Earwig fan designing: Biomimetic and evolutionary biology applications

Significance

We report a geometrical drawing method enabling to reproduce the complex wing-folding pattern of earwigs. Although the earwig wing has unique properties with an outstanding potential for engineering, such as an extreme compactness when fully creased or self-folding behavior, its design process had not been resolved, which limited practical applications. We provide the means of reconfiguring the modeled earwig wing to satisfy flexible designing needs, including a dedicated software. The new method can also reconstruct the wing folding of Paleozoic earwig relatives, which provides the rare chance to infer evolutionary patterns based on spatial (morphofunctional) constraints. This research represents a step toward using the earwig wing as a model for artificial deployable structures of various sizes and materials.

Abstract

Technologies to fold structures into compact shapes are required in multiple engineering applications. Earwigs (Dermaptera) fold their fanlike hind wings in a unique, highly sophisticated manner, granting them the most compact wing storage among all insects. The structural and material composition, in-flight reinforcement mechanisms, and bistable property of earwig wings have been previously studied. However, the geometrical rules required to reproduce their complex crease patterns have remained uncertain. Here we show the method to design an earwig-inspired fan by considering the flat foldability in the origami model, as informed by X-ray microcomputed tomography imaging. As our dedicated designing software shows, the earwig fan can be customized into artificial deployable structures of different sizes and configurations for use in architecture, aerospace, mechanical engineering, and daily use items. Moreover, the proposed method is able to reconstruct the wing-folding mechanism of an ancient earwig relative, the 280-million-year-old Protelytron permianum. This allows us to propose evolutionary patterns that explain how extant earwigs acquired their wing-folding mechanism and to project hypothetical, extinct transitional forms. Our findings can be used as the basic design guidelines in biomimetic research for harnessing the excellent engineering properties of earwig wings, and demonstrate how a geometrical designing method can reveal morphofunctional evolutionary constraints and predict plausible biological disparity in deep time.

Since wings evolved in insects more than 320 million years ago (1), different lineages have undergone selective pressures to effectively move and shelter on the ground while maintaining the advantages of flight. Once insects gained the ability to withdraw the wings upon their body, multiple ways to decrease the area of the stored wings repeatedly evolved. Earwigs fold their hind wings once fanwise and twice axially, reaching packing areas up to about 1/15 of the original wing surface (2, 3). This extreme compactness allows these insects to fully flex their abdomen, enabling them to use their forcepslike cerci (4) and wriggle into narrow spaces, including digging in the soil (5, 6), while usually maintaining fully functional flight capability (2, 7). Unlike the patterns that typically occur in other insects that can fold their wings axially, such as most beetles (8–11), some cockroaches (12), and a few wasps (13, 14), true bugs (15) and moths (16), the crease pattern of the earwig wing is conservative across the whole group and likely evolved only once (17). The fanlike foldable area of the earwig wing, which is the anal lobe characteristic of polyneopteran insects, occupies most of the wing surface, where long and short fan ribs alternate (Fig. 1A). Only long ribs connect to the rib base, which is circle-shaped (Fig. 1B). Each rib has an oval-shaped bending point (i.e., hinge) situated at the middle of the fan and where the ribs slightly bend (Fig. 1C). The folding line uniting all of the hinges is known as the ring fold (17), which increasingly zigzags its way toward the basal area of the wing (Fig. 1 A and D). The elastic energy stored in the hinges and conferred by resilin, a rubberlike protein (3), provides self-folding properties to the earwig wing. Therefore, the wing becomes elastically stable in fully folded shape (18) (Fig. 1E) and can only be unfolded actively (19, 20). All these remarkable properties and others, such as in-flight reinforcement (2) and snap-through stabilizing mechanisms (21), have revealed the vast potential for engineering of the earwig wing. However, the geometrical rules needed to reproduce its complex crease patterns have remained uncertain. Here we show the geometrical method to design an earwig-inspired fan by considering the flat foldability (22, 23) in the origami model, as informed by X-ray microcomputed tomography (micro-CT). The earwig fan can be customized into artificial deployable structures of multiple sizes, materials, and configurations, as the dedicated designing software that we provide shows. The proposed method is also valid to reconstruct the wing crease patterns of a Permian earwig relative, the fossil Protelytron permianum (24), emphasizing its accuracy and allowing evolutionary inferences based on morphofunctional constraints.

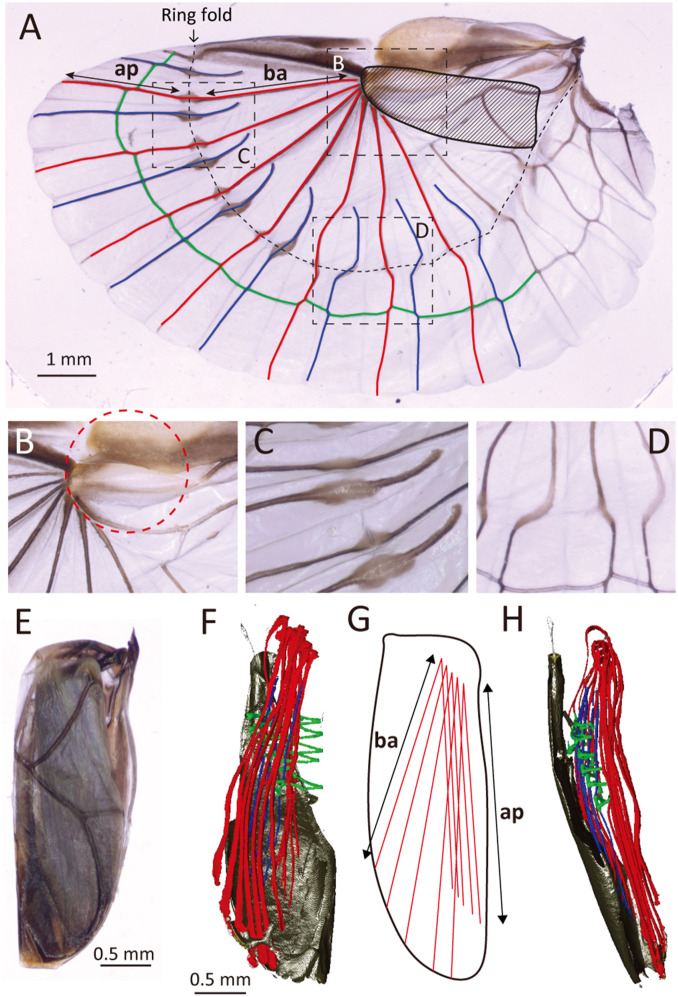
Fig. 1.

Earwig hind wing in unfolded and folded shapes. Long and short ribs are in red and blue, respectively; bridge veins are in green. (A) Unfolded left hind wing of F.auricularia. (B) Detail of rib base. (C) Oval-shaped bending points (hinges). (D) Zigzagging of long and short ribs. (E) Folded left hind wing of F. auricularia as seen from above, corresponding to the shaded area in A. (F) Micro-CT image showing the conformation of veins inside a folded right hind wing of A. harmandi in underside view. (G) Diagram of F. (H) Same as F, in lateral view. Ap, apical stretch of long ribs; ba, basal stretch of long ribs.

Results

We determined the spatial positions of the main structural components of the earwig hind wing (long ribs, short ribs, and bridge veins) when fully folded using micro-CT (Fig. 1 F–H, SI Appendix, Fig. S1, and Movie S1). The roots of the long ribs are arranged in a circular arch along the shape of the base (Fig. 1B). The long ribs turn to the backside of the base around the roots. The basal stretches of the long ribs, from their base to the ring fold, align in the same direction while converging. The apical stretches of the folded long ribs run almost in parallel (Fig. 1G). Based on these characteristics, the geometrical requirements for designing the crease pattern of an earwig fan are as follows: a) the swivel center of the ribs must be at the middle of the wing, not at its base; b) the fold lines must simultaneously satisfy the flat foldability on both the ring fold and the connection between the ribs and rib base; c) the ribs must deploy uniformly in the unfolded shape; and d) the ribs and hinges must be aligned without conflicting in the folded shape.

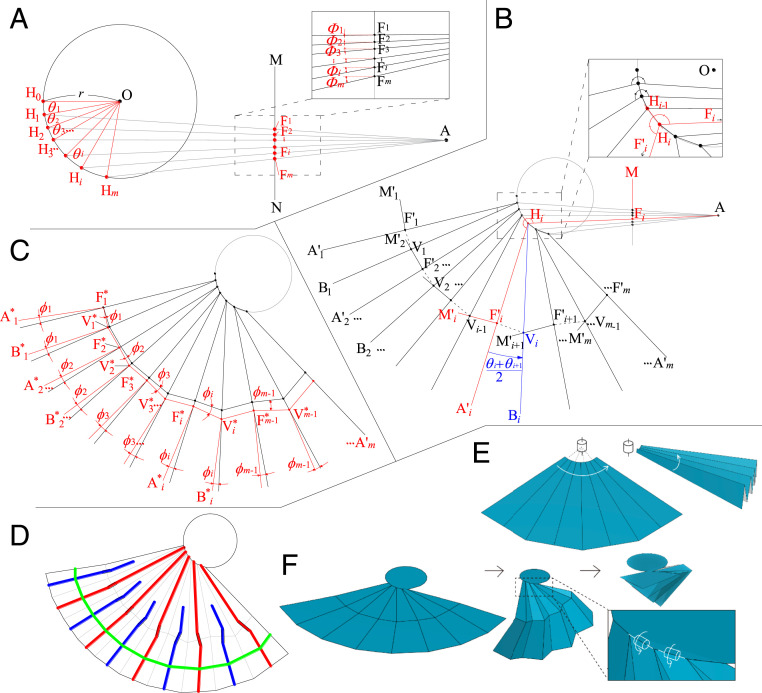
We propose a geometrical drawing method that can create crease patterns that satisfy the above geometrical requirements. First, a circle O, a point A, and a line MN are defined, giving the outline of the folded rib shape (Fig. 2A). Points H₀, H₁,… H_m, the root points of the radial fold lines, are plotted by dividing the arc of circle O with angles θ₁, θ₂,…, θ_m. Points H₀, H₁,… H_m are connected with A and the crossing points of these lines with MN are set as F₁, F₂,..., F_m. Here, the lines H_iF_i correspond to the direction of the long ribs in folded positions. The lines of the ring fold are aligned along the line MN in the folded shape. Next, the radial mountain crease lines (H_iA´_i) and the part of the ring fold (F´_iM´_i) are drawn by mirroring H_iA and F_iM on chord H_i-1H_i (red lines in Fig. 2B). Valley crease lines (H_iB_i) are drawn by rotating H_iA´_i with angles that meet the flat foldability around H_i. In this case, the angle equals to (θ_i+θ_i+1)/2 (blue lines in Fig. 2B). The cross-points of F´_i+1M´_i+1 and H_iB_i provide the remaining vertices of the ring fold (V_i). This drawing process can guarantee the symmetrical relation of angles: ∠H_iF´_i V_i−1=∠H_i F´_iV_i, ∠H_iV_iF´_i =∠H_iV_iF´_i+1 (see SI Appendix, Fig. S2 for detailed proof). These equations also imply that the flat foldability (22, 23) is satisfied around these vertices. Therefore, all vertices included in this crease pattern maintain the flat-foldable condition. However, if the paper is folded using this pattern, the crease lines of the ring fold conflict at the same position in the folded shape, therefore not getting completely folded due to the paper thickness. The crease patterns in the actual earwig wings are designed so that the positions of these hinges are slightly shifted in the folded state (Fig. 1 F and G). This can be incorporated into the design pattern using the following process. The modification proceeds sequentially from F*₁ (at the same position of F´₁). The modified V*₁ is plotted on the intersection of the rotated F´₁V₁ and the radial fold line H₁B₁. V*₁F*₂ is parallel to original V₁F´₂, and F*₂ is plotted on the intersection with H₂A´₂. Continuing this process provides the modified vertices of the ring fold, V*_i and F*_i. According to this modification of the ring fold, the apical part of the radial fold lines, F´_iA´_i and V_iB_i, are modified by rotating with the same angle ϕ_i around F*_i and V*_i. Movies S2 and S3 show a simple example of this design process via classic drawing techniques.

Fig. 2.

Geometrical drawing method of the earwig fan. (A) Construction of the starting geometric elements (circle O, point A, and line MN) and projection of lines H_iF_i. (B) Construction of the radial folding lines and the ring-fold lines. (C) Modification system of the ring fold used to adjust the clearances between ring-fold lines in the folded shape, without interference to the flat foldability. (D) Idealized earwig venation drawn on a constructed crease pattern, showing the same characteristics as in the actual earwig wings (Fig.1 A–D). (E and F) Schematic folding movements of the normal fan and the designed earwig fan, respectively.

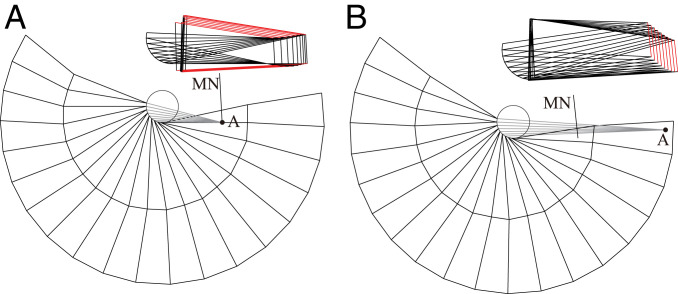
In order to apply the earwig-fan crease patterns to actual deployable structures, each parameter must be determined so that the designs can be stored in a compact shape without the fold lines conflicting. We provide two strategies to design the earwig fan depending on materials and purpose. In the “parallel-edge” approach, the facet edges after the ring fold are parallel (red lines in Fig. 3A). To achieve this conformation, ϕ_i can be selected according to the angle of AH_i, i.e., Φ_1,Φ_2,…Φ_m (Fig. 2A). Then, by placing point A on the lower part of the line MN, the fan facet can be efficiently overlapped and folded in a compact shape (Fig. 3A). Conversely, the second design strategy equates clearances between the folded ring-fold lines (red lines in Fig. 3B) by simply using the same value ϕ for all ϕ_i. As this “equal-clearance” approach, in contrast to the first, causes variations in the direction of the folded ribs, determining the parameters needed to create the compact folded shape is complex. Thus, we developed a software that can seek the proper positions of A and MN and angles ϕ by interactively changing the parameters while obtaining the folded shapes (Movie S4). This software implements the abovementioned two design strategies, enabling us to output appropriate crease patterns according to the target shape and size of the fans. Some useful design options provided by this software are shown in Fig. 4 A–C and Movie S5.

Fig. 3.

Two basic design strategies of earwig-fan inspired deployable structures. (A) Parallel-edge approach. (B) Equal-clearance approach.

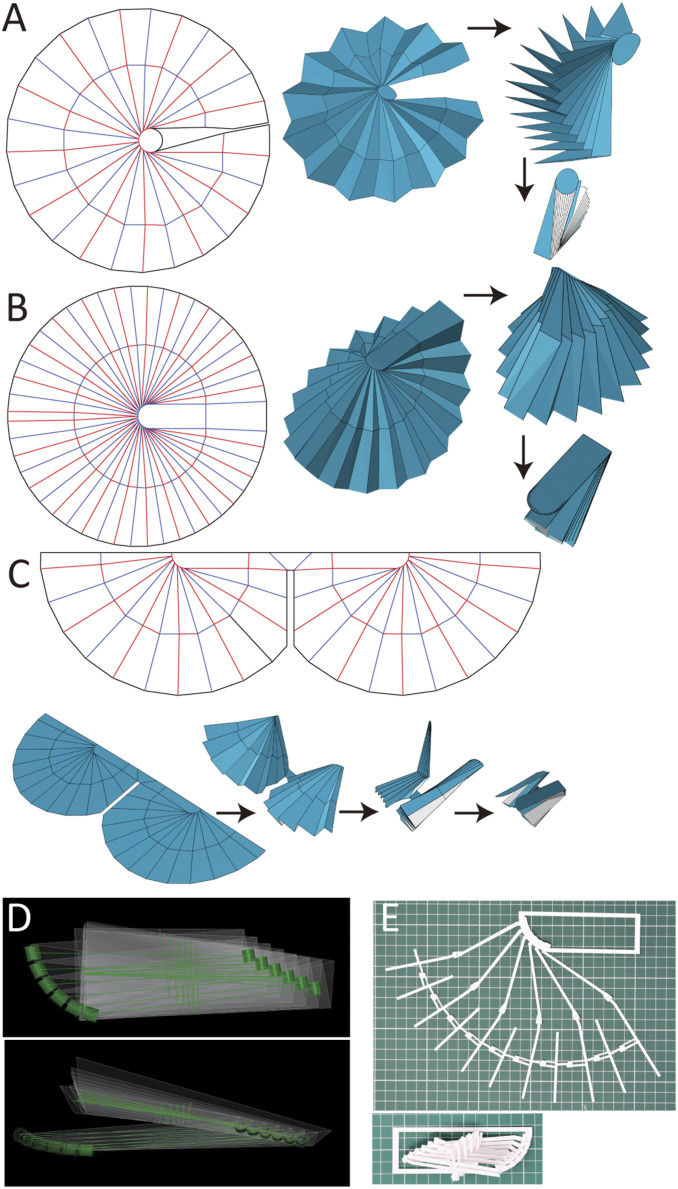
Fig. 4.

Examples of models using the design software. (A) Extended circular model, resulting from extending the pattern around the rib base. This design can be used for deployable structures such as antenna reflectors and umbrellas. (B) Symmetrical circular model. (C) Deployable wing for microair vehicle, obtained by simplifying the earwig folding patterns. See Movie S5. (D) Interference control of the hinge parts by the provided designing software. (E) Three-dimensional printed earwig fan frame based on the model shown in D. All hinge parts can be stored compactly without interference.

Discussion

The geometrical model of the venation in the earwig fan obtained by drawing the frames on the center of the facets from the constructed crease pattern (Fig. 2D) shows the same characteristics as the actual venation in earwigs (Fig. 1 A–D). The long and short ribs found in the earwig wings fall onto the middle of the quadrilaterals and triangles from the inner part of the drawn fan, respectively. The circular rib base (Figs. 1B and 2) helps spread the ribs uniformly while satisfying the flat-foldable conditions at both the root and the ring fold. In a normal fan, radial ribs converge to one point and the rotational axis is perpendicular to the wing plane (Fig. 2E); this causes the concentrations of weight and volume. Unlike the fanlike anal lobe of other polyneopteran insects such as grasshoppers (25), where the fan base is at the base of the wing and the rib axes are positioned on the body side, earwig hind wings have the fan base at their center. Therefore, the weight and volume concentrations of this part are undesirable for the flight properties of the wing. The earwig fan successfully distributes the weight of the fan center by adopting a flat-foldable degree-four vertex at the joint of the ribs and decentralizing the joints on the circular rib base. The rotational axes of the long ribs are parallel to the wing plane (Fig. 2F), which help make the rib base thinner.

The parallel-edge design approach can confer highly efficient storing to isometric materials such as papers and films. However, if used in structures consisting of frames and membranes, the fan frames––usually positioned at the center of the facets––tend to conflict. In actual earwig wings, the point A is positioned out of the MN line so that the facets are gradually shifted. The crease patterns drawn using this approach show good correspondence with the actual earwig wings (SI Appendix, Fig. S3). The challenge when reproducing this fold with the mechanical mechanism is determining how to efficiently store the hinge parts without conflicts on the ring folds, where many hinges are concentrated in the folded shape. This is particularly important in consideration of large-scale applications such as architectural elements and space deployable structures. The equal-clearance design approach can overcome this challenge by providing the proper clearances according to size and shape of the hinge parts. In addition, it is possible to achieve highly efficient storing by adjusting the positions of the hinge parts along the ring-fold lines based on the folded shape simulated by the design software (Fig. 4D). Fig. 4E shows a simple artificial earwig fan frame constructed by using this method and three-dimensional (3D) printer. Detailed design process is available in Movie S6. Overall, our drawing method can design the earwig fan folding for artificial deployable structures in various configurations with different shapes and sizes of the membrane, rib base shape, number of ribs, materials, and types of structures.

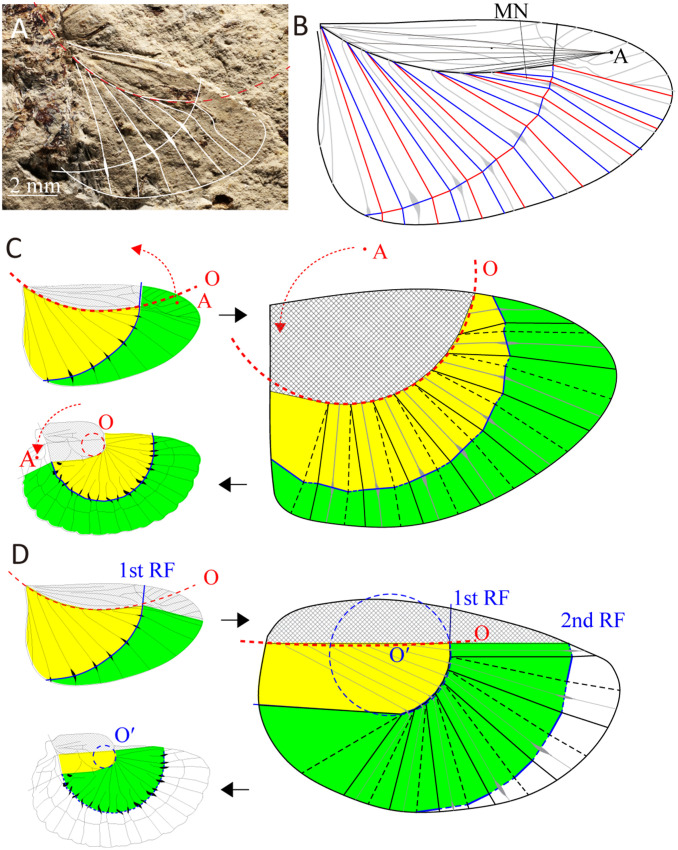
A geometrical designing method can be useful in reconstructing the wing-folding mechanisms of fossil insects, as folds are rarely preserved in rock fossils and the crease patterns in partially to fully folded fossil wings, if preserved, range from challenging to virtually impossible to assess. Our method allows us to recreate the wing-folding pattern of P. permianum (24), classified in the Permian Protelytroptera, a group including relatives of extant earwigs (SI Appendix, Text 1 and Fig. S4). This fossil species had radially spreading veins showing evidence of a ring fold (26) (Fig. 5A), and was able to fold the anal lobe fan transversally (24, 26). Interestingly, the roots of the ribs distribute around a circumference (red broken line, Fig. 5) as seen in current earwigs, albeit with a larger radius. The reconstructed crease pattern has two possible folding modes depending on mountain or valley assignment for each fold line (Fig. 5B). Folding mode A results from the red lines and blue lines in Fig. 5B being assigned as mountains and valleys, respectively. Previous studies have essentially employed this folding mode (17, 24, 26). We propose the alternative folding mode B, obtained by assigning the reverse mountain–valley configuration of model A. We used the proposed design tool to determine the possible evolutionary transformations from the hind wing folding mechanism of P. permianum to the mechanism of the extant earwigs, thereby predicting the wing morphology and crease pattern of hypothetical, extinct transitional forms (Fig. 5 C and D and SI Appendix, Figs. S5C and S6D). This process was performed with the assumption that extant earwigs derive from a protelytropteran or, at least, from a form closely resembling that group (SI Appendix, Text 1). Using folding mode A, our geometric model can explain the crease pattern of extant earwigs by shrinkage and migration toward the wing apex of the circle O, and by migration of the point A from the wing apex to its base (Fig. 5C), as hypothesized by previous works (17, 24, 26). This “shrinking and moving rib base” hypothesis considers both the rib base and the ring fold in P. permianum and Dermaptera as homologous (7). Folding mode B implies a different evolutionary pathway (Fig. 5D). In this “second ring fold” hypothesis, the protelytropteran ring fold migrated anteriorly and became the rib base of the current earwigs, and a new ring fold developed on the rib apical region. The current fossil evidence cannot support either of these hypotheses as being more plausible than the other. Even if the shrinking and moving rib base hypothesis does not entail the generation of a new ring fold, it implies the inversion of both the rib-folding direction and the ring-fold direction (SI Appendix, Text 2 and Figs. S5 and S6).

Fig. 5.

Wing-folding pattern in P. permianum using the proposed geometrical designing method, and two hypothetical evolutionary pathways explaining the folding pattern of extant earwigs. (A) Right hind wing of P. permianum, MCZ-ENT-PALE-3366b. Image credit: Museum of Comparative Zoology, Harvard University. Copyright President and Fellows of Harvard College. (B) Reconstructed crease pattern of the wing of P. permianum. Black thick lines indicate mountain folds. Red and blue lines indicate mountain and valley folding, respectively, in mode A; the opposite assignment corresponds to mode B. (C) Shrinking and moving rib base hypothesis, in folding mode A, and the predicted crease pattern in a hypothetical transitional form (Right). Continuous and dashed lines indicate mountain and valley fold, respectively. (D) Second ring fold hypothesis, in folding mode B, and the predicted crease pattern in a hypothetical transitional form (Right). RF = ring fold. See SI Appendix, Text 2 and Figs. S5 and S6.

The same geometrical model can explain the wing folding in both earwigs and their deep time relatives, thereby highlighting its accuracy. This fact also implies that the mathematical rules elucidated herein for the earwig-type hind wing have likely exerted a strong selective pressure during evolution, which is consistent with the highly conservative crease pattern across all extant earwigs. Our findings illustrate how geometrical designing can be used as a tool to comprehensively explore morphofunctional constraints on biological structures throughout evolution. We have proven that it is possible to use in diverse biomimetic applications the excellent mechanical properties of a deployable structure that an insect lineage has been employing for at least 280 My.

Materials and Methods

The Forficula auricularia Linnaeus, 1758 hind wing depicted in Fig. 1 and SI Appendix, Fig. S3, was obtained via dissection of specimens gathered in a house garden from Oxford, United Kingdom. The folded hind wings of the Anechura harmandi (Burr, 1904) used for the micro-CT scanning were obtained from specimens gathered in a mountain area from Nara, Japan. The fossil specimen of P. permianum used in Fig. 5A and SI Appendix, Fig. S4 is currently deposited at the Museum of Comparative Zoology (MCZ), Harvard University, USA, under the number MCZ-ENT-PALE-3366b. This fossil is from the Wellington Fm. at the Elmo locality, Kansas (USA), early Permian in age (∼280 Ma). The earwig hind wings shown in SI Appendix, Fig. S3 B and C are housed at the Oxford Museum of Natural History (OUMNH), United Kingdom, and are among the few earwig specimens therein that were pinned with their hind wings unfolded. Proreus simulans (Stal, 1860) used in SI Appendix, Fig. S3D was gathered in fields near Okinawa, Japan.

The F. auricularia specimen was imaged using a Zeiss AXIO stereomicroscope with an attached Axiocam 105 color digital camera. The wing was kept flat by gently placing a cover glass on its surface. The P. permianum specimen was photographed using a Canon EOS 6D with an MP-65-mm macrolens mounted on a photographic stand under low-angle light. For the micro-CT imaging, an inspeXio SMX-100CT (Shimazdu Corporation) was used, which comprises a nonenclosure tube-type X-ray generator operating at 35 kV and 100 mA. The hind wings were stained with a 2% iodine ethanol solution for 30 d. CT images were acquired for each 10-μm length at a resolution of 1,024 × 1,024 × 928 voxels and reconstructed into 3D images using the visualization software VGStudio MAX (Volume Graphics GmbH).

The crease-pattern designing software proposed was developed on Rhino 6.0 (Robert McNeel & Associates) and Grasshopper (27). An origami simulation tool box of Grasshopper, Crane (28), was used to simulate the folded shape of the generated crease patterns. The folding processes in Figs. 2 and 4 and Movie S5 were drawn via the online application Origami Simulator (29).

A Fused Deposition Modeling-type 3D printer, RAISE3D Pro2 (Raise 3D Technologies, Inc.) with a 0.4-mm nozzle diameter was used to build the earwig fan frame (Fig. 4E). The material used was a polylactic acid (PLA) Filament with a 1.75 mm diameter (Raise3D Standard PLA Filament, Raise 3D Technologies, Inc.).

Data Availability Statement.

All crease patterns, 3D models, and custom codes used in this study are available in ref. 30.