Contextual Adaptation of Cognitive Flexibility is driven by Task- and Item-Level Learning

Abstract

Adaptive behavior requires finding, and adjusting, an optimal tradeoff between focusing on a current task-set (cognitive stability) and updating that task-set when the environment changes (cognitive flexibility). Such dynamic adjustments of cognitive flexibility are observed in cued task-switching paradigms, where switch costs tend to decrease as the proportion of switch trials over blocks increases. However, the learning mechanisms underlying this phenomenon, here referred to as the list-wide proportion switch effect (LWPSE), are currently unknown. We addressed this question across four behavioral experiments. Experiment 1 replicated the basic LWPSE reported in previous studies. Having participants switch between 3 instead of 2 tasks, Experiment 2 demonstrated that the LWPSE is preserved even when the specific alternate task to switch to cannot be anticipated. Experiment 3a and 3b tested for the generalization of list-wide switch-readiness to an unbiased “transfer task,” presented equally often as switch and repeat trials, by intermixing the transfer task with biased tasks. Despite the list-wide bias, the LWPSE was only found for biased tasks, suggesting that the modulations of switch costs are task set and/or task stimulus (item) specific. To evaluate these two possibilities, Experiment 4 employed biased versus unbiased stimuli within biased task sets and found switch-cost modulations for both stimuli sets. These results establish how people adapt their stability-flexibility tradeoff to different contexts. Specifically, our findings show that people learn to associate context-appropriate levels of switch readiness with switch-predictive cues, provided by task sets as well as specific task stimuli.

Introduction

Life in a changing environment frequently confronts us with cognitive conundrums. Chief among these is the so-called the shielding-shifting dilemma (Goschke, 2013), which refers to two antagonistic challenges: On the one hand, to accomplish our goals we often need to strongly focus on a current task (requiring cognitive stability, the shielding of an ongoing task-set from distraction); on the other hand, we also need to remain sensitive to possible changes in our environment that might require us to quickly update our goals and cognitive strategies (requiring cognitive flexibility, the shifting of attention from one task set to another). Overly rigid goal-shielding may lead to negligence of crucial cues in the environment that should be prioritized; for example, a novice driver may neglect a light that changed from green to red because they were fixated on the task of changing into the right turn lane. Conversely, an overly flexible processing mode may render the agent easily distractible when concentration is required, as when a driver takes their eyes off the road to glance at a new notification from their phone.

To meet this challenge, the brain needs to find – and continually adapt – a contextually optimal level of cognitive flexiblility. Despite the central importance of this process to adaptive behavior (and survival), relatively little is known about the learning processes that underpin the ability to strategically match flexibility (or “switch readiness”) to changing contexts. The present study therefore sought to elucidate how people adjust their level of cognitive flexibility to suit changing task demands in the form of time-varying frequency (or likelihood) of having to switch tasks.

We begin with a brief literature review and some definitions of our theoretical assumptions and terminology. We investigate the topic of cognitive flexibility through the prism of cued switching between task sets (for reviews, see Kiesel et al., 2010; Monsell, 2003; Vandierendonck, Liefooghe, & Verbruggen, 2010; Koch et al., 2018). We define a task-set as a rule that specifies a set of task-relevant stimuli or stimulus features and their associated responses (cf. Kiesel et al., 2010; Monsell, 2003; Rogers & Monsell, 1995). We assume that implementing a task-set involves the attentional selection of the relevant stimulus features and activation of their respective responses, and the shielding of these stimulus-response translations from potential interference by task-irrelevant information (e.g., Dreisbach & Haider, 2008; Dreisbach & Wenke, 2011; Meiran, 2010). In line with a large literature, we further assume that cued switching between task-sets (or task-set updating) requires (1) reconfiguration, that is, the active replacing of the previously active task-set with a new set of stimulus-response rules (e.g. Meiran, 1996; Monsell & Rogers, 1995; Monsell, 2003), and (2) the inhibition of, or resolution of interference from, the most recently active task set (overcoming “task set inertia”, Allport et al., 1994) and from other task sets previously associated with the stimulus set (e.g., Waszak, Hommel, & Allport, 2003). Together, these processes result in switch costs, slower and less accurate responses when a task has to be switched from the previous trial than when it is repeated (Kiesel et al., 2010; Monsell, 2003; Vandierendonck, Liefooghe, & Verbruggen, 2010; Meiran, Chorev, & Sapir, 2000). The ease with which switch processes are carried out can be modulated by a number of factors, including the frequency with which tasks have to be switched over periods of time, which we investigate in the current study.

Finally, we assume that the size of the switch cost can be considered indicative of someone’s current level of cognitive stability (or flexibility) (Braem & Egner, 2018; Dreisbach & Fröber, 2019). This level can be conceived of as a set-point on a stability-flexibility continuum, which has been conceptualized by Goschke (2003, 2013) as a meta-control parameter termed the “updating threshold”: when this threshold is low, tasks can be switched more easily (flexibility is high), but this necessarily bears the cost of poor task-set shielding against interference (stability is low); when this threshold is high, switching is rendered more difficult (cognitive flexibility is low) but in turn the current task-set is well protected against intereference (stability is high). In the present article, we will use the term “switch readiness”, which is inversely related to the updating threshold and task-set shielding. Moreover, we use these terms to denote different set-points on the stability-flexibility continuum (e.g., low vs. high switch-readiness), but we treat them as neutral with respect to the underlying processes that are modulated to produce changes in switch costs (e.g., reconfiguration vs. inhibition/interference resolution processes). We will speculate in the General Discussion on the most likely aspect of switch cost that is modulated by switch frequency manipulations, however.

In summary, successfully navigating the shifting-shielding dilemma can be conceptualized as learning to strategically adjust one’s updating threshold to suit changes in environmental demand for relatively more or less cognitive flexibility (Goschke, 2003). Importantly, behavioral evidence for these types of dynamic adjustments in switch readiness has been obtained in cued task-switching protocols that manipulate the frequency (and thus, likelihood) of switch trials between blocks of trials. Specifically, a number of studies have shown that the magnitude of switch costs tends to scale inversely with the frequency that task switches occur within a given block of trials (Bonnin, Gaonac’h, & Bouquet, 2011; Dreisbach & Haider, 2006; Dreisbach, Haider, & Kluwe, 2002; Duthoo, De Baene, Wühr, & Notebaert, 2012; Mayr, 2006; Monsell & Mizon, 2006) or at a specific spatial location (Crump & Logan, 2010; Leboe et al., 2008). For instance, Monsell & Mizon (2006, Experiment 4) varied switch proportions from 25% to 50% to 75% between blocks of trials and observed the greatest switch costs at a switch frequency of 25% and the smallest switch costs at a switch frequency of 75%. We will here refer to these block-based modulations of switch cost as the list-wide proportion switch effect (LWPSE), leaning on a similar nomenclature in the congruency effect literature (e.g., Bugg & Chanani, 2011; Bugg & Crump, 2012). While the above demonstrations of a LWPSE provides basic evidence that people can adapt their switch readiness to varying task statistics, the exact scope of this adaptation, as well the particulars of the underlying learning processes, are presently not known.

In the present study, we ask in particular what kind of learning drives these effects, and we distinguish between three ways in which changes in updating threshold could become associated with features of low vs. high frequency switch blocks: the listwide level (producing sustained and generalizable changes in flexibility), the task-set level (where a particular level of switch readiness becomes associated with a specific task-set), and the item level (where a particular level of switch readiness becomes associated with specific task stimuli). To investigate the kinds of learning that drive the LWPSE, we ask several questions that have not been previously addressed in the literature: First, because previous studies that found these context-sensitive switch cost modulations only required that participants switch between two tasks, it is not clear to what degree the LWPSE reflects a generic change in cognitive flexibility or task-specific preparation processes. In other words, reduced switch costs in high proportion switch blocks could reflect participants preparing for the particular alternate task, rather than general preparation for a task switch (to any other task). Intuitively, the latter would stand as stronger evidence for a genuine adjustment of cognitive flexibility, since flexible engagement with a changing environment requires increased aptitude to respond to events that are often unexpected.

Second, it is not yet known to what extent the LWPSE is driven by associating switch readiness with the global switch likelihood of the current block context (list-wide learning), or by using the specific task-sets and/or task stimuli (also referred to as “items”) as cues for adjusting switch readiness: in prior studies, in high switch frequency blocks all tasks and all task stimuli were also presented more frequently as switch versus repeat trials (and vice versa for low switch frequency blocks). Therefore, any reductions in switch costs that were observed could have resulted from participants’ learning of task- and/or item-specific associations with switch frequencies instead of linking the temporal, list-wide context to a greater need for flexibility.

In the current paper, we present a series of four experiments that shed light on these unanswered questions about the scope and mechanisms of meta-control over the stability-flexibility tradeoff, as indexed by the LWPSE. Experiment 1 attempts to replicate the LWPSE using the design of Monsell & Mizon (2006) with a different stimulus set. Using three instead of two tasks, Experiment 2 tests whether the LWPSE is preserved when participants do not know which specific alternate task they will switch to. To tease apart list- and task- level biases, Experiment 3a and 3b probed for the generalization of the LWPSE to an unbiased “transfer task” that occurred equally often as switch and repeat trials, presented in blocks with overall high or low switch bias. Following a similar logic, Experiment 4 used switch proportion biased versus unbiased stimuli to investigate whether the LWPSE can be observed in the absence of item-level biases. The data and materials for all experiments are available at https://osf.io/5cxam/, and none of the experiments were preregistered.

Experiment 1

The first experiment was a conceptual replication of Monsell & Mizon’s (2006) Experiment 4. We sought to replicate the switch proportion dependent switch cost to validate a basic task protocol with which to assess the determinants of the LWPSE in the subsequent experiments. Specifically, participants performed cued letter and digit categorization tasks under within-subject manipulations of task sequence (task repeat vs. task switch trials), CSI (short: 190 ms or long: 840 ms) and the proportion of switch trials per block (30%, 50%, or 70%). The CSI factor was included because the pattern of results in prior work suggested that the LWPSE may be CSI-dependent, with maximal effects of switch proportion evident at short CSIs (cf. Monsell & Mizon, 2006). In other words, participants may rely more on context in aiding their task-set updating strategy when they have less time to utilize the trial-by-trial cue for task set reconfiguration. We therefore expected to find reduced switch costs with an increasing proportion of switch trials to be most pronounced in the short CSI condition.

Method

Participants.

A power analysis based on the effect size of the smallest switch cost modulation (switch cost difference between the 50% and 75% switch condition) in Monsell & Mizon (2006, Experiment 4) suggested a total sample size of 26 to achieve 0.95 power. To be conservative and to take into account larger participant exclusion rates for online testing, we roughly doubled this estimate and recruited 56 participants from MTurk. The experiment lasted ~60 minutes and 16 participants were excluded from data analysis for lower than 75% overall accuracy on the task, leaving a final sample size of 40.

Stimuli.

Task stimuli consisted of a letter and a digit displayed simultaneously at either side of the center of the screen for each trial. The letter was randomly selected from ‘A’, ‘E’, ‘I’, ‘U’, ‘G’, ‘K’, ‘M’, or ‘R’ and the digit was randomly selected from ‘2’, ‘3’, ‘4’, ‘5’, ‘6’, ‘7’, ‘8’, or ‘9’. Whether the letter or the digit was presented on the left or right was randomized across trials.

Procedure.

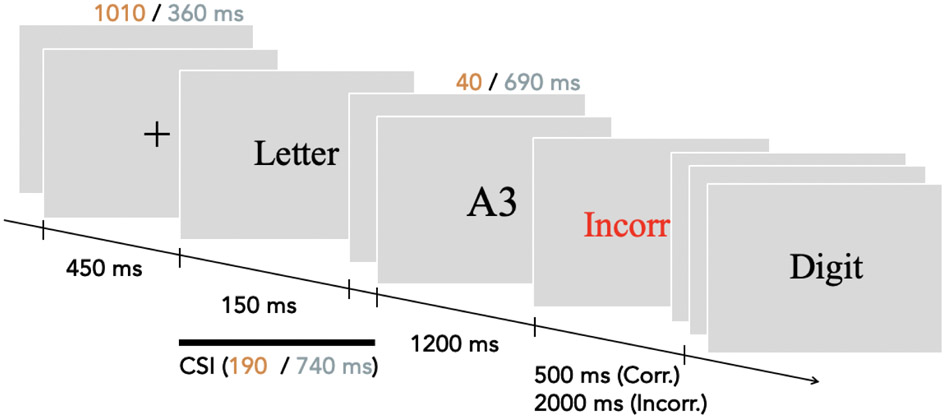
Experiment procedures roughly followed experiment 4 of Monsell & Mizon (2006). Each trial began with a blank interval of 1010 ms (short CSI condition) or 360 ms (long CSI condition), followed by a 450 ms long fixation display, a cue display lasting 150 ms, and another blank interval of either 40 ms (in the short CSI condition) or 690 ms (in the long CSI condition). Finally, the task stimuli appeared and remained on screen for 1200 ms. The lengths of the blank intervals were varied so that the RSI, or the sum of the blank intervals, fixation display, and cue display, was a constant 1650 ms for both short and long CSI trials (see Figure 1).

Figure 1.

Experimental protocol. The basic trial structure of Experiments 1-4 involved a task cue, followed by a cue-to-stimulus-interval (CSI) preceding a target stimulus display, followed by accuracy feedback. Experiment 1 included two CSI conditions (timing parameters for the short CSI condition are shown in orange, the long CSI condition in gray). Experiments 2-4 employed only the short CSI condition, and Experiments 2 and 3 added a colored frame to the target stimulus (see main text).

Participants were required to perform a letter classification task (“Is the letter a vowel or consonant?”) if they saw the cues “Letter” or “Alphabet” and to perform a digit classification task (“Is the digit odd or even?”) if they saw the cues “Digit” or “Number.” The 2:1 cue-to-task mapping allowed us to change the cue on every trial, regardless of whether the task was switched or repeated, thus eliminating the contribution of possible response time benefits that come from repeating cues on task repeat trials (e.g. Logan & Bundesen, 2003; Mayr & Kliegl, 2003) to our computation of task switch costs. Participants had to press the ‘d’ or ‘k’ key to categorize the stimuli as vowel/consonant or odd/even. Participants were randomly assigned to different response mappings for each task. Correct responses were followed by a 500 ms blank screen, and incorrect responses were followed by the word “ERROR” displayed for 2000 ms. Responses made while the task stimulus was not onscreen were considered incorrect.

Each participant completed 18 blocks of 31 trials. All trials except the first in each block were coded as belonging to either the task switch (preceded by a different task) or task repeat (preceded by the same task) condition. The percentage of switch trials per block was 30, 50, or 70; there were six blocks of each switch proportion condition. The trial sequence for each block was generated pseudo-randomly according to an algorithm that ensured each task was presented an approximately equal number of times. In the 30% switch block, each task was presented either 4 or 5 times as a switch trial and 11 or 10 times as a repeat trial, creating a 9:21 switch to repeat ratio. In the 70% switch block, the number of switch v. repeat trials per task was reversed, creating a 21:9 switch to repeat ratio; in the 50% switch block, each task was presented either 7 or 8 times as repeat and as switch trials. For a table depicting switch/repeat frequencies for each task in this and subsequent experiments, refer to Appendix A, Table 2. All 6 blocks of the same switch proportion were presented consecutively to increase the saliency of the switch/repeat context, but the presentation order of the chunk of blocks with the same switch proportion was counterbalanced across participants. CSI alternated from block to block beginning with the short CSI. Before starting the main experiment, participants completed two short CSI blocks and one long CSI block for practice. All practice blocks had 50% switch proportion.

Design.

The experiment followed a 2 (task sequence: switch vs. repeat) × 2 (CSI: long vs. short) × 3 (switch proportion: 30% vs. 50% vs. 70%) repeated-measures factorial design.

Results and Discussion

For assessing performance accuracy, we analyzed data from all trials after excluding practice blocks and the first trial of each block. For RT analyses, we additionally excluded incorrect trials, and trials following incorrect trials. After applying these exclusion criteria, trials with response times (RT) outside 1.5 times the interquartile RT range of the remaining sample were filtered out for the RT analyses. Descriptive statistics are displayed in Table 1. Excluded trial counts and the number of remaining trials per smallest and largest cells are included in Supplementary Materials, Appendix A, Table 1.

Table 1.

Mean Response Times (ms) and Accuracy (%) with Standard Errors in Experiment 1 and 2 as a Function of CSI and Switch Proportion

	Exp 1 (2 tasks)						Exp 2 (3 tasks)
	30%		50%		70%		30%		70%
190 ms CSI	RT	Acc	RT	Acc	RT	Acc	RT	Acc	RT	Acc
Switch	816.9 (14.9)	81.9 (1.8)	805.7 (14.3)	79.4 (2.5)	809.7 (15.9)	78.7 (2.4)	860.2 (14.7)	78.0 (1.8)	853.7 (14.1)	78.5 (1.6)
Repeat	771.4 (13.8)	87.42 (1.5)	781.3 (14.4)	84.9 (2.2)	782.6 (15.1)	84.0 (2.1)	788.9 (12.8)	86.5 (1.6)	812.4 (12.6)	85.2 (1.7)
740 ms CSI
Switch	676.5 (12.2)	88.1 (2.3)	678.4 (15.2)	87.2 (2.0)	688.9 (15.8)	85.9 (2.0)
Repeat	656.8 (11.7)	90.8 (1.8)	661.1 (13.4)	89.7 (1.6)	670.5 (15.0)	90.1 (1.8)

Note. Data refers to group mean RTs (excluding error trials, trials following error trials, and RT outliers) and percentage accurate with SE in parentheses.

We ran a repeated-measures analysis of variance (ANOVA) with the independent variables of task sequence (switch vs. repeat), CSI (long vs. short), and switch proportion (30% vs. 50% vs. 70%). Replicating classic effects in the task switching literature, we observed a main effect of task sequence (i.e., switch costs), as reflected in slower RTs for switch trials (M_switch = 734.59 ms) compared to repeat trials (M_repeat = 712.15 ms), F(1,39) = 84.02, p < .0001, η_p² = .68; a main effect of CSI, as short CSIs yielded longer RTs (M_short = 784.74 ms) than long CSIs (M_long = 665.79 ms), F(1, 39) = 312.72, p < .0001, η_p² = .89; and a task sequence × CSI interaction (F(1, 39) = 10.77, p = .002, η_p² = .22), wherein short CSI trials produced larger switch costs (M_switchcost = 32.33 ms) than long CSI trials (M_switchcost = 18.45 ms).

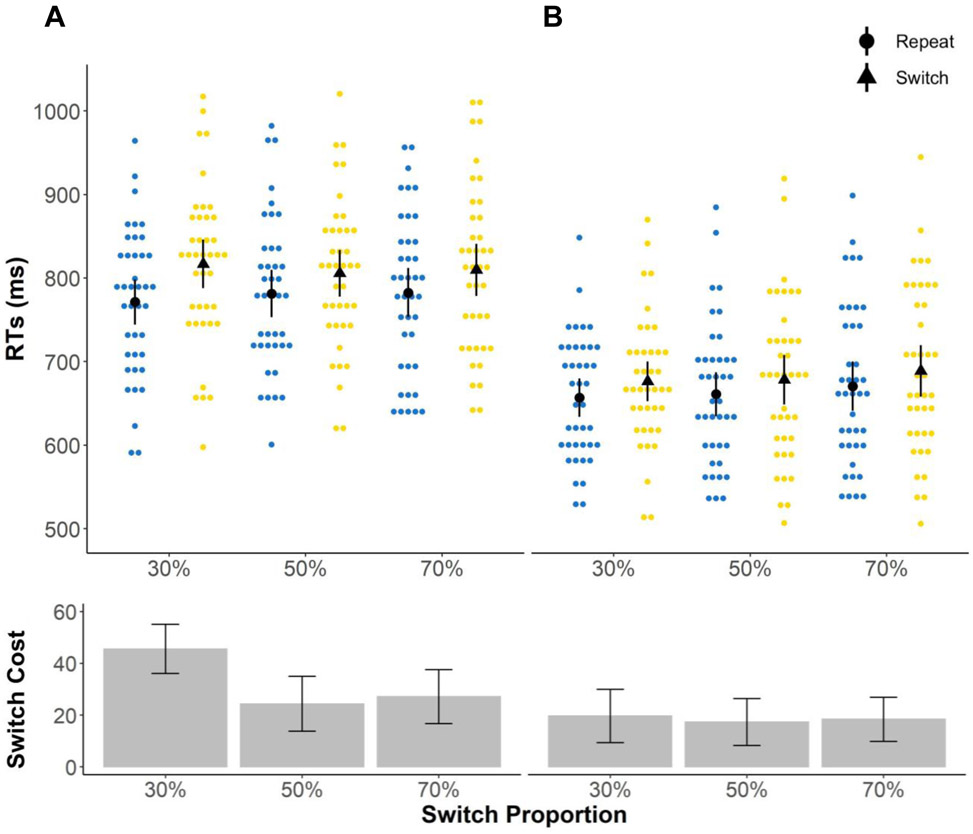
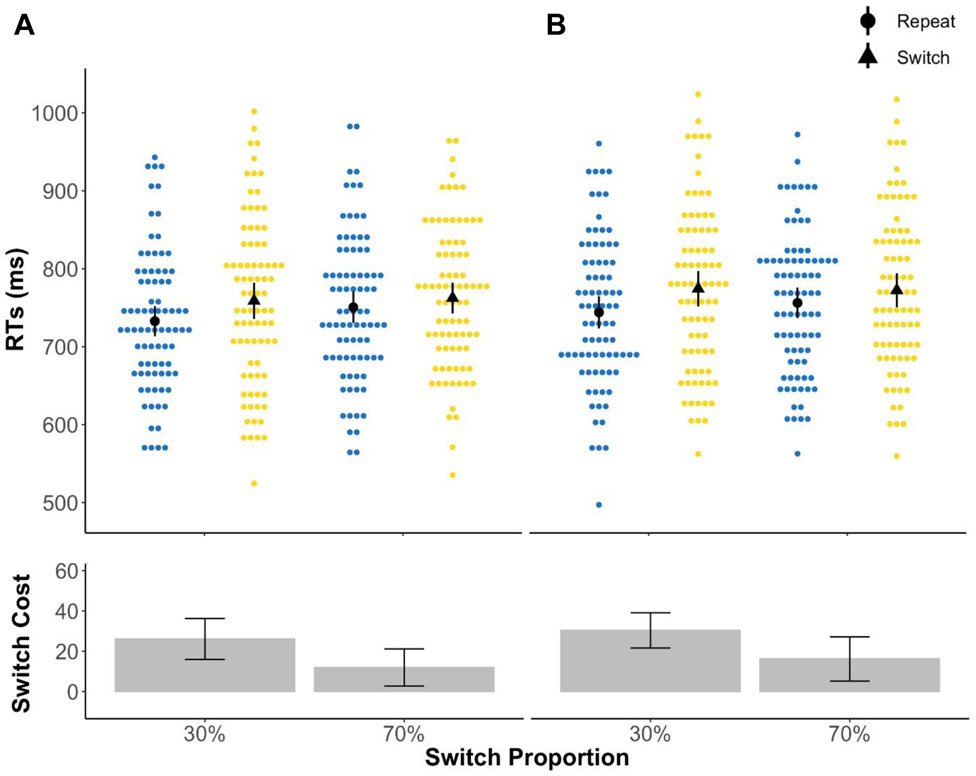
More crucial to the focus of the current study, there was a significant interaction effect of task sequence × switch proportion, F(2, 78) = 3.87, p = .02, η_p² = .09, as switch cost was greater in the 30% switch condition (M_switchcost = 32.6 ms) than in the 50% (M_switchcost = 20.84 ms) and 70% (M_switchcost = 22.73 ms) switch conditions. Moreover, as anticipated, the interaction effect of task sequence × switch proportion was driven by a modulation of switch cost by switch proportion in the short but not in the long CSI condition (see Figure 2), as supported by a three way interaction between task sequence × CSI × switch proportion (F(2, 78) = 3.14, p = 0.05, η_p² = .07). Post hoc tests revealed that, in the short CSI condition, switch cost for the 30% switch condition (M_switchcost = 45.56 ms) was significantly larger than the 50% switch condition (M_switchcost = 24.34 ms, p = .004) and the 70% switch condition (M_switchcost = 27.10 ms, p = .025). On the other hand, in the long CSI condition, there were no significant switch cost differences between any of the three different switch proportions (p = 1). No other main or interaction effects were significant.

Figure 2.

Experiment 1 mean RTs and switch costs in the (A) short CSI and (B) long CSI conditions. Upper panels depict group mean RTs in black circles (repeat) or triangles (switch) and individual mean RTs in blue (repeat) or yellow (switch) dots. Lower panels depict mean switch costs in bars. All error bars indicate confidence intervals (1.96 × standard error). For trials with short CSI, switch cost in the 30% switch condition was significantly greater than the 50% and 70% conditions. Trials with long CSIs did not show significant switch cost moderations by switch proportion.

An identical ANOVA was run on subject’s mean accuracies. There was an expected main effect of task sequence (F(1,39) = 28.63, p < .0001, η_p² = .42) as participants performed with lower accuracy on switch (M_accuracy = 0.83) compared to repeat trials (M_accuracy = 0.88). We also observed a main effect of CSI, as trials with shorter CSI periods (M_accuracy = 0.83) produced significantly lower accuracy rates (F(1,39) = 34.63, p < .0001, η_p² = .47) compared to long CSI trials (M_accuracy = 0.89). There was also a significant task sequence × CSI interaction (F(1,39) = 6.19, p = .02, η_p² = .14), wherein short CSI trials were associated with larger accuracy switch costs (repeat - switch) (M_switchcost = 0.05) than long CSI trials (M_switchcost = 0.03). Unlike the RT data, all other effects were nonsignificant.

For this experiment and all following experiments, congruency effects in RTs and accuracy are reported in Supplementary Analyses (see Appendix B).

Experiment 1 successfully replicated the key results of Experiment 4 of Monsell & Mizon (2006) in RTs: switch costs were reduced in conditions where switching was more frequent, but only for short CSIs. However, it is noteworthy that, unlike in Experiment 4 of Monsell & Mizon (2006), switch cost reductions in the current experiment seemed to be mainly driven by increases in repeat trial RTs, rather than decreases in switch trial RTs. This pattern of results is observed across all four experiments in this study and is discussed in depth in the General Discussion, where a probable explanation of the lack of switch trial RT improvements is offered.

Another caveat to interpreting our results is that switch frequency may be confounded with run length, i.e. the number of consecutive task repeats (Bonnin et al., 2011). Since run lengths are longer in low switch frequency blocks, repeated exposure to the same task could promote within-run RT speeding and produce greater task-set inertia that requires more laborious inhibition when participants finally encounter a switch trial, leading to RT slowing. However, finding switch cost adjustments even after restricting their analysis to the first three positions in a run, Bonnin et al. (2011) demonstrated that run length is not the primary contributor to LWPSE.

Nontheless, the switch cost reductions we observed suggest that participants employ the statistics of control demands – the incidence of switch trials in the different blocks – to guide their cognitive strategies. Moreover, this context-sensitive adjustment in switch-readiness is only evident under conditions where the cue-to-target interval is too short to engage in substantial task-set reconfiguration prior to target onset on a trial-by-trial basis. In the following experiments, we sought to characterize more closely the scope and sources of this form of learned cognitive flexibility.

Experiment 2

Experiment 1 replicated the basic effect of switch proportion (Monsell & Mizon, 2006), demonstrating that the costs of switching are lower when switches are more frequent. However, since participants were only switching between two tasks, they always knew which particular task they would be switching to when they expected a switch. Therefore, the results of Experiment 1 may reflect specific preparation for the particular alternate task instead of a general adjustment of switch-readiness or cognitive flexibility. To test whether the changes in switch cost reflect a modulation of generalizable switch readiness rather than better preparation for a specific alternate task, we adapted the design of Experiment 1 to involve three tasks instead of two (see Chiu & Egner (2017) for an equivalent approach in the context of an item-specific switch proportion manipulation). If switch cost were still moderated by switch proportion in Experiment 2, this would constitute evidence that participants are capable of using context to facilitate task switching even when they do not know what task they are switching to. That three task paradigms make actively anticipating the upcoming task more difficult in turn implies that inhibition (or lack thereof) of the previous task (Mayr & Keele, 2000) should have larger influences on the size of switch costs than anticipatory task-set reconfiguration (Rogers & Monsell, 1995; Monsell, 2003) .

In Experiment 2, a color classification task was included as the third task, in addition to the letter and digit tasks. Participants were cued from trial-to-trial as to which of the three tasks to perform. Only a short CSI (200 ms) was used because Experiment 1 demonstrated that a long CSI eliminated the effect of switch proportion on switch costs. Additionally, only 30% and 70% switch blocks were used, because the switch cost difference between 50% and 70% switch proportion blocks was nonsignificant in Experiment. The 50% condition is also more difficult to compare to the other two conditions, as that condition has a greater level of overall task uncertainty (0.5 in a two-task design) compared to the 30% and 70% blocks, which are equated in terms of uncertainty (0.3 in a two-task design).

Method

Participants.

58 participants were recruited from MTurk. The experiment lasted ~30 minutes, and participants were compensated $3.00 if they performed at 50% accuracy or above. 17 participants were excluded from data analysis for lower than 65% overall accuracy on the task, leaving a final sample size of 41. The accuracy threshold for participant inclusion was modified from Experiment 1 (where it was 75%) due to the increased difficulty associated with switching between three rather than two tasks.

Stimuli.

Task stimuli were the same as before, except that a colored frame was placed around the letter/digit pair. The color of the frame was randomly selected from four warm colors (shades of red, orange, and yellow) and four cold colors (shades of green, blue, and purple).

Procedure.

Experiment procedures were largely identical to Experiment 1, with a few changes to timing in order to accommodate the third task and the increased difficulty of switching between three tasks. First, 10 ms were added to the cue display period, bringing the CSI to 200 ms. Second, the target stimulus display period was increased by 100 ms (totaling 1300 ms) to give participants more time to respond (as before, correct responses had to be made while the stimuli were on screen). Finally, cued by the word “Color” or “Hue,” the color task was added requiring participants to indicate whether the color of the frame was cold or warm (cf. Cooper et al., 2019). As in Experiment 1, the cue was always switched between consecutive trials. Participants were randomly assigned to different response mappings for each task. The experiment consisted of 8 blocks of 31 trials each. Four blocks had a 30% switch proportion and the other four had a 70% switch proportion. Trial sequence and the block presentation order were generated in the same way as in Experiment 1.

Design.

The experiment followed a 2 (task sequence: switch vs. repeat) x 3 (switch proportion: 30% vs. 70%) repeated-measures factorial design.

Results and Discussion

The same exclusion criteria as in Experiment 1 were applied. Descriptive statistics are displayed in Table 1, side-by-side with those of Experiment 1.

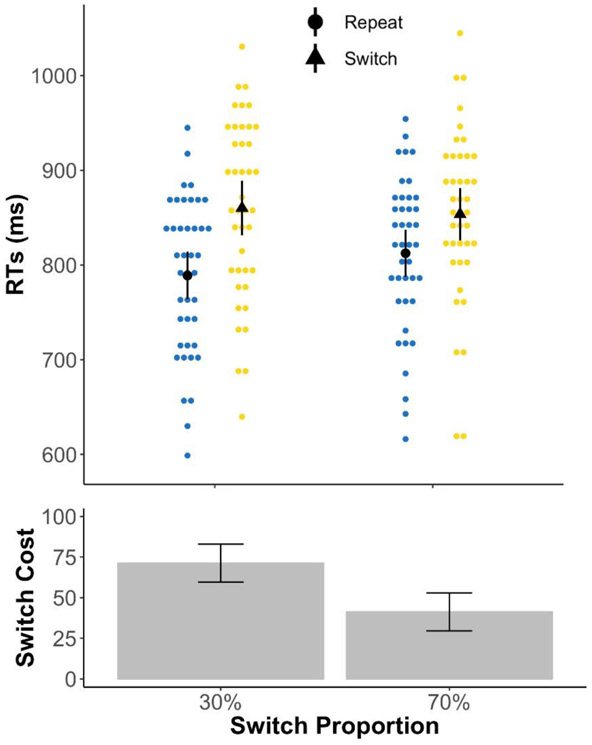
We ran a repeated-measures ANOVA with the independent variables of task sequence (switch vs. repeat) and switch proportion (30% vs. 70%). The main effect of task sequence on RT (i.e., the switch cost) was significant, F(1, 40) = 149.59, p < .0001, η_p² = .79, as participants responded slower on switch (M_switch = 852.07 ms) compared to repeat trials (M_repeat = 795.26 ms). There was no main effect of switch proportion. Crucially, we found an interaction effect between task sequence and switch proportion, F(1, 40) = 15.60, p = .0003, η_p² = .28. Switch cost was significantly higher in the 30% (M_switchcost = 71.26 ms) than in the 70% switch condition (M_switchcost = 41.26 ms) (see Figure 3).

Figure 3.

Experiment 2 mean RTs and switch costs collapsed across three tasks. Upper panel depicts group mean RTs in black circles (repeat) and triangles (switch) and individual mean RTs in blue (repeat) and yellow (switch) dots. Lower panel depicts mean switch costs in bars. All error bars indicate confidence intervals (1.96 × standard error). Switch cost in the 30% switch condition was significantly greater than the 70% condition.

The accuracy analysis only found a significant effect of task sequence where accuracy for switch trials (M_switch = 0.78) was lower than repeat trials (M_repeat = 0.86), F(1, 40) = 64.10, p < .0001, η_p² = .62. The main effect of switch proportion and the interaction of task sequence and switch proportion that were significant in the RT data were nonsignificant in the accuracy data.

In Experiment 2, the three-task design makes anticipating switching to one particular alternate task impossible. The observation of a significant modulation of switch cost by switch proportion therefore provides evidence that the reduction of switch cost in high switch blocks is not limited to situations in which the task that will be switched to is known. Thus, Experiment 2 indicates that the LWPSE cannot be explained via trial-by-trial preparation for a specific alternative task.

Experiment 3a

Thus far, we have demonstrated that switch readiness can be adjusted based on the frequency of switches within blocks (Experiments 1 and 2), and that reduced switch costs under high switch frequency do not depend on there being only a single alternate task to switch to (Experiment 2). However, it is unclear whether these adjustments in switch-readiness reflect learning processes that are tied to the specific tasks, which all occurred at biased switch frequencies, or whether participants instead entered some kind of global flexible state in a high switch proportion context, which should be transferable to tasks that are not biased in their switch frequency. Experiments 1 and 2 could not answer this key question because the 30% and 70% switch blocks were biased both at the block (list-wide) level and at the task level. That is, in blocks where the overall proportion of switch trials was higher, each task was also presented more frequently as switch rather than repeat trials. (The reverse was true for low proportion switch blocks.) So, for instance, even though in high switch proportion blocks in Experiment 2 participants could not anticipate which task they would be switching to, any one of the three tasks had in fact been encountered more frequently as switch than repeat trials in that block.

Although paradigms that associate biased switch proportions with spatial locations (Leboe et al., 2008, Exp 2; Crump & Logan, 2010) are not contaminated by task- and item-level biases (i.e. tasks and stimuli are presented equally likely across the two biased spatial locations), list-wide paradigms are not controlled in the same way. Our novel manipulations allow us to investigate whether contextual adaptation to list-wide temporal context can occur when we control for task (Exp 3a and 3b) and item (Exp 4) bias.

To find out whether there is a global, transferable effect of block-wise switch proportion that is independent of task-level switch proportion, in Experiment 3a we introduced an unbiased third task, presented alongside two heavily biased tasks that drove the 30% or 70% switch proportion in each block. The unbiased task always appeared equally often as switch and repeat trials, regardless of the block-wise switch proportion (for an equivalent approach in the realm of conflict-control, see (Bugg, 2014; Bugg & Chanani, 2011; Hutchison, 2011). If participants do enter a globally more cognitively flexible state in high switch proportion blocks, then the unbiased task should also show reduced switch cost. On the other hand, if the switch proportion effect operates at the level of specific task sets, then we should not observe a transfer of this effect to the unbiased task.

Method

Participants.

59 participants were recruited from MTurk. The experiment lasted ~45 minutes and participants were compensated $4.50 if they performed at 50% accuracy or above. 18 participants were excluded from data analysis for lower than 65% overall accuracy on the task, leaving a final sample size of 41.

Stimuli and Procedures.

Task stimuli, trial components, and timing were identical to Experiment 2. Participants were randomly assigned to different response mappings for each task and the identity of the unbiased task (i.e. whether it was the letter, digit, or number task).

The experiment consisted of 16 blocks of 31 trials each. The number of blocks was doubled compared to Experiment 2 in order to ensure that each participant was exposed to 160 trials of the unbiased task (there were 10 trials per block). Eight blocks had a 30% switch proportion and eight blocks had a 70% switch proportion. Trial sequences were pseudo-randomly generated. In the 30% switch proportion block, the two biased tasks were each presented twice as switch trials and 8 times as repeat trials and the unbiased task was presented 5 times as switch and 5 times as repeat trials, creating an overall switch to repeat ratio of 9:21. In the 70% switch proportion block, the number of switch versus repeat trials was reversed for the biased tasks, while the unbiased task was still presented 5 times as switch and 5 times as repeat trials. Participants were randomly assigned to conditions where either the letter, digit, or color task appeared as the unbiased task.

Design.

The experiment followed a 2 (task sequence: switch vs. repeat) x 2 (task bias: biased vs. unbiased) x 3 (switch proportion: 30% vs. 70%) repeated-measures factorial design.

Results and Discussion

The same exclusion criteria (including RT exclusion) as Experiment 1 and 2 were applied. Descriptive statistics are displayed in Table 2.

Table 2.

Mean Response Times (ms) and Accuracy (%) with Standard Errors in Experiment 3a and 3b as a Function of Task Bias and Switch Proportion

	Exp 3a				Exp 3b
	30%		70%		30%		70%
Biased Tasks	RT	Acc	RT	Acc	RT	Acc	RT	Acc
Switch	844.4 (14.7)	77.4 (2.2)	839.6 (15.2)	80.3 (2.7)	807.4 (13.2)	80.0 (1.6)	805.0 (13.2)	79.5 (1.4)
Repeat	756.4 (11.6)	87.3 (1.6)	785.8 (14.2)	87.2 (1.6)	756.6 (12.2)	86.4 (1.3)	770.5 (12.8)	85.8 (1.5)
Transfer Task
Switch	830.5 (12.2)	79.8 (2.1)	828.1 (18.9)	83.6 (1.8)	807.5 (15.3)	76.5 (2.1)	803.3 (15.4)	76.5 (2.1)
Repeat	762.4 (15.9)	85.1 (1.9)	766.2 (18.6)	87.3 (1.9)	758.4 (14.0)	85.3 (1.7)	755.2 (13.8)	83.3 (1.8)

Note. Data refers to group mean RTs (excluding error trials, trials following error trials, and RT outliers) and percentage accurate with SE in parentheses.

We ran a repeated-measures ANOVA with the independent variables of task sequence (switch vs. repeat), task bias (biased vs. unbiased task), and switch proportion (30% vs. 70%). We observed a main effect of task sequence on RT, F(1, 40) = 127.63, p < .0001, η_p² = .76, as responses on switch trials were slower (M_switch = 829.25 ms) comparted to repeat trials (M_repeat = 758.51 ms). As in Experiments 1 and 2, there was a significant interaction effect of task sequence × switch proportion, F(1,40) = 8.34, p = .006, η_p² = .17, wherein switch costs were higher in the 30% switch condition (M_switchcost = 78.06 ms) compared to the 70% switch condition (M_switchcost = 57.82 ms).

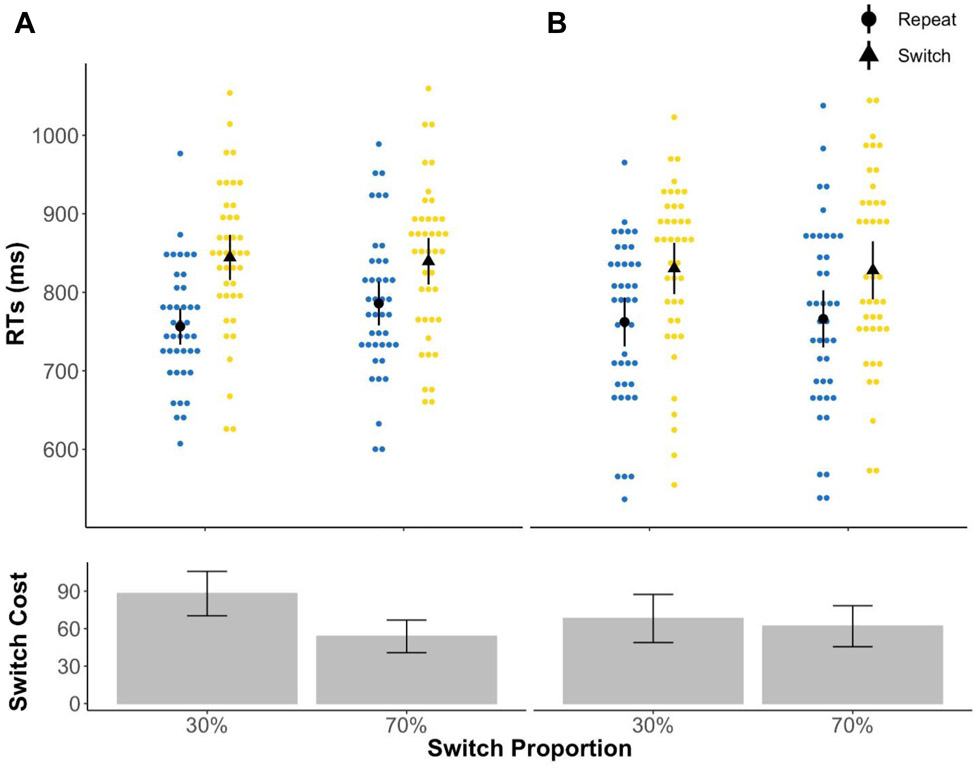
Most pertinently, we observed a three way interaction between task sequence, switch proportion, and task bias (F(1, 40) = 4.16, p = .048, η_p² = .09), which was due to the fact that the interaction effect of task sequence × switch proportion was driven by the biased tasks only (see Figure 4). Post hoc tests confirmed that, in the biased task condition, switch cost in the 30% switch condition (M_switchcost = 88.01 ms) was significantly higher than in the 70% switch condition (M_switchcost = 53.75 ms, F(1,40) = 11.53, p = .002, η_p² = .22).

Figure 4.

Experiment 3a mean RTs and switch costs for (A) biased and (B) unbiased transfer tasks. Upper panels depict group mean RTs in black circles (repeat) and triangles (switch) and individual mean RTs in blue (repeat) and yellow (switch) dots. Lower panels depict mean switch costs in bars. All error bars indicate confidence intervals (1.96 × standard error). In the biased task condition, switch cost in the 30% switch condition was significantly greater than the 70% condition. Switch cost differences were not significant in the unbiased transfer task.

To ensure that the three-way interaction was not due to greater power for detecting effects of the biased tasks (there were two biased tasks, which meant there were more total biased task trials), we ran three separate ANOVAs on each of the two biased tasks and the transfer task. The task sequence × switch proportion interaction effect was significant for both biased tasks (F(1,40) = 4.14, p = .05, η_p² = .09; F(1,40) = 11.39, p = 0.002, η_p² = .22), but not for the unbiased task (F(1,40) = .43, p = .52, η_p² = .01).

As before, the accuracy data showed a main effect of task sequence, reflecting significant switch costs (M_repeat = .87; – M_switch = 0.80), F(1, 40) = 49.43, p < .0001, η_p² = .55. There was also an interaction between task sequence and task bias (biased v. unbiased task), wherein participants exhibited lower mean switch cost in the transfer task (M_switchcost = 0.045) compared to the biased tasks (M_switchcost = 0.071), F(1, 40) = 4.54, p < .04, η_p² = .10. All other main effects and interactions were nonsignificant, including the crucial three-way interaction between task sequence, switch proportion, and task bias we observed in the RT data.

Experiment 3a found that the inverse relationship between switch cost and switch proportion did not hold for a transfer task that did not exhibit a switch frequency bias, even while it could be found in the biased tasks that occurred in the same block. One factor to consider when interpreting Experiment 3a’s results is that manipulating task-level switch proportion biases may have introduced inadvertent determinacies in the task-sequence that could have affected switch cost. In the 30% switch proportion blocks, in order to keep overall switch proportion low while presenting the transfer task half of the time as switch and half of the time as repeat trials, the transfer task had to be presented as a switch trial every time participants were switching away from one of the biased tasks. In other words, in order to present the transfer task enough times on switch trials, every switch from one of the other tasks had to be utilized as a switch to the transfer task. This pattern within the task sequence may have made it easier for participants to switch to the transfer task, compared to either of the biased tasks, in the 30% switch probability condition, thereby lowering switch cost for only the transfer task in the low switch likelihood condition, where one would have expected greater switch costs, thus potentially counteracting the detection of a possible LWPSE. We designed Experiment 3b to control for this possibility.

Experiment 3b

In order to control for the potential confound posed by the inadvertent determinative task sequences in Experiment 3a, in Experiment 3b we reduced the number of transfer task trials in each block, from a third of all trials to around one fifth. Note that while the relatively rare occurrence of the transfer tasks may generally affect performance on transfer task trials, it should do so in the same manner across the two switch frequency conditions. Since we are separately comparing how the transfer and biased tasks performance changes in different switch frequency contexts, the differential number of task presentations between biased and transfer tasks should therefore not affect our comparisons of interest. Importantly, reducing trial numbers of the transfer task allowed us to create a scenario where only a minority of the switches away from either of the biased tasks represented a switch to the transfer task. In this manner, Experiment 3b tested whether Experiment 3a’s results – the lack of transfer of block-wise proportion biases to the unbiased transfer task – would still hold after removing potential confounds due to predictable transitions between tasks.

Method

Participants.

A total of 120 participants were recruited from MTurk. The experiment lasted ~44 minutes and participants were compensated $5.60 if they performed at 65% accuracy or above. 59 participants were excluded from data analysis for lower than 65% overall accuracy on the task, leaving a final sample size of 61.

Stimuli and Procedures.

Task stimuli, trial components, and timing were identical to Experiment 3a, except that error feedback was only presented for 500 ms instead of 2000 ms to cut down on experiment time. (In Experiment 3a, participants were shown a blank screen for 500 ms after stimulus offset if their response was correct or the word “ERROR” in red for 2000 ms if their response was incorrect.) Participants were randomly assigned to different response mappings for each task and the identity of the unbiased task (i.e. whether it was the letter, digit, or number task).

The experiment consisted of 18 blocks of 39 trials each. The number of blocks was increased compared to Experiment 3a in order to ensure that each participant was exposed to 144 trials of the rarely occurring transfer task (there were 8 transfer task trials per block). Nine blocks had a 39% switch proportion and nine blocks had a 61% switch proportion. Trial sequences were pseudo-randomly generated. In the low switch proportion block, the two biased tasks were each presented either 5 or 6 times as switch trials and 10 or 9 times as repeat trials and the unbiased task was presented 4 times as switch and 4 times as repeat trials, creating an overall switch to repeat ratio of 15:23, or 39% switch trials. Thus, in low switch proportion blocks, a switch away from either of the biased tasks was associated with a switch to the transfer task in ~33–40% of cases. In the high switch proportion block, the number of switch v. repeat trials was reversed for the biased tasks, while the unbiased task was still presented 4 times as switch and 4 times as repeat trials, creating an overall switch to repeat ratio of 23:15, or 61% switch trials. Thus, in high switch proportion blocks, a switch away from either of the biased tasks was associated with a switch to the transfer task in ~17-18% of cases. Participants were randomly assigned to conditions where either the letter, digit, or color task appeared as the unbiased task.

Design.

The experiment followed a 2 (task sequence: switch vs. repeat) x 2 (task bias: biased vs. unbiased) x 2 (switch proportion: 39% vs. 61%) repeated-measures factorial design.

Results and Discussion

The same exclusion criteria (including RT exclusion) as Experiment 3a were applied. Descriptive statistics are displayed in Table 2, side-by-side with those of Experiment 3a.

We ran a repeated-measures ANOVA with the independent variables of task sequence (switch vs. repeat), task bias (biased vs. unbiased task), and switch proportion (low vs. high). We observed a main effect of task sequence on RT, F(1, 60) = 162.52, p < .0001, η_p² = .73, as responses on switch trials were slower (M_switch = 802.32 ms) compared to repeat trials (M_repeat = 756.07 ms). The interaction effect between task sequence × switch proportion only reached marginal significance, F(1,60) = 3.75, p = .06, η_p² = .06, wherein switch costs were marginally higher in the low switch condition (M_switchcost = 49.96 ms) compared to the high switch condition (M_switchcost = 41.28 ms) (See Figure 5).

Figure 5.

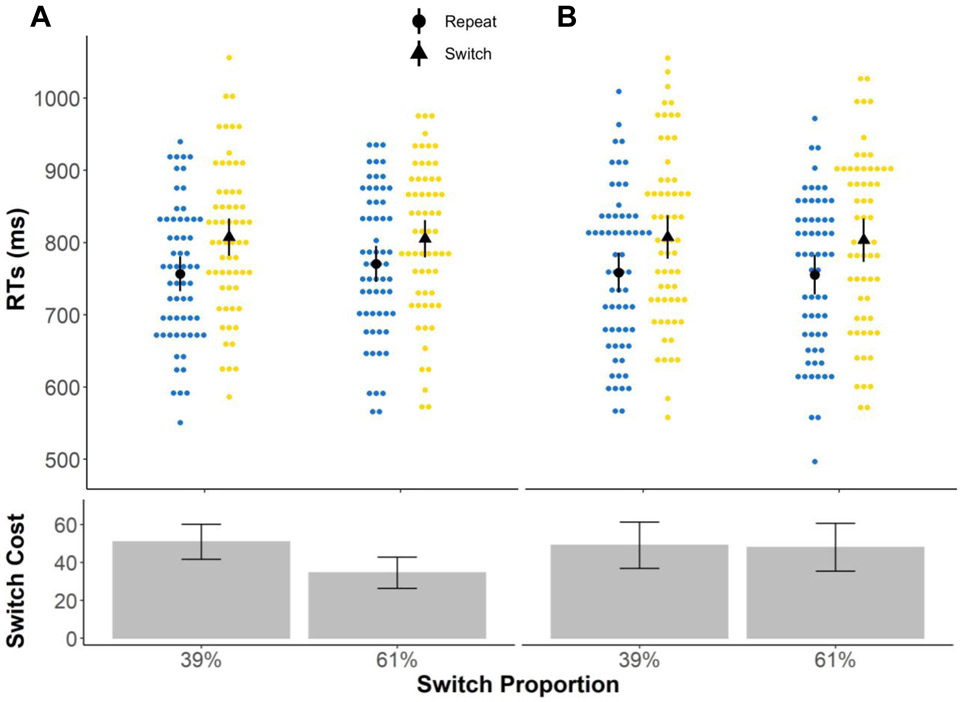
Experiment 3b mean RTs and switch costs for (A) biased and (B) unbiased transfer tasks. Upper panels depict group mean RTs in black circles (repeat) and triangles (switch) and individual mean RTs in blue (repeat) and yellow (switch) dots. Lower panels depict mean switch costs in bars. All error bars indicate confidence intervals (1.96 × standard error). In the biased task condition, switch cost in the 39% switch condition was significantly greater than the 61% condition. Switch cost differences were not significant in the unbiased transfer task.

The previously observed three-way interaction between task sequence, switch proportion, and task bias reached marginal significance (F(1, 60) = 3.44, p = .07, η_p² = .05). Figure 5 shows that, as in Experiment 3a, the trending interaction effect of task sequence × switch proportion was driven by the biased tasks only. Post hoc tests confirmed that, in the biased task condition, switch cost in the low switch proportion condition (M_switchcost = 50.83 ms) was significantly higher than in the high switch proportion condition (M_switchcost = 34.58 ms, F(1,60) = 13.63, p < .0005, η_p² = .19).

To ensure that this marginally significant three-way interaction was not due to greater power for detecting effects of the biased tasks, which had much larger trial counts, we ran three separate ANOVAs on each of the two biased tasks and the unbiased task. As in Experiment 3a, the task sequence × switch proportion interaction effect was significant for both biased tasks (F(1,60) = 6.81, p = .01, η_p² = .10; F(1,60) = 8.72, p = .004, η_p² = .13), but not for the unbiased task (F(1,60) = .02, p = .88, η_p² = .0004).

The accuracy data showed a main effect of task sequence, reflecting significant switch costs (M_repeat = .86; – M_switch = 0.79), F(1, 60) = 91.32, p < .0001, η_p² = .60. The three-way interaction between task sequence, switch proportion, and task bias did not reach significance. Separate ANOVAs on the two biased tasks and the transfer task found no task sequence × switch proportion interactions. All other main effects and interactions were non-significant.

In Experiment 3a and 3b, we modeled task bias as factor with two levels, rather than capturing the manipulation as the independent variable “task” (biased task 1, biased task 2, transfer task) with three levels, for clarity and ease of presentation. We also ran a supplemental analysis of an ANOVA model with task as a three level factor (see Appendix C). This did not change the general results except that the previously significant three-way interaction between task sequence, switch proportion, and task bias (F(1,40) = 4.16, p = .048, η_p² = .09) in Experiment 3a became marginally significant (F(1.91, 76.34) = 3.08, p = .05, η_p² = .07). In Experiment 3b, the previously marginally significant interaction between task sequence and switch proportion (F(1,60) = 3.75, p = .06, η_p² = .06) became significant (F(1,60) = 7.91, p = .007, η_p² = .12) and the previously marginally significant three way interaction between task sequence, switch proportion, and task bias (F(1, 60) = 3.44, p = .07, η_p² = .05) became nonsignificant (F(1, 60) = 2.17, p = .12, η_p² = .03).

The results of Experiment 3b replicated those of Experiment 3a, thus suggesting that the lack of transfer effects of the LWPSE in the former was not solely an artifact of determinacies in the task transitions. Experiment 3a and 3b jointly indicate that the LWPSE does not transfer to an unbiased task inserted into biased blocks of low or high switch proportion. This suggests that the adjustments of switch-readiness mediating the effect are tied to task-specific learning of switch proportions. We speculate on how switch proportion biases could operate on the level of task-sets in the General Discussion. Consequently, these results imply that participants do not enter a globally more flexible state in high switch proportion blocks.

Experiment 4

Experiment 3a and 3b investigated whether the adjustments of switch readiness observed in Experiments 1 and 2 occur in a global, generalizable fashion, which would allow them to transfer to an unbiased task embedded within biased blocks. Our results suggest that the adjustments of switch readiness were instead task specific, as modulation of switch costs were observed only for tasks whose switch frequency was biased. In other words, learned switch readiness seems to be directly tied to those task sets that are switched to more frequently. This finding, however, still leaves open two possible drivers of the list-wide proportion switch effect, as a given task set associated with frequent switching in our protocol also entails a specific set of task stimuli that also occur more (or less) frequently in the context of task repetitions or switches in different blocks. That is, all the stimuli in high switch proportion blocks are presented more often as switch than repeat trials (and the opposite is true for low switch proportion blocks). Thus, in addition to introducing task-level biases, biased blocks also create item-specific biases. Given that it has previously been shown that switch readiness can become associated with specific stimuli (Chiu & Egner, 2017; Leboe, Wong, Crump, & Stobbe, 2008, Exp 1), it is possible that the list-wide switch proportion effect investigated here is entirely due to a cumulative item-specific switch proportion effect.

In a final experiment, we therefore examined the role of biased associations at the stimulus- vs. task- level. This was accomplished by reverting to the two-task design of Experiment 1, but now adding a manipulation that divided the stimuli used in each task set into a biased set (driving the overall switch proportion) and an unbiased set that was associated with an equal number of task repetitions and switches (cf. Bugg & Chanani, 2011). This set-up allowed us to segregate possible item-specific switch proportion effects (analyzing biased stimuli) from possible task-level switch proportion effects (analyzing unbiased stimuli).

Method

Participants.

Due to the fact that we used a total of 16 stimuli, participants were only exposed to each letter or number one, two, or four times (depending on the experimental conditions) in each block of 60 trials. This may be a problem for Experiment 4 as it depends on an item-level manipulation of switch proportion associations; in order to establish these item-level associations, participants must encounter each letter/digit a sufficient number of times. Given power concerns due to participants’ reduced chance of exposure to each stimulus condition, we doubled the target sample size compared to Experiment 1,2, and 3a. 120 participants were recruited from MTurk. The experiment again lasted ~45 minutes and the same payment and exclusion criteria as Experiment 3 were applied, leaving a final sample size of 82.

Stimuli and Procedures.

Task stimuli, trial components, and timing were identical to Experiment 1. For each participant, half of the stimuli items (i.e. 2 vowels, 2 consonants, 2 odd digits, and 2 even digits) were pseudo-randomly selected as biased stimuli and the other half of the stimuli items were selected as unbiased stimuli.

The experiment consisted of 8 blocks of 61 trials each. The number of trials per block was doubled compared to previous 3 experiments to ensure that participants encountered each of the 16 stimuli items at least once as a switch and once as a repeat trial per block. Four blocks had a 30% switch proportion and four had a 70% switch proportion. Trial sequences were pseudo-randomly generated according to the same algorithm as in Experiment 1. Additionally, the item relevant to the task cued on a given trial was predetermined to create the biased v. unbiased stimulus manipulation. For example, if the current task was the digit task, the digit in the digit and letter stimulus pair was predetermined while the letter was randomly selected from the 8 possible ones. The task-relevant items were pseudo-randomly generated via an algorithm that ensured the following: In the 30% switch block, the 8 biased items were each presented 4 times as repeat trials and once as a switch trial (total of 32 repeat and 8 switch trials with biased stimuli items) and all the unbiased items were presented once each as a switch and repeat trial except 2 which were presented twice each (total of 10 repeat and 10 switch trials with unbiased stimuli items). This created an overall switch to repeat ratio of 18:42. In the 70% switch block, the number of switch to repeat trials was reversed for the biased stimuli, but it remained 10:10 for the unbiased stimuli.

Design.

The experiment followed a 2 (task sequence: switch vs. repeat) x 2 (stimulus bias: biased vs. unbiased) x 2 (switch proportion: 30% vs. 70%) repeated-measures factorial design.

Results and Discussion

The same exclusion criteria (including RT exclusion) as in Experiment 1, 2, and 3 were applied. Descriptive statistics are displayed in Table 3.

Table 3.

Mean Response Times (ms) and Accuracy (%) with Standard Error in Experiment 3a and 3b as a Function of Task Bias and Switch Proportion

	Exp 4
	30%		70%
Biased Items	RT	Acc	RT	Acc
Switch	758.8 (11.9)	77.9 (1.6)	762.5 (10.2)	81.1 (1.2)
Repeat	732.7 (9.9)	85.1 (1.1)	750.5 (10.4)	86.5 (1.1)
Unbiased Items
Switch	774.4 (11.6)	76.7 (1.4)	773.4 (11.1)	78.7 (1.2)
Repeat	744.0 (10.6)	82.7 (1.3)	756.2 (10.0)	84.5 (1.2)

Note. Data refers to group mean RTs (excluding error trials, trials following error trials, and RT outliers) and accuracy percentage with SE in parentheses.

We ran a repeated-measures ANOVA with the independent variables of task sequence (switch vs. repeat), stimulus bias (biased vs. unbiased stimulus), and switch proportion (30% vs. 70%). We observed a main effect of task sequence, as switch costs were significant (M_switch = 763.01 ms; M_repeat = 740.07 ms), F(1, 81) = 38.82, p < .0001, η_p² = .32. Moreover, RT for unbiased items (M = 760.51 ms) was significantly slower than for biased items (M = 746.64 ms), F(1, 81) = 33.77, p < .0001, η_p² = .29. There was again no main effect of switch proportion.

Importantly, we detected a task sequence × switch proportion interaction, F(1,81) = 12.54, p = .0007, η_p² = .13, wherein switch cost for the 30% switch condition (M_switchcost = 28.20 ms) was higher than for the 70% switch condition (M_switchcost = 14.04 ms). There was no interaction between stimulus bias and switch proportion. More relevant to our assessment of differential contributions of biased vs. unbiased stimuli to the LWSPE, there was no significant three-way interaction (F(1,81) = 0.00, p = >.99, η_p² < .0001) (see Figure 6).

Figure 6.

Experiment 4 mean RTs and switch costs for A) biased and B) unbiased stimuli sets. Upper panels depict group mean RTs in black circles (repeat) and triangles (switch) and individual mean RTs in blue (repeat) and yellow (switch) dots. Lower panels depict mean switch costs in bars. All error bars indicate confidence intervals (1.96 × standard error). In both biased and unbiased stimuli sets, switch cost in the 30% switch condition was greater than in the 70% switch condition.

To directly examine whether the switch proportion effect could be observed for unbiased stimuli, we ran separate ANOVAs for biased and unbiased items, respectively. This analysis confirmed that the task sequence × switch proportion interaction was significant both for the biased stimuli, F(1,81) = 8.46, p = .005, η_p² = .09, and the unbiased stimuli, though the effect was numerically weaker for the latter, F(1,81) = 4.86, p = .03, η_p² = .06.

The accuracy data showed a main effect of task sequence, reflecting significant switch costs (M_repeat = .85; – M_switch = 0.80), F(1, 81) = 113.37, p < .0001, η_p² = .58. There was also a significant effect of stimulus bias, F(1,81) = 18.38, p < .0001, η_p² = .18, wherein biased stimuli were associated with higher accuracy (M_accuracy = .83) than unbiased stimuli (M_accuracy = .81). Accuracy was also significantly higher in the 30% switch condition (M_accuracy = .823) compared to the 70% switch condition (M_accuracy = .820), F(1,81) = 4.93, p = .03, η_p² = .06. Unlike in the RT data, there was no significant interaction effect between task sequence × switch proportion. Separate ANOVAs on the two biased tasks and the unbiased task also found no task sequence × switch proportion interactions. All other main effects and interactions were non-significant.

In summary, though trials containing biased items produced larger switch proportion modulations of switch costs, significant switch cost adjustments were also detectable for unbiased items. Experiment 4’s results therefore suggest that item-lev el biases are not the sole driving factor behind the LWPSE that we observed in Experiments 1, 2, and 3. The LWPSE observed in unbiased items is likely driven by task-level proportion biases. Unlike task-level bias, the presence of item-level bias is therefore not a necessary condition for making switch cost adjustments.

General Discussion

This study set out to characterize the nature of the learning processes driving meta-control over cognitive flexibility, as indexed by the LWPSE. In four experiments that manipulated switch proportion, we demonstrated that the inverse relationship between switch cost and the frequency of switches in a block is driven by item- and task-level associations, rather than the global, block-level context. We find these modulations of switch costs primarily in the RT but not in accuracy data, similar to several previous studies on the LWPSE (Bonnin et al, 2011; Dreisback & Haider, 2006; Dreisbach et al., 2002). In line with previous work, Experiments 1 and 2 found reliable switch cost reductions for high proportion switch blocks when the cue-stimulus interval was short (Monsell & Mizon, 2006), and that these reductions occur even when participants cannot reliably predict which specific task they would be switching to (Chiu & Egner, 2017). Experiment 3a and 3b found that switch cost for an unbiased transfer task was unaffected by the block-wide switch-proportion context, suggesting that block-level biasing of switch likelihood does not result in a global, trans-task enhancement of cognitive flexibility. In turn, this indicates that the LWPSE is driven by task- and/or item-level learning of switch associations. Chiu & Egner (2017) found item specific switch proportion effects on biased stimuli embedded in overall unbiased (50:50 switch/repeat trials) blocks, thus demonstrating that item-level biases can elicit switch cost adjustments. Experiment 4 in the current study extends this finding by demonstrating that item-level biases are not the only drivers of switch cost adjustments. Rather, we also identified switch cost modulation in the unbiased (presented equally often as switch versus repeat trials) stimuli sets, indicating that task-level bias can produce adaptation in flexibility even in the absence of item-level bias.

As we alluded to in the discussion of Experiment 1, the smaller switch costs in the high switch proportion conditions across all 4 experiments were carried mainly by slower RTs to repeat trials, rather than faster RTs to switch trials (though switch trials were numerically faster in high vs. low switch proportion blocks in all four experiments). Most previous studies reported switch costs adjustments driven by both switch and repeat trial types (e.g. Duthoo et al., 2012; Monsell & Mizon, 2006) but some have also found them driven predominantly by RT changes in repeat trials (Dreisbach & Haider, 2006). Bonnin et al. (2011) provides one possible explanation of the lack of switch trial RT adaptations: they propose that backwards inhibition (Mayr & Keele, 2000) may increase average switch trial RTs in high switch frequency blocks, since high frequency blocks contain more frequent switches back to the previous task (i.e. “ABA” task sequences) compared to low switch frequency blocks. In support of this conjecture, Bonnin et al. (2011, Experiment 1) documented numerically smaller switch RT reductions in conditions with shorter (800 ms) versus longer (1300 ms) response-stimulus intervals (RSI), the latter of which should decrease the potency of backwards inhibition effects. We employed a 810 ms RSI in the current series of experiments, which falls in the same range as the short RSI condition in Bonnin et al. (2011). Thus, even though our participants may have been exhibiting greater switch-readiness in high switch frequency blocks, the resultant performance benefits may have been be masked by concurrent backward inhibition effects, an interpretation that is supported by the fact that we did not actually observed slowed switch RTs due to backwards inhibition effects in high switch frequency blocks . However, additional systematic research into backwards inhibition as another variable that can influence block-wise switch cost adjustments is clearly warranted.

Task sets form the boundaries of control strategies

The lack of evidence for global list-wide proportion switch effects in the present study appears to clash with findings from conflict-control experiments that utilized a conceptually equivalent design of unbiased transfer items embedded within biased blocks (list-wide proportion congruency (LWPC) effects. For example, Bugg & Chanani (2011) designed a picture-word Stroop task where sets of biased items (presented more frequently as incongruent or congruent trials) were used to create mostly-congruent or mostly-incongruent blocks, and intermixed with unbiased transfer items (presented equally often as congruent and incongruent stimuli). Hence, as in our design, the biased items were biased both at the list-wide and item-specific levels, while the unbiased items were biased only at the list-wide level. Bugg & Chanani (2011) (see also Bugg, 2014; Hutchison, 2011) found that conflict (the RT difference between congruent and incongruent trials) was reduced in mostly incongruent compared to mostly congruent blocks for both stimulus sets, thus providing evidence for the existence of list-wide (global) effects of adjustments in conflict control.

Why would list-wise proportion-based adjustments in cognitive control strategy generalize in this manner for conflict control but not for task switching? We posit that this difference can be attributed to the key role that task sets play in determining processing strategies, including attentional sets (cf. Egner, 2014; Hazeltine, Lightman, Schwarb, & Schumacher, 2011; Schumacher & Hazeltine, 2016; Grant, Cookson, & Weissman, 2020). In particular, in the case of conflict-control, the generalization of list-wide proportion effects to transfer items generally takes place within a single task set (but see Surrey, Dreisbach, & Fischer (2017; Exp 2) for an example of how context specific proportion congruence (CSPC) effects generalized to a different task set in a transfer block that maintained the same proportion congruency bias). For example, in Bugg & Chanani’s (2011) picture-word Stroop task, the task is always to name the picture while ignoring the superimposed word, regardless of whether items are biased or unbiased. Since conflict-driven adaptation effects are thought to reflect the reinforcement of an ongoing task set (Botvinick, Braver, Barch, Carter, & Cohen, 2001; Egner, 2008; Goschke, 2000), it makes sense that they would generalize to other stimuli that are processed within the same attentional set (here, “focus on pictures, ignore words”). These LWPC transfer effects from the conflict control literature are in fact directly comparable to the findings of task-level effects for unbiased items we observed in Experiment 4; here, the unbiased items for which we detected a transfer effect of the switch proportion manipulation were part of the same task set(s) within which the switch proportion bias occurred (driven by other biased items), just as in the case of the LWPC effects. Moreover, in a similar vein to our finding that task-level control effects can be observed independently of item-specific learning, Schneider (2015) found response congruency effects in a cued-task switching paradigm even when stimulus items were never repeated (see Appendix B for supplementary response congruency analyses for the current study).

By contrast, we found no evidence for a transfer of switch cost modulation to unbiased stimuli that were associated with a distinct, unbiased task set. We are not aware of any other studies in the proportion switch domain where effects generalized in a trans-task fashion, though one study in the realm of proportion congruency (Surrey et al., 2017; Exp 2) showed transfer of CSPC effects when participants performed a new task (categorizing numbers as odd/even versus categorizing letters as consonant/vowel) in the same proportion congruence context. Our results are not directly comparable with Surrey et al. (2017) because the transfer task in our paradigm was presented with unbiased switch associations regardless of block-wide context. More future experiments would be required to delineate the exact conditions under which cross-task transfer occurs. Nonetheless, findings from the current study suggest that task sets might form the overarching cognitive structure within which frequency-driven learning of context-appropriate control strategies takes place: people are able to adapt cognitive flexibility to the specific statistics of the task(s) at hand, but they do not generalize those flexibility settings to the broader temporal (list-wide) context when having to switch to a different, unbiased task.

A potential caveat to these conclusions is that we did not assess potential transfer effects in the context of more extreme switch proportion biases than 70:30. While we (and previous studies) observed reliable switch proportion effects on the biased task sets and biased and unbiased item-levels using 70:30 (and even 61:39) trial type proportions in the absence of any evidence for cross-task transfer, we cannot technically rule out the possibility that such effects could be observed under more extreme statistics (e.g. 90:10). However, one could also predict that a more extreme switch proportion bias would make detection of cross-task transfer less likely, as it would also make easier for participants to distinguish between the heavily biased tasks and the transfer task which remains neutral. Likewise, it is possible that cross-task transfer may develop if block numbers were increased further and participants had more time to acquire switch bias associations. We tested this idea in supplementary analyses conducted on Experiment 3a and b, where we examined how task phase (early or late) interacted with our other experimental variables (see Appendix D). The analyses indicated that task phase did not interact significantly with task sequence, switch proportion, or task in either experiment, indicating that it is unlikely that transfer effects would emerge if we substantially increased trial numbers.

How are task-specific switch readiness adjustments implemented?

In assessing possible drivers of learning that may mediate the LWPSE, we have shown that strategic shifts in switch readiness are mediated by associating task sets and task stimuli with their respective switch likelihood. But how exactly are these adjustments carried out in terms of the underlying mechanisms of task-set regulation? We consider two, not mutually exclusive, possible sites of action: one related to the processes involved in switching (that is, task set reconfiguration and/or resolution of interference), and the other related task set representation (that is, the level of activation or shielding of the task rules).

In terms of switch processes, we believe that the current data are more in line with effects of switch proportion on task-set reconfiguration than on the processes of overcoming task-set inertia or resolving associative interference. First, the present study replicated the finding that the LWSP effect is dependent on CSI in the presence of constant RSIs (Experiment 1, and Monsell & Mizon, 2006). Since the former is typically assumed to affect task-set reconfiguration processes (Rogers & Monsell, 1995) while that latter is thought to modulate effects of task-set inertia (e.g., Sohn & Anderson, 2001), this indicates that the present switch proportion effects are more likely related to modulation of reconfiguration processes than of those involved in overcoming interia from the previous-trial task-set. Moreover, the present study employed univalent stimuli (presented side-by-side), and task stimuli associated with the uncued tasks did not systematically vary between different switch frequency conditions. The former aspect is likely to reduce associative task-set interference triggered by uncued task stimuli (Waszak, Hommel, & Allport, 2003), and even if such effects contributed to switch costs in the present study, it is not clear how they would differentially affect the different switch proportion conditions.

Monsell & Mizon (2006) proposed that the switch proportion effect observed in their study, which did not distinguish block-wide from task-set or item-related learning, may reflect either a strategy whereby participants shift from a default carryover of the prior task set to preparation of the alternative task that is implemented either before or after task cue onset (or both). The present study constrains these possibilities in important ways: first, Experiment 2 has shown that any such strategy shift is not dependent on preparation for one specific other task but can be effective in conditions of three tasks, where no single alternate task is predictable. Second, since we did not observe transfer to an unbiased task (Experiment 3a, b), it seems unlikely that the switch frequency driven change in preparation processes occurred prior to the task cue or stimulus onset, as in that case one would anticipate transfer effects. Rather, it appears that under high switch likelihood, the shift from preparing for task-set repetition to preparing for a switch is bound to specific task cues or items, and therefore only becomes effective after task cue or stimulus onset.

If the CSI is long, the strategy (or expectation) invoked by the biased switch proportions can be overridden (Experiment 1), but at short CSIs, these effects can be observed (Experiments 1-4), such that when the actual requirements do not match the expected control settings, performance costs will be incurred (in the present case, slower task repetition performance when the task cue or item is predictive of switching). Together, these results suggest that the effects of switch proportion are mediated via fast, bottom-up (task cue- or item-triggered) priming of the context-appropriate control setting (cf. King et al., 2012). This explanation is conceptually equivalent to the account of stimulus-triggered reactive conflict-control processes mediating the item-specific proportion congruency effect (e.g., Bugg & Hutchison, 2013), but in the present case the process in question relates to task-set reconfiguration rather than conflict resolution, and can be triggered both by biased task cues and task stimuli.

In terms of effects mediated by the relative levels of activation (and/or shielding) of task-set representations, there are two a priori possibilities; either frequently switched-to tasks are retained in a more activated state or they become less activated (or less stable). First, it seems superficially plausible that frequently switched-to task-sets incur smaller switch costs because they are maintained at a higher level of activation (compared to conditions where they are not switched to very often). However, we believe that this is an unlikely scenario, since in that case one would predict a general RT reduction for the switch-biased tasks, regardless of whether they occur on switch or repeat trials, rather than the observed switch cost reductions that are in great part driven by repeat trial RT increases. Similarly, generally heightened activation of task-sets under high switch frequency would also predict a greater degree of task-set inertia, i.e. involuntary priming by the previous task set (Allport & Wylie, 1999), which should again result in reduced repeat trial RTs, contrary to the observed data. These factors make it unlikely that switching to tasks more frequently increases the strength of their activation.

In contrast, the possibility that task set representations become less activated (less stable or less well-shielded) under conditions of frequent switching seems more congruent with the current findings: less stable sets would be expected to be switched to and from more easily but also provide less benefits of task repetitions, which is in line with the repeat RT increases we observed in the current study under high switch frequency conditions. The idea that greater flexibility corresponds to weaker task-set activation is also supported by recent neuroimaging evidence from Qiao, Zhang, Chen, & Egner (2017), who found via multi-voxel pattern analysis on frontoparietal cortex activity patterns that neural task-set representations are less stably encoded on task switch compared to repeat trials.

Note that the two speculative explanations that we offer, modulation of task-set reconfiguration and differential task-set activation/shielding, are not mutually exclusive – it is quite likely that both processes contribute to our observed results. In sum, our data thus suggests that instead of entering flexible versus stable global cognitive states that span the duration of a block, people seem to shift between more flexible versus more stable processing modes based on learning which specific tasks or items require greater switch-readiness or greater task-set shielding. In other words, people learn to link a context-appropriate meta-control state (e.g., an “updating threshold” setting) to task sets and stimuli, and are capable of rapidly retrieving or activating that state in a bottom-up manner. These results carry practical implications for attempts to train cognitive flexibility and stability, as they demonstrate that not only external context, such as the degree of volatility in an environment, but also internal context, such as task-sets or goals, matters for learning or improving on a particular cognitive strategy.

Finally, an interesting additional question might be to what degree the learning process that we here conceptualize as reflecting the acquisition of strategic (goal-directed) meta-control settings is an implicit or explicit one. We can only speculate on this, as we neither manipulated nor probed participants’ awareness of the different switch proportion conditions. However, while the role of conscious awareness and understanding of cues for control is generally still ill-understood (see e.g., Farooqui & Manly, 2015; Bejjani, Dolgin, Zhang, & Egner, 2020), a number of related studies in the domain of conflict-control, specifically proportion congruent manipulations, have tested participants for their understanding of the experimental manipulations and have typically detected little or no explicit insight (Crump, Vaquero, & Milliken, 2008; King, Korb, & Egner, 2012; Reuss, Desender, Kiesel, and Kunde, 2014; Schmidt, Crump, Cheesman, & Besner, 2007; Bejjani, Tan, & Egner, 2020). It therefore seems likely that the same was true for the current experiments. If this assumption were correct, it would in turn indicate that meta-control, defined as adjusting the balance between complimentary control modes in a context-appropriate manner (Goschke, 2013), can in fact be accomplished by implicit learning processes. This would be consistent with perspectives that ground cognitive control in associative binding and learning processes, which do not necessarily require explicit awareness of the triggers and/or implementation of contextual adapatation in processing strategies (Egner, 2014; Abrahamse, Braem, Notebaert, & Verguts, 2016).

Possible Neural Mechanisms

How may the type of adjustments in cognitive flexibility that we document here in behavior play out in the brain? In the cognitive neuroscience literature, the effective maintenance of task sets has traditionally been associated with the dorsolateral prefrontal cortex (dlPFC) (Waskom, Kumaran, Gordon, Rissman, & Wagner, 2014; Wisniewski, Reverberi, Momennejad, Kahnt, & Haynes, 2015; Woolgar, Hampshire, Thompson, & Duncan, 2011) and, as alluded to before, recent work by Qiao et al. (2017) suggests that the stability of task set representations – as assessed by their decodability using fMRI multivoxel pattern analysis – is reduced during task switch compared to repeat trials. So one possibility is that an increase in switch-readiness under conditions of high switch-likelihood may be mediated by a strategic destabilization of dlPFC task-set representations (see our speculation on less activated task sets, above). Another, not mutually exclusive possibility is that learned changes in cognitive flexibility are mediated by the basal ganglia (BG), which are thought to play the role of a gating mechanism for updating (or not) dlPFC working memory content (Frank, Loughry, & O'Reilly, 2001; O'Reilly & Frank, 2006) including task sets (e.g. Cools, Sheridan, Jacobs, & D'Esposito, 2007). Here, greater switch-readiness may be associated with a lower threshold for gate-opening in the BG. In line with this latter possibility, it has been shown that item-specific proportion congruency effects involve prominent contributions by the caudate nucleus (Chiu, Jiang, & Egner, 2017). However, no neuroimaging study to date has directly assessed the neural signature of the LWSPE, such that a proper evaluation of the above hypotheses is left to future studies.

Conclusions

We presented a novel, systematic comparison of block-, task-, and item-level effects of switch proportion biases to elucidate the underlying mechanisms of the LWPSE. We observed reliable modulation of switch costs by switch proportion that was driven by participants forming associations between switch-likelihood and specific task sets and stimuli. These learned adjustments in cognitive flexibility did not generalize to an unbiased task within the same block, suggesting that task sets define a critical boundary for learning and applying suitable meta-control settings. Thus, cognitive flexibility (switch-readiness) can be strategically adapted to varying contextual demands, but the context that matters is not temporal (experimental block) but rather the task goal and task stimuli.