Quantitative Measurement of Redox State in Human Brain by ³¹P MRS at 7T with Spectral Simplification and Inclusion of Multiple Nucleotide Sugar Components in Data Analysis

Abstract

Purpose:

To develop a simplified method for quantitative measurement of NAD⁺/NADH levels in human brain by ³¹P MRS without interference from the α-ATP signal and with inclusion of multiple UDP-sugar components.

Methods:

Simple pulse-acquire ³¹P MR spectra were collected at 7T with and without a frequency-selective inversion pulse to remove the dominant α-ATP signal from the underlying NAD(H) signal. Careful inspection of the ³¹P signal at −9.8 ppm previously assigned to UDP-glucose revealed multiple UDP-sugar components that must also be considered when deconvoluting the NAD(H) signal to quantify NAD⁺ and NADH. Finally, the overlapping NAD(H) and UDP(G) resonances were deconvoluted into individual components using Voigt lineshape analysis and UDP(G) modeling.

Results:

The frequency-selective inversion/subtraction method enabled clean separation of the NAD(H) signal from the otherwise dominant α-ATP signal. In addition, the upfield signal near −9.8 ppm appears more “quartet-like” than a simple doublet consistent with contributions from other nucleotide sugars such as UDP-galactose, UDP-N-acetyl-galactosamine, and UDP-N-acetyl-glucosamine in addition to UDP-glucose. Deconvolution of the combined NAD(H) and UDP(G) signals showed that the measured NAD⁺/NAD ratio was heavily influenced by UDP(G) modeling (7.5±1.8 when the UDP(G) signal was fitted as multiple doublets versus 5.3±0.6 when a simplified pseudo doublet model was used). In a test/re-test experiments separated by two weeks, consistent NAD⁺/NADH ratios were measured in the brain of seven human subjects.

Conclusions:

The NAD⁺/NADH ratio in human brain can be measured using ³¹P MR spectra simplified by spectral editing and with inclusion of multiple UDP-sugar components in the data analysis.

Introduction

The nicotinamide adenine dinucleotides (NAD⁺ and NADH) are ubiquitous cofactors in many redox reactions in multiple cell compartments (1,2). While NAD⁺ serves as the primary electron acceptor in oxidative catabolic processes, it also participates as a substrate for synthesis of poly(ADP-ribose) (PAR), a polymer needed for maintenance of DNA integrity, gene expression and cell division (3). The phosphorylated analogs, NADP⁺ and NADPH, participate in reductive anabolic reactions for synthesis of fatty acids, nucleotides and other cellular building blocks while NADPH serves to modulate levels of cellular reactive oxygen species (4). It has long been known that low availability of NAD(H) can lead to altered metabolism, cold intolerance, and delayed brain development (5,6), whereas a deprivation of NAD(H) may occur in association with alcoholism, malabsorption, tuberculosis and eating disorders (7). During an energy deficit or reduced carbohydrate intake such as fasting and exercise, NAD(H) can activate sirtuins to deacetylate histone and proteins, triggering cellular adaptation toward more efficient metabolism (5). Recent studies suggest that brain NAD(H) levels decrease with aging (8), implying a potential role of NAD(H) in cognitive decline and other aging-associated conditions (1). Given the tight coupling of NAD(H) with major metabolic pathways (Figure 1), there has been a great interest in using the NAD⁺/NADH ratio as imaging biomarker in schizophrenia (9) and psychotic disorders (10), and in using NAD(H) as a therapeutic target to treat various metabolic conditions ranging from oxidative stress to cancer and neurodegenerative diseases (11–13).

Figure 1.

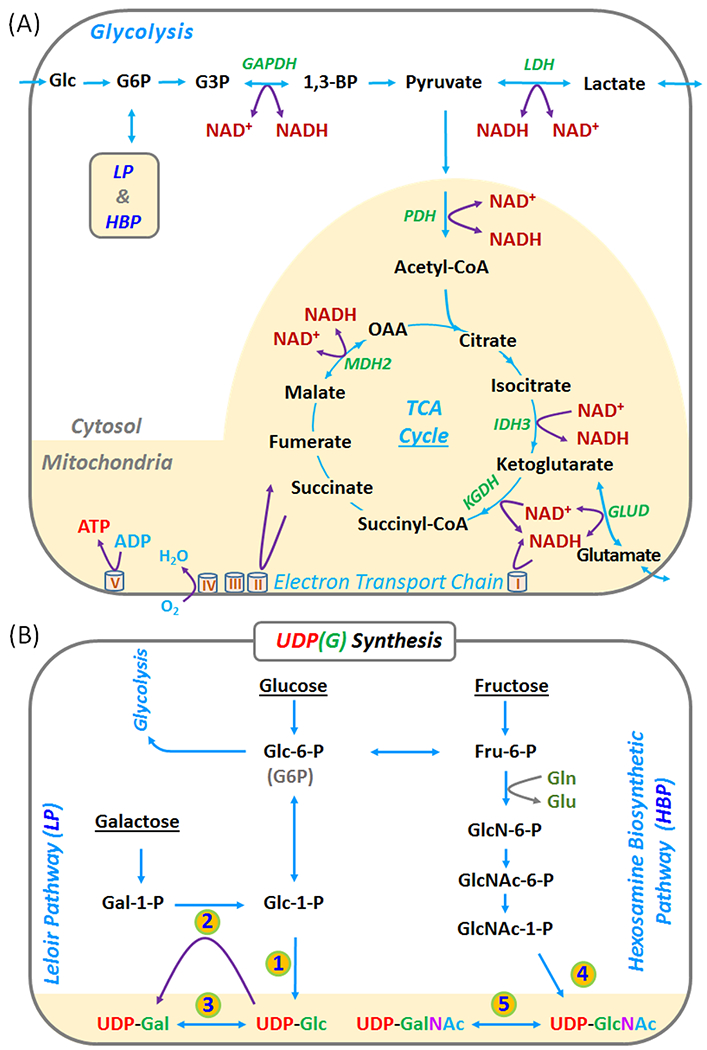
(A) Coupling of NAD(H) redox reactions with metabolic pathways in glycolysis and mitochondrial TCA cycle. (B) Production of UDP-Gal and UDP-Glc in the Leloir pathway (LP), and of UDP-GalNAc and UDP-GlcNAc in the hexoamine biosynthetic pathway (HBP). Abbreviations: ATP, adenosine triphosphate; NAD(H), nicotinamide adenine dinucleotides (reflecting the sum NAD⁺ and NADH); UDP, Uridine diphosphate; UDP-Gal, UDP-galactose; UDP-Glc, UDP-glucose; UDP-GalNAc, UDP-N-acetyl-galactose; and UDP-GlcNAc, UDP-N-acetyl-glucose; UDP(G) reflects the sum of UDP-Gal, UDP-Glc, UDP-GalNAc, and UDP-GlcNAc. Enzymes in the numbered steps: 1. glucose-1-phosphate uridyltransferase; 2. galactose-1-phosphate uridyltransferase; 3. UDP-galactose 4-epimerase; 4. UDP-N-acetyl-glucosamine diphosphorylase; and 5. UDP-N-acetyl-glucosamine 4-epimerase.

Given the abundance of NAD⁺ and NADH in brain, the sum of these two species (referred to here as NAD(H)) is easily detected by ³¹P MRS at high magnetic fields (14–18). The ³¹P signal of NAD(H) consists of a singlet (NADH) and an AB quartet (NAD⁺) with the quartet typically dominating (19,20). Curve fitting of the NAD(H) signal allows a direct measure of the NAD⁺/NADH ratio (8,14,15) provided that this region of the spectrum does not contain other underlying signals. However, removing the contribution of the dominant α-ATP resonance plus underlying signals from sugar dinucleotides makes measurement of an accurate NAD⁺/NADH ratio difficult even at ultrahigh magnetic fields. As a result, the reported values of NAD⁺/NADH ratios have been quite variable (8,12,13). In the current study, we aimed to explore a novel ³¹P spectral editing method based on T₁ differences between the NAD(H) the α-ATP resonances to facilitate more consistent measurements of NAD⁺/NADH. While the classical J_1H-1H-based editing methods are successful for resolving overlapping resonances in ¹H MRS, a similar J_31P-31P-based editing approach is impractical given the unfavorably large ²J_31P-31P/T₂ ratio of the α-ATP resonance. Fortunately, the T₁ differences between α-ATP and NAD(H) is sufficiently large (14) to permit spectral editing of these nucleotides using relatively simple inversion-recovery (IR) methods.

Assessment of NAD⁺/NADH in brain by ³¹P MRS is also sensitive to varying levels of UDP-glucose (UDP-Glc), a sugar nucleotide that has a ³¹P doublet underlying the NAD(H) signal near - 8.2 ppm. The presence of UDP-Glc in brain is typically identified by the appearance of a J-coupled doublet at −9.8 ppm but this signal often appears more complex than a simple doublet (14,15). The high-resolution ³¹P MRS spectra collected in the current study clearly show that the −9.8 ppm signal appears more like a “quartet-like” resonance rather than a single doublet. A lineshape analysis shows that this signal is best described by four overlapping doublets with small differences in chemical shift. We tentatively assign these doublets to UDP-glucose (UDP-Glc,), UDP-galactose (UDP-Gal), UDP-N-acetyl-galactosamine (UDP-GalNAc), and UDP-N-acetyl-glucosamine (UDP-GlcNAc). These four sugars reflect two pairs of interconvertible epimers in the Leloir (LP) and hexosamine biosynthetic (HBP) pathways (Figure 1). These four UDP(G) components have been documented as the most dominant nucleotide sugars in extracts of brain tissues by HPLC (21–23) and in cells and various tissue extracts by NMR (24–28). Given that each UDP-sugar would also contribute a small ³¹P doublet that also co-resonates with NAD(H), it is important to remove these components before deconvoluting the NAD(H) resonance for evaluation of the NAD⁺/NADH ratio.

Methods

Human Subjects

The protocol was approved by the Institutional Review Board of the University of Texas Southwestern Medical Center. Prior to the MRS study, informed written consent was obtained from all participants. A total of 14 subjects (7F/7M, aged 18 – 65 yr) participated in the study. Seven subjects (3M/4F), aged 56 ± 7 yr (46 – 65 yr), BMI 27 ± 7, resting heart rate 69 ± 9, and peripheral capillary oxygen saturation (SpO₂) 96 ± 2%, were scanned twice on separate days for reproducibility testing. The remaining seven subjects were scanned for protocol development. All subjects were in good general health with no history of psychiatric or neurological diseases. No subjects were on keto-diet. Heart rate and blood oxygen saturation levels were monitored during the scan. The study was well tolerated by all subjects.

MRS Protocol

All subjects were positioned head-first and supine in the 7T MRI scanner (Achieva, Philips Healthcare, Cleveland, OH), with the back of the head positioned in the center of a half-cylinder-shaped partial volume RF coil (Philips Healthcare, Cleveland, OH). The subjects were asked to remain awake in the MRI scanner. The RF coil was a double-tuned ¹H/³¹P quadrature TR coil consisting of two tilted, partially overlapping 10 cm loops, with a solid base that can be firmly attached to the scanner table. The brain ³¹P signals were mainly from the occipital lobe as confined by the sensitivity profile of the RF coil B₁ field. Axial, coronal, and sagittal T2-weighted turbo spin echo images were acquired for shimming-voxel planning. Typical imaging parameters included field-of-view 180 × 180 mm (FOV), repetition time (TR) 2.5 s, echo time (TE) 80 ms, turbo factor 15, in-plane spatial resolution 0.6 × 0.7 mm², slice thickness 6 mm, gap 1 mm, bandwidth 517 Hz, number of acquisitions (NA) one, and acquisition time 2.1 min. Second order ¹H-based automatic volume shimming was applied prior to ³¹P spectral acquisitions. The average PCr linewidth was 11.5 ± 0.7 Hz (n = 14 subjects).

Brain ³¹P spectra were acquired at 120.6 MHz using pulse-acquire and inversion-recovery (IR) sequences using a constant TR of 1 s, a hard readout pulse and a nominal 90° flip angle (B₁ = 59 μT). Compared to the pulse-acquire reference spectra, the IR sequence included an adiabatic inversion pulse with a bandwidth of 1 kHz to selectively invert the upfield region that includes the α-ATP, NAD(H) and sugar nucleotides resonances (Figure 2B). A fixed post-inversion delay of 0.37 s was used to null the NAD(H) signal prior to readout (Figure 2A). For practical reasons to facilitate monitoring of the spectral quality, all free induction (FID) decays were collected in eight sequential blocks each consisting of 256 scan averages and later examined, aligned and summed for data analysis. Other common ³¹P NMR parameters were as follows: 4K data points, transmitter carrier frequency offset 50 Hz downfield from α-ATP signal. The chemical shifts of all ³¹P metabolites were referenced to PCr at 0 ppm.

Figure 2.

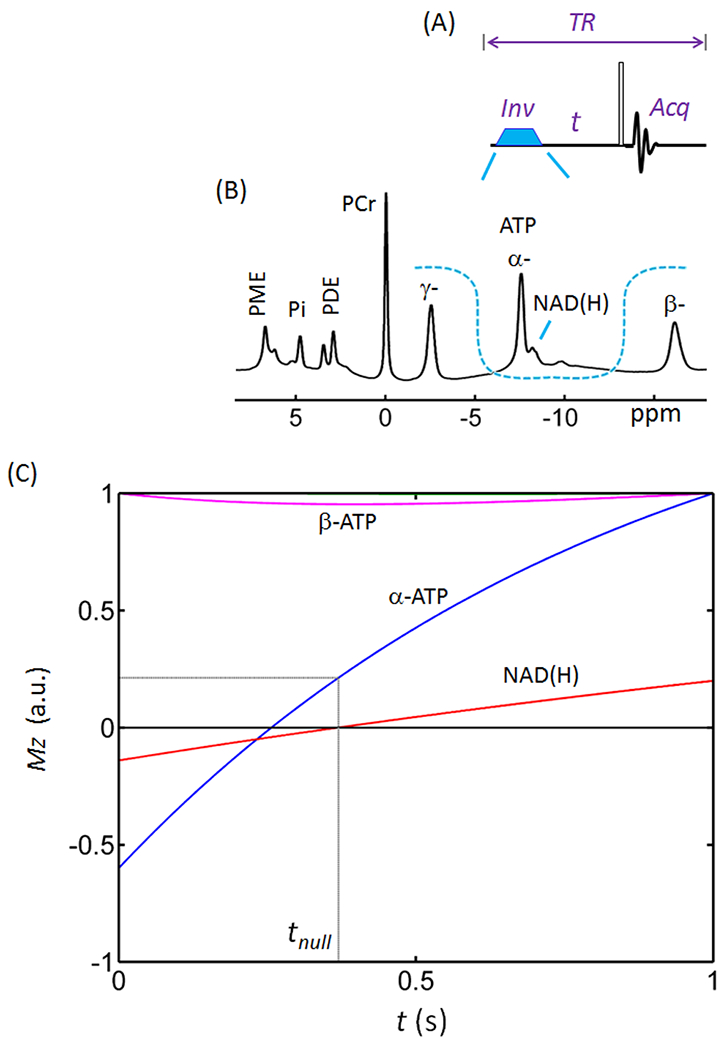
Inversion recovery spectral editing of NAD(H). (A) Diagram of inversion-recovery (IR) pulse sequence. (B) Profile of the inversion band (U-shaped dashed line) over a brain ³¹P spectrum acquired with TR = 1.0 s using a pulse-acquire sequence without baseline correction. Note the baseline distortion and the signal overlap between NAD(H) and α-ATP. The inversion bandwidth covers α-ATP, NAD(H) and UDP(G). (C) Simulated inversion-recovery curves for the ³¹P Z-magnetizations of NAD(H) (red trace) and α- (blue) and β- (magenta) ATP. The simulation was based on steady-state Z-magnetization with 90° readout pulse and constant TR = 1.0 s. Abbreviations: ATP, adenosine triphosphate; NAD(H), nicotinamide adenine dinucleotide; PCr, phosphocreatine; PDE, phosphodiesters; PME, phosphomonoesters; and Pi, inorganic phosphate.

To evaluate reproducibility, a sub-cohort of seven subjects (3M/4F) were scanned twice on two visits separated by 2 weeks but at the same time of the day and under the same scan conditions and procedures. To examine the effect of ¹H-³¹P coupling on ³¹P resonance pattern, three subjects were scanned with and without ¹H decoupling at TR = 5 s. The wide-band ¹H decoupling was applied during the ³¹P MRS acquisition using WALTZ-16 composite pulse (B₂ = 4 μT, estimated effective bandwidth 100 Hz) with the center frequency varied stepwise in 25 Hz over the range of −250 - 125 Hz from the water signal (in 15 increments).

³¹P MRS procedures

The time-domain FID signals were post-processed by zero-filling (to 8 K data points), apodization (with exponential and Gaussian filtering), Fourier transformation, and phasing (zero- and first-order), using the scanner software (SpectroView, Philips Healthcare). To improve the spectral resolution, a Lorentz-to-Gaussian lineshape transformation routine was used, which does not alter the area under a resonance but considerably narrows the linewidth especially at the base of the peaks. The frequency-domain ³¹P spectra were analyzed using an in-house program written in Matlab (The MathWorks, Inc. Natick, MA), which is featured with baseline fitting and lineshape analysis. For baseline and the residual α-ATP lineshape fitting, a combination of Matlab spline and pchip functions was used. For model-based lineshape analysis of the NAD(H) and UDP(G) signals, a Voigt lineshape (a combination of Lorentz and Gaussian) was used. To de-convolute NAD(H), it was assumed that the ³¹P signals of NADH and NAD⁺ are a singlet and AB quartet, respectively, as described by Lu et al (19,20), while the linewidths of NADH and NAD⁺ were allowed to vary. To deconvolute UDP(G), each of the four components, UDP-Gal, UDP-Glc, UDP-GalNAc, and UDP-GlcNAc, was treated as two separated doublets (weak AB pattern). For comparison, in a separate analysis, the UDP(G) multiplet was fitted as a single “pseudo” doublet rather than four individual doublets. The ³¹P spectra were also fitted using the more conventional approach by including the signals of α-ATP, NAD(H), UDP(G) where the α-ATP signal was treated as a doublet reflecting J-coupling to the β-ATP resonance. When comparing the IR and conventional fitting approaches, the integral of β-ATP signal served as an internal reference at 2.8 mM for quantification of the NAD(H) and UDP(G) concentrations.

³¹P MRS inversion-recovery parameters

To determine the best IR parameters for resolving the NAD(H) resonance from the α-ATP signal, the time-dependent Z-magnetization (M_z) of NAD(H) and α-, β- and γ-ATP resonances were simulated using a constant TR of 1 s, a 90° readout pulse, an inversion fraction of 60% and 70% for α-ATP and NAD, and intrinsic T₁ of 2.07, 0.95, 0.68, 0.98 for NAD(H) and α-, β- and γ-ATP, respectively. Intramolecular NOE effects within ATP were taken into account for α- ↔ β-ATP and β- ↔ γ-ATP pairs with a rate constant σ −0.20 s⁻¹ (17). A ³¹P NMR spectrum of an authentic sample of UDP-Glc (pH 7) provided an estimate of ²J_PP = 20.5 ppm and Δδ = 1.62 ppm for the two coupled ³¹P resonances. The linewidth of the resulting simulated UDP-Glc spectrum was adjusted to match the observed UDP(G) signal at −9.8 ppm in the human brain.

Statistical Analysis

All data are reported as mean ± standard deviation (SD) as analyzed using Matlab. Paired two-tailed t-tests were performed to compare the means of redox ratio between the IR and conventional fitting approaches, with statistically significant difference determined by p < 0.05.

Results

Editing of the NAD(H) signal

To optimize the IR delay time (t) for NAD(H)-editing, we simulated the time dependence of Z-magnetization (Mz) of the NAD(H) and α-ATP spins after band-inversion at a constant TR of 1.0 s. As illustrated in Figure 2, the NAD(H) magnetization (T₁ = 2.07 s) recovered more slowly than the α-ATP magnetization (T₁ = 0.95 s) after band-inversion. The NAD(H) signal was nulled at ~ 0.37 s while α-ATP was nulled at 0.28 s. For practical reasons (see discussion), we chose to null the smaller NAD(H) resonance rather than the larger α-ATP resonance. When the NAD(H) signal was nulled at 0.37 s, the α-ATP signal had recovered to 22% of its initial intensity before inversion (blue trace, Figure 2C). Note that this narrow-band inversion had no impact on γ-ATP and only minimal impact on β-ATP (~5%, magenta trace, Figure 2C).

In vivo editing of NAD(H)

Figure 3 compares two ³¹P spectra acquired from the human brain at TR = 1 s with and without inversion. Spectral subtraction of these two images, reference (3A) - inversion (3B), results in 100% of the NAD(H) signal, ~80% of the α-ATP signal and a flattened baseline (Figure 3C). This results in improved resolution of the NAD(H) and α-ATP resonances but increased baseline noise. To further improve the resolution without increasing the noise level, we fit the α-ATP resonance in the inversion spectrum (3B) to obtain a noise-free α-ATP signal. This signal was then amplified and subtracted from the reference spectrum (3A) to achieve maximal separation between the NAD(H) signal and the remaining α-ATP signal. This resulted in a flat baseline around the NAD(H) resonance and no increase in noise.

Figure 3.

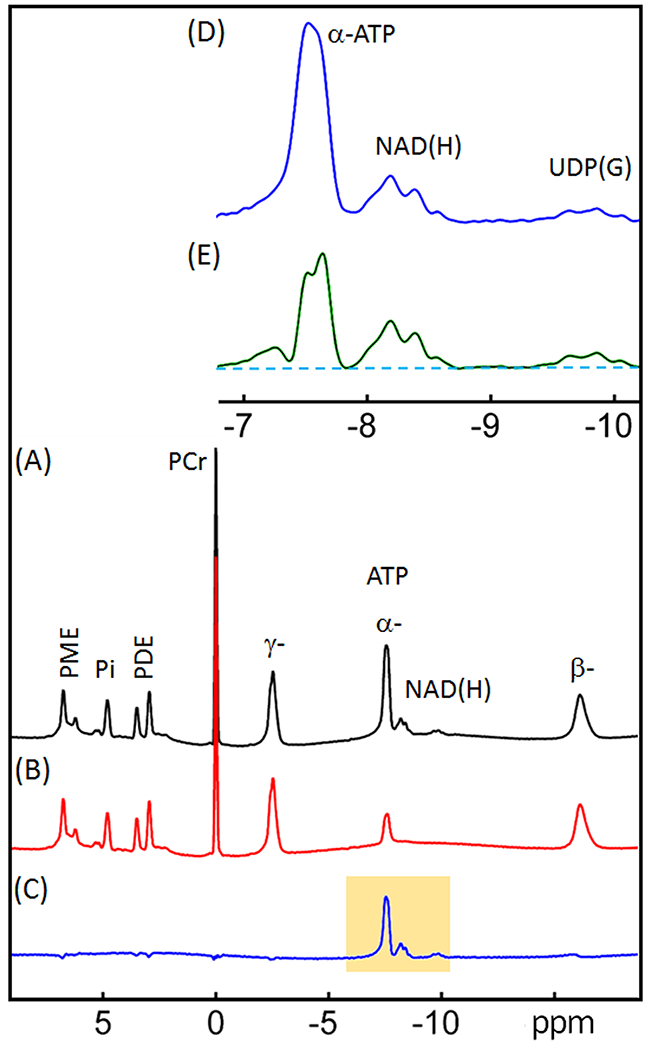
³¹P spectra of human brain acquired with (A) a simple pulse-acquire sequence (“reference spectrum”), and (B) an inversion-recovery sequence (“inversion spectrum” with t_null = 0.37 s). (C) difference spectrum obtained by subtracting the inversion spectrum from the reference spectrum ((C) = (A) - (B)). (D) Enlarged region as highlighted in (C). (E) same as D except a fitted α-ATP and baseline spectrum with α-ATP scaled up to near full intensity prior was used for subtraction rather than B. All data were acquired with constant TR = 1.0 s. Abbreviations: ATP, adenosine triphosphate; NAD(H), nicotinamide adenine dinucleotide; PCr, phosphocreatine; PDE, phosphodiesters; PME, phosphomonoesters; and PI, inorganic phosphate; UDP(G), a combination of UDP-Gal, UDP-Glc, UDP-GalNAc, and UDP-GlcNAc.

Revisiting the UDP-Glc Assignment

The presence of a UDP(G) signal affects the deconvolution of NAD(H) signal. Previously, it was assumed that UDP-glucose is the only nucleotide sugar present in brain and solely contributes to the appearance of the ³¹P signal at −9.8 ppm. This assumption was based on the hypothesis that the −9.8 ppm signal would be a doublet, which is J-coupled to a second doublet at −8.2 ppm hidden by the larger NAD(H) signal. The high resolution spectrum in Figure 4A, however, clearly reveals a “quartet-like” pattern for the signal at −9.8 ppm. This signal also has a large chemical span comparable to that observed for the NAD(H) multiplet at −8.2 ppm, which is much larger than one would expect for a doublet from a single UDP-Glc species (phantom simulation spectrum, Figure 4B). Although the −9.8 ppm signal can appear as a broad doublet when using a large line-broadening factor during post-processing, such a broadened doublet still differs significantly from a true UDP-Glc doublet, in terms of chemical shift span, splitting, and relative peak magnitudes (Figure 4B).

Figure 4.

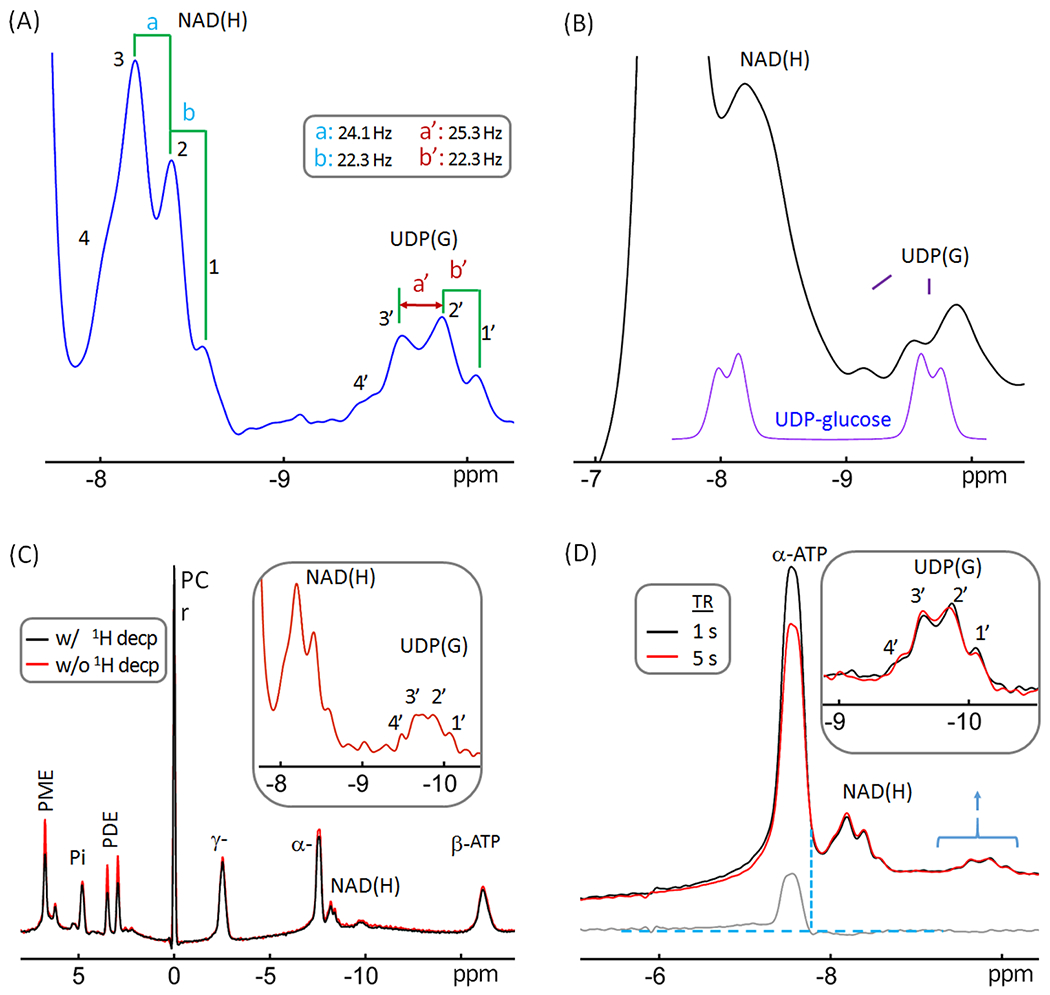
Reexamination of the resonance pattern observed in the −9.8 ppm resonance previously assigned exclusively to UDP-glucose. (A) A regional brain ³¹P spectrum showing the splitting features of resonance signals at −8.2 pm and −9.8 ppm. Note that the resonance pattern of the −9.8 ppm signal is not a simple doublet, suggesting the presence of additional UDP(G) species beside UDP-glucose. (B) (Bottom purple trace) UDP-glucose ³¹P signals at 7T simulated with aqueous solution NMR data (Δδ = 1.6 ppm and ²J_PP = 20.5 Hz) acquired at 202.5 MHz. (Top black trace) A brain ³¹P MR spectrum post-processed with a line-broadening factor of 25 Hz. Note the difference in span, splitting, and relative peak magnitude of the upfield doublet between the simulated and in vivo data. (C) Brain ³¹P MR spectra acquired at TR 5 s with (red trace) and without (black trace) wideband ¹H-decoupling, showing that the large splitting of the upfield signal at −9.8 ppm does not reflect weak ¹H-³¹P coupling. (D) Regional brain ³¹P spectra acquired at TR = 1 s (black trace) and 5 s (red trace), scaled to the signal at −9.8 ppm to facilitate comparison of resonance patterns. The bottom trace (gray) shows the spectral difference. Note the similarity in linewidth and relative intensity between the NAD(H) signal and the upfield signal at −9.8 ppm. Abbreviations: ATP, adenosine triphosphate; NAD(H), nicotinamide adenine dinucleotide; PCr, phosphocreatine; PDE, phosphodiesters; PME, phosphomonoesters; and PI, inorganic phosphate; UDP(G), a combination of UDP-Gal, UDP-Glc, UDP-GalNAc, and UDP-GlcNAc.

The splitting in the −9.8 ppm signal was 22 – 25 Hz (Figure 4A), showing that this is not from a typical ³J_H-C-O-P coupling (1 - 9 Hz). Indeed, broad band ¹H decoupling failed to collapse the additional splitting into a simple doublet (Figure 4C), despite that it substantially increased the signal intensity of several metabolites in the down field region such as PME and PDE (by ~ 25 – 50%, red versus black trace, Figure 4C), which confirms the effectiveness of the ¹H decoupling. Together, this suggests that more than one UDP(G) components contribute to the ³¹P signal at −9.8 ppm.

Given the fact that the linewidth of the −9.8 ppm signal is similar to that observed for NAD(H) (Figure 4A), it is unlikely that the −9.8 ppm signal reflects a less-mobile cellular di-phosphate species. Moreover, the signals at −9.8 ppm and −8.2 ppm are J-coupled (14), and both are insensitive to TR variation (TR = 1 s versus 5 s), in contrast to the α-ATP signal which does change due to a much shorter T₁ (Figure 4D). Taken together, these spectral features support the presence of multiple UDP(G)-like chemical species. With reference to the documented ³¹P NMR data on tissue extracts and relevant HPLC results in literature (21–29), we tentatively assign these different chemical species, collectively referred to as UDP(G) to include UDP-Gal, UDP-Glc, UDP-GalNAc, and UDP-GlcNAc, listed in the order of their chemical shifts.

UDP(G) and NAD(H) Signal Deconvolution

Following the spectral editing, we performed lineshape fitting on NAD(H) and UDP(G) to de-convolute the NAD(H) signal into NADH (a singlet) and NAD⁺ (an AB-quartet), and the UDP(G) signals into four components including UDP-Gal, UDP-Glc, UDP-GalNAc, and UDP-GlcNAc (each as two separate doublets), as shown in Figure 5A. The resultant best-fit chemical shifts and metabolite concentrations are summarized in Table 1 and 2, respectively. The ²J_PP coupling constants were 20.14 Hz for NAD⁺, 20.3 Hz for UDP-Gal and UDP-Glc, and 20.5 Hz for UDP-GalNAc and UDP-GlcNAc.

Figure 5.

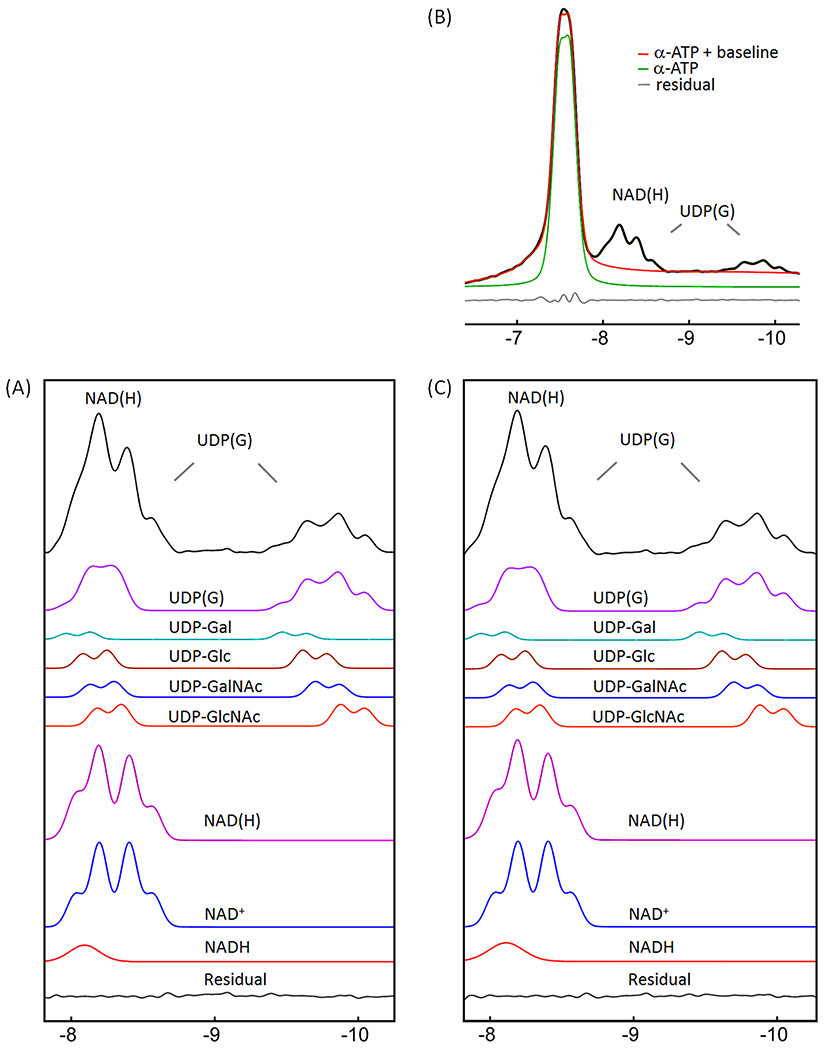
Lineshape analysis for deconvoluting NAD(H) into NADH and NAD⁺, and UDP(G) into UDP-Gal, UDP-Glc, UDP-GalNAc, and UDP-GlcNAc components. (A) IR-based approach. (B and C) Conventional approach with inclusion of α-ATP in the fitting. The black trace in (A) is the inversion-edited spectrum from Figure 3E. The black trace in (B) is the reference spectrum from Figure 3A. The red trace in (B) is the fitted α-ATP with baseline to the reference spectrum. The black trace in (C) is the reference spectrum subtracted by the fitted α-ATP with baseline (= black trace – red trace, in (B)). Abbreviations: ATP, adenosine triphosphate; NAD(H), nicotinamide adenine dinucleotide, a combination of NADH and NAD⁺; UDP(G), a combination of UDP-Gal, UDP-Glc, UDP-GalNAc, and UDP-GlcNAc.

Table 1.

³¹P Chemical shifts (ppm) of UDP(G) and NAD(H) components measured in human brain at 7T.

	UDP(G) multi-doublet		UDP(G) (pseudo-)doublet
	IR-based	Conventional	IR-based	Conventional	Perlmana (24)	de Graaf(14)	Kim(9)
NADH	−8.092	−8.111	−8.132	−8.132		−8.1	−8.13
NAD+	−8.132	−8.131	−8.141	−8.140		−8.15	−8.15
	−8.467	−8.467	−8.453	−8.452		−8.45	−8.47
UDP-Gal	−8.047	−8.022
	−9.554	−9.543	UDP(G)		−9.490
UDP-Glc	−8.165	−8.162	−8.200	−8.196		−8.23	−8.23
	−9.697	−9.699	−9.794	−9.802	−9.688	−9.83	−9.83
UDP-GalNAc	−8.215	8.218
	−9.785	−9.782			−9.769
UDP-GlcNAc	−8.265	−8.265
	−9.961	−9.963			−9.961

^aFrom rat extract at pH 8.2, corrected for difference in reference by setting the chemical shift of hexose phosphate of UDP-GlcNAc to −9.961 ppm. Chemical shifts obtained from the summed spectrum.

Table 2.

Comparison of brain redox ratio ([NAD+]/[NADH]) and concentrations of NAD(H) and UDP(G) components evaluated using IR-based versus conventional fitting approaches (n = 7)^a

	UDP(G) multi-doublet			UDP(G) (pseudo-)doublet
	IR-based	Conventional	p-value	IR-based	Conventional	p-value	Xinb (15)	de Graaf c (14)	Kimd (9)
NAD+/NADH	7.5±1.8 [7.6]	6.0±2.1 [5.9]	<0.05	5.3±0.6 [5.2]	4.7 ± 0.5 [4.8]	<0.05	5.6±1.0	4.2±0.9	5.3
NAD(H)	0.362±0.030	0.375±0.031	0.33	0.358±0.045	0.374±0.051	0.32	0.276	0.387	0.269
UDP(G)	0.332±0.031	0.335±0.038	0.51	0.323±0.033	0.324±0.029	0.96	0.180±0.010	0.339±0.099	0.074
NAD+	0.318±0.031	0.317±0.031	0.90	0.301±0.039	0.311±0.036	0.49	0.233±0.005	0.312±0.065	0.226
NADH	0.044±0.007	0.058±0.017	<0.05	0.057±0.008	0.066±0.003	0.06	0.043±0.007	0.075±0.016	0.043
UDP-Gal	0.048±0.011	0.047±0.011	0.63
UDP-Glc	0.089±0.015	0.091±0.019	0.33
UDP-GalNAc	0.079±0.006	0.080±0.005	0.50
UDP-GlcNAc	0.116±0.013	0.117±0.014	0.44

^aThe metabolite concentrations are reported as the mean ±SD relative to β-ATP at 2.8 mM without T₁ corrections; the NAD⁺/NADH ratios in square brackets were from the fittings to the summed spectrum (n = 7).

^a,b,cData acquired from brain posterior at 7T with TR = 1 s,^a 3 s,^b and 5 s.^c .

^dData acquired from the brain frontal lobe at 4 T; TR unreported.

The fitting of the mixed signal (NAD(H) + UDP(G)) at −8.2 ppm was sensitive to the linewidth of NADH relative to NAD⁺. The best fit to the summed spectrum yielded a redox ratio (NAD⁺/NADH) of 7.6 when the linewidth was allowed to vary in the fitting. In this case, the NADH linewidth was 1.7X that of the NAD⁺ linewidth (Figure 5A). When the two linewidths were fixed to an equal value, the calculated redox ratio increased to 12.4 and the fitted residual increased 3-fold. When the UDP(G) multiplet was fitted as a pseudo-doublet ((²J_α-β-UDP(G) = 20.5 Hz) instead of multiple doublets, the best-fit gave a reduced redox ratio of 5.4 and a linewidth ratio of 1.3 (Figure 6A). In comparison, when only the two inner lines of the UDP(G) multiplet were fitted (pseudo-doublet at peak splitting 25.5 Hz), the redox ratio was 10.1 (Figure 6C). The fitting residual increased substantially when UDP(G) was fitted as a pseudo-doublet compared to when it was fitted as multiple doublets (Figure 6 versus 5). Without including UDP(G), the fit of NAD(H) signal at −8.2 ppm yielded a smaller NAD+/NADH ratio of 4.1 at equal linewidths between NAD⁺ and NADH. The redox ratio was further reduced to 3.2 with worse residuals when the linewidth ratio between NADH and NAD⁺ was fixed at 1.7 (data not shown). For the group of seven subjects studied, the measured NAD⁺/NADH averaged 7.5 ± 1.8 when UDP(G) was fitted as multiple doublets and 5.3 ± 0.6 when UDP(G) was fitted as a pseudo-doublet (Table 2).

Figure 6.

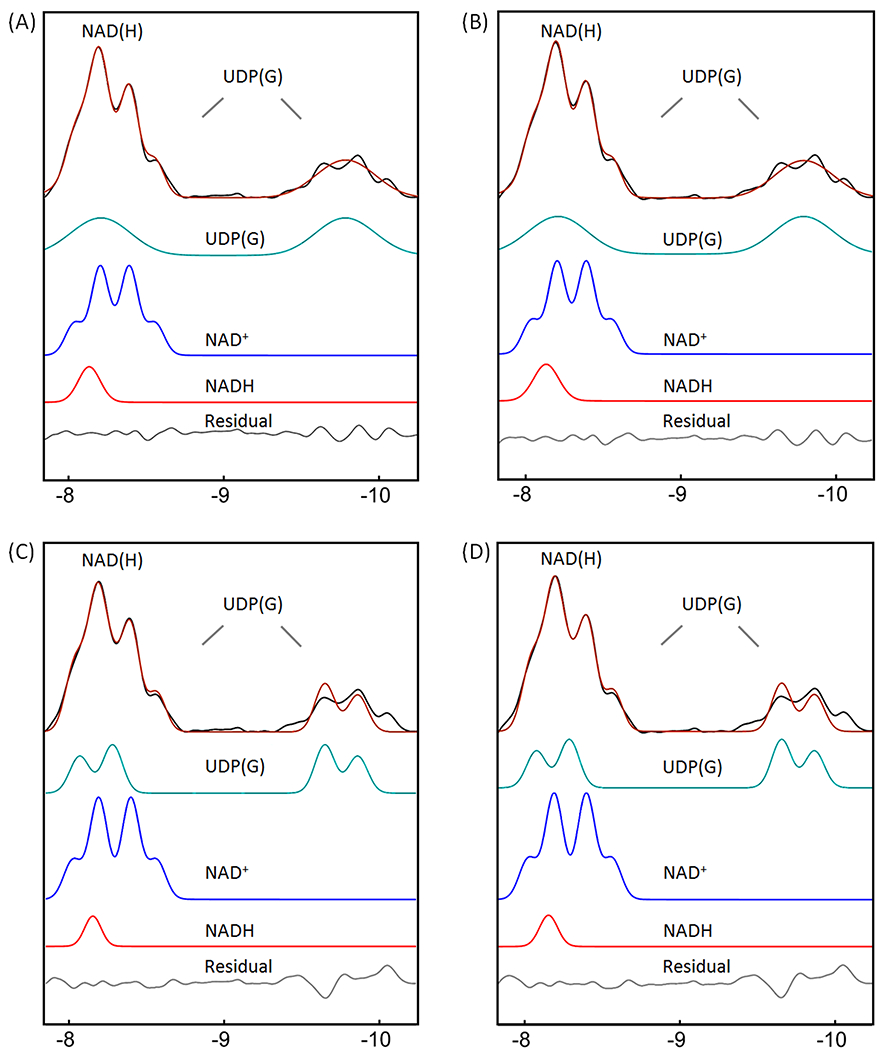
Lineshape analysis for deconvoluting NAD(H) into NADH and NAD⁺, with UDP(G) fitted as a pseudo-doublet. (A and C) IR-based approach. (B and D) Conventional approach with inclusion of α-ATP in the fitting. The black traces in (A) and (C) represent the same inversion-edited spectrum from Figure 3E. The black traces in (B) and (D) are obtained from the reference spectrum subtracted by the fitted α-ATP with baseline. (A and B) Pseudo-doublet fitting to the entire UDP(G) multiplet. (C and D) Pseudo-doublet fitting to the two central peaks of UDP(G). Abbreviations: NAD(H), nicotinamide adenine dinucleotide (a combination of the oxidized form NAD⁺ and reduced form NADH); UDP(G), a combination of UDP-Gal, UDP-Glc, UDP-GalNAc, and UDP-GlcNAc.

Conventional approach

For comparison, we also analyzed the summed spectrum using a conventional approach with inclusion of α-ATP in the lineshape fitting. The α-ATP signal was fitted as a doublet, J-coupled to the β-ATP resonance (²J_α-β-ATP = 16.3 Hz, δ = −7.553 ppm). The best fit to the summed spectrum by the conventional approach yielded a lower NAD⁺/NADH ratio of 5.9, with a higher linewidth ratio of 2.1 between NADH and NAD⁺ (Figure 5C versus 5A), and a slightly increased fitting residual (0.022 vs 0.019) in the NAD(H) downfield region (−7.81 – −8.69 ppm). When the linewidth ratio between NADH and NAD⁺ was fixed at 1.7, the resultant NAD⁺/NADH ratio increased to 7.1, similar to the result with the IR-based fitting (7.6). When the UDP(G) multiplet was fitted as a pseudo-doublet, the resulting redox ratio was 4.8 and the linewidth of NAD(H) was 1.3 greater than the NAD⁺ linewidth (Figure 6B). In comparison, when only the two central peaks of UDP(G) multiplet was fitted (pseudo-doublet, peak splitting 25.5 Hz), the redox ratio was 9.3, with worse residual (Figure 6D vs 6B). These trends are similar to those observed with the IR-based approach (Figure 6C vs 6A).

For the group of seven subjects studied, the measured NAD⁺/NADH averaged 6.0 ± 2.1 when UDP(G) fitted as multiple doublets and 4.7 ± 0.6 when UDP(G) was fitted as a pseudo-doublet (Table 2). This is also consistent with the trend found with the IR-based approach (Table 2), and the results are linearly correlated between these two approaches (Figure 7A).

Figure 7.

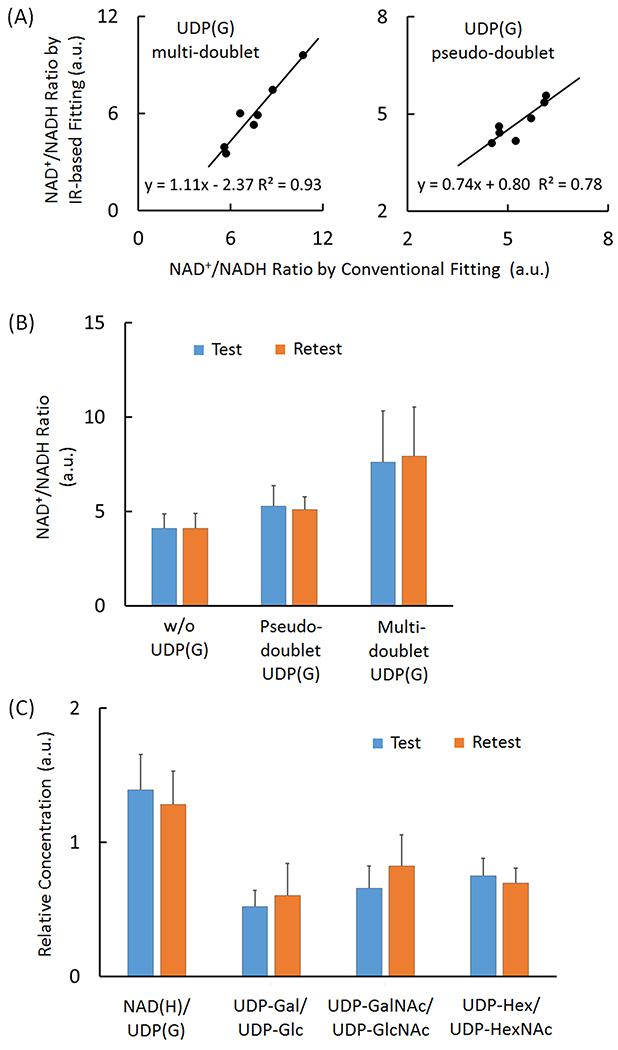
(A) Linear correlations between in the measured redox ratios (NAD⁺/NADH) as measured using the IR versus conventional lineshape fitting methods, with UDP(G) fitted as four doublets (left panel) and a single pseudo-doublet (right panel). (B) Comparison of the measured NAD⁺/NADH ratio between different fitting approaches in test and retest separated by two-weeks. (C) Comparison of the relative concentration of various UDP(G) components in test and retest after two-week. The data were from the IR-based fitting analysis with UDP(G) fitted by multi-doublet model. Abbreviations: ATP, adenosine triphosphate; NAD(H), nicotinamide adenine dinucleotide, a combination of NADH and NAD⁺; UDP(G), a combination of UDP-Gal, UDP-Glc, UDP-GalNAc, and UDP-GlcNAc.

In terms of the measured UDP(G) concentrations, only very small differences were seen between the IR-based and the corresponding conventional fitting approaches (Table 2).

Reproducibility Test

The reproducibility in measuring the NAD⁺/NADH ratio was tested by fitting inversion-edited spectra collected in a cohort of seven subjects on two visits separated by 2 weeks (Figure 8A). Without inclusion of UDP(G), the fitting yielded an average intra-subject variance of 5.8 ± 4.8 % (standard deviation / average), without significant gender difference (female: 5.9 ± 4.1 % versus male 5.7 ± 6.5 %). With inclusion of all four UDP(G) species in the fitting, the measured NAD⁺/NADH ratio averaged 7.6 ± 2.7 for the test and 7.9 ± 2.6 for the retest. With the pseudo-doublet approximation, the averaged NAD⁺/NADH ratio was 5.3 ± 1.0 for the test and 5.1 ± 0.6 for the retest (Figure 7B).

Good reproducible results were measured for four different metabolite ratios, NAD(H)/UDP(G), UDP-Gal/UDP-Glc, UDP-GalNAc/UDP-GlcNAc, and UDP-Hex/UDP-HexNAc, as shown in Figure 7C.

Discussion

New findings

We have demonstrated using IR-based spectral editing that the NAD(H) signal at −8.2 ppm can be largely resolved from the residual α-ATP resonance (the subtraction spectrum, Figure 3). We also provided ³¹P MRS evidence for the presence of multiple nucleotide sugars in human brain (Figures 4 and 5) and tentatively assigned these to UDP-Gal, UDP-Glc, UDP-GalNAc, and UDP-GlcNAc (Figure 1B). Furthermore, we have shown that the measured NAD⁺/NADH ratio is highly dependent upon whether the combined UDP(G) resonance at −9.8 ppm is fitted as a single pseudo-doublet or as four separate doublets each reflecting a single UDP-sugar species (Figures 5, 6 and 7). To the best of our knowledge, this is the first report of simultaneous measurement of multiple nucleotide sugars (including both hexoses and hexoamines) in the human brain in vivo by ³¹P MRS. Thus, this ³¹P MRS study represents an extension of previously reported brain redox measurements initiated by Lu (17,18) and extended by de Graaf (14).

Coexistence of multiple UDP(G) species

The four nucleotide sugars identified as the contributors to the UDP(G) signal consist of two pairs of interconvertible epimers. Of these, the hexose pair, UDP-Gal and UDP-Glc, are generated in the LP pathway while the hexosamine pair, UDP-GalNAc and UDP-GlcNAc, are formed in the HBP pathway (Figure 1B). One would expect that UDP-Glc should coexist with UDP-Gal in brain, given that conversion of UDP-Gal ↔ UDP-Glc is catalyzed by galactose-1-phosphate uridyltransferase. A defect in this enzyme is known to cause galactosemia, a metabolic disorder in galactose processing that is associated with high risk of cataracts, delayed growth, and intellectual disability (29,30). Indeed, co-existence of UDP-Glc and UDP-Gal in cells and tissue extracts has been well-documented in the literature (21–28).

Regarding the relative content, we found that UDP-Gal/UDP-Glc ratio was approximately 0.5 by ³¹P MRS (Figure 7B) as compared to ~0.33 measured by HPLC in brain tissue extracts (21, 22). Similarly, the UDP-GalNAc/UDP-GlcNAc ratio was ~0.7 by ³¹P MRS (Figure 7B) compared to ~ 0.5 previously found in brain tissue by HPLC (21,22). In terms of the total tissue content, the UDP-Hex/UDP-HexNAc ratio of 0.65 by in vivo ³¹P MRS also agrees well with previous results measured in brain tissue extracts by HPLC (21,22).

In addition to the two pairs of interconvertible UDP(G) epimers, UDP-glucuronic acid (UDP-GlcA) is another potential contributor to the nucleotide sugar signal at −9.8 ppm (24). However, an inclusion of this nucleotide sugar as a 5^th species failed to improve the lineshape fitting (data not shown), consistent with a report of negligibly low UDP-GlcA concentrations in brain extracts (21).

Spectral Evidence of Multiple UDP(G) Species

The presence of multiple UDP(G) was evidenced by a “quartet-like” resonance pattern at −9.8 ppm (Figure 4). This spectral pattern is distinctly different from that expected if UDP-Glc was the sole contributor to this signal (14). Such a complex resonance pattern cannot be reasonably explained by ¹H-³¹P coupling, given the large splitting (22 - 25 Hz, rather than 1 - 9 Hz, Figure 4A and 4C), nor can it be realistically attributed to a single species in multiple cellular compartments, or to a single species bound to macromolecules (Figure 4D). It should be noted that the −9.8 ppm resonance could be easily described as “doublet-like” if additional line broadening is added to enhance SNR during post-processing. However, the appearance of this “pseudo-doublet” differs from that collected on an authentic sample of UDP-glucose in terms of chemical shift, apparent ³¹P-³¹P coupling and relative peak magnitude (Figure 4B).

Impact of the UDP(G) signals on de-convolution of NAD(H)

Our data showed that inclusion of all four UDP(G) species led to a nearly 90% increase in the measured NAD⁺/NADH ratio (4.1 versus 7.6, Figure 7B). A similar trend was also found previously by de Graff et al (14), who reported that the NAD+/NADH ratio was 2.4 without inclusion of UDP(G), and 4.2 with inclusion of UDP-glucose as a single contributor. This dramatic sensitivity in measuring the NAD⁺/NADH ratio with/without inclusion of UDP(G) is due to the fact that the UDP(G) signal at −8.2 ppm is more populated in the downfield part of NAD⁺ quartet where the resonance of NAD(H) signal is centered (Figure 5).

Regarding the structural assignment, the signal at −9.8 ppm is assigned to the phosphate group (Pβ) directly attached to the sugar residue in each UDP(G) species while the signal at −8.2 ppm is assigned to the phosphate (Pα) directly bonded to the uridine residue common to all four UDP-sugars. The chemical shifts of Pα and Pβ do differ among each UDP(G) species although the difference chemical shift is smaller for Pα than for Pβ. In both cases, their chemical shifts follow the same order UDP-Gal > UDP-Glc > UDP-GalNAc > UDP-GlcNAc. Several previous reports support this finding (24–28) despite small differences in reported chemical shifts due to differences in pH, buffer media, and referencing. For example, Perlman et al (24) identified multiple nucleotide sugars in liver extracts using 2D NMR and reported a Δδ (Pβ) value of 0.2 ppm between UDP-Gal and UDPGlc, 0.1 ppm between UDP-Gal and UDP-GalNAc, and 0.2 ppm between UDP-GalNAc and UDP-GlcNAc. In comparison, a smaller Δδ (Pα) of 0.1 ppm was reported between UDP-Gal and UDP-Glc, and between UDP-GalNAc and UDP-GlcNAc (24–26). These values and orders match the results found here in human brain when using the IR-based fitting (Figure 5A, Table 1). Similarly, the J-coupling constant between Pα and Pβ (20.3 Hz for UDP-Gal and UDP-Glc and 20.5 Hz for UDP-GalNAc and UDP-GlcNAc) measured here agree well with values reported by Teleman et al (28).

The presence of multiple UDP(G) components requires that each of these species is fitted as a separate doublet when deconvoluting the mixed NAD(H)-UDP(G) signal. In comparison, if one assumes a single pseudo-doublet UDP(G) signal, the fitting results in a significantly reduced NAD⁺/NADH ratio (by 20 – 30%), but it does not significantly affect the total NAD(H) and UDP(G) concentrations (Table 2). Furthermore, the pseudo-doublet approximation results in smaller inter-subject differences in the measured NAD⁺/NADH ratio, as suggested by the smaller standard deviations (24% vs 11% using the IR approach, and 35% vs 11% using conventional lineshape fitting).

Reproducibility in Measuring the NAD⁺/NADH Ratio

Despite the presence of multiple UDP(G) species in brain, consistent results were obtained between the first and second measurements of the NAD⁺/NADH ratio and other UDP(G) species (Figure 7). As a group (n = 7 subjects), with inclusion of UDP(G), the test-retest variation in NAD⁺/NADH ratio was 4% (7.6 ± 2.7 versus 7.9 ± 2.6), while the intra-subject variance in NAD⁺/NADH ratio was 19.7 ± 7.9 %. Without inclusion of UDP(G) in the fitting, the intra-subject NAD⁺/NADH variance averaged 5.8 ± 4.8 %. A smaller intra-subject NAD⁺/NADH variance of 5.8 ± 4.6 % was also found when the UDP(G) multiplet was fitting by a pseudo doublet (n = 7 subjects).

IR-based vs. Conventional Fitting Approach

As shown in Table 2, the concentration of NAD⁺ is much higher than NADH in brain so small variations in NADH levels can impact the measured redox ratio quite significantly. It was found that the measured NAD⁺/NADH ratio was consistently higher when measured using the IR method reported here compared to the ratio measured using conventional lineshape fitting methods (7.5 ± 1.8 vs 6.0 ± 2.1 for the UDP(G) multi-doublet model, and 5.3 ± 0.6 vs 4.7 ± 0.5 for the UDP(G) pseudo-doublet model). This translates to small differences in NADH concentration (44 ± 7 μM vs 58 ± 17 μM for the UDP(G) multi-doublet model, and 57 ± 8 μM vs 66 ± 3 μM for the UDP(G) pseudo-doublet model). As a group evaluated with the UDP(G) multi-doublet fitting model, the IR-based approach yielded a smaller inter-subject NAD⁺/NADH variance compared to conventional fitting (24% vs 35%), while no difference was found with the UDP(G) pseudo-doublet model (11% for both). Another difference between these two approaches was found in the fitted chemical shift of the Pα resonance of UDP-Gal (Δδ= 0.025 ppm, Table 1), which resonates near NADH and α-ATP. Otherwise, the outputs of these two fitting routines are largely identical in the remaining upfield region (< −8.4 ppm, Figure 5).

The difference in the measured NAD⁺/NADH ratio between these two fitting routines (15 – 20%) was statistically significant. The difference may be attributed to imperfect nulling of the mixed NAD(H) signal by the inversion sequence and/or imperfect fitting of α-ATP line shape by the conventional approach (given the distorted baseline and the potential interference from other unresolvable endogenous nucleotides). Despite a lack of gold standard, the results of the measured NAD⁺/NADH ratio by these two approaches are linearly correlated (Figure 7A). Note that, the IR-based approach, allowing straightforward deconvolution of NAD(H) and UDP(G), i.e. without interference from the overwhelming large α-ATP signal and from the underlying distorted baseline, does represent a technical advantage. Of course, this simplicity is at the cost of an additional scan, a common problem in all spectral editing methods.

NAD(H) Spectral Editing

The spectral simulations in Figure 2 show that separation of NAD(H) from α-ATP can be achieved by three possible ways: 1) null α-ATP at t ~ 0.25 s; 2) null NAD(H) at t ~ 0.37; or 3) reduce both α-ATP and NAD(H) signals to a level so that these two signals no longer overlap near t ~ 0.20 s. In this study, we chose option #2 because it provided the best SNR. Technically, it is also relatively easy to null a small NAD(H) signal and to correct any residuals in case of imperfect nulling.

An optimal inversion will provide the largest possible α-ATP recovery during the chosen TR. For improving inversion efficiency and robustness, we selected an inversion bandwidth that excites only the α-ATP-NAD(H)-UDP(G) region without perturbing the β- and γ-ATP resonances. This takes advantage of the known effect of NOE on post-inversion recovery of the α-ATP signal (15). Using this inversion sequence, we were able to null both NAD(H) and UDP(G) signals while allowing the α-ATP signal to recover as much as possible (Figure 3B). This residual α-ATP signal and the underlying baseline can then be fitted and scaled up to mirror the α-ATP signal in the reference spectrum. The difference spectrum then yields a clean NAD(H)/UDP(G) signal (Figure 3E) for deconvolution (Figure 5A).

This work has limitations. First, not all aspects of the new and conventional fitting approaches were fully explored and compared due to the limited scope. Second, in nulling NAD(H), we assumed that the two constituents (NAD⁺ and NADH) have the same T₁ values in human brain at 7T. This assumption is based on the structural similarity between these two molecules and supported by T₁ values measured in cat brain at higher fields (20): 1.50 s for NAD⁺ versus 1.58 s for NADH at 9.4 T, and 0.82 s for NAD⁺ versus 0.87 s for NADH at 16.4 T. In case of imperfect nulling due to minor differences in T₁, this can be corrected during post-processing during baseline fitting, since the residual signal is expected to be small. Third, although we established the method to analyze UDP(G) composition in human brain in vivo, there is a lack of validation by an independent approach. In terms of UDP(G) assignments, relative populations, and optimized chemical shifts, our findings agree well with the documented results in tissue extracts of animal models by HPLC and 2D NMR analysis. It is unrealistic to anticipate similar validation by biopsy of human brain or by in vivo 2D NMR spectroscopy due to low abundance of UDP(G). Nevertheless, we hope future studies at even higher magnetic fields will independently validate our results by offering better resolution of the separate UDP-sugar resonances. Fourth, our lineshape analysis indicates that an optimal NAD(H) lineshape fitting was achieved when the linewidth of the NADH singlet is ~70% broader than the NAD⁺ quartet. At first glance this seems counter-intuitive, but it may occur as a consequence of exchange between NADH, the less-abundant form, and NAD⁺, the more-abundant form. A second possibility is that a greater percentage of total tissue NADH is bound to enzymes and this adds to its ³¹P linewidth. Such kinetic features so far have not been fully explored by ³¹P MRS in vivo. NAD⁺ binding interactions with enzymes and the impact of this binding on NAD⁺ linewidths have been reported and discussed based on in vitro observations (ref. 14 and references cited therein).

In summary, we successfully resolved the NAD(H) signal from the otherwise interfering α-ATP resonance using IR-based spectral editing. We also presented a method to analyze multiple UDP(G) species that contribute to the nucleotide sugar ³¹P resonances at −9.8 ppm and −8.2 ppm. These species include two pairs of interconvertible epimers: UDP-galactose ↔ UDP-glucose, and UDP-N-Acetyl-galactose ↔ UDP-N-Acetyl-glucose. The capability of measuring these species and NAD⁺/NADH ratio in human brain may advance our understanding of altered redox states and sugar metabolism related to aberrant glycosylation during development of neurodegenerative diseases.