Modeling of active shimming of metallic needles for interventional MRI

Abstract

Purpose

Artifacts caused by large magnetic susceptibility differences between metallic needles and tissue are a persistent problem in many interventional MRI applications. The signal void caused by the needle can hide procedure targets and prevent accurate image‐based monitoring. In this paper, a solution to this problem is presented in the form of an active shim insert inspired from degaussing coils used in naval vessels, that is designed to correct the field disturbance (ΔB₀) caused by the needle.

Methods

The ΔB₀ induced by a 10 gauge hollow single‐beveled titanium needle at 3T is modeled in different orientations. A set of 63 orthogonal coil pairs with unique tip paths are evaluated for shimming performance, and an optimal coil pair is chosen. Shimming performance and current demands are evaluated over a range of needle orientations.

Results

Robust correction of the titanium needle induced ΔB₀ is predicted using a flat no‐loop coil combined with an orthogonal 1½ turn loop coil angled at the bevel angle for most orientations, with currents well below 1 amp per coil. Reductions in ΔB₀ standard deviations with shimming ranged from ~49% to ~10% depending on needle orientation, with performance worsening as the needle is aligned more along B₀.

Conclusion

Simulations predict that it is possible to minimize metallic probe induced ΔB₀ and signal losses using externally supplied direct current shim coil inserts in arbitrary orientations for potential benefits in many interventional MRI applications.

1. INTRODUCTION

Needle artifacts are a recognized challenge in the field of interventional MRI (iMRI). ¹ , ² , ³ , ⁴ , ⁵ The large difference in magnetic susceptibilities between metallic needles and the surrounding tissue induces significant field perturbations (ΔB₀) in the vicinity of the needle and causes a range of artifacts, including intravoxel signal loss, distortions, and signal pileups due to voxel mismapping. ¹ , ² , ³ , ⁴ , ⁵ The severity of the artifacts scale linearly with field strength, which is  one reason why most iMRI procedures remain restricted to 3 Tesla (3T) and lower field strengths.

Needle artifacts hinder a wide range of diagnostic, therapeutic, and basic research applications in iMRI. In MR‐guided biopsies, artifacts obscure target lesions, vital anatomies such as nerves and blood vessels, and the actual device position. In core needle breast biopsy for example, the void caused by a 14 gauge (2.11 mm outside diameter [OD]) titanium needle was reported to be 4 mm at 1.5T and almost 9.5 mm at 3T. ⁶ , ⁷ , ⁸ , ⁹ , ¹⁰ Similar needle artifacts have been discussed in MR‐guided prostate, ¹¹ , ¹² head and neck, ¹³ musculoskeletal, ¹⁴ spine, ¹⁵ and liver biopsies. ¹⁶ Susceptibility artifacts also create difficulties in MR‐guided brachytherapy ¹⁷ , ¹⁸ where both the metallic stylet and the radioactive pellet generate signal voids that make placement under MR guidance inaccurate. ¹⁹ Other MR‐guided therapeutic applications, such as radiofrequency, ²⁰ microwave, ²¹ and cryo‐ablation, ²² , ²³ , ²⁴ also suffer from susceptibility artifacts that are especially damaging close to the probe where it is most important to monitor temperature and tissue damage. Often, radiologists use more than one probe to treat targets, in which case susceptibility artifacts create significant visualization challenges. Furthermore, quantitative MR phase‐based thermometry is often made impossible by the signal void or inaccurate due to high phase noise. ²⁵

Needle artifacts fall under the larger category of metal artifacts in MRI and therefore, metal artifact reduction techniques, such as MAVRIC/MAVRIC‐SL, ²⁶ , ²⁷ SEMAC, ²⁸ VAT³, or imaging parameter adjustments (MARS), ³ , ²⁹ , ³⁰ , ³¹ could be in principle applied to partially tackle this issue. However, these sequences, while well suited for anatomical imaging around implants, are primarily based on 2D/3D spin echo sequences and, therefore, are not ideal for iMRI applications where high speed of imaging is important for dynamic 3D tracking, targeting of moving organs, or continuous quantitative imaging (e.g., in phase contrast thermometry). Therefore, a compensation method that tackles the issue at the source, that is, the needle, could be significant in (1) enabling imaging with a variety of sequences, (2) imaging at a high frame rate, and (3) pushing these applications to higher field scanners.

While needle artifacts have been characterized in previous studies, ⁴ , ³² , ³³ there have been very few presented needle‐based solutions that satisfy the speed and sequence requirements of iMRI. Glass and plastic needles have been presented that have lesser artifacts, but they are mechanically weak and prone to bending and breaking. ⁵ Another proposed design was to coat paramagnetic titanium with diamagnetic bismuth to produce a composite material needle. ³⁴ However, this is still a problem open to new solutions.

The goal of this work is to introduce a potential solution to this problem in the form of a multicoil active shim insert that is designed to fit inside the metallic needle and produce a field that corrects the ΔB₀ induced by the needle outside of it. Field inhomogeneity and signal simulations are presented that demonstrate the correction of the ΔB₀ and reduction of the signal void produced by a 10 gauge titanium needle at 3T.

2. METHODS

The concept and design of active shims for metallic needles is inspired from similar coils used in naval defense ³⁵ , ³⁶ , ³⁷ , ³⁸ , ³⁹ as well as recent work in local shim coils for brain shimming in MRI. ⁴⁰ , ⁴¹ , ⁴² In ships and submarines, special tri‐directional current carrying cables called “degaussing coils” are built into the vessel’s hull to compensate the magnetic fields induced by the hull’s interaction with the earth’s magnetic field. ³⁵ , ³⁶ , ³⁷ , ³⁸ , ³⁹ In iMRI, the needle is like the metallic vessel and the scanner’s B₀ field is the earth’s uniform magnetic field. The ΔB₀ and the image artifacts produced by the needle can, therefore, be potentially corrected by current carrying coils built around or placed within the needle. In the following sections, a basic framework and design of such shim coils is presented based on simulations of field shimming. To ease the design process, two different coordinate frames are defined: (1) the needle coordinate frame (X_N, Y_N, Z_N), with X_N defined along the cylindrical needle’s length, Y_N and Z_N along the needle’s radial axes; and (2) the MRI scanner’s coordinate frame, (X_M, Y_M, Z_M), with X_M as up‐down, Y_M as left‐right, and Z_M as in and out of the bore. Rotations about the X_M, Y_M, and Z_M axes are defined in the left‐handed system and denoted by three values in degrees, respectively (Figure 1B,C).

FIGURE 1.

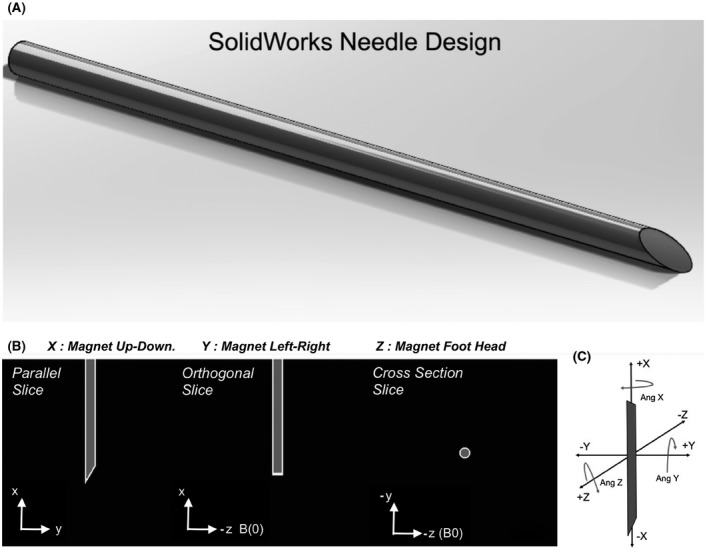
Needle design and susceptibility distribution. A, Solidworks rendering of the single 30 degree beveled closed tip 10 Gauge needle. B, Midline views in three planes of the needle’s distal 30 mm tip’s susceptibility distribution. Black voxels represent water outside the needle (χ = −9.05 × 10⁻⁶), gray voxels represent air (χ = 0.37 × 10⁻⁶) inside the needle and the white voxels represent titanium (χ = 182 × 10⁻⁶). C, Definition of the magnet axes and positive angle rotations. The needle is shown in the (0, 0, 0) degree orientation in the scanner bore.

2.1. Needle design and field modeling

The ΔB₀ around a 10 gauge (3.4/2.7 mm outside/inside diameter ) titanium needle (volume susceptibility: χ = 182 × 10⁻⁶) ⁴³ with air inside (χ = 0.37 × 10⁻⁶) ⁴³ placed in a surrounding medium of Water (χ = −9.05 × 10⁻⁶) ⁴³ was modeled at 3T. A 100 mm long hollow cylindrical needle was designed in SolidWorks (Dassault Systemes, MA, USA) with a 30° single‐sided closed bevel at the tip. The design was exported as an .STL file into MATLAB (MathWorks, MA, USA) and voxelized to a 0.1 mm³ isotropic resolution 3D grid of points (Figure 1). ⁴⁴ From this larger grid, a sub‐grid of 40 × 40 × 40 mm³ (400³ voxels) was used for modeling the field from the distal 3 cm of the needle. Prior to field modeling, the needle volume was transformed from the needle frame to the magnet frame, so that all field modeling could be performed in the magnet frame. Without any rotations applied (0, 0, 0 degree orientation), the needle was oriented vertically with the beveled tip pointing down along ‐X_M and the longer bevel edge along the magnet’s ‐Y_M axis (Figure 1B,C). The voxels were assigned susceptibility values χ(r) based on the material distribution in space.

The field distortion induced by the needle was modeled using Fourier‐analysis field modeling. ⁴⁵ , ⁴⁶ , ⁴⁷ Only the z component of the field was considered for further analysis. To avoid wraparound field errors originating from Fourier transformation, χ(r) was zeropadded to a grid of 600³ voxels before field modeling and cropped back to 400³ voxels subsequently. To design an optimal shim coil pattern that would provide reasonably robust shimming across needle orientations, the needle field was initially modeled at four orientations which represented the limits of possible needle angles in one octant: two with the needle orientated perpendicular to B₀ along the magnet’s up‐down (X_M) axis at (0, 0, 0) and (90, 0, 0) degrees, and two with needle oriented parallel to B₀ at (0, −90, 0) and (90, −90, 0) degrees.

2.2. Shim coil design

2.2.1. Field computation

In a naval vessel, multiple independently powered degaussing coils are distributed along the vessel’s hull for maximum field control in all directions. In contrast, the only practical route for shim power supply in an interventional device is through the proximal end of the device. Therefore, it is most practical to design the shim structure as a set of two or three externally supplied coils (referred to here as “shim coil set”) that run the length of the needle and best compensate the needle’s induced field at any orientation.

All simulations of shim coil fields were performed in Matlab using an implementation of Biot‐Savart’s law. ⁴⁸ Coil paths were also defined in Matlab, matching the 10 gauge needle dimensions, so that the coils fit inside the needle. A wire thickness of 0.4 mm (26 Gauge), 400³ voxel target grid of 0.1 mm resolution, elemental wire length of 0.4 mm and a unit current of 1 amp were assumed for the field calculations. For all field calculations, coil geometry was first defined in the needle frame and then transformed into the scanner’s coordinate frame to match the needle orientation.

2.2.2. Shim coil geometry

Two single‐turn shim coils were first defined in the needle’s coordinate system with normals along Z_N (CN0) and Y_N (CN90) as shown in Figure 2A. The rationale for this geometry can be understood from direct observation of the needle’s induced B _z field in the (0, 0, 0) degree orientation (Figure 3A). This field has a bipolar structure along the body of the needle that is most apparent in the cross‐section slice. In comparison, Figure 3C shows the 1 amp field produced by a flat no‐loop CN0 coil shown in Figure 2B (top row, green box). The needle and the coil generated field patterns match closely, and it is clear that a coil path as shown can potentially compensate the induced field along the needle’s body. However, as the needle and the coil rotate in space, for example about the X_M axis in Figure 3, the field produced by the coil can no longer compensate the induced field. It is necessary to add a second coil that is placed orthogonal to the first coil to produce a correcting field in this orientation. In general, a minimum of two coils are required to compensate the field in a phased manner as the needle changes orientation inside the scanner.

FIGURE 2.

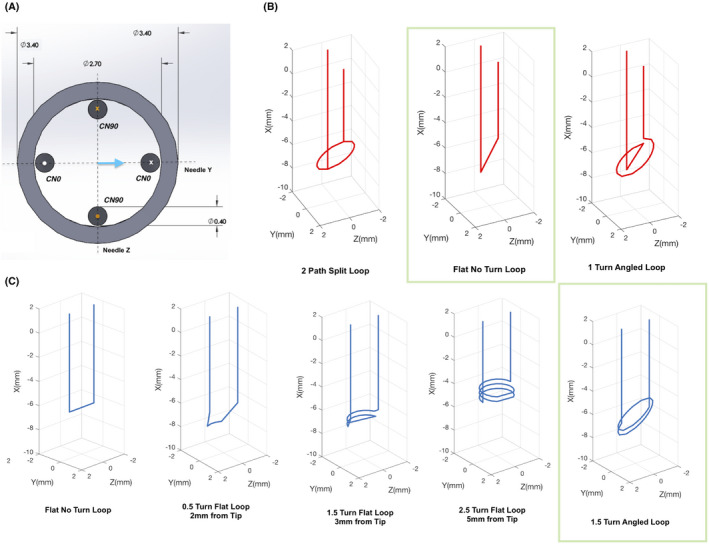
Design of the shim coils. A, Solidworks sketch of two example shim coils in the needle’s coordinate frame. All dimensions are in mm. CN0 and CN90 are designed orthogonally with the angle representing the coil’s deviation from the needle’s Y axis (blue arrow). Only one angle is used to define the coils in the needle frame, since all coils are designed orthogonal to the needle’s radial plane. X and O represent directions of current flow. B,C, 3 CN0 (red) and 5 of the 21 CN90 (blue) paths considered for optimization are shown. All coils are shown in the magnet coordinate frame with orientation (0, 0, 0). The complete set of coils is shown in Supporting Information Figure S1. Green boxes highlight the pair of coils chosen for the optimized shim set

FIGURE 3.

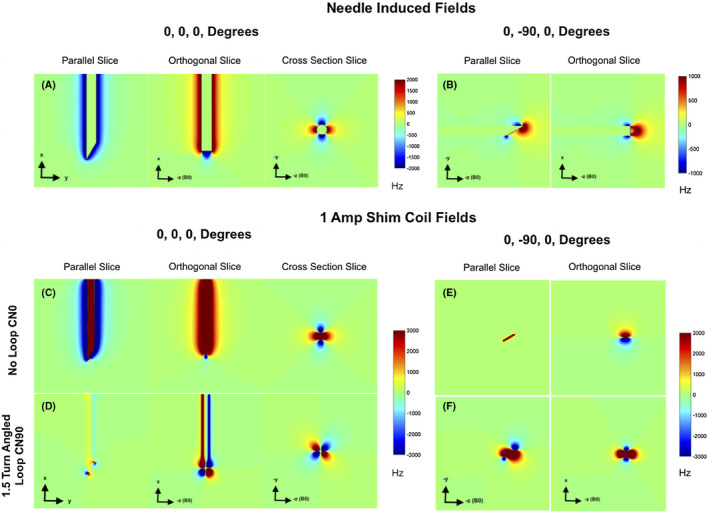
Needle and coil induced fields in Hertz. A, B, Estimated needle induced ΔB₀ at 3T for (0, 0, 0) degree and (0, −90, 0) degree orientations. Midline planes parallel to the bevel, orthogonal to the bevel and a cross section slice are shown. In the (0, 0, 0) degree orientation, these align with the axial, sagittal, and coronal planes, respectively. The resolution is 0.1 mm/voxel isotropic. C‐F, 1 Ampere B_z fields produced by the flat no‐loop CN0 and 1.5 turn angled loop CN90 coil in the two orientations. Strong field production is seen in all cases. The cross‐section slices in (A) and (C) best demonstrate the potential of field correction

While the above coil paths target field correction along the needle’s body, any number of tip paths can be conceived that will compensate the field around the tip to different extents. Also, the tip can present very different field patterns in different orientations. In this work, this problem was approached by comparing the shimming performance from a set of candidate CN0 and CN90 tip path combinations in the four needle orientations described earlier. To simplify the path choices, a constraint was added that the tip path be symmetric about at least one radial axis. This constraint is based on the fact that the needle is symmetric and asymmetric coil paths will produce skewed fields that may be suboptimal for correction. A total of 21 coil paths were considered for CN90, which included ½, 1½, and 2½ turn flat (at 90° with X_N) loops at 2, 3, 4, 5, and 6 mm clearances from the tip, ½, 1, 1½, 2, 2½, and 3 turn angled (at 30° bevel angle) loops at 3.85 mm clearance from the tip and a flat no loop path at 3.85 mm clearance from the tip. There was a 3.85 mm clearance distance from the plane of the needle tip to the air space inside the needle. Three coil paths were considered for CN0, which included a one‐turn angled loop, a flat no‐loop path, and a split two path loop, all 3.85 mm from the tip. All loops were defined with a pitch of one wire diameter. Figure 2 shows schematics of some of the tip paths considered. The complete set of coils is shown in Supporting Information Figure S1. Shimming performance was evaluated by fitting the needle induced fields with each of the 63 CN0 and CN90 combinations for all four orientations. The combination with the lowest summed shimmed to unshimmed ΔB₀ standard deviation (SD) ratio over all four orientations was selected as the final tip path, that is, we minimized,

$$\sum _{i=1}^4\frac{\sigma \left(B_i^T-B_i^S\right)}{\sigma \left(B_i^T\right)}\text{where}{B}^s=\sum _{c=1}^2{A}_c{B}_c$$ (1)

where B^T is the target needle field, B^S is the summed field of the two shim coils, A are the shim currents and B are the unit 1 amp shim coil fields. Shimming involved a ±0.5 Amperes current‐constrained least squares fit to the target field in MATLAB. The target and shim fields were both masked to exclude voxels lying within the needle during shimming.

2.3. Shimming a needle in arbitrary orientation

Since an interventional device is free to move in any orientation, a shimming solution has to ideally work well in all orientations. For a device with known geometry, the induced fields hold constant for any orientation; therefore, the corresponding shim currents can be estimated a priori and used to adaptively compensate the ΔB₀ during a procedure. To evaluate this, we modeled the fields produced by the distal 2 cm of the needle in orientations ranging from −90 degrees to +90 degrees, in steps of 15 degree rotations about each magnet axis. This yielded 2197 different orientations for which corresponding shims were computed. To evaluate the impact of shimming on the signal void around the needle, gradient echo (GRE) signal fractions were also simulated (neglecting RF and T₂ effects) in the volumes as ⁴⁹ :

$$\left|S\right|/S_0=sinc\left(\pi TE\mathrm{\Delta }x\frac{\mathit{df}}{\mathit{dx}}\right)sinc\left(\pi TE\mathrm{\Delta }y\frac{\mathit{df}}{\mathit{dy}}\right)sinc\left(\pi TE\mathrm{\Delta }z\frac{\mathit{df}}{\mathit{dz}}\right)$$ (2)

where Δx, Δy and Δz are the image voxel dimensions, TE is the echo time (assumed to be 0.5 mm, 0.5 mm, 0.5 mm and 3 ms respectively) and df/dx, df/dy and df/dz are the ΔB₀ gradients across a voxel in x, y and z. S₀ is the signal magnitude assuming a zero field gradient across the voxel. For any arbitrary orientation within this range, the optimal shim currents can be estimated by interpolation. For orientations outside this range, the symmetry of the needle enables the prediction of the necessary shim currents.

3. RESULTS

Figures 3A,B show the ΔB₀ induced by the 10G titanium needle at 3T. Central volume slices parallel and orthogonal to the needle’s bevel are shown. When the needle is perpendicular to B₀ (0, 0, 0 degrees), a bipolar pattern is observed across the needle’s body (best seen in the cross‐section slice). When the needle is parallel to B₀ (0, −90, 0), the ΔB₀ is significantly reduced, unipolar, localized mainly to the tip, and asymmetric due to the bevel. Figures 3C‐F show the 1 amp fields produced by two coils highlighted in green boxes in Figure 2, in the same orientations. The 1 amp coil fields are seen to be significantly stronger than the needle induced fields. When the needle is perpendicular to B₀, the shim fields match the needle induced ΔB₀ closely indicating the possiblity of effective shimming. When the needle is parallel to B₀, shimming might be more challenging since the needle ΔB₀ is unipolar and non‐monotonic (Figure 3B), while terminal fields produced by the coil loops are mostly bipolar and monotonic (Figure 3E,F).

The analysis of 63 shim coil combinations based on Equation 1 indicated that the combination of a flat no‐loop CN0 and 1.5 turn angled loop CN90 gave the best shimming performance (detailed results in Supporting Information Figure S2). These two coil designs are highlighted in the green boxes in Figure 2. Figure 4 shows the results of shim simulations with this pair. ΔB₀ maps are shown for two of the four orientations without and with shimming. Excellent compensation of ΔB₀ is predicted in the 0, 0, 0 orientation where the SD of the field over the volume reduced from 206.6 Hz before shimming to 106.4 Hz after shimming (~49% reduction) with currents of −0.5 amps (fit constraint) in CN0 and −0.005 Amps in CN90. The ΔB₀ is well compensated all along the needle, except for the extreme tip, which is difficult to compensate due to its sharp beveled geometry and only two independent coils. Profiles across the needle’s body show that the unshimmed fields of up to ~−2800 Hz are brought down to less than ~−100 Hz close to the needle. As expected, using a higher constraint of 1 amp provides better correction. A slightly undesirable feature of the correction seems to be field overcompensation in the voxels closest to the needle (field spikes seen in the profiles). This will cause some unavoidable signal loss, in the <1 mm extent along this axis. In the future, coil paths can be designed to minimize this overcompensation. Compared to the perpendicular orientations, field compensation is modest when the needle is parallel to B₀ (~10% reduction in SD). This is primarily due to two reasons: (1) compensating the monopolar fields at the tip ideally requires multiple independent loop coils at the tip, which is difficult to achieve; and (2) due to the bevel, the field at the tip is not monotonic (Figure 4C,D), while the shim coil fields are monotonic. Nevertheless, some sections of the needle do show significant reduction in ΔB₀ even in these orientations. Table 1 gives a summary of the shim performances in the four orientations.

FIGURE 4.

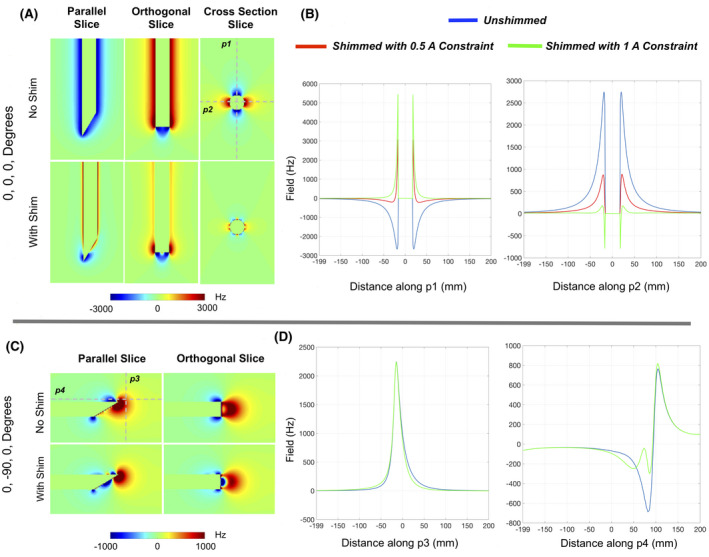
Results of simulated needle shimming for two orientations. Excellent compensation of the needle induced ΔB₀ is predicted around the needle for the perpendicular orientation. Field profiles along the gray dotted lines (p1‐p4) are shown alongside for the No Shim, shimming with 0.5 amp and 1 amp constraint conditions. Field spikes closest to the needle in the shimmed conditions are indicative of overcompensation in the nearest voxels in order to a get good shim in farther voxels. Shim performance is lower in the parallel orientation, but good correction is still observed in some sections of the needle (along p4)

TABLE 1.

Shim performance and current demands for shimming the needle in the four orientations at the limits of an octant ^a

Orientation angle X, Y, Z (degrees)	No shim		With shim 0.5 amp constraint				With shim 1 amp constraint
	SD (Hz)	Vol 50 mm3	SD (Hz)	Vol 50 mm3	Shim currents (amps)		SD (Hz)	Vol 50 mm3	Shim currents (amps)
					CN0	CN90			CN0	CN90
0, 0, 0	206.63	2920	106.47	1549	−0.5	−0.005	99.17	1228	−0.716	0
90, 0, 0	205.25	2915	110.69	1434	−0.012	0.408	110.23	1433	−0.012	0.408
0, −90, 0	48.42	275	44.64	208	0.006	−0.126	44.64	208	0.005	−0.126
90, −90, 0	47.87	328	44.06	271	0.013	−0.132	44.05	272	0.013	−0.132

^aVol 50 refers to the volume of voxels around the needle (excluding the needle volume) with signal fraction <50% of maximum signal.

Figure 5 shows slices across a simulated 40 mm side GRE signal fraction volume with the needle at an oblique (90, 30, 0) degree orientation, along with the needle image for reference. Shimming enables significant signal recovery all around the needle, that is especially apparent in the orthogonal plane. Note that the increased signal loss evident in the proximal tip in the shimmed case is artifactual, stemming from residual wraparound field from the Fourier transform field modeling. Figure 6 shows results of shim performance in a range of needle angles for the 20 mm side volume. Results from the complete set of 2197 orientations are presented in Supporting Information Videos S1 and S2, which are available online. The results show that shim performance is robust and a significant volume of lost signal around the needle is recovered over a wide range of needle orientations (maximum recovery of ~ 50%). The video data show the phased manner in which the two coils operate with changing orientation to achieve the best shims.

FIGURE 5.

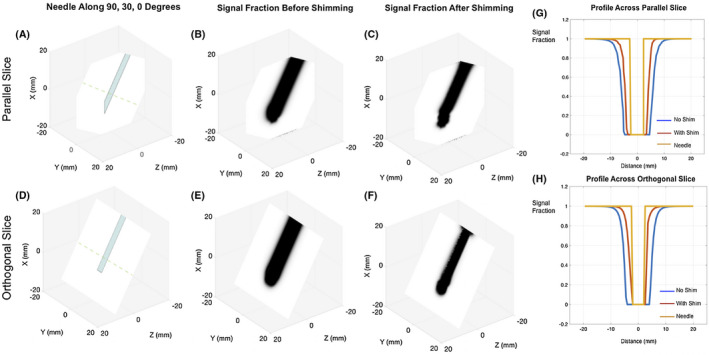
Simulated 0.5 mm side voxel GRE signal fraction maps for the needle at an arbitrary 90, 30, 0 degree orientation. A,D, Needle shown as a baseline to compare the signal void. Maps without (B,E) and with (C,F) shims at a TE of 3 ms. Significant signal recovery predicted with shimming is visible in both planes parallel and orthogonal to the needle bevel. G,H, Profiles across the parallel and orthogonal slices for all conditions along the dotted lines in (A) and (D). Shimming recovers a large volume of the lost signal around the needle that is especially apparent in the orthogonal plane

FIGURE 6.

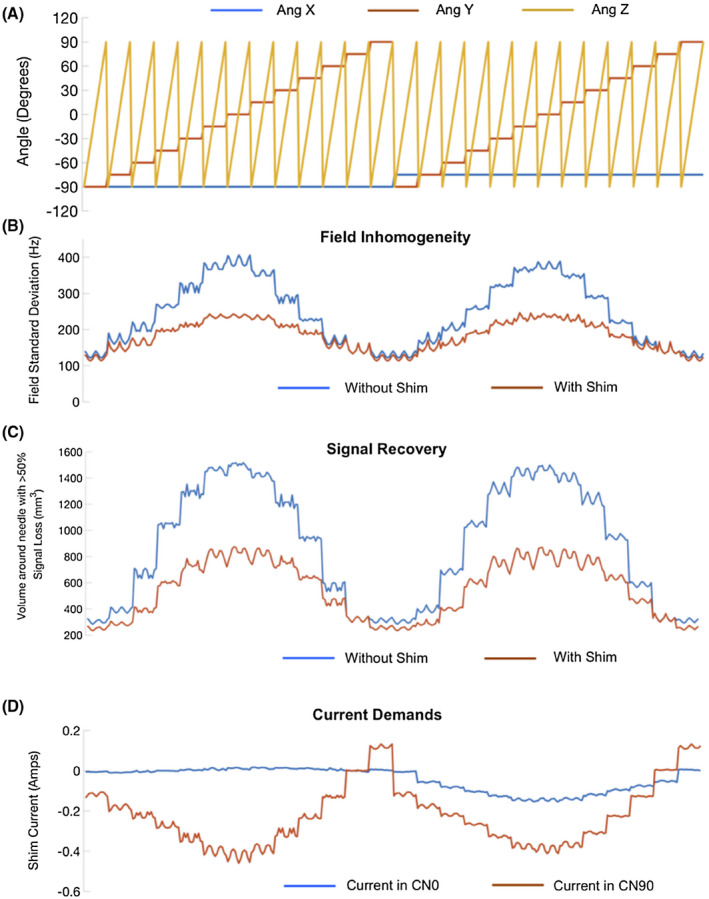
Needle shim performance at arbitrary orientations. A, A subsample of the −90 to +90 degree range of angles evaluated for shim performance. B, Fieldmap SDs without and with shimming for the angles in (A). C, Total volume of voxels around the needle with signal fraction <50% of maximum signal (estimated assuming 0 field gradient across a voxel) without and with shimming. D, Current demands in the two coils for the same angles. Results from the complete set of 2197 orientations are presented in two supporting video files, Supporting Information Videos S1 and S2

4. DISCUSSION AND CONCLUSION

This paper presents the concept, design, and modeling of active shimming of metallic probes used in iMRI. Simulations predict that it is possible to obtain significant compensation of the metallic probe induced fields and signal loss at 3T at arbitrary orientations using just two independent shim coils.

Shim performance better than the one achieved here can likely be obtained using larger number of independent shim coils or with better optimized coil paths. Within the coils considered here, coils with integral number of turns in general performed worse than those with additional half turns because of the need for an extra diagonal connection to complete the return path. In general, the performance of the coils decreased with distance from the tip. Also, adding turns did not necessarily improve performance in all coils. For flat loop coils, the performance worsened, while for angled loop coils, performance improved only slightly. In this work, the problem of shim coil design was approached in the forward sense. The traditional spatial harmonic expansion construct of magnet shims is challenging here, since each coil has to produce fields that can shim the body as well as the tip to the best extent. A target field stream function technique may, therefore, be the best approach to obtain optimized coil paths. ⁵⁰ , ⁵¹ , ⁵² Studies to identify such optimized current paths are currently underway. One might consider optimizing the coils for shimming only the tip which is usually closest to the target of the procedure at the cost of a poor shim across the probe’s body. In addition, coil design can be guided by the expected range of orientations for specific applications, which might relax the design requirements.

Active shimming should work with varying effectiveness in any metallic probe with any arbitrary material, body shape or tip geometry. Lower artifact levels can reduce procedure times and error rates, especially when multiple probes are used in the same procedure. Furthermore, active shimming should be compatible and synergistic with most imaging‐based approaches for minimizing needle artifacts. ²⁶ , ²⁷ , ²⁸ , ²⁹ , ³⁰ , ³¹ , ⁵³ Therefore, a combination of techniques could be used in materials such as stainless steel that have large susceptibility differences with water. This could facilitate wider adoption of stainless steel probes that have greater gauge and size availability than titanium, which might be currently preferred in some applications solely due to low artifact levels. Reduced artifact levels should also improve the performance of needle tip detection using traditional and more recent deep‐learning based image processing techniques. ⁵⁴ , ⁵⁵ , ⁵⁶ For example, in Figure 5C, the orientation of the bevel becomes apparent after shimming, which could be further elucidated by image processing.

Some practical difficulties will have to be overcome for fabrication of actively shimmed needles. The needle modeled here was hollow with a closed tip, without any inbuilt components or channels. In open tip hollow needles, shim coils will take up some of the internal working channel and therefore, design practicality considerations will have to be made on a device per device basis. For example, instead of a flat loop chosen here, a combination with a split loop, which gives almost the same performance (Number 38 in Supporting Information Figure S2) could be chosen to leave the internal channel open. For higher gauges, microfabrication techniques could be considered for developing the inserts. Importantly, the ΔB₀ will be inversely proportional to needle gauge due to lower volumes of metal, and so will be the current demands and required wire diameters. In this work, the needle was filled with air. Filling it with water makes only a slight difference in the induced field and the required shim currents. Demand in CN0 changes from −0.716 A to −0.723 A in the 0, 0, 0 orientation and CN90 demand remains unchanged. For real time tracking and adaptive shimming, a setup using optical or inductively coupled fiducials attached to base of the needle could be used to provide fast updates of device position and adaptive current updates. ⁵⁷ , ⁵⁸

This work does not address potential effects such as radiofrequency (RF)/gradient induced eddy current related B₁ effects ⁵⁹ and shielding of the shim field. In practice, all shim coils will incorporate broadband chokes to suppress RF and gradient induced currents. Shielding effects are also expected to be minimal given the relatively low permeability materials used in making iMRI probes although some field reductions might be observed in stainless‐steel probes. Our future work will focus on actual fabrication of such needles and demonstrating signal recovery in iMRI applications.

CONFLICT OF INTEREST

The topic of this work has been submitted for a United States patent application.

Supporting information

FIGURE S1 21 CN90 (blue) and 3 CN0 (red) candidate coils considered for the shim optimization in pairs. All coils are shown in the magnet frame in the 0, 0, 0 orientation. In all coils, the leads were designed such that they were either along the needle’s Y = 0 (for CN0) or Z = 0 (for CN90) axes to maintain orthogonality in the body of the needle. This was irrespective of the clearance from the beveled tip that caused some coils to be truncated. Truncation was not required for coils with clearance greater than ~6 mm

FIGURE S2 Results of shim optimization with the 63 coil combinations (21 CN90 and 3 CN0 coils) in 4 orientations. Plots show the ratio of the standard deviation of the field after over before shimming in (A) 0, 0, 0 and 90, 0, 0 degree (B) 0, −90, 0 degree and 90, −90, 0 degree needle orientations. (C) Sum of the four ratios and identification of combination 17 (Flat No Turn loop CN0 and 1.5 Turn Angled Loop CN90, black arrow) as the best pair. It can be seen that many coil combinations perform well in certain orientations but fail in others

VIDEO S1 Shim performance and current demands for 2197 needle orientations ranging from −90 to +90 degrees in steps of 15 degrees rotations about all axes. Fieldmap slice planes parallel and orthogonal to the needle bevel are shown with and without shimming, along with fieldmap standard deviation values and current demands. Shim current requirements for orientations in between can be estimated by interpolation

VIDEO S2 Simulated GRE signal fraction maps for the 2197 needle orientations ranging from −90 to +90 degrees in steps of 15 degrees rotations about all axes along with volume of voxels around the needle with signal fraction <50% of maximum signal (assuming 0 field gradients in all three axes)

Sengupta S. Modeling of active shimming of metallic needles for interventional MRI. Magn Reson Med. 2020;84:2858–2870. 10.1002/mrm.28320