Nanothermometry: From Microscopy to Thermal Treatments

Abstract

Measuring temperature in cells and tissues remotely, with sufficient sensitivity, and in real time presents a new paradigm in engineering, chemistry and biology. Traditional sensors, such as contact thermometers, thermocouples, and electrodes, are too large to measure the temperature with subcellular resolution and are too invasive to measure the temperature in deep tissue. The new challenge requires novel approaches in designing biocompatible temperature sensors—nanothermometers—and innovative techniques for their measurements. In the last two decades, a variety of nanothermometers whose response reflected the thermal environment within a physiological temperature range have been identified as potential sensors. This review covers the principles and aspects of nanothermometer design driven by two emerging areas: single-cell thermogenesis and image guided thermal treatments. The review highlights the current trends in nanothermometry illustrated with recent representative examples.

Graphical Abstract

Hot or cold? The review highlights the general mechanisms and principles behind temperature measurements using nanothermometers within a physiologically relevant temperature range (20–80°C) in cells and in vivo.

1. Introduction: Importance of Thermometry in Biomedical Studies

Biological objects, such as cells, tissues, and bodies are tightly regulated systems that represent a good example of a heat-generating object that operates within narrow limits of a few degrees. These limits are controlled through numerous physiological pathways that regulate the kinetics of heat loss and its production for attaining balance. The loss of balance leads to severe life-threatening conditions, such as hyperthermia and heatstroke. From pain to emotional distress, relatively small temperature fluctuations have large effects on many physiological functions and might be symptoms of serious diseases such as viral and bacterial infection, diabetes, vitamin deficiency, autoimmune disease, and cancer. Yet, local applications of high and low temperatures might have a strong healing effect. Controlled heating or cooling has been known for centuries to provide therapeutic intervention for treating various conditions as it employs destruction of bacteria, viruses, and dysfunctional cells and tissues, all within a targeted region.

Nanothermometry is an emerging area that has attracted attention for its ability to answer fundamental questions of temperature regulation in cell biology, provide understanding of the mechanism behind the disease, and assist with the thermal treatment of deep tissue. The search for nanothermometers has been driven by primarily two fields: fundamental cell biology to understand cell thermogenesis on a single-cell level, and in vivo imaging to monitor and control clinically important thermal ablation procedures. Being conceptually different, both fields came to rely on the same class of biologically compatible, temperature-sensitive nanosensors, collectively known as molecular nanothermometers and (later denoted as nanothermometers) which enable temperature readout remotely and in real time.

The size, sensitivity and response time of the nanothermometers are critical for both fields. The nanodimension is important to not affect biological functions within the cell, while whenever possible to either evenly distribute within the cells or to localize to a specific subcellular location. Extremely high sensitivity is needed to resolve temperatures of less than 0.1 K and a rapid response (millisecond) is required to map thermogenesis and detect temperature fluctuations due to fast metabolic processes. For thermal ablation applications, the size of the nanothermometers is critical in the prevention of toxicity and immune responses, as well as providing fast clearance. Sensitivity is less critical in this application and 1 K is considered to be sufficient. Since the thermal ablation procedure takes several minutes, a response time of 1 sec is adequate. Regardless of the application, nanometre size, biocompatibility, rapid equilibration with the environment, and the independence from the type of cell or tissue are the key parameters considered in nanothermometer design.

In this review, we provide a brief rationale for measurements on the cellular and in vivo levels, as their importance, impact, and challenges. The review highlights some of the general mechanisms and principles behind temperature measurements using nanothermometers within a physiologically relevant temperature range (20–80°C). Methods of measurements, also known as imaging modalities (i.e., fluorescence lifetime and anisotropy, fluorescence correlation spectroscopy, photoacoustics and ultrasound), that could be tailored for specific applications are presented. The design of nanothermometers for non-biological applications, such as for monitoring microelectronics,^[1] fuel cells,^[2] or their uses in thermochromics materials,^[3] will not be considered specifically in this review, but are expected to motivate a biology-driven researcher to adapt these advanced technologies for biological use.

2. Nanothermometry for Cell Studies with Temperature-Sensitive Constructs

A high thermal resolution technique originally used for cell studies in the 80s and 90s, microcalorimetry,^[4] reported changes in cells’ temperature within a few degrees as a response to certain stimuli, such as drugs, toxins, and mutations. These studies provided the initial foundation of cell thermo-genesis, required a large number of cells in suspension (i.e., 10⁶ mL),^[5] and had poor spatial and temporal resolution. Detailed information of the biochemical processes in a single cell demands a high spatial resolution technique, nanothermometry, with the goal to map temperature within a single living cell. Although the feasibility of accurate single-cell temperature measurements has been recently questioned,^[6] the search for highly sensitive nanothermometry techniques has led to the development of many exciting materials with diverse mechanisms of thermal sensing. The current list includes: lanthanide nanoparticles,^[7] quantum dots,^[8] gold nanorods,^[9] molecular beacons,^[10] polymers with encapsulated fluorophores,^[11] and nanodiamonds,^[12] which have been extensively reviewed.^[13]

2.1. Fluorescence-Intensity-Based Nanothermometers: Absolute Intensity and Shifts

Fluorescence intensity of the fluorophores (i.e. fluorescent dyes, nanocrystals, organometallic complexes) is in general sensitive (usually decreases) to temperature due to the increase in the non-radiative rate caused by temperature-induced vibrations and rotations. For this reason, it is no wonder that intensity-based nanothermometers represent the largest class of published thermal sensors. However, their applications are limited to emitters that elicit a very large change in signal to compensate concentration artefacts caused by differences in the probes’ distribution, different rates of extravasation, and leaking through cell membranes. This concentration dependence is the principal bottleneck in nanothermometry. Fortunately, the change in intensity for some of the nanothermometers is accompanied by a shift in emission (from a few nanometres to tens of nanometres) that can be used for ratiometric measurements. The ratiometric approach with nanothermometers eliminates concentration artefacts, which leads to more reliable temperature measurements and higher sensitivity.

The nanothermometer sensitivity discussed in this review and commonly used in literature is quantified according to Equation (1):^[13]

$$S=\frac{\Delta Q}{Q_{\text{T}}\Delta T}\times 100\%$$ (1)

where S is sensitivity [%K⁻¹], Q_T the reading at low temperature, DQ corresponds to the change in the signal over the temperature span (DT). Another metric that also appears in the literature is a temperature resolution that indicates the minimal detectable signal change that can be estimated from the standard deviation of residuals in the fit of the experimental data and the sensitivity.^[13b,14]

2.1.1. Eu³⁺ Complexes

We start from the europium-based complexes, since the first attempt (published in 1998) to measure thermogenesis on a single-cell level with intensity-based nanothermometers was based on Eu-TTA.^[15] Due to its hydrophobic nature, the complex readily integrates into cell membranes, and was used to image intracellular heat waves after activation of muscarinic receptors by acetylcholine. A few years prior Eu-TTA was recognized as an efficient temperature-sensitive emitter for the hot-spot monitoring of integrated circuits with a theoretically limited thermal resolution of 0.001 K, and a diffraction-limited spatial resolution to 300 nm.^[16]

The principle of the Eu-TTA nanothermometer is shown in Figure 1. The TTA ligand absorbs UV light as an antenna and transfers the energy to the Eu³⁺ ion. Further transition from the ⁵D₀ energy level to the ⁷F₂ produces a photon at 612 nm that is temperature sensitive. The quantum efficiency of the overall process is quite low, less than 0.5%, but the quantum yield is highly sensitive to temperature as illustrated with a sharp decrease in the physiological range, which makes this intensity-based nanothermometer suitable for temperature measurements in cells and tissue/living organisms.

Figure 1.

Mechansim of Eu-TTA emission and its thermal sensitivity. a) The TTA ligand absorbs UV light, as an antenna, and transfers the energy to the Eu³⁺ ion. Further transition from the ⁵D₀ energy level to the ⁷F₂ producesa photon at 612 nm that is temperature sensitive. b) Temperature-dependent change in the absolute quantum yield of the Eu-TTA complex. From Ref. [16].

Encouraged by this study, several constructs and applications of Eu-TTA, nanothermometers, and micro-thermometers (a glass micropipette filled with the Eu-TTA) have been described.^[17] Recently, the TTA ligand has been replaced with other UV-absorbing ligands and nanoparticles. The Eu³⁺-doped TiO₂ nanoparticles showed a large improvement in sensitivity, reaching 2.43%K⁻¹.^[14] Addressing the problem of the inaccuracy of intensity-only measurements, Arai et al^[18] added the reference emitter [Ir(ppy)₃] to the design. In this study, instead of the TTA, a different ligand that was excitable by the lower energy of blue light, was used. Both the sensor Eu complex and the reference Ir complex were embedded into polymeric nanoparticles of ca. 120 nm diameter to achieve a sensitivity of4.0%K⁻¹.

2.1.2. Quantum Dots (QDs)

QDs (CdSe, CdS, Ag₂S, PbS and some others) are attractive contrast agents in cell biology primarily because of their small size, unsurpassed brightness, and in many cases commercial availability. Similar to Eu complexes and other luminescent nanomaterials (carbon nanotubes, nanodiamonds, fluorescent polymers and dyes), the intensity of QDs decreases with increasing temperature. This decrease is due to shrinkage of the energy bandgap of semiconductors in the physiological temperature range.^[19] QDs have only one relatively narrow emission that cannot be used for ratiometric imaging. However, there is a noticeable, although small, red-shift in QD emission (ca. 0.1 nmK⁻¹ for CdSe^[20]) that can be used for ratiometric temperature measurements. Overall, QDs show a relatively low thermal sensitivity of <0.5%K⁻¹,^[21] which is below the limit of a recently introduced “quality threshold” for nanothermometers.^[13a] Still, the efforts to increase QD sensitivity and applicability for nanothermometry remain a focus of many studies recently reviewed in Ref. [13b] Interestingly, the low thermal sensitivity of QDs can be significantly enhanced by two-photon excitation.^[22]

2.1.3. Upconverting Nanoparticles (UCNPs)

Another interesting class of materials extensively tested for nanothermometry is based on UCNPs.^[23] Typical UCNPs are composed of a host crystal, such as metal fluorides (NaYF₄), oxides (Y₂O₃), phosphates (YPO₄), and vanadates (GdVO₄) doped with lanthanide ions, either individually (Er³⁺, Yb³⁺, Ho³⁺, Gd³⁺, Tm³⁺) or with their combinations.^[24] An example of the mechanism for two-step upconversion of the Er³⁺,Yb³⁺/NaYF₄ NPs is shown in Figure 2. One of the major advantages of UCNPs is the virtually zero background stemming from a negative Stokes shift, which makes them ideal for optical imaging.

Figure 2.

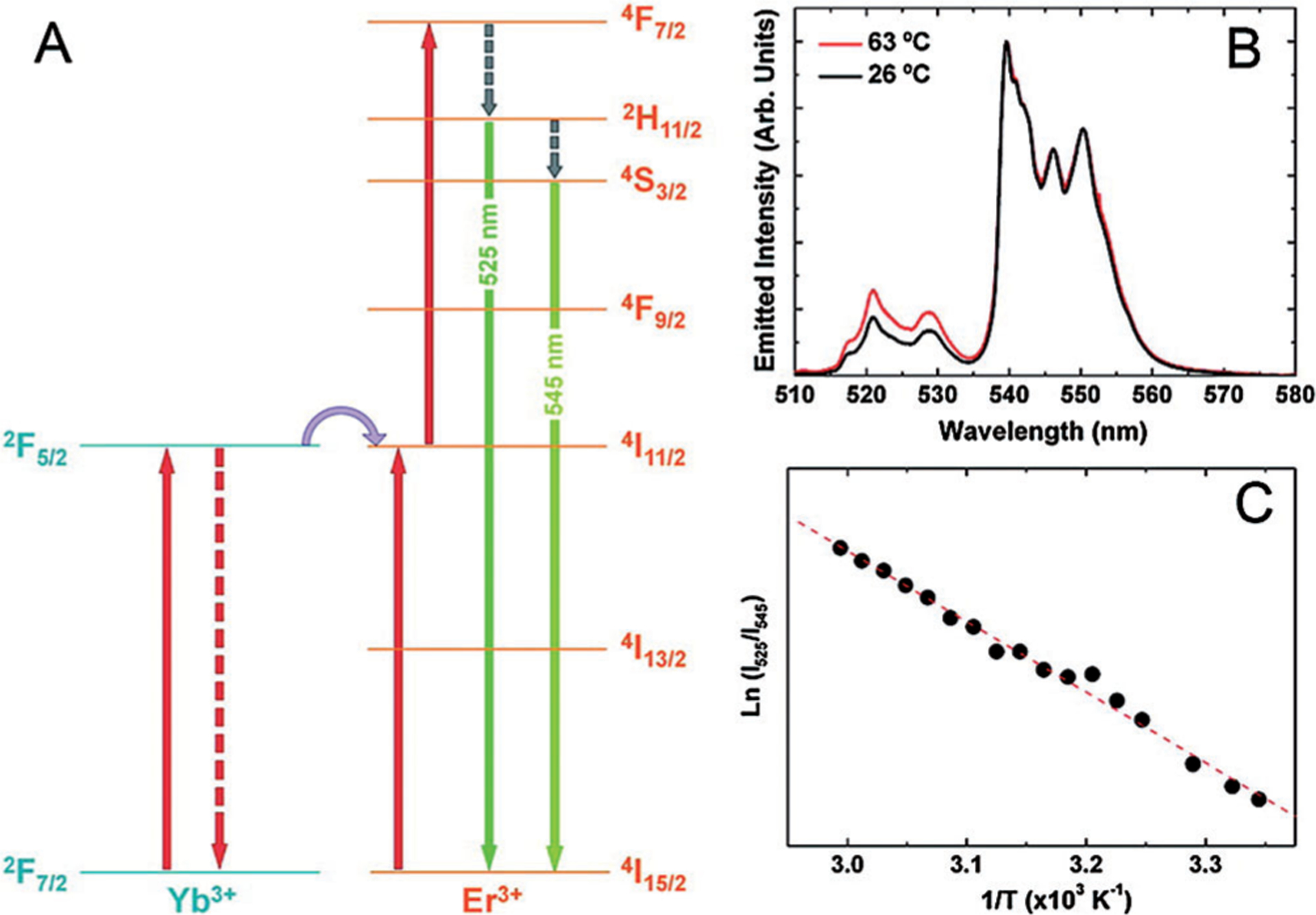
Mechanism of temperature sensitivity of Er³⁺,Yb³⁺/NaYF₄ upconverting nanoparticles. a) Energy-level diagram showing the relevant states of the Yb³⁺ and Er³⁺ ions and the two-step upconversion excitation mechanism. The temperature sensitivity of the UCNPs occurs as a result of the closely spaced ²H_11/2 and ⁴S_3/2 energy states. (b) Upconversion emission spectra obtained at two different temperatures (λ_exc= 920 nm). (c) Plot of thermal sensitivity [ln(I₅₂₅/I₅₄₅) vs 1/T]. From Ref. [7].

Luminescence upconversion from the bulk of upconverting materials has been utilized for temperature measurement since the early 1990s (reviewed in Ref. [25]). The mechanism of the UCNPs thermal response lies in the different thermal sensitivities of different electronic transitions. Since not all transitions show the same temperature dependence, this forms the basis of using UCNPs as ratiometric nanothermometers.^[26] However, temperature sensitivity of the bulk in general is poor. In contrast, nanoparticles made from the same upconverting materials were found to exhibit much stronger thermal sensitivity. One of the first demonstrations of UCNPs in cell imaging was achieved with Er/Yb in a NaYF₄ matrix.^[7] In these nanothermometers, ratiometric temperature evaluation has been realized by measuring the ratio of the green emission intensity ²H_11/2 (525 nm) of Er³⁺ions to that of the ⁴S_3/2 level (545 nm) with an overall sensitivity of ca. 1.2%K⁻¹.

2.1.4. Fluorescent Organic Dyes

From the synthetic point of view, organic dyes provide far more flexibility than metal-based nanoparticles since dyes structures are highly tunable and their synthesis is reproducible while also being easily scaled up. The best organic small-molecule temperature sensors are usually with rotatable bonds (molecular rotors). The most common example of this strategy is rhodamines. The N-ethylenic group in rhodamine B is free to rotate and at higher temperatures the increased rotation decreases its fluorescence intensity and the lifetime. In contrast, the fluorescent properties of rhodamine 640 (also known as rhodamine 101), with a fixed N-ethyl bond, is practically insensitive to temperature.^[27] Rhodamines have been originally utilized to measure temperature in microfluidic devices^[28] and later used as temperature sensors in microfluidic polymer chain reaction systems.^[29]

However, individual dyes show moderate fluorescence intensity sensitivity (generally less than 2%K⁻¹, with some exceptions), which makes them impractical to use as intensity-based nanothermometers. In addition, organic dyes have only one emission band whose position is weakly sensitive to temperature, hampering their use as ratiometric nanothermometers as well.

To alleviate this problem, our lab has explored a strategy of assembling two fluorophores with different thermal sensitivities into a single construct.^[30] Coumarin, with a strong temperature sensitivity (6.6%K⁻¹), and rhodamine 640, with almost no thermal response (<0.1%K⁻¹), were covalently connected to each other. To minimize the fluorescence energy transfer that complicates the readout, these dyes were selected from different spectral ranges, since this prevented spectral overlap. The ratio of the two emissions provided the basis for temperature measurement. The overall response of the construct, however, showed only a marginal thermal sensitivity of 0.5%K⁻¹. In an other design, Zhegalova et al^[31] combined two fluorophores trapped in a hollow polymethacrylate nanocapsule (Figure 3).

Figure 3.

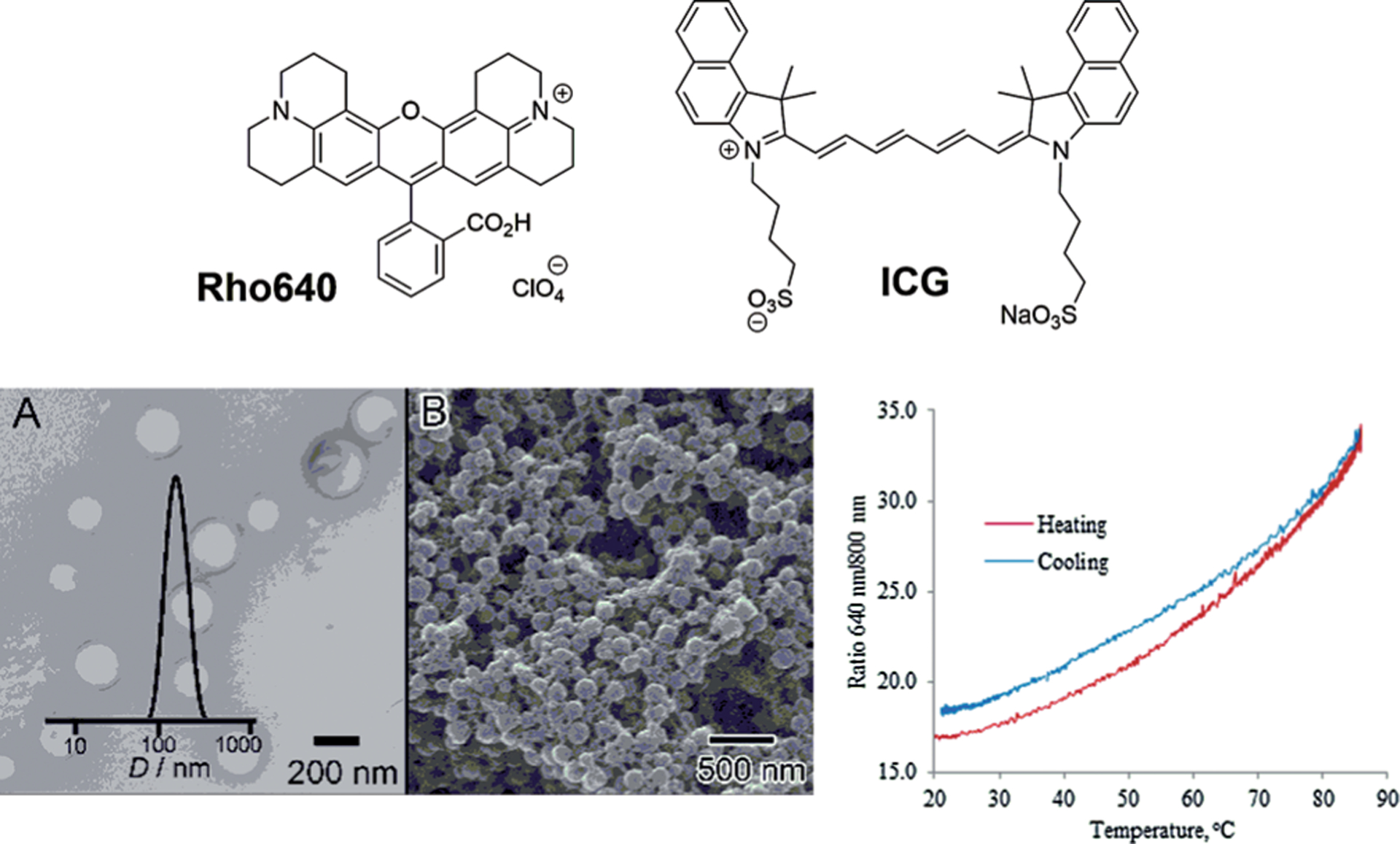
Temperature-sensitive nanocapsules. Structures of rhodamine 640 (Rho640) and ICG used to construct nanothermometers. Temperature-dependent ratiometric emission of Rho640-ICG/nanocapsule emission 640/800 nm emission intensity as a function of temperature (heating/cooling cycle from 20 to 85 °C) S=1.7%K⁻¹. a,b) TEM and SEM images of the nanocapsules correspondingly. From Ref. [31].

Instead of coumarin, a near-infrared (NIR) dye approved by the FDA for imaging in humans, known as indocyanine green (ICG),^[32] was used as a sensor. The nanocapsule shell around the dyes created a well-defined and stable microenvironment that reflected only changes in temperature, while preventing other factors from affecting the dyes’ emission. The thermometer was found to be reversible after heating-cooling cycles, with an overall improved sensitivity of ≈ 1.7%K⁻¹.

2.1.5. Molecular Beacons (OFF-ON)

Although most of the reported nanothermometers rely on a decrease in fluorescence intensities at higher temperatures, there is a growing class of nanosensors that is based on fluorescence activation. These sensors are highly quenched at low temperatures and their activation is specific to certain temperatures. Rather than providing continuous measurement over a relatively large temperature scale, such sensors report the threshold. The high sensitivity of these probes to a specific temperature makes these nanothermometers attractive for intensity-based measurements, and therefore can potentially be useful for controlling thermal ablations, as discussed in Section 4.

One of the first examples of activatable sensors was based on hairpin-type structures, also known as molecular beacons.^[33] A molecular beacon is a strand of DNA containing a number of bases dually labelled by a fluorophore and a quencher at two opposite ends (Figure 4). The DNA sequence is chosen to let the two ends hybridize and form a stem–loop (hairpin) structure. In the closed hairpin form, the beacon is non-fluorescent but becomes highly fluorescent in the open form. Thermal activation can be efficiently regulated by choosing a proper oligonucleotide sequence. The fundamental problem with using molecular beacons for cell thermometry is their instability in a complex cellular environment. In a study conducted by Ke et al.,^[10] this issue was addressed by forming a beacon from the non-natural l-DNA backbone that prevented digestion of the stand by nucleases and other enzymatic degradations inside cells. In line with this concept, Ebrahimi et al.^[34] designed a beacon labelled with a fluorophore at one end and attached to the surface of a gold nanoparticle at the other end. This design previously introduced by Maxwell et al.^[35] ensured quenching of the fluorophores near the gold surface. Heating the beacon above the melting point (T_m) increased the distance between the fluorophores and the gold, leading to fluorescence enhancement.^[34]

Figure 4.

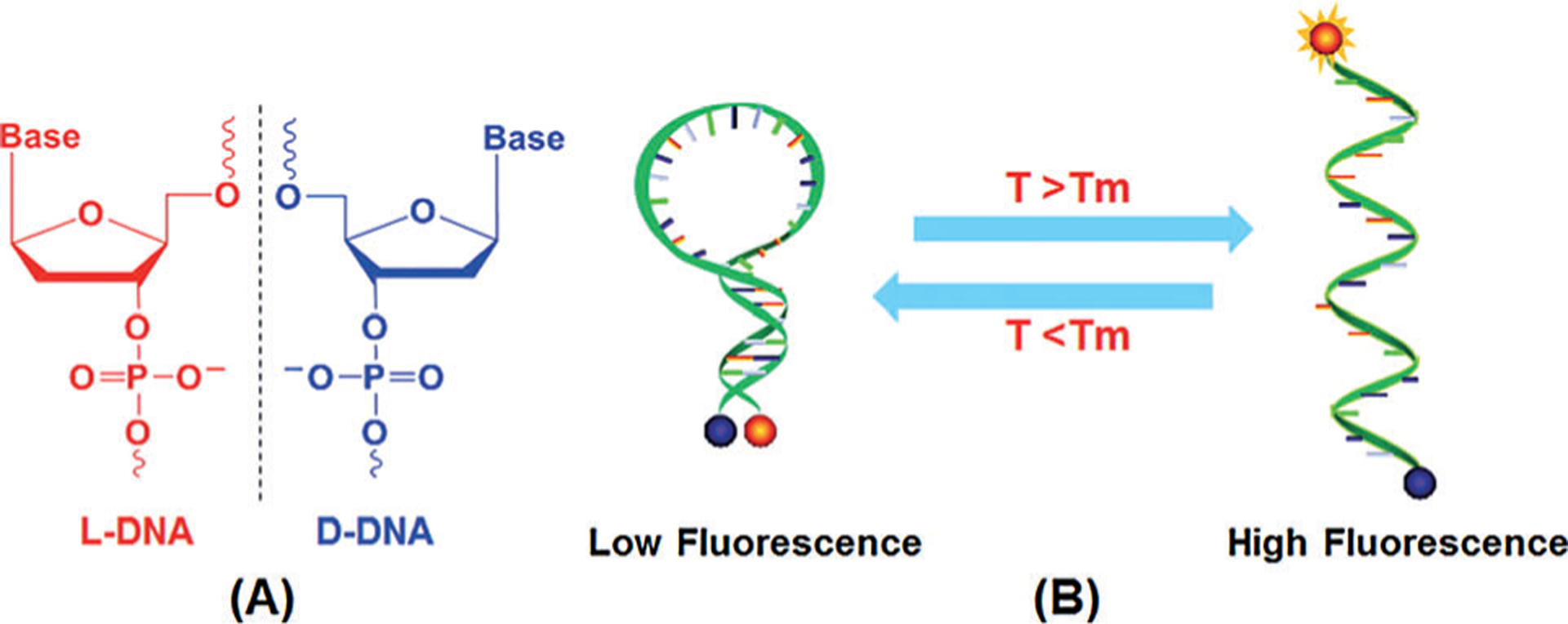
Principle of molecular-beacon-based intracellular nanothermometer. a) Structure of l-DNA. b) By increasing the temperature, the hydrogen bonding between the bases weakens and the stem of beacon structures starts to open up depending on their melting temperature points (T_m). From Ref. [10].

2.2. Fluorescent Lifetime (FL) Thermometry

FL is potentially an attractive way of measuring temperature, as this parameter is independent of concentration artefacts^[36] and has often been used in measuring temperature in microfluidic devices.^[37] As compared to the ratiometric molecular thermometers, FL-based constructs require only one fluorophore, simplifying the thermometer design. In principle, any fluorescent organic dye or nanocrystal with fluorescence intensity-based temperature sensitivity can be used as a lifetime probe. However, FL nanothermometers, based on organic dyes in general, have lower sensitivity than intensity-based sensors. For example, the encapsulated NIR dye ICG showed FL thermal sensitivity of only 0.58%K⁻¹, as compared to ≈ 1.7%K⁻¹ in the intensity measurements.^[31]

Okabe et al.^[36b] reported a highly sensitive polymeric nanothermometer suitable for FL temperature mapping. This thermometer has two major components, a polymeric backbone whose confirmation is sensitive to temperature and a fluorescent unit containing a water-sensitive fluorophore, benzofurazan, which can be quenched by neighboring water molecules at low temperatures, when the thermo-responsive polymer assumes an extended structure. At higher temperature hydration weakens and the polymeric sequence shrinks back, resulting in the release of water molecules and hence, stronger fluorescence. The FL of this nanothermometer increases from 5.06 ns to 7.09 ns as temperature increases from 30 to 38°C, or 5%K⁻¹, which is unusually high for FL constructs. An even higher sensitivity of ≈ 8%K⁻¹ was achieved after optimizing the polymeric backbone and introducing a polycationic block.^[38]

An interesting application of FL nanothermometry is time gating, which might serve, for example, to locate hot spots in cells. Organic dyes have a short FL of less than 10 ns and time gating is difficult to achieve. In contrast, many metal-based nanomaterials (QDs, rare-metal based constructs) have long FL (hundreds of nanoseconds to microseconds), and time gating can be implemented with fast detectors. However, the FL of most of these materials decreases with temperature, which is not optimal for time-gating temperature applications. For example, the change in temperature leads to an average lifetime decrease in gold nanoclusters (AuNCs) from 834 ns at 25°C to ≈ 660 ns at 43°C, or 1.4%K⁻¹.^[39] A better option would be an increase in lifetime with temperature.

3. Nanothermometry Based on Temperature-Induced Brownian Motions

For many biological systems, such as cells, soft tissues, and biofluids, small particles undergo random thermal motion known as Brownian motion. This random motion, composed of rotational and translational movement, is modelled by the Stokes–Einstein equation, which connects the diffusion coefficient to temperature and viscosity, which is also a function of temperature. Hence, temperature can be measured by probing the motional properties of particles. If the particles are fluorescent, the temperature can be deduced from two complementary molecular dynamic techniques, fluorescence correlation spectroscopy (FCS) and fluorescence anisotropy (polarization) (FA).^[40]

3.1. Temperature Measurement with Fluorescence Correlation Spectroscopy (FCS)

FCS utilizes statistical analysis of fluorescent fluctuations to assess the diffusion of the fluorophores. A thermally-induced Brownian motion of molecules and particles in solution is macroscopically described by the diffusion coefficients (D) that can be measured with relatively good precision using FCS.^[41] Any fluorophore that is photostable, with no blinking or significant triplet states^[42] can be used. For spherical molecules and nanoparticles, the Stokes–Einstein equation [Eq. (2)]:

$$D=\frac{k_{\text{B}}T}{3\pi \eta d}$$ (2)

where D is the translational diffusion coefficient, d the dynamic diameter, θ_rot the rotational correlation time and η the viscosity, relates the diffusion coefficient to the hydrodynamic radius, which results in a change in temperature such as shown in Figure 5.

Figure 5.

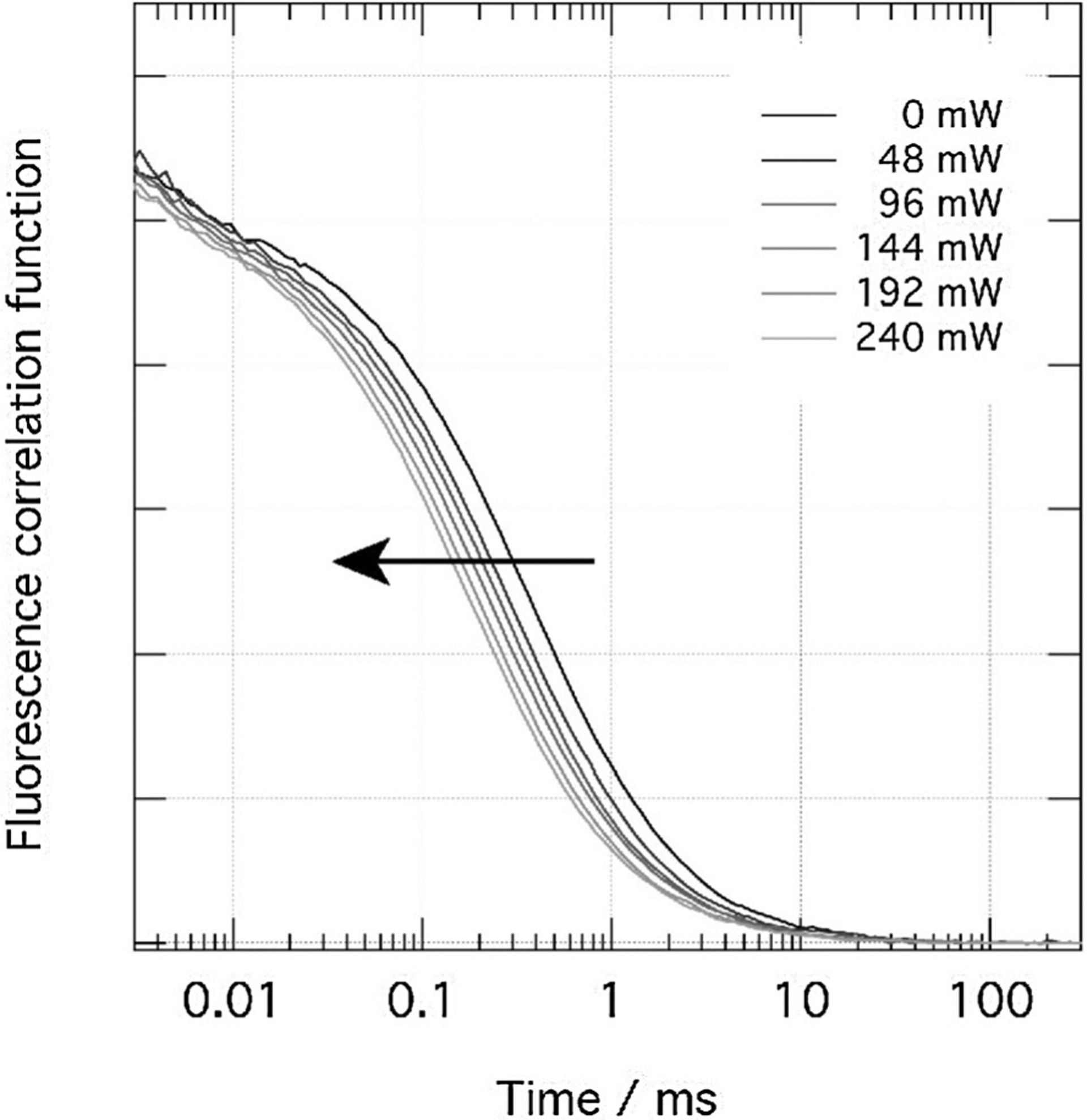
Temperature sensitivity based on FCS. Dependence of the autocorrelation curve of rhodamine 6G in ethylene glycol on the temperature induced by NIR laser light.^[43]

Several groups explored FCS as a method for temperature measurements.^[44] Jung et al.^[44a] applied FCS to measure changes in the diffusion properties of organic dyes, QDs, and fluorescent beads. As the temperature was increased, the diffusion times were reduced, which indicated an increase in the diffusion coefficient. An interesting application of nanothermometry with FCS has been demonstrated by Bag et al.,^[44b] where the authors measured the diffusion of a fluorophore across the membranes of different cell types. Using temperature-sensitivity profiles for these cells, the authors identified differences in the cell membrane structures.

Recently, an innovative dual-focus fluorescence correlation spectroscopy (2fFCS) was introduced for the absolute and precise measurement of diffusion coefficients of small fluorescing molecules. This technique has been applied for determining temperature by measuring the diffusion of fluorescing molecules of a known size.^[44c] The method facilitated probing of the temperature within 350 nm with an accuracy of 2 K. Al though the authors proposed to use this method for monitoring temperature in microfluidic systems, the technique could also be utilized in cell studies.

3.2. Fluorescence Anisotropy (FA) Nanothermometry

FA is commonly used in diverse life science applications, anywhere from analytical chemistry^[45] and drug design,^[46] to probing the cellular microenvironment^[47] and imaging.^[48] FA directly relates to the rotational correlation time (q) of the molecules and is inversely proportional to temperature according to the Stokes–Einstein–Debye equation [Eq. (3)]:

$${\theta }_{\text{rot}}=\frac{\eta V}{k_{\text{B}}T}$$ (3)

where V is the hydrodynamic volume, k_B is Boltzmann’s constant (1.38 × 10⁻²³) and T is the temperature in Kelvin. A well-known Perrin equation [Eq. (4)]^[49] connects the measurable anisotropy value r with the temperature:

$$\frac{r_0}{r}=1+\frac{\tau }{{\theta }_{\text{rot }}}$$ (4)

where r₀ is the limited (fundamental, maximum) fluorescence anisotropy, usually r₀ ≤ 4, and τ is the fluorescence lifetime of the fluorophore.

Fluorescence anisotropy has a complex dependence on temperature.^[50] Higher temperature leads to a shorter rotational correlation time, and therefore, lower anisotropy according to the Perrin equation. This increase in temperature decreases the fluorescence lifetime, especially in molecules with strong thermal sensitivity, such as previously mentioned coumarin and cyanine dyes, leading to the opposite effect. Since the role of temperature is difficult to predict, the fluorophores with no rotatable bonds,^[51] and thus stable FL, are preferable for FA-based temperature measurements. These FL-stable molecules are also superior due to their low environmental sensitivity to solvent polarity and viscosity which would otherwise complicates the readout.

Utilizing this rationale, Baffou et al.^[52] reported an FA-based thermal imaging technique using fluorescein with a stable fluorescence lifetime of ≈ 4 ns. The method has been success fully applied to map local temperature around gold nanorods heated by a NIR laser (Figure 6). Addressing the availability of fluorescent, stably transfected cell lines, Donner and colleagues^[53] proposed FA for mapping temperature with green fluorescent protein (GFP). GFP is quite suitable for this task due to its relatively long rotational time of 4.1 ns (because of its large size), which is close to its fluorescence lifetime of 2.5 ns.^[46] This criterion is an important prerequisite for accurate measurements of FA. Furthermore, the method has been tested on GFP transfected cancer cell lines and a temperature sensitivity of about 0.6 K⁻¹ has been achieved.

Figure 6.

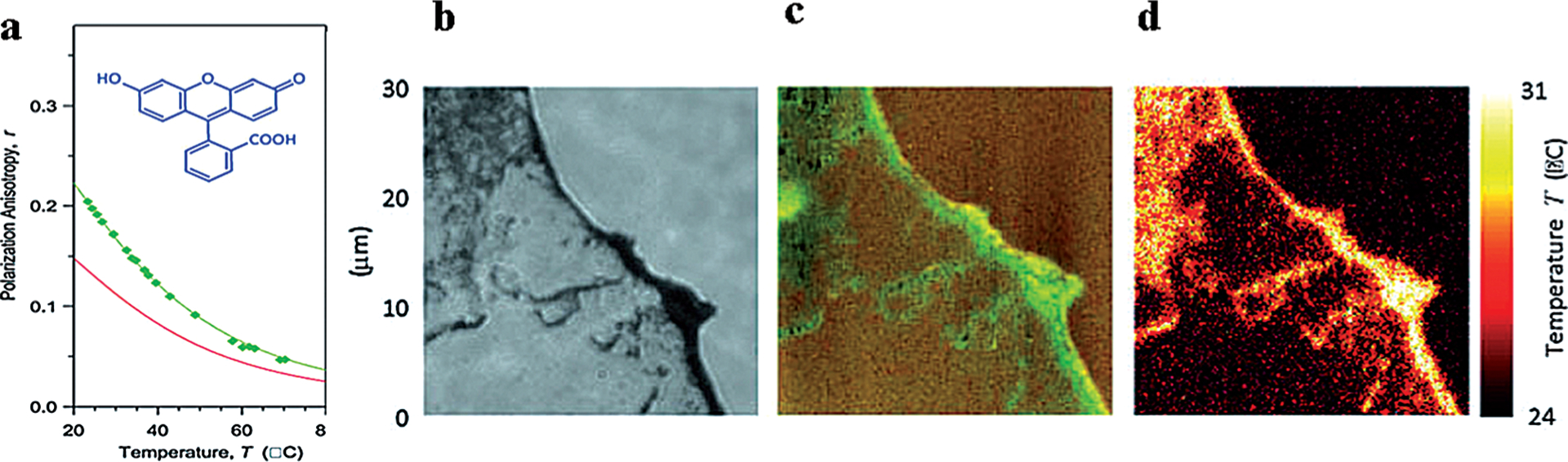
Temperature mapping with FA. a) FA of fluorescein as a function of the temperature a glycerol-water mixture. b) Optical image of dispersed and agglomerated nanorods. c) FA image of the fluorescein surrounding the gold nanorods and sensing the temperature variations. d) Temperature map calculated from (b). From Ref. [52].

In many of the studies, the simultaneous effect of both temperature and viscosity on the optical behavior of fluorophores is rarely considered. Addressing this problem, Vysniauskas et al.^[54] prepared a sensor based on a conjugated porphyrin dimer that is capable of decoupling temperature from viscosity effects and therefore, enables accurate temperature measurements in viscous environments.

4. Nanothermometry for Image-Guided Thermal Ablation

While the measurement of body temperature has been implemented for centuries, measuring the temperature on a submillimetre scale in vivo within deep tissue remains a significant challenge. Recently, this problem became critical in monitoring thermal ablation of tumors, as well as other lesions, such as atherosclerotic plaques and benign masses. In cancer therapy, tumor ablation is a treatment in which a source of energy, such as a radiofrequency, microwave, laser, focused ultrasound, or cryogen (for cryoablation) is used to destroy tumor cells through tissue heating or cooling.^[55] By the middle of 2015, more than 40 active clinical trials were underway utilizing high-temperature ablations and more than 100 trials involved cryoablations.

A major flaw with thermal treatment is the lack of suitable methods to detect temperature at the treatment site in order to control the power and duration of the ablation technique. Precise monitoring of temperature to minimize the damaging effect of overheating or underheating is essential for the efficacy and safety of ablation procedures, and it has been particularly stressed that temperature guidance is critical for the success of thermal therapies.^[56] The use of imaging methods to measure temperature changes has been tested with ultrasound (based on changes in the speed of sound and thermal expansion),^[57] CT (based on density changes),^[58] tissue impedance (based on tissue electrical properties),^[59] and MRI [based on temperature dependence of T1 relaxivity, the diffusion coefficient, magnetization, or water proton resonant frequency (PRF) shift].^[60] Despite the slow response, PRF is the only FDA-approved method of temperature measurement during thermal ablation procedures. Overall, quantifying temperature changes during thermal ablation with most of these techniques has proven difficult, due to tissue-type specificity and heat-induced changes in the corresponding temperature dependencies.^[60a] Following the demand, new approaches with novel temperature-sensitive nanoparticles and nanothermometry techniques, described below, have emerged.

4.1. Photoacoustic (PA) Temperature Measurements

In the PA-assisted thermal ablation technique, temperature is measured directly from the tissue, while nanoparticles (nanoheaters) are used as absorbers of laser, microwave, or magnetic energy. When a pulsed light (typically of the order of nanosecond) irradiates and consequently is absorbed by a tissue of a nanoheater, the object expands and generates an acoustic wave with the measurable amplitude of the PA signal P, as described by Equation (5):

$$P=\Gamma \cdot {\mu }_{\text{a}}\cdot F;\Gamma =\frac{\beta \cdot c^2}{C_{\text{p}}}$$ (5)

where P is the pressure of the generated acoustic wave, Γ the Grueneisen parameter, μ_a the absorption coefficient, F the laser fluence, β the termal coefficent of volume expansion, c the speed of sound and C_p the heat capacity at constant pressure. As is evident from Equation (5), the amplitude P is directly dependent on the Grueneisen parameter. The coefficient b and the speed of sound are both temperature-dependent and linearly proportional to the temperature for body tissues, in the physiologically relevant temperature ranges. Therefore, the Grueneisen parameter, and thus the PA signal, are directly related to temperature and is linearly proportional to the measurable PA signal, according to Equation (6):

$$\Delta T=a\frac{\Delta P}{P}=a\frac{\Delta \Gamma }{\Gamma }$$ (6)

where a is a tissue-dependent constant that can be determined experimentally, ΔP is the increase in pressure when the temperature rises by ΔT, and ΔG is the corresponding change in the Grueneisen parameter. To demonstrate the proof-of-principle in using PA for temperature monitoring, Shah et al.^[61] utilized PA in conjunction with gold nanorods as photoabsorbers and local heat sources in order to achieve a good thermal sensitivity of 5%K⁻¹. Following this study, other PA nanothermometry techniques to monitor thermal ablations of tissue have been developed.^[62] Later, Chen with colleagues^[63] demonstrated that silica-coated gold nanorods provided a multi-fold improvement, reaching a sensitivity of 20%K⁻¹ in comparison to the non-coated nanorods (Figure 7). The authors further applied this technology to visualize photothermal therapy of atherosclerotic plaques.^[64]

Figure 7.

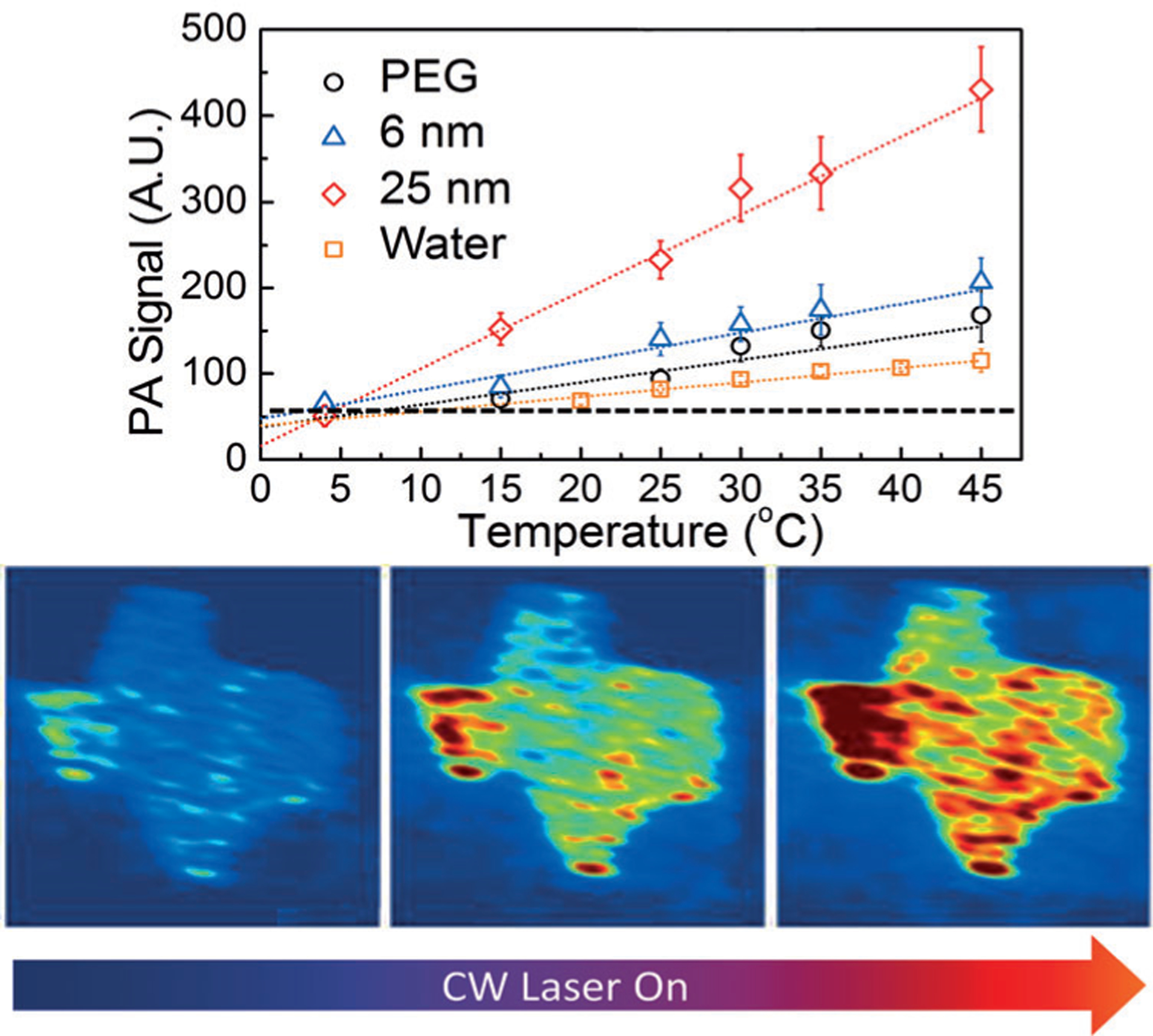
PA in temperature mapping. Top) PA response of silica-covered gold nanorods. Bottom) Mapping of temperature in the tissue phantom with silica-covered gold nanorods. The tissue was heated with a NIR laser. From Ref. [63].

4.2. Ultrasound Microthermometers

In general, ultrasound signal is weakly sensitive to temperature. However, ultrasound contrast agents might show a stronger response due to their temperature-dependent ultrasonic attenuation coefficients. To explore this concept, Biagioni and co-authors^[65] used an ultrasound contrast agent SonoVue as a potential sensor for thermometery. This contrast agent used clinically in echographic imaging techniques to enhance image contrast^[65] is, essentially, a suspension of microbubbles ranging from 1–10 μm in diameter containing an inert SF₆ gas enclosed in a phospholipid membrane.^[66] The SonoVue membrane consists of two types of phospholipids with hydrocarbon chains of different melting temperatures, around 42 and 55°C. Due to the phase transition, the ultrasonic attenuation coefficient of SonoVue has strong dependence on temperature in that range. Thermal testing displayed an almost linear increase of the SonoVue attenuation coefficient, from 45 to 60°C, providing the promising sensitivity of 11%K⁻¹.

4.3. Optical Nanothermometers

Compared to their applications in microscopy, optical nanothermometers are quite rare for deep-tissue measurements. Part of this problem is that the tissue has limited optical transparency due to high absorption and scattering properties of the tissue in the visible range. To be detected by optical techniques, the nanothermometers have to be active in the NIR (700–950 nm also known as Optical Window I), or in the recently discovered extended NIR (exNIR, 950–1400 nm, Optical Window II) range, where the photons penetrate much deeper.^[67]

Our lab approached this requirement by developing nanothermometers that can work both as a local heat source for the laser ablation procedures and as a temperature source.^[9] The nanothermometers were composed of a gold nanorod core absorbing NIR light appended by a temperature-sensitive linker with a fluorescent dye attached (Figure 8). In this design, at normal body temperatures the nanoparticles’ fluorescence is quenched, rendering them invisible; upon heating, the nanoparticle rapidly becomes fluorescent and detectable. Selection of the linker was the major challenge in tuning the temperature sensitivity to the desired ablation range. Overall, the nanothermometers demonstrated negligible fluorescence below 50°C and high fluorescence above 70°C with a thermal sensitivity 70%K⁻¹ (Figure 8). This is so far the highest sensitivity for nanothermometers ever reported, at an order of magnitude higher than other temperature-sensitive designs (from the current review of temperature-responsive materials on a nanoscale^[13a]).

Figure 8.

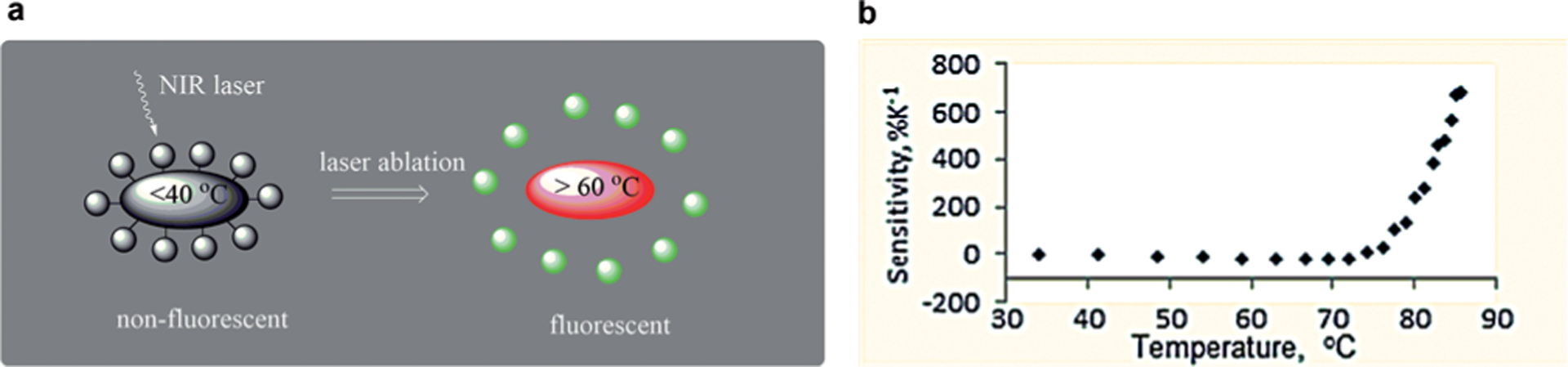
Optical activatable nanothermometers for monitoring laser ablation procedures: a) conceptual design, b) change in fluorescence as the function of temperature. From Ref. [9].

In principle, any temperature-sensitive nanomaterials absorbing and emitting in the NIR or exNIR can be used for deep-tissue thermometry. Thus, certain lanthanides emitting in the NIR range, were investigated in deep-tissue imaging. Benayas et al.^[68] reported on nanothermometers made from Nd:YAG, a well-known material known as “laser glass” that is used for solid-state lasers. Under excitation at 808 nm, the relative intensity of the two spectrally isolated luminescence peaks located at around 940 nm was found to be temperature-dependent, allowing for ratiometric luminescence nanothermometry. Similar thermal properties have been observed in Nd:NaYF₄ glass.^[69] In both cases, the sensitivity was quite low—less than 0.15%K⁻¹.

Reflecting the interest in nanothermometry in the Optical Window II, Klaus et al.^[70] investigated novel 1D polymeric Pt-complexes that emitted in exNIR. The nanostructure represents a “stack-of-chips” configuration that emit at 1060 nm while excited with NIR light (i.e. at 770 nm). The nanomaterials displayed temperature-dependent fluorescence intensity with the sensitivity of 2%K⁻¹ accompanied by a small blue-shift in the broad range of temperatures from −50 to +50°C (Figure 9). Interestingly, the fluorescence intensity of the complexes was increasing, which is quite unique among fluorophores.

Figure 9.

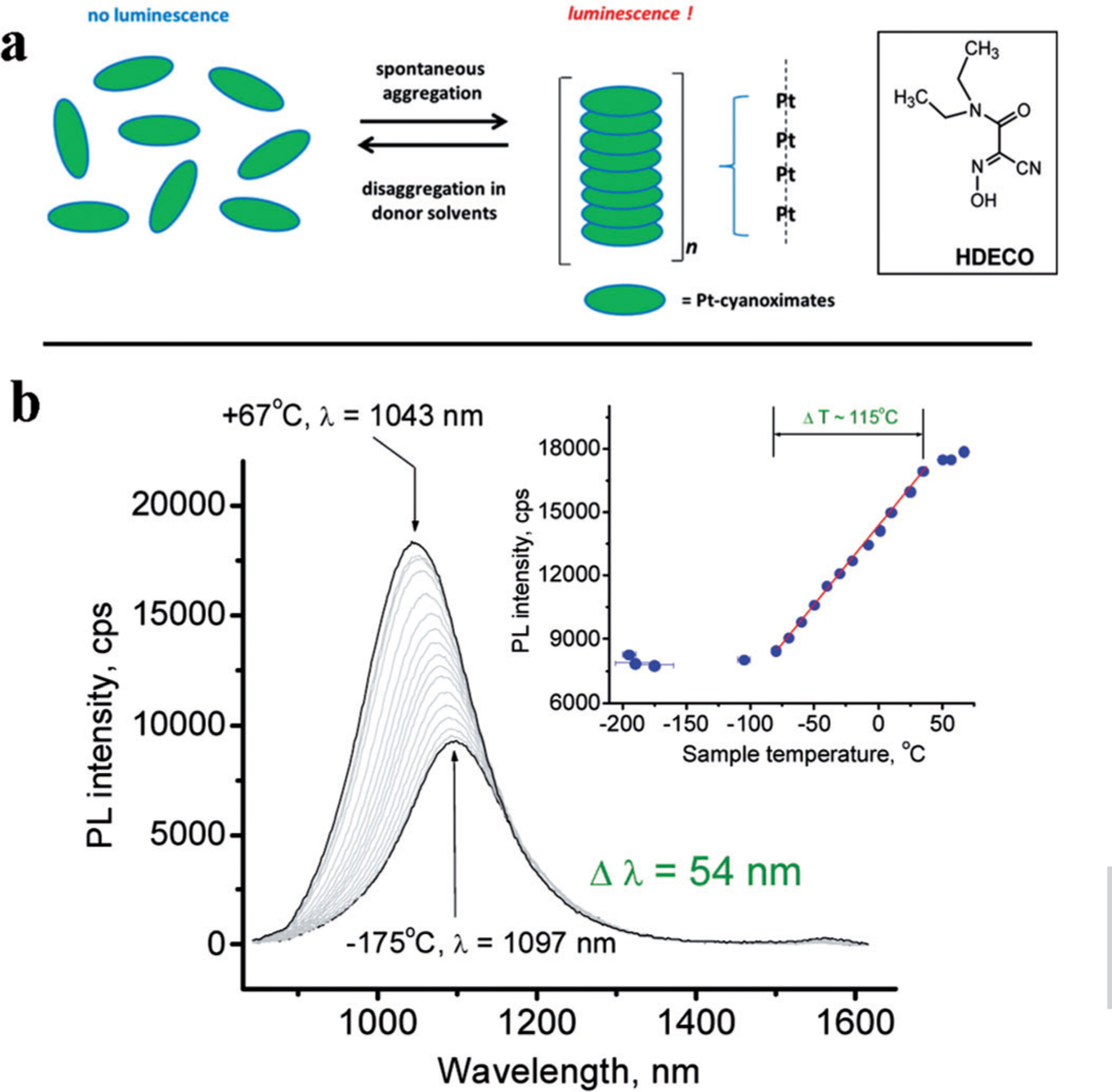
Temperature dependence of the emission of Pt complexes emitting in the exNIR. a) Structure of a 1D Pt(DECO)₂ forming stack-of-chips configuration, b) Thermal sensitivity of the complexes embedded in KBr pellets. λ_ex=770 nm; monitored at 1061 nm. The inset shows a linear response in the emission intensity change with the temperature. From Ref. [70].

5. Concludings and Outlook

The search for efficient nanothermometers to measure temperature in biological tissues is an active area of research, comprising advances in materials science, synthetic and analytical chemistry, engineering, and biology. The motivation comes from both fundamental studies of cell thermogenesis and the controlling of thermal ablations of diseases. One of the promising new directions include the control of optoporation techniques—where holes are created in the cell membrane using femtosecond lasers to allow sterile, non-contact transfection.^[71] Translating optoporation to an in vivo setting offers great potential for investigating the pathogenesis of complex diseases in living animal models.^[72] Another emerging area is in vivo thermogenesis with the goal to understand temperature regulation within and between the organs and monitor metabolic, stress and disease-induced processes in deep tissue.^[73]

Today, there are hundreds of different designs of nanothermometers, or related type of measurements, that have been proposed. Despite the relatively large and rapidly growing activity, the field is still young since no generally accepted methods exist, yet. There are several common issues that withhold this area of research from becoming generally applied in practical situations. One of these issues is the lack of high-accuracy reference standards, which allows stable readings that is independent of cell type, cellular pH, as well as tissue heterogeneity, and in vivo depth. Another drawback is the need for specialized, and thus expensive, equipment that every lab has to develop in order to test a new nanothermometer design. This problem is especially prominent in high-spatial resolution imaging studies. If further developed, nanothermometry promises to be an innovative tool for understanding a variety of cell mechanisms, a method for high-throughput screening in drug design, and a necessary component for targeted treatments of cancer and other diseases.

Biographies

Dr. Haiying Zhou, PhD, received her BS in Chemistry from Zhengzhou University, her MS in Analytical Chemistry from the University of Science and Technology Beijing, another MS in Biochemistry from Wichita State University and her PhD in Organic Chemistry from University of Missouri, Columbia. She is currently a postdoctoral researcher at Washington University School of Medicine. Her research is focused on synthesis of small and macro-molecular agents for non-invasive multi-modal molecular imaging probes for PET, SPECT, MRI and NIR optical imaging.

Monica Sharma is a graduate of Case Western Reserve University located in Cleveland, Ohio. Currently, she is a student in the Masters of Public Health program at Washington University with a specialization in Epidemiology and Biostatistics. She has a long-term interest in the application of imaging modalities and understanding clinically relevant biomarkers that are present in the pathophysiology of various disease states.

Dr. Oleg Berezin, PhD, has graduated from Lomonosov Moscow State University with a major in Physical Chemistry. He is currently a Director of Mobichem Scientific Engineering Ltd., a company that develops innovative optical materials for research and industry.

Dr. Darryl Zuckerman, MD, is a board-certified radiologist with a certificate of added qualification in interventional radiology, the specialty that deals with using imaging guidance to perform a variety of minimally invasive diagnostic and therapeutic procedures. He currently holds the position of program director for the interventional radiology fellowship at Washington University School of Medicine. He is a fellow of the American College of Radiology as well as the Society of Interventional Radiology.

Dr. Mikhail Berezin, PhD, graduated from the Institute of Oil and Gas and the Institute of Organic Chemistry Academy of Science (Moscow, Russia), majoring in Chemistry. After being a research scientist at Monsanto, he moved to an academic career. He is currently an Assistant Professor in Radiology at Washington University School of Medicine. His laboratory develops image-guided minimally invasive optical methods for biomedical applications.