Structure and Stability of Aromatic Nitrogen Heterocycles Used in the Field of Energetic Materials

Abstract

Understanding the stabilization of nitrogen heterocycles is critical in the field of energetic materials and calls for innovative knowledge of nitrogen aromatics. Herewith, we report for the first time that nitrogen lone pair electron (NLPE) delocalization in five-membered nitrogen heterocycles creates a second σ-aromaticity in addition to the prototypical π-aromaticity. The NLPE delocalization and the attendant dual-aromaticity are enhanced as more carbon atoms in the ring are substituted by unsaturated nitrogen atoms. The presence of adjacent nitrogen atoms in the ring can enhance the aromaticity of the nitrogen heterocycles and improve in-crystal intermolecular binding strength but will decrease the firmness of the individual molecular architecture. Notably, such σ-aromaticity is not present in six-membered nitrogen heterocycles, probably due to the longer bonds and broader regions of their rings; therefore, six-membered heterocycles present overall lower aromaticity than five-membered heterocycles. This work brings new knowledge to nitrogen aromatics and is expected to inspire broad interest in the chemistry community.

1. Introduction

Compared to organic chemistry, the development of nitrogen chemistry has been very slow since the Haber–Bosch process was invented in the early 1900s to produce ammonia industrially from nitrogen [1]. A typical example is the full-nitrogen substance pentazole anion cyclo-N₅⁻, which has super-high energy storage in its N−N bond and is considered the ultimate pursuit of energetic materials. The cyclo-N₅⁻, albeit known to be π-aromatic like benzene, exhibits completely opposite properties to benzene—it is surprisingly unstable, difficult to obtain, and susceptible to electrophilic attack. After the first failed attempt in 1903 [2], the cyclo-N₅⁻ was finally isolated in a stable crystal after 114 years of continuous effort [3]. However, the mechanism of the stabilization of cyclo-N₅⁻ and the means of achieving productive separation of cyclo-N₅⁻ need further exploration [4,5].

Coincidentally, anomalous phenomena also occur in the aza systems of alicyclic amines, which are an important composition of energetic materials [6]. According to valence shell electron pair repulsion (VSEPR) theory, the nitrogen lone pair electrons (NLPEs) in a cyclic system should repel the neighboring C-N bonds and other lone pairs in the ring [7,8,9], thereby destabilizing the cyclic aza system. However, the presence of nitrogen in the ring has been proved to confer more degrees of stability to these molecules than their hydrocarbon analogues [6,7], suggesting the failure of VSEPR theory in interpreting the stabilization of the cyclic aza species. Some researchers have proposed that delocalization of the nitrogen lone pair (n→σ*) in the cyclic aza systems accounts for the enhancement of the stability of the cycles [6,10]. However, better understanding of the “aza-stabilization” anomaly calls for new knowledge of nitrogen chemistry.

Herewith, we report a series of quantum calculations on the structure, molecular orbital, electron density, magnetic shielding, and energetics of dozens of compounds composed of various homocycles and nitrogen heterocycles. We discovered for the first time the presence of a second σ-aromaticity in five-membered nitrogen heterocycles, in addition to the prototypical π-aromaticity; however, such σ-aromaticity is not present in six-membered nitrogen heterocycles. This work presents the key role of NLPEs in distinguishing the chemical properties of nitrogen aromatics from those of carbon aromatics and is expected to inspire broad interest in nitrogen chemistry.

2. Results and Discussion

2.1. Enhanced Aromaticity of Nitrogen Heterocycles Due to NLPE Delocalization

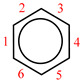
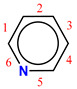
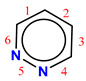
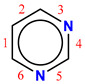
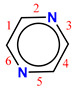
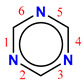
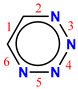
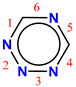
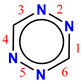
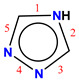
We collected 22 types of molecules, with increasing carbon atoms substituted by nitrogen atoms (see Table 1). All the molecular structures were first optimized by energy minimization and then used for visualization of molecular orbital (MO) and analysis of charge density, magnetic shielding, and bond characteristics. Notably, after geometry optimization, 14 presented slight distortion from the planar conformation (by 0.18 Å), and all the other cyclic molecules remained planar.

Table 1.

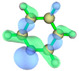
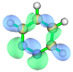
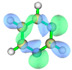
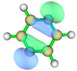
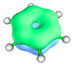
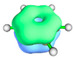
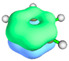
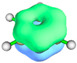
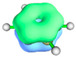
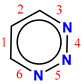
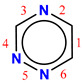
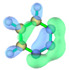
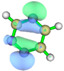
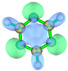
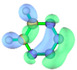
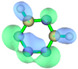
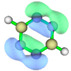
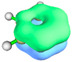
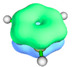
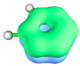
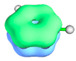
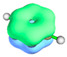
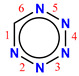
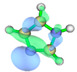
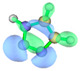
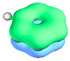
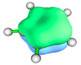
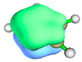
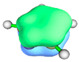
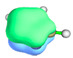
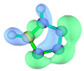
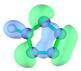
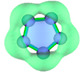
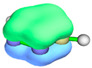
Chemical structures of ammonia (1), benzene (2), six-membered nitrogen heterocycles (3–14), and five-membered nitrogen heterocycles (15–22). The isosurfaces (0.05) of the lowest σ MO containing nitrogen lone pair electrons (MO_min-σ(LP)) and the lowest π MO (MO_min-π) are presented for each of the 22 compounds.

Label	1	2	3	4	5	6
Structure	NH3
MOmin-σ(LP)		-
MOmin-π	-
Label	7	8	9	10	11	12
Structure
MOmin-σ(LP)
MOmin-π
Label	13	14	15	16	17	18
Structure
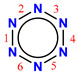
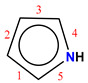
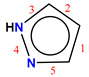
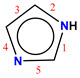
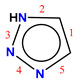
MOmin-σ(LP)			-
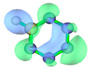
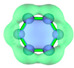
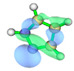
MOmin-π
Label	19	20	21	22
Structure
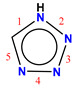
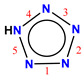
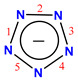
MOmin-σ(LP)
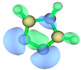
MOmin-π

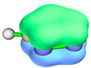
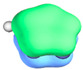
2.1.1. Visualization of the NLPE Delocalization

The nitrogen in 1 (ammonia) was sp³ hybridized, and the carbon and nitrogen in all the cyclic compounds (2–22) were sp² hybridized. The σ NLPE delocalization, as well as the π electron delocalization of the 22 systems, was visualized by the isosurfaces of each lowest molecular orbital (MO), as shown in Table 1. The quantities with min-π/min-σ(LP) subscripts were the components contributed by the lowest energy level of π-electrons/σ-NLPEs.

We first studied the cases with a single unsaturated nitrogen atom (1, 3, 16, and 17), with each of these systems presenting only one pair of σ-NLPEs. For example, ammonia (1) has one pair of NLPEs at the top of the trigonal pyramidal of the structure; 3 has one pair of NLPEs in the ring; for 16 and 17, the NLPEs of the saturated nitrogen join the lower-energy π MO, so there is only one pair of σ-NLPEs affiliated with the unsaturated nitrogen in each heterocycle. As shown by the shapes of their MO_min-σ(LP) in Table 1, these σ-NLPEs were highly localized in the region of the unsaturated nitrogen atom. The high localization of the σ-NLPEs makes these systems basic and attractive to electrophiles, which is consistent with traditional organic/inorganic chemistry knowledge [7].

However, the presence of more than two unsaturated nitrogen atoms in the ring, partially in the ortho positions, made the NLPEs delocalized in a broader region. For example, 4, 7, 10–12, and 18–21 had the isosurfaces of their MO_min-σ(LP) continuously distributed in the region between the unsaturated nitrogen atoms, as shown in Table 1. Notably, although 8 and 13 had adjacent unsaturated nitrogen atoms in the ring, some of these nitrogen atoms contributed their NLPEs to the relative lower energy π orbital instead of the σ orbital. Therefore, these two compounds did not have ortho-NLPEs, but showed para- and para-NLPEs in each MO_min-σ(LP). Table 1 indicates that the σ-NLPEs in 5, 6, 8, 9, and 13, which had para or meta position in each ring, were generally more localized compared to those NLPEs in the ortho positions.

In extreme cases, when all carbon atoms were substituted by unsaturated nitrogen atoms in the ring, the delocalization of the NLPEs formed into a circle and achieved a maximum. For example, the MO_min-σ(LP) of 14 and 22 spread out over each molecule into a flower shape in the equatorial plane, as shown in Table 1. This is consistent with our previous study on pentazolate anion [11,12].

In brief summary, the substitution of carbon atoms by unsaturated nitrogen atoms in the heterocycles improved the extent of the delocalization of NLPEs. More unsaturated nitrogen atoms led to a higher extent of NLPE delocalization, and the preferable order of the NLPE positions that contributed to such delocalization was ortho > meta > para.

2.1.2. Quantification of the NLPE Delocalization

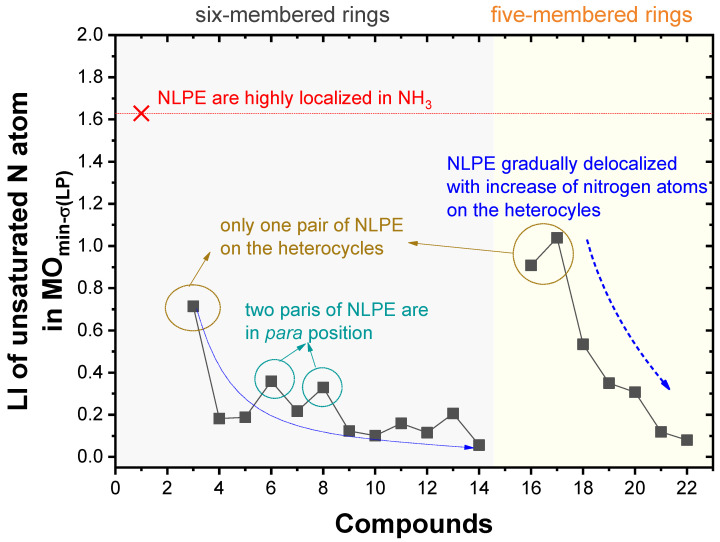
In order to quantify the delocalization extent of the NLPEs, we calculated the electron-based aromaticity LI [13,14]. The LI quantitatively measured how many electrons were localized in a region; a higher LI value suggested stronger localization, but weaker delocalization of the NLPEs. The LI of the unsaturated nitrogen atoms projected in MO_min-σ(LP) for each of the 22 studied compounds is shown in Figure 1.

Figure 1.

Localization index (LI) of unsaturated nitrogen atom in each lowest σ(LP) orbital for the 22 studied compounds.

Figure 1 confirms that, in the systems with a single unsaturated nitrogen atom, such as 1 (LI = 1.63), 3 (LI = 0.71), 16 (LI = 0.91), and 17 (LI = 1.04), the NLPEs were highly localized. The NLPEs in the para positions (LI = 0.36 for 6 and LI = 0.33 for 8, with 2 pairs of NLPEs in the para positions) contributed less to the delocalization of the heterocycles, compared to those NLPEs in the ortho and meta positions (LI = 0.18 for 4, with 2 pairs of NLPEs in the ortho position; LI = 0.19 for 5, with 2 pairs of NLPEs in the meta position).

The extent of the NLPE delocalization gradually increased as a function of the number of unsaturated nitrogen atoms in the ring. Notably, the change of the NLPE delocalization in the five-membered heterocycles (with LI varying in 1.04–0.08) was more dramatic than in the six-membered heterocycles (with LI varying in 0.71–0.06).

2.1.3. Discovery of Additional σ-Aromaticity in Five-Membered Nitrogen Heterocycles

To determine how aromaticity (including prototypical π-aromaticity, newly proposed σ-aromaticity, and total aromaticity) varies in these heterocycles, we further calculated the magnetic index of aromaticity–NICS_zz(r), which is the NICS value along the z axis, by far the most widely used method for diagnosing aromaticity [15,16]. The indices with π/σ subscripts were the components contributed by all the π-electrons/σ-electrons. The more negative the NICS values, the more aromatic were the rings.

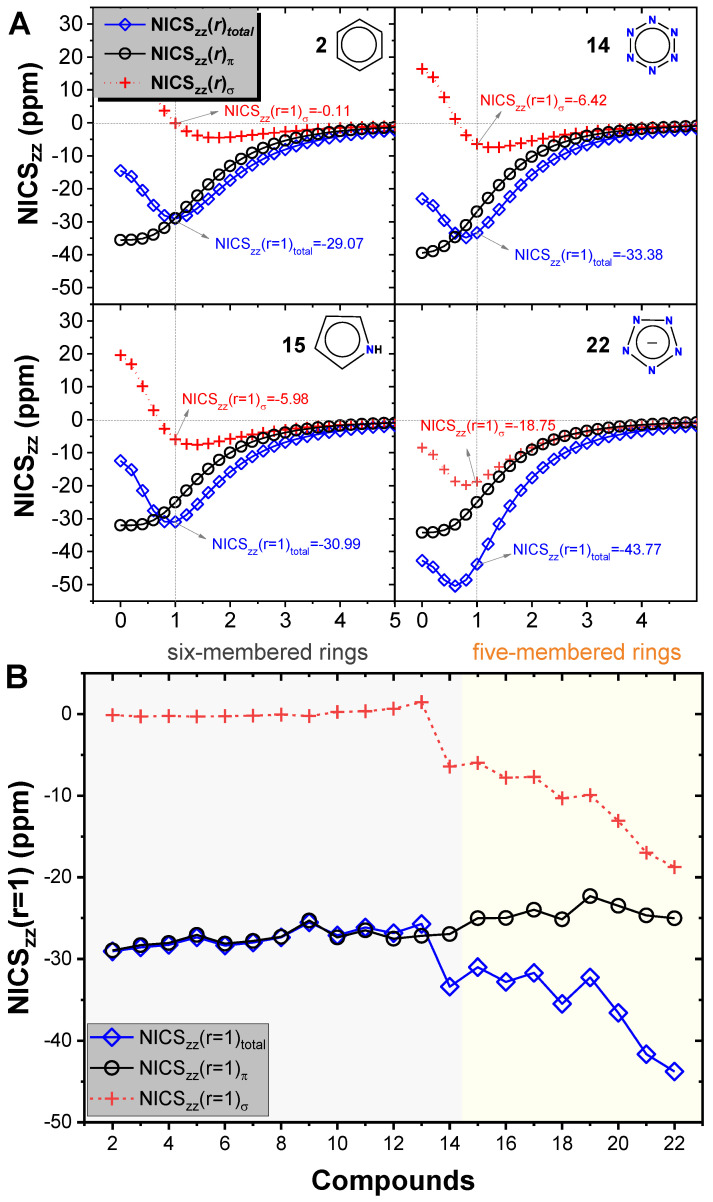
Taking 2, 14, 15, and 22 as examples, we showed the NICS_zz(r)_total, as well as the π and σ orbital components (NICS_zz(r)_π and NICS_zz(r)_σ) in Figure 2A. As the vertical distance relative to the ring critical point varied from r = 0.0 to 5.0 Å, NICS_zz(r)_π was always negative for 2, 14, 15, and 22, suggesting the presence of π-aromaticity in these systems. NICS_zz(r)_σ was always negative in 22, whereas it was positive or close to zero in 2; the situations of 14 and 15 were between 2 and 22. This indicated the presence of σ-aromaticity in the all-nitrogen compound 22, whereas benzene 2 lacked such σ-aromaticity; 14 and 15 had only weak σ-aromaticity.

Figure 2.

(A) NICS_zz(r)_total, NICS_zz(r)_π, and NICS_zz(r)_σ of 2, 14, 15, and 22 as a function of r, the vertical distance relative to the ring critical point. (B) NICS_zz(r = 1)_total, NICS_zz(r = 1)_π, and NICS_zz(r = 1)_σ of all 21 of the studied cyclic systems.

The order of the σ-aromaticity of the four compounds could be quantified by the absolute values of NICS_zz(1)_σ: 22 > 14 > 15 > 2. Here NICS_zz(1) was the NICS_zz value when the vertical distance relative to the ring critical point was 1 Å. Due to the significant contribution of σ-aromaticity in the four compounds, their overall aromaticity presented an identical order to the σ-aromaticity, with the order of the absolute values of NICS_zz(1)_total being 22 > 14 > 15 > 2.

We further performed NICS_zz(r)_total, NICS_zz(r)_π, and NICS_zz(r)_σ calculations for all other cyclic systems when r varied from 0.0 to 5.0 Å. The highest absolute value of the NICS_zz(r)_total for 13 and 15 was r_extreme = 1.0 Å vertically above the ring critical point; for 14 and 16–20, r_extreme = 0.8 Å; for 21 and 22, r_extreme shifted to 0.6 Å, identical to the P₂N₃⁻ anion [17]. In order to evaluate the aromaticity of all 21 cyclic systems in identical conditions, we uniformly took the NICS_zz(r) values at r = 1 Å to compare their aromaticity, as shown in Figure 2B.

Figure 2B clearly indicates that σ-aromaticity was present in all five-membered rings, and it was gradually enhanced as the number of nitrogen atoms in the ring increased; σ-aromaticity reached a maximum in 22, in which all carbon atoms were substituted by unsaturated nitrogen atoms. In addition, we found a significant influence of bond length in the ring on the aromaticity of the compound; longer bonds in the ring led to weaker aromaticity. For example, 16 and 17 were isomers; the latter had longer bonds in the ring (Figure 3) and thereby had smaller π-aromaticity, σ-aromaticity, and total aromaticity. Similar phenomena occurred also in isomeric 18 and 19. Interestingly, except for 14, no obvious σ-aromaticity was present in the six-membered rings, probably due to the longer bonds and broader regions of their rings compared to the five-membered rings.

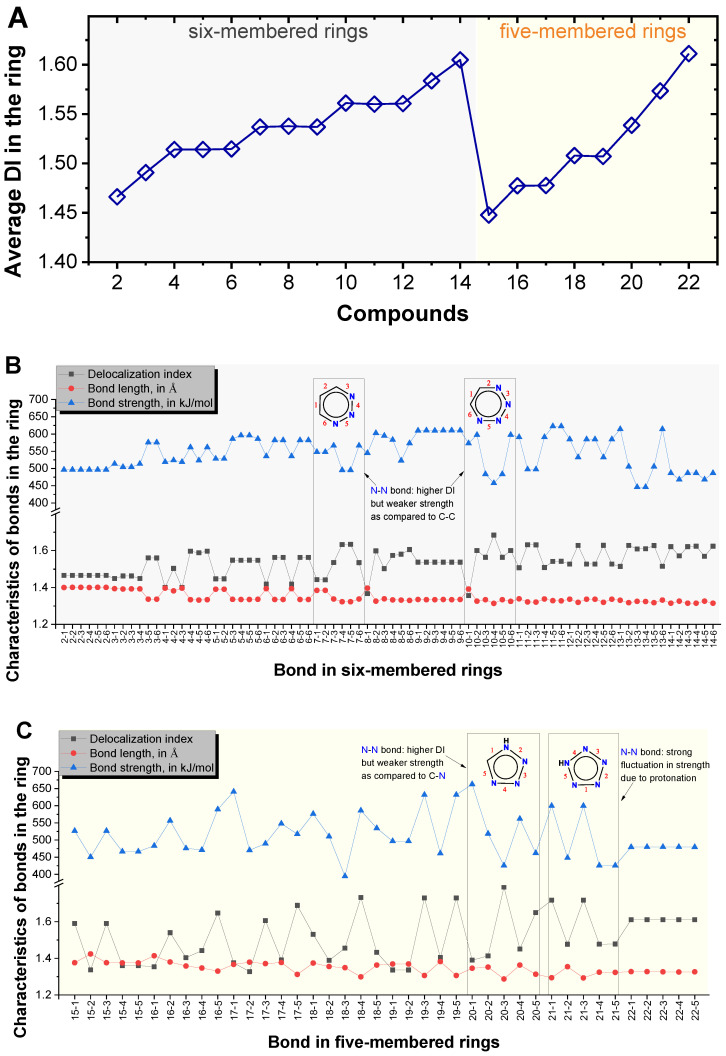
Figure 3.

(A) Average delocalization index (DI) of the bonds in the ring for the 21 cyclic compounds. (B) DI, length, and strength for individual bonds in the rings of the six-membered compounds and (C) five-membered compounds. X-Y in x-axis denotes bond Y of compound X; the Y bond indices for each compound are illustrated in Table 1.

Due to the contribution of the NLPE delocalization, the five-membered rings showed dual-aromaticity, namely π- and σ-aromaticity. Figure 2B indicates that dual-aromaticity of the five-membered rings, with NICS_zz(1)_total in the range of −43.77 to −30.99, was significantly higher than the prototypical aromaticity of the six-membered rings, which had their NICS_zz(1)_total in the range of −29.07 to −25.53.

We note that the dual aromaticity in five-membered nitrogen heterocycles is very different from the double aromaticity of metallic compounds. The dual aromaticity of, for example, Al₄²⁻ dianion means that four σ electrons and two π electrons together form a single aromatic system due to the electron deficiency of the dianion [18,19,20]. However, the dual aromaticity of five-membered nitrogen heterocycles was derived from two separate aromatic systems, with independently delocalized π-electrons and σ(LP)-electrons, like those present in 3,5-dehydrophenyl cation [21], saturated inorganic rings [22], and probably in pnictogen five-membered rings like P₅⁻ and As₅⁻ anion [23,24].

Therefore, the “dual” aromaticity in five-membered nitrogen heterocycles means two types of electrons and two separate aromatic systems. As we declared in one of our previous works, the two aromatic systems are independent in real space but are coupled in energy space. The competition between the nonbonding interactions in both aromatic systems and the LP–LP repulsive interactions in the σ aromatic system makes the dual-aromatics show different reactivity to electrophilic attack in different acidic solutions [11].

2.2. Effect of Enhanced Aromaticity of Heterocycles on Structure Stability

In this section, we investigate the effect of enhanced aromaticity of nitrogen heterocycles on their structure stability, at both the molecular and crystal levels. Notably, the calculation method for crystal systems considers periodic boundary condition and intermolecular interactions and thereby can reflect the effect of aromaticity on the energetics of solid-state systems.

2.2.1. Reduced Molecular Structure Firmness

Structure stability of nitrogen heterocycles is closely related to the firmness of their backbone bonds. Herewith, we quantified the firmness of the bonds in the ring by their DI, bond length, and bond strength, as shown in Figure 3.

DI [14], also called fuzzy bond order [25,26], measures the number of shared electrons between two atoms. Figure 3A clearly indicates that the average DI of the ring, namely the electron delocalization over the cyclic backbone, was enhanced as the number of unsaturated nitrogen atoms increased.

The characteristics of each individual bond in the rings of the 21 cyclic compounds, including DI, length, and strength, are shown in Figure 3B,C. Bond length was calculated using the HASEM application [11,27]. Figure 3 indicates that higher DI and smaller bond length generally corresponded to higher bond strength. However, we found that N−N bonds presented significantly lower strength as compared to C−C or C−N bonds, even when they had higher bond orders (applicable when DI ≤ 2); this finding is consistent with a previous report [28].

When more carbons are substituted by nitrogen atoms, the attendant phenomenon is that more N−N bonds, which have low strength and are very likely to rupture, will be present. Therefore, although NLPEs are more delocalized in the ring and even create additional σ-aromaticity, the firmness of the entire molecular architecture is reduced once adjacent nitrogen atoms are present in the ring. For example, bond 4 and 5 in compound 7 (7-4 and 7-5) in Figure 3B; bond 4 in compound 10 (10-4) in Figure 3B; bond 3 in compound 20 (20-3) and so on. These mentioned N–N bonds have much lower strength compared to C−C or C−N bonds in the rings.

The very low N-N bond strength of cyclo-pentazolate anion (22) is the reason that 22 is difficult to productively separate, because these N-N bonds easily break prior to the C−N bond cleavage in the precursor 3,5-dimethyl-4-hydroxyphenylpentazole [3]. One practical way, as reported in our recent work [11], is to introduce an appropriate concentration of hydronium or ammonium in the solution, which strengthens all the N–N bonds in 22 with the aid of the electron delocalization of the formed hydrogen bonds.

2.2.2. Improved In-Crystal Intermolecular Binding Strength

Crystal structure stability depends significantly on the interspecies binding strength of the constitution components. Therefore, the stability of the crystals composed of nitrogen heterocycles is closely related to one of the important intermolecular–aromatic interactions.

Herewith, we collected 32 crystal structures composed of ammonia and various homocyclic and nitrogen heterocyclic molecules (Table 2). Lattice energy (LE), the energy difference between total energy of constituent molecules in the free state and total energy of the crystal, was employed to quantify the in-crystal binding strength, as shown in Figure 4. The number of hydrogen atoms in each molecule was also plotted to evaluate the effect of hydrogen bonding on LE.

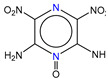
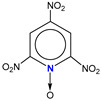
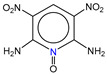
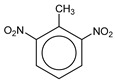
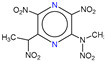
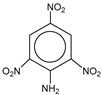
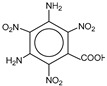
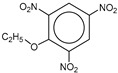
Table 2.

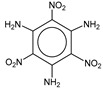
Lattice energies (LE, in kcal·mol⁻¹) of 32 crystals composed of ammine and various nitrogen heterocycles. Cambridge Crystallographic Data Centre (CCDC) number of the crystal structures, as well as the chemical structures of the constituent molecules are provided.

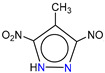
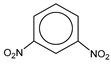
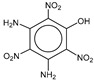
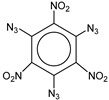
Label	CCDC No.	Structure	LE	Label	CCDC No.	Structure	LE
c1	1644462	NH3	13.01	c17	1272845		24.35
c2	725244		12.83	c18	1272852		24.49
c3	1177301		12.50	c19	1214795		24.53
c4	1166481		17.52	c20	125117		24.73
c5	1142965		18.28	c21	1255528		25.17
c6	213311		18.97	c22	1910475		25.22
c7	201615		19.78	c23	1105564		25.50
c8	171054		19.91	c24	1136625		26.26
c9	258373		20.27	c25	166510		27.22
c10	667816		20.40	c26	938305		28.93
c11	258373		20.49	c27	910889		29.28
c12	225824		20.65	c28	1266837		30.17
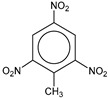
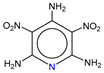
c13	227799		21.32	c29	1270764		30.22
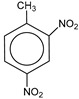
c14	225823		21.48	c30	273637		31.14
c15	947035		22.32	c31	1135164		32.58
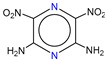
c16	1272856		24.13	c32	938305		32.67

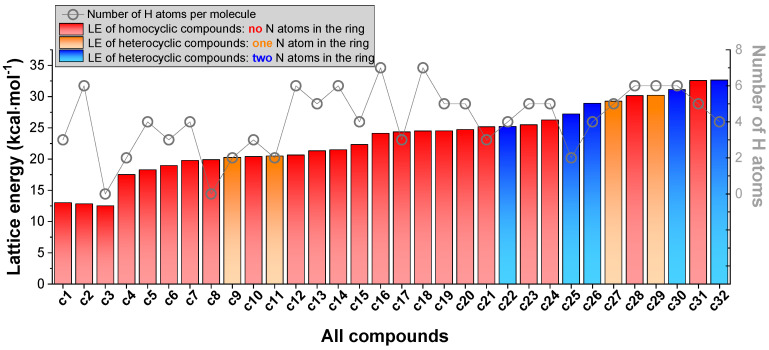
Figure 4.

Lattice energy (LE) of 32 crystals composed of ammonia (red bar), homocycles (red bar), and heterocycles (with one N in the ring, orange bar; two N in the ring, blue bar). Number of hydrogen atoms in each molecule is plotted by grey open circles.

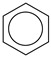
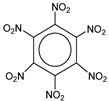
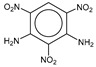
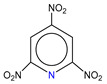
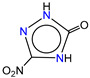
As shown in Figure 4, c1 (ammonia), which has no aromaticity, is gaseous at ambient condition and has the lowest LE of 13.01 kcal·mol⁻¹. As for the cyclic systems, Figure 4 indicates that the crystals composed of C–N heterocycles generally have higher stability as compared to those composed of all-C homocyclic molecules. One typical example is c9 and c11, which have one nitrogen atom in each heterocycle. Both have relatively less hydrogen bonding than c5–c7, but present higher LE (20.27 and 20.49 kcal·mol⁻¹ for c9 and c11, respectively) than c5–c7 (LE in the range of 18.28–19.78 kcal·mol⁻¹). Another typical example is c25 and c32, which have two nitrogen atoms in each heterocycle. Both have much less hydrogen bonding than c23 and c24, whereas they present higher LE (27.22 kcal·mol⁻¹ for c25 and 32.67 kcal·mol⁻¹ for c32, respectively) due to their relatively stronger aromaticity. In addition, the presence of nitro group is conducive to provoking dipole–dipole interactions, thereby further enlarging LE of the crystal.

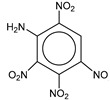
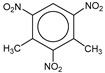
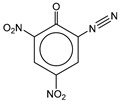
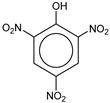
c2–c8, on the other hand, have no nitrogen atoms in their rings, relatively less hydrogen bonding, and present very low LE (in the range of 12.83–19.91 kcal·mol⁻¹, respectively). For example, c2 (benzene) has very low LE (12.83 kcal·mol⁻¹) and is liquid at ambient condition. c3 (HNB explosive), with a low LE = 12.50 kcal·mol⁻¹, is very sensitive to light and easy to decompose. c12–c21 generally have abundant hydrogen bonding, whereas they have relatively lower LE than the crystals composed of heterocyclic molecules (like c22, c25, c26, c27, c29, c30, and c32) due to the absence of nitrogen atoms in their rings and therefore relatively weaker aromaticity.

In brief, we found that strong aromaticity of heterocyclic molecules is conducive to enhancing in-crystal intermolecular binding, and vice versa.

3. Computational Methodology

In order to study NLPE delocalization characteristics and the attendant changes in aromaticity and structure stability of nitrogen heterocycles, we collected 22 molecular structures and 32 crystal structures composed of ammonia and six- and five-membered homocycles and nitrogen heterocycles. All of these are functional groups or molecules of commonly seen energetic materials.

At the molecular level, the structure optimization was performed using Gaussian 09 at the B3LYP/6-311++G(d,p) level of theory [29]. The optimized structures were then used for charge density analysis. All the electron-based aromaticity indices, namely the localization index (LI) and the delocalization index (DI) [14,25,26], were calculated at the CCSD(T)/6-31G+ level, and the magnetic based aromaticity index (nucleus-independent chemical shifts, NICS [15,16]) were calculated at the B3LYP/6-311++G(d, p) level. Using natural bond orbital (NBO) analysis and the quantum theory of atoms in molecules (QTAIM) method, the Multiwfn application [13] was used to separate DI and NICS into individual components contributed solely by specified orbitals.

The crystal level calculations were performed using High Accuracy Atomistic Simulation for Energetic Materials (HASEM) software [27,30], with the inputs taken from the lattice parameters and atomic coordinates of the CIF files stored in the Cambridge Crystallographic Data Centre (CCDC) database [31]. All the geometry optimization was performed using the conjugate gradient method. The simulated structures were considered to be optimized when the residual forces were less than 0.03 eV/Å, and the stress components were less than 0.01 GPa. The optimized structures were then used for energetics evaluation.

4. Conclusions

We performed a quantum a chemistry study on 54 aza systems (22 molecules and 32 crystals) and studied the aromaticity of various nitrogen heterocycles from the perspectives of structure, molecular orbital, electron density, magnetic shielding, and energetics. The main conclusions are as follows:

• (1)More unsaturated nitrogen atoms present in the heterocycles lead to a higher extent of nitrogen lone pair electrons (NLPE) delocalization, and the preferable order of the NLPE position that contributes to such delocalization is ortho > meta > para.
• (2)σ-aromaticity is discovered in five-membered nitrogen heterocycles, in addition to the prototypical π-aromaticity; however, such σ-aromaticity is not present in six-membered nitrogen heterocycles.
• (3)The presence of adjacent nitrogen atoms in the ring of nitrogen heterocycles (ortho) decreases the firmness of the molecular structure, but can increase the in-crystal intermolecular binding strength.

Author Contributions

Conceptualization and manuscript writing, L.Z.; molecular structure design, validation, and manuscript writing, J.-G.Z.; calculations and data analysis, H.-H.Z.; discussion and manuscript co-writing, C.Y. and C.Q.S. All authors have read and agreed to the published version of the manuscript.

Funding

The authors greatly acknowledge the financial support from the National Natural Science Foundation of China (Grant Nos. 11604017, U1830134, 21911530096, 11702262, and 11572294).

Conflicts of Interest

The authors declare no conflict of interest.