Limitations and challenges in protein stability prediction upon genome variations: towards future applications in precision medicine

Graphical abstract

Abstract

Protein stability predictions are becoming essential in medicine to develop novel immunotherapeutic agents and for drug discovery. Despite the large number of computational approaches for predicting the protein stability upon mutation, there are still critical unsolved problems: 1) the limited number of thermodynamic measurements for proteins provided by current databases; 2) the large intrinsic variability of ΔΔG values due to different experimental conditions; 3) biases in the development of predictive methods caused by ignoring the anti-symmetry of ΔΔG values between mutant and native protein forms; 4) over-optimistic prediction performance, due to sequence similarity between proteins used in training and test datasets. Here, we review these issues, highlighting new challenges required to improve current tools and to achieve more reliable predictions. In addition, we provide a perspective of how these methods will be beneficial for designing novel precision medicine approaches for several genetic disorders caused by mutations, such as cancer and neurodegenerative diseases.

1. Introduction

Protein structure is determined by the interactions among the amino acids and with the environment, resulting in a stable 3D structure. In the folding process, a stable 3D conformation of the protein corresponds to a minimum of the Gibbs free energy (ΔG) of the protein-environment system. ΔG of folding includes both the entropic contributions (hydrophobic effects and protein configurations) and the interaction energies within the protein (like Van der Waals interactions, hydrogen and electrostatic bonding, etc.). In many cases, the functional cycle of the protein is accomplished by switching among a few stable 3D conformations, implying the existence of several local free energy minima experienced by the same protein and the need of keeping the energy barriers among them relatively low. Non-synonymous DNA variations, which alter the amino acid sequence, may change protein function by either increasing or decreasing protein stability, which may prevent the conformational changes required for the protein to function [1]. Mutations occurring at the surface of a protein domain are often neutral. Yet, they may affect the binding affinities for other proteins or the inter-domain compactness in multi-domain proteins. Mutations occurring in the core may alter the stability in the domain fold [2]. Indeed, protein stability changes have been shown to constitute one of the major underlying molecular mechanisms in several mutation-induced diseases [3] and might prove to be an even more frequent cause of function loss and disease than previously thought. Understanding how specific mutations in a patient affect protein stability or interactions can identify possible drug resistance/sensitivity in that patient, allowing better therapeutic approaches. In addition, such knowledge is important for improving the protein design through site-directed or random mutagenesis, leading to promising new approaches for precision medicine.

The effects of non-synonymous variants on protein stability are quantified in terms of the Gibbs free energy of unfolding (ΔG). ΔG is a nonlinear function of several factors, like temperature, pH values, concentrations of salt, organic solvents, urea and other chemical agents. From the experimental point of view, the measure of interest is the difference of the unfolding free energy between the mutated and wild-type proteins (ΔΔG^u). Thus ΔΔG^u = ΔG^u_mutant- ΔG^u_wild-type, which is the difference of the free energy of unfolding between the mutated and wild-type proteins (Fig. 1, central box). The sign of ΔΔG indicates if the variation decreases (ΔΔG^u < 0) or increases (ΔΔG^u > 0) the protein stability. However, the opposite convention is also possible (ΔΔG^f = ΔG^f_mutant − ΔG^f_wild-type). Thus, it is crucial to specify which definition is adopted. In this review, we will use the symbol ΔΔG to refer to ΔΔG^u.

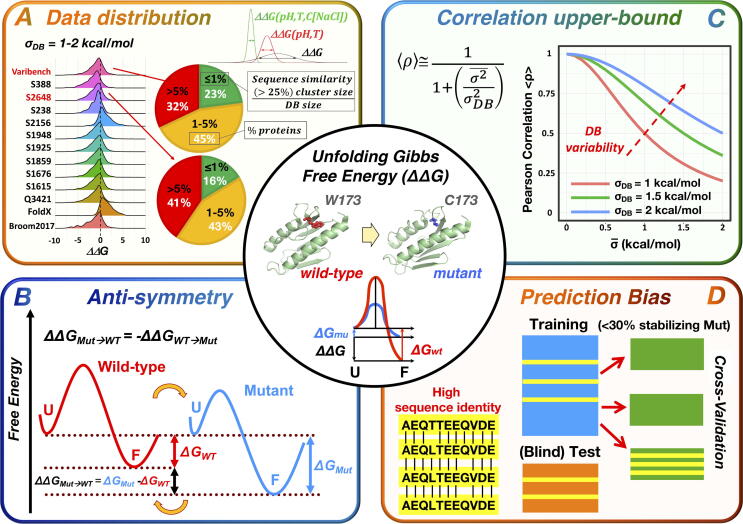
Fig. 1.

Summary of the main issues affecting the prediction of stability changes upon mutation. A) Distribution of ΔΔG values from current databases (DB), characterized by σ_DB < 2 kcal/mol, and intrinsic variability of the available ΔΔG values, which are obtained under different experimental conditions (upper-right corner of panel A). The pie-charts represent the distribution of proteins clustered by sequence similarity for the two largest and most widely used datasets (S2648 and VariBench). Clusters were obtained using blastclust (www.ncbi.nlm.nih.gov/Web/Newsltr/Spring04/blastlab.html), using a threshold cut-off of 25% of identity. The proportion of proteins belonging to clusters with a size representing <= 1%, 1–5% and > 5% of the size of the entire DB are highlighted in the pie-charts in green, orange and red, respectively. The smaller the cluster size, the lower the probability of choosing proteins with sequence identity or high sequence similarity. Only a small fraction of the datasets can be randomly selected (green slices). B) Anti-symmetric properties of the folding process. U = unfolded; F = folded. C) Low upper-bound for correlation estimates due to low variability of ΔΔG values in current databases. D) Biased datasets, due to unbalance between destabilizing and stabilizing (< 30%) variants and to the presence of proteins with high sequence identity, which generate inappropriate training/testing sets leading to over-fitting issues during the learning process (e.g yellow-green set in cross validation and the blind test set in panel D). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Protein stability has been traditionally measured with circular dichroism, differential scanning calorimetry, fluorescence spectroscopy using thermal and denaturant unfolding methods [4]. Although experimental approaches to measure differences between mutant and wild-type proteins are accurate, they are demanding in terms of time and costs. Therefore, several computational methods have been developed for assessing and predicting how protein stability is affected by single-point mutations [5]. Most of them aim at either classifying the effect (stabilizing/destabilizing/neutral) or quantifying the ΔΔG values.

Several tools for predicting pathogenic variants have been developed and reviewed [6], [7], [8], [9], [10]. In this work, we focus on the methods and issues related to the robust prediction of ΔΔG values, providing a comprehensive evaluation of both the limits of current approaches and some possible solutions to achieve better predictions by minimizing the bias in the performance assessment. Recent critical reviews were already provided by Pucci et al. [11] and Fang [12]. Here we will extend those reviews by introducing some further crucial points, discussing: 1) the unbalance and intrinsic variability of the thermodynamic data; 2) the failure of taking into account the anti-symmetric property of the folding process (ΔΔG^u = −ΔΔG^f ); 3) the best practices for providing a fair assessment of prediction performance. Beyond discussing these critical points, an additional aim of the present review is to provide a perspective in using these prediction approaches for direct biomedical applications. Such tools could help clinicians in selecting the most appropriate treatments and creating novel therapeutic strategies based on a more thorough genetic understanding of the patient's disease.

2. Stability data and benchmark sets

As pointed out by Pucci and Rooman [13], current experimental and computational techniques provide only a partial picture of protein folding and adaptation processes, making the comparison between different prediction approaches a non-trivial task. Furthermore, despite the large number of benchmark datasets provided by VariBench and VariSNP used for variation interpretation [14], only a few sources are available for protein stability studies. The main repository to retrieve protein stability information used to be ProTherm [15], which provided a collection of thermodynamic measures including Gibbs free energy change, enthalpy change, heat capacity change, transition temperature etc. for both wild-type and mutant proteins. The last version (5.0) contained ~ 17,000 entries from 771 proteins. Reported thermodynamic measurements for wild-type proteins, single, double and multiple mutants were 7014, 8202, 1277 and 620, respectively. However, this database is not available anymore, and it is known to present several inconsistencies [14], including missing thermodynamic values and ΔΔG values with opposite sign. Data need to be filtered and manually cleaned for collecting reliable datasets. For these reasons, a large number of curated benchmark datasets was derived from ProTherm. The most used ones are reported in Table 1. Despite the several considered subsets, there is an urgent need for new experimental data, particularly for stabilizing mutations: they account for <30% of the datasets reported above; the worst case is represented by S388, with only 11% stabilizing mutations. Indeed, the available datasets are still limited compared to the thousands of three-dimensional (3D) protein structures available in the Protein Data Bank (PDB) [34], which in total includes ~ 167,000 proteins (as of July 2020). A major limitation of the currently available data is the intrinsic variability characterizing the ΔΔG values. Two experimental ΔΔG measurements of the same variant may disagree if not carried out under the same conditions and by the same experimental technique. Therefore, methods have to deal with ΔΔG values that have different uncertainties associated with their measurements (see Fig. 1A) and multiple experimental ΔΔG values for the same mutation. As an example, in Keeler et al. [35] the variation of Histidine 180 to Alanine in the human prolactin measured at 25 °C, but different pH, corresponds to a ΔΔG = 1.39 kcal/mol at pH = 5.8 and ΔΔG = -0.04 at pH = 7.8. In Ferguson and Shaw [36], the variation of Leucine 3 to Serine in the calcium-binding protein S100B, measured under two different starting conditions and techniques but at the same temperature (25 °C) and pH (7.2), yielded two different ΔΔG: 1.91 and −2.77 kcal/mol. In addition, some works used all the ΔΔG values for training/testing, while other analyses focused on selected subsets of ΔΔG values obtained under specific experimental conditions (e.g. S388) or took their average or weighted average (e.g. S2156 and S2648). Considering the overall ΔΔG value distributions for the most used databases, the observed variability is high (Fig. 1A); e.g. ΔΔG standard deviation is 2.06 kcal/mol in ProTherm, 1.91 kcal/mol in Varibench [31], 1.47 kcal/mol in S2648 [25]. Actually, a meaningful comparison of different methods should be based on the same datasets.

Table 1.

The most used datasets and subsets derived from ProTherm Database.

Dataset	Total Variants (Proteins)	Stabilizing Variants (Proteins)	Destabilizing Variants (Proteins)	Additional Details
Broom2017 [16]	605 (58)	147 (37)	458 (54)	Unique Variants/Background Variants
Cao Test [17]	276 (37)	79 (21)	197 (35)	Replicated Variants
Cao Train [17]	5,444 (2 0 4)	1,233 (1 5 0)	4,211 (1 8 5)	Replicated Variants
Fold-X [18]	964 (38)	110 (25)	854 (36)	Unique Variants
Myoglobin [19]	134 (1)	36 (1)	98 (1)	One Protein
p53 [20]	42 (1)	11 (1)	31 (1)	One Protein
PTmul [21]	914 (90)	310 (57)	604 (68)	Unique Variants/Multiple Variants
Q3421 [22]	3,421 (1 4 8)	763 (1 1 4)	2,658 (1 3 1)	Unique Variants/Averaged ΔΔG
S1615 [23]	1,615 (41)	449 (35)	1166 (35)	Unique Variants
S1676 [24]	1676 (95)	453 (53)	1,223 (62)	Unique Variants/Averaged ΔΔG
S1859 [25]	1,859 (64)	583 (48)	1,276 (55)	Replicated Variants/Averaged ΔΔG
S1925 [20]	1925 (55)	582 (42)	1,343 (48)	Replicated Variants
S1948 [26]	1,948 (58)	592 (45)	1,356 (50)	Replicated Variants
S2156 [27]	2,156 (84)	472 (61)	1,684 (68)	Unique Variants/Averaged ΔΔG
S238 [28]	238 (25)	45 (16)	193 (20)	Unique Variants/Subset of S1948
S2648 [28]	2,648 (1 3 1)	602 (96)	2,046 (1 1 8)	Unique Variants/Averaged ΔΔG
S3366[29]	3,366 (1 3 0)	836 (1 0 3)	2,530 (1 1 0)	Unique/Single and Multiple Variants
S350 [28]	350 (67)	90 (35)	260 (57)	Unique Variants/Subset of S2648
S388 [23]	388 (17)	48 (12)	340 (15)	Unique Variants/Physiological Conditions
S3568 [30]	3,568 (1 5 4)	947 (1 1 0)	2,621 (1 3 8)	Replicated Variants
S630 [30]	630 (39)	467 (26)	163 (32)	Replicated Variants
Ssym* [11]	342 (15)	90 (10)	251 (13)	Unique/Symmetric Variants
VariBench [31]	1,564 (89)	436 (70)	1,128 (78)	Unique Variants
VariBench3D[31]	1,423(79)	382 (60)	1,041 (68)	Variants with available structures from [31]

Unique Variants: Only one ΔΔG value for each variation. Replicated Variants: Multiple data for the same variant are included. Averaged ΔΔG: Multiple ΔΔG values for the same variant are replaced with their average. Multiple Variant: The dataset includes variation data for protein with multiple-site variants. Background Variants: The initial protein used as a reference for calculating the ΔGs is different from the wild-type. Physiological Conditions: Temperature 20–40 °C and pH: 6–8. *Reported data only for direct variants.

A possible solution to generate new ΔΔG data might be the application of molecular dynamics (MD) simulations. MD is a powerful tool that enables the investigation of conformational changes in proteins [32], [33], [34], [35]. However, to use this approach, an extensive number of simulations under different conditions (e.g. with different force fields) would be necessary, given the high number of experimental variations with a ΔΔG lower than single hydrogen-bond energy. This requires a super-accurate force field and MD tuning. Nonetheless, with the increasing computational power and force field accuracy, MD simulations might play a relevant role in this field in the future, at least as data-augmentation tools.

3. Computational tools for predicting protein stability change

Existing prediction algorithms use one or a combination of the following features, characterizing protein stability:

• -Structural-based features: residue contact networks, residue/atom distances, protein geometry, etc.
• -Sequence-based features: based on conserved sequences and amino acid positions. They can provide the impact on protein viability but no information at a functional level.
• -Energy-based features: energy of unfolding of the target protein as the sum of various energies such as Van der Waals interactions, solvation energy, extra-stabilizing free energy, etc.
• -Molecular-based features: solvent accessible surface area of the interface, hydrophobic and hydrophilic area. Most of these features are derived by the structure-based ones; however, some of them, such as hydrophobicity or molecular weight, are related to the chemistry of the residue, and can be described without the structure information.

Most of the current methods use a mixture of all the above-described features, although some of them focus only on a specific subset. The first predictive approaches for protein stability have been developed through the application of force fields based on physical free energy functions derived from molecular mechanics [32], which are often combined with molecular dynamics or Monte Carlo simulations [33], [34], [35]. A force field is a collection of bonded and non-bonded interaction terms that are related by a set of equations, which can be used to estimate the potential energy of a molecular system. However, these approaches are computationally intensive, and this limits their practical application to small sets of protein mutants. For this reason, problem-specific physical-based methods have been introduced, such as methods based on empirical energy functions [18], [28], [36], which apply the Maxwell-Boltzmann statistics to estimate the propensities of interaction between atoms from a set of known protein structures. These functions are also known as scoring functions, empirical potentials, knowledge-based potentials, or statistical potentials. In contrast to the force fields approaches, empirical potentials are based on geometrical descriptors, reporting information from experimental data of known protein structures. The advantage of these models, based on principles from statistical physics, is that they provide a trade-off between computational cost and accuracy of the free energy function. Among the most popular approaches, FoldX [18] uses van der Waals and electrostatic energies with additional hydrogen bond and solvation contributions. Model parameters are fitted to a given set of experimental data and the resulting model is used to predict new mutation-induced folding free energy changes. To model mutations, FoldX uses a rotamer approach, allowing conformational changes of sidechains and keeping the backbone fixed.

Another group of classical linear ΔΔG predictors are based on Molecular Mechanics/Poisson − Boltzmann Surface Area (MM/PBSA) or Molecular Mechanics/Generalized Born Surface Area (MM/GBSA) methods [37], [38]. These methods typically use ensembles of conformations from molecular dynamics simulations, combining the molecular mechanics energies with solvation energies. Among the most recent of these approaches, SAAFEC [39] combines a MM/PBSA component and a set of knowledge-based terms of biophysical characteristics into a multiple linear regression model. The goal is not only to accurately predict ΔΔG values, but also to characterize the structural changes induced by mutations and the physical nature of the predicted folding free energy changes. In general, these MM/PBSA‐based methods demonstrate a rather good prediction performance at a reasonable computational cost.

Data-driven computational tools based on both simple regression or machine-learning approaches like Support Vector Machine (SVM), Random Forest (RF) and Artificial Neural Network (ANN) methods have also been explored to predict ΔΔG. Most known and recent approaches are reported in Table 2, together with the tools mentioned above. These methods are based on a first training phase using examples of proteins and their mutants, for which the ΔΔGs have been experimentally measured. Machine learning approaches do not require a full understanding of the principles underlying the target function, since these are modeled during the learning process. This aspect increases the flexibility of these approaches in building new features, revealing unrecognized patterns, relationships and dependencies not considered by knowledge-based models. By construction, these methods can combine all kinds of computable features. In addition, these approaches are much less time-consuming compared to the previous techniques since, once a model is built from the data, the prediction is immediate. Most of these methods use statistical potentials of environmental propensities, substitution frequencies and correlations of adjacent residues found experimentally in protein structure, enabling non-energy-like terms to be incorporated into the scoring function. However, these estimations are highly dependent on the availability of large and diverse experimental training data, increasing the risks of over-fitting issues, and their results might not be easily interpreted in physical terms.

Table 2.

A selection of the most popular methods to predict the functional effects of missense variants in terms of protein stability, i.e. prediction of ΔΔG values.

Method	3D/1D features required	Algorithm	Basic idea and advantages	Anti-Symmetry	Multiple mutations	URL
FoldX [18]	3D	linear regression	Based on empirical physical-based energies	NO	YES	http://foldxsuite.crg.eu/
MUpro [51]	3D and 1D	ANN and SVMs	It predicts from sequence	NO	NO	http://mupro.proteomics.ics.uci.edu/
CUPSAT [36]	3D	combined statistical potentials	It provides information about the site of mutation and protein structural features	NO	NO	http://cupsat.tu-bs.de/
I-Mutant(3.0/2.0) [26], [40]	3D or 1D	SVM	It classifies the predictions into three classes: neutral, large increase or decrease	NO	NO	http://gpcr2.biocomp.unibo.it/cgi/predictors/I-Mutant3.0/I-Mutant3.0.cgi
iPTREE-STAB [25]	1D	Decision trees and adaptive boosting	It also provides numerical stability values	NO	NO	http://bioinformatics.myweb.hinet.net/iptree.htm
AUTO-MUTE (2.0) [69]	3D	Random Forest	It considers spatial perturbations or 3D neighbors of the modified residue	NO	NO	http://binf.gmu.edu/automute/
Prethermut [29]	3D	SVM + Random Forest	It predicts single- and multi-site mutations	NO	YES	http://www.mobioinfor.cn/prethermut/download.htm
POPMUSIC(3.1/2.1) [28]	3D	ANN + Statistical potential	Linear combination of statistical potentials whose coefficients depend on the solvent accessibility of the modified residue	NO	NO	http://babylone.ulb.ac.be/popmusic
Pro-Maya [52]	3D and 1D	Random Forest regression	It uses available data on mutations occurring in the same position and in other positions	NO	NO	http://bental.tau.ac.il/ProMaya
PROTS-RF [51]	3D and 1D	Random Forest	Derived from a non-redundant representative collection of thousands of thermophilic and mesophilic protein structures	YES	YES	Unavailable
iStable(2.0) [30], [53],	3D or 1D	meta-predictor	It uses either sequence or structure information	NO	NO	http://predictor.nchu.edu.tw/iStable/
NeEMO [54]	3D	ANN regression	Based on residue-residue interaction networks	NO	NO	http://protein.bio.unipd.it/neemo/help.html
DUET [41]	3D	meta-predictor (SVM regression)	It integrates mCSM and SDM in a consensus prediction	NO	NO	http://biosig.unimelb.edu.au/duet/stability
mCSM [20]	3D	Gaussian process regression and random forest	It translates the distance patterns between atoms into graph-based signatures providing complementary data to potential energy-based approaches	NO	NO	http://biosig.unimelb.edu.au/mcsm/
EASE-MM [24]	1D	SVM	It combines 5 SVM models and makes the final prediction from a consensus of 2 models selected based on the predicted secondary structure and accessible surface area of the mutated residue	NO	NO	http://sparks-lab.org/server/ease
INPS(3D) [43], [55]	3D or 1D	SVM regression	It takes into account evolutionary information from sequence	YES	NO	http://inps.biocomp.unibo.it
STRUM [22]	3D and 1D	Gradient boosting regression trees	It combines sequence profiles with low-resolution 3D models constructed by iterative threading assembly refinement simulations	NO	NO	https://zhanglab.ccmb.med.umich.edu/STRUM/
ELASPIC [56]	3D and 1D	Stochastic Gradient Boosting of Decision Trees	It predicts the mutation effects on protein folding using homology modeling	NO	YES	http://elaspic.kimlab.org/
SAAFEC [39]	3D	Molecular Mechanics Poisson-Boltzmann	It represents the non-polar solvation energy through a linear relation to the solvent accessible surface area	NO	NO	http://compbio.clemson.edu/SAAFEC
MAESTRO(web) [57]	3D	Multi-agent prediction (ANN + SVM + linear regression)	It provides confidence estimations and multiple-site predictions	NO	YES	https://biwww.che.sbg.ac.at/maestro/web
SDM [46]	3D and 1D	environment-specific substitution tables (ESSTs)	It uses conformationally constrained environment-specific substitution tables from 2,054 protein family sequence and structure alignments	YES	NO	http://marid.bioc.cam.ac.uk/sdm2
TML-MP [58]	3D and 1D	Gradient boosting	Topology-based predictor using persistent homology to reduce the geometric complexity and the number of degrees of freedom of proteins	NO	NO	http://weilab.math.msu.edu/TML/TML-MP/
ThreeFoil [16]	3D and 1D	meta-predictor using 11 tools	It assigns weight to any tool's prediction proportionally to its performance on similar types of mutations	YES	NO	http://meieringlab.uwaterloo.ca/stabilitypredict/
DynaMut [59]	3D	meta-predictor based on Normal Mode Analysis	It allows the study of harmonic motions in a system, providing insights into its dynamics and accessible conformations	YES	NO	http://biosig.unimelb.edu.au/dynamut/.
DDGun [21]	3D or 1D	Linear combination of features	Untrained method introducing anti-symmetric features based on evolutionary information; it predicts also for multiple site variations	YES	YES	http://folding.biofold.org/ddgun/
DeepDDG [17]	3D and 1D	ANN	It is based on a deep neural network architecture trained on > 5,700 manually curated experimental data	YES	NO	http://protein.org.cn/ddg.html
ProTstab [60]	1D	Gradient boosting of regression trees	It exploits a cellular stability based on limited proteolysis and mass spectrometry	NO	NO	http://structure.bmc.lu.se/ProTstab/index/

According to the type of data considered, there might be some restrictions. Structure-based approaches (e.g. methods using 3D structure in Table 2) cannot be used if the 3-dimensional structures of the proteins are unavailable. This limitation can be resolved by using sequence-based prediction tools (referred as 1D in Table 2), which use the amino acid sequence of proteins along with different machine-learning methods to predict changes in the folding free energy. These methods have the advantage of being applicable when the three-dimensional (3D) structure is not available. Methods using the 3D structure of the wild-type protein, e.g. I-Mutant [23], [26], [40], PoPMuSiC [28] or DUET [41], turned out to perform better than purely sequence-based approaches in general [42]. Interestingly, the recent sequence-based method INPS [43] was shown to complement and improve structure-based approaches. However, so far, no known polynomial-time and polynomial-space algorithms are available to solve the full-optimization of protein geometry since it is a combinatorial NP-hard problem [44]. Therefore, every tool implements heuristics and approximations. When no experimental structure is available, predicted structures can be used as models [45]. However, evaluations of the current methods have been systematically performed on the basis of the experimental structures and of the modeling procedure used for generating the predicted structures [16].

3.1. ΔΔG Anti-symmetry

An important property considered only by few predictors is the ΔΔG anti-symmetry, which represents a physical principle at the basis of any thermodynamic transformation (Fig. 1B). Given a chemical (or conformational) transformation from A to B, the relative concentrations of A and B (i.e. [A] and [B]) at equilibrium (and at constant temperature and pressure) are described by the following Gibbs free energy difference:

$$\mathrm{\Delta }{G}_{\mathit{AB}}=-RT\mathrm{l}\mathrm{o}\mathrm{g}\left(\frac{\left[A\right]}{\left[B\right]}\right)$$

This relation is anti-symmetric in A and B, since the inverse transformation (from B to A) is described by:

$$\mathrm{\Delta }{G}_{\mathit{BA}}=-RT\log \left(\frac{\left[B\right]}{\left[A\right]}\right)=-\mathrm{\Delta }{G}_{\mathit{AB}}$$

This general principle, which can be also applied to the protein folding/unfolding process, leads to the basic anti-symmetry of the free energy change upon residue variation. In the case of a protein variation, if the unfolded and folded states of a protein X are defined as U(X) and F(X), two protein sequences p and q that differ by few aminoacids will be characterized by the following anti-symmetric equation:

$$\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{pq}}=RT\log \left(\frac{\left[U(p)\right]}{\left[F(p)\right]}\right)-RT\log \left(\frac{\left[U(q)\right]}{\left[F(q)\right]}\right)=-\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{qp}}$$

Machine learning approaches have started to consider reverse variants with inverse ΔΔG signs in the training step. Referring to Table 2, only the following methods consider this aspect: SDM [46], DDGun(3D) [21], ThreeFoil [43], PROTS-RF [47], INPS [43] and DeepDDG [17]. In particular, PROTS-RF was the first approach to assess its performance by taking into account also reverse mutations, while DDGun(3D) implemented anti-symmetric scoring functions used in the prediction model, i.e. evolutionary, hydrophobicity and residue contact scores.

The simplest way to measure the anti-symmetry bias is to compute the Pearson correlation between the predictions on a variation set against the predictions on the corresponding reverse variation set. Correlation values shifted away from −1 indicate the extent of the anti-symmetry bias (Table 3). To fulfill the anti-symmetry constraint, Usmanova et al. [48] showed that the methods should generate the lowest energy structure of the mutant starting from the native one and vice versa, which may be hard, considering internal specific features of the programs. FoldX, for instance, keeps fixed the backbone and side-chain of all residues but neighbors upon mutation. As a result, the modeled structure of the mutant (B) is expected to be less stable than the native structure (A) by some value δ_AB and vice versa. Thus, the average mutation bias (<δ > ) can be calculated as <δ> = <(δ_AB + δ_BA)/2> = <(ΔΔG_AB + ΔΔG_BA)/2>. This bias does not depend on the experimental determination of the free energy of the protein structure nor on the definition of wild-type and mutant proteins.

Table 3.

Performance evaluation reported for each method, highlighting possible biases.

Method	Validation	Training data	Test Data	Correlation (ρ)	Anti-symmetry (ρ_dir-inv)	Sequence Identity/homologs
FoldX [18]	none	S339	S625	0.82	Biased* (−0.38)	not declared
MUpro [51]	20‐fold CV and LOO	S1615	S1615, S388	0.13–0.76	Biased* (−0.02)	Homologs removed from S1615 (SR1496, SR1135, SR1023, SR1539)
CUPSAT [36]	3/4/5-fold CV	S1538, S1603	S1538, S1603	0.55–0.78	Biased* (−0.54)	not declared
I-Mutant(3.0/2.0) [26], [40]	10/20/30-fold CV	S1948	S1948	0.62–0.71	Biased* (0.02)	not declared
iPTREE-STAB [25]	4/10/20-fold CV	S1859	S1859	0.7	not evaluated	not declared
AUTO-MUTE (2.0) [69]	20‐fold CV	Subsets of S1948, S1615, S388,S1791, S1396, S2204	Subsets of S1948, S1615, S388,S1791, S1396	0.74–0.79	Biased* (−0.06)	not declared
Prethermut [29]	10-fold CV	S3366, S2156	S3366, S2156	0.67–0.72	not evaluated	not declared
POPMUSIC(3.1/2.1) [28]	5-fold CV	S2648	S2648	0.63–0.79	Biased* (−0.29); unbiased version POPMUSICsym (−0.77)	not declared
Pro-Maya [52]	5/10-fold CV and LOO	S2648, S2156	S2648, S2156	0.59–0.8	not evaluated	<30% identity and keeping information on the mutation site
PROTS-RF [51]	5/10-fold CV	S2156	S2156 + D180, D140 (27 and 19 proteins)	0.62–0.86	Unbiased	<30% identity in CV
iStable(2.0) [30], [53]	5-fold CV v2.0: 10-fold CV	S2648, S1948 v2.0: S3528	M1311, M1820 (from S2648, S1948, no redundancies) v2.0: S630	0.85 v2.0: 0.67–0.71	Biased* (−0.05) v2.0: not evaluated	Meta predictor combining several predictors and using the same protein variant to train the combined model
NeEMO [54]	10-fold CV	S2399 (113 proteins)	IM_631 (from S2399)	0.5–0.79	Biased* (0.09)	Evaluated but not used in CV
DUET [41]	S350, p53	S2648	p53,S350	0.71–0.82	Biased* (−0.21)	not declared
mCSM [20]	5/10/20-fold CV	S2648, S1925	S350	0.51–0.82	Biased* (−0.26)	5-fold cross-validation separating by protein (Pearson = 0.51)
EASE-MM [24]	10-fold CV and blind	1676 mutations from S1948	S543, S236	0.51–0.59	not evaluated	max 25% sequence identity between folds and train/test sets
INPS(3D) [43], [55]	5-fold CV	S2648, p53	S2648, p53	0.53–0.71	Unbiased for sequence-only* (−0.99 1D, −0.86 3D)	5-fold cross-validation separating by protein as in mCSM
STRUM [22]	5-fold CV	Q3421	S2648, S350, Q306 (subset of S2648)	0.4–0.8	Biased* (0.34)	Q306 as test, with sequence identity < 60%
ELASPIC [56]	20‐fold CV and LOO	S3463 (159 proteins)	S2636 (134 proteins), S2104 (79 proteins)	0.77	not evaluated	90% sequence identity redundancy reduction
SAAFEC [39]	5-fold CV	983 mutations from Protherm (42 proteins)	983 mutations from Protherm (42 proteins)	0.61	not evaluated	not declared
MAESTRO(web) [57]	5/10/20-fold CV	S2648, S1925 (from S1948), S1765, S2244	S2648, S350	0.63–0.76	Biased* (−0.34)	Lowest correlation (0.63) when separating by protein in 5-fold CV as in mCSM
SDM(2) [46]	None	None	S2648, S350, p53, S140	0.52–0.63	Biased* (−0.75)	not declared
TML-MP [58]	5-fold cross validation	S2648 S350, M233	2648 S350, M233	0.54–0.82	not evaluated	not declared
ThreeFoil [16]	2-fold CV with 1000 reshuffling	Broom2017	Broom2017	0.73	not evaluated	not declared
DynaMut [59]	10-fold CV and blind TS	S2648	S351	0.58–0,70	Biased	Homology included, use in input Duet, trained on the same S2640
DDGun [21]	S2648, Ssym, p53, Myoglobin	Untrained	S2648, Ssym, p53, Myoglobin	0.45–0.71 (0.54–0.68)	Unbiased* (−0.99)	not applicable
DeepDDG [17]		Cao Train	Cao Test	0.56	not evaluated	Homologs (>25%) removed from test set
ProTstab [60]	10-fold CV	Varibench	Varibench	0.79	not evaluated	not declared

Possible biases can be due to anti-symmetry and lack of checking for sequence identity on training/test data. CV = cross-validation, LOO = leave-one-out, TS = test-set, MCC = Matthews Correlation Coefficient, ρ = correlation, ρ_dir-inv = correlation between direct and inverse variation. *Evaluated on Ssym database [11].

3.2. Multiple-site variations

Another challenge is the prediction of protein stability in the occurrence of multiple mutations. Multiple-point mutations are common variations of the protein sequence that may be needed in protein engineering when a single-point mutation is not enough to yield the desired stability change. Dealing with multiple-site variations adds another level of complexity beyond the prediction of the effect of a single variant on protein stability, since it requires the learning of many types of combinatorial effects (compensatory, additive, following linear or nonlinear combinations, threshold effects, etc.) [49]. Moreover, experimental ΔΔG data for multiple-point mutations are less abundant than for single-point ones. This shortage of data, together with difficulties arising from the combinatorial nature of the problem, make the effects of multiple-point mutations hard to predict. For these reasons, most of the methods only handle single-point mutations.

Generally speaking, it is expected that substitutions that are closer (in sequence or structure) interact more than those that are farther away from each other. In this latter case, predicting the ΔΔG values due to each substitution independently and then adding the predicted values should provide a good approximation of the multiple-point mutation ΔΔG [50]. This additive approach is most naturally employed by linear methods like FoldX [18] and DDGun [21]. However, it can be trivially used to extend all single-point methods to multiple-point mutations. Another approach, implemented by PROTS-RF [47] and Prethermut [29], calculates the average input features across multiple substitutions. However, averaging may not be appropriate in case of cooperative effects.

4. Best practice and pitfalls in prediction assessment

4.1. A prediction accuracy upper bound

As shown above (see Fig. 1A), given a set of experimental ΔΔG values for a specific variation, two samples can be considered as having similar ΔΔG values if they are within the experimental error (uncertainty). However, since a certain variability characterizes each dataset, a question to address is: given the standard deviation of the dataset (${\sigma }_{\mathit{DB}}$) and the measure uncertainty (σ), is there an upper bound to the prediction performance? Starting from a set of measured ΔΔG protein variations, the best predictor can be estimated according to its similarity to another set of experimentally-determined ΔΔG values. The assumption is that no computational method can be better than a set of similar experiments. To derive an upper bound of the Pearson correlation as a function of the noise and distribution of the ΔΔG data, the idea is that, starting from a narrow dataset distribution with a variance having the same order of magnitude of the experimental uncertainty, the theoretical upper bounds can be lower than expected. Some studies provided a theoretical estimation of the upper bound of the Pearson correlation as a function of the average uncertainty of the data (σ) and the standard deviation of the dataset (${\sigma }_{\mathit{DB}}$ see Fig. 1C) [61], [62]. As an example, the popular datasets S2648 and VariBench have a σ_DB < 2 kcal/mol, leading to an upper bound for the Pearson correlation coefficient of ~ 0.8 and a lower bound for the root mean square error between experimental and predicted ΔΔG values of ~ 1 kcal/mol. This implies that the methods using these data for estimating their performance and reporting Pearson correlation above 0.8 are likely to be affected by over-fitting biases in the training step.

4.2. The burden of sequence identity

The reliability of machine learning approaches depends on the size and quality of the training dataset. Therefore, it is essential to use high-quality experimental observations with high consistency when training and testing these methods. Table 3 reports the main features characterizing the performance evaluations of each method listed in Table 2. In particular, the size and balance of training data must be considered carefully. Datasets with a few hundred or thousand cases, as those mostly used, might be too small to identify useful descriptors in the learning process. In addition, low heterogeneity within training datasets might lead to prediction tools not able to generalize. As a consequence, the weights assigned to the descriptors identified by these predictive models can be biased by the over-representation of some partial descriptors in the training data, sometimes ignoring general predictive descriptors. A common error made by the current methods is not taking into account similarities between training and test sets, leading to over-fitting issues (see Fig. 1D).

Evolution has selected proteins that are well-suited to maintain certain specific functions. Although evolutionary pressure constrains protein structure, sequence-level variations can be high, with very different sequences having a similar structure. Two proteins with different sequences but evolutionary or functionally-related are called homologs. Quantifying these evolutionary relationships is very important for preventing undesired information leakage between data splits. However, we mainly rely on sequence identity, which measures the percentage of exact amino acid matches between aligned subsequences of proteins. For example, filtering at a 25% sequence identity threshold means that no pairs of proteins in the training and test sets have >25% exact amino acid matches. Unfortunately, not all the current approaches have considered sequence identity in dividing training and test sets (Table 3), which means measuring the performance of the method using test sets not containing proteins similar (or identical) to those of the training set. One of the most representative examples explaining the similarity issue between training and testing is shown in Pires et al. [20]. The Pearson correlation of the method mCSM ranges between 0.7 and 0.8 when a random selection of the variations is used. However, the correlation drops down to the range 0.54–0.51 when the cross-validation is performed using ‘per site-’ and ‘per protein-’ clustering, respectively. Different protein positions tend to be more or less sensitive to mutations independently of the residue substitution (Pro-Maya [52]). Thus, using the same site (or same protein) in training and testing leads to a wrong and over-optimistic performance. Furthermore, a method trained under these conditions tends not to generalize well. For these reasons, a simple random split of the datasets should be avoided.

The problem of similarities among training and testing sets is more pronounced when meta-predictors are used. In the last years new stacked methods, combining multiple different predictors, have been developed, e.g. DUET [41], iStable(2.0) [30], [53], Dynamut [59] and ThreeFoil [16]. Meta-predictors offer the main advantage that even a simple majority voting approach over several methods yields better results than any individual method, each characterized by its strengths and weaknesses. However, the performance reported by these methods might be misleading. For example, ThreeFoil combines predictions from 11 freely available tools, each originally trained on different datasets, all derived from ProTherm. The meta-predictor was built such that the weight given to the prediction from any particular tool was based on that tool's performance against similar types of mutations from a training set of 605 mutations. Matthews Correlation Coefficient (MCC) values were determined through cross-validation and a dataset of 605 mutations was split into halves, with one half used to determine MCC values as weights and the other half used to test the overall performance, repeating the procedure 1000 times. However, 60% of the proteins used for this dataset were used by some of the predictors during their training step, introducing the similarity issues between training and test sets described above. Similarly, Dynamut combines the effects of mutations on protein stability and dynamics calculated by Bio3D [63], ENCoM [82] and DUET to generate an optimized and more robust predictor. DUET, in turn, combines two approaches, SDM and mCSM. These approaches were trained on S2648, which was the same dataset used by Dynamut for training the meta-predictor, making cross-validation, and for extracting a “blind” set of 351 variations for the performance evaluation. In iStable 2.0 the authors introduced two datasets for training and testing [30]. In the test set of 630 variations, 442 were derived from the same proteins used in the training sets. The two datasets contain repeated mutations, 703 and 77 for training and test sets, respectively. In terms of protein sequence similarity, only three proteins (corresponding to 81 mutations) can be safely used in S630 to test the methods. Therefore, there is an urgent need of reviewing these methods by testing their predictive models with data that have no sequence similarity (trained on similar proteins) to those of the training set.

4.3. Unbalanced experimental datasets and anti-symmetry

Unbalanced training datasets with large differences in the number of cases representing specific categories might also lead to erroneous estimations (see Fig. 1D). As an example, a training dataset with 80% of destabilizing mutations would allow the predictor to erroneously classify most mutations as destabilizing. This can hamper both classification (ΔΔG sign) and regression (ΔΔG value). Given this unbalance, the most recommended measures of accuracy in the context of classification are the MCC and the harmonic mean between precision and recall (F1) [64].

Another important feature described above, which has a great impact on the algorithm performance, is represented by the anti-symmetric properties of the free energy changes. Recently, different studies addressed this problem as bias in most predictors [11], [12], [48], [61], [65], and specifically designed datasets including both the variations and the corresponding inverses (such as A->B and B->A on the same protein) have been introduced: Ssym [11], Usmanova-DB [48] and Fang-DB [12]. The results show that only INPS and PopMusic [11] were sufficiently robust to be defined compliant with the anti-symmetric properties [61], [65]. The Pearson correlation between the predictions on a variation set and the predictions on the corresponding inverse variation set (ρ_dir-inv) can measure the method bias. In Table 3 we report the anti-symmetry bias of different methods (when measured). A perfect method should show a Pearson correlation equal to −1.

4.4. Developing a new method

Most of the predictors were trained using random splits of the selected datasets (Table 1). However, as mentioned above, this procedure is not correct since there is a huge level of redundancy in the datasets. Considering the pie-charts represented in Fig. 1A, only few protein sequences show no significant sequence similarity (<25%) with other proteins of the same database (only 15 and 5 proteins in S2648 and Varibench, respectively). The percentage of proteins clustered into large groups (i.e. clusters including > 5% of the proteins present in the entire database) with high sequence similarity is significantly high, involving 32% and 41% of the proteins annotated in S2648 and Varibench, respectively. This redundancy characterizes all the available datasets. Thus, given the difficulty of comparing methods and assessing the performance on fair bases, here we provide sequence-identity-reduced datasets (see Supplementary Materials). We clustered the variants according to the sequence identity of the protein sequences they belong to, using a threshold cut-off of 25% identity. The variants of S2648, VariBench3D, sSym, P53 and Myoglobin datasets are grouped in a way that it is possible to perform 10-fold cross-validation on S2648 and, using the models trained in the different folds, to predict the variations of the other datasets excluding sequence similarity issues. With our clustering, new methods can be developed and fairly compared. We adopted a circular cross-validation procedure (with either 10 or 5 sets): 8 (or 3) folds at a time are kept for the training while the other 2 are considered for validation and test, respectively. By rotating along all the folds, it is possible to use the whole dataset both for the validation and for the test (see Supplementary). It is compulsory that the tuning of the hyper-parameters or method selections should be done by analyzing the performance computed on the validation sets, without “peeping” at those obtained on the test sets, otherwise the whole procedure would be spoiled.

5. The test case of CAGI experiments

The Critical Assessment of Genome Interpretation (CAGI) is a community experiment aimed at fairly assessing the computational methods for genome interpretation [66]. In the latest edition (CAGI 5) data providers measured unfolding free energy of a set of variants with far-UV circular dichroism and intrinsic fluorescence spectra on Frataxin (FXN), a highly-conserved protein fundamental for the cellular iron homeostasis in both prokaryotes and eukaryotes. These measurements were used to calculate the change in unfolding free energy between the variant and wild-type proteins at zero concentration of denaturant (ΔΔG^H2O). The experimental dataset [67], including eight amino acid substitutions, was used to evaluate the performance of the web-available tools for predicting the value of ΔΔG^H2O associated with the variants and to classify them as destabilizing or not-destabilizing [68]. Eight performance measures were applied to test the methods, five for assessing the predictions in regression (Pearson and Spearman Correlation Coefficients, Kendall-Tau Coefficient, Root Mean Square and Mean Absolute Errors) and three for the classification performance, i.e. Accuracy, Matthews Correlation Coefficient and Area Under the Receiving Operator Characteristic Curve (AUC). A prediction threshold equal to −1 kcal/mol was set to discriminate between destabilizing (ΔΔG < −1 kcal/mol) and not-destabilizing (neutral) variants (ΔΔG$\ge$−1 kcal/mol) [69]. According to this classification, 5 variants destabilize the protein structure and 3 variants are non-destabilizing. These protein variations were submitted to the web server of each method for the assessment of its predictions. The results confirmed that ELASPIC and INPS3D, as well as DDGun and PopMusic that were optimized for the anti-symmetric property, are among the best methods in predicting the ΔΔG associated with the variants included in the challenge (see Table 4). Although the FXN dataset includes only 8 variants, it represents a first attempt to validate the performance of ΔΔG prediction tools using a blind test set.

Table 4.

Performance of state-of-the-art methods on 8 variants of the CAGI FXN challenge.

Method	rP	rS	Kτ	RMSE	MAE	Q2	MCC	AUC
DDGun [21]	0.90	0.69	0.57	2.15	1.93	0.70	0.45	0.80
ELASPIC [56]	0.82	0.69	0.50	2.38	1.71	0.80	0.60	0.93
SAAFEC [39]	0.74	0.83	0.71	2.71	2.08	0.83	0.75	0.93
PopMusic [28]	0.83	0.54	0.40	2.68	2.00	0.90	0.78	0.80
EASE-MM (1D) [24]	0.81	0.64	0.64	2.88	2.22	0.70	0.45	0.80
INPS (3D) [55]	0.76	0.60	0.43	3.18	2.36	0.80	0.60	0.87
NeEMO [54]	0.83	0.62	0.50	3.39	2.44	0.70	0.45	0.87
INPS (1D) [43]	0.70	0.60	0.43	3.35	2.52	0.80	0.60	0.87
MAESTRO [57]	0.72	0.60	0.43	3.40	2.48	0.70	0.45	0.67
iStable [30], [53]	0.82	0.55	0.43	3.57	2.73	0.70	0.45	0.80
DUET [41]	0.53	0.55	0.36	3.34	2.46	0.70	0.45	0.73
DeepDDG [17]	0.73	0.38	0.29	3.10	2.43	0.53	0.07	0.67
I-Mutant2 (1D) [26], [40]	0.69	0.36	0.21	3.52	2.68	0.80	0.60	0.67
SDM [46]	0.54	0.52	0.36	3.49	2.73	0.63	0.26	0.67
mCSM [20]	0.54	0.43	0.21	3.30	2.49	0.37	−0.26	0.60
I-Mutant2 (3D) [26], [40]	0.75	0.04	−0.05	3.60	2.55	0.63	0.35	0.58
AUTOMUTE (TR) [69]	0.33	0.26	0.14	3.64	2.67	0.53	0.07	0.73
DynaMut [59]	0.37	0.29	0.14	3.94	2.89	0.60	0.29	0.67
MUpro (1D) [51]	0.14	−0.10	−0.07	3.89	2.80	0.70	0.45	0.53
CUPSAT (DN) [36]	0.20	−0.12	−0.14	4.98	3.97	0.50	0.00	0.20

Methods are ranked using 8 measures of performance. r_P and r_S: Pearson and Spearman Correlation Coefficients, respectively. K_τ: Kendall-Tau Coefficient. RMSE and MAE: Root Mean Square and Mean Absolute Errors. Q2: Accuracy: MCC: Matthews Correlation Coefficient. AUC: Area Under the Receiving Operator Characteristic (ROC) Curve. A binary classification threshold between destabilizing and neutral variants has been set to −1.0 kcal/mol. Measures of performance were defined as in Baldi et al. [69]. DN: Denaturant. TR: Tree Regression. 1D and 3D: sequence-based and structure-based predictions, respectively. ΔΔGs were calculated at the experimental conditions of pH = 8 and T = 20C.

6. Challenges in the applications of protein stability predictions in biomedicine and precision medicine

Sequence variations and structural changes that cause disease were first linked in 1949 for sickle-cell anemia [70], [71], which is an autosomal recessive disorder caused by the amino acid substitution E6V in the β-chain of human hemoglobin [72], i.e., a replacement of glutamic acid (E) by a valine (V) at position 6. Currently, the Human Gene Mutation Database (HGMD [73]), Online Mendelian Inheritance in Man (OMIM [74]), the Catalogue of Somatic Mutations in Cancer (COSMIC) [75], and other resources collect thousands of such single amino acid variants causative of, or associated with, diseases, in addition to many other types of sequence variations. However, the number of pathogenic variants in those databases represents only a small fraction of the potential number of pathogenic mutations in the world-wide human population.

Engineering stability-changing mutations are opening promising perspectives for several approaches in precision medicine. Analyses linking the effects of a mutation on a protein thermodynamic stability with pathogenicity indicate that loss of stability could be a main driver of inherited diseases. Thus, an improved understanding of the complex relationships among protein sequence, structure, folding and stability could provide new possibilities for diagnosis and even novel treatments specific for the patients. Casadio et al. [76] made the first effort in assessing the relationships among stability changes in proteins and their involvement in human diseases at large-scale by analyzing the Human Proteome [2]. By estimating for each single amino acid polymorphism the probability of being disease-related, they showed that protein stability changes can also be disease-associated at the proteome level. The probability indexes were statistically derived from a dataset of 17,170 single amino acid variations in 5,305 proteins retrieved from data available at UniProtKB (release 2010_04), dbSNP (build 132), OMIM and ProTherm [15]. SDM2, mCSM and DUET have been used to evaluate the effects of stability changes in different applications: human cancer-related genes in the COSMIC database [77], inhibition of inosine-5′-monophosphate dehydrogenase, isoniazid and rifampicin resistance in Mycobacterium Tuberculosis [78], phosphodiesterase somatic mutations implicated in cancer and retinitis pigmentosa [79], protein presenilin 2 linked to familial Alzheimer’s disease [80].

A challenging task for medical applications is predicting how mutations in proteins alter their ability to function, distinguishing mutations that are “drivers” of disease or drug resistance from “passengers” that are neutral, or even selectively advantageous for the organism. This task requires understanding the impact of missense mutations in protein function, and mapping genetic variations to 3D protein structures [81]. In particular, mutations on protein surfaces in the protein–protein interfaces were associated with larger global effects than mutations occurring elsewhere in protein surfaces [2], [81]. Protein stability may directly be related to functional activity, and changes in stability or incorrect folding could be the major effects of pathogenic missense mutations. In most cases, missense mutations are deleterious due to the decrease in stability of the corresponding protein [82]. In other cases, missense mutations may cause diseases by enhancing the stability of the corresponding protein [83]. The mutant kinase EGFR can be taken as an example of both kinds of disease-inducing changes, at the same time illustrating emblematically how complex the path from the detection of mutation-induced free energy changes to precision medicine might be. Kinase activation commonly involves a rotation and shift of the αC-helix between these states, a conformational change that is governed by an allosteric switch. Driver mutations can control that switch. Oncogenic driver mutations act by either stabilizing the active conformation, or disrupting interactions that stabilize the inactive one. 41% of the EGFR mutations in lung cancer present the oncogenic Leu858 driver mutation [84], which stabilizes the αC-helix in the active conformation. By contrast, the T790M mutation in EGFR stabilizes the hydrophobic R-spine, which destabilizes the inactive conformation. The outcome is similar: the mutations allosterically switch the preferred states towards a constitutively activated kinase. In brief, driver mutations can adopt one of three mechanisms: destabilize the inactive state, stabilize the active state, or both. In terms of free energy, those effects can be seen as changes in the relative depths of minima, with the outcome of favoring or disfavoring the asymmetric or symmetric dimer conformation [85]. This kind of knowledge clearly impacts on the choice of treatment for lung cancer patients. For instance, Gefitinib is an EGFR inhibitor used to treat lung cancer, but, as expected by the reasons described above, it improves the outcome only in a subset of patients bearing very specific genetic changes.

Another research field that might benefit from future applications of engineering stability-changing mutations is represented by the immunogenomics studies. In the last years, immunotherapies have shown high rates of success as treatments for several types of cancer. Recent approaches employ the adoptive transfer of autologous T cells from a patient, genetically modified either with an engineered Chimeric Antigen Receptor (CAR) or with an engineered T Cell Receptor (TCR), for recognition of the appropriate peptides in complex with the Major Histocompatibility Complex class I (MHC-I).

However, finding suitable candidates (for CAR-T and TCR-T cell therapy) is very costly and time-consuming. For this reason, computational methods for predicting the immunogenicity of peptide-MHC-I complexes are being developed.

In particular, the role of protein-complex stability has been recognized as crucial for the immunogenicity prediction of the peptide-MHC-I complexes (for example NetMHCstab [86] and NetMHCstabpan [87]). These methods are expected to speed up therapy implementation for each patient significantly. The intrinsic effects of fold stability on immunogenicity have wide potential applications also in the vaccine field. The first examples of stability-optimized vaccines have been demonstrated [88], and further major advances on protein design for novel therapies within the next years are expected.

7. Summary and outlook

The prediction of protein stability changes upon variation is essential for protein design and precision medicine. The current methods, although far from being perfect, achieved sufficient levels of performance to complement experimental studies [68]. However, several issues need to be addressed to enhance such levels of performance, in particular:

• 1.increasing the quality and the size of the current datasets, adding more carefully curated experimental data;
• 2.building methods that are intrinsically anti-symmetric (ΔΔG(A->B) = -ΔΔG(B->A));
• 3.for machine-learning approaches, it is essential that the model training has to be performed using low levels of sequence identity between learning and testing sets. To facilitate the scientific community in this task, we provide similarity-free cross-validation folds for the most relevant datasets (Supplementary materials).

If these indications are taken into account, the next generation of predictors can achieve more reliable and more consistent performances.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have influenced the work reported in this paper.

Appendix A. Supplementary data

The following are the Supplementary data to this article: