TREXMO plus: an advanced self-learning model for occupational exposure assessment

Abstract

In Europe, several occupational exposure models have been developed and are recommended for regulatory exposure assessment. Only some information on the substance of interest (e.g., vapor pressure) and the workplace conditions (e.g., ventilation rate) is required in these models to predict an exposure value that will be later used to characterize the risk. However, it has been shown that models may differ in their predictions and that usually, one of the models best fits a given set of exposure conditions. Unfortunately, there are no clear rules on how to select the best model. In this study, we developed a new modeling approach that together uses the three most popular models, Advanced REACH Tool, Stoffenmanger, and ECETOC TRAv3, to obtain a unique exposure prediction. This approach is an extension of the TREXMO tool, and is called TREXMO+. TREXMO+ applies a machine-learning technique on a set of exposure data with the measured values to split them into smaller subsets, corresponding to exposure conditions sharing similar characteristics. For each subset, TREXMO+ then establishes a regression model with the three REACH tools used as the exposure predictors. The performance of the new model was tested and a comparison was made between the results obtained by TREXMO+ and those obtained by conventional tools. TREXMO+ model was found to be less biased and more accurate than the REACH models. Its prediction differs generally from measurements by a factor of 2–3 from measurements, whereas conventional models were found to differ by a factor 2–14. However, as the available test dataset is limited, its results will need to be confirmed by larger-scale tests.

Introduction

In 2007, the European Union parliament adopted a new chemical regulation that concerns Registration, Evaluation, Authorization, and restriction of CHemicals (REACH) [1]. The purpose of REACH is to improve the protection of human health and the environment against the risk posed by chemicals. To comply with this legislation, for substances manufactured or imported ≥10 tons per year, registrants should conduct a Chemical Safety Assessment (CSA). The CSA includes risk characterization and exposure assessment based on the established exposure scenarios. An exposure scenario is a document describing the conditions that ensure adequate control of risk when a substance is used in a specific task or several processes or uses. These conditions defined for every step of the manufacturing, any anticipated use down in the supply chain, and every substance in a product. Collection of exposure measurements to support a CSA requires a large sampling size and high costs. The sampling size can be further enlarged to cover the between-and within-user variability [2]. Statistical exposure models, such as ECETOC TRA [3, 4], on the other hand, present a cheap and fast assessment alternative. Although the exposure measurements are still considered the gold standard and their collection should not be completely replaced [5], the models can discriminate between well-controlled situations and situations that may pose risk to the human health.

Within the context of REACH, several generic exposure models are recommended for the exposure assessment purposes [1]. Tier 1 models, such as EMKG-EXPO-TOOL [6], ECETOC TRAv2 [3], and TRAv3 [4], are simple screening tools that are supposed to predict more conservative (i.e., protective) estimates, as compared with higher tier tools, such as Advanced REACH Tool (ART) [7, 8] and Stoffenmanager (SM) [9, 10]. To calculate a tier 1 estimate, a few exposure parameters regarding substance and workplace properties are required. EMKG-EXPO-TOOL, for example, uses only three parameters, i.e., volatility (for liquids) or dustiness band (for solids), amount of substance, and applied exposure control. SM and ART, however, require more exposure descriptive information to calculate estimates that are supposed to be more precise compared with the results of tier 1 models. ART, for example, besides the vapor pressure (VP) of a substance, requires its concentration and activity coefficient to assess how the substance properties contribute in the final exposure. Also, these higher tier tools provide estimates at different percentiles of the exposure distribution, i.e., 50th, 75th, 90th, 95th, and 99th (only ART).

A broad study, known as the eteam study [11], has extensively compared several tier 1 models, including ECETOC TRAv2 and v3, EMKG-EXPO-TOOL, and SM (tier 1.5), with nearly 4000 exposure measurements [12]. The authors reported that overall, the tier 1 models performed satisfactorily for a wider range of considered exposure situations (ESs), by overestimating the corresponding exposure measurement data; this was the desired outcome as the tier 1 models are intended to overestimate the measurements and thus behave more protective. For certain exposure conditions, the study also found underestimations of the measured values. In another study [13], ART (the only tier 2 model of REACH) was compared with almost 600 measurements from Switzerland. By evaluating the fraction of the measurements found within the 90% confidence interval of the 50th and 90th percentiles, Savic et al. [13] found that ART tends to accurately predict exposures to volatile liquids and powders. The authors also reported that ART overestimates exposures to volatile liquids but underestimates exposures to powders and solids. Similarly, Lee et al. [14, 15] tested the performance of these models against a U.S. dataset for liquids with VP > 10 Pa and reported results similar to those of the eteam for the tier 1 models and SM. For ART, however, Lee et al. [15] found a tendency to underestimate exposure measurements. Several other studies also focused on the performance of these models under REACH [8, 16–18]. Most of these studies showed that the models could be reliable for certain ESs, but in some cases, their algorithms need to be improved. Nevertheless, the models’ performance remains unknown for a great number of ESs for which no adequate data are available. To the best of our knowledge, none of the published studies has established straightforward rules on which model is the best choice for a given set of ESs.

Furthermore, Savic et al. [19] compared, in silico, the estimates of ART, SM (version 4.0) [10], and TRAv3 for 300,000 combinations of exposure parameters. The authors addressed ESs for which the modeled exposures can differ by several orders of magnitude, indicating that a wrong selection of model may have serious consequences on assessment of risk. Because no workplace measurements were involved in the inter-model comparison [19] (i.e., in silico study), it was impossible to determine the actual performance of the three REACH models. Savic et al. [20] then introduced the usefulness of TREXMO, which promotes and facilitates the simultaneous use of sereval exposure models.

The purpose of this study, therefore, was to develop a new modeling approach that combines the exposure outputs of three existing REACH models to derive a refined prediction. The three inhalation models used as the exposure predictors in our model were ART, SM (version 4.0) [10], and TRAv3. We developed an algorithm that adjusts its prediction coefficients depending on the evaluated exposure conditions. This means that the model will use available exposure data to learn about the models’ weaknesses and strengths for different ESs. Whenever new exposure data are supplied to the model, it will perform a self-refinement of its prediction coefficients. We hypothesized that this new approach, compared with the three REACH models, would perform better in terms of bias and accuracy with an assumption that those three models were developed using different and independent exposure data. To calculate its estimates, TREXMO+ will only use indirectly the data on which the three models are based. Depending on how similar is a given exposure situation with the data in these three models, the new model will assign them different prediction coefficients.

Methods

TREXMO

TREXMO [20], an integrated tool of six exposure models, i.e., ART, SM, ECETOC TRAv3, MEASE, EMKG-EXPO-TOOL, and EASE, is designed to predict estimates of the six models simultaneously. By starting from a set of the parameters established in one of the models (preferably ART), TREXMO recommends the most appropriate parameters in the other five. For a given ES, six exposure predictions can thus be provided from a single parameter set. TREXMO v2, however, neither provides its own estimates nor recommends which of the six predictions could be the most suitable, regarding a given ES, for the risk characterization. Detailed information is provided in Savic et al. [20].

TREXMO+

This is an advanced model developed based on the inter-model translations established for TREXMO. It was consequently named TREXMO+. This new model is intended to derive its exposure estimates by using three REACH models, i.e., ART, SM, and TRAv3, as its independent predictors. The remaining three models of TREXMO were not considered in this study because of the following reasons:

MEASE. Regarding the inhalation exposure, the model predicts the values similar to those of TRAv3. Its contribution in TREXMO+ was thus not expected to improve the performance.

EMKG-EXPO-TOOL and EASE. These two models are conceptually much simpler compared with the three considered once. Also, they do not predict the point value estimates, but the range. Moreover, EASE was used as a basis for the development of ECETOC TRA and it can thus be expected that the exposure data, on which the two models are based, is mostly overlapped.

TREXMO+ concept

For both ART and SM, the 50th percentile estimates of the exposure distribution is the direct output of their calibrations against the exposure measurements [8, 10]. According to the ECETOC’s technical guidance [4], the exposure estimates in TRAv3 are considered to represent the 75th percentile estimate of the exposure distribution. Because neither the model calculations nor the supporting material provides a way to obtain the 50th percentile, the 75th percentile estimate was used here. For the model developed in this study, which predicts the geometric mean (GM), the choice of the percentiles of the three REACH models was not crucial, because these models are used only as predictors of the exposure. This is explained in detail next.

To predict exposure estimates of the three REACH models, appropriate exposure parameters (such as VP and activity task) must be coded for the given models. To automatize this step, we integrated the parameter translation rules of TREXMO [20] into our model. ART was used as the starting model as recommended by Savic et al. [20]. Since some input parameters in ART can be translated into multiple ways (especially for PROC and type of use in TRAv3) and thus lead to different exposure estimates, TREXMO+ for these cases is programmed to require additional expert judgments. Fortunately, the data (Table 2) that were used in our study included a PROC value for each ES. For a smaller fraction of ESs, professional use (i.e., more conservative option) was selected to represent the type of use for TRAv3, since the corresponding information was missing.

Table 2.

Summary of the number of exposure situations (ESs) and exposure measurements (EMs) provided by the Swiss Insurance Fund (SUVA, Switzerland) and the National Institute for Occupational Safety and Health (NIOSH, US).

Exposure type	SUVA		NIOSH
	Total ESs (EMb)	Processed ESsa (EM)	Total ESs (EMb)	Processed ESs (EM)
Volatile liquids (VP > 10 Pa)	146 (346)	135 (317)	50 (425)	50 (425)
Non-volatile liquids (VP ≤ 10 Pa)	5 (5)	0	4 (9)	0
Powders (non-abrasive dust)	59 (113)	59 (113)	10 (40)	10 (40)
Solids (abrasive dust)	52 (120)	24 (57)	0	0

VP vapor pressure.

^aProcessed data: only ESs that were applicable in all the three REACH models used in the study; in case of non-volatiles, the data were not processed due to the small data size.

^bSUVA included 1–3 exposure measurements per ES, while NIOSH 5–12.

The structure of TREXMO+ is shown in Fig. 1a. The algorithm consists of three layers: (1) classification, (2) learning, and (3) assessment.

Fig. 1. Schematic illustration of TREXMO+ algorithm and a regression tree example.

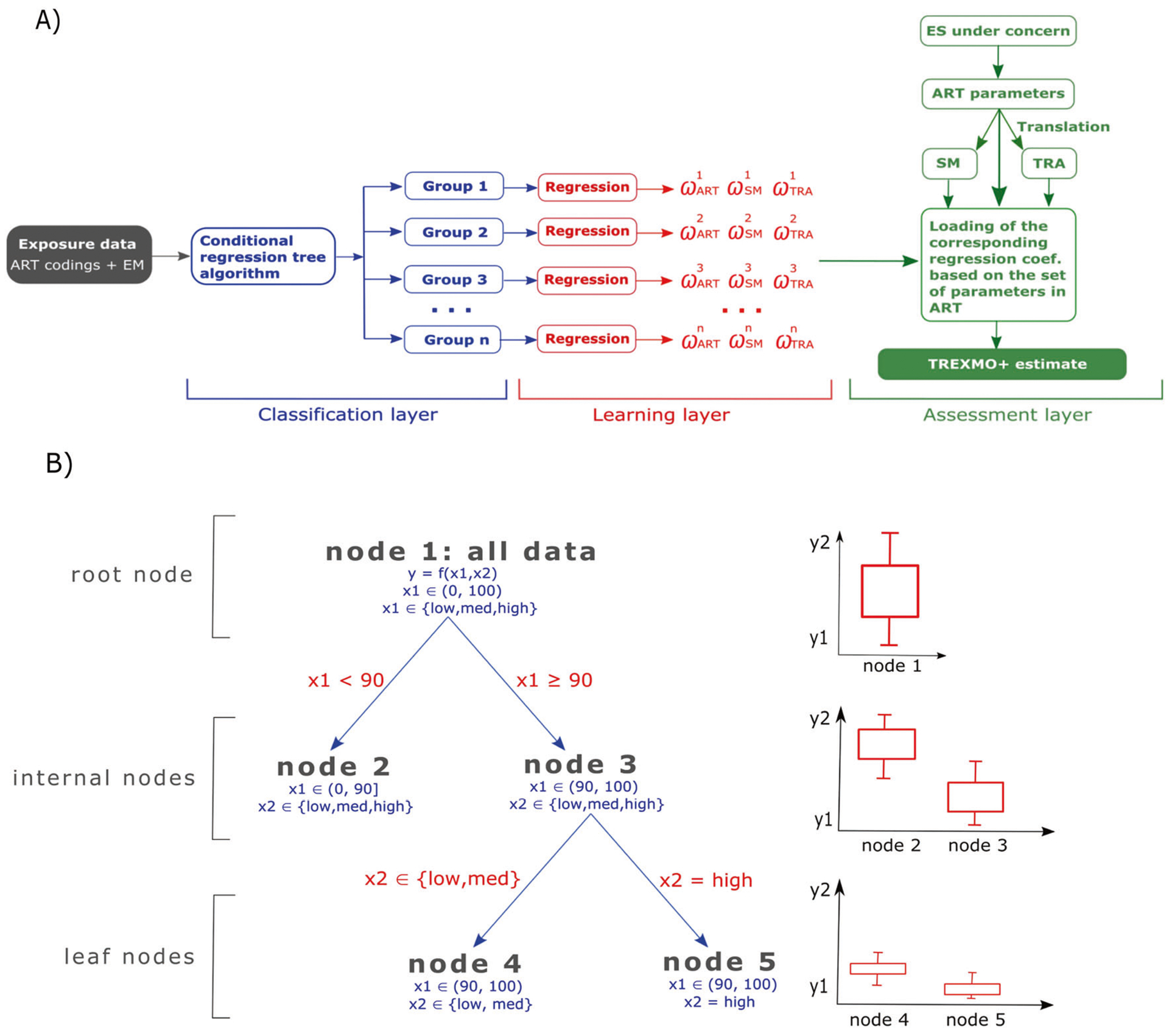
a - TREXMO+ algorithm and b - regression tree.

Classification layer

Exposure data containing the exposure parameters coded for ART (+PROC/TRAv3 per ES) are supplied to this layer. This database must not include exposure data that were used to calibrate any of ART, SM, or TRAv3. Exposure data from two different sources were available for the purpose of this study.

The classification layer is designed to split the supplied data into similarly exposed groups with the addressed exposure conditions. To classify the data, we used a conditional inference regression tree (RT) [21]. This is a machine-learning (ML) method [22] that constructs a tree-like structure from a dataset containing a continuous dependent variable (such as exposure measurement data). The method has been explained in detail by Strasser and Weber [21]. A brief explanation is provided in the next paragraph. In this study, the RT algorithm was used only to classify the exposure dataset into smaller subsets and not to derive a prediction algorithm. For each subset of the data obtained by using the RT, the corresponding prediction coefficients are established in the next, learning, layer of TREXMO+.

Figure 1b illustrates an example of the workflow of the RT algorithm. The most-top, root node (node 1) contains data consisting of two independent variables (x1 and x2) to determine a dependent (or response) variable (y) using a function of f(x1, x2). At this point, the response covers a wider range of possibilities between y1 and y2, shown in the bar graph in Fig. 1b. RT tests a null hypothesis of independence of the two (x) predictors with the response. As the independence measure, a p value corresponding to a given level of confidence (such as 95% confidence interval) was used. If the null hypothesis cannot be rejected, then a binary split is performed. When more splits are possible, the most discriminative one (with the lowest p value) is performed. In Fig. 1b, the first, most discriminant, binary split is found for x1 = 90 (arbitrary number used for explaining the logic). The data are then split in two smaller subsets; node 2 contains the records with x1 < 90, while node 3 contains only the data with x1 ≥ 90. Compared with the root node, the response in these two child (internal) nodes is narrower. Every binary split results in narrower data and the response with smaller standard deviations. The recursive data splitting continues until the null hypothesis cannot be rejected. The nodes that cannot be split are leaf (or terminal) nodes.

In this study, the variables (as such, in Fig. 1b), for which the independence with the response was tested, were the exposure determinants of ART. Table 1 lists all exposure determinants, grouped by the principal modifying factor of ART [7]. The RT algorithm evaluated how significant these determinants are in predicting the measured values. Only VP and concentration were used as continuous variables. It is important to keep the independence between the used variables. For activity emission potential, for example, the parameter list for underlying determinants (such as amount of product) depends on activity class (such as surface spraying of liquid products). These underlying determinants were thus not used as the variables in RT.

Table 1.

ART exposure determinants used for testing independence with the measurements in RTs.

Modifying factor	RT variables (example)	Variable type
Substance emission potential	Vapor pressurea	Continuous
	Product concentrationa	Continuous
	Dustinessb	Categorical
Activity emission potential	Activity (sub)classes (e.g., surface spraying of liquid products)	Categorical
Local control	Category of primary local control (e.g., enclosing LEV)	Categorical
Segregation	Segregation (e.g., partial segregation)	Categorical
Dilution	Room volume Air-exchange per hour	Categorical
Separation	Separation (e.g., partial separation with ventilation)	Categorical
Surface contamination	Surface contamination (e.g., good housekeeping)	Categorical

ART Advanced REACH Tool, LEV local exhaust ventilation, RT regression tree.

^aFor volatile liquids, fugacity was calculated as log(vapor pressure × concentration).

^bFor powders and solids, log-concentration was calculated.

Learning layer

Here, TREXMO+ evaluates the regression coefficients (w) in Eq. 1 for each leaf node from the previous layer (see Fig. 1a). It is assumed that the performance of the three models (ART, SM, and TRAv3) varies less over different conditions in the leaf nodes, as compared with data in the root node. For each leaf node, the regression analysis in Eq. 1 is conducted. It uses the three models’ estimates (E) to predict the GM of measurements.

$$\text{GM}=w_{\text{ART}}{E}_{\text{ART}}+w_{\text{SM}}{E}_{\text{SM}}+w_{\text{TRA}}{E}_{\text{TRA}}+\epsilon$$ (1)

For n number of leaf nodes, this layer outputs a (3 × n) matrix containing three regression coefficients (for ART, SM, and TRAv3) per node. These regression coefficients define how a given predictor (i.e., exposure model) determines the GM found in the SUVA and NIOSH datasets. As already mentioned, it is not crucial to know which percentile of the exposure is used for these three predictors. If, for example, the 90th percentile was used for SM (or ART), it would not change the performance of the final prediction of TREXMO+, but only the evaluated regression coefficient of the given model. This means that even if unitless predictors were used, the outcomes from Eq. 1 would be still prediction of GM in mg/m³.

Since all predictors in Eq. 1 are REACH exposure models, some collinearity could exist between them. To address this issue, variance inflation factor (VIF) [23, 24] was evaluated for each leaf node as a measure of collinearity between the predictor models. The predictors for which VIF was higher than five [24] was excluded from Eq. 1 and the regression coefficients were reevaluated for the remaining predictors. Furthermore, R-squared was calculated for each node to show how much of the variance is explained by using the model in Eq. 1.

Assessment layer

For a new ES, this layer predicts an exposure estimate. For the given ES, it requires a set of ART exposure parameters to be provided. Following the rules established by Savic et al. [20]; TREXMO+ performs the parameter translations to SM and TRAv3 and calculates the three estimates of the three REACH models. In the next step, TREXMO+ calls the RT from its first layer. Based on the provided ART parameters, the algorithm assigns the given ES to an appropriate leaf node. TREXMO+ then loads the corresponding regression coefficients from its second layer and calculates a final TREXMO+ estimate by using Eq. 1.

Evaluation of RTs and regression coefficients

Table 2 shows the exposure data used in the classification layer of TREXMO+. The complete data were coded using the exposure parameters of ART. Also, a PROC and type of use parameter were assigned to each ES to allow the calculations in TRAv3. For the ESs with more than one exposure measurement, the GM was calculated. 80% of the data was selected into the training set, i.e., the TREXMO+ development, while the remaining data—the testing set— were used to test the performance of the new models (explained in the next section). The redistribution of exposure data into two subsets (the training set and testing set) was randomly conducted by iterating until an RT with the maximal possible number of the binary splits was achieved. Then, an RT based on the training set was established and compared with the RT from the previous iteration. The goal was to cover as much variance as possible in the training set in order to result in more binary splits. This step is especially important for the exposure types in which fewer data were available (that is, powders and solids) and a single random selection may have resulted in no splits.

The ART parameter sets (+PROC and type of use), with their corresponding GMs, were supplied to the classification layer of TREXMO+. One RT and one matrix holding the regression coefficients (w in Eq. 1) were obtained for each of the exposure types, that is, volatile liquids, powders, and solids.

It is important to address that the official TREXMO+ tool includes the RTs and the matrices holding the evaluated regression coefficients for the whole data (both training and testing set). The RT algorithm and the coefficient matrices were evaluated for the total data. Again, one RT and one matrix with these coefficients were evaluated for each exposure type, separately. The results are given in Figs. S1–S3 and Table S1 (see Supplementary Information 2).

TREXMO+ validation

For each ES, based on a given set of the exposure parameters, the third layer of TREXMO+ loaded the corresponding coefficients from its second layer. The TREXMO+ predictions were then calculated by using these coefficients with the estimates of ART, SM, and TRAv3, in Eq. 1.

Several statistical analyses were conducted to investigate the performance of TREXMO+ and to compare the results with those predicted individually from three models. Residuals (Eq. 2), measuring the difference between modeled $(\widehat{y})$ and individual exposure measurement (i.e., not GM) (y), were calculated and plotted against the measurements. According to Eq. 2, positive residuals mean overestimation, while negative residuals implicate underestimation of the measurements by the modeled predictions.

$$r_i=\text{log}{\widehat{y}}_i-\text{log}{y}_i$$ (2)

LOcally-WEighted Scatterplot Smoothing (LOWESS) [25] was used to present the changes of the residuals for different models in the same graph. LOWESS converted residual data points into smoothed lines.

Relative bias (Eqs. 3 and 4) and accuracy (Eq. 5) were also evaluated. Accuracy is calculated as mean absolute error (MAE). While the former shows how much, overall, the models overestimate or underestimate exposure; the latter quantifies the average distance between the model’s central estimate and GM of the measurements. Because the bias (Eq. 3) accounts for the sign of the log-difference, it cannot be used to quantify the average distance between the measured and modeled values.

$$\text{bias}=\frac{1}{n}\sum _{i=1}^n\text{log}{\widehat{y}}_i-\text{log}{y}_i$$ (3)

$$\text{relative}\text{bias}=\left(e^{\text{bias }}-1\right)\times 100\%$$ (4)

$$\text{accuracy}=\frac{1}{n}\sum _{i=1}^n\left|\text{log}{\widehat{y}}_i-\text{log}{\text{GM}}_i\right|$$ (5)

Since the ML algorithm in the classification layer of TREXMO+ can also be used to predict GM, the corresponding relative bias and accuracy were also evaluated.

Finally, regression parameters, slope and intercept, were calculated for TREXMO+ and its three predictor models. The log-estimates of each model were plotted against the log-exposure measurements.

Software

The entire study was performed in R language and environment for statistical computing [26], version 3.5.0. To establish the RTs needed for the first layer of TREXMO+, ctree function was called from R’s party package. For the multicollinearity test, car package and its function vif were used. Furthermore, for the graphs in this paper, ggplot function from ggplot2 package [27] was used.

Results

Established RTs and regression coefficients

Figure 2 shows RTs established for the training dataset for volatile liquids (A) and powders (B) (Eq. 1). For solids, the exposure conditions were insufficiently different to allow for a statistically significant binary split. The iterative random redistribution of the ESs failed to result in a training set with enough variance for a binary split. Solid ESs thus remained in the root node, and no RT is shown for solids in Fig. 2. For liquids, three determinants—fugacity, activity (sub)classes, and local controls—were found to significantly affect the GM of the measurements. For powders, these determinants were dustiness and concentration.

Fig. 2. Regression trees established for the evaluated exposure forms.

a Volatile liquids and b powders.

Table 3 shows the calculated regression coefficients for the three REACH models and different nodes in Fig. 2 (w; see Eq. 1). For solids, because no RT was established, one set of these coefficients was obtained. A high collinearity (i.e., VIF > 5) was often found between ART and SM. Therefore, most of the time, only two models (e.g., ART and TRAv3 or SM and TRAv3) were used as predictors in Eq. 1. Finally, the found R-squared values in Table 3 varied drastically from node to node. For liquids, for example, while the regression explained 86% for node 6, only 13% was explained for node 3.

Table 3.

The TREXMO+ coefficients evaluated for the three predictor models and the corresponding R-squared values found for different exposure subsets (i.e., nodes).

Exposure type (ESa/EMb)	Node	Number of ES	ART	SM	TRAv3	Error	R2
Liquids (185/742)	3	40	0.32	c	0.16	1.31	0.13
	4	11	0.03	2.44	−0.99	1.14	0.69
	6	67	0.36	c	0.37	0.74	0.82
	7	30	c	−0.51	0.49	0.84	0.30
Powders (69/153)	3	7	−0.19	1.62	−0.69	1.00	0.54
	4	38	0.18	0.15	0.01	0.68	0.15
	5	10	c	0.98	−0.88	0.71	0.82
Solids (24/57)	/	24	0.13	c	0.39	0.60	0.35

The node numbers correspond to the leaf nodes in Fig. 2.

^aNumber of exposure situations.

^bNumber of exposure measurements.

^cModel not used as predictor due to a high multicollinearity.

To illustrate the concept of TREXMO+, residuals with LOWESS smoothing were also evaluated for the training dataset. Figure 3 (the training dataset) shows how TREXMO+ balances its estimates by shifting it to a REACH model that locally performs best. Our model, however, kept the overall behavior of the three models. This is especially evident for liquids, where the three REACH models tend to overestimate lower exposures and underestimate higher exposures. Here, TREXMO+ resulted in a similar, but alleviated, trend.

Fig. 3. Residuals obtained for the training and testing dataset for the three exposure types.

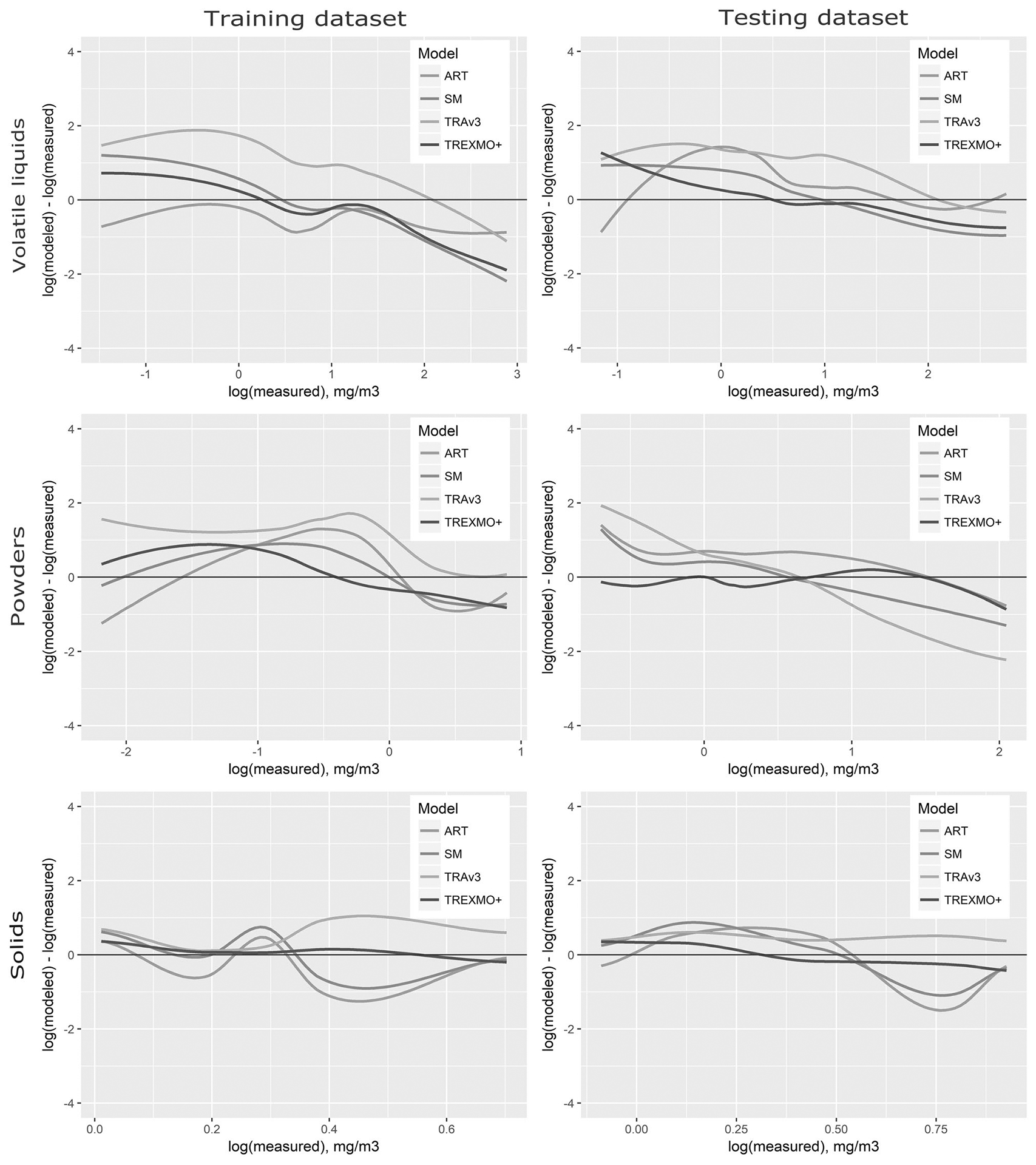
The LOWESS method was applied to plot data points as smoothed lines for the four exposure models.

Validation results

The RTs in Fig. 2 and the corresponding coefficients in Table 3 were used to calculate the TREXMO+ estimates for the ESs in the testing dataset.

Figure 3 (the testing dataset) shows trends in the residuals for the three REACH models and TREXMO+. As for the training set, the models tend to overestimate lower exposures and underestimate higher exposures. The TREXMO+ line is the least deviated from the central “zero” line. This means that the mentioned trend is alleviated for TREXMO+. It also means that compared with the three REACH models, the difference between the TREXMO+ estimates and the exposure measurements is smaller.

The results found for relative bias (Table 4) show that TREXMO+ underestimates the measurements (relative bias from −24 to −41%). Even lower values (relative bias from −49 to −90) were found when the ML algorithm was used to assess the exposure. Except for solids, for which ART and SM were found to underestimate the exposures, the REACH models were found to overestimate more frequently the measurements. For powders, for example, the extent and the number of overestimations by ART resulted in a high relative bias (=1004%). Figure 3 illustrates this finding (the testing dataset); the ART’s line is above the central “zero” line over almost the entire domain.

Table 4.

Relative bias and accuracy of the three REACH models, the machine-learning algorithm only and TREXMO+.

Model	Relative bias (%)			Accuracy
	Liquids	Powders	Solids	Liquids	Powders	Solids
ART	86	1004	−57	1.00	0.85	0.61
SM	9	325	−34	0.66	0.63	0.53
TRAv3	410	818	171	1.16	1.04	0.45
ML	−49	−90	−66	0.61	0.58	0.34
TREXMO+	−41	−24	−30	0.46	0.48	0.31

For all three exposure types, TREXMO+ was the most accurate model (Table 4). This means that the average difference between the estimates of TREXMO+ and the calculated GM was the smallest. Regarding different exposure forms, this difference was found to be, on average, between 0.31 and 0.48. As the accuracy is expressed on the log-scale (see Eq. 5), the estimates of TREXMO+ are expected to be two to three times lower or higher than the measured GM. The second most accurate was when using only ML of TREXMO+, for which MAE was 0.31–0.61. Only a small difference (MAE, 0.31 vs 0.34) was found between TREXMO+ and ML for solids, which can be explained by the fact that the regression layer failed to perform binary splits for this form of exposure. Of the three REACH models, SM was the most accurate, with a log-difference of 0.53–0.66 (or three to five times GM).

Finally, the relationship between the modeled and measured exposures is shown in Fig. 4 and Table 5. The corresponding 90% confidence interval for ART and the 90% confidence interval and prediction interval for TREXMO+ are also plotted in Fig. 4.

Fig. 4. Measured versus modeled exposure values for three different exposure types.

Red dotted lines (for ART and the inner dotted lines for TREXMO+) illustrate the 90% confidence intervals, whereas the blue dotted lines (only for TREXMO+; the outer lines) illustrate the prediction interval.

Table 5.

Regression coefficients obtained for the models.

Exposure type (ESb/ EMc)	Model	Intercept (a)	Slope (b)	R2	p value
Liquids (185/742)	ART	0.47	0.38	0.20	4.6e-9a
	SM	−0.13	1.09	0.34	1.2e-15a
	TRAv3	0.03	0.55	0.15	2e-6a
	TREXMO+	0.18	0.92	0.41	<2e-16a
Powders (69/153)	ART	−0.41	0.37	0.06	0.16
	SM	0.06	−0.18	0.01	0.63
	TRAv3	0.86	−0.97	0.49	0.47
	TREXMO+	0.12	0.87	0.65	<2e-16a
Solids (24/57)	ART	0.50	0.16	0.05	0.55
	SM	0.56	−0.08	0.01	0.86
	TRAv3	−0.43	1.00	0.94	<1e-5a
	TREXMO+	−0.7	3.01	0.68	0.01a

^aStatistically significant at the 95% confidence level.

^bNumber of exposure situations.

^cNumber of exposure measurements.

For liquids, all four models were significantly correlated with the measurements (p < 0.05). The variance in the measured exposure was best explained by TREXMO+ (R-squared = 0.41). For powders, the correlation was significant only for TREXMO+, whereas SM and TRAv3 were even negatively correlated with the measurements. For SM, this was also the case for solids (slope = −0.08). The relationship between the modeled and measured exposure for this exposure form was significant only for TRAv3 and TREXMO+.

Discussion

In this study report, we presented the development and validation of a new, “meta” exposure model, called TREXMO+. This model applies the concept of the multi-model approach of TREXMO [20]. By using between-model translations to calculate a refined estimate, TREXMO+ calculates exposure for three REACH models: ART, SM, and TRAv3. Furthermore, the model incorporates an RT algorithm to account for different performances of these individual models for different exposure conditions. This concept, in which three existing models are used only as exposure predictors of another model, was expected to perform better than the predictor models alone. A small fraction (20%) of the measured data was used to test the performance of TREXMO+ and confirmed this hypothesis. For all tested criteria, including residuals, bias, accuracy, and regression, TREXMO+ led to improved results over the three REACH models considered.

RTs and regression coefficients

The splitting criteria in the established RTs, which were the ART exposure parameters, were in accordance with the results in Savic et al. [19]. Those authors reported that the parameters of substance properties (such as VP or dustiness), activity type (such as spraying), and local control have the most significant influence on determining measured exposure levels. Moreover, a sensitivity analysis [28] and a computational comparison [19] have also shown that these parameters affect most the final models’ predictions and the differences among the predictions of ART, SM, and TRAv3. Regarding the RTs established for different exposure types, the most binary splits (three) were obtained for volatile liquids. This was driven by three factors: data size, variability between ESs, and how well the exposure parameters account for the variance in the measurements. Nearly 65% of the exposure data in this study addressed the exposure to volatile liquids. The given ESs for liquids covered a wide range of different exposure conditions. For example, the data included substances with VPs from 18 Pa to 59 kPa. Also, all activity (sub)classes of ART were covered. A smaller amount of data and less variable ESs led to a smaller RT (that is, two splits) for powders, in comparison with liquids. The RT did not branch further to include splits for different activities and local controls. Finally, the training data, on which the RTs were based, included only 19 ESs for solids. These data were insufficiently different to result in a significant binary split. Almost all ESs (18 of 19) addressed exposure to wood dusts with the contaminant concentration of 100%. Almost half of these ESs included no local control, whereas exposure in the other half was controlled with on-tool extraction.

In some cases, the binary splits in Fig. 2 were not in accordance with the dimensionless scores assigned to the parameters of ART. It is expected that exposure parameters with substantially different scores would be classified in different nodes. However, the extremely fine dust (score = 1.0) category appeared in the same node as firm granules (score = 0.01) instead with fine dust (score = 0.3). The explanation for this can be found in Savic et al. [13], where the same SUVA data were used to investigate the performance of ART. In that publication, the authors stated that where the raw data were unclear, the most conservative parameters were assigned. This means that most likely the selection of extremely fine dusts was too conservative. A more appropriate parameter would be coarse dust for the ESs with extremely fine dust.

This study also found strong collinearity between ART and SM for certain exposure conditions (Table 3). For these two exposure models, similar results were obtained in our previous, in silico, study [19]. These results could be explained by the fact that both ART and SM follow the same source-receptor approach. Also, this could mean that there is some overlapping between the exposure data used to develop these models.

Model validation

Overall, the results showed that TREXMO+ is less biased and more accurate. The estimates of this model better explained the variance (that is, higher R-squared) of the measurements. Somewhat higher underestimations and lower accuracy were found when ML alone was used to predict the exposure. This was the least noticeable for solids, for which no binary split was obtained. However, it is difficult to imagine how the two approaches will differ as more data becomes available. Moreover, the relatively small data size and the similarity between the exposure conditions (both from SUVA and NIOSH) in the training and testing datasets might have biased the final results and conclusions.

For all three exposure types considered, the correlation between TREXMO+ and the measurements was significant at the 95% confidence level. This was not the case, however, for the REACH models for powders and solids, for which only TRAv3 had a significant correlation with the measurements. The three REACH models were found to overestimate the measurements. For liquids (excluding SM) and powders, these models were too conservative. With relative bias between 300 and 1000%, powders were the most overestimated. Such overprotectiveness might obscure the practical use of these models.

Conversely, TREXMO+ underestimated the measurements. The extent of these underestimations (that is, the magnitude of absolute value of relative bias) was small, as compared with the overestimations obtained for the REACH models. Overall, TREXMO+ was thus the least biased model, a determination which was the goal of this study. This model was more biased than SM only for liquids. According to Eq. 3, bias is a measure of the average difference between the modeled and measured exposures. If, for example, the number and extent of over- and underestimates is equal, then the bias in Eq. 3 equals zero. However, this does not mean that the model is not locally biased (e.g., for lower exposures). A better representation on how a model performs locally was thus obtained with LOWES smoothing of the residuals in Fig. 3. For liquids, the residuals for TREXMO+ were closer to the measured exposure over the measurements range. For SM, however, the extent of overestimation of lower exposures and underestimation of higher exposures was greater than for our model. The results for accuracy confirmed these findings. It was shown that the estimates of TREXMO+, on average, differ only two to three times from the GM of the measured exposures.

Regarding the relationship with the measurements, only the estimates of TREXMO+ were significantly correlated with all three exposure types considered. For powders and solids, SM and TRAv3 (only for powders) were even negatively correlated. However, this may be due to the relatively small number of measurements in the testing data, which were also the most distributed within a small range (0.1–10 mg/m³).

The recommendations on the risk management measures that should be communicated down the supply chain when assessing the exposure by using TREXMO+ should be the same as with ART. This is because the users of TREXMO+ will require the same exposure information in TREXMO+ as in ART. Another reason is that, regarding its concept, TREXMO+ is expected to calculate values that could be seen as tier 2 estimates.

Limitations

Two major limitations of this study were the amount of data and the reliability of the established exposure parameters for ART. As already mentioned, most of the ESs addressed exposure to volatile liquids. Although for this exposure type, 37 different ESs were used to investigate the performances of TREXMO+, only 14 powder ESs and 5 solid ESs were in the testing dataset.

Regarding the quality of information in the two exposure databases, it was more likely that erroneous selection of input parameters for ART occurred when interpreting the SUVA dataset. This statement is drawn from the fact that only two assessors (one expert and one trainee) interpreted the raw SUVA data. The input parameters for the NIOSH database were coded based on the consensus between six assessors from different agencies [15]. Nevertheless, this might create a space for mistakes that could lead to, for example, miscoding of the dustiness categories.

In addition, the current version of TREXMO+ predicts only the GM exposure values, while the 90th percentile is used under REACH for risk characterization [1]. When more data becomes available, required statistical analyses will be conducted to provide the parameters for the calculation of higher percentiles in TREXMO+.

Conclusion and outlook

Compared with the three REACH models, TREXMO+ performed better with regard to bias, accuracy, and its correlation with measurements. The most important outcome is that the model’s predictions differ only by a factor between 2 and 3 in comparison with corresponding exposure measurements, relatively smaller than factors of the three REACH models. The small testing dataset, however, might raise concerns on the validity of these results, especially for powders and solids. More exposure data will thus be needed to further test the performances of TREXMO+ or refine its algorithm. It is important to note that a future refinement of any of the predictor models will also improve the predictions of TREXMO+.

The new model solves the problem with the multi-models approach recommended in Savic et al. [20], in which several exposure estimates are calculated for the same ES. Instead of the three or more exposure values calculated from REACH models, which may differ by several orders of magnitude [19], TREXMO+ provides a single, refined estimate that corresponds the most to given exposure conditions.

TREXMO+ is not limited to the three REACH models (see Eq. 1) and its input parameters. Estimates of other exposure algorithms, such as physical-chemical models, could be considered in the future for inclusion in TREXMO+. Furthermore, regarding the limited exposure data that was available for this study, the classification layer identified only the exposure parameters of the three REACH models as significant for the exposure assessment. It is, however, important to mention that with more exposure data available, other variables, if found significant, could be used to extend Eq. 1.

By the end of 2019, TREXMO+ will be available as a user-friendly web-application. The corresponding URL address will be shared with all current users of TREXMO v2 and added to the Google search engine. This publicly available freeware will include all data in the SUVA and NIOSH datasets.