Skip to main content
PMC home page
Genome Research logoLink to Genome Research
. 2020 Jul;30(7):1040–1046. doi: 10.1101/gr.258228.119

TRACE: transcription factor footprinting using chromatin accessibility data and DNA sequence

Ningxin Ouyang 1, Alan P Boyle 1,2
PMCID: PMC7397869  PMID: 32660981

Abstract

Transcription is tightly regulated by cis-regulatory DNA elements where transcription factors (TFs) can bind. Thus, identification of TF binding sites (TFBSs) is key to understanding gene expression and whole regulatory networks within a cell. The standard approaches used for TFBS prediction, such as position weight matrices (PWMs) and chromatin immunoprecipitation followed by sequencing (ChIP-seq), are widely used but have their drawbacks, including high false-positive rates and limited antibody availability, respectively. Several computational footprinting algorithms have been developed to detect TFBSs by investigating chromatin accessibility patterns; however, these also have limitations. We have developed a footprinting method to predict TF footprints in active chromatin elements (TRACE) to improve the prediction of TFBS footprints. TRACE incorporates DNase-seq data and PWMs within a multivariate hidden Markov model (HMM) to detect footprint-like regions with matching motifs. TRACE is an unsupervised method that accurately annotates binding sites for specific TFs automatically with no requirement for pregenerated candidate binding sites or ChIP-seq training data. Compared with published footprinting algorithms, TRACE has the best overall performance with the distinct advantage of targeting multiple motifs in a single model.

Identification of cis-regulatory elements where transcription factors (TFs) bind remains a key goal in deciphering transcriptional regulatory circuits. Standard approaches to identify sets of active TF binding sites (TFBSs) include the use of position weight matrices (PWMs) (Stormo et al. 1982) and ChIP-seq (Barski et al. 2007). Although these methods have been successful, both suffer from drawbacks that limit their usefulness. PWMs are able to identify high-resolution binding sites but are prone to extremely high false-positive rates (FPRs) in the genome. On the other hand, although ChIP-seq binding measurements are highly specific and have a significantly reduced FPR, the resolution is comparatively low, is labor intensive, and depends on suitable antibodies that are only available for a limited number of TFs. Newer experimental techniques for the identification of DNA-bound protein binding sites, such as ChIP-exo (Rhee and Pugh 2012) and CUT&RUN (Skene and Henikoff 2017), have the advantage of high resolution and cost efficiency but still share the same labor intensive and limited antibody availability disadvantages as ChIP-seq.

To complement these approaches, another experimental method has been developed using data from high-throughput sequencing after DNase I digestion (DNase-seq) (Boyle et al. 2008). DNase-seq identifies stretches of open regions of chromatin where DNase I cuts at a higher frequency. Within these regions, TFBSs can be identified at nucleotide resolution by searching for footprint-like regions with low numbers of DNase I cuts embedded in high-cut peaks.

Hesselberth et al. (2009) first proposed a DNase-seq signal–based computational method to detect footprints at base-pair resolution in Saccharomyces cerevisiae. Since then, several computational footprinting algorithms have been developed to detect TFBSs by investigating chromatin accessibility patterns, which can be categorized as de novo (the Boyle method, DNase2TF, HINT, PIQ, and Wellington) and motif-centric (DeFCoM, BinDNase, CENTIPEDE, FLR) (Boyle et al. 2011; Pique-Regi et al. 2011; Piper et al. 2013; Sherwood et al. 2014; Sung et al. 2014; Yardımcı et al. 2014; Kähärä and Lähdesmäki 2015; Gusmao et al. 2016; Quach and Furey 2017). De novo methods detect footprints across input regions based on their DNase digestion pattern. However, most of these methods were not designed to distinguish between binding sites for specific TFs and cannot automatically label TF-specific binding sites of interest. In contrast, motif-centric methods can predict TF-specific sites but require pregenerated candidate binding sites for TFs and assess their probability of being TF bound (active binding sites). This limits their performance as these methods are unable to detect additional regions of candidate binding sites. Moreover, some of these methods are supervised, requiring ChIP-seq data to generate positive and negative training sets, and can only be applied to TFs with high-quality antibodies. This is a constraint as only a minority of TFs have ChIP-seq data available (Wang et al. 2012).

In addition to DNase digestion patterns, more detailed modeling of sequence preference information has been used in TFBS identification. Hoffman and Birney (2010) have previously proposed a hidden Markov model (HMM)–based method, termed Sunflower, to predict TFBSs based solely on sequence data. Instead of scanning for motif sequences directly, this model takes into consideration the competition between multiple TFs to provide a binding profile for all factors included in the model. Although Sunflower still suffers from sequence-only method limitations for identifying TFBSs, it has a greater ability to distinguish the specific TF that binds at each predicted site.

We have developed an unsupervised footprinting method, TRACE, based on a HMM framework (Rabiner 1989; Durbin et al. 1998) and inspired by the success of Sunflower and other existing footprinting methods. TRACE predicts footprints and label binding sites for a set of desired TFs by integrating both DNase-seq data and PWMs. Our method is not dependent on pregenerated candidate binding sites or available ChIP-seq data, making it more flexible and broadly applicable compared to previous methods.

Results

The TRACE model

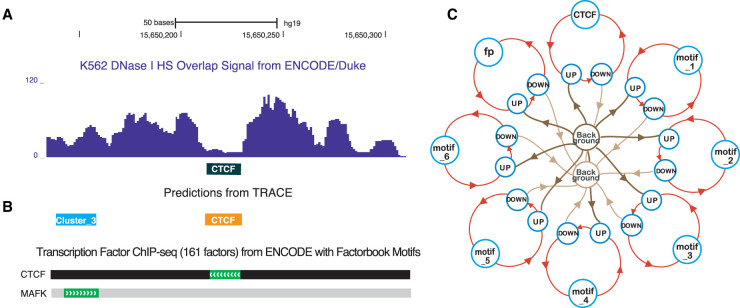
TRACE is an HMM-based unsupervised method with the number of hidden states dependent on the numbers and lengths of included PWMs (Fig. 1). The basic structure of our model includes two background states (the start and end of each open chromatin region delineated by DNase I cut sites), a target TF state (Fig. 1C, CTCF), a generic footprint state (Fig. 1C, fp), and a series of bait motif states (Fig. 1C, motif_1-motif_6). Each of the nonbackground states is surrounded by a set of UP, TOP, and DOWN states (upslope, summit, and downslope of small peaks surrounding each footprint). Target TF states and bait motif states contain a number of discrete chains of states representing binding sites for each motif included in the model. The generic footprint state represents the regions that have a footprint-like digestion pattern but do not match any PWMs in the model. TRACE includes a series of bait motifs representing commonly co-occurring motifs that significantly increase the performance of the model. For example, the seven-motif CTCF model in Figure 1C includes a CTCF binding site state chain, six additional bait motifs (motif_1, motif_2, …, motif_6), and generic footprints whose sequences do not match any of the included motifs. For each of these motifs, our model can distinguish its TF-bound states from unbound states based on the distinct DNase-seq digestion patterns of the motif sites (Supplemental Fig. S1).

Figure 1.

Figure 1.

Open in a new tab

Computational footprinting can detect TFBSs at nucleotide resolution. (A) An example of digestion pattern at footprints: DNase I base overlap signal centered at CTCF motif sites (black box). (B) Predicted binding sites from TRACE using our 10-motif CTCF model match a corresponding region of TF binding obtained by ChIP-seq experiments with DNA-binding motifs by the ENCODE Factorbook repository. (MAFK is a member of cluster 3 motifs.) (C) Simplified example schematic of a seven-motif CTCF model. Circles represent different hidden states including multiple motifs; lines with arrows represent transitions between different states. For simplicity, TOP states are not shown in the model structure.

TRACE takes PWMs and DNase-seq signals as inputs and models the emission distribution as a multivariate normal distribution using cut count signal and its derivative, as well as PWM scores at each genomic position. Each binding site (footprint) is expected to be in a region of low sequence density surrounded by a peak of density to either side with a high PWM score (Fig. 1A,B).

TRACE outperforms existing methods

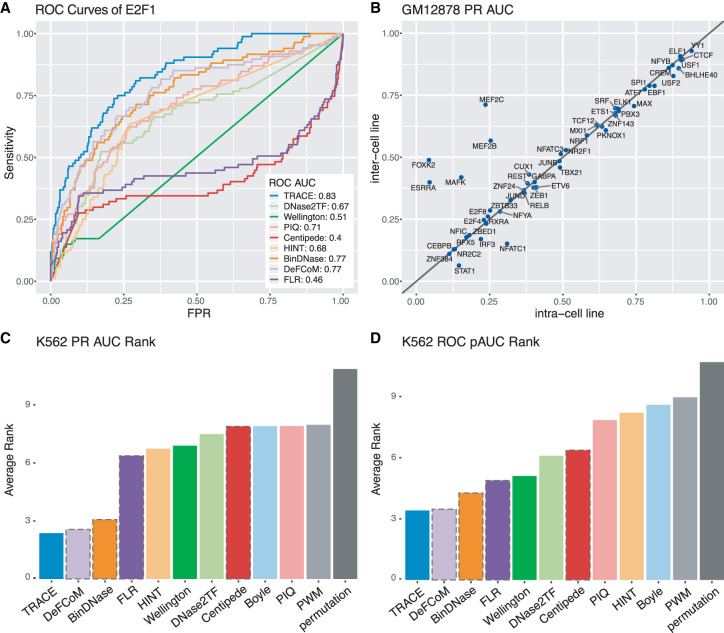
To evaluate the performance of TRACE relative to published computational footprinting methods, we tested nine methods (DeFCoM, BinDNase, CENTIPEDE, FLR, DNase2TF, HINT, PIQ, Wellington, and a PWM-only comparison) on 99 TFs. For a fair comparison across all methods, de novo methods were applied to DNase-seq peaks containing the same sets of motif sites that were assessed by motif-centric methods. Receiver operating characteristic curve area under the curve (ROC AUC) and precision-recall (PR) AUC of predictions of each TF were computed for each method based on the P-values or scores provided and were ranked across all methods (Fig. 2A; Supplemental Figs. S2, S3).

Figure 2.

Figure 2.

Open in a new tab

TRACE's performance is stable across cell lines, and it outperforms other computational methods. (A) Example ROC curves of E2F1 for all methods evaluated. (B) Cross–cell line comparison of binding site prediction in GM12878. Each point represents a TF tested; the x-axis and y-axis are PR AUCs of applying TRACE using models trained from GM12878 and models trained from K562, respectively. Points above the diagonal line indicate TFs for which the inter–cell line model performed better. (C,D) Average rank of PR AUC and ROC pAUC of existing methods across all TFs tested. The bars with a dashed outline represent motif-centric methods.

Previous studies evaluating computational footprinting methods focus on ROC AUC as a measurement of performance. Although this is a decent classification performance assessment, the number can be inflated by false positive predictions. For example, the ROC AUC statistic might imply a relatively favorable classification if the method tends to call most samples as positive hits when the data are highly unbalanced, as is the case for many of TFs tested. In addition, partial ROC AUC (ROC pAUC) were computed at a 5% FPR cutoff. PR AUC was also included in the evaluations as it provides a better assessment of false positives. Compared with other footprinting methods, TRACE has the best overall performance based on average rank in both ROC pAUC and PR AUC across the 99 tested TFs (Fig. 2C,D). It ranked first overall for 25.5% of TFs and in the top five for 96.9% of TFs. Compared with other unsupervised methods, TRACE ranked first for 87.7% of TFs. TRACE also outperformed supervised approaches, including DeFCoM and BinDNase. TRACE can predict TF footprints with a performance equal to or better than the best published methods without the requirement of positive and negative training data sets.

Bait motifs improve footprinting prediction accuracy

TRACE provides identification of binding sites for any desired TFs at nucleotide resolution. By incorporating DNase-seq data and PWM information, it can detect footprints with an anticipated DNase digestion pattern and matching motifs (Fig. 1B). One important feature of our model is that states for different motifs are independent of each other, enabling its ability to distinctly label binding sites for multiple TFs. In addition, adding extra motifs to the model for a specific TF can potentially increase the accuracy of identifying TF-specific binding sites. These additional motifs serve as baits, discouraging the prediction of weakly matching sites and introducing competition, thus decreasing FPRs (Hoffman and Birney 2010). However, including PWMs with similar sequence preference does not provide useful information and could decrease our model's ability to distinguish between binding sites of different motifs. To avoid this, only root motifs from each motif cluster in the JASPAR CORE vertebrates clustering were used (Khan et al. 2018), and the cluster that contains the TF of interest was excluded (Supplemental Methods). Each root motif encompasses all of the position-specific scoring matrices (PSSMs) of a cluster generated by the RSAT matrix-clustering tool (Castro-Mondragon et al. 2017). In a N-motif model, the root motifs from N − 1 clusters with the greatest number of occurrences were selected. These N − 1 motifs provide additional information, making the model more sensitive to identifying binding sites for the TF of interest.

Overall, the addition of bait motifs to the model yielded significant improvements over our original method, which had a similar HMM structure but did not include motif information (an option provided in TRACE) (Boyle et al. 2011). Using a 10-motif model (the TF of interest plus nine extra motifs), the average PR AUC from TRACE increased by 0.20 (63.1%) over our original method, and ROC pAUC improved by 20%.

By comparing models containing different numbers of extra motifs, we found that additional TFs can increase the quality of TFBS identification in most cases. However, this was at the expense of considerably increased computational time (Supplemental Table S3). We determined that an optimal trade-off between performance increase and computational time was the 10-motif model, which is used in the remainder of this study.

TRACE can be applied accurately across cell lines

Cross–cell line validation was performed using models trained from K562 DNase-seq data and subsequently applied to GM12878 to test their performance compared with models trained on GM12878. Because there is less available validation data in GM12878, this comparison used 52 TFs. The results indicated that TRACE can provide accurate predictions in one cell line using a model trained from another cell line and that intra–cell line and inter–cell line predictions have comparable overall performance (Fig. 2B). This suggests that the data processing steps can successfully capture the signature information of DNase digestion and diminish between–data set variance to a degree sufficient for effective prediction across cell lines. It also indicates that the DNase digestion pattern of binding sites is preserved for most TFs across cell types. Some exceptions were observed, however; for example, ESRRA had significantly better performance in the inter–cell line test compared with the intra–cell line test. This TF has far fewer active binding sites in GM12878 (7.6% prevalence) than K562 (31.3% prevalence), and TRACE may not be able to learn an accurate model from the GM12878 data. This suggests that the model should be trained using the highest quality and most representative of the true genome-wide binding data sets, and the trained model can be applied across all cell types of interest.

TRACE's cross–cell line application allows for fast and large-scale TFBS prediction using existing models without repetitive model training, which is the most time-consuming step. It also shows TRACE's advantage over the supervised methods’ limited usage as only a very small fraction of TFs have ChIP-seq data available (Supplemental Fig. S4). To further showcase this flexibility, we have generated models for 526 JASPAR motifs and made them available through our GitHub site (see Software availability).

TRACE calls accurate footprints using ATAC-seq data

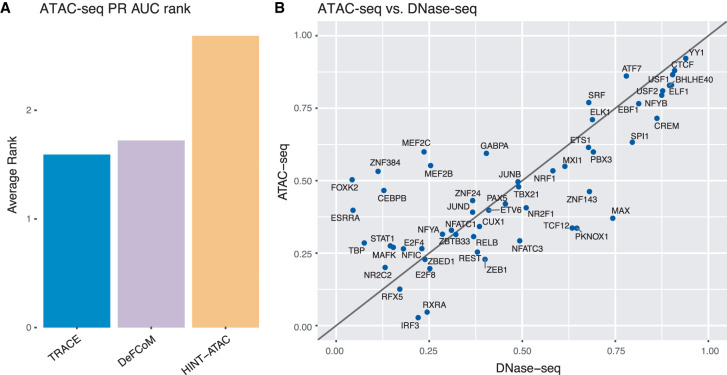
ATAC-seq provides chromatin accessibility information (Buenrostro et al. 2013) and has been proposed to be useful in footprinting analyses. TRACE was tested using ATAC-seq and OMNI-ATAC-seq data (Supplemental Methods) to evaluate the performance of our model compared with other models designed to work with this particular data type. The results were compared with HINT-ATAC (Li et al. 2019) and DeFCoM, as their original publications included ATAC-seq–based evaluation, and showed similar improvement in performance as in the case of DNase data.

Overall, TRACE maintains the best performance among these three methods, as it ranked first for both PR AUC and ROC pAUC (Fig. 3A; Supplemental Fig. S5). Prediction accuracy for TRACE was compared using DNase-seq and ATAC-seq data for each TF in GM12878 (Fig. 3B; Supplemental Fig. S6). This analysis showed that ATAC-seq data provide comparable TFBS identification potential as DNase-seq but that TRACE works slightly better at comparing PR AUCs using DNase-seq data (60% of TFs). TFs that showed a significantly lower PR AUC using DNase-seq were caused by training data imbalances from GM12878 DNase-seq peaks. For example, training sets from ATAC-seq data for FOXK2, ZNF384, CEBPB, and TBP all have at least a 100% increase of prevalence compared with DNase-seq training sets. To determine that the performance difference between these two data sets was not owing to the deeper sequencing depth of DNase-seq, TRACE was performed on a DNase-seq data set that had comparable and/or fewer reads than ATAC-seq. This had minimal effect on TRACE's performance, and similar results were obtained (Supplemental Fig. S12). We further down-sampled our data sets and found that footprinting performance would drop significantly if the number of reads was below 50 million.

Figure 3.

Figure 3.

Open in a new tab

TRACE can perform well on ATAC-seq data. (A) Average rank of PR AUC across all TFs tested using ATAC-seq data for TRACE, DeFCom, and HINT-ATAC. (B) DNase-seq–based and ATAC-seq–based TRACE performance comparison on PR AUC.

DNase footprinting has stable performance despite variable levels of data imbalance

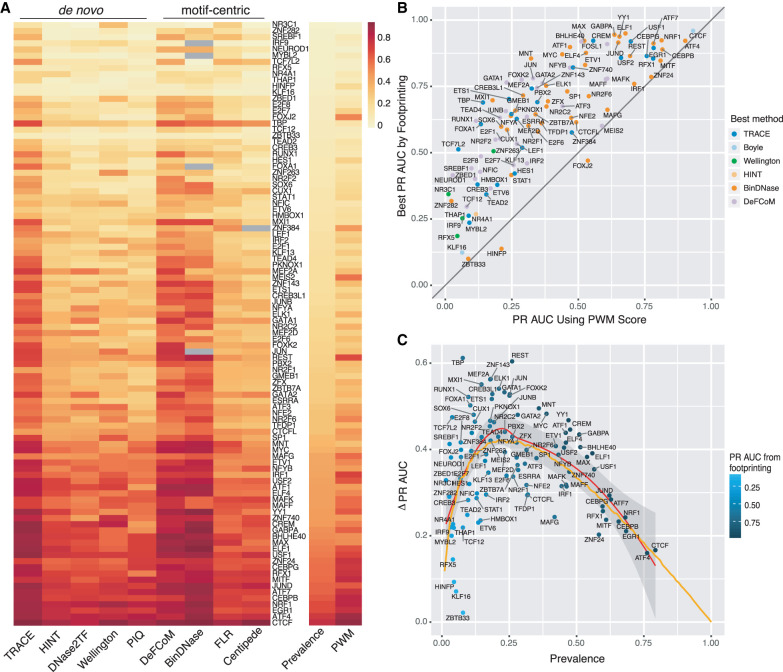
It has been noted that not all TFs have accurately predicted active binding sites by computational footprinting, regardless of the algorithm applied. Our evaluation of existing footprinting methods indicates that all methods share similar performance trends across all TFs (Fig. 4A, left panel; Supplemental Fig. S9). This pattern also exists when assessing candidate binding sites by PWM scores alone (Fig. 4A, right panel). The footprinting performance gain against PWMs is only marginal for some TFs, and using PWM scores alone can even outperform all footprinting methods for two TFs among the 99 TFs tested here (Fig. 4B).

Figure 4.

Figure 4.

Open in a new tab

Computational footprinting methods share similar performance patterns. (A) Heatmap of PR AUC of all TFs tested from existing methods sorted by prevalence. (B) Comparison between the best PR AUC among all footprinting methods (y-axis) and PR AUC from using PWM score alone (x-axis) for every TF tested. (C) Performance improvement of footprinting methods over permutation for each TF colored by its best PR AUC from footprinting. Orange line is from a simulation test using positive instances drawn from N(10, 8), and negative instances from N(0, 7) to show expected PR AUC trend as binding prevalence changes.

The poor performance from footprinting might be partially owing to the imbalance of positive (P) and negative (N) examples in data sets, as evaluation statistics of prediction for each TF were shown to be associated with its prevalence (fraction of positive samples, P/(P + N); see Methods) (Fig. 4A). Data imbalance affects the quality of model training, and if the data distribution is too skewed, training quality will likely be diminished. Some poor performing models were associated with too few positive examples, owing to their inability to distinguish active and inactive states in model training. However, this only accounts for a small subset and cannot explain the general trend of poor performance in TFBS predictions. Comparing final models for each TF did not reveal significant correlation between prediction accuracies and statistics from different models.

To further explore how computational footprinting may be limited by data imbalance, the best footprinting performance for each TF was compared with a matched-imbalance permutation test of labeled sites (Fig. 4C; Supplemental Figs. S7, S8, S10). To complement this, simulations were performed with different levels of classification skill and varying imbalance to estimate how PR AUC and ROC AUC values reflect the classifier performance (Supplemental Fig. S7). As imbalance changes within a classification skill, we can expect that the PR AUC will change correspondingly but that ROC AUC and ROC pAUC will stay the same (Saito and Rehmsmeier 2015). However, the ROC curve often provides an overly optimistic assessment caused by true negatives used in FPR calculation, especially when there is a large skew in the data distribution (Davis and Goadrich 2006).

Instead of comparing AUCs across TFs directly, their performance improvement over random labels (baseline) was measured. To examine the general performance gain using computational footprinting, max PR AUCs or ROC AUCs were collected from all existing methods, including TRACE, and then AUCs were subtracted from the corresponding permutation test. This number was used as a measurement of footprinting performance advantage over randomly predicted labels. The regression line of PR AUC increase against baseline has a skewed bell-like shape, consistent with the shape of simulated performance generated from a steady model skill (Fig. 4C; Supplemental Figs. S7, S10). This suggests that the performance of footprinting is roughly at a stable level and not associated with data imbalance. A higher evaluation statistic does not necessarily mean a better classification quality for that TF in some cases. Although prevalence may affect evaluation statistic values, no evidence was found that the true classification quality is determined by this data imbalance. Instead, there tends to be a stable level of footprinting classification performance increase compared with random across all TFs.

Discussion

Incorporating DNase-seq data and PWM information enables TRACE to detect footprints with the desired DNase digestion pattern and matching motifs. By including multiple motifs in the same model, our method provides a better overall TFBS prediction than other existing computational footprinting methods. Because different motifs are treated as separate states in our model, TRACE also has the potential of targeting multiple TFs in a single model. Our method annotates binding sites for the desired TFs across input regions automatically, without requiring pregenerated candidate binding sites or additional motif matching steps. In addition, as an unsupervised algorithm, its application is not limited to TFs with available ChIP-seq data.

Although computational footprinting has shown the ability to predict TFBSs at an approximately consistent level, variation in evaluation statistics is still observed across TFs. A previous study showed that not all TFs will leave clear footprint-like nuclease cleavage patterns, and their protection of DNA from cleavage is correlated with residence time (Sung et al. 2014). For some TFs, this can result in footprinting methods being unable to detect a consistent footprint-like DNase digestion pattern and failing to correctly label its binding sites. However, there is only limited residence time data available for a small number of TFs, and no comprehensive examination on residence time's impact on footprinting quality has been completed. Although residence time is known to be associated with enzymatic digestion patterns, it is also correlated with the number of active binding sites. GR, AP-1, and CTCF were tested by Sung et al. (2014) as TFs or TF subunits with short, intermediate, and long residence times, respectively. For those TFs included in our test (NR3C1 as GR group, JUN, JUNB, JUND as AP-1 group, and CTCF), we observed that TFs with a longer residency time tend to have a greater prevalence and a better PR AUC from footprinting (Supplemental Fig. S11). However, neither the ROC AUC nor ROC pAUC of these TFs was correlated with residence time. This indicates the possibility that the association between residence time and footprinting ability might be caused by the correlation between performance evaluation statistics and TFBS prevalence. The observed performance disparity may only reflect the changes in fraction of active binding sites among all putative motif sites.

Our evaluation on all footprinting methods indicates that there might be a limited classification accuracy gain that computational footprinting achieves, as the best performance for different TFs all centered at a certain level of classification quality. Our analysis suggests that evaluation statistics of classification from footprinting may be largely influenced by TFBS prevalence, and comparing them directly across TFs may be misleading. Computational footprinting in general might have a maximum potential for how well it can detect TFBSs, and only very limited improvement can be achieved beyond this point.

Methods

Data and software

DNase-seq data in BAM and BED formats and ChIP-seq data in BED format were retrieved from the ENCODE download portal (Supplemental Table S1). ATAC-seq data for GM12878 cells using the standard ATAC-seq protocol were obtained from the NCBI Gene Expression Omnibus (GEO) under accession number GSE47753 (Buenrostro et al. 2013). Omni-ATAC-seq data were obtained from the NCBI Sequencing Read Archive (SRA) with the NCBI BioProject accession PRJNA380283 (Corces et al. 2017). One hundred twenty-nine PWMs and cluster information (Supplemental Table S2) were downloaded from the JASPAR database (Khan et al. 2018). Motif sites were identified using FIMO (MEME v5.0.3) with default parameters (Grant et al. 2011). Evaluation statistics were generated using the Python package scikit-learn (Pedregosa et al. 2011).

Data processing

After bias correction based on model and bias values reported by He et al. (2014), we first counted the number of DNase-seq reads at each location using the 5′ end of the reads, which is the DNase I digestion site. These cut counts were then normalized by the nonzero mean of the surrounding 10,000-bp window (within data set normalization), as well as the percentile and standard deviation from the entire region (between data set normalization) (Supplemental Methods). Normalized signals were then smoothed using the local regression method R (R Core Team 2018) function LOESS (Cleveland et al. 1992), and their derivatives were calculated using the savitzky-golay filter in the Python package Scipy (Vertanen et al. 2020). The first derivatives represent the slope of the processed signal curve, and their signs indicate the increase or decrease in data changes. UP, TOP, and DOWN states in the peak have positive, zero, and negative slopes, respectively.

Evaluation

To assess the performance of TRACE and existing computational footprinting tools, we evaluated DeFCoM, BinDNase, CENTIPEDE, FLR, PWM score only, DNase2TF, HINT, PIQ, and Wellington based on scores or P-values provided by each method. Candidate binding sites (motif sites) that overlapped with DNase-seq peaks confirmed by ChIP-seq were used as the positive set, and those not in ChIP-seq peaks but still overlapping DNase-seq peaks made up the negative set. Prevalence was calculated as number of active binding sites (positive set) divided by total number of motif sites (positive set and negative set).

To provide a fair comparison across all methods, we applied de novo methods to DNase-seq peaks (with 100-bp flanking regions to each side) containing the same sets of motif sites that were included in motif-centric method tests. For de novo methods, only the predictions overlapping with motif sites of tested TFs were included in our evaluation; candidate binding sites that were missing from their predictions were also included with an assigned minimum score. For motif-centric methods and PWM-only evaluations, only candidate binding sites provided are assessed; thus, all predictions were included in the evaluation (Supplemental Methods). Annotations and corresponding scores or P-values were used to calculate the ROC AUC, ROC pAUC at a 5% FPR cutoff, and PR AUC values for all TFs.

Permutation tests were performed by shuffling labels from footprinting prediction results. Multiple simulation tests were also included based on different levels of positive and negative sample separations and different positive example fractions. Scores for positive and negative groups were randomly drawn from the normal distribution of different means and standard deviations.

Software availability

TRACE is an open source software; the source code, trained models, and predictions are available on GitHub (https://github.com/Boyle-Lab/TRACE) and as Supplemental Code.

Competing interest statement

The authors declare no competing interests.

Supplementary Material

Supplemental Material
supp_30_7_1040__index.html (1.1KB, html)

Acknowledgments

N.O. and A.P.B. were supported by National Institutes of Health (National Human Genome Research Institute) U41 HG009293.

Footnotes

[Supplemental material is available for this article.]

Article published online before print. Article, supplemental material, and publication date are at http://www.genome.org/cgi/doi/10.1101/gr.258228.119.

References

  1. Barski A, Cuddapah S, Cui K, Roh T-Y, Schones DE, Wang Z, Wei G, Chepelev I, Zhao K. 2007. High-resolution profiling of histone methylations in the human genome. Cell 129: 823–837. 10.1016/j.cell.2007.05.009 [DOI] [PubMed] [Google Scholar]
  2. Boyle AP, Davis S, Shulha HP, Meltzer P, Margulies EH, Weng Z, Furey TS, Crawford GE. 2008. High-resolution mapping and characterization of open chromatin across the genome. Cell 132: 311–322. 10.1016/j.cell.2007.12.014 [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Boyle AP, Song L, Lee B-K, London D, Keefe D, Birney E, Iyer VR, Crawford GE, Furey TS. 2011. High-resolution genome-wide in vivo footprinting of diverse transcription factors in human cells. Genome Res 21: 456–464. 10.1101/gr.112656.110 [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Buenrostro JD, Giresi PG, Zaba LC, Chang HY, Greenleaf WJ. 2013. Transposition of native chromatin for fast and sensitive epigenomic profiling of open chromatin, DNA-binding proteins and nucleosome position. Nat Methods 10: 1213–1218. 10.1038/nmeth.2688 [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Castro-Mondragon JA, Jaeger S, Thieffry D, Thomas-Chollier M, van Helden J. 2017. RSAT matrix-clustering: dynamic exploration and redundancy reduction of transcription factor binding motif collections. Nucleic Acids Res 45: e119 10.1093/nar/gkx314 [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Cleveland WS, Grosse E, Shyu WM. 1992. Local regression models. In Statistical models in S (ed. Chambers JM, Hastie TJ), pp. 309–376. Wadsworth & Brooks/Cole, New York. [Google Scholar]
  7. Corces MR, Trevino AE, Hamilton EG, Greenside PG, Sinnott-Armstrong NA, Vesuna S, Satpathy AT, Rubin AJ, Montine KS, Wu B, et al. 2017. An improved ATAC-seq protocol reduces background and enables interrogation of frozen tissues. Nat Methods 14: 959–962. 10.1038/nmeth.4396 [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Davis J, Goadrich M. 2006. The relationship between precision-recall and ROC curves. In Proceedings of the 23rd international conference on Machine learning–ICML ‘06, pp. 233–240, ACM Press, New York, New York, USA. [Google Scholar]
  9. Durbin R, Eddy SR, Krogh A, Mitchison G. 1998. Biological sequence analysis. Cambridge University Press, Cambridge. [Google Scholar]
  10. Grant CE, Bailey TL, Noble WS. 2011. FIMO: scanning for occurrences of a given motif. Bioinformatics 27: 1017–1018. 10.1093/bioinformatics/btr064 [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Gusmao EG, Allhoff M, Zenke M, Costa IG. 2016. Analysis of computational footprinting methods for DNase sequencing experiments. Nat Methods 13: 303–309. 10.1038/nmeth.3772 [DOI] [PubMed] [Google Scholar]
  12. He HH, Meyer CA, Hu SS, Chen M-W, Zang C, Liu Y, Rao PK, Fei T, Xu H, Long H, et al. 2014. Refined DNase-seq protocol and data analysis reveals intrinsic bias in transcription factor footprint identification. Nat Methods 11: 73–78. 10.1038/nmeth.2762 [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Hesselberth JR, Chen X, Zhang Z, Sabo PJ, Sandstrom R, Reynolds AP, Thurman RE, Neph S, Kuehn MS, Noble WS, et al. 2009. Global mapping of protein–DNA interactions in vivo by digital genomic footprinting. Nat Methods 6: 283–289. 10.1038/nmeth.1313 [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Hoffman MM, Birney E. 2010. An effective model for natural selection in promoters. Genome Res 20: 685–692. 10.1101/gr.096719.109 [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Kähärä J, Lähdesmäki H. 2015. BinDNase: a discriminatory approach for transcription factor binding prediction using DNase I hypersensitivity data. Bioinformatics 31: 2852–2859. 10.1093/bioinformatics/btv294 [DOI] [PubMed] [Google Scholar]
  16. Khan A, Fornes O, Stigliani A, Gheorghe M, Castro-Mondragon JA, van der Lee R, Bessy A, Chèneby J, Kulkarni SR, Tan G, et al. 2018. JASPAR 2018: update of the open-access database of transcription factor binding profiles and its web framework. Nucleic Acids Res 46: D260–D266. 10.1093/nar/gkx1126 [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Li Z, Schulz MH, Look T, Begemann M, Zenke M, Costa IG. 2019. Identification of transcription factor binding sites using ATAC-seq. Genome Biol 20: 45 10.1186/s13059-019-1642-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Pedregosa F, Michel V, Grisel O, Blondel M, Prettenhofer P, Weiss R, Vanderplas J, Cournapeau D, Pedregosa F, Varoquaux G, et al. 2011. Scikit-learn: machine learning in Python. J Mach Learn Res 12: 2825–2830. [Google Scholar]
  19. Piper J, Elze MC, Cauchy P, Cockerill PN, Bonifer C, Ott S. 2013. Wellington: a novel method for the accurate identification of digital genomic footprints from DNase-seq data. Nucleic Acids Res 41: e201 10.1093/nar/gkt850 [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Pique-Regi R, Degner JF, Pai AA, Gaffney DJ, Gilad Y, Pritchard JK. 2011. Accurate inference of transcription factor binding from DNA sequence and chromatin accessibility data. Genome Res 21: 447–455. 10.1101/gr.112623.110 [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Quach B, Furey TS. 2017. DeFCoM: analysis and modeling of transcription factor binding sites using a motif-centric genomic footprinter. Bioinformatics 33: 956–963. 10.1093/bioinformatics/btw740 [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Rabiner LR. 1989. A tutorial on hidden Markov models and selected applications in speech recognition. Proc IEEE 77: 257–286. 10.1109/5.18626 [DOI] [Google Scholar]
  23. R Core Team. 2018. R: a language and environment for statistical computing. R Foundation for Statistical Computing, Vienna: https://www.R-project.org/. [Google Scholar]
  24. Rhee HS, Pugh BF. 2012. ChIP-exo method for identifying genomic location of DNA-binding proteins with near-single-nucleotide accuracy. Curr Protoc Mol Biol 100: 21.24.1–21.24.14. 10.1002/0471142727.mb2124s100 [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Saito T, Rehmsmeier M. 2015. The precision-recall plot is more informative than the ROC plot when evaluating binary classifiers on imbalanced datasets. PLoS One 10: e0118432 10.1371/journal.pone.0118432 [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Sherwood RI, Hashimoto T, O'Donnell CW, Lewis S, Barkal AA, van Hoff JP, Karun V, Jaakkola T, Gifford DK. 2014. Discovery of directional and nondirectional pioneer transcription factors by modeling DNase profile magnitude and shape. Nat Biotechnol 32: 171–178. 10.1038/nbt.2798 [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Skene PJ, Henikoff S. 2017. An efficient targeted nuclease strategy for high-resolution mapping of DNA binding sites. eLife 6: e21856 10.7554/eLife.21856 [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Stormo GD, Schneider TD, Gold L, Ehrenfeucht A. 1982. Use of the ‘Perceptron’ algorithm to distinguish translational initiation sites in E. coli. Nucleic Acids Res 10: 2997–3011. 10.1093/nar/10.9.2997 [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Sung M-H, Guertin MJ, Baek S, Hager GL. 2014. DNase footprint signatures are dictated by factor dynamics and DNA sequence. Mol Cell 56: 275–285. 10.1016/j.molcel.2014.08.016 [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Virtanen P, Gommers R, Oliphant TE, Haberland M, Reddy T, Cournapeau D, Burovski E, Peterson P, Weckesser W, Bright J, et al. 2020. SciPy 1.0: fundamental algorithms for scientific computing in Python. Nat Methods 17: 261–272. 10.1038/s41592-019-0686-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Wang J, Zhuang J, Iyer S, Lin X, Whitfield TW, Greven MC, Pierce BG, Dong X, Kundaje A, Cheng Y, et al. 2012. Sequence features and chromatin structure around the genomic regions bound by 119 human transcription factors. Genome Res 22: 1798–1812. 10.1101/gr.139105.112 [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Yardımcı GG, Frank CL, Crawford GE, Ohler U. 2014. Explicit DNase sequence bias modeling enables high-resolution transcription factor footprint detection. Nucleic Acids Res 42: 11865–11878. 10.1093/nar/gku810 [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplemental Material
supp_30_7_1040__index.html (1.1KB, html)
supp_gr.258228.119_Supplemental_Materials.docx (2.8MB, docx)
supp_gr.258228.119_Supplemental_Code.zip (127.4MB, zip)
supp_gr.258228.119_Supplemental_Table_S1-S2_JDeditt.xlsx (24.6KB, xlsx)

Articles from Genome Research are provided here courtesy of Cold Spring Harbor Laboratory Press

RESOURCES