Abstract
The COVID-19 has become a pandemic. The timing and nature of the COVID-19 pandemic response and control varied among the regions and from one country to the other, and their role in affecting the spread of the disease has been debated. The focus of this work is on the early phase of the disease when control measures can be most effective. We proposed a modified susceptible-exposed-infected-removed model (SEIR) model based on temporal moving windows to quantify COVID-19 transmission patterns and compare the temporal progress of disease spread in six representative regions worldwide: three Chinese regions (Zhejiang, Guangdong and Xinjiang) vs. three countries (South Korea, Italy and Iran). It was found that in the early phase of COVID-19 spread the disease follows a certain empirical law that is common in all regions considered. Simulations of the imposition of strong social distancing measures were used to evaluate the impact that these measures might have had on the duration and severity of COVID-19 outbreaks in the three countries. Measure-dependent transmission rates followed a modified normal distribution (empirical law) in the three Chinese regions. These rates responded quickly to the launch of the 1st-level Response to Major Public Health Emergency in each region, peaking after 1–2 days, reaching their inflection points after 10–19 days, and dropping to zero after 11–18 days since the 1st-level response was launched. By March 29th, the mortality rates were 0.08% (Zhejiang), 0.54% (Guangdong) and 3.95% (Xinjiang). Subsequent modeling simulations were based on the working assumption that similar infection transmission control measures were taken in South Korea as in Zhejiang on February 25th, in Italy as in Guangdong on February 25th, and in Iran as in Xinjiang on March 8th. The results showed that by June 15th the accumulated infection cases could have been reduced by 32.49% (South Korea), 98.16% (Italy) and 85.73% (Iran). The surface air temperature showed stronger association with transmission rate of COVID-19 than surface relative humidity. On the basis of these findings, disease control measures were shown to be particularly effective in flattening and shrinking the COVID-10 case curve, which could effectively reduce the severity of the disease and mitigate medical burden. The proposed empirical law and the SEIR-temporal moving window model can also be used to study infectious disease outbreaks worldwide.
Keywords: COVID-19, SEIR, Transmission rate, Dynamic, Distancing measures, Climatic factors
Graphical abstract
Highlights
-
•
SEIR model can simulate the transmission spread of COVID-19.
-
•
Transmission rate followed a modified normal distribution in three regions of China.
-
•
Following strict measures, transmission rate reduced to 0 after 11-18 days.
-
•
Effective measures can flatten and shrink the curve of COVID-19 cases.
-
•
Temperature showed stronger association with COVID-19 than humidity.
1. Introduction
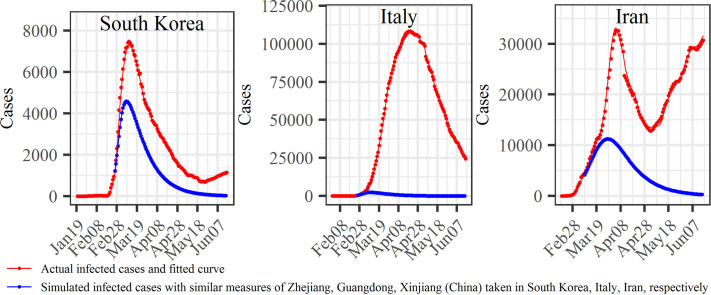
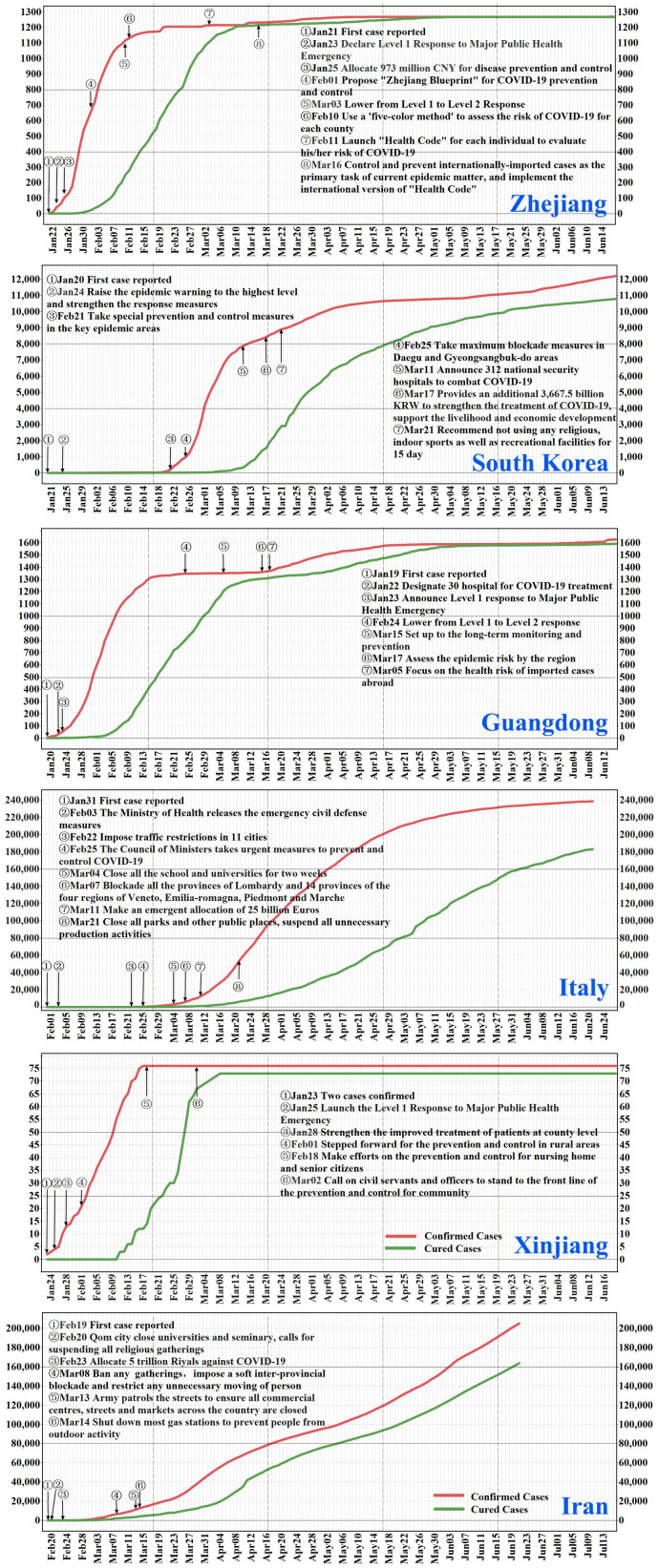
The coronavirus 2019 (COVID-19) outbreak occurred in the Wuhan city (Hubei province) of China during mid-late January 2020. It was found that the COVID-19 spread more rapidly compared to the Severe Acute Respiratory Syndrome (SARS) and the Middle East Respiratory Syndrome (MERS) (Peeri et al., 2020). Responding to the emerging infectious disease, the Chinese authorities acted quickly by taking strict prevention and control measures and by providing necessary support in terms of medical teams, instruments, supplies, and funds; a detailed outline and timetable of the Chinese efforts are provided in Fig. S1 (National Health Commission of People's Republic of China, 2020) in the Supporting Information. By March 18th, 2020 (i.e., after nearly two months of fighting the disease nationwide), the number of newly confirmed COVID-19 patients had dropped to zero in Mainland China (National Health Commission of People's Republic of China, 2020). Elsewhere, the disease spread widely; at early April, over 1.8 million COVID-19 cases have been recorded in more than 213 countries worldwide (World Health Organization, 2020). Facing the increasing numbers of COVID-19 cases, the governments of many impacted nations and regions adopted various measures to control disease spread (Fig. 1 ). The Chinese regions of Zhejiang, Guangdong and Xinjiang each announced a 1st-level Response to Major Public Health Emergency on January 23rd, January 23rd and January 25th, respectively; these orders came just two, four and two days after the first COVID-19 case was reported in each region (Health Commission of Zhejiang Province, 2020; Health Commission of Guangdong Province, 2020; Health Commission of Xinjiang Uygur Autonomous Region, 2020). The South Korean government imposed strict blockades in Daegu city and North Gyeongsang province on February 25th when 977 cases were already diagnosed and 10 deaths were reported (Ministry of Health and Welfare, South Korea, 2020). On the same day, the Italian Council of Ministers took urgent control measures to prevent and control COVID-19 when 322 cases were already diagnosed and 10 deaths were reported (Ministry of Health, Italy, 2020). The Iranian government banned any gathering, imposed a soft inter-provincial blockade and restricted any unnecessary population movements on March 8th when 6566 cases were already diagnosed and 194 deaths were reported (Ministry of Health and Medical Education, Islamic Republic of Iran, 2020) (more detailed descriptions of these responses can be found in the Text S1 and Text S2). The present study seeks to better understand the impact of control measures on the course of COVID-19 outbreaks in these three Chinese regions and three nations.
Fig. 1.
Temporal evolution of accumulated and cured cases of COVID-19 diseases in Zhejiang, Guangdong and Xinjiang of China, South Korea, Italy and Iran. Major events concerning disease control and prevention are labeled at their corresponding date.
2. Materials and methods
2.1. Study regions and data collection
The locations of the six regions are shown in Fig. 2 . The reasons for choosing these study regions can be found in Text S1. In Zhejiang, Guangdong and Xinjiang the study period covered the first 28 days (i.e., from January 21th to February 17th, from January 19th to February 15th, January 23th to February 19th for the three Chinese regions, respectively) since the first COVID-19 cases were detected, because the disease spread could be controlled during this time period. On the other hand, in South Korea, Italy and Iran the study period lasted from the time when the first cases were reported (i.e., January 20th, January 31st, February 19th, respectively) until June 15th 2020. The numbers of infected, cured and dead individuals were collected from the Health Commissions of Zhejiang, Guangdong and Xinjiang (Health Commission of Zhejiang Province, 2020; Health Commission of Guangdong Province, 2020; Health Commission of Xinjiang Uygur Autonomous Region, 2020) and from the Health Departments of South Korea, Italy and Iran (Ministry of Health and Welfare, South Korea, 2020; Ministry of Health, Italy, 2020; Ministry of Health and Medical Education, Islamic Republic of Iran, 2020). The surface relative humidity and the surface air temperature data at each region within the same study period mentioned above were obtained from the Atmospheric Infrared Sounder (AIRS) L3 products with spatial resolution 1°×1° and temporal resolution 12 h (http://disc.gsfc.nasa.gov/datasets/AIRS3STD_006/summary). Specifically, the AIRS L3 products provide surface relative humidity and surface air temperature data at 1:30 A.M. local time and 1:30 P.M. local time. Then, the geographical boundary of each region was used to extract the daily surface relative humidity and surface air temperature at 1:30 P.M. local time in each region for averaging. The descriptive statistics of daily averaged surface relative humidity and surface air temperature in each of the six regions during the study period are presented in Table 1 .
Fig. 2.
Geographical locations of the six study regions.
Table 1.
Descriptive statistics of surface relative humidity and surface air temperature in the six regions.
| Regions | Surface relative humidity (%) |
Surface air temperature (K) |
||||
|---|---|---|---|---|---|---|
| Min. | Max. | Average | Min. | Max. | Average | |
| Zhejiang | 45.6786 | 82.0000 | 61.6806 | 279.6250 | 292.4063 | 286.7089 |
| Guangdong | 37.2574 | 76.4107 | 60.9771 | 288.2610 | 297.8906 | 293.1130 |
| Xinjiang | 32.0828 | 54.3339 | 43.8759 | 267.2240 | 275.1417 | 270.8881 |
| South Korea | 31.2500 | 82.1250 | 52.5640 | 273.9250 | 300.7557 | 287.4800 |
| Italy | 38.7348 | 73.0288 | 54.5595 | 277.2092 | 294.9395 | 287.0715 |
| Iran | 11.4475 | 63.0950 | 31.9835 | 282.0582 | 308.2978 | 294.5224 |
2.2. Methodology framework
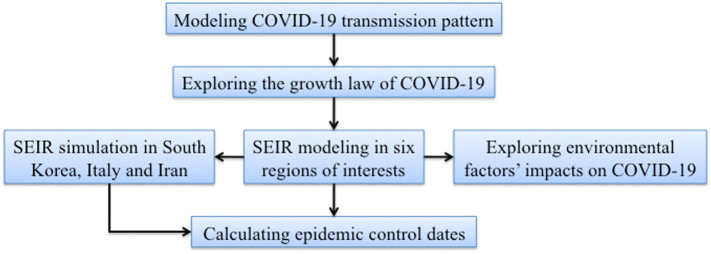
An outline of the modeling framework used in the present study is given in Fig. 3 . The methodology of the present study consisted of three parts: (a) the disease spread over time in each of the six study regions was represented mathematically by an epidemic model and an empirical law describing the evolution of the disease during the critical early phase was established; (b) the effects of the measures taken at the various study regions to control the disease were compared quantitatively in terms of the epidemic model parameters; and (c) linear regression relationships linking the environmental factors and the disease transmission rates were derived. A more detailed discussion of the various parts follows next.
Fig. 3.
Outline of the workflow in this study.
2.3. Transmission pattern modeling
Many models linking the evolution of susceptible, infected and removed cases have been used in the study of infectious disease distributions (Anderson et al., 1992; Alonso et al., 2007; Angulo et al., 2012, Angulo et al., 2013; Yu et al., 2014). Some of these works used susceptible-infected-removed (SIR) models to characterize the evolution of a disease. This kind of models, however, are suitable in cases in which once an individual is infected, the symptoms can be detected immediately. In other words, a SIR model is not suitable for modeling diseases with distinct incubation periods (such as the COVID-19 with about 5 days incubation period), because once an individual is infected with the disease, no symptoms are detected in the following several days, which means the infected but asymptomatic people will unknowingly infect others before they develop any symptoms. Therefore, a modified susceptible-exposed-infected-removed model (SEIR) was developed in this study to simulate the COVID-19 spread in the six study regions. The basic outline of the SEIR model is shown in Fig. S2, and the corresponding equations are as follows:
| (1a-e) |
where N denotes the population sizes of the regions of interest, S(t), E(t), I(t), C(t) and D(t) represent, respectively, the number of susceptible, exposed (may or may not become infected), infected, cured and dead individuals at time t. The exposed and infected individuals constitute the total number of affected individuals A(t) = E(t) + I(t). The cured and dead individuals constitute the total number of removed individuals R(t) = C(t) + D(t). The time-varying parameters β 1(t) and β 2(t) denote the rate of COVID-19 transmission when an individual comes in contact with infected and exposed individuals, respectively, the constant α represents the probability that the exposed individuals become infected, and the time-varying parameters γ(t) and λ(t) denote the COVID-19 cure rate and death rate, respectively.
The SEIR model parameters above are very important because they determine (to varying extents and within different contexts) the epidemic spread and its severity. The values of the infection transmission rate β 1(t), the exposure transmission rate β 2(t) and the infection probability α of exposed individuals depend on the measures taken by responsible individuals and authorities prior to disease exposure (e.g., hygiene, disinfection, protective equipment, social distancing, testing, isolation, etc.). The cure rate γ(t) and the death rate λ(t) depend on a range of disease and social factors (e.g., lethality of the pathogen, pre-existing health condition of the infected individuals, the timeliness and quality of health care available).
One of the objectives of this work is to investigate how the COVID-19 epidemic can be better understood and how its control might be improved by adjusting the corresponding SEIR model parameters according to the disease prevention and control measures. That is, to prevent or control an epidemic means to control the model parameters such as β 1(t), β 2(t) and α. In this work, the following modeling and computational choices were made concerning the SEIR model of Eq. (1a-e).
(i) The sum of the number of infected, cured and dead individuals at time t is equal to the accumulated number of confirmed infected individuals at the same time. The populations N of the regions of interest were large enough so that they can be assumed to remain constant during the epidemic. It holds that S(t) ≤ S 0, i.e., the susceptible population S(t) at any time is smaller than the initial number of susceptible cases (S 0).
(ii) In the SEIR equations, the exposure rate includes two parts: one part is proportional to the contacts between susceptible and infected individuals (assessed by β 1), and the other part is proportional to the contacts between susceptible and exposed individuals (assessed by β 2). Since individuals that are confirmed as infected in the three regions of China were immediately sent to hospitals for isolation and medical treatment, it was assumed that the infection transmission rate was smaller than the exposure transmission rate, i.e., β 1 < β 2. Specifically, following the current COVID-19 literature (Yang et al., 2020), it was assumed that β 2 = 5β 1, and that the probability that an exposed individual becomes infected was . The cured and dead individuals are removed at the rate γ(t) + λ(t). In the regions of interest, the values of γ and λ were zero at the beginning (t = 0), i.e., γ 0 = λ 0 = 0.
(iii) Given that the COVID-19 disease spread has been controlled in the three Chinese regions, only data from the first 28-days were taken into account in the present study. For South Korea, Italy and Iran, complete datasets covering each entire country were used, including areas in which epidemic spread is still underway.
(iv) Transmission, cure, and mortality rates are unknown and dynamic. We estimated these parameters for each region using particle swarm optimization (PSO), a nonlinear computational fitting procedure (Kennedy and Eberhart, 1995; Banks et al., 2007). A 6-day moving window was introduced for computational model parameter fitting (i.e., the infection transmission rate, β 1, the cure rate, γ, and the mortality rate, λ). The computational modeling procedure included the steps listed in Table 2 . The actual (empirical) values of the three rates varied during the 6-day window period, but in Table 2 the values of the three PSO-fitted parameters were assumed constant, corresponding to the minimum residuals (observed vs. fitted numbers of infected, cured and dead cases) during the same period. The β 1, γ and λ values at the regions of interest were compared by considering the effective measures taken by the various regions to control the disease. In addition, considering that the increasing number of infected individuals in China has become very small, the COVID-19 transmission pattern (law) resulting from control measures implemented in the Chinese regions was investigated by fitting the transmission rate curve to empirical mathematical models, shown in Text S3.
Table 2.
The SEIR computational modeling procedure.
| Step | Description |
|---|---|
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
(v) Disease spread cases were simulated in the present study based on the modeling assumption that the disease control measures taken in Zhejiang, Guangdong and Xinjiang (actual implementation) were also implemented in South Korea, Italy and Iran, respectively (hypothetical implementation). As noted earlier, the transmission rates are directly related to these measures (i.e., the effects of the measure are reflected in the corresponding transmission, cured and mortality rates, which quantify them); then, disease spread simulations in South Korea, Italy and Iran were generated by the SEIR model using the transmission law observed in the three Chinese regions. In symbolic terms:
More details can be found in Text S4. The simulated COVID-19 infected cases and accumulated infected cases in South Korea, Italy and Iran were compared to real ones.
2.4. Epidemic control dates calculation
According to the proposed SEIR model, the infection contact rate expresses the fraction of population that comes into contact with an infected individual during the infection period. Τhe reproductive ratio R 0(t) = q(t)S 0 represents the number of secondary infections at any time t in the population caused by an initial primary infection. The epidemic would be considered under control at the time t ECT (epidemic control time, ECT) after which the R 0(t) is consistently smaller than L 0(t), i.e., the inequality
| (2) |
holds for all t ≥ t ECD. The transmission, cure and mortality rates were used to calculate R 0(t), and the infected and exposed case numbers to calculate L 0(t) in each one of the six regions. The epidemic would be considered under control at the epidemic control time t ECT after which Eq. (2) holds.
2.5. Environmental factor-transmission rate association
Linear regression models were developed in order to explore the potential relationship of both the “surface relative humidity-transmission rate” and the “surface air temperature-transmission rate”. For this purpose, the surface relative humidity and the air temperature values at various temporal lags (i.e., 0, 1, 2, …, 6 days lag) were viewed as the independent variables and the transmission rates at various regions as the dependent variables. The coefficient of determination (R 2) and the significance (p-value) of the regression model were used to quantify the strength of the “environmental factor-transmission rate” association.
3. Results
3.1. The case increment trends in the six regions
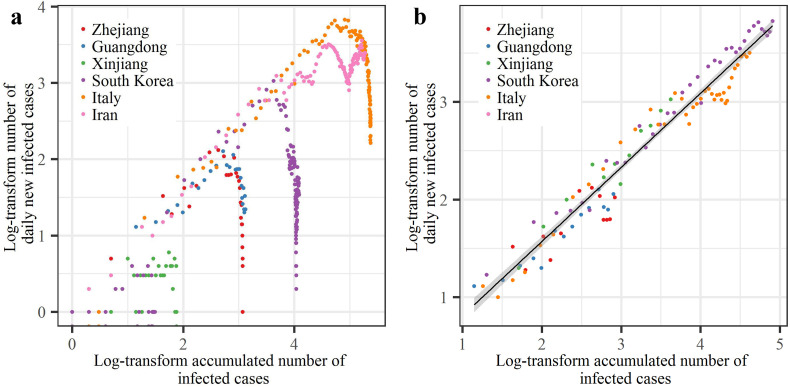
Comparative analysis of disease spread trends in the six study regions was conducted first by using the accumulated number of infected case and the number of daily new infected cases. The dots representing cases in Zhejiang, Guangdong, Xinjiang, South Korea and Italy showed that after they reached their peaks, the numbers of daily new infected cases exhibited decreasing trends (Fig. 4a). In contrast, the dots representing cases in Iran showed that the numbers of daily new infected cases exhibited increasing trends, indicating the worsening situations in these countries. It was found that during the exponential growth period of the epidemic (Fig. 4b), COVID-19 variation in the six study regions closely followed the log-linear differential equation law
| (3) |
with T(t) = I(t) + R(t), where I(t) and R(t) represent the infected and removed case numbers at time t, respectively; R(t) is the sum of cured C(t) and death D(t) cases. Given that Eq. (3) fits the data with high accuracy (R 2 = 0.95, p < 2.2 × 10−16 ≈ 0), it can be viewed as an empirical COVID-19 growth law linking the log-number of daily new infected cases and the log-accumulated number of infected cases, thus providing a measure of the COVID-19 transmission speed. This is a general law, that is potentially applicable to COVID-19 spread cases in other world regions, and, accordingly, it could be a useful tool in subsequent investigations.
Fig. 4.
Relationship between the numbers of daily new infected cases vs. the accumulated numbers of infected cases. (a) Scatter-plots of this relationship for the six regions; (b) linear fitting of the scatter-plots with 95% confidence interval shown as shaded areas (excluding points showing declining trends or where the number of daily new infected cases ≤10).
3.2. COVID-19 transmission patterns in the six regions
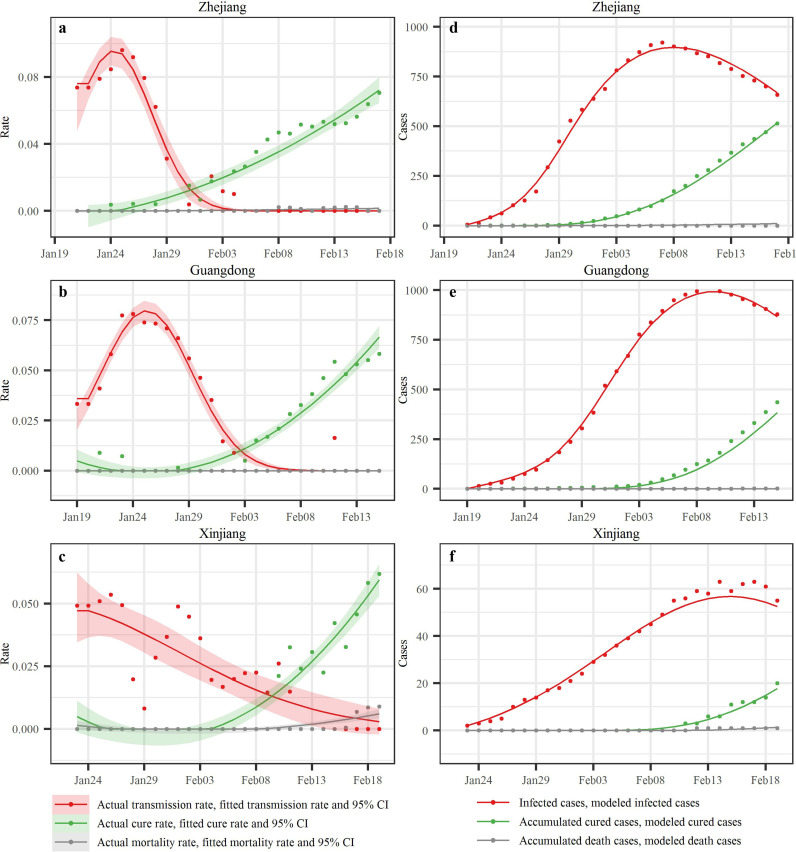
We employed a modified susceptible-exposed-infected-removed (SEIR) model with 6-day temporal window to characterize COVID-19 transmission in the six study regions. The SEIR parameters were estimated by introducing the number of infected, cured, and dead individuals during the first 28 days of the COVID-19 outbreak in Zhejiang, Guangdong and Xinjiang, and during the time period since the first case was reported through June 15th in South Korea, Italy and Iran. Regarding the empirical transmission rates, Zhejiang and Guangdong showed similar single-peaked patterns, with a rapid rise in rates followed by a drop (Fig. 5a–c). Empirical transmission rates in Xinjiang also showed this pattern but with noticeable fluctuations. Transmission rate peaked within 1 day in both Guangdong and Xinjiang and 2 days in Zhejiang, following the declaration of a 1st-Level Response to Major Public Health Emergency in each region. The highest transmission rates were 0.096 (Zhejiang), 0.075 (Guangdong) and 0.053 (Xinjiang), respectively. The empirical transmission rate dropped to zero after 11 days (Zhejiang and Guangdong) and 18 days (Xinjiang) following the declaration; the modified normal distribution provided a good fit to the transmission rates, and the quadratic function also provided good fits to the cure and mortality rates (the function parameters are shown in the Table S1). Using the fitted rate curves above, the case numbers of these three groups of individuals (infected, cured and dead) generated by the SEIR model are denoted by continuous lines in Fig. 5d–f, whereas the actual case numbers are denoted by dots (the R 2 values of the infected case numbers vary from 0.980 to 0.999). Following the first infected individual confirmed in each region, the infected case numbers exhibited a clearly defined first increasing, peaking and subsequently decreasing trend. The peak infected case numbers occurred on the 17th (Zhejiang), 21st (Guangdong) and 22nd (Xinjiang) day, respectively, after the first case was reported.
Fig. 5.
SEIR modeling results in the three Chinese regions. The first column displays the empirical transmission rates (red dots), cure rates (green dots) and mortality rates (gray dots) together with the corresponding fitted lines and the 95% confidence interval (shadows) in Zhejiang, Guangdong and Xinjiang (China); the second column displays the reported infected case numbers (red dots), accumulated cured case numbers (green dots) and dead case numbers (gray dots) together with the corresponding SEIR-produced values (lines) in the three Chinese regions. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
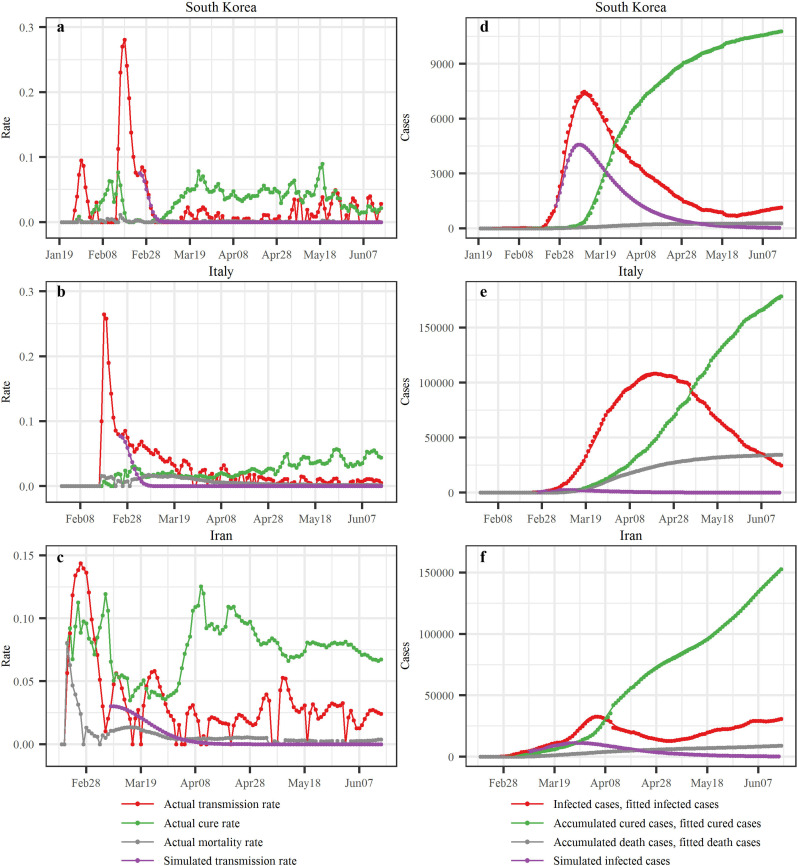
Similarly, the transmission, cure and mortality rates in South Korea, Italy and Iran were calculated by SEIR (Fig. 6a–c). In South Korea, the transmission rate initially displayed a remarkable double-peaked pattern and then decreased until a low level was reached. The second period of transmission rate increase started on February 13th, 2020, and it reached its peak (0.281) on February 18th. Then, and until early May, rather low transmission rates were observed, which were followed by rates fluctuating around an intermediate rate value during the period from May 3rd to June 15th. The cure rate reached its first peak (0.077) on February 15th, and then decreased rapidly to a low level, then commenced a steady rise since March 1st and reached its second peak (0.071) on March 25th; after that it remained at a stable level until it reached its third peak (0.090) on May 19th, and then it dropped to a lower level. In Italy, the transmission rate initially increased rapidly and reached its peak (0.264) on February 18th, and then it decreased until it reached a relatively stable level. The cure rate in Italy exhibited an increasing trend, while the mortality rate exhibited an increasing-decreasing trend. In Iran, the transmission rate reached its highest value (0.144) on February 26th, and decreased subsequently; and then it showed a fluctuating behavior. The cure rate variation was irregular, with a first peak (0.113) on February 25th, followed by a second peak (0.119) on March 6th, then it reduced showing several local (fluctuating) peaks; after a small period, on March 28th the cure rate began to grow again reaching the third peak (0.125) on April 10th and then it remained at a stable level. The mortality rate in Iran reached its first peak (0.063) on February 22nd, then decreased considerably but continued to fluctuate.
Fig. 6.
SEIR modeling results in South Korea, Italy and Iran. The first column displays empirical values of the three rates together with the transmission rates based on simulations of the Chinese control measures assumed since February 25th, February 25th and March 8th in South Korea, Italy and Iran, respectively; and the second column displays the reported numbers, SEIR-produced values and the simulated infected case numbers in the three countries.
Due to the different disease spread control measures taken in South Korea, Italy and Iran, the transmission, cure and mortality rates exhibited irregular variations. These irregularly varying rates were directly inserted in the SEIR model to calculate case numbers. The R 2 values of the infected case numbers were all above 0.995. The case number curves for South Korea differed from those for Italy and Iran. Until March 11th, the infected case numbers in these countries displayed a constantly increasing trend, although the increment pace of infected cases in South Korea had slowed down by that time. Between March 11th and May 25th, infected cases in South Korea decreased considerably. On the other hand, in Italy and Iran the case number curves reached their peaks on April 19th and April 5th, respectively, and then followed a decreasing trend. The case number curves in South Korea and Iran began to increase again on May 25th and May 3rd, respectively. The accumulated cured cases in South Korea started increasing sharply on March 11th. In Italy and Iran, the accumulated cured cases started increasing on March 14th and March 1st, respectively, but these increases were very slow. The accumulated death cases in South Korea were kept at a low level, whereas those for Italy and Iran started increasing on March 13th and March 10th, respectively; and they are still increasing.
Furthermore, we selected a date in each country when major disease control measures were launched: February 25th (South Korea), February 25th (Italy) and March 8th (Iran) (Fig. 1). For policy comparison purposes, we assumed that South Korea, Italy and Iran had taken the same control measures as adopted in Zhejiang, Guangdong and Xinjiang regions, respectively. The simulated transmission rate curves corresponding to the assumed control measures for South Korea, Italy and Iran are shown as purple dot-lines in Fig. 6a–c (more detailed information can be found in Text S4), and the cured rates in the three countries were assumed to be , , and , respectively. For illustration purposes, the values in the denominators are the average number of days between the green and red lines in Fig. 1 (more details can be found in Text S4), i.e. the 18.17, 19.23 and 19.07 days that are assumed to be the time needed to cure the disease in South Korea, Italy and Iran, respectively, under the simulated conditions. Using these simulated rates to run the SEIR model, it was found that the infected case numbers in South Korea, Italy and Iran would have reached their highest values on March 9th, 10th and 28th, respectively, and the corresponding infected case numbers would have been 4575, 2434 and 11,243 (Fig. 6), which are much smaller than the reported infected case numbers (7212, 8514 and 11,466) at the same days. Also, the observed maximum infected case number in South Korea on March 11th was 7470, which is also much larger than the maximum simulated number (4575), and the number of days required to reach the infected case peak could have been reduced to two days. In Italy, the observed maximum number of infected cases on April 19th was 108,257, which is >44 times larger than the maximum simulated infected case number (2434). Similarly, the maximum observed infected case number in Iran on April 5th was 32,612, around three times of the maximum simulated infected case number (11243); noteworthy, the observed infected case number in Iran on June 15th was 30,336 and it was still increasing since then. We also compared the accumulated confirmed case numbers (sum of infected, cured and dead cases) between the simulated and the observed situations up to June 15th. The simulated vs. reported accumulated cases were 8206 vs. 12,155 in South Korea, 4362 vs. 237,290 in Italy, and 27,101 vs. 189,876 in Iran, i.e., a reduction in the accumulated infected case numbers of 3949, 232,928 and 162,775 for South Korea, Italy and Iran, respectively, accounting for 32.49%, 98.16% and 85.73% of the accumulated cases in these countries. These simulations were based on the assumption that the control measures taken in the three Chinese regions would have similar effects in the three countries given their considerable socio-economic and cultural similarities. In this respect, it is noteworthy that the transmission rate in the three countries, indeed, followed a similar modified normal distribution law as in the three Chinese regions.
3.3. COVID-19 epidemic control dates in the six regions
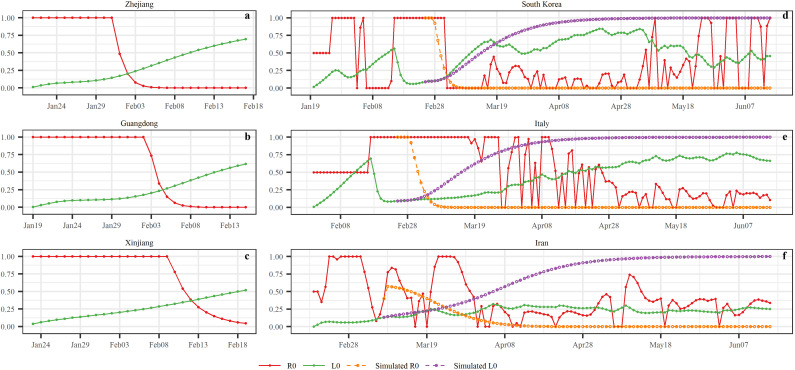
We computed the epidemic control time (ECT) when the COVID-19 was under control. As can be seen in Fig. 7 , in the three Chinese regions the inequality of Eq. (2) holds on the dates t ECT=February 2rd (Zhejiang), t ECT=February 5th (Guangdong) and t ECT=February 13th (Xinjiang), i.e. 10, 13 and 19 days, respectively, following the 1st-Level Response to Major Public Health Emergency, and 2, 4 and 1 days before the infected case numbers reached their peak values. This means, that the COVID-19 should have been under control after these t ECT dates (the epidemic reached an “inflection point” at the corresponding dates). The observed reproductive ratio R 0(t) and L 0(t) curves in South Korea, Italy and Iran were more irregular than in the Chinese regions. This may happen because the measures taken in these countries were different from those in the three Chinese regions. Specifically, in South Korea the R 0(t) and L 0(t) curves fluctuated around each other until the inequality R 0(t) > L 0(t) was definitely satisfied starting on t ECT= March 4th, i.e., 7 days before the infected case numbers reached their peak values; unfortunately, the situation R 0(t) > L 0(t) re-occurred on May 8th, i.e., the epidemic has been spreading since then. In Italy, it was found that t ECT= April 26th. In Iran, the R 0(t) and L 0(t) curves continued fluctuating around each other, and no definite t ECT dates could be determined, at least until the end of the study period, i.e., June 15th. If, on the other hand, it is assumed that the measures taken in Zhejiang, Guangdong and Xinjiang were implemented in South Korea, Italy and Iran, respectively, the following simulated results would be obtained: in South Korea, t ECT=March 5th; in Italy, t ECT=March 6th; and in Iran, t ECT=March 24th.
Fig. 7.
The trends of R0(t) and L0(t) variations in each of the six study regions (for better visualization, we set R0(t) = 1 whenever the R0(t) value was computed to be greater than 1).
3.4. Linear relationship between environmental factors and COVID-19 transmission rates
The performance of the developed linear regression models linking surface relative humidity (or surface air temperature) and COVID-19 transmission rate are shown in Table 3 , including the coefficient of determination (R 2) and its significance (p value). It was found that the surface relative humidity exhibited a poor relationship with the transmission rate because the R 2 values were less than 0.07 in Zhejiang, Guangdong, South Korea, Italy and Iran (except Xinjiang). On the other hand, the “surface air temperature-transmission rate” association was stronger than the “surface relative humidity-transmission rate” association. Table 3 shows that the surface air temperature in Guangdong within the same day was significantly related to the transmission rate (R 2 = 0.15, p=0.042). Otherwise said, we explored the lagged impacts (i.e., temporal lag = 0–6 days) of surface air temperature on transmission rate; specifically, when the temporal lag was equal to 0 (i.e., the temperature and transmission rate data came from the same day), a significant “air temperature-transmission rate” association was found. In Xinjiang, the surface air temperature was strongly related to the transmission rate at various temporal lags (R 2 varies from 0.24 to 0.62, with p values varying from 6.14E-7 to 0.0075). Regarding South Korea, Italy and Iran, the temporal lagged impacts of environmental factors on transmission rate were explored. It was found that although the temporal lagged impacts (with temporal lags 0–6 days) on surface air temperature on the transmission rate were significant, the values of R 2 were less than 0.14 (not that high).
Table 3.
The performance of the linear regression models.
| Factor | Lag (days) | Zhejiang |
Guangdong |
Xinjiang |
South Korea |
Italy |
Iran |
||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R2 | p value | R2 | p value | R2 | p value | R2 | p value | R2 | p value | R2 | p value | ||
| Surface relative humidity | 0 | 6.82E−02 | 2.29E−01 | 4.62E−02 | 2.72E−01 | 1.10E−01 | 8.50E−02 | 3.39E−02 | 2.78E−02 | 8.93E−03 | 2.72E−01 | 2.71E−02 | 7.46E−02 |
| 1 | 8.50E−03 | 6.76E−01 | 8.73E−03 | 6.36E−01 | 2.10E−01 | 1.41E−02 | 3.51E−02 | 2.50E−02 | 1.15E−02 | 2.12E−01 | 3.88E−02 | 3.25E−02 | |
| 2 | 4.65E−06 | 9.92E−01 | 1.34E−04 | 9.53E−01 | 2.92E−01 | 2.98E−03 | 3.62E−02 | 2.29E−02 | 5.95E−03 | 3.70E−01 | 3.97E−02 | 3.06E−02 | |
| 3 | 4.91E−04 | 9.22E−01 | 3.06E−03 | 7.80E−01 | 3.89E−01 | 3.89E−04 | 3.75E−02 | 2.05E−02 | 9.48E−04 | 7.21E−01 | 4.43E−02 | 2.21E−02 | |
| 4 | 1.95E−03 | 8.41E−01 | 1.44E−02 | 5.43E−01 | 5.22E−01 | 1.41E−05 | 4.27E−02 | 1.33E−02 | 1.82E−04 | 8.76E−01 | 4.27E−02 | 2.48E−02 | |
| 5 | 6.94E−03 | 7.06E−01 | 1.53E−02 | 5.30E−01 | 5.36E−01 | 9.56E−06 | 3.78E−02 | 1.99E−02 | 1.68E−03 | 6.34E−01 | 3.59E−02 | 3.98E−02 | |
| 6 | 4.43E−03 | 7.57E−01 | 1.82E−02 | 4.94E−01 | 5.67E−01 | 3.81E−06 | 2.57E−02 | 5.58E−02 | 5.97E−03 | 3.70E−01 | 3.19E−02 | 5.28E−02 | |
| Surface air temperature | 0 | 9.59E−02 | 1.50E−01 | 1.50E−01 | 4.16E−02 | 2.44E−01 | 7.49E−03 | 5.48E−02 | 4.88E−03 | 1.44E−01 | 4.90E−06 | 1.01E−01 | 4.69E−04 |
| 1 | 9.63E−02 | 1.50E−01 | 3.81E−02 | 3.20E−01 | 3.75E−01 | 5.28E−04 | 3.53E−02 | 2.47E−02 | 1.17E−01 | 4.25E−05 | 1.03E−01 | 3.85E−04 | |
| 2 | 3.71E−02 | 3.78E−01 | 6.88E−03 | 6.75E−01 | 4.56E−01 | 7.99E−05 | 2.07E−02 | 8.64E−02 | 9.81E−02 | 1.94E−04 | 9.39E−02 | 7.39E−04 | |
| 3 | 2.58E−02 | 4.75E−01 | 1.04E−02 | 6.06E−01 | 5.62E−01 | 4.46E−06 | 1.07E−02 | 2.19E−01 | 8.98E−02 | 3.74E−04 | 8.25E−02 | 1.61E−03 | |
| 4 | 6.84E−04 | 9.06E−01 | 4.01E−02 | 3.07E−01 | 6.22E−01 | 6.14E−07 | 5.72E−03 | 3.69E−01 | 9.42E−02 | 2.65E−04 | 7.27E−02 | 3.16E−03 | |
| 5 | 5.42E−03 | 7.39E−01 | 7.24E−02 | 1.66E−01 | 6.14E−01 | 8.06E−07 | 3.72E−03 | 4.69E−01 | 9.69E−02 | 2.14E−04 | 6.92E−02 | 4.00E−03 | |
| 6 | 8.36E−03 | 6.71E−01 | 8.11E−02 | 1.42E−01 | 6.03E−01 | 1.19E−06 | 6.00E−03 | 3.58E−01 | 9.53E−02 | 2.43E−04 | 7.51E−02 | 2.68E−03 | |
4. Discussion
COVID-19 is an infectious disease with largely unknown characteristics but with very considerable apparent societal impacts. Accordingly, everyone must contribute to its prevention and control. Otherwise, the cost in human and material resources will be very high before the disease can finally be controlled. With the current lack of effective drugs and vaccination, the alternative way to control disease spread is the timely detection of the infection source and elimination of its transmission paths. Chinese authorities proposed a slogan for fighting against the COVID-19: “Quarantine all who need to be quarantined, medically treat all who need to be treated, test all who need to be tested” (National Health Commission of the People's Republic of China, 2020). In order to explore the behavior of COVID-19 spread under various disease control measures, the current study employed a modified SEIR model to quantitatively assess the variations of the temporal trajectory of COVID-19 spread in three regions of China as well as in three COVID-19 affected countries.
4.1. Advantages of SEIR model with temporal moving window
The standard SEIR model treats the transmission, cured and mortality rates as constants during the entire outbreak period, despite the varying levels of prevention and control measures. This is not a realistic assumption, especially for a new infectious disease at its early phases, like COVID-19, whose transmission, cured and mortality rates will vary considerably (according to the ongoing disease understanding, the public's reaction etc.). Although some staged SEIR models have been developed by setting different transmission rate values during the various disease periods (e.g., Yang et al., 2020), these models still cannot capture the transmission pattern at the required high temporal resolution level. The proposed SEIR model with temporal moving window, on the other hand, avoids this shortcoming, since it can characterize the dynamics of the transmission, cured and mortality rates during the entire disease period under varying COVID-19 measures, see, Fig. 5, Fig. 6. The transmission rates shown in these two figures assess quantitatively the effects of the measures taken at each region of interest. So, e.g., if the transmission rate remains high, it means that the measures are not efficient; while low transmission rate implies that the disease is under control. On the other hand, the cured and mortality rates may assess the effectiveness of the medical treatment and the availability of medical resources. E.g., if the cured rate is low and mortality rate is high, they indicate ineffective medical treatment and/or insufficient medical resources to support the large number of COVID-19 patients. Public health managers or policy makers can implement immediate measures to control the disease spread and consequently reduce the transmission rate. Moreover, they can adjust their response strategy to the COVID-19 emergency situations. E.g., when the transmission rate reaches a peak (see the curves in Fig. 6), this may be due to some particular events or weaknesses of the control measures. Facing this kind of situation, the policy makers may decide to change the intervention and control measures. When the cured rate is high and mortality rate is rather low in one area, such as in Zhejiang and Guangdong (Fig. 5), the policy makers may consider that that the medical resources are sufficient in these regions, and they may decide to transfer some of these resources (including medical doctors, nurses, equipment and supplements) to other areas that need them (such as Hubei province during February of 2020). Moreover, the transmission, cured and mortality rates can be used to calculate the epidemic control dates (Eq. 2), which are also important in the determination of whether the disease is under control or it will continue to spread further, as discussed in Sub-section 3.3. Last but not least, the modeled daily transmission rate can be used to explore the climate factors-transmission association, as discussed in Sub-section 3.4. In all cases, the disease transmission pattern can be obtained at a high resolution level (say, day unit) from the SEIR model with temporal moving windows.
Some other sophisticated models have also been developed to characterize the temporal or space-time spread pattern of COVID-19 at various countries worldwide. For instance, Giuliani et al. (2020) used an endemic-epidemic multivariate time-series mixed-effected generalized linear model for area disease case counts to model the contributions of three components: the temporal disease dynamics, the connection between neighboring provinces, and the province-specific contributions to the temporal evolution of the disease at specific areas, i.e., the three components can simultaneously influence the disease spread. They found that the dominant component differed between the various provinces, e.g., provinces implementing containment measures were not affected by the disease situation in their neighboring regions, while provinces that were strongly hit by the disease were also dominated by the disease situation in their surrounding regions. This model does a good job as regards the incorporation of the detailed contribution of the three components on the spread of COVID-19 in different small downscaled sub-regions. On the other hand, as noted earlier, the transmission rate used in the proposed SEIR model with temporal moving window can also be regarded as the sum of the three above components, because the current study explored the spread pattern in a large upscaled region (i.e., regarding all small downscaled sub-regions as an entire upscaled region of interests), while Giuliani et al. (2020) focused on the disease spread between downscaled sub-regions. In addition, the three regions of China remained in isolation from other severely affected regions or countries worldwide by the policies taken to shut down migration and transportation, so the influence of the surrounding regions on the transmission can be ignored in the three regions of China. Moreover, transmission rate offers a more direct way to describe the spread speed of the disease than the number of disease cases (newly or accumulated cases). More discussions can be found in Sub-section 4.6.
4.2. COVID-19 spread patterns in the three regions of China
The measures taken to control the COVID-19 spread in China during the early transmission period (including limiting social contacts and outside activities as much as possible, quarantining the infected individuals and their close contacts as soon as possible) were shown to effectively prevent the disease from spreading to larger groups of people by lowering the transmission rate (Fig. 5). With such control measures, the transmission rates reached their peaks within one or two days, and were reduced to zero within 11, 11 and 18 days after a 1st-Level Response to Major Public Health Emergency was declared in Zhejiang, Guangdong, and Xinjiang, respectively. As more knowledge was gained about clinical treatments, the cure rate increased and the mortality rate decreased during the first 28 days of the COVID-19 outbreak.
It was also found that a normal distribution function adequately represented the variation of the transmission rate in the Zhejiang, Guangdong and Xinjiang regions of China under the above control measures. In contrast, the transmission rate at Xinjiang exhibited considerable fluctuations around the normal distribution model, and it took more time (18 days) for the transmission rate to drop to zero than it did in Zhejiang (11 days) and Guangdong (11 days). This may be associated with the advanced socio-economic development in Zhejiang and Guangdong. Also, the governance capability in Xinjiang is different from that in Zhejiang or in Guangdong, which led to varied enforcement degrees of disease prevention and control measures in these regions. Some clues can be found in Fig. 1, i.e., after Xinjiang launched the 1st-Level Response to Major Public Health Emergency, it seems likely that the most stringent prevention and control measures were only taken initially in the largest cities. Then, on January 28th, 2020, Xinjiang strengthened the improved treatment of patients at the county level. Furthermore, on February 1st Xinjiang intensified its implementation of the prevention and control in rural areas.
4.3. COVID-19 spread patterns in the three countries
The disease transmission rates in South Korea, Italy and Iran during the study period experienced much higher peak values (0.281, 0.264 and 0.144, respectively) than in Zhejiang, Guangdong and Xinjiang (0.096, 0.075 and 0.053, respectively), suggesting that some special events took place that caused these higher peaks in the three countries. Specifically, the Daegu Church gathering in Daegu city, and the infections in Daenam hospital (Gyeongsangbuk-do province) were found to be two major events that produced large infected populations, which comprised 82% of the accumulated infected cases on March 29th, 2020. In the same day, it was reported that 84.1% of the accumulated infected cases were related to group outbreaks (Ministry of Health and Welfare, South Korea, 2020). On February 22nd, an infected individual was confirmed in Lombardia (Italy) who had not traveled abroad. This was a key indicator that COVID-19 had spread domestically in Italy. Due to the multi-day incubation period of the disease, the number of confirmed patients is a lagging indicator of transmission. Moreover, the Italian professionals were initially unaware of the highly infectious nature of COVID-19; therefore, a large number of medical staff got sick in Lombardia. Up to June 15th, the number of infected cases in Lombardia accounted for 38.74% of the infected cases nationwide. In Iran, although the transmission rate decreased significantly during the period from February 26th to March 5th, 2020, unfortunately the rate increased again after March 5th, indicating that the disease was not yet under control. The apparent high cure rate in Iran could be linked to the relatively loose hospital rules that allowed the early release of patients. Due to inadequate medical resources in these hospitals, the patients were sent to isolation facilities for further monitoring after leaving the hospital.
Moreover, the simulation tests performed in the present study concerning disease spread in South Korea, Italy and Iran were based on two modeling conditions: (a) the disease transmission law implemented in the three Chinese regions was also used for the three countries under consideration, and (b) similar measures as in the three Chinese regions were assumed to have been taken to control the disease spread at these three countries. Based on these conditional disease simulations, it was found that the COVID-19 spread in South Korea, Italy and Iran could be controlled significantly, resulting to a much smaller infected cases and a shorter time to reach the maximum number of infected individuals, i.e., flattening and shrinking of the infection curves (Fig. 6). If effective measures could be implemented at the early stage of a regional COVID-19 outbreak, the number of infected cases would be controlled and kept at relatively low levels, which would reduce the burden on the medical system; in return, the population health risk, the mortality rate, and the public health costs could be considerably reduced at both the nationwide and the local levels. For example, the mortality rates and the accumulated infected case numbers in the three regions of China were much smaller than those of the three countries considered. Specifically, the mortality rates during the first 28 days of the COVID-19 outbreak were 0.0% in Zhejiang, 0.15% in Guangdong and 1.32% in Xinjiang, respectively. During the period since the first case was reported through June 15th, the mortality rates were 0.08% (Zhejiang), 0.49% (Guangdong), 3.95% (Xinjiang), 2.29% (South Korea), 14.48% (Italy) and 4.71% (Iran). In addition, the difference between the simulated and the observed accumulated infected case numbers on June 15th in South Korea was smaller than those in Italy and Iran, suggesting that the control measures taken in South Korea had better effects on prevention and control than in the other two countries, and that the prevention and control measures in Italy and Iran could have been considerably improved. This finding supports contentions by other scholars that infection control measures such as national lockdowns in many European countries could lead to a reduction in the number COVID-19 related deaths between 21,000 and 120,000 at the end of March (Nature, 2020).
4.4. Disease control measures in China
The early implementation of these measures can lead to lower infected case numbers and a lighter burden on the medical system, which, in turn, can lead to higher cure and lower mortality rates (this is best reflected in the Zhejiang case). In terms of the actual Chinese experience, self-isolation was a key measure of controlling disease spread and transmission. Moreover, wearing facemasks, and practicing hand hygiene, cough etiquette and social distancing are also effective ways to mitigate the disease spread among people (Gilbert, 2020; Chan and Yuen, 2020). Below, the disease control measures taken in China are briefly reviewed with references to local authorities and communities, the medical system, the industry, and the prevailing societal and individual perspectives (Zhejiang Daily, 2020). By implementing these measures, the resulting drop in travel was as high as 90% during the period from January 23rd to February 18th, 2020 compared to the same period (lunar calendar) in 2019 (additional information can be found in Text S5).
Naturally, a country's medical community is at the forefront of the war against an epidemic. In the COVID-19 case, the main measures taken by this community are aimed at the timely and accurate diagnosis of the disease, and the best possible treatment or curing for the infected individuals. The specific measures are listed in Table S3 (National Health Commission of People's Republic of China, 2020; Health Commission of Hubei Province, 2020; Wuhan Municipal Health Commission, 2020; Zhejiang Daily, 2020). Given the long COVID-19 incubation period and the fact that even asymptomatic infections can result in transmission to others, national and local governments needed to act fast and do their best to control the interactions of local people. Three key points should be highlighted: avoid importing infected individuals to a region, control the local disease spread, and prevent exporting infected individuals to other areas. Table S4 (National Health Commission of People's Republic of China, 2020; Health Commission of Hubei Province, 2020; Wuhan Municipal Health Commission, 2020; Zhejiang Daily, 2020) lists the main measures implemented by local governments during the COVID-19 pandemic. Citizen communities are the basic contributing units in a country's overall effort to prevent a disease from spreading further. Therefore, key functions of Chinese communities were to assist in identifying infected patients, restricting community access, and providing the basic needs of daily life to its members. The specific measures taken by local Chinese communities are listed in Table S5 (National Health Commission of People's Republic of China, 2020; Health Commission of Hubei Province, 2020; Wuhan Municipal Health Commission, 2020; Zhejiang Daily, 2020). The contribution of a country's industrial sector can also offer considerable support in the effort to control an epidemic. Some of the actions taken by the country's industry are listed in Table S6 (National Health Commission of People's Republic of China, 2020; Health Commission of Hubei Province, 2020; Wuhan Municipal Health Commission, 2020; Zhejiang Daily, 2020). Lastly, the best way for each individual to contribute is to self-isolate and pay close attention to personal hygiene. Some basic guidelines are as follows: wash hands frequently, wear a facemask when going outside, and stay at home for a 14-day self-isolation period.
Two recent examples about point COVID-19 outbreak in Chinese cities and the quick actions of local authorities are described in Text S6. On the other hand, the Italian and Iranian authorities didn't act as fast as was necessary during the critical early phase of the disease (Fig. 1), e.g., and the important self-isolation policy was not strictly implemented as was done in China. That may be the reason that disease control was not achieved during a short time-period, which had severe consequences. For South Korea, the strategy to fight COVID-19 was based on testing; as a result, South Korea tested the largest number of people per capita worldwide on March 17th, nearly 0.3 million people in total worldwide at that time (Zastrow, 2020). The biggest difference between the measures taken in South Korea and China was that in South Korea the government did not lock down the disease-torn city as was done in China.
4.5. Data quality and uncertainty
Data quality is of vital importance in assessing disease transmission patterns. Aside from Hubei, Zhejiang and Guangdong were the two Chinese provinces with the largest number of reported COVID-19 cases. This provides a prerequisite for obtaining reliable statistical patterns. The large number of COVID-19 cases in Zhejiang and Guangdong was due to their high-level social and economic interactions with Hubei Province. Zhejiang and Guangdong were also the most developed provinces in China, which also translated in better health care system capacities, social readiness and governance. In Xinjiang, the total number of confirmed cases was relatively low, and did not cause any challenge to the local health care capacity. Surveillance throughout China was very high with systems capable of quickly locating any confirmed cases at the geographic scale of a specific building (see, also, the efforts described in Tables S3–S6 and the slogan presented at the beginning of the discussion section). Although these measures may damage the local economy and lower the population's living standards, they play a very important role in the quick detection of the infected individuals and they allow effective epidemiological investigations and quarantine implementation to control disease spread. Also, the measures decisively reduce the number of infected cases and ensure sufficient medical resources are available for testing potentially infected individuals and curing infected individuals. Situations are avoided where the infected individuals cannot get confirmed and sent to the hospital due to the lack of nucleic acid testing kit, thus leading to underreported numbers of accumulated infected cases. Similarly, situations are avoided where infected individuals are not detected and remain dead at home, leading to underreported numbers of accumulated death cases. As a result, the measures can decrease considerably data uncertainty. In this context, it was estimated that data reporting uncertainties in Zhejiang, Guangdong and Xinjiang were low, which is also supported by the present study's very good fit of the models to the observed transmission, infected, cure and mortality rate curves. On the other hand, a series of uncertainty sources characterized the reported data in South Korea, Italy and Iran. When the outbreak occurs, the local health care system capacities maybe unable to confront the epidemic outbreaks, leading to under-diagnosis and data under-reporting uncertainties. This could be a reflection of the irregularities of transmission, cured and mortality rates; e.g., the transmission rates in South Korea, Italy and Iran subsequently failed to comply with the modified normal distribution law unlike in the Chinese regions.
4.6. Impacts of environmental factors on COVID-19 transmission rate
Environmental factors (such as humidity and temperature) can improve the understanding of the COVID-19 spread pattern, because they are regarded as key factors influencing coronaviruses spread (Sajadi et al., 2020). The present study demonstrated that the COVID-19 transmission rate was significantly correlated to the surface relative humidity in Xinjiang, and surface air temperature in Guangdong, Xinjiang, Italy and Iran. Our results suggested that the impacts of surface relative humidity or surface air temperature on the transmission of COVID-19 may vary at different regions, which is in line with relevant findings in the literature (Shahzad et al., 2020), i.e., the environmental effects on COVID-19 turned out to have distinct regional characteristics. E.g., Briz-Redón and Serrano-Aroca (2020) pointed out that no evidence of a relationship between COVID-19 cases and temperature was found in Spain.
In the relevant literature, correlation analysis and generalized addictive model (GAM) are two popular tools for exploring the association between environmental factors and COVID-19. For instance, Bashir et al. (2020) employed the Kendall and Spearman correlation coefficients to quantify the relationship between climatic factors (including temperature, humidity, wind speed, air quality and rainfall) with COVID-19 cases (new cases, total cases, mortality) in New York City and found that temperature and air quality have significant correlation with the COVID-19 epidemic. Similarly, Tosepu et al. (2020) used the Spearman-rank correlation test to explore the relationship between climatic factor and daily new confirmed COVID-19 cases and found that the cases were significantly correlated with the average temperature. Moreover, using GAM it was found that in 122 Chinese cities the number of COVID-19 confirmed cases exhibited a positive linear relationship with mean temperatures less than 3 °C (Zhu and Xie, 2020). Using GAM analysis, Prata et al. (2020) found that in Brazil the annual average temperature compensation exhibited an approximately linear relationship with COVID-19 confirmed cases when the temperature is less than 25.6 °C. Using GAM, Qi et al. (2020) suggested that the association between daily average temperature (or relative humidity) and COVID-19 cases was not consistent throughout Mainland China.
All the previous studies above focused on associations between environmental factors and COVID-19 cases where the COVID-19 transmission rate was assumed constant. Specifically, they used COVID-19 count data (such as new and total numbers of cases) to implement statistical analysis. It should be noted that, as an infectious disease, the reported COVID-19 count cases might be related to historical data by means of the transmission rate. If the number of cases is large, the number of newly confirmed cases in the near future will also be large assuming the same transmission rate in terms of Eq. (1a-e). Subsequently, field situations may emerge in which environmental factor variations have distinct impacts on the number of infected cases; e.g., there may be field situations where large environmental variations lead to apparently small changes in the number of infected cases when the number of these cases is very small (say, 10), and situations where small environmental variations lead to apparently large changes in the number of cases when this number is very large (say, 10,000). For illustration, let the daily change of the surface air temperature in places A and B be from 10 °C to 11 °C. At the same time, assume that the total number of COVID-19 cases in places A and B change, respectively, from 100 to 120, and from 10,000 to 11,000. Based on the fact that in A the increase in the number of cases was 20 whereas in B it was 1000 (and ignoring the different sizes of the base case counts in the two places, 100 vs. 10,000), one could conclude that the surface air temperature in place B had a greater impact on COVID-19 than in place A, which is not necessarily be true. Therefore, it may not always be a rigorous approach to directly use the number of confirmed cases to explore its association with environmental factors. Some previous studies have overcome this shortcoming by using the transmission rate to quantify the relationship between environmental factors and COVID-19 spread. E.g., based on COVID-10 case data from Feb 15th to March 22th, 2020, Jahangiri et al. (2020) assumed a constant transmission rate in various provinces of Iran; they also found that COVID-19 has low sensibility to ambient temperature but high sensitivity to population size. In the current study, on the other hand, we explored this association in the more realistic case that the transmission rate changed both under the influence of various kinds of control measures and, also, with time. We believe that the dynamic transmission rate can help better define the association between environmental factors and COVID-19 than the previous studies.
The impacts of surface relative humidity and surface air temperature on the COVID-19 transmission rates in the six study regions of the present study demonstrated distinct regional characteristics. Specifically, surface air temperature showed stronger association with transmission rate than the surface relative humidity. The reason why surface air temperature and relative humidity have different effects on COVID-19 transmission in different geographical regions maybe that non-meteorological factors make non-negligible contributions to disease transmission, such as population density, age distribution, the number of travelers, and the number of open companies (as noted in Briz-Redón and Serrano-Aroca, 2020). Some of these factors can, to a certain extent, reflect the measures taken to control disease spread, e.g., if strict social distancing and self-isolation measures are implemented, the numbers of travelers and opened companies will decrease rapidly and reach a low level. It was also found that at the early phase of the disease, the population density, per capita GDP and number of medical doctors (MDs) have a significant impact on COVID-19 spread. Moreover, robust government responses to COVID-19 played a determinant role in disease containment (Qiu et al., 2020). Lack of medical resources (such as isolation rooms, number of MDs and nurses, tests etc.) at the early phase of the disease will lead to large transmission rates in the severely hit regions or countries (such as Hubei province of China, and in Italy and Spain) because the infected patients cannot be quarantined and treated in hospitals, but will continue to have the potential of transmitting the disease to others (Rosenbaum, 2020). Moreover, the social environments and life styles can also affect the transmission of COVID-19 (Yancy, 2020). In sum, given that the measures taken to control the disease as well as the meteorological factors vary in different regions, the environmental COVID-19 factors may show regional differences too. Particularly, in the current study, transmission rate reductions were significantly affected by the measures taken to control the spread of COVID-19 and the medical resources available, as discussed in the previous sub-sections.
4.7. Future work
Beyond being used to quantitatively describe the current transmission conditions in the six study regions, the proposed approach has the potential to monitor disease transmission rates and predict disease case numbers in future situations. Health authorities could assimilate this valuable information into their disease prevention and control decision-making process. Future work could also focus on employing the dynamic transmission rate to forecast any trends in the numbers of COVID-19 cases, or to model patterns in future epidemics. Further, spatiotemporal disease characteristics (including the composite space-time disease dependencies and spread patterns using modern geostatistics methods, and their inter-association or tele-connection with climatic factors using time series, time-frequency methods (Christakos and Olea, 2005; Christakos et al., 2005; Chirstakos, 2017; He et al., 2017, He et al., 2018a, He et al., 2018b, He et al., 2019a, He et al., 2019b, He et al., 2019c; Xiao et al., 2019; Jahangiri et al., 2020; Qi et al., 2020; Shi et al., 2020) could be explored by considering various levels of data, such as county-level or even individual-level disease data. More specifically, as was documented in the above literature, the geostatistics methods can help detect the trends, spread directions and core areas of the infectious disease. The spread patterns can be also detected by using composite space-time disease dependencies (say, covariance functions). Wavelet coherency analysis and Hilbert-Huang spectra analysis (both of them are time-frequency analyses) can be used to study the inter-association between disease and climatic factors. Autoregressive integrated moving average model with exogenous variables (ARIMAX) and distributed lag non-linear model (DLNM) with random-effect model can be used to study the climatic impacts with lagged effects on COVID-19. Lastly, the two basic modeling assumptions of the present study were as follows: (a) the effects of the disease control measures were directly reflected in the corresponding model disease rates (transmission, cured and mortality), which quantified these effects; and (b) given that the critical time periods of early disease spread coincided in the corresponding regions and in view of the socio-economic and cultural similarities of these regions, the control measures taken in the Chinese regions (Zhejiang, Guangdong and Xinjiang) would have similar effects if taken in the corresponding countries (South Korea, Italy and Iran). These two modeling assumptions are worth further investigation, and their potential implementation in future studies with similar objectives should be considered.
5. Conclusion
The modified SEIR model was shown to provide an adequate framework to represent the patterns of COVID-19 transmission in Zhejiang, Guangdong, and Xinjiang of China, as well as in the three sample countries (Italy, South Korea and Iran) examined. The proposed SEIR model accounts for the interplay of medical, physical and social processes. Not only it can make useful predictions, but it can also offer guidance about what disease spread parameters should be controlled and how to prevent undesirable outcomes from the epidemic. The early implementation of the control and prevention measures can lead to a dramatically lower number of infected cases and a lighter burden on the medical system, which, in return, can lead to a larger cure rate and a smaller mortality rate.
The temporal moving window scheme implemented here helps characterize the dynamics of the COVID-19 transmission rates in these regions during the disease outbreak, which can also benefit public health management. The transmission rates associated with the control measures in the three Chinese regions under study (including the immediate quarantine of the infected patients and their close contacts, and the considerable restrictions on social contacts) followed a modified normal distribution function. Thus, in terms of the experience gained in China concerning the prevention and control of disease spread, simultaneously restrict self-isolation and quarantining every suspected individual and infected individual were key measures of controlling the spread and the transmission during the early phase of disease spread in the Chinese regions; and wearing facemask is another key self-action to control disease spread. Furthermore, our simulation results showed that if the SEIR epidemic model parameters for South Korea, Italy and Iran were selected on February 25th, February 25th and March 8th that they corresponded to the disease control measures implemented in China, respectively, then considerably better results would have been obtained in the three countries, i.e., up to June 15th, the simulated reduction in the accumulated infected case numbers would have been 3949 for South Korea, 232,928 for Italy and 162,775 for Iran, respectively, accounting for 32.49%, 98.16% and 85.73% of the accumulated number of infected cases. In other words, the infected case curves would be flattened and shrank, and they would also have peaked at an earlier time than the observed curves in these countries. Such earlier response would have led to a faster and more efficient control of COVID-19 in these countries than it actually happened. Lastly, it was found that the association between surface air temperature and transmission rate was stronger than that between surface relative humidity and transmission rate; and it was noticed that these associations exhibited regional characteristics.
CRediT authorship contribution statement
Junyu He: Conceptualization, Methodology, Software, Validation, Formal analysis, Investigation, Data curation, Writing - original draft, Writing - review & editing, Visualization. Guangwei Chen: Software, Investigation, Data curation, Visualization, Writing - review & editing. Yutong Jiang: Software, Investigation, Data curation, Visualization, Writing - review & editing. Runjie Jin: Investigation, Data curation, Writing - review & editing. Ashton Shortridge: Investigation, Writing - review & editing. Susana Agusti: Investigation, Writing - review & editing. Mingjun He: Investigation, Data curation. Jiaping Wu: Conceptualization, Methodology, Validation, Investigation, Data curation, Writing - original draft, Writing - review & editing, Visualization, Supervision, Project administration, Funding acquisition. Carlos M. Duarte: Investigation, Writing - review & editing. George Christakos: Conceptualization, Methodology, Investigation, Writing - original draft, Writing - review & editing, Supervision, Project administration, Funding acquisition.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
We would like to thank Mr. Jimi He (The Chinese University of Hong Kong, Shenzhen) for his assistance with the R software coding. This work was supported in part by the National Science Foundation of China (41671399) and the Science and Technology Department of Zhejiang Province (2016C04004).
Editor: Jay Gan
Footnotes
Supplementary data to this article can be found online at https://doi.org/10.1016/j.scitotenv.2020.141447.
Appendix A. Supplementary data
Supplementary material
References
- Alonso D., McKane A.J., Pascual M. Stochastic amplification in epidemics. J. R. Soc. Interface. 2007;4:575–582. doi: 10.1098/rsif.2006.0192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson R.M., Anderson B., May R.M. Oxford university press; 1992. Infectious Diseases of Humans: Dynamics and Control. [Google Scholar]
- Angulo J.M., Yu H.L., Langousis A., Madrid A.E., Christakos G. Modeling of space–time infectious disease spread under conditions of uncertainty. Int. J. Geogr. Inf. Sci. 2012;26:1751–1772. doi: 10.1080/13658816.2011.648642. [DOI] [Google Scholar]
- Angulo J., Yu H.L., Langousis A., Kolovos A., Wang J., Madrid A.E., Christakos G. Spatiotemporal infectious disease modeling: a BME-SIR approach. PLoS One. 2013;8 doi: 10.1371/journal.pone.0072168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Banks A., Vincent J., Anyakoha C. A review of particle swarm optimization. Part I: background and development. Nat. Comput. 2007;6:467–484. doi: 10.1007/s11047-007-9049-5. [DOI] [Google Scholar]
- Bashir M.F., Ma B., Komal B., Bashir M.A., Tan D., Bashir M. Correlation between climate indicators and COVID-19 pandemic in New York, USA. Sci. Total Environ. 2020;728 doi: 10.1016/j.scitotenv.2020.138835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Briz-Redón Á., Serrano-Aroca Á. A spatio-temporal analysis for exploring the effect of temperature on COVID-19 early evolution in Spain. Sci. Total Environ. 2020;728 doi: 10.1016/j.scitotenv.2020.138811. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chan K.H., Yuen K.-Y. COVID-19 epedemic: disentangling the re-emerging controversy about medical facemasks from an epidemiological perspective. Int. J. Epidemiol. 2020 doi: 10.1093/ije/dyaa044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chirstakos G. Elsevier; 2017. Spatiotemporal Random Fields: Theory and Applications. [Google Scholar]
- Christakos G., Olea R.A. New space-time perspectives on the propagation characteristics of the black death epidemic and its relation to bubonic plague. Stoch. Env. Res. Risk A. 2005;19:307–314. doi: 10.1007/s00477-005-0236-6. [DOI] [Google Scholar]
- Christakos G., Olea R.A., Serre M.L., Wang L.L., Yu H.L. Springer; New York: 2005. Interdisciplinary Public Health Reasoning and Epidemic Modelling: The Case of Black Death. [DOI] [Google Scholar]
- Gilbert G.L. SARS, MERS and COVID-19 –- new threats; old lessons. Int. J. Epidemiol. 2020 doi: 10.1093/ije/dyaa061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giuliani D., Dickson M.M., Espa G., Santi F. 2020. Modelling and Predicting the Spatio-Temporal Spread of Coronavirus Disease 2019 (COVID-19) in Italy. (Available at SSRN 3559569) [DOI] [PMC free article] [PubMed] [Google Scholar]
- He J., Christakos G., Zhang W., Wang Y. A space-time study of hemorrhagic fever with renal syndrome (HFRS) and its climatic associations in Heilongjiang province, China. Front. Appl. Math. Stat. 2017;3:16. doi: 10.3389/fams.2017.00016. [DOI] [Google Scholar]
- He J., Christakos G., Wu J., Cazelles B., Qian Q., Mu D., Wang Y., Yin W., Zhang W. Spatiotemporal variation of the association between climate dynamics and HFRS outbreaks in eastern China during 2005–2016 and its geographic determinants. PLoS Negl. Trop. Dis. 2018;12 doi: 10.1371/journal.pntd.0006554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He J., He J., Han Z., Teng Y., Zhang W., Yin W. Environmental determinants of hemorrhagic fever with renal syndrome in high-risk counties in China: a time series analysis (2002−2012) Am. J. Trop. Med. Hyg. 2018;99:1262–1268. doi: 10.4269/ajtmh.18-0544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He J., Christakos G., Wu J., Jankowski P., Langousis A., Wang Y., Yin W., Zhang W. Probabilistic logic analysis of the highly heterogeneous spatiotemporal HFRS incidence distribution in Heilongjiang province (China) during 2005-2013. PLoS Negl. Trop. Dis. 2019;13 doi: 10.1371/journal.pntd.0007091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He J., Wang Y., Mu D., Xu Z., Qian Q., Chen G., Wen L., Yin W., Li S., Zhang W., Guo Y. The impacts of climatic factors and vegetation on hemorrhagic fever with renal syndrome transmission in China: a study of 109 counties. Int. J. Env. Res. Pub. He. 2019;16:3434. doi: 10.3390/ijerph16183434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He J., Yang Y., Christakos G., Liu Y., Yang X. Assessment of soil heavy metal pollution using stochastic site indicators. Geoderma. 2019;337:359–367. doi: 10.1016/j.geoderma.2018.09.038. [DOI] [Google Scholar]
- Health Commission of Guangdong Province Health Commission of Guangdong Province. 2020. http://wsjkw.gd.gov.cn/ (assessed 5 April 2020)
- Health Commission of Hubei Province Health Commission of Hubei Province. 2020. http://wjw.hubei.gov.cn/ (assessed 5 April 2020)
- Health Commission of Xinjiang Uygur Autonomous Region Health Commission of Xinjiang Uygur Autonomous Region. 2020. http://www.xjhfpc.gov.cn/ (assessed 5 April 2020)
- Health Commission of Zhejiang Province Health Commission of Zhejiang Province. 2020. http://www.zjwjw.gov.cn/ (assessed 5 April 2020)
- Jahangiri M., Jahangiri M., Najafgholipour M. The sensitivity and specificity analyses of ambient temperature and population size on the transmission rate of the novel coronavirus (COVID-19) in different provinces of Iran. Sci. Total Environ. 2020;728 doi: 10.1016/j.scitotenv.2020.138872. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kennedy J., Eberhart R. Proceedings of ICNN’95-International Conference on Neural Networks. vol. 4. IEEE; 1995. Particle swarm optimization; pp. 1942–1948. [DOI] [Google Scholar]
- Ministry of Health and Medical Education, Islamic Republic of Iran Ministry of Health and Medical Education, Islamic Republic of Iran. 2020. http://behdasht.gov.ir (assessed 5 April 2020)
- Ministry of Health and Welfare, South Korea Ministry of Health and Welfare, South Korea. 2020. http://www.mohw.go.kr/react/index.jsp (assessed 5 April 2020)
- Ministry of Health, Italy Ministry of Health, Italy. 2020. http://salute.gov.it/portale/home.html (assessed 5 April 2020)
- National Health Commission of the People's Republic of China National Health Commission of the People's Republic of China. 2020. http://www.nhc.gov.cn/ (assessed 5 April 2020)
- Nature Coronavirus updates: the first three months as it happened. Nature. 2020 doi: 10.1038/d41586-020-00154-w. [DOI] [PubMed] [Google Scholar]
- Peeri N.C., Shrestha N., Rahman M.S., Zaki R., Tan Z., Bibi S., Baghanzadeh M., Aghamohammadi N., Zhang W., Haque U. The SARS, MERS and novel coronavirus (COVID-19) epidemics, the newest and biggest global health threats: what lessons have we learned? Int. J. Epidemiol. 2020 doi: 10.1093/ije/dyaa033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prata D.N., Rodrigues W., Bermejo P.H. Temperature significantly changes COVID-19 transmission in (sub) tropical cities of Brazil. Sci. Total Environ. 2020;729 doi: 10.1016/j.scitotenv.2020.138862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qi H., Xiao S., Shi R., Ward M.P., Chen Y., Tu W., Su Q., Wang W., Wang X., Zhang Z. COVID-19 transmission in Mainland China is associated with temperature and humidity: a time-series analysis. Sci. Total Environ. 2020;728:138778. doi: 10.1016/j.scitotenv.2020.138778. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qiu Y., Chen X., Shi W. Impacts of social and economic factors on the transmission of coronavirus disease 2019 (COVID-19) in China. J. Popul. Econ. 2020;33:1127–1172. doi: 10.1007/s00148-020-00778-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenbaum L. Facing Covid-19 in Italy—ethics, logistics, and therapeutics on the epidemic’s front line. N. Engl. J. Med. 2020;382:1873–1875. doi: 10.1056/NEJMp2005492. [DOI] [PubMed] [Google Scholar]
- Sajadi M.M., Habibzadeh P., Vintzileos A., Shokouhi S., Miralles-Wilhelm F., Amoroso A. 2020. Temperature and Latitude Analysis to Predict Potential Spread and Seasonality for COVID-19. (Available at SSRN 3550308) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shahzad F., Shahzad U., Fareed Z., Iqbal N., Hashmi S.H., Ahmad F. Asymmetric nexus between temperature and COVID-19 in the top ten affected provinces of China: a current application of quantile-on-quantile approach. Sci. Total Environ. 2020 doi: 10.1016/j.scitotenv.2020.139115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi P., Dong Y., Yan H., Zhao C., Li X., Liu W., He M., Tang S., Xi S. Impact of temperature on the dynamics of the COVID-19 outbreak in China. Sci. Total Environ. 2020;728 doi: 10.1016/j.scitotenv.2020.138890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tosepu R., Gunawan J., Effendy D.S., Lestari H., Bahar H., Asfian P. Correlation between weather and Covid-19 pandemic in Jakarta, Indonesia. Sci. Total Environ. 2020;728 doi: 10.1016/j.scitotenv.2020.138436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- World Health Organization (WHO) Coronavirus disease 2019 outbreak situation. 2020. http://who.int/emergencies/diseases/novel-coronavirus-2019 (assessed 12 April 2020)
- Wuhan Municipal Health Commission Wuhan Municipal Health Commission. 2020. http://wjw.wuhan.gov.cn/ (assessed 5 April 2020)
- Xiao X., He J., Yu Y., Cazelles B., Li M., Jiang Q., Xu C. Teleconnection between phytoplankton dynamics in north temperate lakes and global climatic oscillation by time-frequency analysis. Water Res. 2019;154:267–276. doi: 10.1016/j.watres.2019.01.056. [DOI] [PubMed] [Google Scholar]
- Yancy C.W. COVID-19 and African Americans. Jama. 2020;323(19):1891–1892. doi: 10.1001/jama.2020.6548. [DOI] [PubMed] [Google Scholar]
- Yang Z., Zeng Z., Wang K., Wong S.S., Liang W., Zanin M., Liu P., Cao X., Gao Z., Mai Z., Liang J., Liu X., Li S., Li Y., Ye F., Guan W., Yang Y., Li F., Luo S., Xie Y., Liu B., Wang Z., Zhang S., Wang Y., Zhong N., He J. Modified SEIR and AI prediction of the epidemics trend of COVID-19 in China under public health interventions. J. Thorac. Dis. 2020;12:165–174. doi: 10.21037/jtd.2020.02.64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu H.L., Angulo J.M., Cheng M.H., Wu J., Christakos G. An online spatiotemporal prediction model for dengue fever epidemic in Kaohsiung (Taiwan) Biom. J. 2014;56:428–440. doi: 10.1002/bimj.201200270. [DOI] [PubMed] [Google Scholar]
- Zastrow M. South Korea is reporting intimate details of COVID-19 cases: has it helped? Nature. 2020 doi: 10.1038/d41586-020-00740-y. https://www.nature.com/articles/d41586-020-00740-y (assessed 23 July 2020) [DOI] [PubMed] [Google Scholar]
- Zhejiang Daily Zhejiang Daily. 2020. http://zjrb.zjol.com.cn/ (assessed 1 April 2020)
- Zhu Y., Xie J. Association between ambient temperature and COVID-19 infection in 122 cities from China. Sci. Total Environ. 2020 doi: 10.1016/j.scitotenv.2020.138201. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary material