Reverse-Engineering Laboratory Astrophysics: Oxygen Inner-shell Absorption in the ISM

Abstract

The modeling of X-ray spectra from photoionized astrophysical plasmas has been significantly improved due to recent advancements in the theoretical and numerical frameworks, as well as a consolidated and reliable atomic database of inner-shell transitions for all the relevant ions. We discuss these developments and the current state of X-ray spectral modeling in the context of oxygen cold absorption in the interstellar medium (ISM). Unconventionally, we use high-resolution astrophysical observations to accurately determine line positions, and adjust the theoretical models for a comprehensive interpretation of the observed X-ray spectra. This approach has brought to light standing discrepancies in the neutral oxygen absorption-line positions determined from observations and laboratory measurements. We give an overview of our current efforts to devise a definitive model of oxygen photoabsorption that can help to resolve the existing controversy regarding ISM atomic and molecular fractions.

INTRODUCTION

The study of the physical and chemical properties of the interstellar medium (ISM) provides useful insights about the formation and evolution of galaxies. ISM observations have been carried out with a variety of techniques that include ultraviolet (UV) spectroscopy [1], infra-red (IR) spectroscopy [2], and 21 cm radio emission [3]. Additionally, X-ray spectroscopy provides an outstanding method for the study of ISM material since X-ray photons have enough energy to travel through longer columns of material without being completely absorbed or scattered. Galactic X-ray binaries can then be used as back-light sources to observe the absorption features imprinted in the X-ray spectra of the relatively cold material before the light reaches the observer. The X-ray band essentially covers the absorption characteristics of all the cosmologically relevant metals, namely C, N, O, Ne, Mg, Al, Si, S, Ca, Fe, and Ni. The unprecedented spectral resolution of the gratings on board the Chandra and XMM-Newton satellite-borne observatories enables accurate detection of both the broad and narrow absorption lines and edges that can be used to estimate the gas chemical composition, structure, and dynamics.

To properly identify and model such spectral traits, detailed knowledge of the inner-shell processes in the absorbing species is required, in particular, bound–bound and bound–free transitions in neutral atoms, ions, and, most possibly, molecules and dust. Interstellar gas and dust absorb X-rays by inner-shell photoelectric transitions producing line features such as the 1s–2p Kα resonances in ions with less than 10 bound electrons, or bound–free continua resembling an opacity step function at the K-shell electron binding energy. In either case, the excited electron decays via an alternate channel (e.g., Auger decay) or radiates in directions away from the line of sight. Free atoms and ions display series of K lines converging to the edge head that display characteristic morphologies. Compounds and solids imprint proper signatures associated with the valence shell binding the atom to the solid crystal structure. Molecules can be detected by the chemical shifts of the K lines; solids (dust), on the other hand, do not exhibit resonances below threshold since the available upper levels are filled, but show characteristic structures above threshold that distinguish them from free atoms. The underlying physical data are usually compiled from a combination of extensive calculations and accurate laboratory measurements, where reliable identifications and precise quantitative accord are crucial for X-ray spectroscopy.

OXYGEN X-RAY ABSORPTION IN THE ISM

After hydrogen and helium, oxygen is the most abundant element in the ISM; however, solar values have been a matter of debate in the last two decades [4]. Oxygen can be found in several compounds other than the atomic form, such as molecules and dust grains. Therefore, it is astrophysically relevant to derive reasonably accurate estimates of the ionic, atom-to-molecule, and gas-to-solid fractions. In this respect, inner-shell electronic transitions are useful diagnostics since the ionization state or chemical bond shift the line energies by predictable amounts [5, 6, 7].

Studies of ISM X-ray absorption date to the pioneering observations of O I toward the Crab Nebula using the Einstein satellite [8]. Seminal calculations of the O inner-shell photoabsorption cross section were carried out using a central potential method [9], and later represented by analytic fits to the low resolution solid-state data [10, 11, 12]. Cross sections were represented in this work with a continuous background and a sharp discontinuity at the K edge whose energy was poorly determined. These atomic data were used to analyze the O K edge observed in the X-ray spectrum of the black-hole candidate Cyg X-1 [13].

More realistic theoretical cross sections were later computed with the R-matrix technique that included resonance effects [14], and were used to describe ISM absorption in the direction of two different X-ray binaries [15, 16]. However, this calculation did not include the effects of orbital relaxation and spectator Auger damping responsible for resonances with symmetric profiles of nearly constant width that smear the K-edge structure. This limitation was resolved in a subsequent calculation [17] that showed a good overall agreement with laboratory measurements [18]. This new cross section was applied in the analysis of seven X-ray binaries observed with Chandra, leading to the first estimates of oxygen ionized species in the ISM. These new results have challenged the previously suggested contribution of dust and molecular components [19]. This study also disclosed significant discrepancies in the position of the O I Kα resonance among several calculations and even the experimental data.

A more complete R-matrix calculation was performed in intermediate coupling for the whole oxygen isonuclear sequence [20], showing an agreement for neutral O near the threshold of ~ 10% with [17]. Note that the O I calculation was carried in LS−coupling due to its large computational size. Following [21], both radiative and Auger dampings were taken into account in order to reproduce the correct K-threshold behavior. Figure 1 compares these cross sections with those computed in [22] for the region near the n = 2 resonance and with the central-field potential calculation [9].

FIGURE 1.

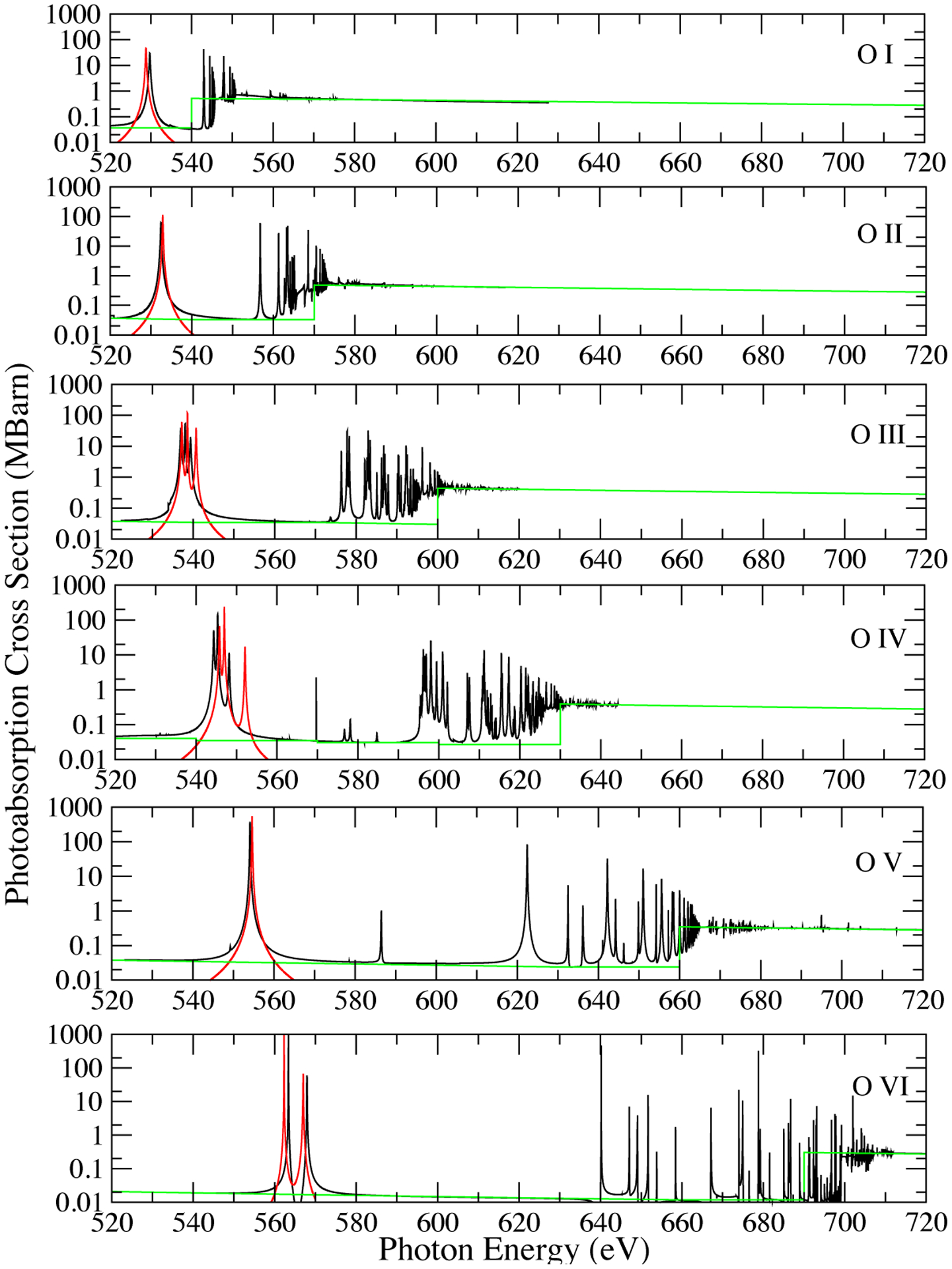
Photoabsorption cross sections of oxygen ions showing the structure near the K edge as calculated in Refs. [20] (black), [22] (red), and [9] (green).

Atoms, Ions, and Dust

Investigations in the infrared and ultraviolet indicate that a fraction of the ISM oxygen may be in solid form [23, 24]. In the X-ray band, it has been argued that oscillatory modulations near the K edge, referred to as X-ray absorption fine structure (XAFS), could be detected. These are condensed matter modulations of the atomic cross section due to the presence of solid particles [25, 26]. Analysis of the soft X-ray spectra from several sources have reported possible detections of molecules that could be linked to XAFS: in the edges of Ne, Mg, and Si [15, 27, 28]; in the L edge of Fe [29, 30]; and in the oxygen K edge [5, 6, 31, 32, 33]. XAFS signatures have also been searched for in the XMM-Newton spectrum of Sco X-1 [5]. XAFS is derived from the differences between the observed and theoretical fluxes; however, the model used by these authors is based on an atomic oxygen absorption cross section [14] that, as mentioned above, has serious limitations in reproducing the correct structure of the O K edge. The same observations have been reanalyzed [34] using the latest O I theoretical cross sections [14, 17, 20], thus evaluating the impact of the atomic data on the interpretation of the observations. It was found that a simple model based on the cross section by [20] was able to reproduce the observed absorption features without evidence of contributions from any other component. A fit using the cross sections by [17] showed a similar improvement, demonstrating that the residuals observed near the K edge are removed by implementing a more accurate atomic model (see Figure 2).

FIGURE 2.

Upper panel: Sco X-1 spectrum covering the O K-edge region. The black/gray data points are the observed data for two different exposures, while the red/blue curves are the corresponding models. The best fits using the cross sections by [14] and [20] are shown with dashed and solid lines, respectively. The middle and lower panels show the residuals in σ units with respect to these two models. From [34].

The case of XTE J1817–330

The resolution of the Chandra gratings is such that the disentanglement of the below-threshold resonance structure in neutral and ionized atomic species and the search for molecules requires reliable physical models. The latter must account for the piling up of resonances below the edge, the widths of the lower members of the K-line series, and the magnitude of the K edge to an accuracy of ~10% and, furthermore, the energy of the resonances must be accurate to a few mÅ. The need of invoking such a model to explain the oxygen K-edge structure observed in the Chandra HETG spectra of the X-ray binary XTE J1817–330 has been firmly shown [35]. The O K-edge region was fitted with a model referred to as warmabs, which is based on the photoionization package XSTAR [36] that incorporates the photoabsorption cross sections of [20]. This study revealed that the ISM absorption toward this object included both ionized and neutral gas, and reported Kα, Kβ, and Kγ lines from O I and Kα from O II and O III. High-ionization lines were also detected (O VI and O VII) although they are not expected to arise in the ISM given their very large equivalent widths. Moreover, it was found that the photoionization cross sections must be shifted in wavelength in order to accurately fit the observed spectra. Figure 3 shows the corrections for the cross sections used in this study, together with the best fit model of the high signal-to-noise Chandra spectrum of XTE J1817–330. The required shifts are 29 mÅ and 75 mÅ for the O I and O II cross sections, respectively. No shift was applied to the O III cross section. Surprisingly, it was also found that the experimental data [18] also required the same shift to fit the observation. This shift is similar to the disagreement already discussed in [19].

FIGURE 3.

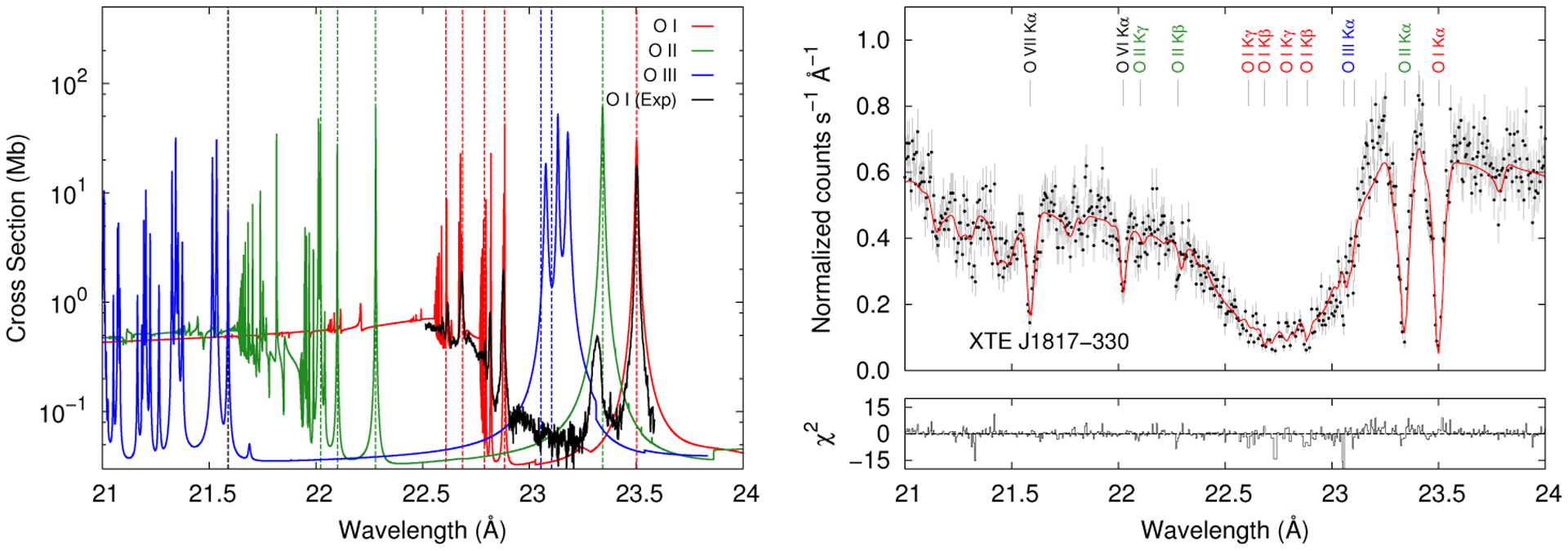
Theoretical atomic cross sections [left; 20] used to model the ISM oxygen K absorption observed in the Chandra HETG X-ray spectra (right) of XTE J1817–330. The experimental O I cross section [18] is also indicated. Wavelength adjustments were required in order to fit the spectra. The ionized components (O II and O III) are present and required by the fits. This analysis allows the determination of ionic abundances, line identifications, and ionization fractions of the ISM.

This benchmark required a careful examination and recalculation of the K-shell absorption spectrum of neutral oxygen and its ions [37], including phenomenological corrections to some resonance energies. In this respect, an analytical formula was developed to accurately represent the O I photoabsorption cross section. However, a 0.6 eV discrepancy remains between the astronomical and experimental measurements of the K-line position, where the accuracy of the molecular data used in the experimental calibration of the wavelength scale would probably need a revision. As a result, we decided to calibrate the theoretical energy scale relative to the astronomical observations.

Oxygen distribution in the ISM

A comprehensive study of O photoabsorption in the ISM was performed by analyzing high-resolution Chandra spectra of eight low-mass X-ray binaries [38]. Using the warmabs physical model, the abundances and the ionization parameter were therein determined for each source. Two different O I cross sections [20, 37] were considered in order to gauge the impact of the atomic data on model output. Figure 4 shows the abundances obtained using [20] (black lines) and [37] (red lines), indicating that, in spite of the differences in the cross sections, similar abundance values are obtained, namely an average oxygen abundance of A_O≈ 0.7.

FIGURE 4.

ISM oxygen abundances obtained from warmabs fits of the spectra towards eight galactic low-mass X-ray binaries. Open black circles: using the O I photoabsorption cross section by [20]. Filled red circles: using the O I photoabsorption cross section by [37]. Average oxygen abundances of A_O = 0.68 and A_O = 0.70 for these two cases are respectively denoted with black and red horizontal lines. From [38].

We are therefore confident about the O I representation since small differences in the atomic data do not seem to affect model predictions. The O abundance is given relative to the solar value in [39], and the average ionization parameter (log ξ =−2.9) from the fits indicates the predominance of the neutral component in the ISM. In Figure 5 we show the total oxygen column density vs. the ionization parameter for all sources. Apparently, the line-of-sight for the sources considered have both low oxygen column densities and low ionization parameters. The column-density ratios N(O II)/N(O I) and N(O III)/N(O I) derived from the model are estimated to be < 0.1. We do not find spectral features corresponding to the solid state in the oxygen absorption region.

FIGURE 5.

Map of the oxygen column density vs. ionization parameter generally showing low ionization parameters and low oxygen column densities. From [38].

CONCLUSIONS

During the last decade great advancements have been achieved regarding the understanding of inner-shell photoabsorption processes relevant to the interpretation of X-ray spectra from astronomical sources. In the case of oxygen ions, a detailed description of the K-shell spectra has been attained due to a combination of computations, laboratory measurements, and high-quality astronomical observations. The latter have been proven to be of utmost importance in order to correct and fine-tune the positions of the absorption features present in both theoretical and experimental photoabsorption cross sections. This unconventional approach has led to a revised O I K-shell cross section that can now be used to obtain reliable ISM abundance diagnostics.

The analysis of high-resolution Chandra spectra toward several galactic X-ray sources has revealed the need for accurate line positions, line identifications, and cross sections in the interpretation of the observed X-ray spectra. A precise knowledge of the cross sections for ionized atomic species is crucial to unravel the atomic contribution from that of possible compounds. We thus recommend the adoption of the most updated atomic data when looking for absorption signatures due to molecules or dust. This methodology is currently being implemented to refine the atomic data for other astrophysically relevant elements such as Ne, Mg, Si, and Fe.