Assessing levels of consciousness with symbolic analysis

Abstract

‘Covert consciousness’ is a state in which consciousness is present without the capacity for behavioural response, and it can occur in patients with intraoperative awareness or unresponsive wakefulness syndrome. To detect and prevent this undesirable state, it is critical to develop a reliable neurobiological assessment of an individual's level of consciousness that is independent of behaviour. One such approach that shows potential is measuring surrogates of cortical communication in the brain using electroencephalography (EEG). EEG is practicable in clinical application, but involves many fundamental signal processing problems, including signal-to-noise ratio and high dimensional complexity. Symbolic analysis of EEG can mitigate these problems, improving the measurement of brain connectivity and the ability to successfully assess levels of consciousness. In this article, we review the problem of covert consciousness, basic neurobiological principles of consciousness, current methods of measuring brain connectivity and the advantages of symbolic processing, with a focus on symbolic transfer entropy (STE). Finally, we discuss recent advances and clinical applications of STE and other symbolic analyses to assess levels of consciousness.

1. Introduction

Understanding the mechanism and measurement of human consciousness is a fundamental pursuit across multiple scholarly disciplines. One of the persistent challenges resulting from our incomplete understanding is the inability to discriminate clearly between conscious and unconscious states in individuals who have lost the capacity for behavioural responsiveness. The presence of conscious experience coupled with the absence of responsiveness is often referred to as ‘covert consciousness’. Although breakthroughs in neuroimaging have demonstrated the possibility of assessing levels of consciousness in behaviourally unresponsive patients, this technology is expensive and cumbersome. Furthermore, neuroimaging modalities are simply not feasible for the real-time detection of consciousness in the operating room setting, where—often due to the effects of paralytic drugs administered by anaesthesiologists—covert consciousness has been repeatedly documented to occur. As such, neurophysiological techniques involving the electroencephalogram (EEG) have been an active area of research for detecting covert consciousness in patients with unresponsive wakefulness syndrome (formerly referred to as the ‘vegetative state’) as well as in patients undergoing surgery with intended general anaesthesia. Unfortunately, the raw EEG is a complex signal that does not have a clear and invariant signature across unconscious states. One current dilemma is how to simplify techniques of EEG analysis while grounding them in the neurobiology of consciousness. Symbolic analysis is one method that has been explored to achieve this balance. In this article, we review the problem of covert consciousness, basic principles of the neurobiology of consciousness, the measurement of cortical connectivity with a form of symbolic analysis known as symbolic transfer entropy (STE), and recent advances in assessing levels of consciousness using other measures based on symbolic analysis.

2. Consciousness versus responsiveness

We are privy to one and only one case of subjective experience: our own. Therefore, all remaining assessments of conscious experience are inferred from behavioural activity and behavioural responsiveness. Imagine walking down the street and saying hello to a neighbour who is walking past you. Although you cannot definitively establish that your neighbour is conscious, you would nonetheless infer the presence of conscious experience based on her activity (walking), her responsiveness (waving and saying hello back to you), and your past experience in which your own responses (such as waving) were coupled with a conscious experience of an environmental stimulus (such as someone saying hello). Conversely, we make inferences of unconsciousness based on lack of behavioural responsiveness. If a friend were lying on a couch with his eyes closed and did not respond to a question you posed, you might conclude that he was sleeping. If you wanted to distinguish between the relatively reversible physiologic state of sleep and the relatively irreversible pathologic state of coma, you might jostle your friend to assess his responsiveness. Movement and awakening would confirm that the observed state was sleep, while unresponsiveness to vigorous shaking and noxious stimuli might suggest a more ominous situation. In short, we rely on behavioural assessments to make inferences of both consciousness and unconsciousness because we cannot directly access or measure consciousness in others.

Although responsiveness generally works well as a surrogate for consciousness in everyday life, pharmacologic interventions or pathologic events can generate conditions for covert consciousness by creating unbridgeable chasms between experience, intent and response. One common example of the pharmacologic dissociation of consciousness and responsiveness is unintended awareness during surgery. In 1–2/1000 surgical patients—and up to 1/100 high-risk patients—undetected consciousness and memory formation may occur in the operating room setting [1,2]. The incidence of undetected conscious experience without memory formation is significantly higher [3], as consciousness becomes dissociated from responsiveness owing to the effects of paralytic drugs. The suppression of voluntary movement is tantamount to the elimination of the primary behavioural measure of consciousness. The experience of awake paralysis—especially coupled with the pain of surgery—can be psychologically devastating [4,5], which motivates prevention of these events.

The pathologic and sometimes irreversible dissociation of consciousness and responsiveness is observed in neurologically impaired patients who have suffered, for example, a stroke or traumatic brain injury. The possibility of covert consciousness in what has classically been termed the vegetative state was illustrated dramatically in an influential case report of a woman who, despite a clinical diagnosis consistent with pathologic unconsciousness, was able to demonstrate brain activation patterns in response to volitional tasks that were similar to those of awake healthy controls [6]. This case led to neuroimaging paradigms intended to detect covert consciousness in those with diagnoses of unresponsive wakefulness syndrome, among other conditions [7]. The need for brain-based rather than behaviour-based diagnoses of pathologic unconsciousness is critical given the high percentage of misdiagnoses (between, for example, vegetative and minimally conscious states) [8].

As noted, functional neuroimaging is an expensive, time-consuming and cumbersome technology that lacks practicality for bedside diagnoses of pathologic states of unconsciousness and lacks feasibility for real-time intraoperative use to prevent awareness during anaesthesia. As such, the fields of neurology and anaesthesiology have focused more intensely on EEG as a diagnostic tool for these conditions. However, the use of EEG protocols to diagnose covert consciousness has been controversial in neurology [9–13], and the use of processed EEG in anaesthesiology has not demonstrated superiority to more traditional pharmacologic metrics in the prevention of intraoperative awareness [14,15]. The potential for successful detection of consciousness in the absence of responsiveness depends on a clearer understanding of the neurobiological principles of conscious experience.

3. Consciousness and neural communication

In order to distinguish between conscious and unconscious states in individuals who may lack normal responsiveness, we need to understand how the brain generates conscious experience as opposed to mere wakefulness. The neuroscientific mechanisms of consciousness remain opaque, although a number of prominent theories are being actively considered, including global neuronal workspace theory [16], predictive coding [17], higher-order representationalism [18] and integrated information theory [19]. Although these theoretical frameworks are clearly distinct, many involve some form of ‘communication’—i.e. an exchange of information—across the brain, as opposed to the isolated function of a particular neural region that is solely responsible for conscious processing. The requirement for communication between specific neural structures in the generation of consciousness becomes obvious when we consider the nature of our experience and the nature of brain function. The nature of our experience is that it is singular but complex, which is often referred to as the unity of consciousness. For example, we do not experience an object's colour independently of its shape or its movement or its spatial location. Rather, these visual features are bound or synthesized into a single percept that is furthermore integrated with other sensory modalities. By contrast, we have known at least since the nineteenth century that the brain is subdivided into discrete neural populations that serve specific functions. As such, the unity of consciousness seems to be at odds with the division of labour in the brain. Since the late twentieth century, the question of how the brain synthesizes discrete and specialized cognitive processing into a singular experience has been known as the cognitive binding problem [20,21]. In the twenty-first century, this line of investigation has evolved to the integrated information theory [19,22,23], which asserts that (i) the capacity of a system to be conscious is directly proportional to its ability to synthesize functionally discrete and specialized neural processing subsystems (in the case of the brain) and (ii) the complexity of integrated information cannot be causally reduced to its individual parts. The past work on the binding of neural information and integrated information theory differ in that the former proposes a necessity relationship to consciousness (i.e. binding is necessary for consciousness), while the latter proposes an identity relationship to consciousness (i.e. integrated information is consciousness). In either case, it should be clear that disrupting the process of information synthesis in the brain would be sufficient for unconsciousness, although the precise mechanism of disruption required for unconsciousness is currently unknown. While certain patterns of neural communication continue to persist in unconscious states, including sleep [24], anaesthesia-induced unconsciousness [25] and seizure [26], the ‘unbinding’ of patterns associated with neural representation has been argued to be the proximate cause and minimally sufficient condition for physiologic, pharmacologic and pathologic states of unconsciousness [27]. Therefore, the measurement of neural communication across the brain, a prerequisite for integration, holds promise as a method of assessing levels of consciousness. As discussed, EEG holds the most practical promise for assessing consciousness in the clinical domain, which means that corticocortical communication would be the primary target of measurement. In the following sections, we discuss the symbolization of EEG signals as well as recent advances in assessing depressed levels of consciousness using symbolic processes.

4. Computational techniques for estimating cortical communication with electroencephalography

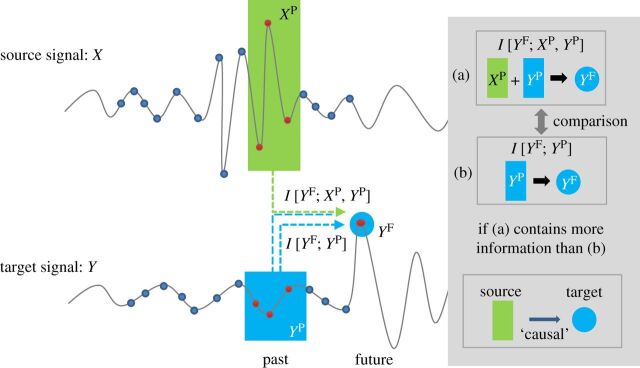
Estimating connectivity between two brain regions is a non-trivial task, with many potential problems caused by characteristics of the EEG itself and the limitations of the connectivity methods employed. Broadly, these methods have been classified as being measures of either functional or effective connectivity [28]. Functional connectivity measures the statistical covariation between signals recorded in different brain regions, while effective connectivity refers to the influence that one neural system exerts over another, at either a synaptic or a population level [28]. In this paper, we will focus on the methods that estimate effective connectivity from EEG, including measures of directed connectivity that have been used to assess level of consciousness [29,30]. Techniques that have been recently employed to estimate effective connectivity can be further divided into two categories: model-based approaches and information-theoretic approaches. Within model-based approaches, the most popular methods are dynamical causal modelling (DCM) [31] and Granger causality (GC) [32]. These two methods estimate the effective connectivity by generating a specific model for the processes underlying the observed data. DCM assumes a bilinear state space model with nonlinear interactions [31,33] and requires a priori knowledge about the underlying connectivity and comparisons of several competing models with respect to the observed data. However, as a priori knowledge about potential connectivity configurations in the brain may not always be available, the application of DCM to exploratory analyses is limited. GC is a linear regression model that quantifies the information transfer relationship between a source and a target signal. The past of the source signal is used to predict the future of the target signal; if its inclusion improves the prediction beyond what is known from the past of the target signal alone, the source signal is said to ‘Granger cause’ the target signal. However, this method is vulnerable to producing spurious results as a result of its linear interpretation, sensitivity to noise and band pass filtering [34,35], and inaccurate inferences in cases where two signals are mutually influenced by a third independent source [36]. These limitations make both DCM and GC non-ideal for assessing effective connectivity in EEG data. Transfer entropy (TE) is a popular information-theoretic approach with a broad range of applications that addresses many of these limitations [37]. While this measure is still susceptible to producing spurious results due to a source that mutually influences the signals of interest, TE is not dependent on a priori knowledge of brain connectivity patterns, is able to detect nonlinear relationships and is robust for a wide distribution of interaction delays [38]. TE is a nonlinear extension of GC and is equivalent to GC for jointly multivariate Gaussian variables [39]. The concept of TE is illustrated in figure 1. TE offers a model-free estimation of the direction and strength of connectivity between two signals, quantifying the degree of dependence of the target signal (Y) on the source signal (X) or vice versa. TE can be defined as the amount of mutual information between the past of X (X^P) and the future of Y (Y ^F), when the past of Y (Y ^P) is already known, i.e.

4.1

where H(Y ^F|Y ^P) is the entropy of the process Y ^F conditional on its past.

Figure 1.

Schematic illustration of TE. TE measures the influence of source signal X on target signal Y and is based on information theory. The information transfer from signal X to Y is measured by the difference of two mutual information values I[Y ^F; X^P, Y ^P] and I[Y ^F; Y ^P], where X^P, Y ^P and Y ^F are, respectively, the past of source and target signals and the future of target signal. The difference corresponds to information transferred from the past of source signal X^P to the future of target signal Y ^F and not from the past of the target signal itself. The average overall vector points measure the information transferred from the source signal to the target signal. (Courtesy of Lee et al. [29].)

The probability distributions of X^P, Y ^P and Y ^F can be written explicitly as

4.2

4.3

Equation (4.3) shows that the TE represents the amount of information provided by the additional knowledge of the past of X describing the information between the past and the future of Y . As TE is by definition sensitive to all orders of correlations, it is able to detect unknown nonlinear interactions, in contrast with linear and model-based methods. However, TE is limited by its sensitivity to the bin size (though non-binning strategies to estimate TE exist, e.g. [40]), its need for large amounts of data in order to produce a reliable probability, and the presence of more embedding parameters. Furthermore, TE is parsimonious in choosing samples of the source, target and conditional signals, which limits its performance in the presence of data with high dimensional dynamics [41] and also introduces the difficult process of optimizing the embedding dimensions of the multivariate space and the delays of interactions [42,43].

5. Interventional methods for assessing causal relationships

Another popular set of approaches in information and network sciences to study the causal relationships between subsystems are interventional methods [44,45]. In the context of these methods, causal influence refers to the extent to which the source signal has a direct influence on the future of a target signal [44], i.e. ‘if I change the present of the source signal with an intervention, to what extent does that alter the future of the target signal?’ By contrast, TE is a measure of observed (conditional) correlations. TE refers to the amount of information that a source signal adds to the future of a target signal, i.e. ‘if I know the present of the source signal, how much does that help to predict the future of the target signal?’ Given that causal interactions can serve the purposes of information transfer, storage and/or modification in a system, and TE only detects information transfer, TE may not accurately measure the underlying causal structure in all situations. In other words, non-zero TE signifies the presence of a causal relationship, but zero TE does not guarantee its absence [46]. However, as we typically do not have the ability to perturb specific brain signals in humans to measure the direct causal effects (though this is attempted more coarsely with interventions such as transcranial magnetic stimulation (TMS) [47]), the interventional method is somewhat limited in its application to assessing level of consciousness based on EEG.

6. Symbolic transfer entropy

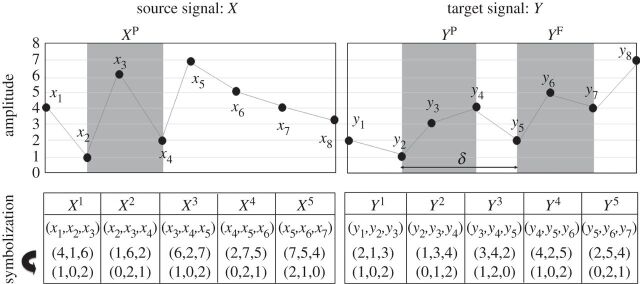
To mitigate the disadvantages of TE, Staniek & Lehnertz [48] modified the method with a symbolization process. In symbolic transfer entropy (STE), each vector for Y ^F, X^P and Y ^P in equation (4.2) becomes a symbolized vector point. For instance, a vector Y ^t consists of the ranks of its components Y ^t=[y₁,y₂,…,y_m], where y_j=y_{t−m×(j−1)τ} is replaced with the rank in ascending order, y_j∈[1,2,…,m] for j=1,2,…,m. Here, m is the embedding dimension and τ is the time delay. The symbolization process for the source and target EEG are illustrated in figure 2. STE is defined in the same way as equation (4.2), but embedded vector points are replaced with symbolized vector points. In comparison with TE, STE has the advantage of requiring no binning and no advanced estimator of the probability density function. Furthermore, the total possible number of vectors is significantly reduced by using ranked vector elements, making the estimation of probability relatively robust to a higher-dimensional dataset. Recently, Kugiumtzis [50] introduced a corrected version of STE by replacing the ranked vector with the rank of sample as the future of Y (Y ^F) in equation (4.1), which measures the direct analogue to TE using ranks. Further improvements to the original STE equation were introduced by extending it to multivariate time series; the resulting partial TE equations account for the influences of confounding variables from the other observed time series [51,52]. In addition to STE, other methods of mitigating the disadvantages of TE include binless estimation techniques, which do not require the selection of a bin size and work well for relatively small datasets [40,53].

Figure 2.

The symbolization of two EEG signals. The amplitudes of source and target signals, X and Y , are symbolized with the ranks of vector components in ascending order. In this example, the embedding dimension is m=3 and the time delay τ=1. Thus, the vector components are symbolized with 0, 1 and 2. For instance, X² = (1,6,2) is symbolized to (0,2,1) in ascending order. The grey shaded parts are X^P(=X²), Y ^P(=Y ²) and Y ^F(=Y ⁵), corresponding to the pasts of source and target EEG signals and the future of target EEG signal, respectively. Here, δ=3 is the interaction delay between the source and target EEG signals. (Courtesy of Jordan et al. [49].)

7. Symbolization of electroencephalography

In general, symbolization involves the transformation of an experimental signal into a series of discrete symbols that are processed to extract important information about the system dynamics. The common approach to symbolization is to partition the range of the original experimental data into a finite number of regions. Each region is associated with a specific symbolic value and uniquely mapped to a particular symbol depending on the region. The number of symbols and symbolization strategy are selected based on how much of the original information is retained in the sequence of symbols, and the sensitivity of the results to the choice of partition requires careful evaluation [54–56]. In broad applications, symbolization of experimental data provides better efficiency when finding and quantifying information from a system, reducing sensitivity to measurement noise and increasing the efficiency of numerical computations [57]. However, symbolization also removes significant amounts of information from the data, resulting in the potential for failure to detect the presence of information transfer [58,59]. Furthermore, the output of the symbolization process is characterized by several important limitations: (i) the generating partitions that are used to guarantee the uniqueness of the mapping are difficult to identify in noisy data, and thus data such as experimental neurophysiological signals may not be accurately represented, and (ii) symbolization relies only upon the relative differences between data points, and information associated with absolute differences between data points are ignored.

In the original presentation of STE, the degree of consistency between the symbolic process of ranked vector elements and the original system was not discussed. The ranked vector elements method was supported with its successful application to permutation entropy, which provided similar results using generating partitions for the interval map and a similar pattern with the Lyapunov exponent in a chaotic system [48]. As a result, STE is a measure mainly focused on the practical task of detecting the direction of information transfer relationships between two noisy systems. Further theoretical explanation for symbolization with ranked vector elements is required to quantify robustly the performance of this measure.

8. Parameter selection in multiscale symbolic transfer entropy

STE applied to EEG data exhibits a multiscale structure because of the multiscale properties inherent in spatio-temporal brain function. The multiscale nature of EEG-based STE creates the problem of needing to select a representative scale to produce a single value of STE for a given set of EEG data. The selection of a representative scale (and, in turn, the selection of appropriate embedding parameters) is critically important when comparing effective connectivity based on EEG with different spectral properties, which is often the case across varying levels of consciousness. For example, compared to EEG recorded during conscious wakefulness, the spectral characteristics of EEG recorded during ketamine-induced unconsciousness exhibit increases in gamma and delta power (corresponding to short- and long-term dynamics) and decreases in alpha power (corresponding to mid-range dynamics) [29]. Such spectral shifts result in distinct changes in the pattern of information transfer between frontal and parietal brain regions in both short- and long-term scales. Consequently, it would be impossible to choose a single scale that produces STE values that are truly representative of both states of consciousness. In order to circumvent this problem, Lee et al. [29] calculated STE for different states of consciousness by systematically searching a broad parameter space for the parameter set (embedding dimension (d_E), time delay (τ) and prediction time (δ)) that produced the maximum information transfer for each individual state of consciousness. By taking the maximum STE, all processes become non-parametric, i.e. without the need to make a subjective decision about embedding parameters. The prediction time was determined by the time lag resulting in maximal cross-correlation, assuming that the time lag represented the interaction delay between the source and target signals. The authors found that this parameter selection method yielded a consistent pattern of change of STE in EEG between consciousness and unconsciousness induced by a diverse group of anaesthetics. However, it is worth while noting that this parameter selection method may not work for all types of complex systems. Further study is required for choosing the appropriate parameter set.

9. Bias and normalization of symbolic transfer entropy

The different temporal and spectral characteristics of EEG recorded across varying states of consciousness can produce different biases in STE, which may be difficult to disentangle from components of the STE value that reflect the true underlying effective connectivity of the dataset. One method of removing the bias of STE for a given EEG dataset is the shuffled data method [58]. In this method, one or more datasets are shuffled such that the randomized data retain the same signal characteristics as the original, but the existing relationship between the set of signals is eliminated. Specifically, this can be accomplished by scrambling the temporal order of samples or segments in a time series. When estimating the bias in STE between two EEG signals, this shuffling process is applied only to the source signal (X), leaving the target signal (Y) intact. The STE with the shuffled source signal (X^P_Shuff), 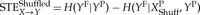, estimates the bias caused by the signal characteristics of the source signal (X). Furthermore, a bias can also be caused if the target signal (Y) exhibits high autocorrelation. This can be addressed by normalizing the STE as follows:

9.1

NSTE is normalized STE (dimensionless), in which the bias of STE is subtracted from the original STE and then divided by the entropy within the target signal, H(Y ^F|Y ^P). By this definition, NSTE represents the fraction of information in the target signal Y not explained by its own past and explained by the past of the source signal X [58].

Papana & Kugiumtzis [51] tested several types of surrogate data and corrected transfer entropies (mean conditional probability of recurrence, TE, effective TE, STE and corrected versions with surrogate data) to remove the bias from information transfer measures. They also examined the direction and strength of coupling with different settings of dynamic complexity, data length, noise levels and embedding dimensions, concluding that these potential factors give bias in both directions depending on their combination. However, among the tested information transfer measures, the corrected STE with surrogate data showed the best performance in detecting direction and strength of coupling as well as minimization of bias [51].

10. Statistical analysis for false positive symbolic transfer entropy connections

While NSTE is an unbiased estimator of effective connectivity that is robust against different signal characteristics, there is still a potential for it to be influenced by false positive information transfer. To mitigate this problem, permutation and time shift tests can be applied to evaluate the significance and the linear mixing effect, respectively, on connectivity. The permutation test is a non-parametrical statistical significance test that is used to assess whether test statistics of two groups are interchangeable [38,42]. The null hypothesis is that there is exchangeability between the test statistics (e.g. NSTE) of the original and shuffled EEG datasets. If NSTE values of the original EEG are significantly different from those of the shuffled EEG, a non-spurious measurement is supported. The time shift test evaluates the possibility of false positive connectivity due to an instantaneous linear mixing effect [42,38]. When instantaneous noise is linearly mixed with X and Y signals, a time shift to the past of X will increase the ability to predict Y because the instantaneous noise in shifted X appears in the future of Y . Thus, one should observe an increase in NSTE. If NSTE values for the original data are not significantly larger than those for the shifted data, then the hypothesis of an interaction between X and Y is not supported. Applying both of these tests to NSTE measures ensures that the resulting estimate of effective connectivity is an accurate representation of the influence of one EEG signal on another.

Alternatively, instead of statistically detecting the linear mixing or instantaneous information transfer, methods have been developed to directly remove confounding simultaneous effects from TE (or NSTE) [60].

11. Assessment of consciousness using symbolic analysis

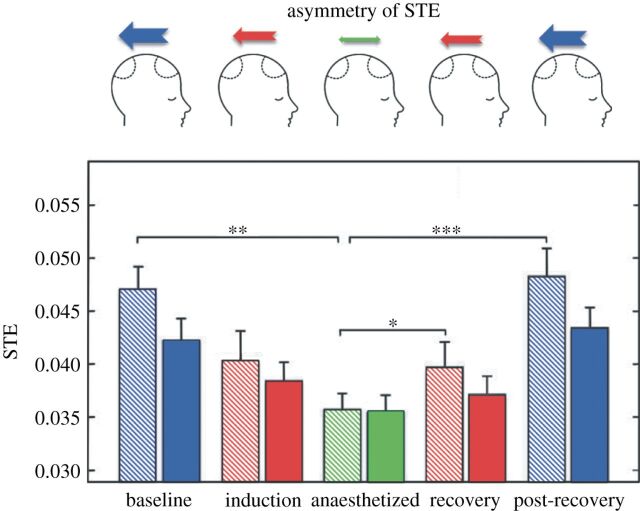
Recently, several advances in detecting changing levels of consciousness have been made by applying symbolic analysis techniques to EEG signals. Ku et al. [30] were the first to apply STE to measure cortical communication for the purposes of assessing levels of consciousness in humans. In their study, the authors recorded EEG from eight electrodes placed over the frontal and parietal regions of 18 surgical patients receiving general anaesthesia with propofol or sevoflurane. STE was used to assess the effective connectivity from frontal to parietal electrodes (i.e. feedback or reentrant connectivity) and from parietal to frontal electrodes (i.e. feedforward connectivity) during baseline consciousness, anaesthetic induction, unconsciousness and recovery states. The authors demonstrated that the dominant feedback connectivity in the baseline conscious states was inhibited after induction, resulting in a reduced asymmetry of feedback and feedforward connections while patients were unconscious. Feedback dominance returned upon recovery of consciousness (figure 3). The results of this study suggested that inhibition of frontoparietal connectivity, as measured by STE, is one neurophysiological correlate of general anaesthesia in surgical patients.

Figure 3.

Inhibition and recovery of frontal–parietal STE. The schematic diagrams in the top row represent the changing asymmetry between feedback and feed-forward STE over the five states. The feedback STE from frontal to parietal electrodes is preferentially inhibited and recovers across states. The feedback and feedforward STE are denoted with striped and solid bars, respectively, for each state. Error bar denotes the standard error (*p<0.005, ^**p<0.01, ^***p<0.001, n=18 patients). (Courtesy of Ku et al. [30].)

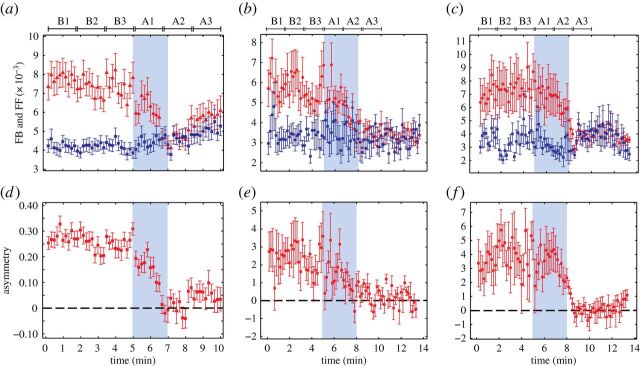
Lee et al. [29] applied NSTE to EEG collected from 30 surgical patients induced with ketamine, an anaesthetic with markedly distinct molecular and neurophysiological properties compared with propofol and sevoflurane. Despite ketamine exhibiting distinct spectral changes, ketamine reduced the feedback dominance observed during the baseline consciousness (figure 4). The novel finding of a consistent communication breakdown pattern across these diverse and major groups of anaesthetics suggests that using STE to measure connectivity in the frontoparietal region could be useful in monitoring brain states in surgical patients. Importantly, commercially available processed EEG monitors designed for assessment of intraoperative level of consciousness are typically insensitive to ketamine (and similar anaesthetics such as nitrous oxide), as their algorithms usually depend on a slowing EEG frequency. As such, symbolic analysis was able to achieve something that has long been elusive with more conventional analytic techniques [61].

Figure 4.

A common neural correlate of anaesthetic-induced unconsciousness. The inhibition of asymmetry between the feedback (FB, red triangles) and feedforward (FF, blue squares) connectivity is a common feature found across three heterogeneous anaesthetics. The FB/FF connections (a–c) and their asymmetry (d–f) in the frontal–parietal network are shown for (a,d) ketamine (n=30), (b,e) propofol (n=9) and (c,f) sevoflurane (n=9). The means and standard errors are denoted in each window. Anaesthetic administration is highlighted with blue shade. Six substates (B1, B2, B3 in baseline state and A1, A2 and A3 in anaesthesia) for the statistical tests are denoted. Each substate consists of ten 10 s long EEG epochs; time scales differ between ketamine and propofol/sevoflurane because data were collected in different studies. (Courtesy of Lee et al. [29].)

While these studies demonstrated a consistent correlation between loss of feedback processing and loss of consciousness, it is unclear whether or not these changes in effective connectivity are related to a functional disconnection between anterior and posterior brain structures, or whether they merely represent an epiphenomenal marker of unconsciousness. To address this gap, Jordan et al. [49] simultaneously recorded functional magnetic resonance imaging (fMRI) and high-density EEG in 15 subjects undergoing propofol-induced loss of consciousness. STE was used to calculate the effective connectivity between all permutations of frontal, parietal, temporal and occipital electrodes, and these measures were then correlated with changes in the functional connectivity of the resting-state network. Consistent with previous studies, but without a priori assumptions, the authors found that the maximum decrease in STE occurred between frontal and parietal electrodes. Functional correlation in higher-order frontoparietal networks was also significantly decreased. Furthermore, the observed propofol-induced decrease in functional connectivity of the anterior default mode network was significantly correlated with the decrease in STE between frontoparietal and frontooccipital electrode pairs—all other correlations between functional connectivity changes and STE changes were insignificant. This study demonstrated that observed changes in information exchange in frontoparietal networks, as measured by STE, directly correlate with changes in the spatio-temporal coherence of spontaneous fluctuations in fMRI.

Technical aspects of STE in the assessment of consciousness have also been explored using empirical data. Untergehrer et al. [62] assessed frontoparietal connectivity in EEG recorded from 15 male volunteers during consciousness and propofol-induced unconsciousness. The authors investigated the effect of varying parameters embedded in STE; two parameters were fixed (embedding dimension m=5 and time delay τ=5) while transfer time was varied systematically from 25 ms (δ=5) to 250 ms (δ=50). Consistent with previous findings, feedback connectivity was decreased during propofol-induced unconsciousness. However, the values of STE varied in the range of transfer times in both conscious and unconscious states, and exhibited different dynamics. During unconsciousness, maximum information transfer values occurred within significantly shorter time intervals than during consciousness. The results of this empirical study demonstrated the need to consider carefully the parameter selection in STE calculations, as discussed theoretically in the section regarding parameter selection. Notably, time intervals that maximize STE between source and target signals are linked to the physical interaction delay between them. Thus, in finding the maximum STE, we may inversely estimate the actual interaction times between two brain regions in conscious and unconscious states [63].

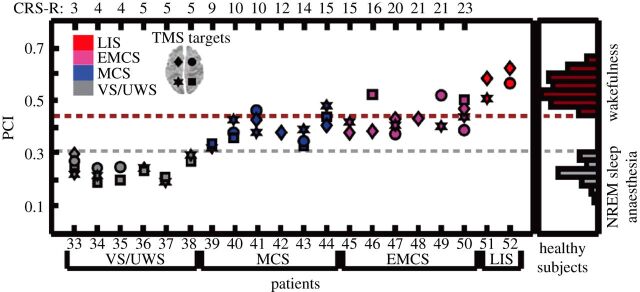
While the focus of this review has been STE, other types of symbolic analysis have been used to assess levels of consciousness. Notably, Casali et al. [59] applied the Lempel–Ziv measure of algorithmic complexity to analyse EEG response to TMS during physiological, pharmacological and pathological loss of consciousness. The authors estimated the primary electromagnetic sources of scalp EEG activity in response to TMS-evoked cortical currents and used the Lempel–Ziv complexity to evaluate the information content of corticocortical causal interactions. The algorithm systematically evaluates a set of five symbols used to represent the amount of non-redundant information contained in the data. From the output of this symbolic analysis, the authors calculated the perturbational complexity index (PCI) as a measure of an individual's level of consciousness. PCI values ranged from 0.44 to 0.67 in 32 healthy awake individuals and were reduced to 0.18–0.28 during non-rapid eye movement (NREM) sleep and to 0.12–0.31 during anaesthetic-induced unconsciousness (figure 5). Furthermore, PCI values also clearly reflected the level of consciousness of patients who suffered brain injury and were thus at risk for covert consciousness. The values systematically increased for patients in the following conditions: unresponsive wakefulness syndrome (0.19–0.31), minimally conscious state (0.32–0.49), recovery from coma (0.37–0.52) and locked-in syndrome (0.51–0.62, which is consistent with values in healthy awake individuals).

Figure 5.

PCI discriminates the level of consciousness in brain-injured patients. PCI values for 48 TMS sessions collected from 20 severely brain-injured patients (TMS was targeted to both left and right BA08 and BA07, as indicated at top left). Distributions of PCI values from healthy individuals and patients are presented. LIS, locked-in syndrome; EMCS, emerging from minimally conscious state; MCS, minimally conscious state; VS/UWS, vegetative state/unresponsive wakefulness syndrome. (Courtesy of Casali et al. [59].)

King et al. [64] have also applied symbolic analysis techniques to this population. They developed a ‘weighted symbolic mutual information’ measure that demonstrated the ability to discriminate among patients in a vegetative state, minimally conscious state and conscious state, as well as healthy controls. Long-range connections were particularly susceptible to decreases in mutual information across brain regions. This study is interesting because it demonstrates a similar set of findings to the PCI approach, but with a non-perturbational technique.

12. Conclusion

Techniques involving symbolic analysis have proved successful in discriminating clearly between states of consciousness and unconsciousness where conventional techniques of EEG analysis have failed. In particular, the use of STE has revealed a consistent disruption of frontoparietal information processing by three molecularly and pharmacologically distinct anaesthetics. Application of STE has also resulted in novel insights into longstanding problems related to consciousness, such as the potential for a neurobiological explanation of near-death experiences. Borjigin et al. [65] found that cardiac arrest stimulates a transient but dramatic surge in cortical communication, estimated using STE analysis of EEG recorded in an animal model.

PCI and weighted symbolic mutual information measures appear to distinguish levels of consciousness in patients with neural injury. Further work is required to assess the most robust and computationally efficient method for clinical use. A particular challenge for symbolic analysis will be the real-time (versus off-line) application to EEG as well as the ability to detect the stability of a given level of consciousness. For example, PCI values are comparable across slow-wave sleep, anaesthetic-induced unconsciousness and unresponsive wakefulness syndrome, yet these states vary considerably with respect to reversibility in the context of a noxious stimulus. Comparisons of different symbolic measures may also shed light on competing theories of consciousness. For example, PCI and weighted symbolic mutual information are rooted in distinct frameworks of consciousness (integrated information theory and global neuronal workspace theory, respectively), yet both have the ability to discriminate among similar pathological states; the implications of this must be carefully considered. In conclusion, symbolic analysis of EEG has resulted in interval advances in the last half-decade in terms of assessing levels of consciousness and promises to be a helpful tool for future investigation and clinical application.