Using traveller-derived cases in Henan Province to quantify the spread of COVID-19 in Wuhan, China

Abstract

Wuhan shutdown was implemented on January 23 and the first level response to public health emergencies (FLRPHE) was launched over the country, and then China got the outbreak of COVID-19 under control. A mathematical model is established to study the transmission of COVID-19 in Wuhan. This research investigates the spread of COVID-19 in Wuhan and assesses the effectiveness of control measures including the Wuhan city travel ban and FLRPHE. Based on the dynamical analysis and data fitting, the transmission of COVID-19 in Wuhan is estimated and the effects of control measures including Wuhan city travel ban and FLRPHE are investigated. According to the assumptions, the basic reproduction number for COVID-19 estimated that for Wuhan equal to 7.53 and there are $4.718\times {10}^4$ infectious people in Wuhan as of January 23. The interventions including the Wuhan city travel ban and FLRPHE reduce the size of peak and the cumulative number of confirmed cases of COVID-19 in Wuhan by 99%. The extraordinary efforts implemented by China effectively contain the transmission of COVID-19 and protect public health in China.

Introduction

In December 2019, the novel coronavirus pneumonia case was reported in Wuhan, a metropolis with a population of 14.1865 million. On 20 January 2020, human-to-human transmission of the novel Corona Virus Disease 2019 (COVID-19) was confirmed [1, 2]. By January 23, 2020, 495 confirmed cases and 23 deaths were reported. However, no vaccine and special medicine are used to treat the patients of COVID-19. Then, a series of control measures were implemented to prevent and control the transmission of COVID-19. To stop the further dispersal of COVID-19 from Wuhan to other cities, Wuhan shutdown was implemented to limit movement of people in and out of Wuhan on January 23, 2020 [3], which is the most stringent quarantine measures for a metropolis with a population of over 10 million in human history. On the same day, the first-level response to public health emergencies (FLRPHE) [4] was launched in Hubei province. After the Wuhan shutdown, confirmed and suspected cases are quarantined, crowds are stopped, close contracts are tracked and isolated at home, public transport, schools and entertainment places are closed, floating population are managed and information and hygienic knowledge are released. The control measures implemented provide lessons for other countries or regions to prevent and control the transmission of COVID-19.

Mathematical modelling could be used particularly to investigate the transmission of diseases such as COVID-19, and can also dynamically forecast the development trend of diseases based on the previous information [5–7]. Using the number of cases detected outside mainland China, Imai et al. [8] estimated the number of cases in Wuhan city by 18th January. Wu et al. [9] posed a transmission dynamics model of COVID-19 in Wuhan and estimated the overall symptomatic case fatality risk. Song et al. [10] developed a mathematical model base on the epidemiology of COVID-19, computed the basic reproduction number, predicted the final size of COVID-19 in China, and investigated the effects of isolation of healthy people, confirmed cases and close contacts on the transmission of COVID-19 in China. Tang et al. [11] assessed the transmission risk of COVID-19 in China and showed the effect of interventions on the transmission of COVID-19.

Although the spread of COVID-19 in Wuhan has been largely studied [8–20], the transmission patterns of COVID-19 and the effectiveness of interventions are unclear [2]. Thus, a quantitative analysis is implemented to study the spread of COVID-19 before Wuhan shutdown and assess the effectiveness of control measures including the Wuhan city travel ban and FLRPHE in Wuhan. Reports provide the evidence that Public health systems in Wuhan were unable to bear a heavy burden, which led to many unconfirmed cases of COVID-19 [12]. Therefore, the spread of COVID-19 in Wuhan is estimated using traveller data from Wuhan to Henan Province. This method is used to estimate the cumulative number of cases based on two assumptions which are that 100% detection in travellers after arrival over the destination and the same infection rate between travellers and residents in Wuhan.

The active track of travellers from Wuhan to Henan Province was traced in detail and 398 imported cases were detected [21–23]. There were over 5 million travellers from Wuhan to other cities, where about 0.3 million travellers entering Henan Province which is the most travellers from Wuhan outside of Hubei province in China. Since the first imported case was reported on January 21, the People’s Government of Henan Province carried out strict surveillance for travellers from Wuhan and confirmed cases. Subsequently, FLRPHE was launched on January 25 over the Henan Province. The imported cases from Wuhan to Henan Province were detected from January 4 to February 14. Among provinces in China, Henan Province received the most travellers and imported cases, and showed the better surveillance of detected imported cases from Wuhan. Where the time of arrival at Henan Province, time of symptoms onset, time of seeing a doctor, time of diagnosis, and time of treatment were reported in detail during the COVID-19 outbreak [21–23]. Then, the information of imported cases tracked in Henan Province could veritably reflect the actual situation.

To estimate the spread of COVID-19 by January 23 and assess the effectiveness of control measures including the Wuhan city travel ban and FLRPHE, a mathematical model with immigration from Wuhan to Henan Province is built. Using the mathematical model, the size of the epidemic on January 23 is estimated, the peak time and value, and the cumulative number of cases without interventions including Wuhan city travel ban and FLRPHE are simulated, and the effectiveness of interventions is assessed.

The paper is organized as follows. The mathematical model and dynamics analysis are shown in Sect. 2. Section 3 gives the estimation of the parameters. The effects of control measures including the Wuhan city travel ban and FLRPHE are investigated in Sect. 4. Section 5 provides the discussion and conclusion.

Mathematical modelling of COVID-19 transmission

The mathematical model is used to estimate the epidemic of COVID-19 in Wuhan. The 6th edition treatment of novel coronavirus pneumonia [23] and report of the WHO-China Joint Mission on COVID-19 [24] imply that most people are susceptible and the infected people in the incubation period has infectivity. Susceptible people are infected by infectious people and become infected people. The patients go to the hospital and are diagnosed. Finally, the patients removed from the hospital. The imported cases in Henan Province are used to estimate the spread of COVID-19 in Wuhan. Then, the population of Wuhan (N) is divided into susceptible people ($S_1$), unfound infectious people ($I_1$), found infectious people ($H_1$) and removed people ($R_1$), respectively. The population of imported cases in Henan Province from Wuhan is divided into unfound infectious people ($I_2$), found infectious people ($H_2$) and removed people ($R_2$), respectively.

In the model, the following assumptions are given. The natural birth and death rates are not incorporated into the model due to that the short period span is considered. The unfound infectious people has the same infectivity. The transmission of COVID-19 in Henan Province is not considered. The susceptible people and unfound infectious people can travel from Wuhan to other places, and found infectious people and removed people cannot travel from Wuhan to other places by January 23.

In this study, the effects of control measures including the Wuhan city travel ban and FLRPHE since January 23 are investigated. The imported cases from Wuhan to Henan Province were detected from January 4 to February 14. Therefore, the initial time is chosen as January 4 and the twentieth day corresponds to January 23. Based on the epidemiological pattern of COVID-19 and previous work [12, 13], the transmission dynamics of COVID-19 is established by the following equations (The flow diagram is shown in Fig. 1):

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill \frac{\mathrm{d}{S}_1(t)}{\mathrm{d}t}& =-\frac{\beta S_1(t)I_1(t)}{S_1(t)+I_1(t)+R_1(t)}\hfill \\ \hfill & -\mu S_1(t),\hfill \\ \hfill \frac{\mathrm{d}{I}_1(t)}{\mathrm{d}t}& =\frac{\beta S_1(t)I_1(t)}{S_1(t)+I_1(t)+R_1(t)}\hfill \\ \hfill & -{\gamma }_1{I}_1(t)-\theta \omega (t)I_1(t),\hfill \\ \hfill \frac{\mathrm{d}{H}_1(t)}{\mathrm{d}t}& ={\gamma }_1{I}_1(t)-{\delta }_1{H}_1(t),\hfill \\ \hfill \frac{\mathrm{d}{R}_1(t)}{\mathrm{d}t}& ={\delta }_1{H}_1(t),\hfill \\ \hfill \frac{\mathrm{d}{I}_2(t)}{\mathrm{d}t}& =\omega (t)I_1(t)-{\gamma }_2{I}_2(t),\hfill \\ \hfill \frac{\mathrm{d}{H}_2(t)}{\mathrm{d}t}& ={\gamma }_2{I}_2(t)-{\delta }_2{H}_2(t),\hfill \\ \hfill \frac{\mathrm{d}{R}_2(t)}{\mathrm{d}t}& ={\delta }_2{H}_2(t),\hfill \\ \hfill \end{array}\right)\end{array}$$ 1

where

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \omega (t)=& b\frac{1}{\sqrt{2\pi }\sigma }{e}^{-{(\frac{t-u}{\sqrt{2}\sigma })}^2},\hfill \\ \hfill \mu =& \left\{\begin{array}{c}\hfill {\mu }_1,t\in [0,20),\\ \hfill 0,t\ge 20.\end{array}\right)\hfill \\ \hfill b=& \left\{\begin{array}{c}\hfill b_1,t\in [0,20),\\ \hfill 0,t\ge 20.\end{array}\right)\hfill \end{array}\end{array}$$

$\beta$ is the transmission rate, ${\gamma }_1$ and ${\gamma }_2$ denote the discovery rates of infectious people, and ${\delta }_1$ and ${\delta }_2$ are the removed rates. According to the real data [21], the imported cases per day from Wuhan to Henan Province satisfy the normal distribution function $\omega (t)$, where u is the expectation and $\sigma$ is the standard deviation, and b is the proposition of outflow of infectious people from Wuhan to Henan Province per day. $\theta$ is an emigration coefficient ratio of infectious people from Wuhan based on the imported cases from Wuhan to Henan Province. $\mu$ (${\mu }_1$) is the emigration rate of susceptible people from Wuhan to other places. $\mu$ (b) is ${\mu }_1$ ($b_1$) before January 23 and 0 after January 23 because that Wuhan city travel was banned on January 23. This model is supplemented by the initial values

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill S_1(0)>0,I_1(0)\ge & 0,H_1(0)\ge 0,R_1(0)\ge 0,\hfill \\ \hfill I_2(0)\ge & 0,H_2(0)\ge 0\mathrm{and}{R}_2(0)\ge 0.\hfill \end{array}\end{array}$$ 2

Fig. 1.

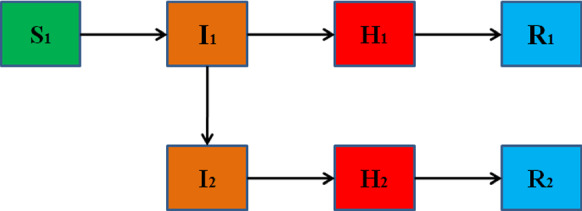
The flow diagram of COVID-19 in the model

Theorem 2.1

For system (1) with initial values (2), the solutions system (1) are nonnegative and ultimately bounded.

Proof

Using the Theorem 5.2.1 in [25], the nonnegativeness of $S_1(t)$, $I_1(t)$, $H_1(t)$, $R_1(t)$, $I_2(t)$, $H_2(t)$ and $R_2(t)$ follows immediately.

From the first equation of system (1),

$$\begin{array}{c}\hfill \frac{\mathrm{d}{S}_1(t)}{\mathrm{d}t}\le -\mu S_1(t).\end{array}$$

Then, ${lim\; sup}_{t\to +\infty }{S}_1(t)\le S_1(0)$. Thus, $S_1(t)$ is ultimately bounded.

Define a Lyapunov function

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill F(t)=& S_1(t)+I_1(t)+H_1(t)+R_1(t)\hfill \\ \hfill & +\theta (I_2(t)+H_2(t)+R_2(t)).\hfill \end{array}\end{array}$$

Obviously, $F(t)\ge 0(\forall t\ge 0)$. Then, differentiating F(t) along the solutions of system (1) leads to

$$\begin{array}{c}\hfill \frac{\mathrm{d}F(t)}{\mathrm{d}t}=-\mu S_1(t).\end{array}$$

Then, $F(t)\le S_1(0)$ for all $t>0$. Therefore, $I_1(t),H_1(t),R_1(t),I_2(t),H_2(t)$ and $R_2(t)$ are ultimately bounded. The proof is completed. $\square$

It follows from system (1) that there is a disease-free equilibrium point $E_0=(S_1^{\ast },0,0,R_1^{\ast },0,0,R_2^{\ast })$ with arbitrary constants $S_1^{\ast }>0$, $R_1^{\ast }>0$ and $R_2^{\ast }>0$. Since that $\omega (t)$ varies as time goes on, then $\omega (t)$ is reduced the mean value $\omega$ in the theoretical analysis. Using the next-generation matrix theory [26, 27], the basic reproduction number in Wuhan is computed as

$$\begin{array}{c}\hfill R_0=\frac{\beta }{{\gamma }_1+\theta \omega }.\end{array}$$

In the following, the stability of the disease-free equilibrium point $E_0$ would be analyzed.

Theorem 2.2

For system (1),

• (i)The disease-free equilibrium point $E_0$ is locally asymptotically stable if $R_0<1$.
• (ii)If $R_0<1$, then the disease-free equilibrium point $E_0$ is globally asymptotically stable.

Proof

Since the stability of $R_1(t),I_2(t),H_2(t)$ and $R_2(t)$ are determined by $S_1(t),I_1(t)$ and $H_1(t)$, it is sufficient to analyze the dynamics of the system with $S_1(t),I_1(t)$ and $H_1(t)$, then system (1) reduces the following differential equations

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill \frac{\mathrm{d}{S}_1(t)}{\mathrm{d}t}& =-\frac{\beta S_1(t)I_1(t)}{S_1(t)+I_1(t)+R_1(t)}\hfill \\ \hfill & -\mu S_1(t),\hfill \\ \hfill \frac{\mathrm{d}{I}_1(t)}{\mathrm{d}t}& =\frac{\beta S_1(t)I_1(t)}{S_1(t)+I_1(t)+R_1(t)}\hfill \\ \hfill & -{\gamma }_1{I}_1(t)-\theta \omega I_1(t),\hfill \\ \hfill \frac{\mathrm{d}{H}_1(t)}{\mathrm{d}t}& ={\gamma }_1{I}_1(t)-{\delta }_1{H}_1(t),\hfill \\ \hfill \end{array}\right)\end{array}$$ 3

Now the Jacobian matrix of system (3) at the disease-free equilibrium point $E_0$ is

$$\begin{array}{c}\hfill J=\left(\begin{array}{ccc}-\mu & -\frac{\beta S_1^{\ast }}{S_1^{\ast }+R_1^{\ast }}& 0\\ 0& \frac{\beta S_1^{\ast }}{S_1^{\ast }+R_1^{\ast }}-{\gamma }_1-\theta \omega & 0\\ 0& {\gamma }_1& -{\delta }_1\\ \end{array}\right).\end{array}$$

Then, the characteristic equation $|\lambda I-J|=0$ at $E_0$ gives

$$\begin{array}{c}\hfill (\lambda +\mu )\left(\lambda ,-,\left(\frac{\beta S_1^{\ast }}{S_1^{\ast }+R_1^{\ast }},-,{\gamma }_1,-,\theta ,\omega \right)\right)(\lambda +{\delta }_1)=0.\end{array}$$ 4

When $R_0<1$, all roots ($-\mu ,-{\delta }_1,\frac{\beta S_1^{\ast }}{S_1^{\ast }+R_1^{\ast }}-{\gamma }_1-\theta \omega$) of Eq. (4) have negative real parts. Therefore, the disease-free equilibrium point $E_0$ is locally asymptotically stable.

Now the global stability of the disease-free equilibrium point $E_0$ is proved. Define a Lyapunov function

$$\begin{array}{c}\hfill L(t)=I_1(t).\end{array}$$

Obviously, $L(t)\ge 0(\forall t\ge 0)$. Then, differentiating L(t) along the solutions of system (3) leads to

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \frac{\mathrm{d}L(t)}{\mathrm{d}t}& \le \beta I_1(t)-{\gamma }_1{I}_1(t)-\theta \omega I_1(t)\hfill \\ \hfill & =I_1(t)(\beta -{\gamma }_1-\theta \omega ).\hfill \end{array}\end{array}$$

If $R_0<1$, then $L^{\prime }(t)\le 0$. Based on the above discussions, the largest compact invariant set in $\{L^{\prime }(t)=0\}$ is the singleton $\{E_0\}$. Using the LaSalle invariance principle [28] and the local stability of $E_0$, the disease-free equilibrium point $E_0$ is globally asymptotically stable. $\square$

Numerical results are used to show the stability of equilibria of the system (1).

Case 1: $\mu >0$.

Setting the parameter $\beta =0.5$, $\mu =0.0018$, ${\gamma }_1=0.09$, $\theta =16.7$, $\omega =0.009$, ${\gamma }_2=0.1$, ${\delta }_1=0.05$, ${\delta }_2=0.1$ and initial value $(S_1(0),I_1(0),H_1(0),R_1(0),I_2(0),H_2(0),R_2(0))$ $=(100,10,0,0,0,0,0)$. The time series of variables in system (1) are shown in Fig. 2. In this case, the susceptible people will vanish as time goes on. Removed people $R_1$ and $R_2$ approach to $R_1^{\ast }$ and $R_2^{\ast }$, respectively.

Fig. 2.

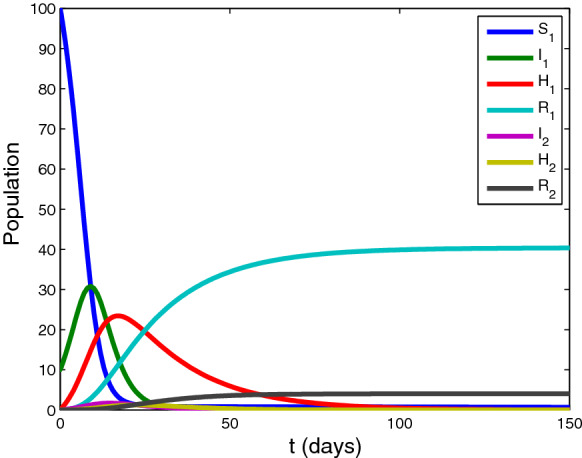
The time series of variables in system (1). $S_1(t)$ approaches to 0

Case 2: $\mu =0$.

Setting the parameter $\beta =0.1$, ${\gamma }_1=0.09$, $\theta =16.7$, $\omega =0.009$, ${\gamma }_2=0.1$, ${\delta }_1=0.05$, ${\delta }_2=0.1$ and initial value $(S_1(0),I_1(0),H_1(0),R_1(0),I_2(0),H_2(0),R_2(0))$ $=(100,10,0,0,0,0,0)$. The time series of variables in system (1) are shown in Fig. 3. In this case, the variable $S_1(t)$ converges to $S_1^{\ast }$, removed people $R_1$ and $R_2$ approach to $R_1^{\ast }$ and $R_2^{\ast }$, and other variables tend to zero.

Fig. 3.

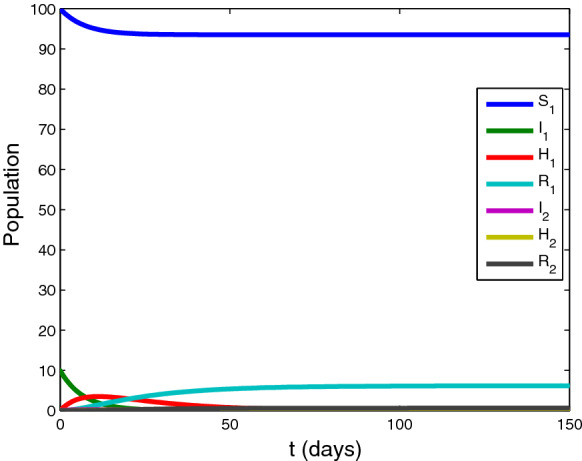
The time series of variables in system (1). $S_1(t)$ approaches to $S_1^{\ast }$

Parameters estimation

Data source

Data of COVID-19 cases in Wuhan are obtained in China from the National Health Commission of the People’s Republic of China and Coronavirus disease (COVID-19) situation reports in WHO [29, 30]. The data set includes the cumulative and new numbers of confirmed cases, suspected cases, death cases and cured cases, and the cumulative number of close contacts and hospitalization time. The data of imported cases from Wuhan to Henan Province were from the Health Commission of Henan Province [21].

As of January 19, 2020, the epidemiological investigation of 198 confirmed cases by the Chinese Center for Disease Control and Prevention (CDC) [22] showed that 22% of patients (43 cases) had direct exposure to the Huanan Seafood Wholesale Market which was closed on January 1, 2020. Since it was difficult to trace all infections of COVID-19 in Wuhan, 82 cases of COVID-19 in Wuhan (twice of 41 cases in our baseline scenario) by a constant zoonotic force of infection are assumed. For sensitivity analysis, 123 and 164 cases (twice and triple higher than the baseline scenario value) are assumed.

The imported cases are people who have travel history from Wuhan to Henan Province. The active track of imported cases from Wuhan to Henan Province was traced in detail. These data provide the date of arrival at Henan Province, date of symptoms onset, date of confirmation, the time between arrival and symptoms onset, the time between symptoms onset and confirmation, and time of treatment. During the Spring Festival from January 21 to February 2, 2019, there was an average outflow of 5.2 million people from Wuhan before the Chinese Lunar New Year. In 2020, about 5 million people travelled out of Wuhan before January 23 which is the time of Wuhan city travel ban. The average number of travellers from Wuhan between January 4 and January 23 was obtained from the Baidu migration data [31], where the first imported cases from Wuhan to Henan Province arrived at Henan Province on January 4, 2020. Then, estimation of the average proposition of daily travel volume from Wuhan was given and about 0.3 million people travelled from Wuhan to Henan Province between January 4 and January 23, 2020. The average proposition of daily exported cases from Wuhan to other places was computed based on the imported cases and the number of travellers from Wuhan to Henan Province and the number of travellers out of Wuhan between January 4 and January 23, 2020. These data used are from publicly available data sources.

Parameters estimation

Wuhan is a metropolis with a population of 14.1865 million including 9.0935 million permanent population and 5.103 million floating population. The cumulative number of cases in Wuhan before January 23, 2020 is estimated based on the confirmed cases exported to Henan Province from January 4 (the arrival time of the first imported case from Wuhan to Henan Province) to January 23. According to the data of imported cases from Wuhan to Henan Province [21], the time between arrival and symptoms onset is defined as the mean incubation period which is 7.9 days, the time between arrival and confirmation is 10.6 days (${\gamma }_2=\frac{1}{10.6}$), and time of treatment in Henan Province is 10 days (${\delta }_2=\frac{1}{10}$), respectively. Since about 5 million people travelled out of Wuhan before January 23 and about 0.3 million people travelled from Wuhan to Henan Province between January 4 and January 23, then the proposition of emigration of susceptible people from Wuhan to other places per day is 0.0018 (${\mu }_1=0.0018$), and the emigration coefficient ratio of infectious people from Wuhan to other places is $\frac{50}{3}$ ($\theta =\frac{50}{3}$). The initial values on January 4 are $S_1(0)=14.1865\ast {10}^6$, $H_1(0)=41$, $R_1(0)=I_2(0)=H_2(0)=R_2(0)=0$, and $I_1(0)$ is defined in Table 1.

Table 1.

Parameters estimation

Parameter	Mean	STD	95% CI	Sources
The baseline scenario $I_1(0)=41$
u	13.7104	0.0158	[13.7099, 13.7108]	Estimated
$\sigma$	2.4370	0.0034	[2.4369, 2.4371]	Estimated
$\beta$	0.6866	0.0003	[0.6865, 0.6867]	Estimated
$b_1$	0.01	0.0000007	[0.0100, 0.0100]	Estimated
${\gamma }_1$	0.0894	0.0003	[0.0893, 0.0895]	Estimated
${\delta }_1$	0.0605	0.0002	[0.0604, 0.0606]	Estimated
The second scenario $I_1(0)=123$
u	9.5819	0.0739	[9.5666, 9.5972]	Estimated
$\sigma$	3.1972	0.0047	[3.1962, 3.1981]	Estimated
$\beta$	0.5785	0.0001	[0.5785, 0.5785]	Estimated
$b_1$	0.01	0.000005	[0.01,0.01]	Estimated
${\gamma }_1$	0.0905	0.0004	[0.0905, 0.0906]	Estimated
${\delta }_1$	0.0576	0.0001	[0.0575, 0.0576]	Estimated
The third scenario $I_1(0)=164$
u	9.3038	0.1796	[9.2666, 9.3410]	Estimated
$\sigma$	3.4477	0.0050	[3.4467, 3.4488]	Estimated
$\beta$	0.5637	0.0043	[0.5629, 0.5646]	Estimated
$b_1$	0.01	0.000001	[0.01, 0.01]	Estimated
${\gamma }_1$	0.0870	0.0051	[0.0860, 0.0881]	Estimated
${\delta }_1$	0.0566	0.0004	[0.0565, 0.0566]	Estimated

(a) The second scenario: the initial infectious people are twice higher than our baseline scenario value; (b) The third scenario: the initial infectious people are triple higher than our baseline scenario value

Based on the mathematical model and the cumulative number of confirmed cases, using Markov Chain Monte Carlo (MCMC) method employing the adaptive Metropolis-Hasting algorithm with 20,000 iterations and a 10,000 iteration burn-in period [32], parameter values $\beta$, $b_1$, ${\gamma }_1$, ${\delta }_1$, u and $\sigma$ are estimated for three different scenarios. Furthermore, the mean value, standard deviation (STD) and 95% confidence interval (95% CI) are given in Table 1 for three different scenarios. Therefore, the basic reproduction number of three different scenarios are 7.53, 6.27 and 6.35, respectively.

Fitting results with three different scenarios

Regarding the uncertainty of estimated parameter values, the MCMC method is used to assess the performance of our model using the estimated parameter values in Table 1. In the baseline scenario, Fig. 4 displays the estimated cumulative number of imported people and real data from Wuhan to Henan Province, and shows the 95% confidence interval of simulation results. It is obvious that our simulations are consistent with the real data, which verifies the exactitude of our model.

Fig. 4.

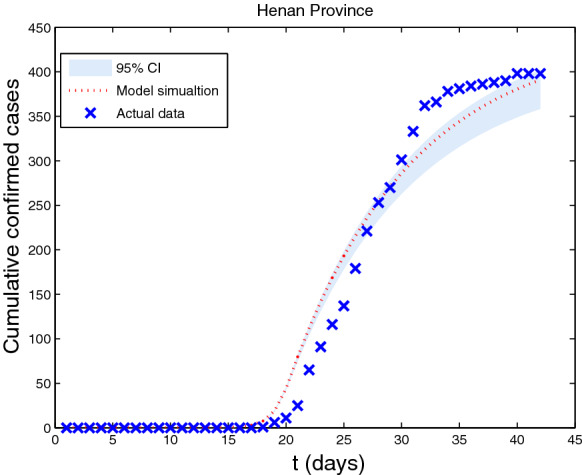
In the baseline scenario, the fitting results of estimated cumulative number of imported cases with real data from Wuhan to Henan Province

The spread of COVID-19 and the effectiveness of interventions in Wuhan

Estimating the spread of COVID-19 in Wuhan

Simulation results for the cumulative number of confirmed cases by January 23 for three different scenarios are given in Figs. 5, 6 and 7. In the baseline scenario, Fig. 5 shows that the cumulative number of cases of COVID-19 in Wuhan arrives at $4.718\times {10}^4$ as of January 23, 2020. If the initial infectious cases by zoonotic force of infection were twice higher than our baseline scenario value, Fig. 6 reveals that the cumulative number of cases of COVID-19 in Wuhan is $3.828\times {10}^4$ as of January 23, 2020, which means that the cumulative number of cases of COVID-19 would be 19% lower than the baseline scenario. If the initial infectious cases by zoonotic force of infection were triple higher than our baseline scenario value, Fig. 7 indicates that the cumulative number of cases of COVID-19 in Wuhan was $4.595\times {10}^4$ as of January 23, 2020, which means that the cumulative number of cases of COVID-19 would be 2.6% lower than the baseline scenario.

Fig. 5.

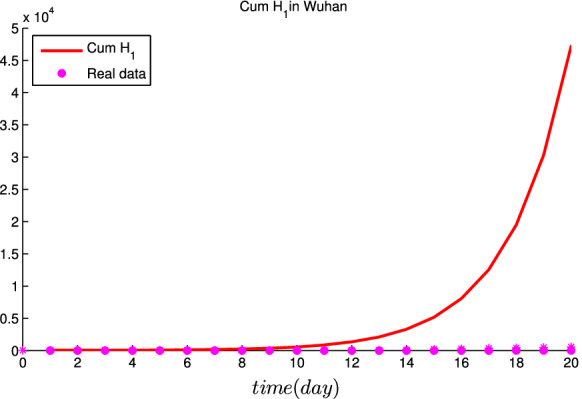
In the baseline scenario, the estimated cumulative number of cases in Wuhan with real data as of January 23, 2020

Fig. 6.

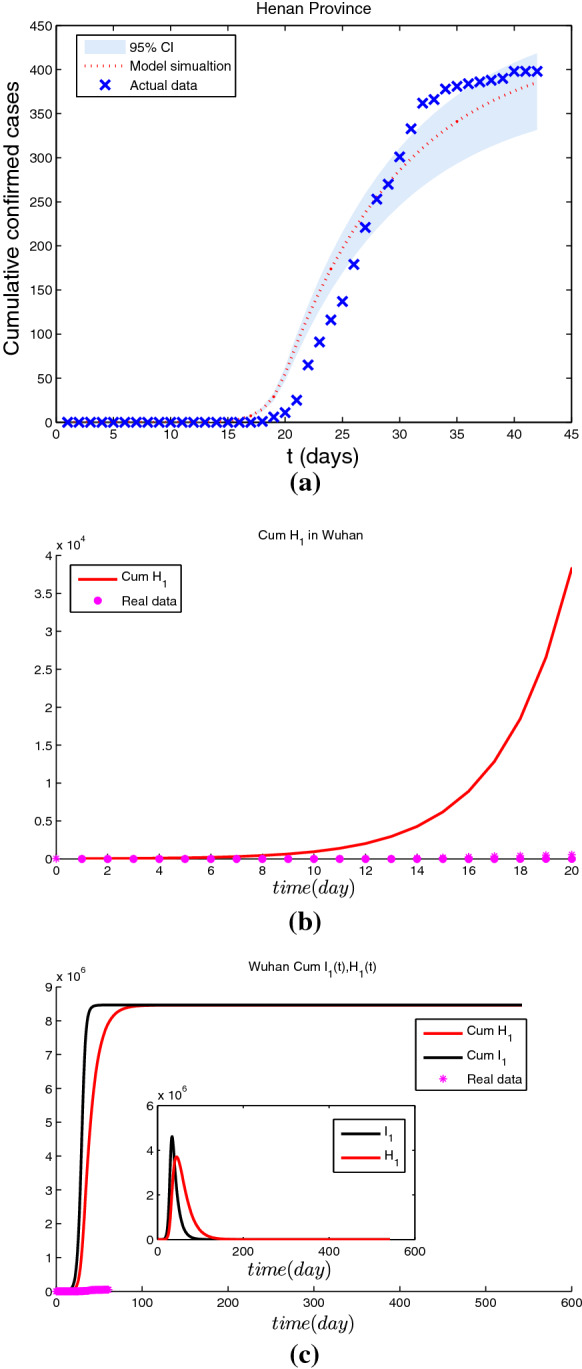
For twice higher than the baseline scenario value, a the fitting results of estimated cumulative number of imported cases with real data from Wuhan to Henan Province; b the estimated cumulative number of cases in Wuhan with real data as of January 23, 2020; c simulation results of the spread of COVID-19 in Wuhan without interventions

Fig. 7.

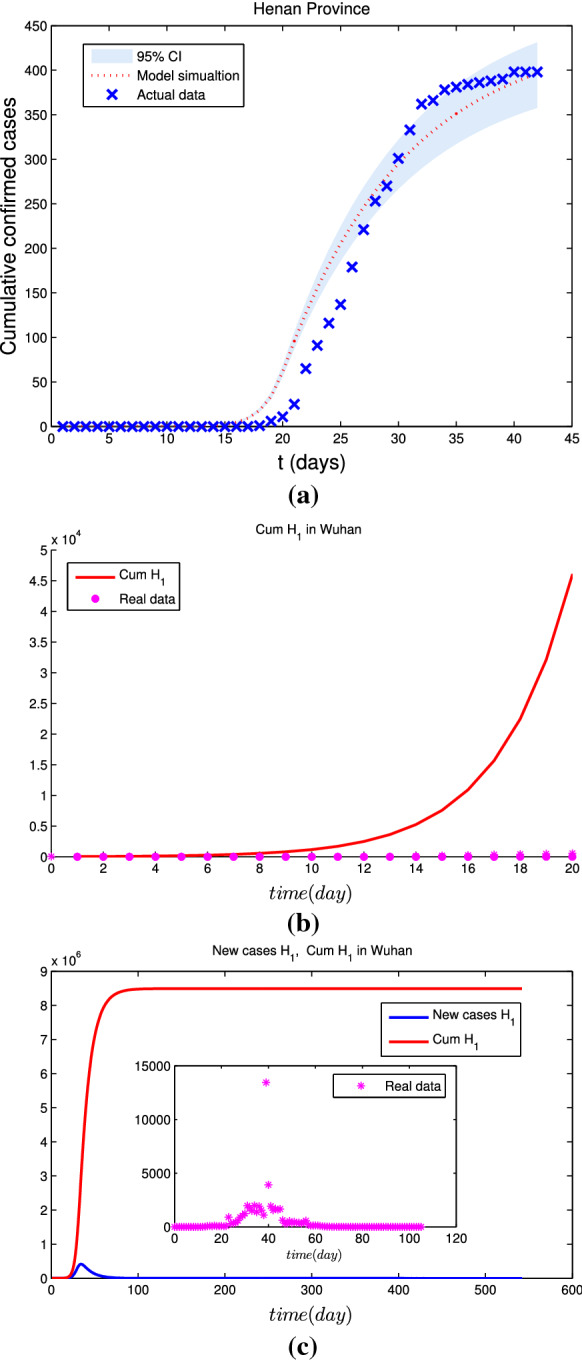
For triple higher than the baseline scenario, a the fitting results of estimated cumulative number of imported cases with real data from Wuhan to Henan Province; b the estimated cumulative number of cases in Wuhan with real data as of January 23, 2020; c simulation results of the spread of COVID-19 in Wuhan without interventions

Assessing the effectiveness of interventions in Wuhan

If there were no interventions including Wuhan city travel ban and FLRPHE (Figs. 6, 7 and 8), the epidemic of COVID-19 in Wuhan will arrive the peak with $4.69\times {10}^5$ ($4.18\times {10}^5$ and $4.168\times {10}^5$) around February 7 (February 9), 2020, and the cumulative number of cases of COVID-19 in Wuhan would arrive $8.83\times {10}^6$ ($8.46\times {10}^6$ and $8.49\times {10}^6$) in the baseline scenario (twice and triple higher than the baseline scenario value), which means that the peak time is consistent with the real data, but interventions including Wuhan city travel ban and FLRPHE reduce peak value and the cumulative number of cases of COVID-19 by about 99%.

Fig. 8.

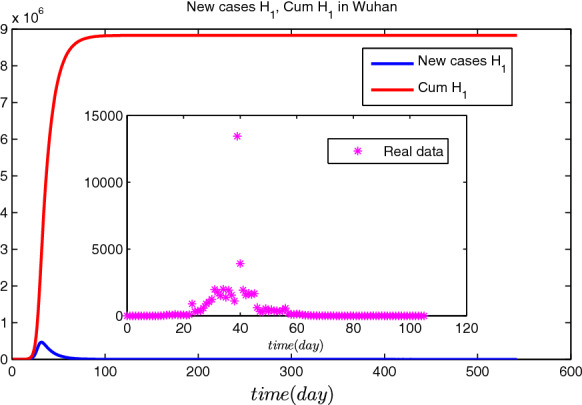
In the baseline scenario, simulation results of the spread of COVID-19 in Wuhan without interventions

Discussion and conclusion

Since the first case of COVID-19 was reported in Wuhan in December 2019, COVID-19 has spread rapidly over all provinces in China and caused 50,008 reported cases and 2574 deaths in Wuhan by April 13. In our study, a mathematical model of the COVID-19 transmission was established. Based on the dynamical analysis and data fitting, the estimated basic reproduction number is 7.53 and the estimated cumulative number of cases of COVID-19 reaches $4.718\times {10}^4$ in Wuhan as of January 23, 2020 which is greater than the cases reported due to the difficulties of tracing all infections and lack of sufficient medical resources. The basic reproduction number estimated is consistent with the value in [33], where a median value $R_0$ of 5.7 (95% CI: 3.8–8.9) is calculated, which means that the epidemic was very serious in Wuhan. The cumulative number of cases estimated in our study is greatly less than the epidemic size estimated in [12] which overestimated the epidemic size of COVID-19 in Wuhan by January 23, 2020. Therefore, our results truly reflect the spread of COVID-19 in Wuhan as of January 23, 2020 since the imported cases in Henan Province from Wuhan were traced in detail. Furthermore, the interventions including Wuhan city travel ban and FLRPHE reduce the peak value and the cumulative number of cases of COVID-19 in Wuhan by over 99%. The interventions effectively contained the spread of COVID-19 and protected public health all over the world [3, 34]. The interventions implemented by China have provided lessons for other countries to prevent and control the transmission of COVID-19.

In our study, there are two assumptions on the estimation of the epidemic size of COVID-19 in Wuhan. The first assumption is that the detection rate of imported cases in Henan Province is 100% sensitive. When our model is correct, the epidemic size of COVID-19 in Wuhan as of January 23, 2020 is estimated using the lower bound of detection rate since that the imported infectious people including asymptomatic patients or low severity cases were not detected. The second assumption is the same infection rate between travellers and residents in Wuhan. According to the discussions in [13], the true prevalence between travellers and residents might be different due to that the people visiting few individuals produced fewer infections and some visitors have less exposure to the infection than residents for a short time. However, the transmission of COVID-19 in Henan Province was not considered in our model which incorporated the transmission of COVID-19 in Wuhan and imported cases in Henan Province from Wuhan.

The mathematical modelling used in our study is similar with the work to model the epidemic dynamics of COVID-19 [8, 9, 14–18]. The mathematical model with emigration from Wuhan to Henan Province provides support for our estimation of the epidemic size of COVID-19 in Wuhan and the assessment of interventions using the imported cases and Baidu migration data. Nevertheless, our study has some limitations. First, the epidemic size of COVID-19 in Wuhan was estimated using the imported cases in Henan Province which might not completely reflect all exported cases from Wuhan. Second, the other interventions were not considered and incorporated into our model, which might overestimate the epidemic size in Wuhan as of January 23, 2020. Third, whether the transmission of COVID-19 was influenced by temperature and precipitation or not, the related study could not be found out.

Although COVID-19 has been under control in China, the normal production and life return to the previous status. But the epidemic of COVID-19 in the world is very serious and the imported cases from overseas continue to appear, which leads to an increase in the transmission risk of COVID-19 in China. Therefore, people must maintain vigilance against the potential second epidemic of COVID-19 in China [10, 35].

Compliance with ethical standards

Conflict of interest

The authors declare that they have no conflict of interest.