Skip to main content
PMC home page
iScience logoLink to iScience
. 2020 Jul 18;23(8):101382. doi: 10.1016/j.isci.2020.101382

Molecular Crowding and Diffusion-Capture in Synapses

Marianna Lamprou Kokolaki 1,2, Aurélien Fauquier 1,2, Marianne Renner 1,3,∗
PMCID: PMC7399191  PMID: 32739837

Summary

Cell membranes often contain domains with important physiological functions. A typical example are neuronal synapses, whose capacity to capture receptors for neurotransmitters is central to neuronal functions. Receptors diffuse in the membrane until they are stabilized by interactions with stable elements, the scaffold. Single particle tracking experiments demonstrated that these interactions are rather weak and that lateral diffusion is strongly impaired in the post-synaptic membrane due to molecular crowding. We investigated how the distribution of scaffolding molecules and molecular crowding affect the capture of receptors. In particle-based Monte Carlo simulations, based on experimental data of molecular diffusion and organization, crowding enhanced the receptor-scaffold interaction but reduced the capture of new molecules. The distribution of scaffolding sites in several clusters reduced crowding and fostered the exchange of molecules accelerating synaptic plasticity. Synapses could switch between two regimes, becoming more stable or more plastic depending on the internal distribution of molecules.

Subject Areas: Neuroscience, Molecular Neuroscience, In Silico Biology

Graphical Abstract

graphic file with name fx1.jpg

Open in a new tab

Highlights

  • •

    The good: molecular crowding enhances the interaction receptors-scaffold

  • •

    The bad: the exchange of molecules with extrasynaptic areas is reduced by crowding

  • •

    Molecular crowding helps synapses to be stable

  • •

    Nanoclusters of scaffold sites reduce crowding effects and favor synaptic plasticity

Neuroscience; Molecular Neuroscience; In Silico Biology

Introduction

The plasma membrane of cells (PM) is a heterogeneous fluid surface in which diffusing molecules can be organized into domains with particular composition (Nicolson, 2014). The spatial patterning of molecules of the PM is essential to cells, as specific membrane domains are dedicated to sense the environment and to communicate with other cells (Recouvreux and Lenne, 2016; Krapf, 2018). An example of these highly specialized domains are neuronal chemical synapses. Importantly, synapses are not static domains; they are able to modulate the intensity of synaptic responses by changing the number of receptors for neurotransmitters that reside in the synapse. This is one of the plasticity mechanisms thought to underlie memory and learning (reviewed in Huganir and Nicoll, 2013; Petrini et al., 2014).

Receptors for neurotransmitters are accumulated at the postsynaptic membrane by interactions with the subjacent meshwork of scaffolding proteins, which transiently capture them by stopping their diffusion (reviewed in Choquet and Triller, 2013; Maynard and Triller, 2019). We can assume that the capture results from the first-order reaction:

R+S⇄koffkonRS

where R are the receptors and S the scaffolding molecules, kon the effective forward binding rate, and koff the effective backward binding rate. kon and koff integrate the contribution of diffusion and intrinsic binding rates (Soula et al., 2014 and references therein) and can be estimated from the frequency and duration of binding events (Renner et al., 2017 and references therein). The affinity of receptors for their scaffolding molecules can be modulated by the phosphorylation state of receptors and scaffolds (Opazo et al., 2010; Specht et al., 2011; Hausrat et al., 2015; Flores et al., 2015; Battaglia et al., 2018). Indeed, changes of receptor-scaffold affinity and/or changes in the number of scaffolding sites underlie many synaptic plasticity phenomena (reviewed in Diering and Huganir, 2018).

The diffusion of receptors and its regulation has been described quite extensively by single particle tracking (SPT) or fluorescence recovery after photo bleaching (FRAP) (reviewed in Choquet and Triller, 2013; Park, 2018; Maynard and Triller, 2019), although the kinetics of their capture in synapses remains obscure. Difficulties to investigate receptor-scaffold interactions experimentally are numerous, notably due to the particularities of reactions occurring in 2D. In classical bulk biochemistry approaches to identify interactions and to quantify molecular affinities, peptides interact in an 3D environment and in conditions that can be quite different from those of membrane molecules in cells. Contrary to 3D, reactions between molecules on a membrane are affected by the distances between molecules that influence their reaction rates at all length scales (reviewed in Mahmutovic et al., 2012). Moreover, reactants are present in relatively small numbers (50–150 receptors and ∼200–300 scaffold sites; Sheng and Kim, 2011; Specht et al., 2013; MacGillavry et al., 2013 and references therein), thus discreteness and stochasticity cannot be disregarded (reviewed in Melo and Martins, 2006; Gillespie et al., 2013). Therefore, we can consider that the interaction receptor/scaffold happens in conditions far from the postulates of the law of mass action: it is a badly mixed system that involves a few numbers of molecules. Moreover, several experimental data support that the postsynaptic membrane is crowded with immobile proteins (Renner et al., 2009a, 2009b; Li et al., 2016). The importance of macromolecular crowding on reaction kinetics is now widely recognized (reviewed in Melo and Martins, 2006; Kalay et al., 2012). Interestingly, it has been shown that fractal reaction kinetics with time-dependent rate coefficients arise from diffusion-hindered systems in 2D (Hellmann et al., 2011). We may wonder how important these factors are in the case of synapses. Given the sizes of molecules and their density, how important is the effect of crowding for the capture of receptors? Does the pattern of distribution of scaffolding sites have an effect at this scale? What type of structure has the highest trapping capacity?

Particle-based Brownian dynamics offer the opportunity to simulate diffusion and reaction of molecules considering the spatial configuration of reactants. Monte Carlo simulations (MC) are ideally suited to study systems where the number of molecules is small and there is an important spatial heterogeneity (Goldman et al., 2004; Burrage et al., 2007). MC has been previously used to simulate AMPA receptors diffusion and recruitment into excitatory synapses (Santamaria et al., 2010; Tolle and Le Novére, 2010; Czöndör et al., 2012; Li et al., 2016; Gupta, 2018).

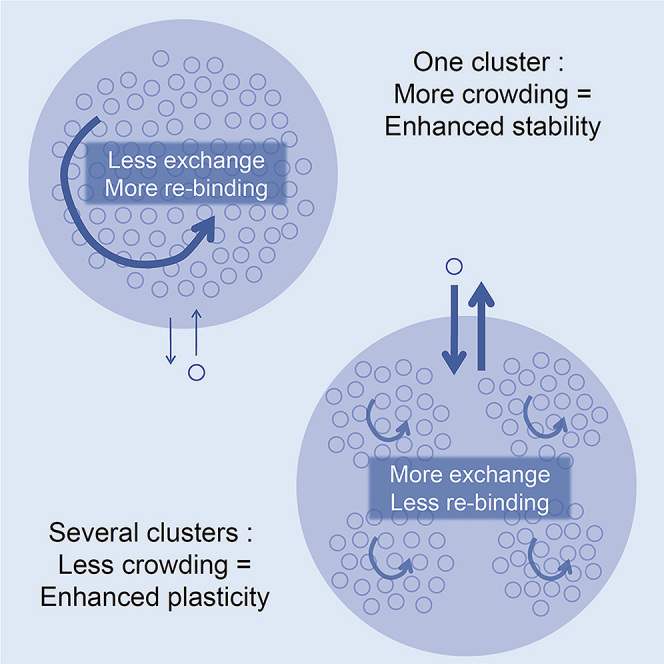
In this work, particle-based MC simulations were used to analyze the capture of receptors depending on the distribution of scaffolding sites and the presence of immobile obstacles. As expected, the distribution of sites in one or multiple clusters had a strong effect on the capture of molecules under crowding conditions, affecting the accessibility of sites. Crowding itself had a negative effect impairing the capture of molecules coming from outside the synapse, thus reducing the capacity of the simulated synapse to recruit new molecules. However, above a certain level, crowding had a positive effect strongly enhancing the re-capture of molecules already inside the synaptic area, thus increasing kon of these molecules. The distribution of scaffolding sites into several clusters decreased the influence of crowding, favoring the exchange of molecules with the extra-synaptic area and thus accelerating plasticity-like changes. Therefore, by rearranging the scaffold and changing the crowding level, synapses could switch between a state prone to change that easily exchanges molecules and a state prone to stability that reduces the exchange.

Results

Simulation of Diffusion-Capture in a Self-Crowded Patch of Membrane

The size of diffusing molecules and the distribution of binding sites were treated explicitly to incorporate the effects of space. The design of the simulation space and the parameters of the simulation were based on experimental data obtained on cultured neurons (Renner et al., 2009a, 2012; 2017; Specht et al., 2013; Patrizio et al., 2017; see Transparent Methods).

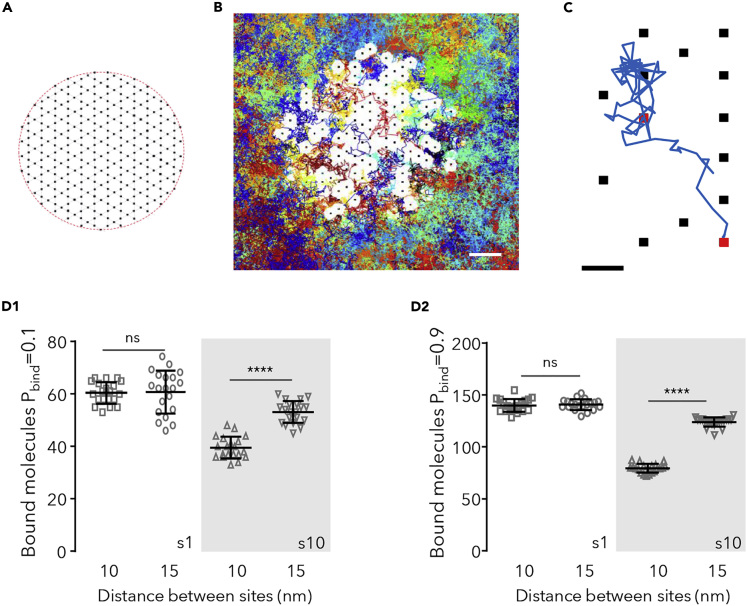
Scaffold interaction sites (3-nm-wide squares) were distributed following a hexagonal grid (Figure 1A) in a circle of 190–300 nm in diameter (depending on the distance between binding sites), in agreement with the expected hexagonal distribution of Gephyrin, the scaffolding molecule of inhibitory synapses (Bedet et al., 2006). The size of the interaction site was meant to represent a reactive radius for the diffusing particles; the binding sites themselves were not considered as obstacles. For a given set of simulations, a chosen number of sites was selected randomly from the possible positions given the distribution used (Figure 1B). The maximum number of sites (250) was always inferior to the number of nodes of the grid, leaving spaces without binding sites. The distance between sites was 10 or 15 nm, consistent with experimental data about the density of scaffolding sites of Gephyrin (Specht et al., 2013) or PSD-95, the main scaffolding molecule of excitatory synapses (MacGillavry et al., 2013).

Figure 1.

Figure 1

Open in a new tab

Capture of Molecules in Simulated Synapses

(A) Scheme of the hexagonal grid where binding sites could occur (black dots).

(B) Detail of the simulation space showing the randomly chosen binding sites (250 in total, black dots) overlaid with all the trajectories cumulated during 75s of simulation (200 molecules in total, 118 molecules bound at t = 75s, each trajectory depicted in a different color). The distance between sites was 15 nm. Molecules were 10 nm in diameter and a probability of binding (Pbind) of 0.9 and a probability of unbinding (Pfree) of 10−4. White spaces correspond to the excluded area due to the bound molecules (self-crowding). Bar: 50 nm.

(C) Detail of one trajectory (in blue) and binding sites (squares). The simulated molecule bound to the sites shown in red. Bar: 15 nm.

(D) Number of bound molecules when sites were distanced 10 nm or 15 nm, in steady state, for small (s1) or large (s10, gray area) molecules and low (D1) or high (D2) Pbind (values of 20 independent simulations overlaid with the mean ± SD, unpaired t test, ns: not significant; ∗∗∗∗p < 0.0001).

The size of typical receptors is 6–13 nm, depending on the type of receptor and the presence of accessory proteins (Schauder et al., 2013; Miller and Aricescu, 2014; Greger et al., 2017). Crowding arise when the distance between obstacles is comparable to the diameter of the diffusing molecule. Given the distance between scaffolding sites, the immobilization of receptors was expected to create significant self-crowding effects. To distinguish between the effects on the capture of receptors raising from crowding and those due just to the occupation of binding sites, two different sets of molecules were modeled. Large molecules representing receptors were simulated as diffusing circles of 10 nm in diameter (s10). Small molecules that could occupy binding sites without creating crowding were simulated as circles of 1 nm (s1).

The starting point of diffusing molecules was randomly chosen in the simulation space. Lateral diffusion of molecules was simulated as random walks (see Transparent Methods). Molecules bounced back when they found an obstacle in their way (immobile or mobile). Molecules were immobilized with a given probability Pbind if they passed on top of a binding site. Once immobilized, they were set free with a given probability Pfree (1 × 10−4 unless indicated, Figures 1B and 1C and Video S1). Experimental observations obtained with FRAP and SPT indicate that effective kon and koff values of the receptor-scaffold interaction are in the order of 10−1-10−2 s−1 (Czöndör et al., 2012; Renner et al., 2017). Pbind and Pfree values were chosen to provide similar values of the rate constants on simulated trajectories “converted” to match the temporal and spatial resolution of trajectories obtained experimentally with SPT (time between trajectory points of 75 ms, localization precision of 15 nm) (Figure S1, see Transparent Methods). The calculation of effective kon and koff was done using Packing coefficient analysis as before (Renner et al., 2017).

Video S1: Sequence (in Accelerated Motion) Corresponding to 37 s of a Simulation Run at Steady State

Only one every 75 time points are shown. Blue circles are diffusing molecules (size: 10 nm) that can bind to scaffolding sites (in black). Related to Figure 1

Download video file (2.1MB, flv)

Simulations were run for a short period of time (37,500 trajectory points, equivalent to 37.5 s) to assess the speed of population of empty synapses or for a longer period (225 s) to reach equilibrium (steady state, Figures S2A1–A2) that was typically attained after 75–100 s (not shown). Analyses of the steady state were done on the last 75 s of the run (Figure S2A2). The number of bound molecules was in the range of the number of synaptic receptors found experimentally (less than 200, Figure S2A1, reviewed in Choquet and Triller, 2013; Patrizio et al., 2017) and reflected the fractional occupancy of scaffolding sites observed in synapses (reviewed in Specht, 2020).

A first series of simulations was performed to describe the system at steady state without (small molecules) or with self-crowding (large molecules). Figure 1D shows the number of bound molecules for the two configurations of sites, the more compact (sites distanced 10 nm) and the less compact one (sites distanced 15) for molecules with low (Figure 1D1) or high (Figure 1D2) Pbind. Figure S2B shows examples of the final distribution of molecules. As expected, small molecules (s1) bound to sites at the same level in both configurations (t test, p < 0.6), the number of bound molecules depending only on Pbind. For large molecules, there was a robust effect of the distance between sites (Fig. 1D, ∼25% and ∼36% reduction in the compact distribution for molecules with Pbind = 0.1 or 0.9, respectively; t test p < 0.0001). Large molecules were overall less captured than the small ones (reduction of ∼34%–43% in case of the compact distribution, of ∼12% in the other case).

These results agree with the facts that (1) bound molecules become immobile obstacles for the moving ones reducing the area available to diffuse (Figure 1B) and (2) self-crowding arise when the distances between sites are in the order of the size of molecules. Small molecules (diameter of 1 nm) had always the possibility to diffuse between bound molecules and thus their capture was not affected.

The effects of crowding are likely to vanish when the relative importance of the reaction increases with respect to diffusion (i.e. in case of strong affinity). We checked the effect of the distribution of sites when molecules have a lower Pfree (0.5 × 10−4, still in the range of what can be observed in experimental data). The overall number of bound molecules (Pbind = 0.9) was higher than before as expected, due to the increased affinity (compare Figures S3 and 1D). The lower trapping due to self-crowding was still observed, although the effect was less important than before (∼30%–34% reduction for large molecules in more compact with respect to less compact configuration, Figure S3).

The hexagonal distribution of sites was meant to represent the expected arrangement of the scaffolding molecule Gephyrin; however, other scaffolds may have a random distribution of sites. We wonder whether the effects of self-crowding were still observable when sites were distributed randomly, with a minimum distance of 10 or 15nm between sites (Figure S4A). Large molecules were still less captured in the more compact configuration although the reduction was less important than on the hexagonal lattice (∼13%–15% reduction, Figure S4B). On the other hand, the random configuration provided distributions that were less dense than the hexagonal grid, with a median distance between sites of 11.18 nm in case of the more compact distribution and 17.02 nm for the less compact one (not shown).

We may expect that some sites became inaccessible to large molecules due to percolation effects. However, it is important to note that the self-crowding simulated here and the configuration of areas above the percolation threshold are continuously fluctuating, as molecules constantly get bound and unbound (Video S1). Indeed, all the sites were able to capture molecules at some point of the simulation run, although those on the borders were logically more efficient principally in the compact case (Figure S5).

Altogether, these data suggest that changing the pattern of distribution of sites could improve the trapping capacity of synapses by increasing the number of effective scaffolding sites. Actually, scaffolding molecules in real synapses are not always evenly distributed in the post-synaptic area. The presence of nanodomains of excitatory and inhibitory receptors and their scaffolding molecules in a fraction of synapses have been shown by several groups (MacGillavry et al., 2013; Nair et al., 2013; Specht et al., 2013; Dzyubenko et al., 2016; Orlando et al., 2017; Pennacchietti et al., 2017; Kellermayer et al., 2018; Hruska et al., 2018). Typically, these synapses contain 2–10 nanodomains (most commonly 2–3, depending on the receptor type; Nair et al., 2013; Kellermayer et al., 2018) that are ∼50–100 nm wide and contain ∼20 or more receptors.

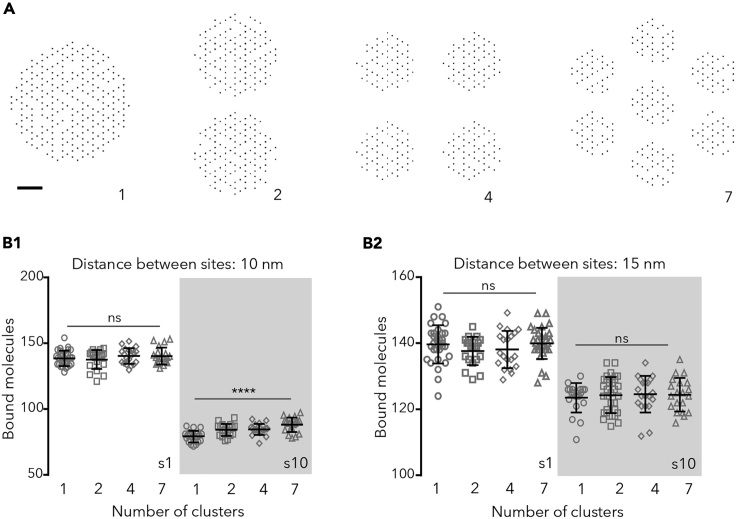
Nanoclusters were simulated by distributing sites in 2, 4, or 7 clusters (Figure 2A). Each cluster contained equivalent numbers of sites, chosen randomly from the nodes of a hexagonal lattice (250 sites in total, see Transparent Methods). The spacing between clusters (minimum 30 nm) was set to hold all the scaffolding sites within a circle of 250–550 nm in diameter, compatible with the reported sizes of the post-synaptic density (Specht et al., 2013; reviewed in Choquet and Triller, 2013).

Figure 2.

Figure 2

Open in a new tab

Capture of Molecules When Sites Are Distributed in Multiple Clusters

(A) Examples of the configuration of sites (250 in total) in 1, 2, 4, or 7 clusters. Bar: 60 nm.

(B) Number of bound molecules in synapses containing 250 sites, in steady state. Binding sites were distanced 10 nm (B1) or 15 nm (B2) and distributed in 1, 4, or 7 clusters. Simulated molecules were 1 or 10 nm in diameter (s1 and s10, respectively) and bound to the sites with Pbind = 0.9 (values of 20 independent simulations, overlaid with the mean ± SD, one-way ANOVA, ns: not significant; ∗∗∗∗p < 0.0001).

At steady state, the number of clusters did not affect the final number of bound molecules if sites were distanced 15 nm (Figure 2B). There was a significant, although modest, effect of multiple clusters (∼6%–10% increase) on the number or large molecules and high Pbind (0.9) bound in the compact distribution (Figure 2B1). The effect was also observed for low Pbind (0.1) molecules, between 1 and 7 clusters (∼9%, not shown, ANOVA with Tukey's multiple comparisons test, p < 0.05). This means that the presence of nanoclusters per se did not imply a systematic improvement on the trapping capacity of synapses at steady state.

Distribution of Sites in Several Clusters Counteracts the Detrimental Effects of Crowding

One important property of synapses is their capacity to change the number of receptors. Crowding, created by receptors themselves but also by other molecules immobilized in synapses, could be an important factor setting the extent of the change and the time needed for it. This point was evaluated by monitoring the recruitment of molecules in absence or presence of extra fixed obstacles, which remained bound to a site during all the simulation period. Obstacles were small (s1) or large (s10): large ones were used to simulate a situation with high molecular crowding, whereas small ones did not generate crowding.

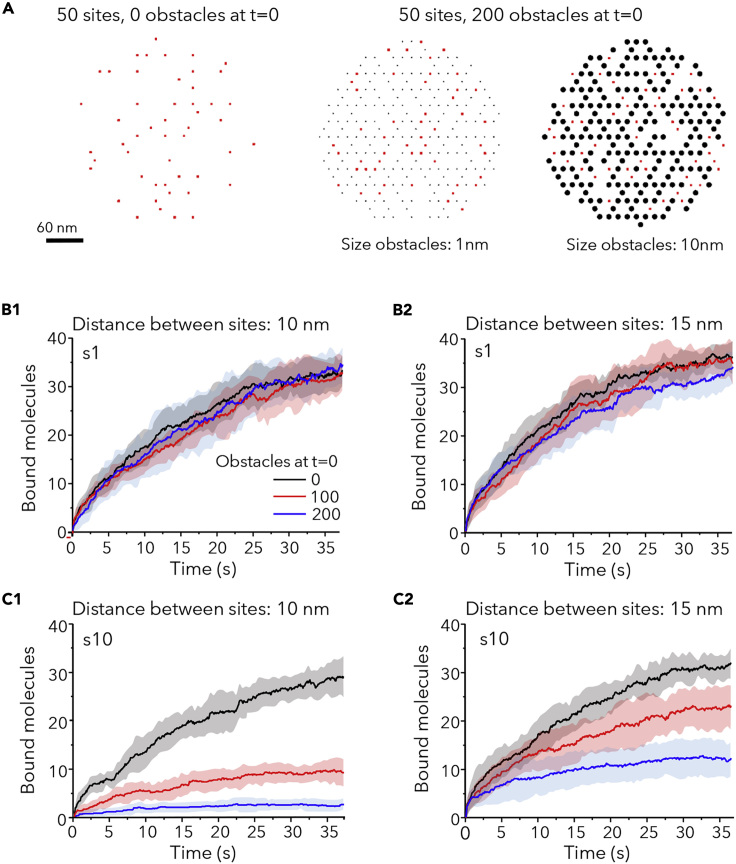
There were two different starting scenarios: an area with 50 free binding sites alone or an area with 50 free sites surrounded by obstacles at t = 0 (Figure 3A). No simulated molecule was bound at t = 0. Figure 3A shows the case of 200 obstacles of 1 nm or 10 nm in diameter. For each scenario, we compared the effect of obstacles on the binding of small or large molecules with different Pbind.

Figure 3.

Figure 3

Open in a new tab

Molecular Crowding Slows Down the Capture of New Molecules

(A) Examples of the distribution of 50 sites (red squares) in the absence of extra immobile obstacles at time point t = 0 (left) or among 200 obstacles (black circles) of size = 1 nm (center) or size = 10 nm (right). Obstacles occupy the position of other sites in the hexagonal grid and remain bound and immobile during all the simulation. Bar: 60 nm.

(B and C) Number of bound molecules in time in synapses (Pbind = 0.9) with initially 50 free sites, in absence of presence of 100 or 200 obstacles at t = 0, for small (B1-2) or large (C1-2) molecules. Distance between sites was 10 nm (B1 and C1) or 15 nm (B2 and C2). Obstacles had the same size than diffusing molecules. Colors as in B1. Mean (lines) ± SD (shaded areas) of 10 independent simulations.

Only the first 37.5s of the simulation are shown (the entire simulations are depicted in Figure S6).

In a first series of simulations, sites were distributed in one cluster. Figures 3B and 3C illustrate early changes (after only 37.5s) for small (Figure 3B) or large (Figure 3C) molecules with Pbind = 0.9. Sites were colonized by small molecules at similar speed independently of obstacles (Figure 3B). Conversely, the trapping of large molecules was strongly affected by the presence of obstacles (Figure 3C), especially for the compact distribution of sites (Figure 3C1). This was also observed at later times (225s of the simulation run, Figure S6).

To further confirm the effect of crowding, we checked the trapping of molecules in presence of obstacles of different size than the diffusing molecule (small molecules with large obstacles and large molecules with small obstacles). All the results are summarized in Tables 1 and 2. Small molecules were less captured in case of crowding created by large obstacles. For large molecules, there was also a significant reduction in case of small obstacles, meaning that the presence of a high number of immobile obstacles could also influence the capacity of synapses to gather new receptors even if they do not create crowding.

Table 1.

Number of Bound Molecules at Early or Late Simulation Times for Small (s1) or Large (s10) Molecules When Scaffolding Sites Were Separated 10 nm (Pbind = 0.9), in Absence or Presence of the Indicated Extra Obstacles at t = 0

Distance 10 nm Early (37.5s) Late (225s)
s1 0 obstacles 32.90 ± 1.08 39.40 ± 0.45
100 obstacles s1 34.00 ± 1.33 (ns) 39.90 ± 0.85 (ns)
200 obstacles s1 34.50 ± 1.45 (ns) 39.17 ± 0.48 (ns)
100 obstacles s10 23.00 ± 1.68 (∗∗∗) 30.60 ± 1.04 (∗∗∗∗)
200 obstacles s10 16.20 ± 0.81 (∗∗∗∗) 24.80 ± 0.97 (∗∗∗∗)
s10 0 obstacles 28.1 ± 1.34 31.3 ± 0.95
100 obstacles s1 22.9 ± 1.48 (∗) 31.2 ± 0.69 (ns)
200 obstacles s1 15.7 ± 1.00 (∗∗∗∗) 24.2 ± 0.94 (∗∗∗∗)
100 obstacles s10 8.8 ± 0.98 (∗∗∗∗) 11.5 ± 0.65 (∗∗∗∗)
200 obstacles s10 2.9 ± 0.43 (∗∗∗∗) 2.2 ± 0.36 (∗∗∗∗)
Open in a new tab

Obstacles had the same size of the molecule or not. Mean ± SD, t test against 0 obstacles condition, ns: not significant, ∗p < 0.05; ∗∗∗p < 0.001; ∗∗∗∗p < 0.0001.

Table 2.

Number of Bound Molecules at Early or Late Simulation Times for Small (s1) or Large (s10) Molecules When Scaffolding Sites Were Separated 15 nm (Pbind = 0.9), in Absence or Presence of the Indicated Extra Obstacles at t = 0

Distance 15 nm Early Changes (37.5s) Late Changes (225s)
s1 0 obstacles 36.80 ± 3.12 36.70 ± 3.06
100 obstacles s1 35.30 ± 3.94 (ns) 36.50 ± 3.74 (ns)
200 obstacles s1 34.40 ± 2.59 (ns) 38.90 ± 2.80 (ns)
100 obstacles s10 30.90 ± 4.50 (∗∗) 36.10 ± 2.68 (ns)
200 obstacles s10 29.00 ± 3.02 (∗∗∗∗) 33.80 ± 3.49 (ns)
s10 0 obstacles 32.70 ± 3.62 37.20 ± 3.19
100 obstacles s1 30.30 ± 3.30 (ns) 34.70 ± 3.62 (ns)
200 obstacles s1 27.50 ± 2.50 (∗∗) 31.50 ± 3.60 (∗∗)
100 obstacles s10 23.70 ± 4.37 (∗∗∗∗) 26.10 ± 10.77 (∗∗)
200 obstacles s10 12.60 ± 3.20 (∗∗∗∗) 20.27 ± 3.13 (∗∗∗∗)
Open in a new tab

Obstacles had the same size of the molecule or not. Mean ± SD, t test against 0 obstacles condition, ns: not significant, ∗∗p < 0.01; ∗∗∗∗p < 0.0001.

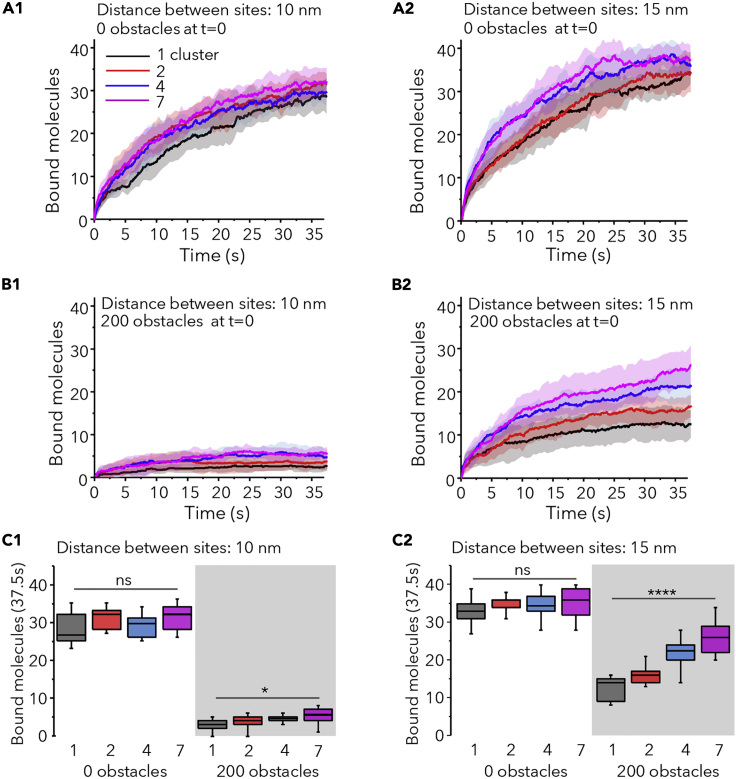
The same scenarios were simulated with sites distributed in several clusters. In absence of extra obstacles, the distribution of sites did not affect the capture of small molecules (not shown) and only apparently improved the speed of recruitment of large molecules (Figure 4A1 and 4A2). This improvement was transient and the number of bound molecules after 37.5s of simulation run was not significantly different between configurations and molecules sizes (Figure 4C, 0 obstacles condition). However, multiple clusters of sites were more performant to capture large molecules in conditions of important crowding (Figures 4B and 4C, 200 obstacles condition). The effect was stronger for the less compact distribution and correlated well with the number of clusters. In the best of cases (7 clusters, distance between sites of 15 nm), the number of bound sites doubled with respect to the one-cluster configuration, but it was still lower than in absence of obstacles (∼28% lower, Figure 4C2).

Figure 4.

Figure 4

Open in a new tab

The Capture of Molecules in Crowded Synapses Is Improved by the Distribution of Sites in Multiple Clusters

(A1-A2 and B1-B2) Number of large molecules bound versus time (Pbind = 0.9) in synapses with initially 50 free sites, with no extra obstacles (A1 and A2) or 200 extra obstacles (B1 and B2) at t = 0. Sites were separated by 10 nm (A1 and B1) or 15 nm (A2 and B2) and distributed in 1, 2, 4, or 7 clusters as indicated. Colors in A1. Mean (line) ± SD (shaded areas), 10 independent simulations.

(C1-C2) Number of bound molecules after 37.5s of simulation run for the simulations described in A1 and B1 (C1) and A2 and B2 (C2) (median and 25%–75% IQR, whiskers: 5%–95% range, one-way ANOVA, ns: not significant; ∗p < 0.05, ∗∗∗∗p < 0.001).

Therefore, crowding had a strong negative impact on the recruitment of new molecules to synapses, but the distribution of sites in several clusters could overcome this drawback at least partially by improving the accessibility of sites.

Crowding Boosts Recapture of Molecules and Increases Stability

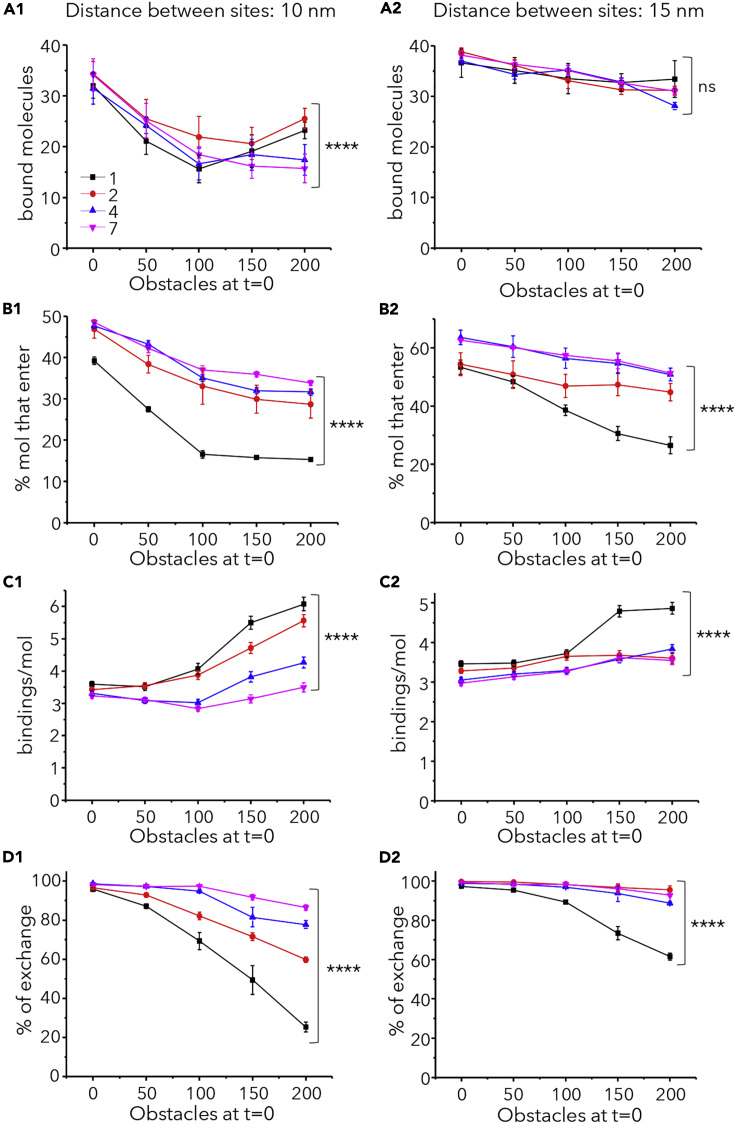
Crowding may affect interactions in a negative and a positive way (reviewed in Minton, 2006; Mugler et al., 2012). Molecular crowding at the post-synaptic domain could impair the capture of new receptors, but at the same time increase the probability of those already captured to bind again after dissociating from the scaffold. To investigate the effect of crowding on the frequency of binding (related to kon), steady state simulations were run in absence or presence of obstacles. As discussed earlier, 50 free sites were available for the capture of diffusing molecules. The number of bound molecules was evaluated together with the fraction of molecules that enter the synaptic area, the number of bindings per molecule, and the percentage of molecules that go in and out the synapse (% of exchange).

Figures 5 and S7 show the results for large molecules with Pbind = 0.9 and Pbind = 0.1, respectively. The number of bound molecules changed in all cases, being reduced by the presence of obstacles (Figures 5A and S7A). The compact distribution of sites was the most affected; but interestingly there was a regain in the number of bound molecules with high crowding (200 obstacles) when sites were distributed in one or two clusters with respect to several clusters (Figures 5A1 and S7A1). This counterintuitive result could be explained by the robust effect of crowding on the number of bindings per molecule (Figures 5C1 and S7C1) and the decrease of the exchange (Figures 5D1 and S7D1).

Figure 5.

Figure 5

Open in a new tab

Molecular Crowding Favors Multiple Bindings and Reduces the Exchange of Molecules

Binding and exchange of large molecules (with Pbind = 0.9) in and out synapses at steady state. Synaptic areas had 50 binding sites and the indicated number of obstacles t = 0. Sites were distanced 10 nm (A1,B1, C1, and D1) or 15 nm (A2, B2, C2, and D2) and distributed in 1 (black), 2 (red), 4 (blue), or 7 (magenta) clusters as indicated in A1. (Mean ± SEM, 10 independent simulations, statistical comparisons in case of 200 obstacles: one-way ANOVA, ns: not significant, ∗∗∗∗p < 0.0001).

(A1-A2) Number of bound molecules at the end of the simulation period (225s).

(B1-B2) Percentage of simulated molecules (total 200) that enter at least once in the synaptic area.

(C1-C2) Number of bindings (to the same or a different site) per molecule during the whole simulation run. (D1-D2) Percentage of exchange (proportion of molecules that enter and exit the synaptic area at least once).

The number of molecules that enter the synaptic area was also reduced by crowding but the distribution of sites in several clusters partially reverted this effect, as expected (Figures 5B and S7B). Importantly, molecules bound more often to scaffolding sites when higher number of obstacles were present, with a stronger effect on the one-cluster configuration (Figures 5C and S7C). Consequently, the exchange of molecules between synaptic and extrasynaptic areas was reduced by obstacles and by the one-cluster configuration (Figures 5D and S7D). Interestingly, compact synapses with two clusters in the more compact configuration were able to keep a high number of bound molecules (Figure 5A1) and at the same time display a higher exchange than synapses with one cluster (Figure 5D1).

Obstacles did not affect the number of bound small molecules; however, the distribution of sites in multiple clusters facilitated the entry of molecules and slightly decreased the number of bindings per molecule (Figure S8).

Synaptic Plasticity-like Changes Were Accelerated by Multiple Clusters of Binding Sites

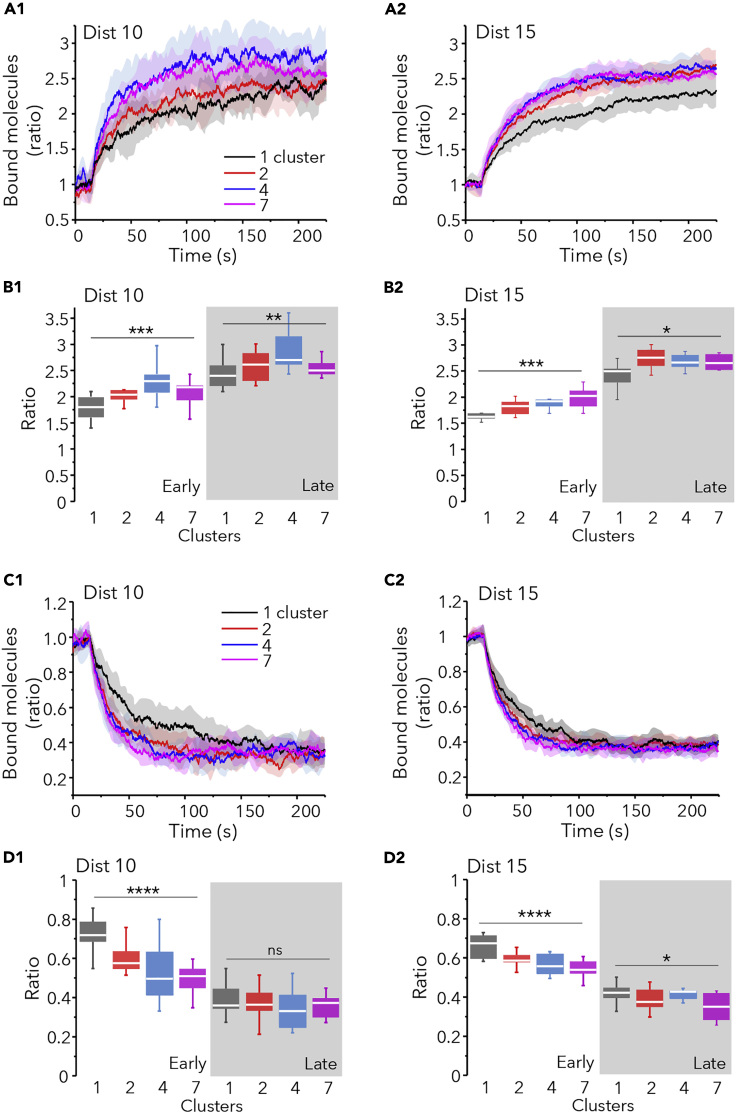
Although one unique cluster of binding sites would support stability, multiple clusters could be a good strategy for crowded synapses to favor plasticity. We investigate this possibility running simulations of large molecules whose Pbind was increased or decreased, to simulate long-term potentiation (LTP) or long-term depression (LTD), respectively. Scaffolding sites (250 in total) were distributed in one or more clusters with a distance between sites of 10 and 15 nm as discussed previously. We added extra 100 obstacles that remained fixed to the scaffold during the whole simulation.

After the increase of Pbind (from 0.1 to 0.9), the number of bound receptors increased progressively in all cases (Figures 6A and 6B). The ratio of bound molecules with respect to the initial state augmented more rapidly when sites were distributed in several clusters (Figure 6A). Differences were significant at early (37.5s) or late (225s) times of simulation, although they were more important at early times (Figure 6B). In case of LTD-like changes, multiple clusters accelerated the loss of bound molecules (Figure 6C). At the end of the simulation (225s) the amount of bound molecules was the same for the more compact distributions (10 nm between sites, Figure 6D1) or it was somewhat reduced in the less compact synapses (15 nm between sites, Figure 6D2). Hence, the presence of multiple clusters of binding sites favored the exchange of molecules accelerating the gain or the loss of synaptic molecules.

Figure 6.

Figure 6

Open in a new tab

Molecular Crowding Accelerate Synaptic Plasticity-like Change

Simulation of LTP-like (A and B) or LTD-like (C and D) changes in receptor trapping in synapses with 250 sites and 100 extra obstacles at t = 0, distributed in 1, 2, 4, or 7 clusters as indicated (colors in A1 and C1). Sites were distanced 10 (Dist 10) or 15 (Dist 15) nm. Pbind was changed at time = 15s (10 independent simulations in each case).

(A and C) Ratio of bound molecules (with respect to those bound at time = 15 s) versus time for LTP (A) or LTD (C) simulations. Mean (lines) ± SD (shaded areas).

(B and D) Ratio of bound molecules (with respect to those bound at time = 15 s) at 37.5s (early) or at 225s (late, shaded area) of simulation run for the simulations shown in A1 (B1), A2 (B2) and C1 (D1) and C2 (D2), respectively (median and 25%–75% IQR, whiskers: 5%–95% range, one-way ANOVA, ns: not significant, ∗p < 0.05, ∗∗p < 0.01, ∗∗∗p < 0.001, ∗∗∗∗p < 0.0001).

Discussion

The synaptic membrane is a crowded environment, yet the efficiency of receptor capture at the postsynaptic membrane is one key element in determining synaptic strength and synaptic plasticity. The demonstration of the mobility of receptors in and out synapses prompted the use of models to understand how synapses can be stable and plastic at the same time. ODE models or abstract representations demonstrated that synaptic strength can be maintained despite the dynamics of the receptors (Holcman and Triller, 2006; Earnshaw and Bressloff, 2006, 2008; Bressloff and Earnshaw, 2009). Czöndör et al. (2012) used numerical trajectories to demonstrate the impact of the location of endo- and exocytotic sites on the trapping of receptors. As geometry and spatial parameters are important when dealing with the diffusion in the postsynaptic membrane (Renner et al., 2009b), other studies made use of particle-based stochastic simulations to address the role of lateral diffusion and crowding (Tolle and Le Novére, 2010; Santamaria et al., 2010). We opted for this kind of approach, reproducing the expected distribution of some scaffolding molecules, to analyze the importance of molecular crowding on the interaction between receptors and scaffold.

Experimental data and models provided hints about the complex role of crowding in synapses. The comparison of the diffusion of lipids and receptors suggest that crowding makes the synaptic membrane to act as a size-exclusion column, excluding molecules from crowded areas and thus increasing their overall diffusivity (Renner et al., 2009b). As crowding is generated in part by receptors themselves, Gupta (2018) showed that diffusion was differentially affected by receptor trapping: overall diffusion was reduced at low and moderate receptor densities but enhanced for high receptor density. On the other hand, crowding can enhance the retention of receptors in synapses depending on its level (Santamaria et al., 2010).

Here we show that crowding may have a bimodal effect on receptor/scaffold interactions. The relative importance of positive or negative effects depended upon the level of crowding, which was created in part by the capture of receptors themselves. Consequently, the net effect of crowding was determined by the compaction and distribution of scaffolding sites. It is interesting to note that the compaction of sites could be modulated for example by the polymerization state of actin cytoskeleton (Renner et al., 2009a and references therein), and therefore it could be regulated by neuronal activity.

Another interesting feature of synapses is that scaffolding sites are always more abundant than receptors (reviewed in Choquet and Triller, 2013; Specht, 2020). The whole structure of the post-synaptic density is proposed to be the result of a network of weak interactions that is able to maintain a steady state, thanks to a high number of free binding sites (reviewed in Specht, 2020). Indeed, some of the scaffolding sites for receptors seem not to be easily available. Many receptors have the same residency time in synapses than molecules that are not stabilized by the scaffold (Renner et al., 2012), which suggest that receptors moved into the synaptic area but they could not establish a scaffolding interaction before diffusing away. This observation highlights the importance of mechanisms that help retaining receptors in the synaptic area by, for example, enhancing reactions. Importantly, theory indicates that molecular crowding may have two opposite effects on the kinetics of interactions: more crowding implies less diffusivity and reaction opportunities, and at the same time, more probability of re-collision and re-binding (reviewed in Minton, 2006; Mugler et al., 2012). The results of our simulations suggest that this is the case of synapses. The frequency of bindings varied upon the local level of crowding and were increased by compact and crowded configurations. Benichou et al. (2010) described analytically this kind of spatial effect on first passage times in case of compact (crowded medium) or not compact exploration. They demonstrated that when a diffusing molecule explores sparsely its environment, the search time of the target is independent of the starting point. However, when the exploration is dense, for example due to crowding, the position of the starting point is not trivial. The results shown here are compatible with this concept of geometry-controlled kinetics and supports its applicability to synapses.

Importantly, our model incorporates recent experimental data about the internal distribution of binding sites in the synapse. Super-resolution microscopy has revealed the nanoscale organization of neurotransmitter receptors, scaffolds, and signaling molecules (Broadhead et al., 2016; MacGillavry et al., 2013; Nair et al., 2013; Hruska et al., 2018). Interestingly, multiple nanoclusters are not systematically observed, implying that it is a feature of a sub-population of synapses (Lee et al., 2017). As the postsynaptic scaffold can display internal rearrangements in living neurons (Kerr and Blanpied, 2012), synaptic nanoclusters seem to be dynamic and depend upon neuronal activity (MacGillavry et al., 2013; Nair et al., 2013; Pennacchietti et al., 2017). Therefore, we may expect that synapses can switch within two states, containing or not nanoclusters of receptors and scaffold. Our results revealed that the distribution of scaffolding sites in more than one cluster could be permissive for synaptic plasticity. The exchange of molecules in crowded synapses was already enhanced in the case of two clusters and increased further with the number of clusters. Thus, the number of nanodomains of receptors could be a proxy of the readiness of synapses to undergo plasticity. This hypothesis is supported by two recent experimental reports. The work of Pennacchietti et al. (2017) showed that inhibitory synapses that responded to the induction of LTP by incorporating more scaffold molecules were those carrying several spots of Gephyrin. Hruska et al. (2018) found multiple nanodomains in excitatory synapses whose number and dynamics positively correlated with the induction of LTP.

Crowding and distribution of binding sites probably play a non-negligible role in other dynamic membrane domains, such as the immunological synapse (Treanor and Batista, 2007), focal adhesions (Rossier et al., 2012), and the initial segment of the axon (Leterrier, 2018). In addition to this, many membrane molecules were shown to create transient nanoclusters (i.e. channels, ion transporters and adhesion proteins; Shrivastava et al., 2013; Chamma et al., 2013, 2016; Heck et al., 2019; reviewed in Garcia-Parajo et al., 2014). It would be interesting to know whether crowding affects the stability of these clusters as well, offering an energetically low-cost and convenient way to control the function of these other signaling platforms.

Limitations of the Study

The main strength of simulations, namely to simplify a complex system to help its understanding, is also its main weakness. Here, synapses were simulated considering only diffusing molecules of uniform size and immobile scaffolds. Molecules were considered as perfect spheres; other steric effects may exist if the irregular shape of molecules is considered. The number of simulated molecules was fixed, so endo- and exocytosis phenomena were not taken into account. Many factors could be introduced to simulate a system closer to real synapses, and this will be the subject of future studies.

Resource Availability

Lead Contact

Further information and requests for resources should be directed to and will be fulfilled by the Lead Contact, Marianne Renner (marianne.renner@sorbonne-universite.fr).

Materials Availability

This study did not generate new unique reagents.

Data and Code Availability

The code generated during this study is available at GitHub repository: https://github.com/mlrennerfr/DiffuTrapClusters.git.

Methods

All methods can be found in the accompanying Transparent Methods supplemental file.

Acknowledgments

Research costs were supported by the Program IDEX Emergence Sorbonne Universités 2016, France, grant no. SU-16-R-EMR-52. Authors declare no conflict of interests.

Author Contributions

Conceptualization, M.R.; Methodology, M.R.; Software, M.R.; Investigation, M.L.K., A.F., M.R.; Formal analysis, M.L.K., A.F., M.R.; Visualization, M.L.K., A.F., M.R.; Writing, M.R.; Funding Acquisition, M.R.; Supervision, M.R.

Declaration of Interests

The authors declare no competing interests.

Published: August 21, 2020

Footnotes

Supplemental Information can be found online at https://doi.org/10.1016/j.isci.2020.101382.

Supplemental Information

Document S1. Transparent Methods and Figures S1–S8
mmc1.pdf (1.5MB, pdf)

References

  1. Battaglia S., Renner M., Russeau M., Come E., Tyagarajan S.K., Levi S. Activity-dependent inhibitory synapse scaling is determined by gephyrin phosphorylation and subsequent regulation of GABAA receptor diffusion. eNeuro. 2018;5:1–20. doi: 10.1523/ENEURO.0203-17.2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Bedet C., Bruusgaard J.C., Vergo S., Groth-Pedersen L., Eimer S., Triller A., Vannier C. Regulation of gephyrin assembly and glycine receptor synaptic stability. J. Biol. Chem. 2006;281:30046–30056. doi: 10.1074/jbc.M602155200. [DOI] [PubMed] [Google Scholar]
  3. Benichou O., Chevalier C., Klafter J., Meyer B., Voituriez R. Geometry-controlled kinetics. Nat. Chem. 2010;2:472–477. doi: 10.1038/nchem.622. [DOI] [PubMed] [Google Scholar]
  4. Bressloff P.C., Earnshaw B.A. A dynamic corral model of receptor trafficking at a synapse. Biophys. J. 2009;96:1786–1802. doi: 10.1016/j.bpj.2008.12.3889. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Broadhead M.J., Horrocks M.H., Zhu F., Muresan L., Benavides-Piccione R., DeFelipe J., Fricker D., Kopanitsa M.V., Duncan R.R., Klenerman D. PSD95 nanoclusters are postsynaptic building blocks in hippocampus circuits. Sci. Rep. 2016;6:24626. doi: 10.1038/srep24626. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Burrage K., Hancock J., Leier A., Nicolau D.V., Jr. Modelling and simulation techniques for membrane biology. Brief Bioinform. 2007;8:234–244. doi: 10.1093/bib/bbm033. [DOI] [PubMed] [Google Scholar]
  7. Chamma I., Heubl M., Chevy Q., Renner M., Moutkine I., Eugene E., Poncer J.C., Levi S. Activity-dependent regulation of the K/Cl transporter KCC2 membrane diffusion, clustering, and function in hippocampal neurons. J. Neurosci. 2013;33:15488–15503. doi: 10.1523/JNEUROSCI.5889-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Chamma I., Levet F., Sibarita J.B., Sainlos M., Thoumine O. Nanoscale organization of synaptic adhesion proteins revealed by single-molecule localization microscopy. Neurophotonics. 2016;3:041810. doi: 10.1117/1.NPh.3.4.041810. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Choquet D., Triller A. The dynamic synapse. Neuron. 2013;80:691–703. doi: 10.1016/j.neuron.2013.10.013. [DOI] [PubMed] [Google Scholar]
  10. Czöndör K., Mondin M., Garcia M., Heine M., Frischknecht R., Choquet D., Sibarita J.B., Thoumine O.R. Unified quantitative model of AMPA receptor trafficking at synapses. Proc. Natl. Acad. Sci. U S A. 2012;109:3522–3527. doi: 10.1073/pnas.1109818109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Diering G.H., Huganir R.L. The AMPA receptor code of synaptic plasticity. Neuron. 2018;100:314–329. doi: 10.1016/j.neuron.2018.10.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Dzyubenko E., Rozenberg A., Hermann D.M., Faissner A. Colocalization of synapse marker proteins evaluated by STED-microscopy reveals patterns of neuronal synapse distribution in vitro. J. Neurosci. Methods. 2016;1:149–159. doi: 10.1016/j.jneumeth.2016.09.001. [DOI] [PubMed] [Google Scholar]
  13. Earnshaw B.A., Bressloff P.C. Modeling the role of lateral membrane diffusion in AMPA receptor trafficking along a spiny dendrite. J. Comput. Neurosci. 2008;25:366–389. doi: 10.1007/s10827-008-0084-8. [DOI] [PubMed] [Google Scholar]
  14. Earnshaw B.A., Bressloff P.C. Biophysical model of AMPA receptor trafficking and its regulation during long-term potentiation/long-term depression. J. Neurosci. 2006;26:12362–12373. doi: 10.1523/JNEUROSCI.3601-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Flores C.E., Nikonenko I., Mendez P., Fritschy J.M., Tyagarajan S.K., Muller D. Activity-dependent inhibitory synapse remodeling through gephyrin phosphorylation. Proc. Natl. Acad. Sci. U S A. 2015;112:E65–E72. doi: 10.1073/pnas.1411170112. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Garcia-Parajo M.F., Cambi A., Torreno-Pina J.A., Thompson N., Jacobson K. Nanoclustering as a dominant feature of plasma membrane organization. J. Cell Sci. 2014;127:4995–5005. doi: 10.1242/jcs.146340. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Gillespie D.T., Hellander A., Petzold L.R. Perspective: stochastic algorithms for chemical kinetics. J. Chem. Phys. 2013;138:170901. doi: 10.1063/1.4801941. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Goldman J., Andrews S., Bray D. Size and composition of membrane protein clusters predicted by Monte Carlo analysis. Eur. Biophys. J. 2004;33:506–512. doi: 10.1007/s00249-004-0391-6. [DOI] [PubMed] [Google Scholar]
  19. Greger I.H., Watson J.F., Cull-Candy S.G. Structural and functional architecture of AMPA-type glutamate receptors and their auxiliary proteins. Neuron. 2017;94:713–730. doi: 10.1016/j.neuron.2017.04.009. [DOI] [PubMed] [Google Scholar]
  20. Gupta R. Self-crowding of AMPA receptors in the excitatory postsynaptic density can effectuate anomalous receptor sub-diffusion. PLoS Comput. Biol. 2018;14:e1005984. doi: 10.1371/journal.pcbi.1005984. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Hausrat T.J., Muhia M., Gerrow K., Thomas P., Hirdes W., Tsukita S., Heisler F.F., Herich L., Dubroqua S., Breiden P. Radixin regulates synaptic GABAA receptor density and is essential for reversal learning and short-term memory. Nat. Commun. 2015;6:6872. doi: 10.1038/ncomms7872. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Heck J., Parutto P., Ciuraszkiewicz A., Bikbaev A., Freund R., Mitlohner J., Andres-Alonso M., Fejtova A., Holcman D., Heine M. Transient confinement of CaV2.1 Ca(2+)-channel splice variants shapes synaptic short-term plasticity. Neuron. 2019;103:66–79 e12. doi: 10.1016/j.neuron.2019.04.030. [DOI] [PubMed] [Google Scholar]
  23. Hellmann M., Klafter J., Heermann D.W., Weiss M. Challenges in determining anomalous diffusion in crowded fluids. J. Phys. Condens Matter. 2011;23:234113. doi: 10.1088/0953-8984/23/23/234113. [DOI] [PubMed] [Google Scholar]
  24. Holcman D., Triller A. Modeling synaptic dynamics driven by receptor lateral diffusion. Biophys. J. 2006;91:2405–2415. doi: 10.1529/biophysj.106.081935. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Hruska M., Henderson N., Le Marchand S.J., Jafri H., Dalva M.B. Synaptic nanomodules underlie the organization and plasticity of spine synapses. Nat. Neurosci. 2018;21:671–682. doi: 10.1038/s41593-018-0138-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Huganir R.L., Nicoll R.A. AMPARs and synaptic plasticity: the last 25 years. Neuron. 2013;80:704–717. doi: 10.1016/j.neuron.2013.10.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Kalay Z., Fujiwara T.K., Kusumi A. Confining domains lead to reaction bursts: reaction kinetics in the plasma membrane. PLoS One. 2012;7:e32948. doi: 10.1371/journal.pone.0032948. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Kellermayer B., Ferreira J.S., Dupuis J., Levet F., Grillo-Bosch D., Bard L., Linares-Loyez J., Bouchet D., Choquet D., Rusakov D.A. Differential nanoscale topography and functional role of GluN2-NMDA receptor subtypes at glutamatergic synapses. Neuron. 2018;100:106–119 e7. doi: 10.1016/j.neuron.2018.09.012. [DOI] [PubMed] [Google Scholar]
  29. Kerr J.M., Blanpied T.A. Subsynaptic AMPA receptor distribution is acutely regulated by actin-driven reorganization of the postsynaptic density. J. Neurosci. 2012;32:658–673. doi: 10.1523/JNEUROSCI.2927-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Krapf D. Compartmentalization of the plasma membrane. Curr. Opin. Cell Biol. 2018;53:15–21. doi: 10.1016/j.ceb.2018.04.002. [DOI] [PubMed] [Google Scholar]
  31. Lee S.H., Jin C., Cai E., Ge P., Ishitsuka Y., Teng K.W., de Thomaz A.A., Nall D., Baday M., Jeyifous O. Super-resolution imaging of synaptic and Extra-synaptic AMPA receptors with different-sized fluorescent probes. Elife. 2017;6:e27744. doi: 10.7554/eLife.27744. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Leterrier C. The axon initial segment: an updated viewpoint. J. Neurosci. 2018;38:2135–2145. doi: 10.1523/JNEUROSCI.1922-17.2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Li T.P., Song Y., MacGillavry H.D., Blanpied T.A., Raghavachari S. Protein crowding within the postsynaptic density can impede the escape of membrane proteins. J. Neurosci. 2016;36:4276–4295. doi: 10.1523/JNEUROSCI.3154-15.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. MacGillavry H.D., Song Y., Raghavachari S., Blanpied T.A. Nanoscale scaffolding domains within the postsynaptic density concentrate synaptic AMPA receptors. Neuron. 2013;78:615–622. doi: 10.1016/j.neuron.2013.03.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Mahmutovic A., Fange D., Berg O.G., Elf J. Lost in presumption: stochastic reactions in spatial models. Nat. Methods. 2012;9:1163–1166. doi: 10.1038/nmeth.2253. [DOI] [PubMed] [Google Scholar]
  36. Maynard S.A., Triller A. Inhibitory receptor diffusion dynamics. Front. Mol. Neurosci. 2019;12:313. doi: 10.3389/fnmol.2019.00313. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Melo E., Martins J. Kinetics of bimolecular reactions in model bilayers and biological membranes. A critical review. Biophys. Chem. 2006;123:77–94. doi: 10.1016/j.bpc.2006.05.003. [DOI] [PubMed] [Google Scholar]
  38. Miller P.S., Aricescu A.R. Crystal structure of a human GABAA receptor. Nature. 2014;512:270–275. doi: 10.1038/nature13293. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Minton A.P. How can biochemical reactions within cells differ from those in test tubes? J. Cell Sci. 2006;119:2863–2869. doi: 10.1242/jcs.03063. [DOI] [PubMed] [Google Scholar]
  40. Mugler A., Bailey A.G., Takahashi K., ten Wolde P.R. Membrane clustering and the role of rebinding in biochemical signaling. Biophys. J. 2012;102:1069–1078. doi: 10.1016/j.bpj.2012.02.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Nair D., Hosy E., Petersen J.D., Constals A., Giannone G., Choquet D., Sibarita J.B. Super-resolution imaging reveals that AMPA receptors inside synapses are dynamically organized in nanodomains regulated by PSD95. J. Neurosci. 2013;33:13204–13224. doi: 10.1523/JNEUROSCI.2381-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Nicolson G.L. The Fluid-Mosaic Model of Membrane Structure: still relevant to understanding the structure, function and dynamics of biological membranes after more than 40 years. Biochim. Biophys. Acta. 2014;1838:1451–1466. doi: 10.1016/j.bbamem.2013.10.019. [DOI] [PubMed] [Google Scholar]
  43. Opazo P., Labrecque S., Tigaret C.M., Frouin A., Wiseman P.W., De Koninck P., Choquet D. CaMKII triggers the diffusional trapping of surface AMPARs through phosphorylation of stargazin. Neuron. 2010;67:239–252. doi: 10.1016/j.neuron.2010.06.007. [DOI] [PubMed] [Google Scholar]
  44. Orlando M., Ravasenga T., Petrini E.M., Falqui A., Marotta R., Barberis A. Correlating Fluorescence and High-Resolution Scanning Electron Microscopy (HRSEM) for the study of GABA(A) receptor clustering induced by inhibitory synaptic plasticity. Sci. Rep. 2017;7:13768. doi: 10.1038/s41598-017-14210-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Park M. AMPA receptor trafficking for postsynaptic potentiation. Front. Cell Neurosci. 2018;12:361. doi: 10.3389/fncel.2018.00361. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Patrizio A., Renner M., Pizzarelli R., Triller A., Specht C.G. Alpha subunit-dependent glycine receptor clustering and regulation of synaptic receptor numbers. Sci. Rep. 2017;7:10899. doi: 10.1038/s41598-017-11264-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Pennacchietti F., Vascon S., Nieus T., Rosillo C., Das S., Tyagarajan S.K., Diaspro A., Del Bue A., Petrini E.M., Barberis A., Cella Zanacchi F. Nanoscale molecular reorganization of the inhibitory postsynaptic density is a determinant of GABAergic synaptic potentiation. J. Neurosci. 2017;37:1747–1756. doi: 10.1523/JNEUROSCI.0514-16.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Petrini E.M., Ravasenga T., Hausrat T.J., Iurilli G., Olcese U., Racine V., Sibarita J.B., Jacob T.C., Moss S.J., Benfenati F. Synaptic recruitment of gephyrin regulates surface GABAA receptor dynamics for the expression of inhibitory LTP. Nat. Commun. 2014;5:3921. doi: 10.1038/ncomms4921. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Recouvreux P., Lenne P.F. Molecular clustering in the cell: from weak interactions to optimized functional architectures. Curr. Opin. Cell Biol. 2016;38:18–23. doi: 10.1016/j.ceb.2016.01.002. [DOI] [PubMed] [Google Scholar]
  50. Renner M., Choquet D., Triller A. Control of the postsynaptic membrane viscosity. J. Neurosci. 2009;29:2926–2937. doi: 10.1523/JNEUROSCI.4445-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Renner M.L., Cognet L., Lounis B., Triller A., Choquet D. The excitatory postsynaptic density is a size exclusion diffusion environment. Neuropharmacology. 2009;56:30–36. doi: 10.1016/j.neuropharm.2008.07.022. [DOI] [PubMed] [Google Scholar]
  52. Renner M., Schweizer C., Bannai H., Triller A., Levi S. Diffusion barriers constrain receptors at synapses. PLoS One. 2012;7:e43032. doi: 10.1371/journal.pone.0043032. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Renner M., Wang L., Levi S., Hennekinne L., Triller A. A simple and powerful analysis of lateral subdiffusion using single particle tracking. Biophys. J. 2017;113:2452–2463. doi: 10.1016/j.bpj.2017.09.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Rossier O., Octeau V., Sibarita J.B., Leduc C., Tessier B., Nair D., Gatterdam V., Destaing O., Albiges-Rizo C., Tampe R. Integrins beta1 and beta3 exhibit distinct dynamic nanoscale organizations inside focal adhesions. Nat. Cell Biol. 2012;14:1057–1067. doi: 10.1038/ncb2588. [DOI] [PubMed] [Google Scholar]
  55. Santamaria F., Gonzalez J., Augustine G.J., Raghavachari S. Quantifying the effects of elastic collisions and non-covalent binding on glutamate receptor trafficking in the post-synaptic density. PLoS Comput. Biol. 2010;6:e1000780. doi: 10.1371/journal.pcbi.1000780. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Schauder D.M., Kuybeda O., Zhang J., Klymko K., Bartesaghi A., Borgnia M.J., Mayer M.L., Subramaniam S. Glutamate receptor desensitization is mediated by changes in quaternary structure of the ligand binding domain. Proc. Natl. Acad. Sci. U S A. 2013;110:5921–5926. doi: 10.1073/pnas.1217549110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Sheng M., Kim E. The postsynaptic organization of synapses. Cold Spring Harb. Perspect. Biol. 2011;3:a005678. doi: 10.1101/cshperspect.a005678. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Shrivastava A.N., Rodriguez P.C., Triller A., Renner M. Dynamic micro-organization of P2X7 receptors revealed by PALM based single particle tracking. Front. Cell Neurosci. 2013;7:232. doi: 10.3389/fncel.2013.00232. [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Soula H., Care B., Beslon G., Berry H. Reply to the comment by V. P. Shkilev on "anomalous versus slowed-down Brownian diffusion in the ligand-binding equilibrium. Biophys. J. 2014;106:2544–2546. doi: 10.1016/j.bpj.2014.03.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Specht C.G., Grunewald N., Pascual O., Rostgaard N., Schwarz G., Triller A. Regulation of glycine receptor diffusion properties and gephyrin interactions by protein kinase C. EMBO J. 2011;30:3842–3853. doi: 10.1038/emboj.2011.276. [DOI] [PMC free article] [PubMed] [Google Scholar]
  61. Specht C.G., Izeddin I., Rodriguez P.C., El Beheiry M., Rostaing P., Darzacq X., Dahan M., Triller A. Quantitative nanoscopy of inhibitory synapses: counting gephyrin molecules and receptor binding sites. Neuron. 2013;79:308–321. doi: 10.1016/j.neuron.2013.05.013. [DOI] [PubMed] [Google Scholar]
  62. Specht C.G. Fractional occupancy of synaptic binding sites and the molecular plasticity of inhibitory synapses. Neuropharmacology. 2020;169:107493. doi: 10.1016/j.neuropharm.2019.01.008. [DOI] [PubMed] [Google Scholar]
  63. Tolle D.P., Le Novére N. Brownian diffusion of AMPA receptors is sufficient to explain fast onset of LTP. BMC Syst. Biol. 2010;4:25. doi: 10.1186/1752-0509-4-25. [DOI] [PMC free article] [PubMed] [Google Scholar]
  64. Treanor B., Batista F.D. Mechanistic insight into lymphocyte activation through quantitative imaging and theoretical modelling. Curr. Opin. Immunol. 2007;19:476–483. doi: 10.1016/j.coi.2007.05.009. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Video S1: Sequence (in Accelerated Motion) Corresponding to 37 s of a Simulation Run at Steady State

Only one every 75 time points are shown. Blue circles are diffusing molecules (size: 10 nm) that can bind to scaffolding sites (in black). Related to Figure 1

Download video file (2.1MB, flv)
Document S1. Transparent Methods and Figures S1–S8
mmc1.pdf (1.5MB, pdf)

Data Availability Statement

The code generated during this study is available at GitHub repository: https://github.com/mlrennerfr/DiffuTrapClusters.git.

Articles from iScience are provided here courtesy of Elsevier

RESOURCES