Elongation Index as a Sensitive Measure of Cell Deformation in High-Throughput Microfluidic Systems

Abstract

One of the promising approaches for high-throughput screening of cell mechanotype is microfluidic deformability cytometry (mDC), in which the apparent deformation index (DI) of the cells stretched by extensional flow at the stagnation point of a cross-slot microchannel is measured. The DI is subject to substantial measurement errors due to cell offset from the flow centerline and velocity fluctuations in inlet channels, leading to artificial widening of DI versus cell size plots. Here, we simulated an mDC experiment using a custom computational algorithm for viscoelastic cell migration. Cell motion and deformation in a cross-slot channel was modeled for fixed or randomized values of cellular mechanical properties (diameter, shear elasticity, cortical tension) and initial cell placement, with or without sinusoidal fluctuations between the inlet velocities. Our numerical simulation indicates that mDC loses sensitivity to changes in shear elasticity when the offset distance exceeds 5 μm, and just 1% velocity fluctuation causes an 11.7% drop in the DI. The obtained relationships between the cell diameter, shear elasticity, and offset distance were used to establish a new measure of cell deformation, referred to as the “elongation index” (EI). In the randomized study, the EI scatter plots were visibly separated for the low- and high-elasticity populations of cells, with a mean of 300 and 3500 Pa, whereas the standard DI output was unable to distinguish between these two groups of cells. The successful suppression of the offset artifacts with a narrower data distribution was shown for the EI output of MCF-7 cells.

Significance

This study establishes a new measure of high-throughput microfluidic deformability cytometry, referred to as the “elongation index,” that is not subject to cell offset artifacts and can sensibly and reliably detect disease-induced changes in mechanical properties of living cells.

Introduction

Malignancy and hereditary blood disorders, such as sickle cell disease, cause reorganization of the intracellular structure that alters the ability of the cell to deform under applied stress (1, 2, 3, 4, 5). Various techniques have been developed to measure deformability of living cells that can be classified into 1) single-cell methods such as micropipette aspiration and atomic force microscopy (6, 7, 8, 9, 10, 11, 12, 13) and 2) microfluidics-based deformability cytometry (14, 15, 16, 17, 18, 19). Microfluidic methods provide several advantages for disease diagnosis over traditional single-cell techniques: 1) high-throughput and easy operation, 2) physiological flow conditions, 3) reduced risk of cell activation, and 4) ability to detect the stage of the cell cycle during deformability measurement. There is a large variation in mechanical properties of living cells measured by single-cell methods, even for healthy cells of the same phenotype, that can be attributed to cell activation and measurement at different stages of the cell cycle.

In microfluidic deformability cytometry (mDC), the cells are stretched by extensional flow at the stagnation point (SP) of a cross-slot microchannel at a rate up to 2000 cells/s. This method specifically produces the cell deformation index (DI) versus cell size scatter plots, with DI defined as the cell’s aspect ratio in a top-view plane. The cells with different mechanical properties (“mechanotype”) are distinguished by comparing the “eyes” of these plots (most populated values of DI and size). mDC has been successfully used to identify nonactivated and activated leukocytes, inflammation and malignancy in blood and pleural fluids, and stem cell pluripotency (14, 15, 16, 17). It operates under inertial flow conditions (Reynolds number (Re) > 10), provided the extensional stress does not rupture the cells.

mDC remains a purely empirical technique that does not go beyond cell size and DI measurement. DI is expected to be a function of cell size, cortical tension, and bulk viscoelasticity of the cell, but it also depends on the lateral position of the cell just before it enters the extensional flow region. The drift of the cells to a lateral position between the centerline and the channel wall always occurs in mDC experiments, leading to measurement errors and, in particularly, to artificially wide distribution of the DI and cell size. Asymmetric cell stretching due to pressure fluctuations, which are caused by flow splitting, also contributes to these errors. None of the modeling studies addressed these issues. Simple analytical expressions that relate the DI with channel geometry and the cell’s viscoelastic properties based on Maxwell and Kelvin-Voigt models exist only for the cell moving along the flow centerline under low velocity, Stokes flow conditions (20, 21, 22, 23). Commercial software packages (e.g., COMSOL Multiphysics) that can only simulate flow, but not cell deformation, in a cross-slot channel have been employed to optimize the channel geometry for mDC (23, 24, 25, 26, 27). This approach worked well for Re ≤ 10 but failed for higher Re. Data analysis based on predictive mDC models that account for DI changes due to cell offset from the centerline and flow disturbances is necessary to further improve mDC accuracy and sensitivity.

In this study, we have used our custom computational algorithm for migration and deformation of a viscoelastic cell to simulate an mDC experiment. The DI of the cell was evaluated for different cell size, shear elasticity, cortical tension, offsets from the flow centerline in the inlet channels, and pressure fluctuations between two inlet channels. Based on this analysis, the approximate relationships between DI and cell offsets were proposed. Using these relationships in the numerical simulation in which the diameter, shear elasticity, and offsets of the cell were randomized, we demonstrated that mDC sensitivity to cell mechanotype can be substantially improved. Specifically, applying this regression analysis to the DI numerical data led to a much narrower distribution of DI and size for MCF-7 cells than the experimental density plots.

Methods

Numerical algorithm

In this work, we have used a custom fully three-dimensional numerical algorithm for living cell migration and deformation, referred to as viscoelastic cell adhesion model (VECAM) (28,29). In VECAM, the cell and its external environment are a multiphase continuum with moving interfaces (e.g., the cell’s cortical layer) tracked by the volume-of-fluid (VOF) method. The velocity field inside and outside the cell is determined from the solution of the continuity and Navier-Stokes equations in a marker-and-cell (MAC) grid with the values of physical parameters for each phase averaged over a grid element. In the VOF method, zero-thickness interfaces between different fluid phases cannot be defined. They are being replaced with transition regions in which the concentration function c = c(t, x) changes between 0 and 1. Here, x = (x, y, z) is the position vector in the Cartesian coordinate system. For that reason, all surface forces in our model are being converted to body forces by using the continuous surface force algorithm (29, 30, 31). In particular, the body force due to cortical tension σ is approximated as

$$\mathit{f}=\sigma \kappa \Vert \nabla c\Vert \mathit{n},$$ (1)

where n = ∇c/||∇c|| is the outward unit normal to the cell surface and κ = −∇ ⋅ n is the local mean curvature of the cell surface. Because the cell’s mass density is nearly the same as the extracellular fluid density, gravity was neglected in the simulation.

The viscoelasticity of the cell cytoplasm is described by the Oldroyd-B model as follows:

$$\begin{array}{c}\mathit{\Pi }=-\nabla p+\nabla \cdot \left[{\mu }_c\left(\nabla \mathbf{u}+{\left(\nabla \mathbf{u}\right)}^T\right)\right]+\mathbf{T},\\ \lambda \left(\frac{\partial \mathbf{T}}{\partial t}+\left(\mathbf{u}\cdot \nabla \right)\mathbf{T}-\left(\nabla \mathbf{u}\right)\mathbf{T}-\mathbf{T}{\left(\nabla \mathbf{u}\right)}^{\text{T}}\right)={\mu }_{cs}\left[\nabla \mathbf{u}+{\left(\nabla \mathbf{u}\right)}^{\text{T}}\right],{\mu }_{cs}=\lambda G.\end{array}$$ (2)

Here, Π is the total stress tensor that includes the contributions from pressure p, cytosolic shear viscosity μ_c, and cytoskeletal viscoelasticity determined by the extra stress tensor T. Other variables in Eq. 2 are the velocity vector u = (u, v, w), mass density ρ, cytoskeletal shear elastic modulus G, cytoskeletal shear viscosity μ_cs, and cytoplasmic relaxation time λ. The cytoplasmic viscosity μ_cp was defined as the sum of cytosolic and cytoskeletal shear viscosities: μ_cp = μ_c + μ_cs. It should be noted that single-phase viscoelastic cell models have been employed for both theoretical and experimental analysis of blood cells and circulating tumor cells (1,9,21,32, 33, 34, 35, 36).

Modeling of mDC experiment

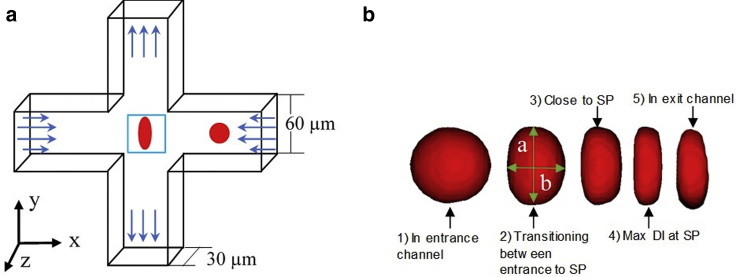
The simulation of cell deformation was performed in a computational domain with a cross-slot channel geometry (Fig. 1 a). The height and width of the channel (30 and 60 μm, respectively) (17) and the volumetric flow rate (425 μL/min in the inflow channel) (14) matched the configuration of previous mDC experiments. The total length of the computational domain, including two 120-μm-long inflow channels, was 300 μm. Fully developed flow was first established in the cross-slot channel. The cell was then placed at 90 μm from the cross-slot center in the flow direction (X direction) and at the flow centerline or varying distance away from the centerline (offset distance) in the cross section of the inflow channel (Y and Z directions). The cell diameter varied from 8 to 26 μm. Its relaxation time was fixed at 0.17 s (1,4), and shear elasticity ranged from 50 Pa to 20 kPa. The shear viscosity of the extracellular fluid, which modeled as a Newtonian fluid, was 0.001 Pa ⋅ s (1 cP). The cytosolic shear viscosity was equal to the extracellular fluid viscosity. The trajectories of the simulated cell motion in the cross-slot channel, as well as cell shape changes at different time instants, were recorded (Fig. 1 b). The DI was calculated from the cell shape data as

$$\mathrm{DI}=\frac{a}{b},$$ (3)

where a and b are the major and minor axes of the cell. The cell continuously deforms as it moves through a cross-slot channel, and as a result, DI changes with time, reaching its maximal value DI_max in the stagnation region of the channel. Because of pressure fluctuations at two inlets of the cross-slot channel and a lateral drift of the cell away from the centerline, most of the cells are displaced from the center (SP) of the channel during mDC experiments. If the cell is perfectly located at the SP, it experiences equal but opposite hydrodynamic forces, which trap the cell and cause extensive cell deformation. This scenario rarely occurs in mDC. To accommodate both these conditions, the initial Y-offset distance of the cell, Y_off, ranged in the numerical simulation from 0 to a maximum of 23 μm. The latter was selected such that to have at least 0.5-μm clearance of the cell from the wall. The initial Z-offset distance, Z_off, was between 0 and 7 μm.

Figure 1.

(a) Schematic of the cross-flow channel geometry with velocity profiles at the inlets and outlets. A cell initially located in one of the inflow channels flows into the cross-slot region, where it experiences maximal deformation at the stagnation point (SP), as shown in the blue box. (b) Shape changes of the cell as it flows through the cross-flow channel, according to the numerical simulation. As the cell progresses through the channel, the major and minor axes of the cells (a and b) were recorded. To see this figure in color, go online.

Before entering the cross-slot channel, the fluid flow is mechanically divided in mDC experiments. This leads to unsteady flow conditions because of uneven and fluctuating pressures at the inlets. To test this effect, we imposed a sinusoidal oscillation on the centerline velocity U_c at both inlets (inlets 1 and 2):

$$U_{c1}=U_c\left[1+\varphi \sin \left(\omega t\right)\right],U_{c2}=U_c\left[1-\varphi \sin \left(\omega t\right)\right],$$ (4)

where ϕ is the dimensionless amplitude of velocity oscillation and ranged from 0 to 0.1 (0–10%) in the simulation and ω is the angular frequency, which was equal to 21 s⁻¹. The maximal variation in the centerline velocity between the inlets was 1.6 m/s.

Correction of the DI data

The numerical data for cell deformation at different Y_off and Z_off were compared to the centerline DI data, and the resulting offset-based errors were fitted into exponential relationships between the DI, cell diameter D, and the total offset distance

$$L_{off}=\sqrt{Y_{off}^2+Z_{off}^2}.$$

The obtained regression data for the errors caused by offsetting the cell were then subtracted from the original DI’s at the centerline, leading to the corrected measure of cell deformation, referred to as the elongation index (EI):

$$EI=DI+{\epsilon }_{off}\left(1-e^{-k_1{L}_{off}}\right)e^{k_{2}D}.$$ (5)

Note that the cell offset causes an artificial decrease in the DI (i.e., the offset-based errors are proportional to a negative of ε_off). The procedure we used to obtain Eq. 5, and the values of its parameters are discussed in the Results and Discussion below. Regression analysis was done by GraphPad Prism (GraphPad Software, La Jolla, CA), with a coefficient of determination R² of at least 87%.

Mesh refinement

All the data were produced on a computational mesh with cubic grid elements of 1.0 μm in size (regular mesh). To test whether this mesh size provides sufficient accuracy, the simulation of single-cell motion initially located at the channel centerline was additionally done on the coarse mesh (2.0 μm in size) and the fine mesh (0.5 μm). In this mesh refinement study, the cell diameter D was 18 μm, and the shear elasticity G was either 1.0 or 5.0 kPa. In the case of a more deformable cell (G = 1.0 kPa), there was a 25% difference in DI_max between the coarse and fine mesh but less than a 3% difference between the regular and fine mesh. For a less deformable cell (G = 5.0 kPa), there was only a 7% difference in DI_max between the coarse and fine mesh and less than a 2% difference between the regular and fine mesh. Thus, the regular mesh simulation had less than 3% error when compared with the fine mesh data but required 4 times fewer computational resources and took half the time of the fine mesh simulation.

Results and Discussion

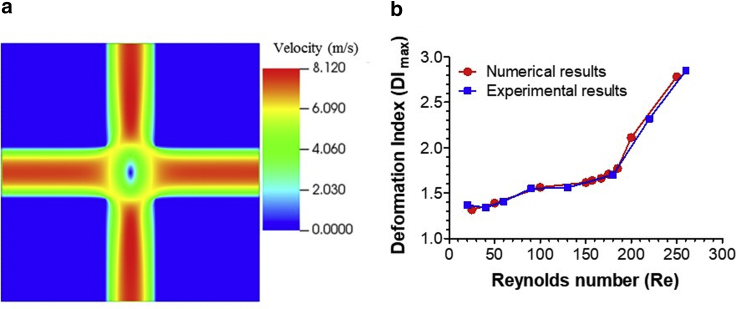
Fig. 2 a shows the fully developed flow field in a cross-slot channel obtained numerically in the absence of the cell. The red color indicates peak velocity achieved, and the blue color designates the zero-velocity areas, which include the SP region in the middle of the computational domain. To test whether our computational model can reproduce the experimental data on HL-60 cell deformation and breakup in a cross-slot channel, we first performed the numerical simulation using the values of parameters provided by Armistead et al. (27): mean diameter D of 12 μm and Young’s modulus E of 301 Pa, which corresponds to G ≈ 100 Pa. The cell was initially located at the inlet channel centerline and exposed to an inlet flow rate from 67.5 to 675 μL/min, corresponding to Re from 25 to 250. Note that the total flow rate is twice the inlet flow rate. The numerical DI data (circles in Fig. 2 b) agreed closely with the experimental data by Armistead et al. (27) (squares), in which only the cells moving along the flow centerline were taken into account. In further analysis, Re was fixed at 157, which was less than the threshold value of 180 at which the cell begins to rupture (27) and agreed with experimental conditions in Gossett et al. (14). The mDC system by Armistead et al. (27) had a width of 35 μm and a depth of 25 μm, whereas the Lin et al. (17) system we modeled had a width of 60 μm and a depth of 30 μm (Fig. 1 a). The critical flow rate for cell rupture in the latter system was 400 μL/min. The extracellular fluid in both systems was a Newtonian liquid with viscosity of 1 cP, and the difference in its mass density was only 5 kg/m³.

Figure 2.

(a) Fully developed flow profile through the midplane of the cross-slot channel without the cell present, according to the numerical simulation. (b) Comparison of the experimental (squares) and numerical relationships (circles) between DI and Re for HL-60 cells. In (b), the numerical cell size and shear elasticity were 12 μm and 100 Pa, respectively. To see this figure in color, go online.

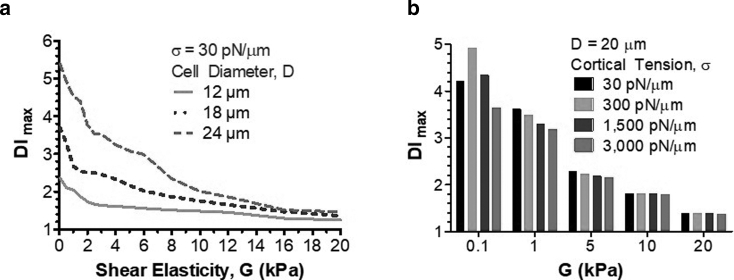
Fig. 3 illustrates how the DI changes with cell size and elastic properties (shear elasticity, cortical tension), provided the cell was originally located at the inlet channel centerline. A bigger cell experienced larger deformation in the SP area even in the absence of changes in shear elasticity (Fig. 3 a). The DI rapidly decreased when shear elasticity changed from 50 Pa to 1 kPa and slowly plateaued at shear elasticity above 10 kPa (Fig. 3 a). Cortical tension had a significant effect on the DI at low shear elasticity (up to 1 kPa) and a nominal effect at higher elasticity (Fig. 3 b). At G = 100 Pa, the DI peaked at 4.9 at σ = 300 pN/μm but decreased to a minimum of 3.6 at 3000 pN/μm. When G = 1 kPa, there was a steady decrease in the DI from 3.6 to 3.2 with σ between 30 and 3000 pN/μm. The bulk shear elasticity of the cell appears because of cross-links between cytoskeletal filaments. These cross-links exist not only within a distinct filament network but also between filaments of different type, such as actin filaments, microtubules, and intermediate filaments (29). In this situation, actin cytoskeleton contributes to both surface and bulk mechanical properties of the cell, which makes cortical tension dependent on bulk shear elasticity. It is likely, however, that this dependence becomes weaker when the cross-link density is high and thus the shear elasticity is large, leading to a diminished role of cortical tension and a dominant contribution of shear elasticity to cell deformation, as evident in Fig. 3 b.

Figure 3.

(a) DI_max versus cytoskeletal shear elasticity for 12-, 18-, and 24-μm diameter cells, according to the numerical simulation. (b) DI_max versus cytoskeletal shear elasticity of a 20-μm cell for different values of the cortical tension.

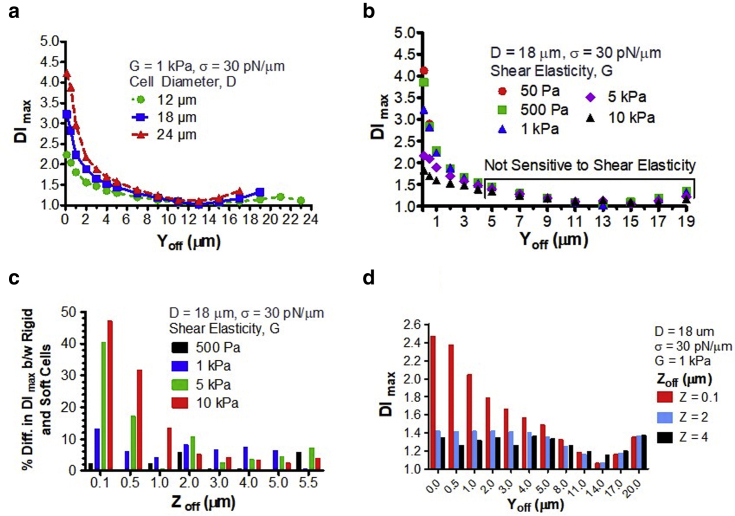
The data shown in Fig. 4 point out that the wide spread of DI and cell sizes in mDC experiments is due to the lateral and transverse displacements of the cell from the centerline (Y- and Z-offsets, respectively). The DI rapidly dropped when the Y_off increased from 0.1 to 1.0 μm, and this effect became more pronounced with an increase in cell size (Fig. 4, a and b). For instance, the DI of a 24-μm cell with shear elasticity of 1 kPa decreased from 4.23 at a Y_off of 0.1 μm to 2.97 at a Y_off of 1.0 μm (30% difference, Fig. 4 a). The DI reached the plateau at a Y_off of ∼5 μm, at which the sensitivity of this parameter to shear elasticity was lost (Fig. 4 b). Even without lateral offset, mDC cannot distinguish the cells with shear elasticities between 500 Pa and 10 kPa when the Z_off becomes 2.0 μm or higher (Fig. 4 c). At a Z_off greater than 2.0 μm, there was less than a 5% difference in the DI between the cells with shear elasticity of 50 Pa and 10 kPa. This indicates that mDC at a large Z_off is not sensitive to elasticity change within three orders of magnitude. Much more drastic changes in the DI were seen when the cell was offset in both lateral and transverse directions (Fig. 4 d). An 18-μm cell with shear elasticity of 1 kPa had the DI of 3.22 at a Y_off of 0.1 μm and no Z_off (Fig. 4 a) or 2.47 at a Z_off of 0.1 μm and no Y_off (Fig. 4 d), which was then decreased to 1.42 at a Y_off of 1.0 μm and a Z_off of 2.0 μm (44% difference; Fig. 4 d). These data also show that the effect of Z_off on the DI reduces with an increase in Y_off. When the Y_off is above 5.0 μm, the transverse displacement of the cells contributes insignificantly to errors of mDC measurement in comparison with their lateral displacement.

Figure 4.

(a) DI vs. Y_off for the cell with shear elasticity of 1 kPa and different cell diameters. (b) DI vs. Y_off for the 18-μm-diameter cells with different values of the cytoskeletal shear elasticity. (c) The effect of Z_off on the percentage difference in DI between the rigid cells (G ≥ 500 Pa) and the soft cell (G = 50 Pa). Y_off was 0 μm. (d) DI vs. Y_off for the 18-μm diameter cells initially located at a different Z_off. To see this figure in color, go online.

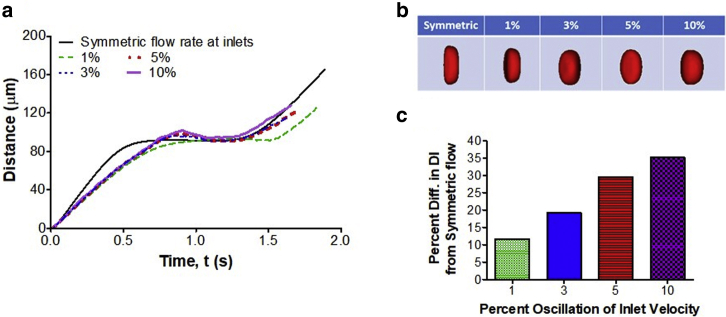
To assess errors in DI measurement resulting from inlet flow perturbations, we studied numerically the cell motion and deformation in a cross-slot channel when the centerline velocity between the inlets oscillated with amplitude ϕ = 0, 1, 3, 5, and 10% (cf. Eq. 4). As seen in Fig. 5 a, there was a significant deviation in the cell trajectory from the symmetric flow case (ϕ = 0%, dark solid line) even when the oscillation amplitude was 1% (green or light dashed line). With this small variation, the cell traveled longer to the cross-slot SP than the cell in symmetric flow. A further increase in ϕ led to the bounce-back effect (rise and drop in the total distance; cf. dotted and solid lines), at which the cell moved past the SP and then returned to it through decaying oscillation in the lateral (Y) direction. This behavior has been already observed in mDC experiments. Fig. 5 b illustrates that the shape of the cell trapped in the SP drastically changed with ϕ. When compared with symmetric flow, the DI decreased by 11.7, 19.2, 29.6, and 35.2% for ϕ = 1, 3, 5, and 10%, respectively (Fig. 5 c).

Figure 5.

The numerical effect of oscillatory perturbation in the inlet velocity on cell motion and deformation in a cross-slot channel. (a) Total distance traveled by the cell and (b) cell shape at the SP region of the cross-slot channel for different amplitudes of sinusoidal flow oscillation between the inlets. (c) Percentage difference in the cell's DI between symmetric flow (no fluctuation between the inlets) and disturbed flow due to velocity fluctuations. The diameter and elasticity of the cell were 18 μm and 1 kPa, respectively. To see this figure in color, go online.

It should be noted that we fully tracked the cell during its motion in the oscillatory flow. The data presented in Fig. 5 are the maximal DI, not the DI averaged over the period of oscillation. For 3% and above oscillation, the cell center deviated from the SP by 3–7 μm in the X direction. In this case, a larger region around the SP was used to track the cell shape and calculate DI_max. For 1% oscillation, the deviation was within 1 μm and did not require a change in the tracking region dimensions. Flow perturbations also caused a small drift of the cell from the centerline in the Z direction; however, this drift insignificantly changed the cell trajectory.

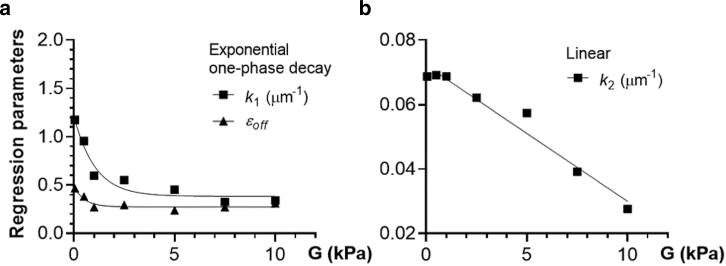
Using the deterministic data in Figs. 3 and 4, we obtained the corrective measure of cell deformation that accounts for cell offset from the centerline (EI, cf. Eq. 5). Specifically, from regression analysis of the centerline data in Fig. 3 a, we first found that DI decreased exponentially with shear elasticity and increased exponentially with cell diameter. We then calculated the errors in the DI_max due to offsets from the data in Fig. 4 and determined the general functional relationship between the DI_max errors and offsets from regression analysis. Based on the exponential behavior of the centerline DI, three parameters of the DI_max error regression model (ε_off, k₁, and k₂) were fitted to the exponential functions of shear elasticity and cell diameter (Fig. 6).

Figure 6.

Dependence of parameters in regression (5) on shear elasticity. (a) ε_off and k₁ vs. G obtained from the deterministic study (symbols, cf. Fig. 4d) and fitting those data to the exponential one-phase decay model (lines). (b) k₂ vs. G for the deterministic study (squares, cf. Fig. 4a) and its fitting to the linear model (line).

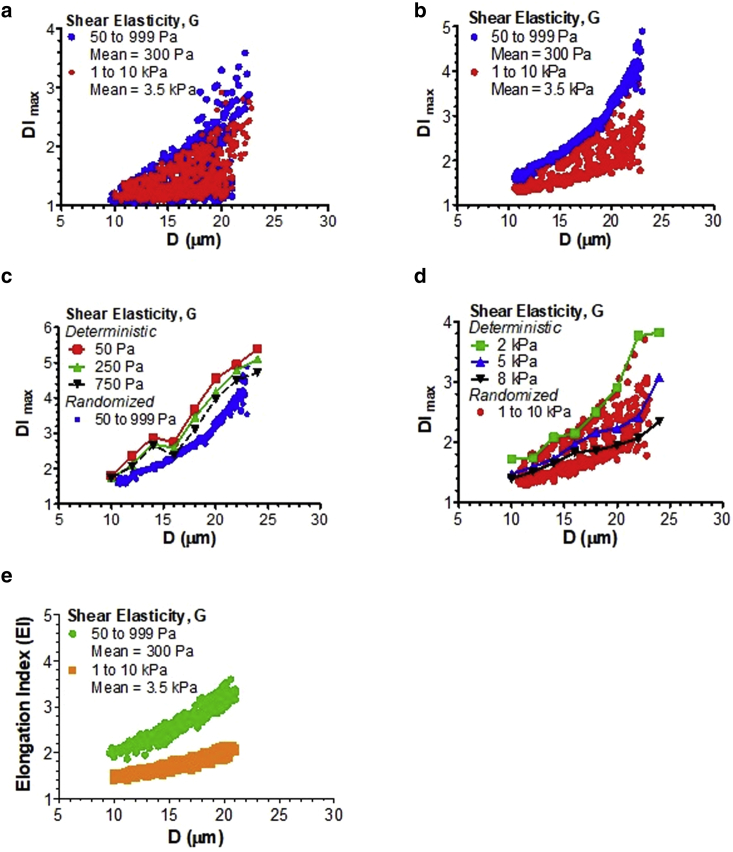
To account for variability in mechanical properties of the cells and their location in the inlet channel during mDC experiment, we conducted the numerical study of cell deformation in a cross-slot channel at which the initial cell placement, cell size, and shear elasticity were randomized via pseudorandom normal sampling (Fig. 7). In this randomization study, the cell diameter D changed from 10 to 24 μm, Y_off ranged between 0.1 and 10 μm, and Z_off was between 0 and 2.5 μm. We considered 24 different types of cells, including healthy epithelial cells and carcinoma cells from several tissues (breast, lung, prostate, ovaries, bladder) as well as healthy and malignant leukocytes (leukemia, lymphoma) (10,18,37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48). The mean diameter of these cells was around 17 μm, whereas there was a larger variation in shear elasticity that caused their separation into low-elasticity (mean G ≈ 300 Pa) and high-elasticity cells (mean G ≈ 3500 Pa).

Figure 7.

Scatter plots for cell deformation versus cell diameter for low- and high-elasticity groups before and after data correction by Eq. 5. (a–d) DI_max vs. D plots, according to the numerical model with normal random distribution of D and G and uniform random distribution of Y_off and Z_off (a) or fixed minimal offset (Y_off = 0.1 μm and Z_off = 0 μm; b–d). In (c) and (d), minimal-offset randomized data for the low- (c) and high-elasticity groups (d) were compared with the deterministic results obtained for the cell with different shear elasticity initially located at the inlet channel centerline. (e) EI vs. D distribution obtained by correcting the offset errors in the original DI_max data (a) via Eq. 5. There was a clear separation of the EI between the low- and high-elasticity groups that was not seen in the DI_max data. The shear elasticity of the cells in the low-elasticity group (blue) ranged from 50 to 999 Pa, with a mean of 300 Pa and an SD of 200 Pa. The high-elasticity group (red) had a shear elasticity between 1 and 10 kPa, with a mean of 3.5 kPa and an SD of 2 kPa. The cell diameter changed from 10 to 24 μm, with a mean of 17 μm and an SD of 4 μm. The ranges for Y_off and Z_off in the randomized study were 0.1–10 and 0.1–2.5 μm, respectively.

Fig. 7 a shows the DI_max versus cell diameter scatter plots for two populations of cells: 1) low-elasticity group (blue circles) and 2) high-elasticity group (red circles). The scatter plots for the same sampling of cell size and elasticity but with a very small offset in the lateral direction (Y_off = 0.1 μm) and no offset in the transverse direction (Z_off = 0 μm) are displayed in Fig. 7 b. The latter study was done to get the DI-values for the cell moving along the inlet channel centerline. (Note that we had to place a small Y_off to avoid complete trapping of the cell within the SP region.) From comparison between Fig. 7, a and b, it is clearly seen that the lateral and transverse offsets led to artificial enlargement of the DI output to the point at which it was no longer possible to distinguish between the cells in the low- and high-elasticity groups that had more than a 10× difference in shear elasticity.

When the cell offset was minimal (Fig. 7 b), randomized data for the low-elasticity group slightly under-predicted the deterministic DI_max-values for the cell moving exactly at the centerline (Fig. 7 c). The high-elasticity group had a wider distribution of DI-values at minimal offset (Fig. 7 b), but all the DI_max data fell within the deterministic centerline values (Fig. 7 d). With applying Eq. 5 to the randomized data in Fig. 7 a, the errors due to offsets had been minimized, and the resulting EI scatter plots were clearly separated for the low- and high-elasticity groups (Fig. 7 e). This indicates that the sensitivity of mDC to shear elasticity can be substantially improved by correcting the DI output by Eq. 5. Based on Fig. 6, ε_off was 0.395 and 0.274, k₁ was 1.007 and 0.412 μm⁻¹, and k₂ was 0.071 and 0.057 μm⁻¹ for the low- and high-elasticity groups in Fig. 7 e, respectively. It should be noted that the EI does not have the same dependence on cell diameter as the centerline data predicts. It rather represents a central tendency for the minimal-offset DI distribution in Fig. 7 b.

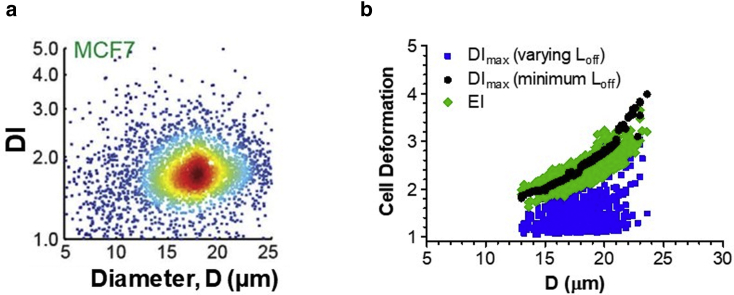
In the last numerical study with randomized values of parameters, we generated the DI_max-values for MCF-7 noninvasive breast cancer cells. The DI output for centered and off-centered MCF-7 cells in the mDC system are shown in Fig. 8 a. The mean shear elasticity and diameter of these cells were selected to be 413 Pa and 18 μm, based on previous measurements (40,49). Fig. 8 b shows the distribution of the DI_max versus cell diameter with uniform random offsets (squares) and minimal fixed offset (circles), as well as the EI versus cell diameter output (diamonds) obtained by correcting the DI_max-values (squares) by Eq. 5. The following values of regression parameters were used in this study: ε_off = 0.372, k₁ = 0.945 μm⁻¹, and k₂ = 0.070 μm⁻¹. The correction of DI_max-values by Eq. 5 led to a narrower, compact distribution of the cell deformation data. The resulting EI-values changed the same way with cell diameter as the minimal-offset DI_max, thus indicating successful suppression of the offset errors.

Figure 8.

(a) Density plot of deformability index versus diameter of MCF-7 cells generated by mDC (reproduced from Fig. 5 d in Masaeli et al. (16) with permission). (b) Numerical scatter plots for MCF-7 cell deformation versus diameter before (squares, circles) and after offset error correction (diamonds). The cell diameter D and shear elasticity G were normally distributed, and the offsets (Y_off and Z_off) were either uniformly distributed (squares) or fixed at a minimal value (Y_off = 0.1 μm and Z_off = 0 μm, circles). The shear elasticity for MCF-7 cells ranged from 200 to 600 Pa, with a mean of 413 Pa and an SD of 100 Pa. The cell diameter range was from 13 to 24 μm, with a mean of 18 μm and an SD of 2 μm. Y_off and Z_off in the fully randomized analysis (squares) varied from 0.1 to 10 μm and 0.1–2.5 μm, respectively. To see this figure in color, go online.

Conclusions

Cross-slot mDC is a promising high-throughput approach for mechanotypic screening of living cells, but it is plagued with measurement errors associated with cell offset from the flow centerline (22,50) and pressure or velocity fluctuations at the inlet channels. One of the ways to reduce offset errors is to eliminate the off-distance DI data (21,27), which can make mDC less powerful in assessing changes in cell mechanotype. We have demonstrated via predictive computational modeling that the mDC output can be sensitized to mechanical properties of the cells, such as shear elasticity, without removing viable off-distance data. In this new approach, the DI is replaced with a new measure, referred to as EI, which accounts for offset errors. The EI formula (Eq. 5) has been derived based on regression analysis of the numerical data for cell deformation in a cross-slot microchannel obtained for different values of cell shear elasticity, diameter, and initial offset from the inlet channel centerline. This formula requires the knowledge of the offset distance and cell diameter, both of which can be measured from acquired images of cells. We also have quantified the effect of flow-splitting-induced fluctuations in inlet velocities on DI measurement. In particular, 1% velocity fluctuation was found to cause an 11.7% drop in the DI. This error further increased to 35.2% at 10% fluctuation. Overall, this study demonstrates that mDC can be significantly improved by its integration with predictive computational models of deformable cell migration such as VECAM.

Author Contributions

S.J.H. and D.B.K. designed this study and wrote the manuscript. H.L. and S.J.H. developed the computational algorithm. S.J.H. performed numerical analysis of cell deformation in a cross-slot microfluidic channel.

Editor: Paul Janmey.