Abstract
Italy was the first country in Europe which imposed control measures of travel restrictions, quarantine and contact precautions to tackle the epidemic spread of the novel coronavirus (SARS-CoV-2) in all its regions. While such efforts are still ongoing, uncertainties regarding SARS-CoV-2 transmissibility and ascertainment of cases make it difficult to evaluate the effectiveness of restrictions. Here, we employed a Susceptible-Exposed-Infectious-Recovered-Dead (SEIRD) model to assess SARS-CoV-2 transmission dynamics, working on the number of reported patients in intensive care unit (ICU) and deaths in Sicily (Italy), from 24 February to 13 April. Overall, we obtained a good fit between estimated and reported data, with a fraction of unreported SARS-CoV-2 cases (18.4%; 95%CI = 0–34.0%) before 10 March lockdown. Interestingly, we estimated that transmission rate in the community was reduced by 32% (95%CI = 23–42%) after the first set of restrictions, and by 80% (95%CI = 70–89%) after those adopted on 23 March. Thus, our estimates delineated the characteristics of SARS-CoV2 epidemic before restrictions taking into account unreported data. Moreover, our findings suggested that transmission rates were reduced after the adoption of control measures. However, we cannot evaluate whether part of this reduction might be attributable to other unmeasured factors, and hence further research and more accurate data are needed to understand the extent to which restrictions contributed to the epidemic control.
Keywords: novel coronavirus, COVID-19, epidemic model, epidemiology
1. Introduction
The novel coronavirus (SARS-CoV-2) that emerged in Wuhan (China) at the end of 2019 quickly spread to another 213 countries, as of 13 April 2020. On the same date, there were 159,516 confirmed SARS-CoV-2 cases with 20,465 deaths in Italy [1]. It is worth mentioning that Italy was the first country in Europe to put its entire population on lockdown [2]. On 10 March, the Italian Government imposed control measures to the entire country, including travel restrictions, quarantine and contact precautions [3,4]. On 23 March, further restrictive measures, which included the shutdown of all non-strategic production in the whole Italian territory, have been adopted [3,4]. Such efforts to contain the virus are still ongoing in all the Italian regions, however, uncertainties regarding SARS-CoV-2 transmissibility and virulence make it difficult to evaluate the effectiveness of restrictions. A major source of uncertainty regards the proportion of unreported cases, a critical epidemiological characteristic that might bias the interpretation of the epidemic curve. Indeed, if one looks at only confirmed data, there has been a reduction in the epidemic spread in Italy after restrictions. Yet, mounting evidence suggested that undocumented infections could greatly contribute to SARS-CoV-2 spread [5,6,7]. Moreover, several outbreaks occurred at different times scattered throughout the Italian territory [1]. For this reason, it is necessary to evaluate the epidemic curve on a region-by-region basis, using data that are less prone to ascertainment bias [8], such as such as those related to hospital admission and deaths [7].
In this study, we employed a Susceptible-Exposed-Infectious-Recovered-Dead (SEIRD) model to assess SARS-CoV-2 transmission dynamics in Sicily (South Italy). The first aim was to estimate the unknown parameters of the model before restrictions of 10 March, also assessing the possibility of unreported cases. We further modeled the epidemic to evaluate changes in transmission rates after the adoption of control measures on 10 and 23 March 2020.
2. Materials and Methods
2.1. Formulating the SEIRD Model
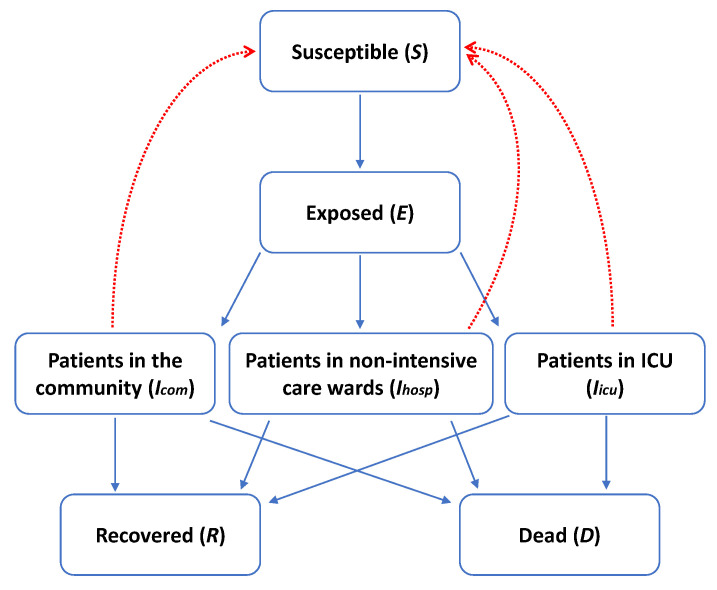
As described in a previous study [7], we modeled the epidemic curve using a Susceptible-Exposed-Infectious-Recovered-Dead (SEIRD) model, where S(t), E(t), I(t), R(t), and D(t) were the number of susceptible (S), exposed (E) (i.e., infected but not yet be infectious), infectious (I), recovered (R) and dead (D) individuals at each time (t). However, to take into account different transmission dynamics in the community and in hospitals, we separated the infectious state into three classes: patients with very mild or no symptoms in the community (Icom), those with mild clinical presentation admitted to non-intensive care wards (Ihos), and those with severe disease who required Intensive Care Unit (ICU) hospitalization (Iicu) (Figure 1).
Figure 1.
The employed Susceptible-Exposed-Infectious-Recovered-Dead (SEIRD) epidemic model for novel coronavirus (SARS-CoV-2) epidemic in Sicily, Italy. This diagram summarizes the flow of individuals across SEIRD compartments (blue lines); red dotted lines, instead, represent the potential transmission of SARS-CoV-2 from infectious to susceptible individuals.
Accordingly, the model was defined by the following system of ordinary differential equations:
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
where:
N was the total population given by the sum of each state;
βcom, βhos, and βicu were the transmission rates in the three infectious categories;
σ was the infection rate (i.e., the inverse of the incubation period) assumed to be the same for each infectious category;
υcom, υhos, and υicu were the probabilities that each exposed individual progressed to Icom, Ihos or Iicu;
γ was the removing rate (i.e., assumed to be the inverse of the infectious period between onset of symptoms and recovering/death);
μcom, μhos, and μicu were the probabilities of dying among infectious individuals.
In brief, Equations (1) and (2) regulated the flow of patients from S to E compartment according to the number of S and I individuals at each time (t), the transmission rates βcom, βhos, and βicu, and the total population N. Specifically, S individuals could become E after contact with I individuals. Equation (3) regulated the flow of patients from E to I compartment according to the number of E individuals at each time (t), the infection rate σ, and the probabilities that each E individual progressed to Icom, Ihos or Iicu. Thus, each E individual could progress to Icom, Ihos or Iicu with different probabilities. Equations (4) and (5) regulated the flow of patients from I to R or D compartments according to the number of I individuals at each time (t), the removing rate and the probabilities of dying or surviving among I individuals. Notably, at each time (t), the sum of Equations (4) and (5) was equal to γI.
2.2. Fitting the Model to the Reported Number of ICU Patients and Deaths
The SEIRD model was formulated to estimate the unknown parameters and to reflect the epidemic curve in a way that was consistent with reported data. However, as discussed in our previous work [7], stringent testing strategies that have been adopted in Italy and other countries might have caused an underestimation of infectious individuals, especially those with mild or no symptoms. To address the uncertainty on reported SARS-CoV-2 infections, we fitted our model to reported data on the daily number of patients hospitalized in ICU and on the number of deaths, which were certainly less prone to be affected by ascertainment bias [8]. These data were obtained from Italy’s Civil Protection department of the Italian Ministry of Health from 24 February to 13 April 2020 [1], and reported in Table S1. In particular, we collected all the data but we fitted our model to minimize the following objective function (6):
| (6) |
where:
Iicu−obs and Iicu−est were the number of observed and estimated ICU patients at each time (t) from 24 February to 17 March. Thus, in the baseline scenario, nicu was set to 23 (i.e., the number of days between start and end dates of the model fitting on ICU patients);
Dobs and Dest were the number of observed and estimated deaths at each time (t) from 24 February to 24 March. Thus, in the baseline scenario, ndeaths was set to 30 (i.e., the number of days between start and end dates of the model fitting on deaths).
In fact, given the lag of 1–2 weeks between the adoption of restrictions (i.e., first restrictions were adopted on 10 March) and their impact on infection and death trends, we were confident in using the above-mentioned periods to fit our model. A summary of this process and data used to fit the model are reported in Figure S1 and Table S1, respectively. To estimate the unknown parameters, we employed a Sequential Quadratic Programming (SQP) algorithm for large-scale constrained optimization, which solved a sequence of optimization subproblems to minimize the objective function (6) satisfying all the constraints [9]. This algorithm has already been used for modeling purposes in the context of SARS-CoV-2 epidemic [10]. The model is based on 10 predefined parameters (i.e., N, S, E, Icom, Ihos, Iicu, R, D, σ, and γ) and 9 parameters to be estimated (i.e., βcom, βhos, βicu, υcom, υhos, υicu, μcom, μhos, and μicu). The modeling started 5 days before the first case was announced in Sicily on 25 February, with one infectious individual in the community. This lag time corresponded to the incubation period of SARS-CoV-2 estimated by Li et al. [11]. The entire set of assumptions and constraints was defined based on the current knowledge on SARS-CoV-2 features and looking at the epidemic curve in Sicily (Table 1). Among these, the infection rate was assumed to be 1/5.2 days according to Li et al. [11]; the removing rate was set to 1/12 days based on infectious and hospitalization periods reported by previous studies in China and Italy [6,12,13]. However, there was no consensus on the removing rate, and hence its uncertainties were further considered in the sensitivity analysis. The above process was iterated 1000 times on randomly generated samples from the distribution functions of reported ICU patients and deaths to obtain 95% Confidence Intervals (CIs). Specifically, the reported number of ICU patients and deaths followed two different third-degree polynomials with R2 = 0.987 and R2 = 0.984, respectively.
Table 1.
Initial parameters of the SEIRD model.
| Initial Model Parameters | Definition | Assumption or Constraints |
|---|---|---|
| Starting date a | The first of the modeling | 20 February 2020 |
| N b | Total population | 5,000,000 |
| S | Susceptible individuals | 4,999,999 |
| E | Exposed individuals | 0 |
| Icom | Non-hospitalized patients | 1 |
| Ihos | Patients hospitalized in non-intensive care wards | 0 |
| Iicu | Patients hospitalized in ICU | 0 |
| R | Recovered | 0 |
| D | Deaths | 0 |
| βcom | Transmission rates in the three infectious categories | 0.1 ≤ βcom ≤ 2 |
| βhos | 0.1 ≤ βhos ≤ 2 | |
| βicu | 0.1 ≤ βicu ≤ 2 | |
| σ c | Infection rate | 0.19 |
| υcom d | Probabilities of progressing to Icom, Ihos or Iicu | 0.1 ≤ υcom < 1 |
| υhos d | 0.1 ≤ υhos < 0.25 | |
| υicu d | 0.1 ≤ υicu < υhos | |
| γ e | Removing rate | 0.08 |
| μcom | Probabilities of dying among Icom, Ihos or Iicu | 0 ≤ μcom < μhos |
| μhos | μcom < μhos < μicu | |
| μicu | μhos < μicu ≤ 1 |
a Assumed to be 5 days (i.e., the incubation period according to Li et al. [11]) before the first case was announced in Sicily on 25 February. b Approximated to the current Sicilian population. c Assumed to be 1/5.2 days according to Li et al. [11]. d Their sum (υcom + υhos + υicu) was assumed to be equal to 1. e γ Assumed to be 1/12 days based on values reported by Wang et al., Chen et al. and Grasselli et al. [6,12,13].
2.3. Modeling the SARS-CoV-2 Transmission after the Adoption of Control Measures
We further modeled the transmission of SARS-CoV-2 in Sicily after 10 March, when the control measures of travel restrictions, self-quarantine and contact precautions have been advocated by the Italian Government. To do that, we re-estimated the transmission rates in the three infectious categories (βcom, βhos, and βicu) maintaining the other parameters obtained previously as unchanged. In this case, we fitted the model to the reported number of daily ICU patients from 18 to 27 March and cumulative deaths from 25 March to 2 April. We used a similar approach to take into account more stringent restrictions adopted by the Italian Government on 23 March, by fitting the model to reported daily ICU patients from 28 March to 13 April and cumulative deaths from 3 to 13 April. Again, the reported number of ICU patients and deaths followed different third-degree polynomials with R2 ranging from 0.981 to 0.992.
2.4. Sensitivity Analysis
Certain parameters of our model could be affected by disease severity, and hence some considerations should be addressed. In the scenario described above, we have already taken into account differences in β, υ, and μ across SARS-CoV-2 patient’s categories. In contrast, σ (i.e., the inverse of incubation period) could be assumed as independent of disease severity. For these reasons, we conducted a sensitivity analysis to account for the effect of disease severity on γ (i.e., the removing rate). Current uncertainties on this parameter and differences between countries make it difficult to establish a proper value. Our hypothesis was that the infectious period increased with increasing disease severity. Considering the inverse relationship between infectious period and removing rate, we assumed that the removing rate of non-hospitalized patients (γcom) was higher than that of patients hospitalized in non-intensive care wards (γhos). Similarly, the removing rate of patients hospitalized in non-intensive care wards was higher than that of patients hospitalized in ICU (γicu). It is worth mentioning that there was still no consensus on the infectious period [12,14,15], and hence its estimates—especially among asymptomatic and mild patients—were not so consistent. In the sensitivity analysis, we assumed three different removing rates for Icom, Ihos, and Iicu according to that used in the baseline scenario. Specifically, we attributed the highest parameter to Iicu (i.e., 1/18 days), an intermediate value for Ihos (i.e., 1/12 days), and the lowest to Icom (i.e., 1/6 days). The highest and the lowest values corresponded to 50% above or below the removing rate used in the baseline scenario. Thus, we performed the analyses by using the above-mentioned removing rates but maintaining the other initial conditions reported in Table 1. Instead, Equations (4) and (5) were replaced with the following:
| (7) |
| (8) |
3. Results
3.1. Description of Reported Data
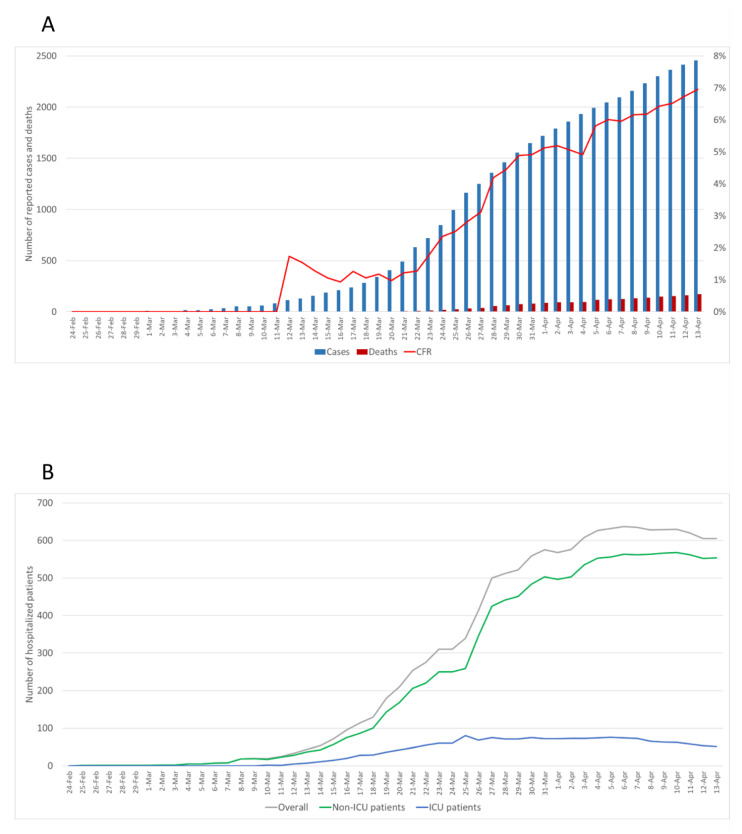
Data on SARS-CoV-2 cases, hospitalized patients and deaths in Sicily, reported by Italy’s Civil Protection from 24 February to 13 April, are shown in Figure 2. As of 13 April 2020, there were 2458 cases, 605 hospitalized patients and 171 deaths. Notably, the daily increment in the number of new cases decreased from 28 March (8.7%) to 13 April (1.7%). Examining the epidemic trend, we also observed that case fatality risk—the number of deaths divided by number of cases—increased from 1.7% to 7.0% as the epidemic spread (Figure 2A). After an exponential growth, instead, the daily number of hospitalized patients reached a steady state from 28 March to 2 April followed by a slight decrement until 13 April. This decline appeared slower for patients hospitalized in non-intensive care wards than those admitted to ICU (Figure 2B).
Figure 2.
Number of cases, hospitalized patients and deaths in Sicily, Italy, reported by Italy’s Civil Protection from 24 February 2020 to 13 April 2020. (A) The bars represent the cumulative number of reported SARS-CoV-2 cases and related deaths while the red line represents the case fatality risk (CFR). (B) The grey line represents the daily number of hospitalized patients, while blue and green lines represent the daily number of patients hospitalized in Intensive Care Unit (ICU) or in other wards.
3.2. The Epidemic Curve Prior to Restrictions
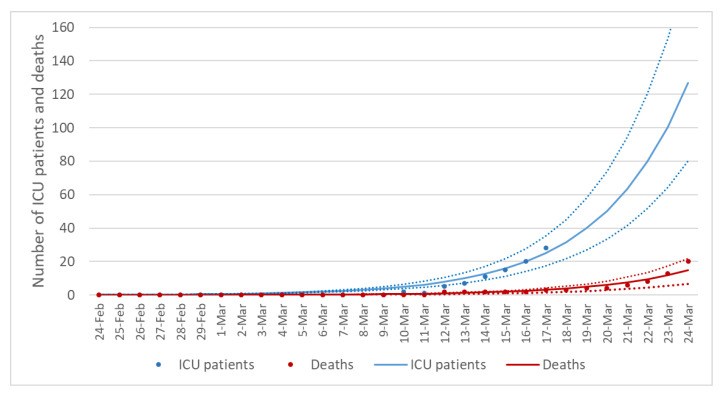
Given the uncertainty on data reported by Italy’s Civil Protection, especially those related to confirmed cases, we first fitted the SEIRD model to the reported daily number of ICU patients and cumulative deaths, obtaining an overall good fit between estimated and reported data (Figure 3). The estimated parameters which best explained the reported numbers of ICU patients and deaths are shown in Table 2. Using the best-fitting parameters, we estimated a total of 76 (95%CI = 60–94) SARS-CoV-2 cases on 10 March, which comprised 65 (95%CI = 51–80) infectious individuals, 20 recoveries (95%CI = 17–23), and 1 (95%CI = 0–1) death. With respect to infectious individuals, we estimated 18 (95%CI = 12–24) hospitalized patients, out of which 5 were in ICU (95%CI = 4–6) and 13 were in other wards (95%CI = 10–16). Although these estimates revealed only a small proportion of unreported cases (18.4%; 95%CI = 0–34.0%), the estimated case fatality risk of 0.7% would remain stable as the epidemic spread.
Figure 3.
Number of estimated and reported patients in Intensive Care Unit and deaths in Sicily (Italy) from 24 February to 24 March 2020. The SEIRD model was fitted to the reported number of patients admitted to Intensive Care Unit (ICU) and deaths. Blue and red dots represent the number of reported ICU patients and deaths, respectively, while the lines represent their estimates and 95% confidence intervals through the SEIRD model.
Table 2.
Best-fitting parameters in absence of control measures.
| SEIRD Parameters | Definition | Estimated Values (95%CI) |
|---|---|---|
| βcom | Transmission rate | 0.99 (0.96–1.04) |
| βhos | 0.37 (0.32–0.43) | |
| βicu | 0.28 (0.24–0.33) | |
| υcom | Probability of progression to Icom, Ihos, or Iicu | 0.76 (0.70–0.82) |
| υhos | 0.19 (0.15–0.23) | |
| υicu | 0.05 (0.03–0.07) | |
| μcom | Probability of dying | 0.01 (0.00–0.02) |
| μhos | 0.07 (0.04–0.10) | |
| μicu | 0.26 (0.20–0.30) |
3.3. The Effect of Control Measures on Transmission Rates
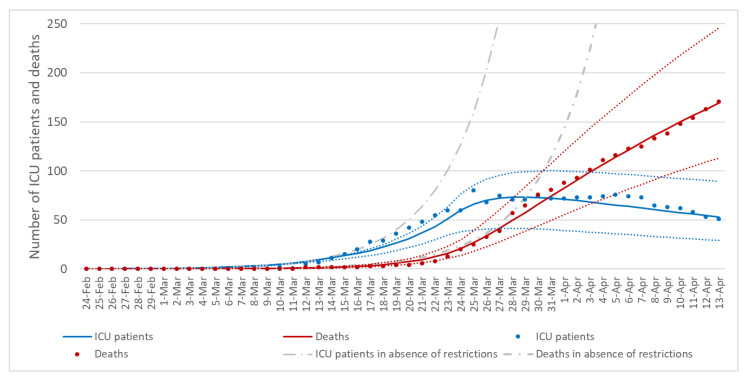
We next applied the SEIRD model to evaluate the effect of restrictions adopted by the Italian Government on 10 March, which were then intensified on 23 March (Figure 4). We estimated that transmission rate in the community was reduced by 32% (95%CI = 23–42%) after the first set of restrictions imposed on 10 March 2020. We estimated that also the transmission rates of patients hospitalized in ICU or in other wards were reduced by 10% (95%CI = 5–15%) and 7% (95%CI = 4–10%), respectively. Interestingly, transmission rate in the community was reduced by 80% (95%CI = 70–89%) after control measures adopted on 23 March, while transmission dynamics remained almost unaltered among hospitalized patients (Table 3).
Figure 4.
Modeling of control measures adopted on 10 March 2020 which were then intensified on 23 March 2020. Blue and red dots represent the number of reported ICU patients and deaths, respectively, while the lines represent their estimates and 95% confidence intervals through the SEIRD model. Grey lines, instead, represent the estimates in absence of control measures.
Table 3.
Transmission rates after the adoption of control measures.
| Control Measures | Transmission Rates | Estimated Values (95%CI) |
|---|---|---|
| First set of restrictions adopted on $$$10 March 2020 | βcom | 0.67 (0.57–0.76) |
| βhos | 0.34 (0.33–0.35) | |
| βicu | 0.25 (0.23–0.27) | |
| Second set of restrictions adopted on 23 March 2020 | βcom | 0.20 (0.11–0.30) |
| βhos | 0.28 (0.25–0.31) | |
| βicu | 0.22 (0.20–0.25) |
3.4. Sensitivity Analysis
Given potential differences in the removing rates across SARS-CoV-2 patient’s categories, we performed a sensitivity analysis and re-evaluated the best-fitting parameters (Table S2). In this scenario, we estimated a total of 74 (95%CI = 58–92) SARS-CoV-2 cases on 10 March, which comprised 3 patients hospitalized in ICU (95%CI = 2–4) and 1 death (95%CI = 0–1). As such, the proportion of unreported cases was 16.2% (95%CI = 0–32.6%). Sensitivity analysis estimated that transmission rate in the community was reduced by 41% (95%CI = 37–46%) after the first set of control measures imposed on 10 March, and by 85% (95%CI = 79–89%) after 23 March 2020.
4. Discussion
In this study, we modeled the SARS-CoV-2 epidemic in Sicily (South Italy) to estimate any instances of undocumented infections and to evaluate the impact of control measures adopted by the Italian Government. Our approach stemmed from the hypothesis that looking at reported cases could lead to biased speculations when interpreting data on an epidemic emergency. For this reason, we further adapted our previously described SEIRD model [7] to investigate the SARS-CoV-2 epidemic curve in Sicily, working directly on data on admissions to ICU and deaths. Although uncertainties of available information on SARS-CoV-2 cases do not allow us to validate this model properly, we have already applied a similar approach to Chinese data [7]. A similar hypothesis has been also formulated by a research group from the Imperial College of London, who is investigating the epidemic curve on the basis of deaths observed over time [16]. However, to our knowledge, our study was the first employing also data on admissions to ICU, another event that was certainly less affected by ascertainment bias. Our findings revealed a smaller proportion of unreported cases in Sicily if compared with previous estimates in Italy [17]. A plausible explanation was that the Sicily’s regional health system did not experience the same emergency observed in other Italian regions, such as Lombardy, Emilia Romagna, and Piedmont [18]. However, despite stringent testing strategies, ~20% of cases were not documented on 10 March. This proportion of unreported cases biased the apparent increase in case fatality risk during the epidemic spread. Instead, taking into account the estimated cases, case fatality risk stably stood around 0.7%. In accordance, the probability of dying among ICU patients was consistent with the ICU mortality reported by Grasselli et al. in the Lombardy region [12]. As stated by previous studies [18], indeed, stringent testing strategies adopted in Italy might explain the higher case fatality risk compared to other countries. This raised the need for caution when comparing preliminary estimates between and within countries.
Looking at the data, we noted a gradual flattening of the epidemic curve after the adoption of restrictive measures by the Italian Government in the middle of March. Although it was not clear to what extent the slowdown in the epidemic spread was exclusively attributable to control measures, restrictions have succeeded, at least partially, to contain SARS-CoV-2 transmission. Specifically, measures such as travel restrictions, quarantine and contact precautions might have modified the transmission rate in the community. Indeed, in our study, we estimated that transmission rate in the community decreased by 32% after 10 March and by 80% after 23 March. Beside this, changes in healthcare worker’s behavior such as wearing of facemasks, social distancing, self-isolation when sick contributed by reducing transmission rates in the hospital setting. Indeed, our estimates on the impact of control measures were in line with those reported by Li and colleagues on the Chinese experience [5]. However, it cannot be ruled out that part of this reduction might be attributable to other factors, including improvements in patient management and seasonal variations [19,20]. For these reasons, we decided to not extend our model beyond 13 April 2020. Indeed, the influence of other factors would be increased with increasing the modeling period, while, in our opinion, working on a limited period could partially reduce these effects.
We recognized that our findings were based on an epidemic model with constant parameters and therefore some points should be considered when interpreting our results. Limitations of these kinds of models significantly hinder their long-term predictive application, and hence we exclusively applied our SEIRD model to estimate the proportion of unreported SARS-CoV-2 cases and to evaluate changes in transmission rates after control measures. To do that, we fitted our model to those data that were considered less biased by uncertainty such as admissions to ICU and deaths. Indeed, in a region where ICU bed needs for SARS-CoV-2 had not yet reached saturation, even the reported number of patients in ICU could be considered less biased. However, our model was characterized by other limitations. First, it was based on the assumption that all the Sicilian population was equally susceptible to SARS-CoV-2. Although the number of susceptible individuals could be a fraction of the entire population, a recent study reported a seropositivity of 3–4% in the city of Wuhan, the epicenter of the epidemic [21]. Even considering a similar proportion in Sicily, our estimates would not change, since they depended on the ratio between S individuals and the total population N. Second, the model did not discriminate cases that were imported from other Italian regions or countries and for the longitudinal flow of patients from symptom onset to recovering/death. Third, our estimates were not adjusted for the age structure of the Sicilian population. We recognized that differentiating by age groups could yield to more precise estimates, however, it would be necessary that data to fit the model were stratified by age [22]. Fourth, our model did not allow the evaluation of the independent effect of different control measures adopted (e.g., contact tracing, travel restrictions, quarantine). Moreover, it was also possible that the reduction in the epidemic spread could be partially due to improvements in patient management and seasonal variations. Finally, the model fitting was based on the SQP algorithm, which required a set of predefined constraints for optimization [9], and multiple simulations applied to obtain 95%CIs. Thus, among an infinite set of combinations which could provide an optimal solution, the algorithm identified the best-fitting parameters in a narrow range of possibilities. This partially explains the narrow 95%CIs of our estimates, which might be wider in the absence of predefined constraints. Thus, our approach certainly relied on several assumptions and constraints based on the current knowledge of SARS-CoV-2 characteristics and relevant references published in recent months. However, we cannot rule out some degree of uncertainty of our estimates, which will be further refined with progresses in the knowledge on SARS-CoV-2.
In conclusion, our approach—which assessed the epidemic curve by estimating backwards from the documented admissions to ICU and deaths—appeared to be useful for the investigation of the SARS-CoV2 epidemic. Our model, on the early phase of the outbreak, delineated the characteristics of SARS-CoV2 transmission in a region without major restrictions or control. Further analysis extended after the adoption of control measures, instead, suggested that restrictions might have reduced SARS-CoV2 transmission rates considerably. However, we cannot rule out that part of this reduction might be attributable to other unmeasured factors. Thus, further research and accurate data are needed to understand which control measures contributed to the epidemic control.
Supplementary Materials
The following are available online at https://www.mdpi.com/1660-4601/17/14/4964/s1, Figure S1: summary of data collection, model formulation and fitting, Table S1: extract of data on SARS-CoV-2 cases in Sicily (Italy), reported by the Italy’s Civil Protection from 24 February to 13 April 2020, Table S2: best-fitting parameters in the sensitivity analysis.
Author Contributions
Conceptualization, A.M. and A.A.; methodology, A.M. and S.B.; software, A.M.; formal analysis, A.M. and M.B.; data curation, A.M. and S.B.; writing—original draft preparation, A.M. and M.B.; writing—review and editing, all the Authors; visualization, A.M.; supervision, A.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Assessorato della Salute, Regione Siciliana-Progetti Obiettivo di Piano Sanitario Nazionale (PSN 2014-4.9.2).
Conflicts of Interest
The authors declare no conflict of interest.
References
- 1.Italian Ministry of Health Covid-19: Situation Report Update at 14 April 18:00. [(accessed on 14 April 2020)]; Available online: http://opendatadpc.maps.arcgis.com/apps/opsdashboard/index.html#/b0c68bce2cce478eaac82fe38d4138b1.
- 2.World Health Organization Health-Topics: Coronavirus. [(accessed on 30 May 2020)]; Available online: https://www.who.int/health-topics/coronavirus#tab=tab_1.
- 3.Italian Ministry of Health Novel Coronavirus. [(accessed on 30 May 2020)]; Available online: http://www.salute.gov.it/portale/nuovocoronavirus/homeNuovoCoronavirus.jsp?lingua=english.
- 4.Signorelli C., Scognamiglio T., Odone A. COVID-19 in Italy: Impact of containment measures and prevalence estimates of infection in the general population. Acta Biomed. 2020;91:175–179. doi: 10.23750/abm.v91i3-S.9511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Li R., Pei S., Chen B., Song Y., Zhang T., Yang W., Shaman J. Substantial undocumented infection facilitates the rapid dissemination of novel coronavirus (SARS-CoV2) Science. 2020 doi: 10.1126/science.abb3221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Wang H., Wang Z., Dong Y., Chang R., Xu C., Yu X., Zhang S., Tsamlag L., Shang M., Huang J., et al. Phase-adjusted estimation of the number of coronavirus disease 2019 cases in Wuhan, China. Cell Discov. 2020;6:10. doi: 10.1038/s41421-020-0148-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Maugeri A., Barchitta M., Battiato S., Agodi A. Estimation of unreported novel coronavirus (SARS-CoV-2) infections from reported deaths: A susceptible exposed infectious recovered dead model. J. Clin. Med. 2020;9:1350. doi: 10.3390/jcm9051350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Lipsitch M., Donnelly C.A., Fraser C., Blake I.M., Cori A., Dorigatti I., Ferguson N.M., Garske T., Mills H.L., Riley S., et al. Potential biases in estimating absolute and relative case-fatality risks during outbreaks. PLoS Negl. Trop. Dis. 2015;9:e0003846. doi: 10.1371/journal.pntd.0003846. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Gill P.E., Murray W., Saunders M.A. Large-scale SQP Methods and their Application in Trajectory Optimization. In: Bulirsch R., Kraft D., editors. Computational Optimal Control. Birkhäuser Basel; Basel, Switzerland: 1994. pp. 29–42. [Google Scholar]
- 10.Zhu H., Li Y., Jin X., Huang J., Liu X., Qian Y., Tan J. Transmission dynamics and control methodology of COVID-19: A modeling study. medRxiv. 2020 doi: 10.1101/2020.03.29.20047118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Li Q., Guan X., Wu P., Wang X., Zhou L., Tong Y., Ren R., Leung K.S.M., Lau E.H.Y., Wong J.Y., et al. Early transmission dynamics in Wuhan, China, of novel coronavirus-infected pneumonia. N. Engl. J. Med. 2020;382:1199–1207. doi: 10.1056/NEJMoa2001316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Grasselli G., Zangrillo A., Zanella A., Antonelli M., Cabrini L., Castelli A., Cereda D., Coluccello A., Foti G., Fumagalli R., et al. Baseline characteristics and outcomes of 1591 patients infected with SARS-CoV-2 admitted to ICUs of the Lombardy Region, Italy. JAMA. 2020 doi: 10.1001/jama.2020.5394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Chen N., Zhou M., Dong X., Qu J., Gong F., Han Y., Qiu Y., Wang J., Liu Y., Wei Y., et al. Epidemiological and clinical characteristics of 99 cases of 2019 novel coronavirus pneumonia in Wuhan, China: A descriptive study. Lancet. 2020;395:507–513. doi: 10.1016/S0140-6736(20)30211-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Yang Y., Lu Q., Liu M., Wang Y., Zhang A., Jalali N., Dean N., Longini I., Halloran M., Xu B., et al. Epidemiological and clinical features of the 2019 novel coronavirus outbreak in China. medRxiv. 2020:02. doi: 10.1101/2020.02.10.20021675. [DOI] [Google Scholar]
- 15.Zhou F., Yu T., Du R., Fan G., Liu Y., Liu Z., Xiang J., Wang Y., Song B., Gu X., et al. Clinical course and risk factors for mortality of adult inpatients with COVID-19 in Wuhan, China: A retrospective cohort study. Lancet. 2020;395:1054–1062. doi: 10.1016/S0140-6736(20)30566-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Imperial College COVID-19 Response Team . Estimating the Number of Infections and the Impact of Non-Pharmaceutical Interventions on COVID-19 in 11 European Countries. Imperial College London; London, UK: 2020. [Google Scholar]
- 17.Tuite A.R., Ng V., Rees E., Fisman D. Estimation of COVID-19 outbreak size in Italy. Lancet Infect Dis. 2020 doi: 10.1016/S1473-3099(20)30227-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Onder G., Rezza G., Brusaferro S. Case-Fatality rate and characteristics of patients dying in relation to COVID-19 in Italy. JAMA. 2020 doi: 10.1001/jama.2020.4683. [DOI] [PubMed] [Google Scholar]
- 19.Scafetta N. Distribution of the SARS-CoV-2 pandemic and its monthly forecast based on seasonal climate patterns. Int. J. Environ. Res. Public Health. 2020;17:3493. doi: 10.3390/ijerph17103493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Torri E., Sbrogiò L.G., Rosa E.D., Cinquetti S., Francia F., Ferro A. Italian public health response to the COVID-19 pandemic: Case report from the field, insights and challenges for the department of prevention. Int. J. Environ. Res. Public Health. 2020;17:3666. doi: 10.3390/ijerph17103666. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Xu X., Sun J., Nie S., Li H., Kong Y., Liang M., Hou J., Huang X., Li D., Ma T., et al. Seroprevalence of immunoglobulin M and G antibodies against SARS-CoV-2 in China. Nat. Med. 2020 doi: 10.1038/s41591-020-0949-6. [DOI] [PubMed] [Google Scholar]
- 22.Davies N.G., Klepac P., Liu Y., Prem K., Jit M., Eggo R.M. CMMID COVID-19 working group. Age-dependent effects in the transmission and control of COVID-19 epidemics. Nat. Med. 2020 doi: 10.1038/s41591-020-0962-9. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.