Comparing Structure-Function Relationships Based on Drasdo's and Sjöstrand's Retinal Ganglion Cell Displacement Models

Abstract

Purpose

To compare structure-function relationships based on the Drasdo and Sjöstrand retinal ganglion cell displacement models.

Methods

Single eyes from 305 patients with glaucoma and 55 heathy participants were included in this multicenter, cross-sectional study. The ganglion cell and inner plexiform layer (GCIPL) thickness was measured using spectral domain optical coherence tomography. Visual field measurements were performed using the Humphrey 10-2 test. All A-scan pixels (128 × 512 pixels) were allocated to the closest 10-2 location with both displacement models using degree and millimeter scales. Structure-function relationships were investigated between GCIPL thickness and corresponding visual sensitivity in nonlong (160 eyes) and long (200 eyes) axial length (AL) groups.

Results

In both the nonlong and long AL groups, compared with the no-displacement model, both the Drasdo and the Sjöstrand models showed that the structure-function relationship around the fovea improved (P < 0.05). The magnitude of improvement in the area was either comparable between the model or was larger for the Drasdo model than the Sjöstrand model (P < 0.05). Meanwhile, structure-function relationships outside the innermost retinal region that were based on the Drasdo and Sjöstrand models were comparable to or were even worse than (in the case of the Drasdo model) those obtained using the no-displacement model.

Conclusions

Structure-function relationships evaluated based on both the Drasdo and Sjöstrand models significantly improved around the fovea, particularly when using the Drasdo model. This was not the case in other areas.

The development of optical coherence tomography (OCT) has enabled the assessment of detailed glaucomatous structural changes, such as changes in the thickness of the circumpapillary retinal nerve fiber layer (RNFL) or the macular RNFL, ganglion cell inner plexiform layer (GCIPL).¹ In the macular area, especially near the fovea, retinal ganglion cell (RGC) bodies are displaced from their receptive fields because the Henle fibers and bipolar cells are connected laterally.^2,3 Drasdo et al.² and Sjöstrand et al.⁴ conducted histologic experiments using enucleated eyes, and their findings shed light on this issue and led them to propose models for calculating the magnitudes of this displacement. The Drasdo and the Sjöstrand models have since been used to adjust for RGC displacement in many previous studies of structure-function relationships,^1,5–13 and some of these studies have supported the usefulness of this approach in improving the structure-function relationship.^1,5,8

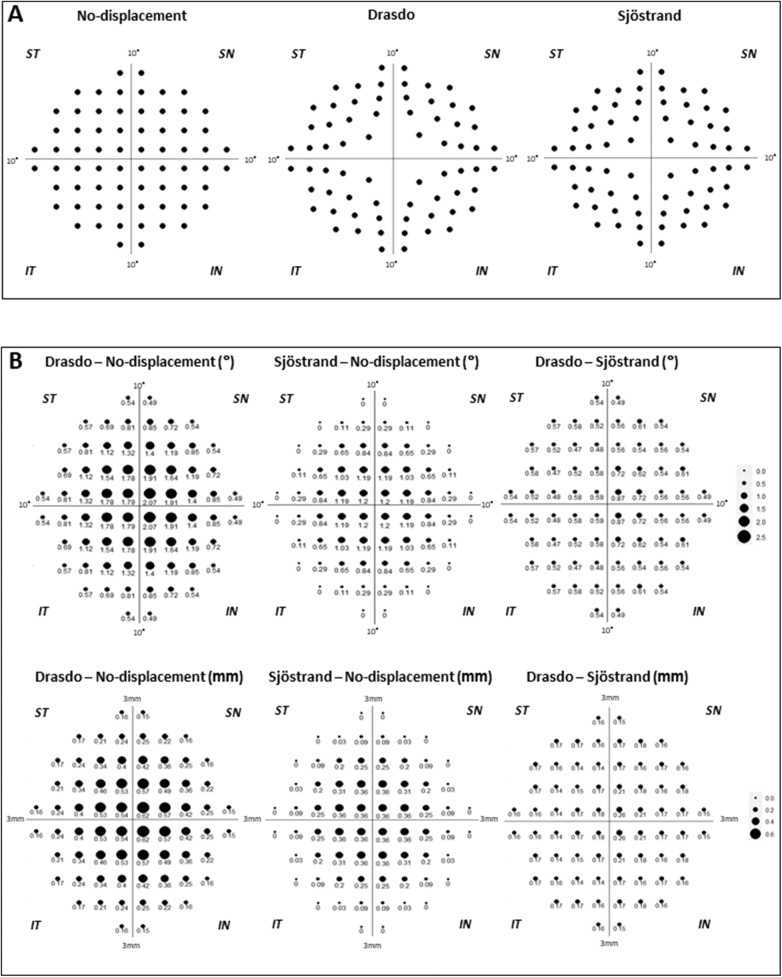
Of note, the magnitudes of RGC displacement are different between the Drasdo and Sjöstrand models, especially within approximately three degrees from the fovea (Fig. 1), because of their differences in the estimated lengths of Henle fibers (406 to 675 µm in Drasdo et al.² and 280 to 400 µm in Sjöstrand et al.⁴). In addition, the magnitude of RGC displacement when evaluated in the Sjöstrand model is laterally symmetrical, whereas in the Drasdo model, there is more displacement in the nasal area than in the temporal area. These differences result in different perceptions of the structure-function relationships; however, no previous study has investigated this.

Figure 1.

The 10-2 visual field test locations after RGC displacement and the difference in the extent of RGC displacement with each model. (A) The no-displacement, Drasdo, and Sjöstrand models are shown from left to right. (B) The differences in the extent of RGC displacement in the model are indicated by the sizes of the circles and numbers in degrees (top) and millimeters (bottom). The numbers under the circles are expressed as degrees. All data are shown as retinal views of the right eye. ST, superior temporal; SN, superior nasal; IT, inferior temporal; IN, inferior nasal.

The purpose of the current study was to compare structure-function relationships in the macular region given RGC displacements evaluated using the Drasdo and Sjöstrand models as well as a no-displacement model. These comparisons were performed separately in nonlong and long axial length (AL) eyes. In addition, the Humphrey Field Analyzer (HFA; Carl Zeiss Meditech, Dublin, CA, USA) 10-2 visual field (VF) was used in the current study because the OCT-scanned area mainly corresponds to the HFA 10-2 test.¹

Methods

This study was approved by the Research Ethics Committee of the Graduate School of Medicine and Faculty of Medicine at the University of Tokyo, Inoue Eye Hospital, Hiroshima Memorial Hospital, and JR Tokyo General Hospital. All patients provided written consent for their information to be stored in the hospital database and used for research. This study was performed according to the tenets of the Declaration of Helsinki.

Participants

In total, 305 eyes from 305 patients with open angle glaucoma and 55 eyes of 55 heathy participants were included in this multicenter, cross-sectional, case-controlled study. All participants were enrolled between May 2013 and October 2017 at either the University of Tokyo Hospital, Inouye Eye Hospital, Hiroshima Memorial Hospital or JR Tokyo General Hospital. All participants underwent complete ophthalmic examinations, including biomicroscopy, gonioscopy, intraocular pressure measurement, fundoscopy, refraction, best-corrected visual acuity test, and AL measurements, as well as OCT imaging and VF measurement.

Open angle glaucoma was defined as (1) the presence of typical glaucomatous changes in the optic nerve head, such as a rim notch with a rim width of ≤0.1 disc diameters or a vertical cup-to-disc ratio of >0.7 and/or an RNFL defect with an edge at the optic nerve head margin with a width greater than a major retinal vessel that diverged in an arcuate or wedge shape; (2) gonioscopically wide open angles with a grade of 3 or 4 based on the Shaffer classification; (3) age 20 years or older; and (4) eyes with visual acuity better than 0.5 LogMAR. Exclusion criteria were possible secondary ocular hypertension and other systemic or ocular disorders that could affect the study results. If both eyes of a patient met these criteria, one eye was randomly chosen.

Healthy participants were recruited from medical staff who were working at each hospital or the other eye of a patient who had unilateral retinal disease, such as age-related macular degeneration, retinal vein occlusion, epiretinal membrane, or retinal detachment. The inclusion criteria for the healthy eyes were as follows: (1) no abnormal findings except for clinically insignificant senile cataract on biomicroscopy, gonioscopy, and fundoscopy; (2) no history of ocular diseases, such as diabetic retinopathy, that could affect the results of OCT examinations; (3) age 20 years or older; (4) normal VF test results of HFA 24-2 or 30-2 according to the Anderson-Patella criteria¹⁴; and (5) intraocular pressure less than 21 mm Hg. Eyes with anomalous discs were cautiously excluded. If both eyes of a participant met these criteria, one eye was randomly chosen.

All eyes were divided into two groups: nonlong AL (22–25 mm) and long AL (25–28 mm).

VF Measurement

VF measurements were performed using the HFA 10-2 test (Swedish Interactive Threshold Algorithm Standard and Goldmann size III stimulus). Only reliable VFs were used in the analysis; these were defined as a fixation loss of less than 20% and a false-positive response of less than 15%.¹⁵ The false-negative rate criteria were not used.¹⁶ The VF of a left eye was mirror-imaged to that of a right eye, and the threshold value was used for statistical analyses.

OCT Imaging

OCT imaging was performed using an RS-3000 (NIDEK Co., Ltd., Aichi, Japan) within a period of 3 months from the HFA 10-2 VF measurement. OCT imaging was performed after pupil dilation with combined eye drops of 0.5% tropicamide and 0.5% phenylephrine hydrochloride (Midrin-P; Santen Pharmaceutical Co., Ltd., Osaka, Japan). In total, 255, 57, 39, 6, and 3 eyes were analyzed with software version 20000/2.00.01, 20300/2.04.00, 20301/2.03.01, 20000/2.00.00, and 21000/2.10.00, respectively. The raster scan protocol for a 30-degree visual angle (128 × 512 pixels) was used for all scans. Data with a signal strength index greater than 7 were included in the current analysis. Images that were unclear due to eye movements or involuntary blinking were acquired again or carefully excluded. All 65,536 (128 × 512) A-scan pixels of GCIPL thickness were exported for each eye, and the data obtained in the left eye were mirror-imaged to those obtained in the right eye for statistical analysis.

RGC Displacement and Calculation of GCIPL Thickness

In the current study, the Drasdo et al.² and the Sjöstrand et al.⁴ models were used to calculate RGC displacement. Figure 1A shows each location expressed as the retinal view of the right eye after RGC displacement by each model corresponding to the HFA 10-2 test locations. In addition, the differences in the magnitudes of RGC displacements associated with each model are shown in Figure 1B. Notably, in Sjöstrand et al.,⁴ the displacement was calculated only within 2 mm (7.5 degrees) from the fovea. Furthermore, displacement is calculated as a minus value when their formula is applied to points outside this area. Instead, we applied no displacement to these test points in the current study.

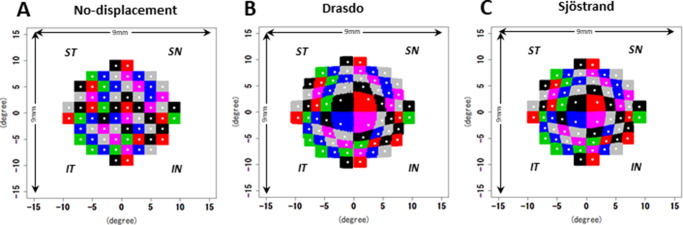
Figure 2 shows the allocation of OCT A-scan pixels to the 68 HFA 10-2 test locations with each model; 68 HFA 10-2 test locations were mapped onto OCT images. In the Sjöstrand et al.⁴ and Drasdo et al.² models, the RGC displacements were measured in millimeters using flat-mounted retina of enucleated eyes, and then the retinal arc lengths were converted from millimeters to degrees according to the formula provided in Dacey¹⁷:

$$\mathrm{y}=0.1+3.4x+0.035x^2$$ (1)

where y is the eccentricity in degrees, and x is eccentricity in millimeters. In the no-displacement model, the GCIPL thickness within a 2-degree square corresponding to 68 HFA 10-2 locations was calculated (Fig. 2A). In the current study, the 2-degree square was displaced based on the Drasdo and Sjöstrand models, and then the GCIPL thickness in the displaced area was calculated (Figs. 2B, 2C).

Figure 2.

The method used to allocate all A-scan pixels (65,536 pixels) to the 10-2 test locations. (A) A 2-degree square corresponding to each 10-2 test location was applied to the no-displacement model. For the Drasdo (B) and the Sjöstrand (C) models, all original A-scan locations within a 2-degree square were displaced by both models, and then the closest locations corresponding with the original A-scan locations were calculated. All data are shown as retinal views of the right eye.

One of the possible caveats of applying these displacements in degrees is that it is not known whether the fovea/macula stretches with eye growth; thus, there is uncertainty in whether the fovea/macula would have similar dimensions between eyes in degrees or in millimeters. Specifically, a 30-degree OCT scan area corresponds to a 9-mm × 9-mm area in eyes with AL = 24.38 mm, but this scan area (in degrees) may correspond to wider or narrower areas in millimeters. To investigate the influence of this aspect, we analyzed the structure-function relationship using displacement in millimeters, and the OCT scan area was exported from the device in millimeters.

Statistical Analysis

In the pointwise analysis, the structure-function relationship between visual sensitivity at each location and the corresponding GCIPL thickness with each model was assessed using a linear regression model, adjusting for age and AL. The obtained correlation coefficient values of paired models were compared using Hittner et al.'s modification¹⁸ of Dunn and Clark's z, in which a back-transformed average Fisher's z procedure was used. This calculation was performed using RGC displacements in degree and millimeter scales.

The structure-function relationship in the whole field was analyzed using a linear mixed model with adjustments for age and AL in which 68 HFA 10-2 test locations were included as a random effect. These calculations were performed using RGC displacements in both degree and millimeter scales. The goodness of the model fit was assessed using the corrected Akaike information criterion (AICc) statistic, which is a corrected value of the Akaike information criterion (AIC), so that an accurate estimation could be made, even when the sample size is relatively small. Any magnitude of reduction in the AICc value is suggestive of an improvement in the model, but the probability that compared with another model, any one particular model minimizes “information loss” can be calculated as follows. When there are n candidate models and the AIC_min is the minimum of the associated AICc values of AIC₁, AIC₂, AIC₃, …, AIC_n, the relative probability that the ith model minimizes information loss is equal to exp((AIC_min – AIC_i) / 2).¹⁹

All of these analyses were carried out in both the nonlong and long AL groups. Adjustment of P values for multiple comparisons was performed using the Bonferroni method.

All analyses were performed using the statistical programming language R (R version 3.5.0; Foundation for Statistical Computing, Vienna, Austria).

Results

The demographic data of the participants are shown in Table 1. Out of 55 healthy eyes, 36 were nonlong AL eyes, and 19 eyes were long eyes. Among 305 glaucomatous eyes, 124 eyes were nonlong AL eyes, and 181 eyes were long AL eyes. The demographic data of the nonlong AL and long AL groups are shown in Table 2. Figure 3 shows the mean VF sensitivity and standard deviation obtained in the nonlong and long AL groups (displayed as retina views in a right eye presentation). The mean deviation (MD) values were not significantly different between the nonlong and long AL groups. However, the mean sensitivity and visual sensitivities at 16 test locations were significantly higher in the nonlong AL group than in the long AL group (P < 0.05). Of these 16 locations, 13 were located in the superior retina (inferior VF test location) and around the fovea.

Table 1.

Demographic Data and Ocular Characteristics of All Participants

Variable	Total (N = 360)	Glaucoma (n = 305)	Healthy (n = 55)	P Value
Eyes, right/left, No.	164/196	145/160	19/36	0.079*
Sex, male/female, No.	149/211	137/168	12/43	0.0016*
Age, y	57.6 ± 14.6 [22 to 90]	60.9 ± 11.0 [22 to 90]	39.3 ± 18.50 [22 to 81]	<0.001†
Axial length, mm	25.20 ± 1.46 [22.01 to 27.97]	25.31 ± 1.45 [22.01 to 27.97]	24.57 ± 1.32 [22.31 to 27.06]	<0.001†
Refraction, D	–3.97 ± 3.65 [–14.00 to 4.00]	–4.05 ± 3.61 [–14.00 to 2.75]	–3.56 ± 3.83 [–13.25 to 4.00]	0.59†
Mean deviation, dB	–9.68 ± 9.24 [–30.37 to 2.41]	–11.36 ± 9.05 [–30.37 to 2.41]	–0.33 ± 1.02 [–2.89 to 2.05]	<0.001†
Pattern standard deviation, dB	8.01 ± 5.38 [0.74 to 16.52]	9.24 ± 4.92 [0.87 to 16.52]	1.19 ± 0.32 [0.74 to 2.71]	<0.001†

Data are expressed as the mean ± standard deviation [minimum to maximum] unless otherwise indicated.

^*Calculated with Fisher's exact test.

^†Calculated with the Wilcoxon rank sum test.

Table 2.

Demographic Data and Ocular Characteristics of the Nonlong and Long Axial Length Groups

Variable	Nonlong AL (n = 160)	Long AL (n = 200)	P Value
Type, glaucoma/healthy, No.	124/36	181/19	<0.001*
Eyes, right/left, No.	65/95	99/101	0.11*
Sex, male/female, No.	45/115	104/94	<0.001*
Age, y	60.0 ± 16.2 [22 to 90]	55.6 ± 13.0 [22 to 85]	<0.001†
Axial length, mm	23.84 ± 0.77 [22.01 to 24.98]	26.28 ± 0.83 [25.00 to 27.97]	<0.001†
Refraction, D	–1.41 ± 2.44 [–9.00 to 4.00]	–6.02 ± 3.12 [–14.00 to 0.50]	<0.001†
Mean deviation, dB	–8.90 ± 9.36 [–29.93 to 2.41]	–10.30 ± 9.11 [–30.37 to 1.59]	0.066†
Pattern standard deviation, dB	7.55 ± 5.67 [0.82 to 16.52]	8.38 ± 5.12 [0.74 to 16.30]	0.19†

Data are expressed as the mean ± standard deviation [minimum to maximum] unless otherwise indicated.

^*Calculated with Fisher's exact test.

^†Calculated with Wilcoxon rank sum test.

Figure 3.

The mean visual field sensitivity and standard deviations obtained in the nonlong and long axial length groups. The mean VF sensitivity (upper) and its standard deviation (lower) are shown as decibels in the nonlong (A) and long (B) AL groups, as indicated. The locations shown in red indicate that the mean VF sensitivity in the nonlong AL group was significantly higher than that obtained in the long AL group. (C) The P values were calculated by the Wilcoxon rank sum test. The locations shown in gray indicate a significant difference in the mean VF sensitivity between the nonlong and long AL groups. All data are shown as retinal views of the right eye.

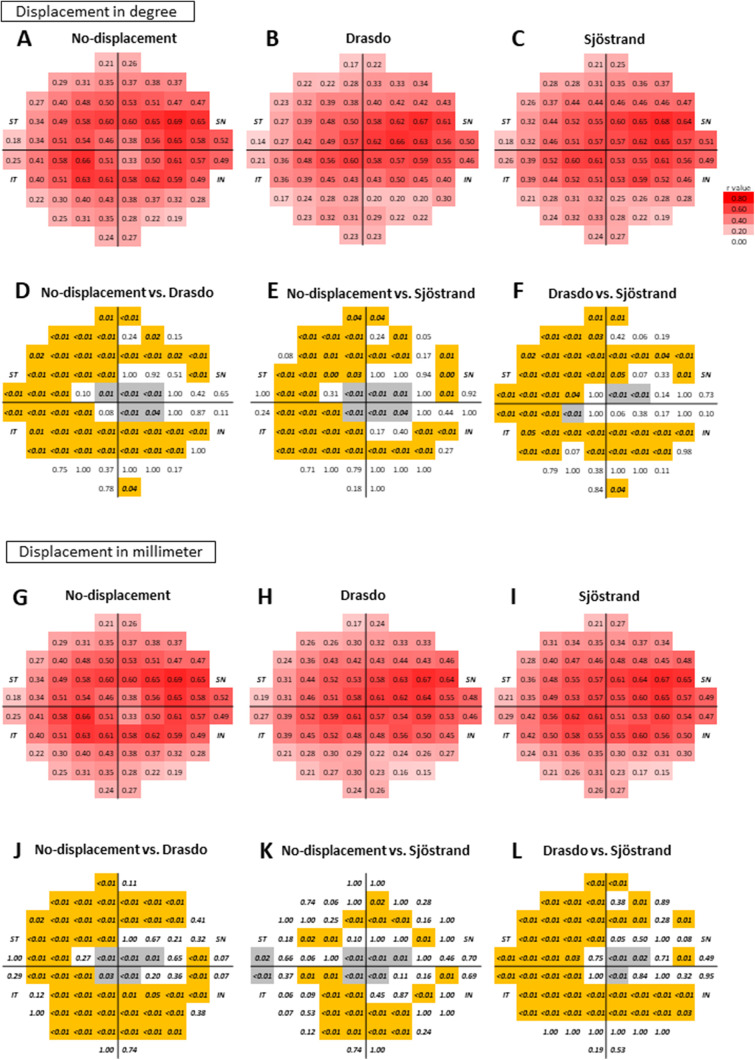
In the nonlong AL group (Fig. 4), the structure-function relationships based on the Drasdo and Sjöstrand models calculated in degrees were significantly tighter around the fovea than those of the no-displacement model, with adjustment for age and AL (P < 0.05, Dunn and Clark's z method modified by Hittner et al.¹⁸ Figs. 4A–4F). A similar tendency was observed when the displacements were calculated in millimeters (with adjustments for age and AL, P < 0.05, Dunn and Clark's z method modified by Hittner et al.¹⁸; Figs. 4G–4L). The distributions of the significantly improved locations were similar between the Drasdo and Sjöstrand models; they were densely distributed around the fovea. In contrast, the structure-function relationships based on the Drasdo and Sjöstrand models were significantly weaker than those of the no-displacement model outside this region, particularly in the temporal area, when using either degrees (Figs. 4A–4F) or millimeters (Figs. 4G–4L) for the displacement (with adjustment for age and AL, P < 0.05, Dunn and Clark's z method modified by Hittner et al.¹⁸). When comparing structure-function relationships between the Drasdo and Sjöstrand models, we found they were equal or significantly tighter in the foveal region when using the Drasdo model than when using the Sjöstrand model, regardless of the scale (degree or millimeters) used to calculate the displacement (with adjustments for age and AL, P < 0.05, Dunn and Clark's z method modified by Hittner et al.¹⁸; Figs. 4A–4L). In contrast, the structure-function relationships in the remaining areas were equal or significantly stronger when using the Sjöstrand model versus the Drasdo model regardless of whether the displacement was calculated in degrees or millimeters (with adjustments for age and AL, P < 0.05, Dunn and Clark's z method modified by Hittner et al.¹⁸; Figs. 4A–4L).

Figure 4.

The correlation coefficients between the ganglion cell inner plexiform layer thickness and visual field sensitivity with the displacement calculation in degrees and millimeters in the nonlong axial length group. The correlation coefficients (A–C: displacement in degrees and G–I: displacement in millimeters) of the nonlong axial length group are shown as r values with a color scale. The P values (D–L) are shown below correlation coefficients to compare the correlation coefficients between each model. The P values written in italic bold letters indicate P values that were less than 0.05. The locations shown in gray indicate that the structure-function relationships based the Drasdo and Sjöstrand models were better than those of the no-displacement model and that the structure-function relationship based on the Drasdo model was better than that of the Sjöstrand model. In contrast, the locations shown in orange indicate that the structure-function relationship based on the Drasdo and Sjöstrand models was worse than those of the no-displacement model, while those based on the Drasdo model were worse than those based on the Sjöstrand model. All data are shown as retinal views of the right eye.

In the long AL group (Figs. 5A–5L), a trend very similar to that found in the nonlong AL group was observed with each displacement model.

Figure 5.

The correlation coefficients between the ganglion cell inner plexiform layer thickness and visual field sensitivity with the displacement calculation in degrees and millimeters in the long axial length group. The correlation coefficients calculated as degrees (A–C: displacement in degree scale and G–I: displacement in millimeters) of the long axial length group are shown with a color scale. The P values (D–L) are shown below correlation coefficients to compare the correlation coefficients between each model. The P values written in italic bold font indicate that the P value was less than 0.05. The locations shown in gray indicate that the structure-function relationships based on the Drasdo and Sjöstrand models were better than those obtained by the no-displacement model, while those based on the Drasdo model were better than those based on the Sjöstrand model. In contrast, the locations shown in orange indicate that the structure-function relationships based on the Drasdo and Sjöstrand models were worse than those based on the no-displacement model and that the structure-function relationships based on the Drasdo model were worse than those obtained by the Sjöstrand model. All data are shown as retinal views of the right eye.

Table 3 shows the structure-function relationship in the whole field of each model. In the nonlong AL group, AICc values were smaller when based on the no-displacement model (80,709.1) than when based on the Drasdo model (81,408.3) and Sjöstrand model (80,870.1), using displacements in degrees. The relative probabilities of the Drasdo and Sjöstrand models minimizing information loss to lower than that obtained by the no-displacement model were 1.5 × 10^–152 and 1.1 × 10^–35, respectively. In other words, these values represent the probabilities that the no-displacement model was a better model than either the Drasdo or the Sjöstrand model for describing the structure-function relationship. In general, similar trends were obtained when the displacement was calculated in millimeters in the nonlong AL group. In this group, the AICc value obtained using the no-displacement model (80,660.3) was smaller than those obtained by the Drasdo (81,288.3) and Sjöstrand (80,782.5) models. The relative probabilities of the Drasdo and the Sjöstrand models minimizing information loss levels to be lower than that obtained by the no-displacement model were 5.1 × 10^–144 and 3.5 × 10^–34, respectively. A similar tendency was observed in the long AL group when the displacement was calculated in degrees; the AICc value obtained using the no-displacement model (104,485.2) was smaller than those obtained by the Drasdo (105,140.9) and Sjöstrand (104,761.6) models. The relative probabilities of the Drasdo and the Sjöstrand model minimizing the information loss level to be lower than that obtained by the no-displacement model were 4.1 × 10^–143 and 9.6 × 10^–61, respectively. In contrast, when the displacement was calculated in millimeters in this group, the Sjöstrand model had a smaller AICc value (104,730.4) than that in the no-displacement (104,809.7) and the Drasdo (105,071.5) models with a relative probability of 6.0 × 10^–18 and 8.5 × 10^–75, respectively.

Table 3.

Comparisons of Models to Explain the Visual Field Sensitivity Values Obtained in the Nonlong and Long Axial Length Groups

	Displacement, Deg					Displacement, mm
Variable	Coefficient	SE	P Value	AICc	RP	Coefficient	SE	P Value	AICc	RP
Nonlong AL group
No-displacement GCIPL thickness	0.38	0.0051	<0.001	80,709.1		0.38	0.0050	<0.001	80,660.3
Drasdo GCIPL thickness	0.38	0.0056	<0.001	81,408.3	1.5 × 10–152	0.38	0.0055	<0.001	81,288.3	5.1 × 10–144
Sjöstrand GCIPL thickness	0.38	0.0052	0.0038	80,870.1	1.1 × 10–35	0.38	0.0051	<0.001	80,782.5	3.5 × 10–34
Long AL group
No-displacement GCIPL thickness	0.25	0.0053	<0.001	104,485.2		0.23	0.0057	0.001	104,809.7	6.0 × 10–18
Drasdo GCIPL thickness	0.23	0.0058	<0.001	105,140.9	9.4 × 10–143	0.24	0.0057	<0.001	105,071.5	8.5 × 10–75
Sjöstrand GCIPL thickness	0.24	0.0055	<0.001	104,761.6	9.6 × 10–61	0.24	0.0054	<0.001	104,730.4

A linear mixed model corrected with age and AL was applied for all analyses.

Relative probabilities were obtained as the probability that the Drasdo or Sjöstrand models would minimize information to less than that of the no-displacement model.

RP, relative probability.

Discussion

In the current study, the structure-function relationships resulting from RGC displacements were investigated using the Drasdo and the Sjöstrand models in both nonlong and long AL eyes. We found that both models resulted in significantly better structure-function relationships than were achieved by the no-displacement model, particularly around the fovea, in both nonlong and long AL eyes. In contrast, the structure-function relationship deteriorated at the periphery of the foveal region in both the Drasdo and Sjöstrand models. When structure-function relationships were compared between the Drasdo and Sjöstrand models, they were comparable or significantly better around the foveal region when based on the Drasdo model, but this was not the case in other macular areas in either nonlong or long AL eyes. In nonlong AL eyes, the structure-function relationships of the whole field were significantly better based on the no-displacement model than with the Drasdo and Sjöstrand models, regardless of whether the scale of the displacement was in degrees or millimeters. A similar tendency was observed in long AL eyes, when the displacement was calculated in degrees or millimeters using the Drasdo and Sjöstrand models.

The mean sensitivity and pointwise sensitivities obtained at 16 locations were significantly higher in the nonlong AL group than in the long AL group. Out of 16 locations, 13 were located in the superior retina (inferior VF) and around the fovea. Aung et al.²⁰ reported that VF sensitivity was reduced in myopic eyes regardless of the method of correction by 0.33 dB and 0.20 dB per millimeter change in AL and per diopter change in refraction, respectively. Araie et al.²¹ reported that the power of myopia was significantly correlated with depression in the inferior VF of 10-2 test locations in glaucoma eyes. Sung et al.²² reported that among 99 eyes with early myopic normal tension glaucoma, 42 (42.42%) showed scotoma within 10 degrees. As implied by these studies, VF sensitivity tends to decrease as myopia increases, and myopic glaucoma eyes tend to show inferior and parafoveal VF defects. The results of the current study agree with these previous reports.^20–22

In the current study, both the Drasdo and the Sjöstrand models resulted in better structure-function relationships than those achieved by the no-displacement model, particularly around the fovea. Ohkubo et al.⁵ compared the pointwise structure-function relationships of patients with glaucoma (average MD value of HFA 10-2 test: –5.49 ± 5.74 dB; range, –20.25 to +2.94 dB) in nonlong AL eyes (more than –6 diopters of myopia) using the Sjöstrand model. They reported that the structure-function relationship improved at the innermost four test points, but the changes were not significant. In agreement with their findings, in the current study, the structure-function relationships at the innermost four test points were significantly better when based on either the Sjöstrand or Drasdo model than when based on the no-displacement model in the nonlong AL group (average MD value of HFA 10-2 test: –8.90 ± 9.36 dB; range, –29.93 to 2.41 dB). This difference in statistical significance could be attributable to differences in sample sizes between the two studies: 60 eyes were included in Ohkubo et al.,⁵ while 160 eyes were included in the current study. Additionally, the stage of glaucoma was more advanced and the range of stages was much wider in the current study than in the previous study,⁵ and this result could have influenced the analysis of the structure-function relationships. The current results suggested that a very similar degree of improvement was also observed in the long AL group (MD value: –10.30 ± 9.11 dB; range, –30.37 to 1.59 dB).

In contrast to findings in the central fovea region, in the periphery of the fovea, structure-function relationships were not improved by either the Sjöstrand or the Drasdo model in the current study. Indeed, the results were significantly better when findings were based on the no-displacement model than when they were based on the Sjöstrand or Drasdo models. The reason for this result is not entirely clear, but we propose the following possible reasons.

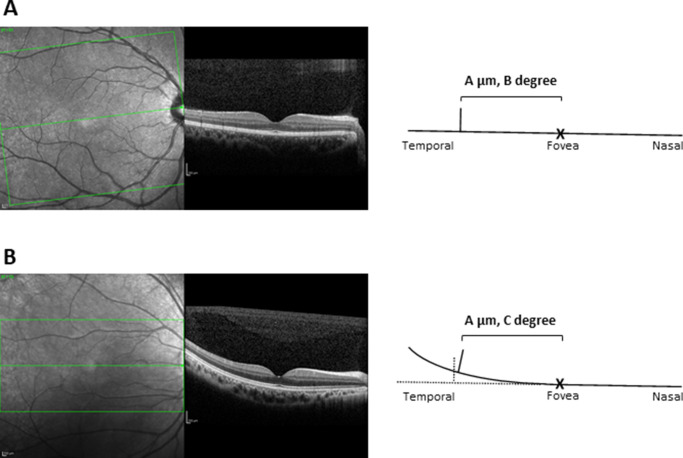
The first possible reason is the tilt of the retina from the visual axis. In the experiments described by Sjöstrand et al.⁴ and Drasdo et al.,² RGC displacements in enucleated eyes were measured in anatomical sections of the flat-mounted retina. However, the retina does not exist in this “flat” shape in the eye in vivo, and the displacement effect over a distance is not identical to that of the angle when the retina is titled. For instance, when the macular area is relatively flat, the influence of retinal tilt would be only marginal (Fig. 6A). However, when the retina is tilted sharply in a more peripheral area, the discrepancy between the displacement in the distance and that at the angle becomes large (the displacement effect by angle decreases more than the displacement effect by distance; Fig. 6B). Finding that structure-function relationships are weaker in the long AL group than in the nonlong AL group in this area would support this theory, because this effect would be exaggerated in more elongated eyes. This could also explain the more obvious tendency for this to occur in the temporal retinal area because individual variation in temporal retinal tilt could not be evaluated in the eyes studied in the current study, and it is therefore necessary to further investigate the relationship between retinal tilt and RGC displacement in the temporal retinal area in the future.

Figure 6.

Influence of temporal retinal tilt on displacement. Representative images of a “flat retina” (A) and a “tilted retina” (B) measured with OCT. Retinal tilt only subtly influenced results in the “flat retina” (A). In contrast, the discrepancy between the displacement in the distance and that found for the angle becomes large in the “tilted retina” (B). For example, OCT (Spectralis; Heidelberg Engineering GmbH, Heidelberg, Germany) images were not obtained from the studied eyes in the current study.

Second, the Dacey¹⁷ formula was used to convert the degree of the angle to the dimensions of the retina (in millimeters) in the current study and in the studies by Sjöstrand et al.⁴ and Drasdo et al.² However, this model involves a conversion of the degree of angle to the dimension of tangent retina (in millimeters) when an image is projected on the retina. In other words, the converted dimension of the tangent retina (in millimeters) is not identical to the circumferential dimension of the retina (in millimeters). Hence, areas closer to the periphery of the fovea would show more exaggerated divergence.

Third, in both the Sjöstrand and Drasdo models, it was not possible to trace any single Henle fiber, and thus, Henle fiber lengths were measured as either the vectoral length parallel to the retinal surface in a slice⁴ or along a path inferred through an aggregate of fiber cross sections that were either long and longitudinally oriented given their origin in the foveal center or that were short and oblique when orienting in the parafovea.² This implies that it may not be possible to obtain a perfectly accurate estimation of Henle fiber length, particularly in the thinner temporal retina. In addition, it is difficult to identify each bipolar cell histologically, and the amount of lateral displacement that occurs at the bipolar cell is unknown in humans. Hence, this displacement was not included in the calculation of RGC displacement in the study by Sjöstrand et al.⁴ (this point was not described in detail in the study by Drasdo et al.²).

Both the Sjöstrand and the Drasdo models were derived from anatomical observations of enucleated eyes; however, different magnitudes of RGC displacements are suggested by each model. In general, they were larger in the Drasdo model, but this tendency was exaggerated near the fovea. Turpin et al.⁶ computed customized RGC displacement for individual eyes by taking into account macular shape parameters in healthy eyes to investigate structure-function mapping. On average, they found that while the displacement agreed when based on the Drasdo model, there was a considerably large amount of individual variations (between 0.9 and 1.4 degrees) in the magnitudes of the RGC displacement at the four innermost locations. This result implies that magnitude of the difference in the RGC displacement between the Drasdo and the Sjöstrand models is between 0.59 to 0.87 degrees, and this difference may be because of individual variance; Drasdo's and Sjöstrand's anatomical observations were made using a very limited number of enucleated eyes (five or six). Our results suggested that around the fovea, improvement in the structure-function relationship is on average better when using the Drasdo model than the Sjöstrand model.

Structure-function mapping²³ and the ganglion cell layer thickness itself have been reported to be highly variable in eyes with long AL.^24,25 Indeed, previous studies have reported that such eyes often have tessellation,^26,27 inferior staphyloma,²⁸ and dome-shaped deformation of the macula,²⁹ which is a mild deformation of the posterior pole caused by stretching of the retina associated with the elongation of the eye.³⁰ Moreover, Li et al.³¹ reported 429 (48.3%) of the 888 long AL eyes (27.51 ± 1.63 mm) had optic disc rotation (or tortion); of these 429 eyes, 367 (85.5%) showed rotation. Other reports suggested similar findings.^32,33 These structural and functional alterations observed in long AL eyes may be the reason that structure-function relationships were weaker in long AL eyes than in nonlong AL eyes in the current study. However, it is worth noting that despite these structural variabilities, structure-function relationships improved more in the foveal area when based on the Drasdo model than when based on the Sjöstrand model, similar to our findings in nonlong AL eyes.

The Dacey formula¹⁷ converts between degrees and millimeters, hypothesizing the AL to be 24.38 mm. The magnitude of the RGC displacement in degrees is larger than that in millimeters because of the magnification effect in long AL eyes. The current results suggested that no obvious difference was observed between displacement calculation in degrees and millimeters (Figs. 4–5). This implies that the lack of improvement seen in the structure-function relationship in the peripheral macular area with either the Sjöstrand or Drasdo model, compared with the no-displacement model, was not simply because of the possible inaccurate conversion from degrees to millimeters using Dacey's formula. The current results should be contrasted with future anatomical experiments in enucleated long AL eyes because it is not known whether Henle fibers stretch with the growth of AL.

The current study has limitations. First, as mentioned above, the individual variation in RGC displacement was not taken into account for each model. Second, we adopted a nonlinear model between dimensions of the retina (in millimeters) and the degree of angle reported by Drasdo and Fowler.³⁴ In general, this approximation is correct more than 50 degrees from the fovea, but there might be marginal deviation within 10 degrees from the fovea. With regard to the reliability of OCT and VF measurement, the reliability was better for OCT measurement than for VF measurement. Recently, we reported that the structure-function relationship measured with fundus tracking perimeter MP-3 was better than that obtained via a traditional HFA VF test. Additionally, we reported that the accuracy of the VF test, which measures macular disease, was improved when measured with a fundus tracking perimeter MP-3.^35,36 These limitations should be considered in future studies.

In conclusion, around the fovea, the use of both the Drasdo and Sjöstrand models significantly improved the structure-function relationships in both nonlong and long AL eyes, while at the periphery of the macula, structure-function relationships based on both models were comparable or were even worse than those obtained using a no-displacement model. Overall, the structure-function relationship was better when using the no-displacement model than when using the Drasdo and Sjöstrand models.