Clinical Corneal Optical Coherence Elastography Measurement Precision: Effect of Heartbeat and Respiration

Abstract

Purpose

Normal physiological movements (e.g., respiration and heartbeat) induce eye motions during clinical measurements of human corneal biomechanical properties using optical coherence elastography (OCE). We quantified the effects of respiratory and cardiac-induced eye motions on clinical corneal OCE measurement precision and repeatability.

Methods

Corneal OCE was performed using low-force, micro-air-pulse tissue stimulation and high-resolution phase-sensitive optical coherence tomography (OCT) imaging. Axial surface displacements of the corneal apex were measured (M-mode) at a 70-kHz sampling rate and three different stimulation pressures (20–60 Pa). Simultaneously, the axial corneal position was tracked with structural OCT imaging, while the heartrate and respiration were monitored over a 90 second period.

Results

Respiratory- and cardiac-induced eye motions have distinctly lower frequency (0.1–1 Hz) and much greater amplitude (up to ± 50 µm movements) than air-pulse-induced corneal tissue deformations (∼250 Hz, <1 µm). The corneal displacements induced during OCE measurements in vivo were –0.41 ± 0.06 µm (n = 22 measurements, coefficient of variation [CV]: 14.6%) and –0.44 ± 0.07 µm (n = 50 measurements, CV: 15.9%), respectively, from two human subjects at 40 Pa stimulation pressure. Observed variation in corneal tissue displacements were not associated with tissue stimulation magnitude, or the amplitude of physiologically induced axial eye motion.

Conclusions

The microsecond timescale and submicron tissue displacements observed during corneal OCE measurements are separable from normal involuntary physiological movements, such as the oculocardiac pulse and respiratory movements.

Translational Relevance

This work advances innovations in biomedical imaging and engineering for clinical diagnostic applications for soft-tissue biomechanical testing.

Introduction

Corneal biomechanical properties (e.g., stiffness) are directly related to structural integrity, ocular health, and vision functions of the human eye,^1–3 and are often changed by corneal diseases⁴ (e.g., keratoconus, ectasia), corneal surgeries⁵ (such as LASIK), and corneal collagen cross-linking surgeries. Elastography is an elasticity imaging method developed to distinguish between normal and diseased tissues by quantifying a tissue's elastic response to mechanical loads.^6–8 Optical coherence elastography (OCE),⁹ based on optical coherence tomography (OCT) imaging, can provide higher axial and lateral spatial resolution with greater measurement precision than ultrasound and magnetic resonance elastographies.¹⁰ Currently, corneal elastography imaging, especially noninvasive in vivo measurement, is still a challenge, and there is no widely accepted standard yet. The development of new methods to measure structural properties of the cornea has become one of the top priorities in the field of corneal biomechanics.¹

Brillouin microscopy has been applied for corneal biomechanical measurements following corneal collagen cross-linking¹¹ and keratoconus in vivo.¹² Mapping of corneal biomechanics using Brillouin microscopy is time-consuming, taking tens of seconds to minutes. Therefore the time this method takes to achieve completion of the requisite confocal depth-scans and to collect the weak scattered signals presents a challenge for patients.¹³ The Ocular Response Analyzer (Reichert Inc.)¹⁴ and CorVis ST (OCULUS Optikgeräte GmbH)¹⁵ are two commercially available clinical devices for evaluating corneal biomechanical properties. Both methods apply large magnitude (70–300 kPa; 10–40 psi), long duration (10–30 ms) air pulse for tissue stimulation that result in global corneal deformation, ocular motion, and aqueous fluid displacement. These factors confound measurements of ocular biomechanics and precludes any possibility of spatially resolved measurements that would be necessary to detect minute variations in spatial stiffness.¹⁶ Previous clinical studies with these instruments have produced conflicting results of measured corneal stiffness for patients following cross-linking treatments.^17–20

OCE imaging systems are comprised of a static^9,21–23 or dynamic^24–26 loading system to induce physical tissue deformation and a high-resolution imaging system, for example, phase-sensitive OCT to analyze the tissue response. Tissue biomechanical properties (e.g., the Young's modulus¹⁰ and viscoelasticity^27,28) can be derived or estimated from the applied deformation force and the observed response. In this study, a microscale air-pulse stimulator was developed for corneal elasticity imaging to provide low force (20–60 Pa; 0.003–0.009 psi), short duration (≤1 ms) tissue excitations that were spatially localized (150 µm diameter).²⁹ The development of phase-sensitive OCT imaging has further improved dynamic OCE imaging by enhancing the displacement detection sensitivity from a micrometer scale (for intensity measurements) to a nanometer or subnanometer scale.^30–37 In our previous studies, we reported displacement detection sensitivities as low as 0.24 ± 0.07 nm.¹⁰ This phase-sensitive OCE system has demonstrated high-resolution quantification of tissue displacement, and it enables the visualization and analysis of laterally propagating elastic waves in dynamic OCE.^8,10,24 Previous studies involving ex vivo measurements of rabbit^32,38–40 and porcine^28,41–43 corneas have demonstrated that the stiffness of the cornea increases after corneal collagen cross-linking,^32,39,42 at higher intraocular pressures (IOPs),⁴¹ and at older ages.

During in vivo corneal stimulation and image acquisition, physiological movements, such as respiration, heartbeat, and ocular pulsations, can cause changes in ocular surface position in addition to involuntary fixational eye motions or head motion.⁴⁴ Although the effects of physiological movements on OCT and OCT angiography have been studied,^45–47 their effects on dynamic OCE measurements have not. Optimally, mechanical tissue stimulation during elastography imaging is aligned normal to the tissue to result in axial tissue displacements. This geometric configuration simplifies the analytical methods required to derive the tissue biomechanical properties.⁴⁸ Other tissue motion during OCE imaging due to normal physiological movements (e.g., breathing, vascular pulsations, or other motion) could result in response amplifications, tissue misalignments during stimulation, as well as variations in the stimulus force delivered. In theory, these uncertainties could cause measurement variability and ultimately ambiguous clinical interpretations.⁴⁹ To address these concerns, we sought to characterize the amplitude, frequency, and timescale of axial eye motion during OCE imaging, to quantify the potential effects of these parameters on measurement variability and precision, and to assess their potential impact on clinical interpretation of in vivo OCE measurements.

In this study, the effects of normal physiological movements, such as respiration and heartbeat, were assessed relative to the measurement precision and repeatability of the prototype corneal phase-sensitive OCT elastography imaging system. We investigated the relationship between axial eye motion, heartbeat, and breathing motion using simultaneous in vivo OCT imaging of the corneal apex and electronic pulse monitoring. We also assessed the effects of axial corneal surface motion on measurement repeatability by simulating the magnitude and frequency of normal physiological eye motion in vitro with a corneal tissue phantom. The mechanical response of corneal tissues and tissue phantoms were measured in M-mode (involving repeated A-scan acquisitions over time at the same location). The primary tissue surface deformation was used as an indicator to evaluate the repeatability and precision of the measurements.

Methods

Human Subjects

This research involved healthy human subjects and adhered to the tenets of the Declaration of Helsinki. Informed consent was obtained from the participants after explanation of the study, as well as the possible consequences of their participation. This research was approved by the institutional review board of the University of Alabama at Birmingham.

Corneal OCE System

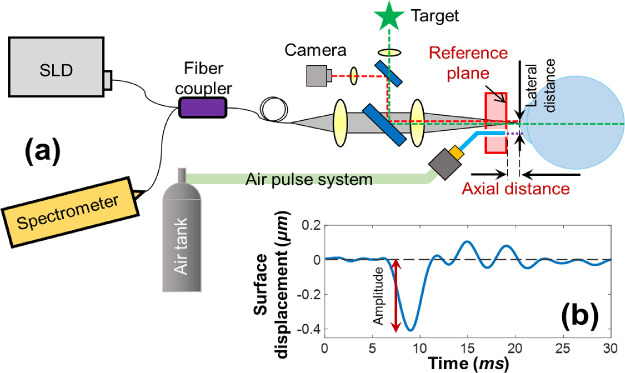
A home-built prototype corneal OCT elastography system was modified from our OCE system presented previously.¹⁰ The axial corneal position was tracked using structural OCT imaging, whereas the corneal displacement response to mechanical stimulation was analyzed using OCE imaging. During imaging, subjects sat in a chair and placed their chin on a chin rest with the forehead stabilized against a head rest using an elastic band. The combination of a fixation target and a camera was used to locate and measure the corneal position. A low-force air-pulse stimulator was used to generate submicron scale corneal tissue displacements,²⁹ and a common-path phase-sensitive OCT system was used to detect the dynamic mechanical responses of the cornea, as shown in Figure 1a. Corneal elastography can be performed as a repeated measure (M-mode) to capture dynamic corneal surface displacement profiles at a single location,¹⁰ or in a scan mode to track elastic wave propagation through the tissue as a function of time.

Figure 1.

Schematic of corneal OCT elastography and the measured tissue displacement profiles. (a) A corneal OCT elastography system was combined with a fixation target and a camera to monitor the measured area, an air-pulse stimulator to provide localized tissue excitation, and a common-path OCT instrument to detect the resulting mechanical wave and tissue deformation. SLD, superluminescent laser diode. (b) A typical in vivo corneal surface displacement profile measured in M-mode. The displacement amplitude was calculated from the surface baseline to the initial negative maximum primary deformation. The lateral distance between the stimulation point and the measurement point was 0.3 mm. The axial distance was varied in this experiment from 0.5 to 2.5 mm.

The common-path OCT system utilized an 845-nm superluminescent laser diode (SLD, D-855, Superlum Diodes Ltd.) with 100-nm waveband. The sample and reference arms shared a common optical path with a reference plane defined as the optical surface of a reference plate (5-mm thick acrylic plate) proximal to the sample. Interference signals from the common path were returned to a spectrometer with 4K pixels and a 70-kHz A-line speed. The structural resolutions were 3.3 µm in the axial direction and 7.8 µm in the lateral direction, and the maximum imaging depth was 6.76 mm (all calculated in air). The phase detection sensitivity was 0.24 nm.¹⁰ A microscale air-pulse stimulator²⁹ was synchronized with the OCT imaging signal to provide short duration (≤1 ms), localized (150 µm), and low force (≤60 Pa) tissue excitations that were normal to the corneal surface. Medical grade air was delivered to the sample through a small diameter cannula (150 µm). This cannula was set at a distance of ∼0.5 mm behind the external surface of the reference plane to prevent contact with the cornea. Previous results from this air-pulse stimulator have demonstrated that the excitation force remains constant over a distance of 10 mm.²⁹

Displacement Measurement

Phase changes at a specified axial depth φ_z(t_J − t₀) can be resolved and unwrapped by tracing one point from time t_J to the referenced time point t₀ among the successive A-scan signals.¹⁰ The change in axial displacement for the sample surface in air, Δz(t_J − t₀), is therefore represented by the observed phase change using Eq. (1), where λ₀ is the center wavelength.³⁵

$$\Delta z\left(t_J-t_0\right)=\frac{{\lambda }_0}{4\pi }\times {\varphi }_z\left(t_J-t_0\right)$$ (1)

Typical induced corneal displacements of one point in M-mode include a baseline before sample excitation (noise level), an initial negative primary surface displacement, a recovery response that is related to tissue viscoelasticity, and a period of damped oscillatory motion (Fig. 1b). Our previous work¹⁰ demonstrated that the primary deformations were directly driven by the applied excitation forces. Stiffer samples tended not to deform as much as less-stiff samples did under the same load. The value of the correlation (stress/strain⁵⁰) between the primary deformations and the applied forces would therefore be useful to distinguish tissues of different stiffness. Here we used the value of the primary deformation as an indicator to evaluate the measurement precision and repeatability.

Axial Motion Quantification

Corneal axial motion was quantified as the change in axial distance (Fig. 1a) by OCT imaging in the absence of any stimulation. Two healthy human volunteers with no history of ocular disease were involved in this study. The IOPs of their individual left eyes were 15 and 14 mm Hg, as measured by Icare ic200 eye tonometer (Icare Oy, Vanda, Finland). The corneal apex positions of their left eyes were tracked by OCT over a time course and were then decomposed in the frequency domain to ascertain the effects of respiration and heartbeat cycles. During corneal position tracking, subjects were allowed to blink, and eye motions were analyzed in the intervals between blinks. The blink interval was usually 3 to 20 seconds. Corneal positions were tracked at least 30 seconds and at most 2 minutes. The pulse rate was measured from a pressure transducer sensing (TN1012/ST, ADInstruments Inc., Colorado Springs, CO) at the subjects’ fingertip of left hands. Ocular position changes owing to inspiration and expiration were noted as a low-frequency sinusoidal pattern as shown in previous studies.⁵¹ We recorded the onset of inspiration and expiration by having subjects press a button to annotate the eye motion record. Heartrate, respiration, and eye position were synchronized using a data acquisition system (PowerLab 8/35, ADInstruments Inc.).⁵²

Surface Displacement Measurement for Corneal Tissue Phantoms

We first assessed the effects of axial eye motion on M-mode elastography measurement precision in vitro with a corneal tissue phantom (2% agar).^10,34,53 This simulation experiment was a simplification of the eye motion observed in vivo with similar motion amplitude and frequency. This model does not consider corneal curvature, surface rotation, or lateral positional effects that could be induced by eye motion. An agar phantom was attached to a translation mount (SM1Z, Thorlabs, minimal readable increment: 1 µm) and moved at amplitudes of ± 5 to 20 µm and at frequencies of 0.2 to 1.4 Hz (speeds: 5.0–26.8 µm/s) to mimic the motions induced by respiration and heartbeats.^45,46 To simulate a range of possible effects due to eye motion, a total of eight measurement conditions were defined with different axial motion amplitudes and speeds, as shown in the Table. The air force was set as 20 Pa and 10 Hz. Therefore each displacement measurement was 100 ms. The elastic responses of agar phantoms from each test group were observed at a lateral distance of 0.3 mm away from the stimulation force. Each measurement was repeated 50 times in 5 seconds.

Table.

Motion Measurement Conditions by Group

Test #	Test 1	Test 2	Test 3	Test 4	Test 5	Test 6	Test 7	Test 8
Amplitude (µm)	± 5	± 5	± 10	± 10	± 15	± 15	± 20	± 20
Speed (µm/s)	5.0	14.0	5.4	19.6	9.0	22.8	8.8	26.8
Frequency (Hz)	0.5	1.4	0.27	0.98	0.30	0.76	0.22	0.67

In Vivo Corneal Surface Displacement Measurements

We evaluated the displacement measurement precision of in vivo corneas at different measurement positions and stimulation forces in M-mode. The lateral distance between the center of the stimulation point and the measurement point was 0.3 mm. The time required for OCE imaging was limited in this experiment by stimulation frequency (100 ms). OCT imaging speed was 70-kHz A-line frequency and a 30-ms B-scan period. The total OCE image acquisition time was 1 second for 10 repeated measurements and could be less if a higher stimulation frequency is used. Signal processing was completed during acquisition and was nearly real-time with a delay that was on the order of milliseconds.

In the first set of measurements, the stimulation pressure was 40 Pa, four groups of repeated measurements (with n = 9, 10, 5, and 10 measurements) were performed on subject 1 as the axial position was changed by a distance of ∼2 mm. Next, we performed a second set of measurements. These were performed at a fixed measurement position (∼1 mm from the reference plane) with air-pulse pressures set as 20 Pa (n = 23 and 22), 40 Pa (n = 22 and 50), and 60 Pa (n = 16 and 52) for both subjects. The variations in axial eye motions during image acquisition and the variations of the resulting displacements for each measurement were recorded and compared.

Results

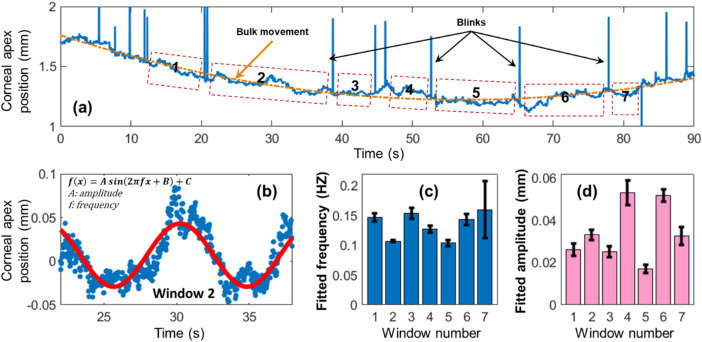
Figure 2 demonstrates an example of respirational eye motion, tracked by OCT imaging in the axial (depth) direction. The corneal apex position of subject 1 was tracked for 90 seconds, as shown inFigure 2a. Bulk motion was fitted to a first-order Fourier curve (orange line). Tracking of the cornea was lost when blinks occurred (shown as spikes) but returned to normal when these blinks had finished. Respirational corneal motions were clearly observed from the raw data and were divided into seven windows between eye-blinks for frequency analysis. Eye motion due to cardiovascular pulsations were low in amplitude for this subject relative to the bulk motion and are not visible unless the timescale is magnified. Figure 2b demonstrates a sinusoidal fitting for window 2 with low-order bulk motion removed. This motion was dominated by respiration based on the temporal and frequency features. Figures 2c and 2d show the calculated (mean ± 95% confidence interval [CI]) motion frequencies and amplitudes for each of the analyzed windows. The respirational motion was calculated as 0.13 ± 0.01 Hz (mean ± 95% CI) in frequency and 34.1 ± 3.3 µm in amplitude for these subwindows.

Figure 2.

Axial corneal positions were observably affected by respiration. (a) Axial corneal position tracking of subject 1 by OCT imaging. Bulk motion (orange line) and respirational fluctuation were clearly seen from the raw data. A total of seven subwindows were selected for analysis. Panel (b) demonstrates a sinusoidal pattern for window 2, which was dominated by respiration. Panels (c) and (d) demonstrate the fitted (mean ± 95% CI) respirational motion frequencies and amplitudes for each subwindow.

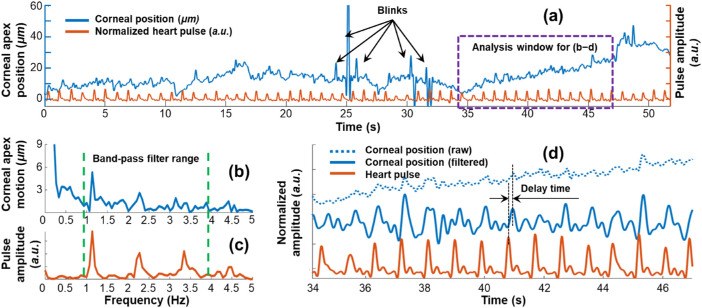
Figure 3 demonstrates a heartbeat-induced eye motion example from subject 2, tracked by OCT imaging in the axial direction for 52 seconds. The pulse amplitude (measured at the finger) was plotted in an arbitrary unit (a.u.). As shown in Figure 3a, a clear correlation was observed between the axial corneal motion and the heartbeat over a time course.Figures 3b–d demonstrate the analysis results for the selected window in Figure 3a. A Fast Fourier Transform method was used to compare the motion frequencies. The corresponding fundamental frequencies and the harmonics of up to four orders were clearly correlated from the eye motion (Fig. 3b) and from the heartbeat (Fig. 3c). We used a band-pass filter (0.8–3.8 Hz) to isolate the main motion frequencies, and then compared the raw and filtered corneal positions and the heartbeat in the temporal domain again (Fig. 3d). We measured the time difference between the heartbeat-related eye motion and the recorded heartbeat as 71.3 ± 22.3 ms (mean ± 95% CI). This delay was generated because the distance between the heart and eye was different from the distance between the heart and the pulse monitor placed on the subject's finger.

Figure 3.

Axial corneal position was affected by cardiovascular pulsations in the time domain and frequency domain. The pulse amplitude was plotted in an arbitrary unit (a.u.). (a) A clear correlation was observed between the corneal position and the heartbeat frequency. Fast Fourier Transform results for the analysis window demonstrates the corresponding frequency components from eye motion (b) and heartbeat (c). A band-pass filter that included the main frequency components was utilized. Panel (d) compares the raw and filtered signals (corneal position and heartbeat) over time for the selected window. Results were normalized and shifted along the Y-axis for comparison. The time delay between the heartbeat and heartbeat-related eye motion was measured as 171.3 ± 22.3 ms (mean ± 95% CI).

Measurements were repeated five times for each participant, and the time duration for each measurement was approximately 30 to 110 seconds. Subwindows between eye-blinks (n = 29 and 18, respectively) were chosen for analysis, and the time duration for each window was 3 to 20 seconds. Figure 4 compares the frequency components from the measured respirations and heartbeats and from the eye motions of the two subjects. Figure 4a shows clear correlations for the frequency components between the breaths (∼0.16 Hz) and breath-related eye motions (∼0.15 Hz), and between the heartbeats (∼1.06 Hz) and heartbeat-related eye motions (∼1.11 Hz). In Figure 4b, the amplitudes of respirational eye-motion (mean: 30.43 and 14.38 µm, respectively) were larger than the amplitudes of heartbeat-related eye-motion (mean: 3.79 and 7.56 µm, respectively).

Figure 4.

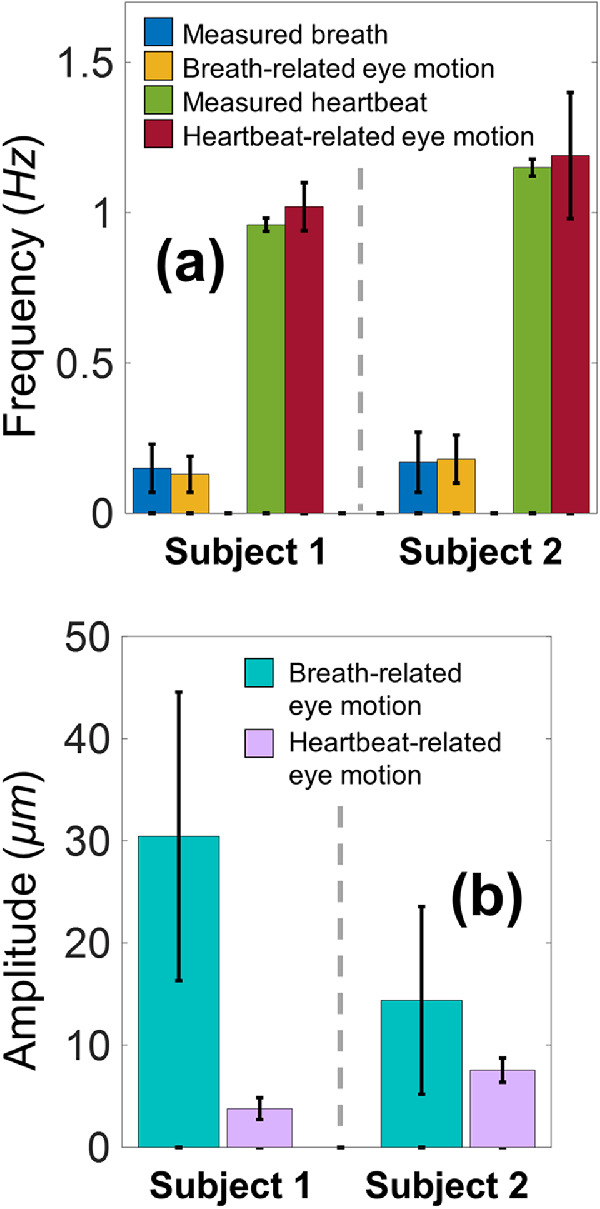
Comparison of the fundamental motion frequency components from the measurements of eye motion, heartbeat, and breathing via Fast Fourier Transform (n = 29 and 18 analyzed windows, respectively, for the two human subjects). (a) Clear correlations were observed for the frequency components between the breaths and breath-related eye motions, and between the heartbeats and heartbeat-related eye motions. (b) Quantification of the breath-related and heartbeat-related eye motion amplitudes.

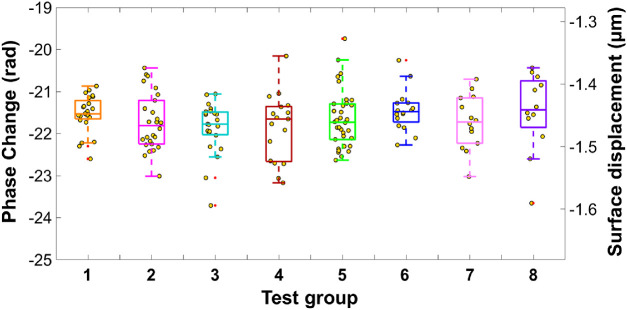
Figure 5 shows the measured surface displacements from tests 1 through 8 (Table) for the 2% agar tissue phantoms. The double y axis demonstrates the phase changes (left axis) and the converted displacements (right axis) using Eq. (1). The median displacement amplitudes for all these tests ranged from –1.441 to –1.467 µm. The maximum difference among the median values was only 0.026 µm, which is close to the range of these tests’ interquartile values, which range from 0.029 to 0.074 µm.

Figure 5.

Elastic displacement measurements (mean ± SD: –1.457 ± 0.044 µm) of 2% agar phantoms show no obvious difference among the eight test groups that were classified by different patterns of motion amplitudes and speeds (Table).

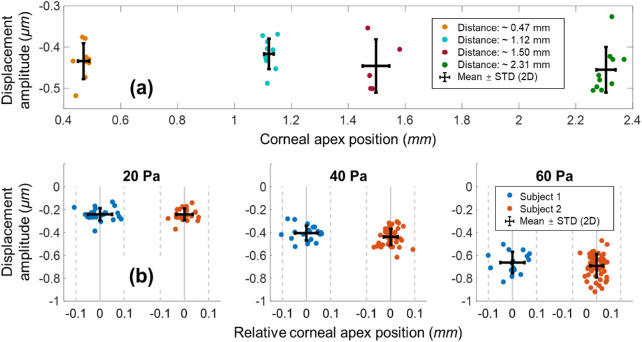
Figure 6a shows the quantification results from the induced corneal displacements from the first set of in vivo measurements. The maximum shift of the corneal axial positions was approximately 2 mm, and the variations in each measurement group along the x axis demonstrate the axial eye motion during image acquisition. The axial distances (mean ± standard deviation [SD]), determined for measurement groups 1 through 4, were 0.47 ± 0.02 mm, 1.12 ± 0.02 mm, 1.50 ± 0.05 mm, and 2.31 ± 0.03 mm, respectively. We used 40 Pa air-pulse stimuli to induce corneal primary deformation amplitudes in measurement groups 1 through 4; these amplitudes are expressed as mean ± SD, and were –434 ± 44 nm, –417 ± 37 nm, –446 ± 65 nm, and –455 ± 55 nm, respectively.

Figure 6.

The measured corneal displacement amplitudes from two human subjects showed no obvious changes related to axial eye motion. (a) Amplitude measurement evaluation when the measured corneal position of subject 1 was shifted by approximately 2 mm (excitation force: 40 Pa). (b) The measured corneal primary displacement was increased with an increasing stimulus force (20‒60 Pa) for subject 1 (n = 61 measurements) and subject 2 (n = 124 measurements).

Figure 6b shows quantification results from the induced corneal displacements from the second set of in vivo measurements. The measured involuntary fixational eye motions for subjects 1 and 2 had SD values of ±0.05 mm (n = 61 total measurements) and ± 0.03 mm (n = 124 total measurements), respectively, in the axial direction. The measured corneal displacements for subject 1 had means ± SDs of –241 ± 54 nm at 20 Pa (n = 23), –405 ± 64 nm at 40 Pa (n = 22), and –663 ± 94 nm at 60 Pa (n = 16). The measured corneal displacements for subject 2 were –242 ± 52 nm at 20 Pa (n = 22), –438 ± 71 nm at 40 Pa (n = 50), and –691 ± 102 nm at 60 Pa (n = 52).

Discussion

We have evaluated the measurement precision of a prototype corneal OCE during involuntary axial eye motion. The respiratory and oculocardiac eye motions were identified as being low-frequency (0.1 to 1 Hz) and large magnitude (5 to 30 µm) compared with the frequency (250 Hz) and amplitude of (<1 µm) of corneal displacements induced during OCE measurements.

The corneal apex position of two human subjects were tracked using OCT imaging, and the primary sources of eye motion for these two subjects were attributable to respiration and cardiovascular pulsations. The magnitude and frequency of axial ocular movements were different between individuals, for example, subject 1 had larger amplitude respiratory-related motion, whereas subject 2 had primarily pulsatile cardiovascular-related motion. Despite this motion, we could easily track eye position and perform elasticity imaging without compromising measurement repeatability.

We performed displacement measurements on agar phantoms and on two human subjects to assess the susceptibility of OCE measurements (nanometer scale) to ocular motions due to normal physiological effects (tens of micrometer scale). We noted that the OCE measurements were not sensitive either to axial eye motions (up to approximately ±50 µm) nor to shifts of measured axial positions (approximately 2 mm). This result was due mainly to two factors. First, the primary surface deformation was easily characterized due to its specific frequency features (∼250 Hz, <1 µm) that were different from the frequency features (± 0.1–1 Hz, up to approximately ±50 µm) of axial motion caused by respiration and cardiovascular pulsations. Second, the air-pulse pressure was constant over the range of axial distances measured (approximately ± 5 to 20 µm). This result agrees with our previously published results, which demonstrated that the excitation force remained constant over a distance of up to 10 mm,²⁹ which is much larger than the shift of measurement positions (approximately 2 mm).

The average coefficient of variation (CV) for the measurements of human subjects was up to approximately 17%, as the displacements were approximately –0.2 to –0.8 µm in amplitude. This was much larger than the CV of 2.1% measured from agar phantoms (∼1.5 µm amplitude). Note that these in vivo corneal measurements depend on many factors. For example, the IOP varies over cardiac cycles and this can change the biomechanical properties of the cornea as we have demonstrated in previous studies.⁴¹ Diseases that influence tissue stiffness (e.g., keratoconus) may likewise have more variable elasticity measurements in vivo if softer tissues are more susceptible to deformation from normal physiological dynamics (oculocardiac pulsations, and others). In addition, eye motion may also change the corneal stiffness. Simulations using finite element analysis could help to explain the effects of motion and IOP on corneal stiffness changes. Future studies will aim to analyze the changes in corneal biomechanics corresponding to cycles of respiration and heartbeat. This insight may also be useful to guide improvements in OCE imaging systems by adding an auxiliary subsystem for motion tracking and correction, if necessary.

Conclusions

We would like to note that the observed oculocardiac pulsations could be, in principle, a source of mechanical stimulation used for biomechanical assessment of the cornea. The displacement of the retina, choroid, and the lamina cribrosa in response to oculocardiac pulsation has been previously reported.^54,55 Using heartbeat-induced fluctuations in IOP as a tool for qualitative and quantitative (with appropriate analytical models) assessment of ocular tissue biomechanics (such as cornea, sclera, and the retina) are the subject of our current investigations.