Fast and accurate calculation of myocardial T₁ and T₂ values using deep learning Bloch equation simulations (DeepBLESS)

Abstract

Purpose

To propose and evaluate a deep learning model for rapid and accurate calculation of myocardial T₁/T₂ values based on a previously proposed Bloch equation simulation with slice profile correction (BLESSPC) method.

Methods

Deep learning Bloch equation simulations (DeepBLESS) models are proposed for rapid and accurate T₁ estimation for the MOLLI T₁ mapping sequence with balanced SSFP readouts and T₁/T₂ estimation for a radial simultaneous T₁ and T₂ mapping (radial T₁‐T₂) sequence. The DeepBLESS models were trained separately based on simulated radial T₁‐T₂ and MOLLI data, respectively. The DeepBLESS T₁‐T₂ estimation accuracy was evaluated based on simulated data with different noise levels. The DeepBLESS model was compared with BLESSPC in simulation, phantom, and in vivo studies for the MOLLI sequence at 1.5 T and radial T₁‐T₂ sequence at 3 T.

Results

After DeepBLESS was trained, in phantom studies, DeepBLESS and BLESSPC achieved similar accuracy and precision in T₁‐T₂ estimations for both MOLLI and radial T₁‐T₂ (P > .05). For in vivo, DeepBLESS and BLESSPC generated similar myocardial T₁/T₂ values for radial T₁‐T₂ at 3 T (T₁: 1366 ± 31 ms for both methods, P > .05; T₂: 37.4 ms ± 0.9 ms for both methods, P > .05), and similar myocardial T₁ values for the MOLLI sequence at 1.5 T (1044 ± 20 ms for both methods, P > .05). DeepBLESS generated a T₁/T₂ map in less than 1 second.

Conclusion

The DeepBLESS model offers an almost instantaneous approach for estimating accurate T₁/T₂ values, replacing BLESSPC for both MOLLI and radial T₁‐T₂ sequences, and is promising for multiparametric mapping in cardiac MRI.

1. INTRODUCTION

Quantitative myocardial tissue relaxometry techniques, such as T₁ and T₂ mapping, are emerging and rapidly evolving cardiovascular MR techniques for noninvasive, quantitative characterization of cardiac tissue. ¹ , ² , ³ , ⁴ , ⁵ , ⁶ , ⁷ , ⁸ , ⁹ To generate a T₁ or T₂ map, multiple images with different T₁ or T₂ weighting are acquired, and the tissue T₁/T₂ parameters are estimated pixel by pixel by fitting the acquired signal to a model‐predicted signal. A commonly used model for T₁ or T₂ calculation is exponential curve fitting. ⁴ , ⁵ , ¹⁰ The exponential curve‐fitting model is accurate under certain conditions and is computationally efficient. However, this basic model cannot model the signal evaluation accurately for some cardiac MRI sequences, such as the widely used MOLLI pulse sequence, ⁴ resulting in inaccurate parameter estimation. ¹¹ To address the issue, Bloch equation simulation–based algorithms have been proposed to model the signal evolution of a sequence to ensure accurate parameters estimation, such as the Bloch equation simulation with the slice‐profile correction (BLESSPC) algorithm for the MOLLI ¹¹ and simultaneous radial T₁‐T₂ mapping ¹² sequences, and the SQAUREMR algorithm for MOLLI. ¹³ Bloch equation simulation is also the key for accurate T₁ and T₂ map calculation in the cardiac MR fingerprinting (MRF) technique. ¹⁴ , ¹⁵ , ¹⁶

However, Bloch equation simulation–based approaches are usually time‐consuming, especially for more comprehensive simulations. ¹¹ , ¹³ , ¹⁵ The computation time of the Bloch equation simulation is important to consider in cardiac application, because the simulation needs to incorporate the scan‐specific heart‐rate variations after each scan. This is different from the applications that use fixed sequence timing, such as brain MRF, ¹⁷ in which the time‐consuming computations can be performed in advance to create the dictionary and then be used for subsequent scans. ¹⁵ Recently, machine learning has been applied in MRF to accelerate Bloch equation simulation–based parameter estimation, ¹⁸ , ¹⁹ including the deep reconstruction network (DRONE). ¹⁸ The DRONE network uses a four‐layer neural network containing two 300 × 300 hidden layers. The network was trained with dictionary‐generated Bloch equation simulations, using the simulated signal as input and T₁/T₂ values as output. ¹⁸ As the timing of the MRF sequence is fixed, the DRONE approach does not use the information of signal acquisition time and therefore cannot be used directly for cardiac parameter mapping without being adapted to scan‐specific heart‐rate variations. To solve this issue, Hamilton et al ²⁰ demonstrated that deep learning can be used to accelerate dictionary generation for cardiac MRF, followed by gridding and pattern matching to calculate T₁ and T₂ values. However, in this work, the effect of ${\mathrm{B}}_1^{+}$ variations was not considered, and gridding and matching were still needed for T₁/T₂ calculation, which could potentially reduce the T₁/T₂ estimation accuracy.

Although the cardiac MRF T₁/T₂ estimation approach is primarily optimized and validated for the cardiac MRF sequence, ¹⁴ , ¹⁵ , ¹⁶ the BLESSPC approach has been shown to generate accurate T₁/T₂ maps for both conventional widely used Cartesian‐based sequences ¹¹ , ²¹ , ²² and radial sequences. ¹² Furthermore, BLESSPC is an optimization‐based approach, whereas cardiac MRF T₁/T₂ estimation needs T₁/T₂ gridding, and the T₁/T₂ estimation accuracy and precision may be limited by the grid size. However, BLESSPC sometimes suffers from relatively long computation time, such as when used for the MOLLI sequence, ¹¹ to improve T₁ estimation accuracy and for the radial T₁‐T₂ mapping sequence when both the inversion pulse and T₂‐preparation pulses were simulated in detail to ensure good accuracy. ¹²

Therefore, we propose a new approach, DeepBLESS, which applies deep learning to BLESSPC to enable rapid myocardial T₁/T₂ parameter calculation. The DeepBLESS model can be adaptive to heart‐rate variations, achieving the same accuracy and precision with BLESSPC, while reducing the reconstruction time to be less than 1 second. Different from the deep learning approach proposed for cardiac MRF T₁ and T₂ estimation, DeepBLESS considers the effect of ${\mathrm{B}}_1^{+}$, and predicts T₁/T₂ values directly without the need for gridding and pattern matching. In this work, we demonstrate the benefits of the DeepBLESS model using two sequences: the MOLLI T₁ mapping sequence at 1.5 T and a recently proposed simultaneous radial T₁ and T₂ mapping sequence ¹² at 3 T.

2. METHODS

2.1. Pulse sequence

The radial T₁‐T₂ sequence is an electrocardiographic‐triggered sequence that uses combined inversion recovery and T₂ preparation with golden angle radial spoiled gradient‐echo readout, acquiring data in a single breath‐hold of 11 heartbeats, ¹² as shown in Figure 1. Based on the acquired multicoil data, 110 images were reconstructed using compressed sensing with spatial and temporal total variation regularization, 10 images for each heartbeat on a sliding temporal window. The signal polarity for the measured signal was assigned using a phase‐sensitive method. ²³ Subsequently, both T₁ and T₂ maps were reconstructed using the extended BLESSPC algorithm. ¹² In detail, BLESSPC for radial T₁‐T₂ mapping simulates the signal evolution of the radial T₁‐T₂ sequence using Bloch equation simulations, considering the effect of nonrectangular slice profile and nonperfect adiabatic inversion, and the T₂ preparation was simulated in detail at a step size of 5 us. In this work, DeepBLESS was compared with BLESSPC for T₁ and T₂ map reconstruction regarding accuracy, precision and calculation speed, based on the 110 reconstructed images generated by the radial T₁‐T₂ sequence. To demonstrate that the proposed network (described in the next section) can be adaptive to the other cardiac parameter mapping applications, DeepBLESS was also applied to the widely used MOLLI 5‐(3)‐3 sequence ¹¹ for T₁ map reconstruction, with the same network structure but with separate network training and different input layer size. In both phantom and in vivo studies, a flip angle (FA) of 6° was used for the radial T₁‐T₂ sequence, and a FA of 35° was used for the MOLLI.

FIGURE 1.

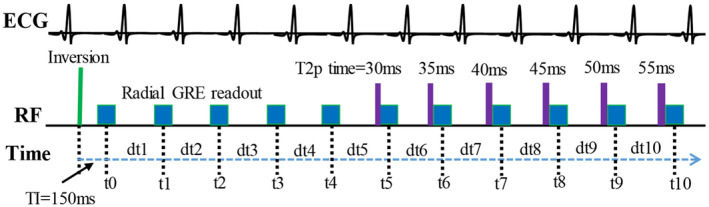
Radial T₁‐T₂ sequence image acquisition, where t0, t1, …, t10 indicate the image acquisition time points, defined as the time when the 40th k‐space line is acquired, and dt1, dt2, …, dt10 are the durations between each acquisition time point, which are needed in the Bloch equation simulation for T₁ and T₂ calculation. ECG, electrocardiogram; and GRE, gradient echo

2.2. Network for DeepBLESS

In DeepBLESS, a deep convolutional neural network was used, which consisted of a cascade of convolutional layers with ResNet blocks ²⁴ and a dense layer as the last layer connected to the output layer, as shown in Figure 2. The input layer consisted of a 1‐dimensional (1D) time‐varying signal with several channels varied depending on the sequence; the first channel corresponds to the acquisition time stamps at each heartbeat, and the other channels store the actual signals acquired. In this study, DeepBLESS was applied to the simultaneous radial T₁ and T₂ mapping sequence (referred to as the radial T₁‐T₂ sequence hereafter) ¹² to predict T₁/T₂ values for each pixel, and the MOLLI 5‐(3)‐3 sequence ¹¹ , ²⁵ was used to predict T₁ value for each pixel. In our implementation, we used 11 convolution layers, including four ResNet blocks (Rn = 4). Each convolutional layer had 32 filters with 3 × 1 size and a strike of one, except the last two convolutional layers, which used a stride of two. These parameters were empirically selected to ensure accurate functional mapping, while avoiding the risk of overfitting (see Supporting Information Document S1 and Table S1 for more information about the optimization). A rectified linear unit activation function ²⁶ was used for the hidden layers and for the output layer. The total number of trainable parameters of DeepBLESS was approximately 31,000 for MOLLI and 32,000 for radial T₁‐T₂. The data sizes of different layers of the network from input to the output are provided in Supporting Information Table S3.

FIGURE 2.

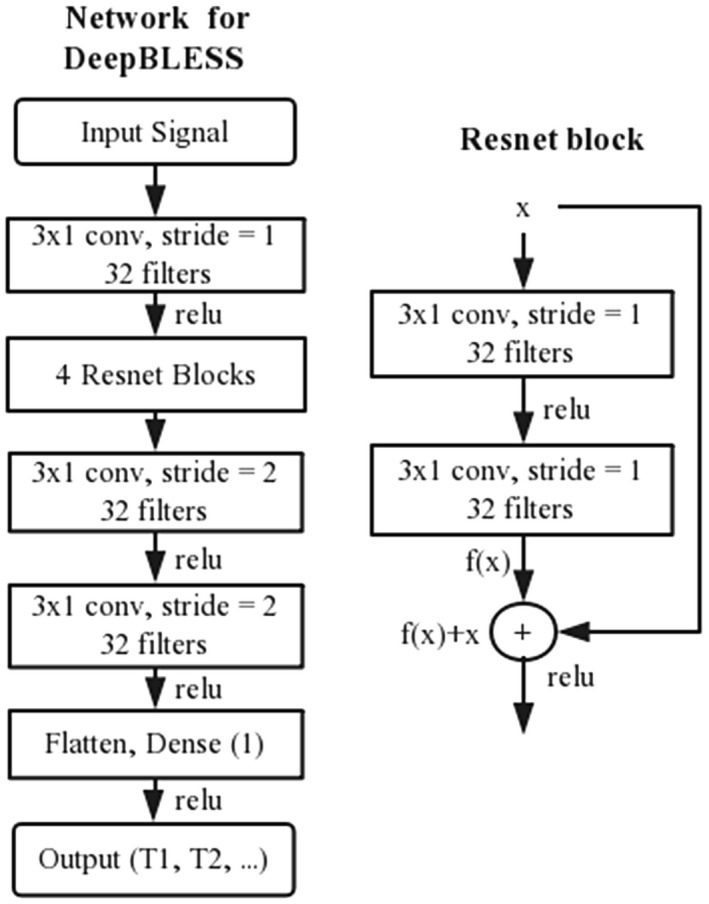
Illustration of the proposed network for deep learning Bloch equation simulations (DeepBLESS). The network consisted of 13 layers, including the input layer, one 3 × 1 convolutional layer (conv), followed by four ResNet blocks and two 3 × 1 convolution layers. Then, a dense layer was added to predict the T₁/T₂ value. The number of filters for each convolutional layer was set to be 32, and the stride was set to be 1 except the last two convolutional layers, which use a stride of 2

2.3. DeepBLESS training

Before applying the proposed model for T₁‐T₂ calculation, DeepBLESS was trained using simulated data for each sequence independently. Bloch equation simulation ¹¹ , ¹² was used to generate the training sets (1,000,000 samples), validation set (100,000 samples), and testing set (100,000 samples) for each sequence. For each simulation, random T₁ and heart rate (HR) were randomly sampled from the range of 200‐2000 ms and 40‐100 bpm, respectively. For T₂, 90% of the simulation data had a randomly selected T₂ between 20 ms and 100 ms, and 10% of the simulation data had a randomly selected T₂ between 100 ms and 200 ms. To consider the possible B₁ variations, the FA (α) was randomly sampled between 3° and 8° for the radial T₁‐T₂ sequence and between 20° and 45° for the MOLLI sequence. For each group of randomly sampled T₁, T₂, α and HR, a HR variation was simulated across the multiple heartbeats of data acquisition according to a Gaussian distribution. In detail, for either the radial T₁‐T₂ or the MOLLI sequence, 10 cardiac cycle lengths (ie, t1‐t10 in Figure 1) were simulated for each simulation data set. For a given randomly selected HR, RandomHR (bpm), the 10 cardiac cycle lengths were generated as follows:

$$\text{Durations}\left(\mathrm{i}\right)=60000/\text{RandomHR}\ast \left(1+0.1\ast {\text{Randn1}}_{\mathrm{i}}\right),$$ (1)

where i = 1, 2, …, 10 and Randn1_i is the ith random value drawn from a Gaussian distribution with mean = 0 and SD = 1.

All of the randomly selected values, such as T₁, T₂, and HR, were random floating point values. To ensure the robustness of our network for missed heartbeats, a common occurrence in clinical cardiac scanning, each simulated heartbeat in our training data had a 1% chance of being skipped. Therefore, approximately 9.5% (based on the simulation results) of our training data had at least one skipped heartbeat. Skipped heartbeats were also simulated for the validation and testing data in a similar fashion.

There were differences in how the sequence was simulated between the radial T₁‐T₂ sequence and the MOLLI sequence. For the radial T₁‐T₂ sequence, both the inversion and the T₂ preparation pulses were simulated in detail, whereas for the MOLLI sequence, the inversion was assumed to be instantaneous and a fixed inversion factor of 0.96 was assumed, which is the estimated average inversion factor on tissues with T₁, T₂ similar to myocardium for the inversion pulse used. ¹¹ , ²⁷

A previous study showed that adding noise to the training data promotes robust learning. ¹⁸ Therefore, real‐valued Gaussian noise was added to the simulated signal before model training. For the MOLLI T₁ mapping, the SNR was restively high in each balanced SSFP image, and the final model was trained by adding 1% SD Gaussian noise to the training data. For radial T₁‐T₂ mapping, the SNR was lower in each reconstructed image, and a wider range of noise levels was simulated. Specifically, four DeepBLESS models were trained after adding Gaussian noise to the training data at SD levels of 1%, 5%, and 9%, and a composite range of 1%‐10%, respectively. To train the networks, we used mean square error as the loss function with a batch size of 2000. For the radial T₁‐T₂ sequence, the input signal was a 1D signal with 11 nodes (representing 11 heartbeats) and 11 channels (1 channel for recording the acquisition time stamp signal, and the remaining channels for the 10 acquired signals in each heartbeat). Essentially, the input signal includes 110 signal intensity values on the T₁ and T₂ relaxation curves for a given pixel, along with the necessary time stamps. The output was the T₁/T₂ value for the corresponding pixel. For the MOLLI sequence, the input signal was a 1D signal with eight nodes (representing eight heartbeats with data acquisitions) and two channels (one acquisition time stamp signal + one acquired signal in each acquisition) for each pixel, and the output was the T₁ value for the corresponding pixel.

Assuming the input values are X, the function of the network to map from input to output is $\mathit{f}\left({\mathit{\theta }}_1,\mathit{X}\right)$ for T₁, and $\mathit{f}\left({\mathit{\theta }}_2,\mathit{X}\right)$ for T₂, where ${\mathit{\theta }}_1$ and ${\mathit{\theta }}_2$ are the trainable parameters. Then the loss functions for T₁ and T₂ are represented as

$$\sum _{\mathit{i}=0}^{\mathit{M}}{\left[\mathit{f}\left({\mathit{\theta }}_1,{\mathit{X}}_{\mathit{i}}\right)-\mathit{T}1\left(\mathit{i}\right)\right]}^2/\mathit{M}$$ (2)

$$\sum _{\mathit{i}=0}^{\mathit{M}}{\left[\mathit{f}\left({\mathit{\theta }}_2,{\mathit{X}}_{\mathit{i}}\right)-\mathit{T}2\left(\mathit{i}\right)\right]}^2/\mathit{M},$$ (3)

where i indicates the ith sample, and M is the batch size.

The Adam optimizer was set with a learning rate of 0.0005 for 500 epochs. The best model parameters were loaded and retrained with a learning rate of 0.0001 for 100 epochs. The model training took about 1 to 1.2 hours using a general‐purpose computer with a NVIDIA GTX 1080 GPU (Santa Clara, CA). Model parameters with the best mean square error from the validation set were saved and used for simulation, phantom, and in vivo studies. The learning rate strategy used in this work is a special case of step decay learning rate annealing approach. The performance of two other learning rate annealing methods was compared in Supporting Information Document S1 and Figure S1.

2.4. Simulation study

After model training, the performance of DeepBLESS was evaluated using testing data sets randomly generated using Bloch equation simulations described in section 2.3. For the radial T₁‐T₂ sequence, the four trained models were used to predict the T₁ and T₂ values in the test data. Random Gaussian noise with SD from 1% (SNR = 100) to 9% (SNR = 11.1) (1% increments) was added to the testing data before the evaluation. The conventional BLESSPC T₁ and T₂ estimation algorithm was applied to the testing data to calculate BLESSPC T₁ and T₂ values for comparison. The predicted T₁ and T₂ values were compared with the corresponding reference values using the following formula: Error = (Predicted – Reference) and Error% = Error/Reference * 100%. The mean of the absolute percent error was calculated.

2.5. Magnetic resonance imaging

For both phantom and in vivo studies, the radial T₁‐T₂ sequence was performed on a 3T MRI scanner (Prisma; Siemens Healthineers, Erlangen, Germany). The MOLLI sequence was performed on a 1.5T MRI scanner (Avanto Fit; Siemens Healthineers, Erlangen, Germany). The manufacturer’s body phased array and the spine coils were used for both scanners.

The radial T₁‐T₂ sequence was acquired with FOV = 320 × 320 mm², TR/TE = 2.5 ms/1.4 ms, slice thickness = 8 mm, pixel size = 1.7 × 1.7 mm², with a reconstructed matrix size of 192 × 192, where 80 radial spokes were acquired in each heartbeat. The images with both magnitude and phase signal were reconstructed off‐line after the data were acquired.

The MOLLI 5‐(3)‐3 sequence was acquired with FOV = 340 × 273 mm², TR/TE = 2.5 ms/1.1 ms, slice thickness = 8 mm, and interpolated pixel size = 1.8 × 1.8 mm². The magnitude and phase images were reconstructed on‐line with 2 $\times$ GRAPPA with 24 k‐space autocalibration lines.

Based on the acquired magnitude and phase images, the real‐valued signal for each pixel was calculated based on a phase‐sensitive method, ²³ , ²⁸ using the phase image with the longest inversion time as the reference phase. Then the real‐valued signal was used for T₁/T₂ estimations using BLESSPC and DeepBLESS.

2.5.1. Phantom studies

For the radial T₁‐T₂ sequence, eight 50‐mL agar and CuSO₄ gel phantoms were used. The radial T₁‐T₂ sequence was performed at simulated HR from 40 bpm to 100 bpm (10‐bpm increments) and were repeated 10 times at simulated HR of 60 bpm to evaluate T₁ and T₂ precision. For MOLLI T₁ mapping, ten 50‐mL agar and CuSO4 gel phantoms were used. The MOLLI sequences were acquired at each simulated HR from 40 to 100 bpm (20‐bpm increments) and were repeated 10 times at simulated HR of 60 bpm to evaluate precision. Although the cardiac cycle lengths were randomly simulated during our model training, the simulated cardiac cycle lengths in the phantom study were different from training data.

Reference T₁ and T₂ values for each gel phantom were determined by a standard inversion‐recovery spin‐echo technique with 12 TIs (TI = 50‐5000 ms) and TR/TE = 10 seconds/4.6 ms. Reference T₂ values were calculated using a standard spin‐echo technique with 11 TEs (TE = 5‐250 ms), with TR = 10 seconds. A region of interest (ROI) was manually drawn for each tube, and the average T₁, T₂ values were used as reference T₁ and T₂ values.

The accuracy was evaluated by calculating the difference and percentile difference between the estimated T₁/T₂ values with reference T₁/T₂ values. The precision was measured using coefficient of variation (CoV), CoV = SD/Mean * 100%, where SD is the standard deviation of the measured T₁ or T₂ values over repeated scans for each ROI.

2.5.2. In vivo studies

The in vivo study was approved by the institutional review board and was compliant with the Health Insurance Portability and Accountability Act. All subjects provided written informed consent. Standard cardiac shimming was applied to reduce off‐resonance variations in the heart region. The radial T₁‐T₂ sequence was performed in 10 healthy volunteers (8 males, ages 35.9 ± 14.0 years, range 24‐65 years) at 3 T. The MOLLI 5‐(3)‐3 sequence was acquired in 8 healthy volunteers (5 males, ages 28.9 ± 4.3 years) at 1.5 T. Images of the mid–left ventricular (LV) short axis were acquired at end‐expiration for each scan. After the radial T₁‐T₂ data were acquired for each volunteer, the average heart rate and heart‐rate variations (represented using CoV) were calculated based on the 11 image‐acquisition time stamps shown in Figure 1. After the multicoil radial data were reconstructed using compressed sensing for radial T₁‐T₂ ¹² or parallel imaging for MOLLI to generate magnitude and phase images, each pixel from the generated images was independently used as input to the corresponding DeepBLESS network. The conventional BLESSPC was also applied to reconstruct T₁/T₂ maps for comparison. The ROIs were drawn in the entire left‐ventricular myocardial region for the radial T₁‐T₂ mapping and in the septal region in the MOLLI T₁ maps. The mean of the T₁/T₂ values within ROIs were calculated.

2.6. Data analysis

For statistical analysis, two‐tailed Student t‐tests were used for pair‐wise comparisons. A P‐value less than .05 was considered statistically significant. The T₁/T₂ estimations by DeepBLESS and BLESSPC were compared using the Pearson’s correlation and Bland–Altman analysis for simulation, phantom, and in vivo studies.

3. RESULTS

3.1. Simulation study

For the radial T₁‐T₂ sequence, the mean absolute T₁ and T₂ percent error using DeepBLESS trained at different noise levels (SNR = 11.1, 20, 100, and composite SNRs = 11.1‐100) compared with BLESSPC as a function of the SNR of the testing data set are shown in Figure 3. Results showed that while the T₁ and T₂ estimation error was increased when the SNR in the testing set was reduced, adding more noise in the training data set helped reduce the T₁ and T₂ estimation error when the testing SNR was lower. In Figure 3, the mean absolute T₁ and T₂ error curves based on the training data with composite SNR were similar to that with SNR = 20, and both curves resembled the BLESSPC curve more than the models trained based on data with SNR = 100 and SNR = 11.1. The detailed T₁/T₂ estimation data for Figure 3 are given in Supporting Information Table S4, which indicates that the SNR = 20 trained model generated the lowest average T₁ and T₂ estimation error compared with the other three models. Therefore, for the radial T₁‐T₂ sequence, we chose to use the DeepBLESS model trained with SNR = 20 for phantom and in vivo studies.

FIGURE 3.

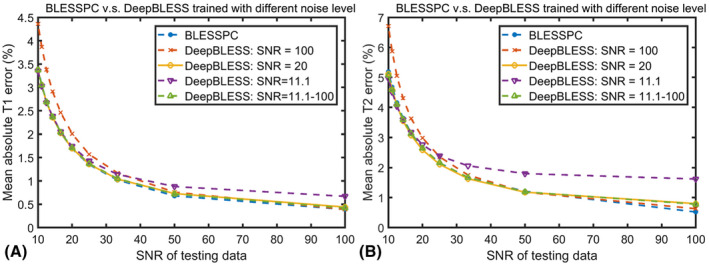
Mean percentile absolute T₁ (A) and T₂ (B) reconstruction error as a function of the testing data noise level (SNR = 10‐100) for radial T₁‐T₂ mapping using the four models trained based on training data with different added noise (SNR = 11.1, 20, 100 and composite SNRs 11.1‐100), in comparison with conventional Bloch equation simulation with slice profile correction (BLESSPC)

Figure 4 shows a comparison of the T₁/T₂ estimation results using DeepBLESS (trained with 5% Gaussian noise, SNR = 20) and BLESSPC on testing data with SNR = 20. The DeepBLESS values were in excellent agreement with BLESSPC (T₁: bias = 0.5 ms, upper 95% limits of agreement = 9.9 ms, lower 95% limits of agreement = −9.0 ms; T₂: bias = −0.1 ms, upper 95% limits of agreement = 1.9 ms, lower 95% limits of agreement = −2.0 ms). The correlation coefficient between DeepBLESS and BLESSPC was 1.0000 for T₁ estimations and 0.9996 for T₂ estimations. For testing data sets (SNR = 20) with at least one missed heartbeat, DeepBLESS still agreed well with BLESSPC with similar bias and 95% limits of agreement (see Supporting Information Figure S2). Example features of DeepBLESS T₁ and T₂ models for a sample (BLESSPC T₁ = 1361 ms, T₂ = 37.7 ms) of the testing set (SNR = 20) simulated based on the radial T₁‐T₂ sequence are shown in Supporting Information Figure S3.

FIGURE 4.

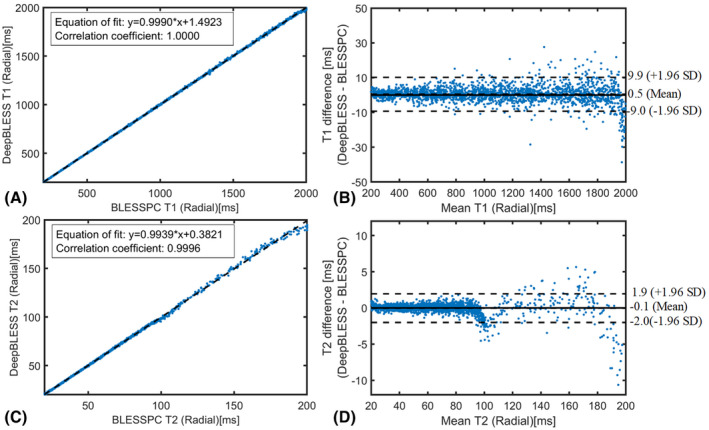
Simulation results for radial T₁‐T₂ mapping: comparison of the T₁/T₂ estimation results using DeepBLESS (trained with 5% Gaussian noise, SNR = 20) and BLESSPC by plotting DeepBLESS against BLESSPC with equation‐of‐fit plot (T₁ [A] and T₂ [C]) and Bland–Altman analysis (T₁ [B] and T₂ [D])

3.2. Phantom study

For both the radial T₁‐T₂ and MOLLI sequences, DeepBLESS generated consistent T₁ and T₂ estimations for heart rates from 40‐100 bpm, with a maximum SD of 4.5 ms for T₁ and 0.6 ms for T₂. For both T₁ and T₂ estimations, DeepBLESS achieved similar accuracy and precision compared with BLESSPC, as indicated in Table 1. The DeepBLESS and BLESSPC models both generated accurate T₁ and T₂ estimations. For radial T₁‐T₂ mapping at 3 T, the average estimation errors over the eight phantoms using DeepBLESS were 1.2 ± 4.5 ms (percent error: −0.1% ± 1.0%) for T₁ and −0.1± 1.3 ms (percent error: −0.2% ± 3.3%) for T₂. In comparison, the average estimation errors using BLESSPC were −0.8 ± 4.6 ms (percent error: −0.3% ± 0.9%) for T₁ and −0.3 ± 1.3 ms (percent error: −0.4% ± 3.2%) for T₂. For MOLLI T₁ mapping at 1.5 T, DeepBLESS and BLESSPC generated T₁ estimation errors of −0.2 ± 18.1 ms (percent error: −0.1% ± 1.7%) and −1.1 ± 18.4 ms (percent error: −0.1% ± 1.8%), respectively. Regarding precision, both DeepBLESS and BLESSPC had similar CoV (0.8% ± 0.1% for both radial T₁ and MOLLI T₁, and 1.3% ± 0.2% for radial T₂; all P > .05).

TABLE 1.

Phantom study: average accuracy and precision of BLESSPC and DeepBLESS for the radial T₁‐T₂ and MOLLI sequences using the standard spin‐echo sequence as reference

Parameter	Method	Accuracy		Precision
		Error	Percent error	Mean CoV
Radial T1	BLESSPC	−0.8 ± 4.6 ms	−0.3% ± 0.9%	0.8% ± 0.1%
	DeepBLESS	1.2 ± 4.5 ms	−0.1% ± 1.0%	0.8% ± 0.1%
Radial T2	BLESSPC	−0.3 ± 1.3 ms	−0.4% ± 3.2%	1.3% ± 0.2%
	DeepBLESS	−0.1 ± 1.3 ms	−0.2% ± 3.3%	1.3% ± 0.2%
MOLLI T1	BLESSPC	−1.1 ± 18.4 ms	−0.1% ± 1.8%	0.8% ± 0.1%
	DeepBLESS	−0.2 ± 18.1 ms	−0.1% ± 1.7%	0.8% ± 0.1%

Abbreviation: CoV, coefficient of variation.

Figure 5 shows a pixel‐level comparison of the DeepBLESS and BLESSPC T₁/T₂ estimations for radial T₁‐T₂ and MOLLI T₁ mapping at selected ROIs by plotting DeepBLESS values against BLESSPC values and using Bland–Altman analysis. Similar to our simulation results, DeepBLESS values were in excellent agreement with BLESSPC (radial T₁: bias = 0.1 ms, upper 95% limits of agreement = 3.9 ms, lower 95% limits of agreement = −3.8 ms; radial T₂: bias = 0.2 ms, upper 95% limits of agreement = 1.0 ms, lower 95% limits of agreement = −0.9 ms and MOLLI T₁: bias = −0.5 ms, upper 95% limits of agreement = 3.7 ms, lower 95% limits of agreement = −4.8 ms).

FIGURE 5.

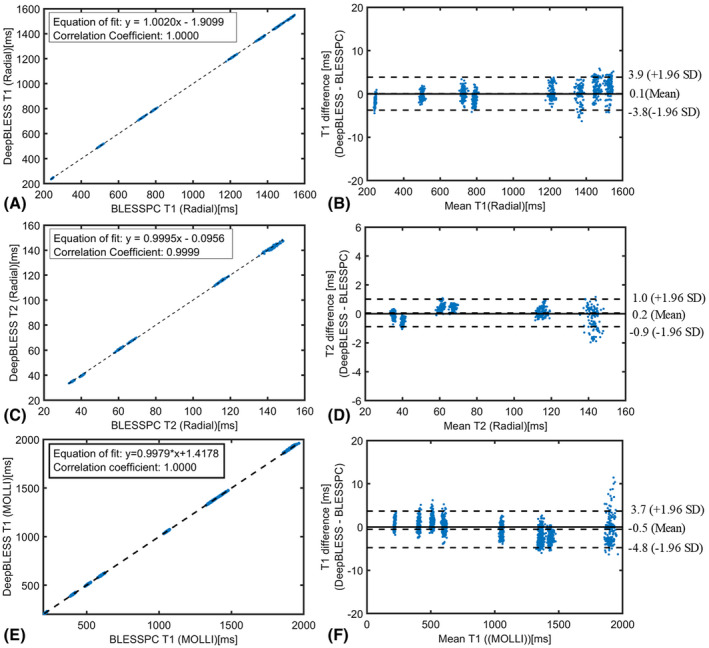
Phantom study results for both radial T₁‐T₂ mapping acquired at 3 T (A‐D) and MOLLI (E‐F) acquired at 1.5 T, comparing DeepBLESS versus BLESSPC. Each data point corresponds to a pixel within the phantom

Figure 6 shows an example of radial T₁ and T₂ maps by DeepBLESS and BLESSPC and their corresponding difference maps. The DeepBLESS and BLESSPC models provided similar T₁ and T₂ estimations.

FIGURE 6.

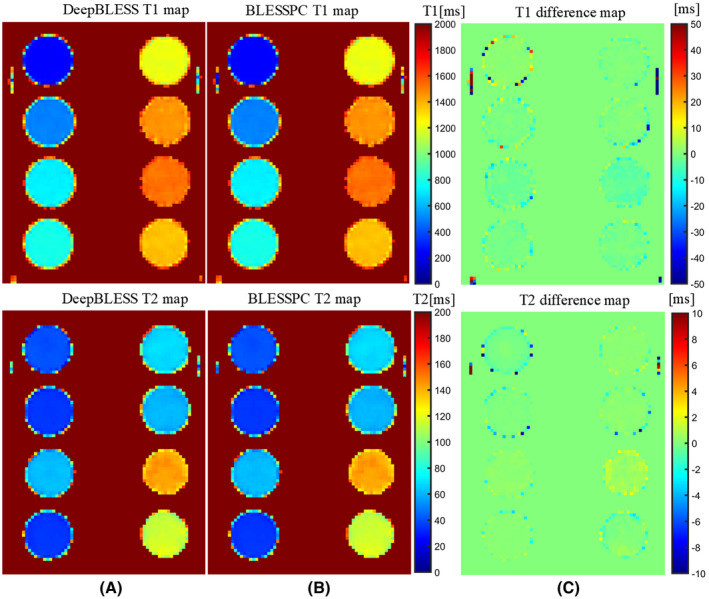
Phantom T₁ and T₂ maps using DeepBLESS (A) and BLESSPC (B) and the corresponding difference maps (C) for the radial T₁‐T₂ mapping sequence acquired at simulated heart rate of 60 bpm. The DeepBLESS and BLESSPC models generated T₁/T₂ maps with similar image quality

3.3. In vivo study

For the radial T₁‐T₂ sequence, the average heart rate in all 10 healthy volunteers was 62.6 ± 7.8 bpm (minimum HR = 50.1 bpm, maximum HR = 77.2 bpm). The average heart‐rate variation (CoV) was 5.5% ± 8.1% (minimum CoV = 0.4%, maximum CoV = 27.9% due to a skipped heartbeat, second maximum CoV = 7.2%). The DeepBLESS and BLESSPC models provided similar myocardial T₁ and T₂ values at 3 T (T₁: 1366 ± 31 ms for both DeepBLESS and BLESSPC, P > .05; T₂: 37.4 ms ± 0.9 ms for both DeepBLESS and BLESSPC, P > .05) in all 10 healthy volunteers studied. The correlation coefficients between DeepBLESS and BLESSPC values were 0.9993 and 0.9984 for radial T₁ and T₂ (Figure 7A,C), respectively. Bland–Altman analysis (Figure 7B,D) demonstrates that DeepBLESS and BLESSPC T₁ and T₂ values were in excellent agreement in vivo (radial T₁: bias = 0.3 ms, upper 95% limits of agreement = 4.5 ms, lower 95% limits of agreement = −3.9 ms; radial T₂: bias = 0.15 ms, upper 95% limits of agreement = 0.5 ms, lower 95% limits of agreement = −0.2 ms). Figure 8 shows example T₁ and T₂ maps generated using DeepBLESS and BLESSPC and their difference maps in 2 healthy subjects, 1 subject without skipped heartbeat (subject A) and 1 with a skipped heartbeat (subject B). For subject B, there was a missed heartbeat after the sixth data acquisition. For both volunteers, the T₁/T₂ difference between DeepBLESS and BLESSPC in the myocardial region was negligible.

FIGURE 7.

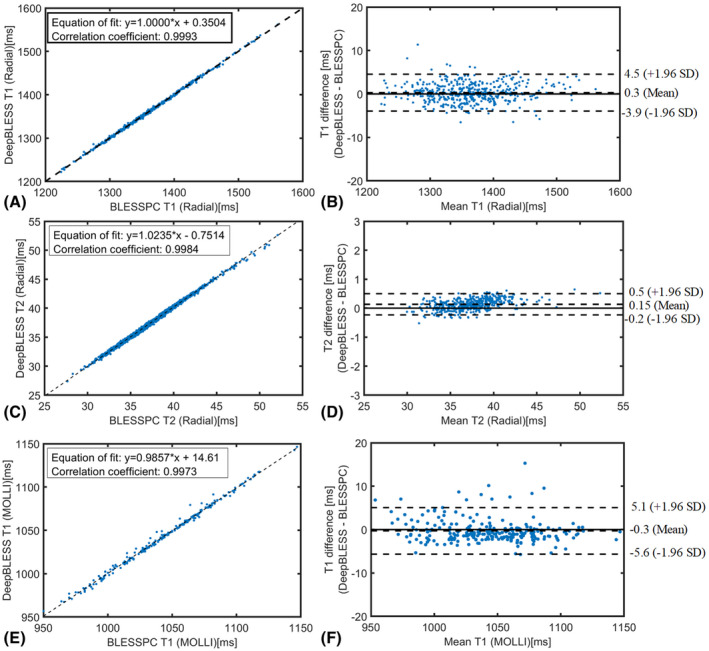
In vivo study results for both radial T₁‐T₂ mapping acquired at 3 T and MOLLI acquired at 1.5 T: pixel‐level comparison of the T₁/T₂ estimation results in the myocardium using DeepBLESS and BLESSPC by plotting DeepBLESS against BLESSPC with equation‐of‐fit plot (radial T₁ [A], radial T₂ [C], and MOLLI T₁ [E]) and Bland–Altman analysis (radial T₁ [B], radial T₂ [D], and MOLLI T₁ [F])

FIGURE 8.

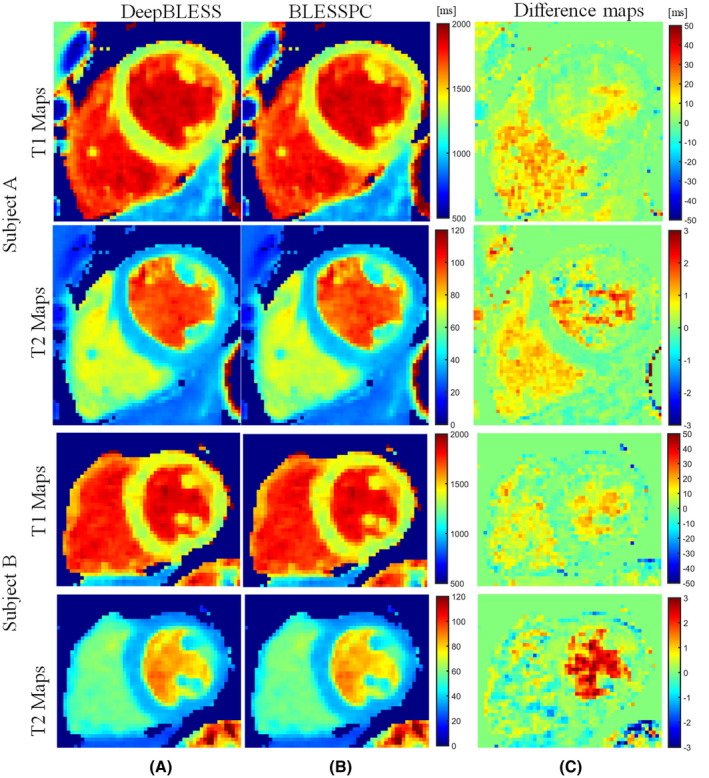
In vivo radial T₁‐T₂ mapping acquired at 3 T: examples of T₁ and T₂ maps generated using DeepBLESS (A) and BLESSPC (B) and the corresponding difference maps (C) in 2 healthy subjects. Subject A had no skipped heartbeat, whereas subject B had a skipped heartbeat after the sixth data acquisition. For both subjects, the maps generated by DeepBLESS and BLESSPC were similar in the myocardium

For the MOLLI sequence, DeepBLESS and BLESSPC generated similar myocardial T₁ values at 1.5 T (T₁ = 1044 ± 20 ms for both DeepBLESS and BLESSPC, P > .05) in all 8 volunteers studied. Correlation coefficient and Bland–Altman analysis (Figure 7E,F) demonstrate that the DeepBLESS and BLESSPC values were in good agreement for in vivo MOLLI T₁ mapping (correlation coefficient = 0.9973, bias = −0.3 ms, upper 95% limits of agreement = 5.1 ms, lower 95% limits of agreement = −5.6 ms). Figure 9 shows example T₁ maps generated using DeepBLESS and BLESSPC for the MOLLI sequence in a healthy subject. In this subject, the average difference between DeepBLESS and BLESSPC T₁ values in the entire left‐ventricular myocardial region was −0.5 ± 1.7 ms.

FIGURE 9.

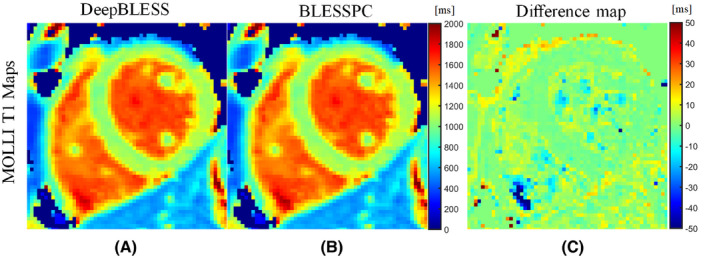
In vivo MOLLI T₁ mapping acquired at 1.5 T: example of T₁ maps generated using DeepBLESS (A) and BLESSPC (B) and the corresponding difference map (C) in a healthy subject. All of the pixels that BLESSPC did not fit well (R₂ < 0.98) were set to 0 for all corresponding maps. The maps generated by DeepBLESS and BLESSPC were similar in the heart region. In the left‐ventricular myocardial region, the average T₁ difference between DeepBLESS and BLESSPC was −0.5 ± 1.7 ms

To compare the computation speed, a general‐purpose desktop computer (Intel Core i7‐8700 CPU, 3.10 GHz) was used for all of the T₁ and T₂ map reconstructions (BLESSPC and DeepBLESS), and a single thread was used for a fair comparison. For radial T₁‐T₂, after compressed‐sensing image reconstruction, a slice of T₁ and T₂ maps could be generated in about 3 hours using BLESSPC (algorithm B in Ref. 12). In comparison, DeepBLESS was able to reconstruct a slice of T₁ and T₂ maps in about 0.6 seconds, achieving up to 18,000‐fold acceleration. For MOLLI, a slice of T₁ map could be generated in about 98 seconds using BLESSPC and about 0.2 seconds using DeepBLESS, achieving 490‐fold acceleration by DeepBLESS.

4. DISCUSSION

In this work, we studied the use of a deep convolutional neural network to learn the Bloch equation simulations (DeepBLESS) to replace the previously reported Bloch equation–based approach (BLESSPC) for rapid myocardial relaxation parameter prediction. Conventional Bloch equation simulation–based approaches enable accurate myocardial relaxation parameter estimation at the cost of increased reconstruction time. ¹¹ , ¹⁵ The proposed DeepBLESS approach enabled almost instantaneous estimation of myocardial relaxation parameters by off‐loading the time‐consuming task of Bloch equation simulations to off‐line. Our results show that, for the radial T₁‐T₂ sequence, DeepBLESS could achieve 18 000 times acceleration while achieving similar accuracy and precision compared with BLESSPC. The DeepBLESS model was also trained for the standard MOLLI 5‐(3)‐3 sequence for rapid T₁ estimation. Our phantom and in vivo results demonstrated that the T₁ values generated using DeepBLESS agreed well with those generated using BLESSPC. We previously reported BLESSPC reconstruction time of 6 seconds when using a spoiled gradient‐echo readout. ²¹ However, a full simulation of the balanced SSFP readout in MOLLI needed 98 seconds to generate a slice of T₁ map, whereas the sequence scan time was only approximately 10 seconds. The relatively long reconstruction time could be a roadblock for widespread clinical utility. The DeepBLESS model reduced the T₁ map reconstruction time from 98 seconds to 0.2 seconds. As the MOLLI image reconstruction used parallel imaging with reconstruction time of less than 1 second, we expect our technique to immediately enable fast and online image reconstruction and T₁ calculation for MOLLI.

For simultaneous myocardial T₁ and T₂ mapping, besides the radial T₁‐T₂ mapping sequence, several other techniques have been proposed. ⁹ , ¹⁴ , ²⁹ , ³⁰ , ³¹ , ³² , ³³ The potential benefits of using radial T₁‐T₂ mapping over other joint T₁ and T₂ mapping techniques have been well described in Shao et al.12 Specifically, most of the techniques used Cartesian acquisition, ⁹ , ²⁹ , ³⁰ , ³¹ , ³² limiting the number of images that can be reconstructed for parameter fitting, and therefore can potentially suffer from reduced precision. The average myocardial T₁ values measured at 3 T using the multitasking ³³ native T₁ and T₂ mapping sequence (1216 ± 67 ms) was lower than the standard MOLLI (1244 ± 48 ms), which itself has been known to underestimate T₁. As for cardiac MRF, improvements have been made to improve its accuracy by also considering the effect of imperfect slice profile, inversion and T₂ preparation, ¹⁵ and the T₁/T₂ calculation speed using deep learning. ²⁰ However, all of these improvements still used the relatively long 16‐heartbeat version cardiac MRF sequence with relatively long acquisition window (240‐280 ms). In comparison, the radial T₁‐T₂ mapping technique requires only 11 heartbeats and a shorter window (~200 ms). In Liu et al, ³⁴ it was stated that the acquisition window may potentially be reduced to 150 ms, and the breath‐hold time may be reduced to 5 heartbeats. However, the T₁/T₂ measurement accuracy/precision using this shortened version of cardiac MRF sequence remains to be evaluated. For shortened cardiac MRF sequences, the precision and reproducibility need to be evaluated carefully due to limited data acquired, which may potentially reduce the parameter‐estimation precision. In comparison, we show that the radial T₁‐T₂ mapping sequence can achieve similar precision and reproducibility, as the widely used MOLLI sequence and conventional cardiac T₂ mapping sequence. ¹² Although there are potential benefits of using radial T₁‐T₂ mapping over the other simultaneous myocardial T₁‐T₂ mapping techniques, further studies are warranted to compare the radial T₁‐T₂ sequence with the other techniques in clinical applications. Although DeepBLESS achieved almost instantaneous T₁/T₂ map reconstruction for the radial T₁‐T₂ mapping sequence, the compressed‐sensing reconstruction took approximately 3 minutes, a limitation for using the radial T₁‐T₂ sequence for simultaneous myocardial T₁ and T₂ mapping. Recent studies have shown that deep learning can be applied to replace compressed sensing, to reduce reconstruction time. ³⁵ , ³⁶ , ³⁷ These techniques may be combined with our proposed T₁ calculation technique to further reduce total imaging time and enable online use of the radial T₁‐T₂ mapping technique.

Recently, deep learning models have been applied to MRF for fast quantitative parameters prediction, such as the MRF DRONE. ¹⁸ However, this model only considers the measured signal as the input, and are only applicable to the sequence that has fixed acquisition timing. For parameter quantification in cardiac applications, the actual image acquisition timing varies due to patient‐specific heart‐rate variations. To be adaptive to heart‐rate variations, DeepBLESS used both the image acquisition time stamps and imaging signal as the input for cardiac parameter prediction. To ensure the robustness of DeepBLESS to various heart‐rate variations, we included variable heart rates in our model training data. Our results demonstrate that DeepBLESS agrees well with BLESSPC for various heart rates. Regarding the deep learning model used in this work, we choose the 3 × 1 size 1D filter for the following two reasons: (1) The input layer size is relatively small (11 × 1 for each channel); therefore, using 3 × 1 size 1D filters should be sufficient. (2) For the same number of trainable parameters, a smaller filter size with deeper network is generally better than a larger filter size with shallower network. Recently, deep learning has been applied to automatic segmentation of cardiac T₁ images. ²⁴ These techniques could potentially be combined with our proposed technique to further improve reliability and efficiency.

Instead of comparing DeepBLESS to conventional dictionary‐matching approaches, ¹⁸ DeepBLESS was compared with BLESSPC, an optimization approach based on the nonlinear least‐squares fitting. ¹¹ , ²¹ The benefit of BLESSPC over the dictionary‐matching approach is that there is no need to generate a large dictionary, which requires more computer memory, and the accuracy and precision is not limited by the size of the dictionary. For cardiac applications, both BLESSPC and the dictionary‐matching approach need Bloch equation simulations after the sequence was performed so that the image acquisition timing is known for simulation. DeepBLESS performs the time‐consuming task of Bloch equations simulations during the off‐line training stage, which learns the nonlinear mapping from acquisition time and signal to relaxation parameters, allowing for fast, accurate, and precise relaxation‐parameter calculation. After the model was trained, the speed of DeepBLESS for parameter calculation is not affected by how detailed the sequence was simulated using Bloch equation simulations, whereas the conventional approaches such as BLESSPC or dictionary‐matching approaches ¹⁴ are substantially affected. Therefore, when more details are considered in Bloch equation simulations, DeepBLESS may achieve more acceleration compared with these conventional approaches. For instance, BLESSPC simulates more details in radial T₁‐T₂ mapping compared with the MOLLI sequence, including simulating the adiabatic inversion pulse and multiple T₂‐prep pulses. As such, DeepBLESS achieved more reconstruction‐time acceleration over BLESSPC for radial T₁‐T₂ mapping (18 000 times) than for MOLLI (490 times). The DeepBLESS model is even more promising for applications that require more timing‐consuming simulations, such as incorporating the effect of magnetization‐transfer effects in parameter mapping, which was not considered in this study, but has been shown to have an effect on myocardial T₁ underestimation using inversion recovery–based sequences. ¹¹ , ³⁸

A previous study has shown that the deep learning approach can help to reduce T₁ and T₂ estimation errors compared with the conventional approach when the noise is higher for MRF. ¹⁷ However, we did not see obvious improvement using DeepBLESS over BLESSPC regarding T₁/T₂ errors for cardiac T₁ and T₂ mapping, despite our demonstrated advantage compared with the DRONE network for cardiac applications (see Supporting Information Document S1 and Table S1). This may be due to the following reasons. (1) The BLESSPC model, because of its comprehensive simulation of essentially every aspect of the pulse sequence, without the need for building a dictionary, may already minimize T₁/T₂ errors. It is not subject to dictionary‐size issues associated with the dictionary‐matching approach compared with the DRONE network. (2) For cardiac applications, the image‐acquisition timing needs to be considered, which may have been more complex for the deep learning network to learn.

To train the network, different from the conventional approach of using a predetermined series of parameters (eg, T₁, T₂) with predetermined step sizes to generate the training data set, we randomly sampled a set of parameters (eg, T₁, T₂, FA, heart rate) in a certain range for each simulation. This has two benefits: (1) flexible training, validation, and testing data size setup; and (2) compared with the conventional approach, the proposed approach will generate more different T₁, T₂, FA, and heart‐rate values for training. For instance, if the conventional approach had n1 different T₁ values, n2 different T₂ values, n3 different FAs, and n4 different heart rates to generate a training set with n1 × n2 × n3 × n4 samples, for the same number of training samples, the proposed approach will generate n1 × n2 × n3 × n4 different values for each parameter. This may improve the training results. Similar to the nonuniform dictionary sampling in DRONE, ¹⁷ we sampled T₂ more densely in the range of 20‐100 ms because this is the expected range of the myocardial T₂. Sampling more data in the 20‐100 ms range gives more weights for T₂ errors in this range in the training, which may help reduce errors in this T₂ range.

In this work, we added Gaussian noise to the training data for two reasons: (1) It is a common approach used in network training to reduce overfitting; and (2) although the noise‐like artifacts from undersampling were certainly not of Gaussian distribution, it was not possible for us to fully characterize the noise characteristics from undersampling. Therefore, assuming a Gaussian distribution would be our alternative approach. The results from phantom and in vivo experiments confirmed that the DeepBLESS trained with added Gaussian noise agreed well with BLESSPC. Similarly, a recent machine‐learning technique for MRF ¹⁷ also added Gaussian noise to the training data, while the signal from the MRF sequence was undersampled. Our results show that using different noise levels will affect the final results. For example, Figure 3 shows that for noisier testing data sets with SNR range of 10‐30, the model trained using less noisy data training data sets with SNR = 100 was less accurate than the model trained using noisier data sets with SNR = 20. For less noisy testing data with SNR greater than 60, the model trained using less noisy training data had better performance. We could not find a model that is always the best for a wide range of SNR from 10‐100; therefore, in this work we chose the model that generated the lowest average T₁ and T₂ estimation error.

To demonstrate that the proposed network can be adaptive to different cardiac T₁/T₂ mapping sequences, we used the same network (except the input) for both radial T₁‐T₂ and MOLLI sequences. Because the MOLLI sequence was simpler than the radial T₁‐T₂ sequence, it is possible to use a shallower network with fewer parameters for MOLLI. However, based on the results from Supporting Information Document S1 and Table S2, even for the MOLLI sequence, the proposed network with four Resnet blocks was still better than the less deep networks using 0 or 2 Resnet blocks, indicating that a deeper network can still help to achieve better results for MOLLI. There was no obvious overfitting using the same network for MOLLI, potentially due to the large training data sets available for the MOLLI network training (1 million training data sets for only 31 000 trainable parameters).

The current annealing approach used in this work is a simple version of traditional step decay annealing approaches (ie, only one‐step decay) with slight modification. We chose to use it because we could tune the first learning rate and epoch number to obtain the best mean square error, load the model with best validation mean square error, and tune the second learning rate and epoch number to further improve the results. In comparison, the conventional step annealing approaches does not load the best model when reducing the learning rate, and the number of training epochs is fixed for each step. Our results in the Supporting Information show that the proposed annealing approach generated better results than the conventional step decay and exponential decay for the hyperparameters tested. However, it does not indicate that the proposed annealing approach is the most accurate way.

We point out that the MOLLI sequence was performed on a 1.5T scanner only, and the radial T₁‐T₂ sequence was performed on a 3T scanner only. The measured average myocardial T₁ values using MOLLI with BLESSPC/DeepBLESS at 1.5 T (1044 ± 20) was higher than the conventional MOLLI T₁ values at 1.5 T (950 ± 21). ³⁹ The measured average myocardial T₁ values using radial T₁‐T₂ with BLESSPC/DeepBLESS at 3 T (1366 ± 31 ms) was also higher than the conventional MOLLI T₁ values at 3 T (1052 ± 23 ms). ³⁹ These are expected, as conventional MOLLI fitting is known to underestimate T₁ values. The measured average myocardial T₂ values using radial T₁‐T₂ with BLESSPC/DeepBLESS at 3 T (37.4 ms ± 0.9 ms) was similar to that measured by cardiac MRF with slice profile, preparation pulse efficiency, and ${\mathrm{B}}_1^{+}$ corrections (37.2 ± 1.5 ms) in Hamilton et al. ¹⁵

In this work, we focused on myocardial T₁/T₂ measurements. The blood T₁/T₂ measurements based on our technique need to be further evaluated, because blood flow was not simulated when building our models. Due to blood flow, the BLESSPC‐fitted apparent FA in the blood region was much lower than that in the myocardial region (usually < 3° for radial T₁‐T₂), whereas in the DeepBLESS training data, we only simulated a reasonable apparent FA range (3°‐8° for radial T₁‐T₂). This could be the main reason why there were larger T₁ differences between BLESSPC and DeepBLESS in the blood region. It is possible to simulate the blood flow to improve blood T₁/T₂ estimation accuracy, and this could be a potential benefit of DeepBLESS over BLESSPC, as adding additional simulations should not affect its T₁/T₂ calculation speed. In BLESSPC for MOLLI, a fixed T₂ of 45 ms was assumed in the Bloch simulation to avoid the need for fitting T₂. In comparison, for DeepBLESS, a wide range of T₂ was simulated, which may potentially be more accurate. The difference map in Figure 9 for MOLLI T₁ mapping shows larger T₁ differences at the edges of the heart between BLESSPC and DeepBLESS, which may be due to cardiac motion, blood flow and off‐resonance, as these effects were not considered in the DeepBLESS model.

Our study has limitations. Although DeepBLESS with the proposed network and hyperparameters was relatively optimal compared with other networks or parameters tested in this work, the current network with the proposed hyperparameters and learning‐rate strategies may not be the most optimized one, as it was not possible to evaluate all possible networks, hyperparameters, and training strategies. Nevertheless, we reached the main goal that the proposed DeepBLESS approach can achieve similar accuracy and precision compared with BLESSPC, while greatly reducing the reconstruction time. As DeepBLESS can be trained on data with noisy data, it can be potentially better than BLESSPC for low SNR data. Further studies are warranted to further optimize the DeepBLESS network and training strategies to achieve better results than BLESSPC. DeepBLESS was trained for heart rates between 40 and 100 bpm with 10% variations in cardiac cycle lengths. It is conceivable that a model training based on larger variations in cardiac cycle lengths could be applied for T₁ and T₂ mapping for patients with arrhythmias. However, a number of other issues need to be addressed, including motion artifacts, cardiac morphology changes due to varying preload and after‐load conditions, which are beyond the scope of the current study. The heart rates between 40 and 100 bpm are suitable for most of the cardiac applications, and for applications out of the current trained range, we can potentially fine‐tune DeepBLESS using the training data with a larger range of heart rates and beat‐to‐beat variations. This study was performed in a small cohort of healthy volunteers at midventricular‐slice location only. Further clinical evaluations on larger cohorts are warranted to evaluate the performance of DeepBLESS. A limitation of training our DeepBLESS network based on simulated data is that it may not entirely reflect the complexity of the in vivo environment. This limitation is not specific to DeepBLESS, and is also true with conventional Bloch equation–based approaches, such as BLESSPC and MRF. Based on our in vivo data, we have shown satisfactory T₁/T₂ accuracy using our network. The simulation data essentially enable the network to learn the nonlinear Bloch equation, which is the foundation for in vivo MRI. Therefore, it would not be surprising that our model worked well for our in vivo studies.

5. CONCLUSIONS

The DeepBLESS model offers an almost instantaneous approach for estimating relaxation‐parameter maps with good accuracy and precision, similar to the conventional Bloch equation–based approach (BLESSPC). The acceleration provided by DeepBLESS is promising for multiparametric mapping in cardiac applications.

Supporting information

FIGURE S1 Training and validation loss against the number of epochs using the proposed learning rate strategy (T₁ [A] and T₂ [B]), conventional learning rate step decay (T₁ [C] and T₂ [D]), and learning‐rate exponential decay (T₁ [E] and T₂ [F]). The proposed learning rate strategy achieved the best validation loss

FIGURE S2 Bland–Altman analysis (2000 data points) between deep learning Bloch equation simulations (DeepBLESS) and DeepBLESS for testing data with at least one missed heartbeat (with 5% added noise, SNR = 20)

FIGURE S3 Example features of DeepBLESS T₁ and T₂ models for a sample (BLESSPC T₁ = 1361 ms, T₂ = 37.7 ms) of the testing set (SNR = 20) simulated based on the radial T₁‐T₂ sequence: first layer feature map for DeepBLESS T₁ (A) and T₂ (C), and the last layer’s input feature, kernels, and final predication results for DeepBLESS T₁ (B) and T₂ (D)

TABLE S1 Mean square error in the validation set (SNR = 20) of the radial T₁‐T₂ sequence using different networks, hyperparameters, and learning rate annealing methods for DeepBLESS

TABLE S2 Mean square error in the validation set (SNR = 20) of the MOLLI sequence using 0‐6 Resnet blocks (Rn = 0, 2 ,4 and 6) for DeepBLESS

TABLE S3 Size of the intermediate features after each of the 11 convolutional layers of the DeepBLESS network

TABLE S4 Mean percentile absolute T₁ and T₂ reconstruction error at different testing data noise levels (SNR = 10‐100)

DOCUMENT S1 Comparison of different networks, hyperparameters, and learning‐rate annealing methods

Shao J, Ghodrati V, Nguyen K‐L, Hu P. Fast and accurate calculation of myocardial T₁ and T₂ values using deep learning Bloch equation simulations (DeepBLESS). Magn Reson Med. 2020;84:2831–2845. 10.1002/mrm.28321