Abstract
Purpose
To determine whether sacrificing part of the scan time of pseudo‐continuous arterial spin labeling (PCASL) for measurement of the labeling efficiency and blood is beneficial in terms of CBF quantification reliability.
Methods
In a simulation framework, 5‐minute scan protocols with different scan time divisions between PCASL data acquisition and supporting measurements were evaluated in terms of CBF estimation variability across both noise and ground truth parameter realizations taken from the general population distribution. The entire simulation experiment was repeated for a single‐post‐labeling delay (PLD), multi‐PLD, and free‐lunch time‐encoded (te‐FL) PCASL acquisition strategy. Furthermore, a real data study was designed for preliminary validation.
Results
For the considered population statistics, measuring the labeling efficiency and the blood proved beneficial in terms of CBF estimation variability for any distribution of the 5‐minute scan time compared to only acquiring ASL data. Compared to single‐PLD PCASL without support measurements as recommended in the consensus statement, a 26%, 33%, and 42% reduction in relative CBF estimation variability was found for optimal combinations of supporting measurements with single‐PLD, free‐lunch, and multi‐PLD PCASL data acquisition, respectively. The benefit of taking the individual variation of blood into account was also demonstrated in the real data experiment.
Conclusions
Spending time to measure the labeling efficiency and the blood instead of acquiring more averages of the PCASL data proves to be advisable for robust CBF quantification in the general population.
Keywords: absolute quantification, cerebral blood flow, labeling efficiency, longitudinal relaxation time of blood, pseudo‐continuous arterial spin labeling
1. INTRODUCTION
Arterial spin labeling (ASL) perfusion MRI is a non‐invasive method to quantify cerebral blood flow (CBF). Over 25 years of research in ASL has brought forth a plethora of protocols, consisting of different labeling methods, readout schemes, and quantification models, along with varying choices for certain acquisition settings, such as the duration of the post‐labeling delay (PLD) and the option of background suppression. In 2015, a recommended implementation of the ASL experiment was published in a consensus paper by the perfusion study group of the International Society for Magnetic Resonance in Medicine (ISMRM) in collaboration with the European consortium for ASL in dementia. 1 The purpose of this consensus was to provide a go‐to methodology for ASL perfusion imaging in a clinical setting. The most notable recommendations were pseudo‐continuous labeling, a single‐PLD for all data acquisition, segmented 3D readout combined with background suppression, and a simplified version of the single‐compartment quantification model. Multiple studies have shown that ASL experiments adhering to the recommended settings result in CBF estimates comparable to those obtained from gold standard ‐PET data. 2 , 3 , 4
While the single‐PLD pseudo‐continuous ASL (PCASL) experiment in combination with the simplified model has proven its reliability, it is prone to several remaining sources of quantification errors. 5 The most important error sources can be divided in 2 categories. First, certain model parameters in the consensus model are fixed to literature values, while the true underlying values may vary significantly in reality. The longitudinal relaxation time of blood changes with factors defining its physiological state, 6 , 7 , 8 such as hematocrit, oxygenation fraction, and blood cell pathologies (eg, observed in sickle cell disease 9 ). The labeling efficiency α depends on magnetic field inhomogeneities and blood flow velocity, and can, therefore, differ between individual arteries, subjects and scan sessions. 10 , 11 In the consensus model, and α are fixed to 1.65 seconds and 0.85, respectively. The discrepancy between fixing these model parameters and the spread of their values in reality may result in significant CBF quantification bias. Second, the consensus model is an oversimplification of the underlying perfusion processes. It is based on 2 main assumptions: the entire bolus has arrived in the imaging voxel at the start of the readout and the labeled spins stay in the blood compartment during the entire experiment. 1 In order for the first assumption to be valid, the PLD has to be longer than the arterial transit time (ATT), which is the travel time of the bolus from the labeling plane to a certain imaging voxel. As the local ATT can vary within the brain and between subjects, 1 , 12 , 13 a sufficiently long PLD of 1800ms was recommended in the consensus experiment. Unfortunately, for ATTs that are significantly shorter than the PLD, the second assumption is invalidated. In that case, labeled spins will have entered the brain tissue where they decay faster, since the longitudinal relaxation time of brain tissue ( ) is shorter than . Therefore, depending on the interplay between the local ATT and the PLD, quantification with the consensus model may lead to relative over‐ or underestimation of CBF. 5
Both error categories described above may lead to local CBF quantification errors varying between regions of the brain, or global quantification errors varying between different subjects or scan sessions, or a combination of both. In other words, CBF can be over‐ or underestimated to varying degrees due to a certain mixture of these confounders. Ultimately, in clinical contexts which depend upon quantitative values, it may impede usability of quantitative ASL scans.
CBF quantification accuracy can be increased by performing additional experiments or using alternative versions of the ASL experiment. Such additional experiments may consist of measuring and α with separate MRI scans, 8 , 14 , 15 , 16 instead of fixing them to literature values. Sampling the perfusion process at multiple time points by means of multi‐PLD PCASL 17 , 18 or time‐encoded PCASL 19 , 20 allows for more accurate CBF quantification along with the possibility to measure the ATT, contrary to the single‐PLD PCASL consensus implementation. However, if the total acquisition time is kept constant, these suggested alterations will limit the number of label‐control pairs that can be acquired during the perfusion phase. Ultimately, this will reduce the precision of CBF quantification.
Clearly, there is a trade‐off between CBF quantification accuracy and precision when sacrificing ASL scan time for additional measurements or acquisition of ASL data at multiple time points, compared to the single‐PLD consensus ASL experiment. Yet, accuracy and precision both impact the ability to compare absolute CBF estimates, both within a subject as well as between subjects. Therefore, the goal of the current study is to optimize the distribution of scan time for a 5‐minute protocol between averaging of ASL data versus performing supporting measurements.
2. METHODS
In order to properly study absolute quantification accuracy, the underlying ground truth values of the parameters of interest need to be known. This requirement can be met in simulation experiments. The building blocks of the simulation experiment in the context of a PCASL experiment with supporting measurements are discussed in Sections 2.1.1, 2.1.2, 2.1.3, 2.1.4. Subsequently, Section 2.1.5 contains an overview of the entire simulation experiment as well as the chosen acquisition strategies for the 5‐minute experiment. The statistical analysis of the simulation results is described in Section 2.1.6. Two slightly different versions of the main simulation experiment with potential significant implications are defined in Section 2.1.7. Finally, the design of a real data experiment serving as a first validation is delineated in Section 2.2.
2.1. Simulation experiment
2.1.1. PCASL data simulation
In this work, the noiseless PCASL difference signal ΔS is simulated as a convolution of an arterial input function (AIF) 21 , 22 and an impulse residue function (IRF). 23 A detailed description of the model is given in Appendix A. A vital part of realistic simulations is the incorporation of realistic noise. As label and control images are usually acquired at low spatial resolutions, resulting in high SNRs, it is reasonable to assume that their signal intensities are Gaussian distributed. 24 , 25 The resulting difference data will also follow a Gaussian distribution. Therefore, Gaussian distributed zero‐mean noise was added to the PCASL difference signals ΔS. An appropriate standard deviation σ for such additive Gaussian noise was determined based on a temporal SNR (tSNR) for 3D GRASE background suppressed single‐PLD PCASL data in gray matter (GM) reported by Vidorreta et al. 26 A single simulated noise disturbed PCASL difference data point ΔM acquired with a labeling duration at a time point , could thereby be defined as:
| (1) |
with the additive noise.
2.1.2. Simulation of supporting measurements
The labeling efficiency α and the longitudinal relaxation time of blood can be estimated from MRI data acquired in separate experiments. 8 , 14 In order to realistically simulate these supporting measurements, information about the estimation precision of the parameter of interest and the associated acquisition time is needed.
Chen et al 14 proposed a sequence for measurement of the PCASL labeling efficiency α. The stability of this measurement was studied by multiple repetitions of the experiment. With cardiac triggering, they found a measurement standard deviation of approximately 0.04. The scan time per repetition was approximately 7 seconds. Assuming the estimation of α is unbiased and is the underlying ground truth labeling efficiency, the estimate from data acquired during a certain scan time can be simulated as
| (2) |
with an estimate of obtained from a single repetition of the experiment, 〈·〉 the mean value of the enclosed subset, and the number of repetitions of the experiment, with ⌊·⌋ the floor operator.
The longitudinal relaxation time of arterial blood can be estimated in the carotid artery as proposed by Li et al. 8 They report an intrasession coefficient of variation (CoV) of 1.1% for the estimation of arterial from ‐weighted data acquired in a scan time of 69 seconds. For an average of 1.65s at 3T, the reported CoV results in an estimation standard deviation s. Assuming the estimation precision scales linearly with the total scan time, scaling the acquisition time with a factor R results in a scaling of the parameter estimation standard deviation with a factor . Therefore, the estimate of from ‐weighted data obtained within a certain scan time and assumed to be unbiased can be simulated as
| (3) |
with the estimate and the true blood longitudinal relaxation time.
The methods described in Equations (2) and (3) were used to simulate supporting experiments for different scan durations with the appropriate associated estimation precision.
2.1.3. Prior distributions of relevant parameters
As it is our goal to assess the CBF estimation over multiple perfusion states in the general population for certain 5‐minute protocols, the simulations should be repeated over a large number of perfusion states. The different perfusion processes representative of the general population can be approximated based upon literature by a prior distribution p(θ) of each parameter that appears in the PCASL data simulation model as presented in Section 2.1.1 and Appendix A (see Table 1). Choosing either a normal or a uniform distribution for a certain parameter was based on the spread of the reported GM values in the considered publications. In terms of this simulation experiment, a perfusion process is defined by a random draw from the prior distribution p(θ) defined in Table 1. The ground truth CBF was kept constant at f = 50 mL/100 g/min for all perfusion states to allow easy interpretation of the results. This has a negligible impact on the generality of the results, as the relative quantification accuracy and precision are approximately independent of the considered CBF value, due to the approximately linear relation between the CBF and the PCASL signal in the single‐compartment quantification model. 27 The equilibrium blood magnetization was kept constant at unity.
Table 1.
The prior distribution p(θ) of the model parameters in GM in the general population
| Parameter | Parameter distribution | |
|---|---|---|
| Parameters | labeling efficiency α [ ] | [39, 40] |
| longitudinal relaxation time of blood [s] | [7, 8, 41] | |
| Specific IRF parameters | longitudinal relaxation time of tissue [s] | [29] |
| blood‐to‐tissue water transit time [s] | [42, 43, 44] | |
| arterial microvascular transit time [s] | [45, 46, 47] | |
| tracer capillary distribution volume [mL/100g] | [37, 48] | |
| tracer venous distribution volume [mL/100 g] | [49, 50] | |
| Specific AIF parameters | arterial transit time Δt [s] | [12, 13] |
| center‐of‐vessel travel time [s] | [21, 22] |
Note: A normal distribution is described as with μ the mean and σ the standard deviation; a uniform distribution is described as with l and u the lower and upper bound, respectively.
2.1.4. Quantification model
After simulating PCASL data and supporting measurements for a certain sequence setting and perfusion state, quantification of CBF is the final step in the simulation experiment. For single‐PLD PCASL experiments, the CBF f was calculated as
| (4) |
with ΔM the mean of the single‐PLD PCASL difference data. For multi‐PLD PCASL or te‐PCASL experiments, the CBF f and ATT Δt were quantified with a nonlinear least squares estimator by fitting the Buxton single‐compartment model 27
| (5) |
to the multi‐time‐point PCASL data. The unit of each estimated CBF value was converted from mL/g/s to mL/100 g/min by multiplication with a factor of 6000.
If scan time was assigned to the additional experiments, α and in Equations (4) and (5) were set to the estimated values as defined in Equations (2) and (3), respectively, otherwise standard literature values were assumed (α = 0.8 and seconds). Measurement of was simulated in each quantification by randomly selecting a value from a normal distribution , which represents the variability in different measurement methods for . 28 For multi‐time‐point PCASL data, the tissue longitudinal relaxation time was fixed at 1.45 seconds, 29 compatible with a 3T scanner.
2.1.5. Overview of the entire simulation experiment
The building blocks of the simulation experiment, discussed in Section 2.1, are summarized in a flowchart in Figure 1. The framework starts with the selection of a ground truth perfusion process, simulates the relevant data and measurements, and ends with the quantification of the CBF. The entire simulation experiment was formed by repeating the steps in this framework on 3 distinct levels.
Figure 1.
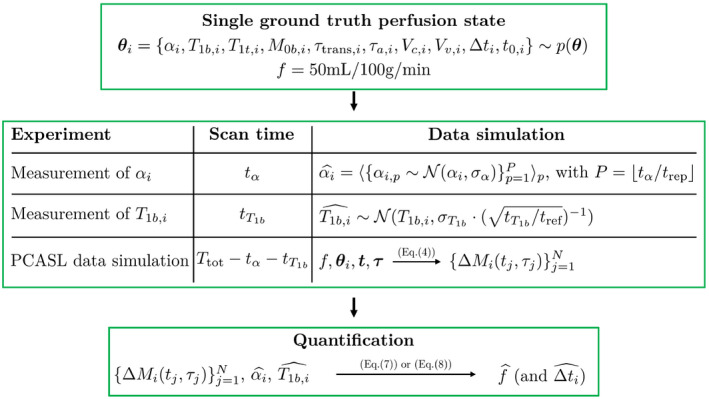
Flowchart of one run of the simulation experiment for a certain 5‐minute protocol and a certain ground truth perfusion state. The amount of PCASL difference data points N depends on the available scan time and the acquisition strategy (single‐PLD, multi‐PLD or time‐encoded)
First, multiple 5‐minute protocols were examined. On the one hand, distribution of the 5‐minute scan time between acquisition of PCASL data and supporting scans was varied. The percentages of scan time assigned to measurement of α and were increased from 0 up to 40% of in increments of 2%, including all possible combinations. On the other hand, 3 acquisition strategies were considered for PCASL: single‐PLD, equidistant sequential multi‐PLD and a free‐lunch version of te‐PCASL (te‐FL PCASL). Details of the PCASL acquisition settings are summarized in Table 2. Each of these PCASL sampling protocols were repeated maximally within the scan time to obtain multiple averages. This process is straightforward for single‐PLD and te‐FL PCASL: fit as many repeats of label‐control pairs or the Hadamard acquisition scheme within the available scan time. For multi‐PLD, after repeating the entire imaging sequence maximally, the remaining scan time was used to acquire data points at a randomized subset of the PLDs.
Table 2.
Details of the PCASL acquisition strategies used in the simulation experiment
| Acquisition strategy | Labeling duration [s] | PLD [s] | # PLDs |
|---|---|---|---|
| Single‐PLD | 1.8 | 1.8 | 1 |
| Equidistant multi‐PLD | 1.8 | 0.2, 0.4, 0.6, 0.8, 1.0, | 10 |
| 1.2, 1.4, 1.6, 1.8, 2.0 | |||
| Free‐lunch time‐encoded | 1.8, 0.175, 0.175, 0.175, | 1.8, 1.625, 1.45, 1.275, | 11 |
| 0.175, 0.175, 0.175, 0.175, | 1.1, 0.925, 0.75, 0.575, | ||
| 0.175, 0.175, 0.175 | 0.4, 0.225, 0.05 |
Second, for each of these 5‐minute protocols, the simulation framework was run for 1000 ground truth perfusion states randomly drawn from the prior distribution p(θ) as defined in Table 1.
Third, for each 5‐minute experiment and for each ground truth perfusion state, 100 repeats of data simulation and quantification were performed with different noise realizations. In this setting, different noise realizations are equivalent to repeated simulation of PCASL data and estimates and .
2.1.6. Statistical analysis
The goal of the current study is to find the 5‐minute protocol that attains the lowest level of CBF estimation variability across all considered confounding sources of variation, namely differences in the underlying perfusion states and random noise in the data. For a certain 5‐minute protocol, multiple runs of data simulation, as described in Figure 1, will result in datasets from different perfusion states and with varying random noise, yet with the same underlying CBF value. A 5‐minute protocol is then considered to have a low CBF estimation variability if the spread in the entire pool of obtained CBF estimates is low. A suitable metric to describe this estimation variability is the standard deviation s of the set of CBF estimates quantified from the Q = 100 repetitions of noisy datasets from each of the P = 1000 considered perfusion processes, that is, the standard deviation over 100.000 CBF estimations:
| (6) |
with the sample mean.
It is important to stress that the standard deviation of such a set of CBF estimates, described by Equation (6), captures CBF estimation variability of a certain protocol on a population level. Statistical measures describing such a set of estimates, like its standard deviation and mean, need to be differentiated from statistical concepts that describe the estimator used for CBF quantification, namely the accuracy (or bias) and precision. Indeed, when referring to the bias or precision of an estimator of CBF, a single underlying perfusion state (ie, fixed α, , and Δt) is assumed. This difference in terminology is followed rigorously in what follows.
2.1.7. Simulation sub‐studies
In the main simulation experiment, a more realistic, more complicated model is used for data simulation than for quantification (see Appendix A). While this option was chosen in order to match a real data experiment as closely as possible, it adds a potential source of bias to the quantification. Therefore, the entire simulation experiment described in Section 2.1.5 was repeated using the single‐compartment model (Equation (5)) for data simulation as well as quantification. The resulting CBF estimate distributions were compared to the ones from the main simulation experiment in order to separate the contribution of supporting measurements to a reduced CBF estimation variability from potential bias caused by an oversimplified quantification.
Simulation of the supporting measurements, as described in Section 2.1.2, assumes estimation of the respective parameters is unbiased. As in reality such supporting measurements could be biased, the entire simulation experiment was also repeated assuming a consistent relative overestimating bias of 5% in both supporting measurements. With this sub‐experiment, it was examined whether such a bias has a detrimental effect on potential benefits of the supporting measurements by comparing the CBF estimate distributions linked to the unbiased and biased versions of the supporting measurements.
2.2. Real data validation experiment
As a first validation of the simulation results, a real data study was designed that allowed for a comparison between CBF quantification using either the population average value or individually estimated values. From a population study with healthy volunteers in which single‐PLD PCASL data (scanner: Siemens 3.0 T, readout: 3D GRASE, spatial resolution = , number of segments for whole‐brain coverage = 2, labeling duration = 1.8 s, PLD = 1.8 s, number of averages = 4, TR = 5 seconds, total acquisition time = 80 seconds) and blood samples prior to scanning were acquired, 5 subjects with a low hematocrit (Hct = 0.345 ± 0.011) and 5 subjects with a high hematocrit (Hct = 0.464 ± 0.015) were selected. From each hematocrit measurement, the of blood was estimated. 7 Furthermore, for each subject, an equilibrium magnetization image (‘ ’) (sequence: 3D GRASE, spatial resolution = mm, number of segments for whole‐brain coverage = 2, TR = 5 seconds, TE = 18 ms), for absolute quantification of the CBF, and a high‐resolution anatomical image (sequence: MPRAGE, spatial resolution = , TR = 2250 ms, TE = 4 ms, TI = 900 ms), for tissue segmentation, were acquired.
The data for each subject was analyzed as follows. First, all relevant MRI data (label images, control images, and the proton density ‘ ’ image) were mutually registered. Second, an averaged perfusion‐weighted image was obtained by pair‐wise subtraction of label‐control pairs and subsequent averaging of the resulting difference images. Third, CBF quantification was performed twice, once using the population average value, and once using the individually estimated value. Finally, CBF values from GM voxels were isolated by downsampling and coregistering a GM mask to the CBF maps, following the procedure described in the work of Bladt et al. 30 The GM mask was obtained from a high‐resolution anatomical image by means of multilevel image thresholding. 31 Potential differences in CBF estimation variability between using the recommended population average value and using individually estimated values were assessed by comparing the standard deviations of the set of GM CBF estimates, pooled over all subjects, for both quantification methods.
As this real data experiment is a simplified version of the main simulation setup, a modified version of the simulation experiment mimicking the real data protocol was also run. For this purpose, the framework of the simulation experiment, described in Section 2.1.5, was slightly adapted: instead of generating 1000 perfusion states with randomized values and a fixed CBF, 1000 perfusion states were generated with randomized CBF values for each of the 10 individually estimated values from the real data experiment; random CBF values were drawn from a normal distribution of GM CBF values (ie, mL/100 g/min) reflecting reported literature ranges 32 ; the set of 1000 perfusion states per value simulates the underlying perfusion variations over different parts of the brain of an individual. Single‐PLD PCASL data were simulated according to the real data acquisition protocol. Subsequently, CBF was quantified from the simulation data twice for each perfusion state: once using the fixed value of 1.65 seconds, which is the recommended population average for , and once using the appropriate individual value. The distributions of the CBF estimates resulting from the real data experiment and those of the modified simulation experiment were compared in terms of the overall CBF estimation variability, allowing for an assessment of the validity of the simulation experiment.
3. RESULTS
3.1. Simulation experiment
Figure 2 shows the standard deviation s of the CBF estimates as defined in Section 2.1.6 for all considered 5‐minute protocols. The value in the top left of Figure 2A, highlighted in black, depicts the CBF estimation variability in the recommended single‐PLD PCASL implementation when separate estimates for and are not made. It serves as a starting point reflecting how differences in perfusion states and noise within and between subjects affect CBF estimation. If the standard deviation s, defined in Section 2.1.6, is a measure for the absolute variability of CBF estimation, the relative variability can be defined as the ratio between s and the underlying ground truth CBF value. For single‐PLD PCASL without supporting measurements, a relative variability of 12.2% was found. While there is no literature study that matches one‐to‐one with this simulation experiment, the between‐subject standard deviation reported in the QUASAR reproducibility study 13 is closely related to the CBF estimation variability reported in this simulation study. The ratio of the reported average between‐subject standard deviation and average mean GM CBF value in 13 is equal to 11.6%, which shows that the relative variability reported above reflects reality. The standard deviations shown in the top left corners of Figure 2B,C represent the CBF estimation variability for the te‐FL and multi‐PLD PCASL protocol without supporting measurements, respectively. The relative variabilities of these protocols (12.6% and 12.2%, respectively) are comparable to the one of their single‐PLD counterpart.
Figure 2.
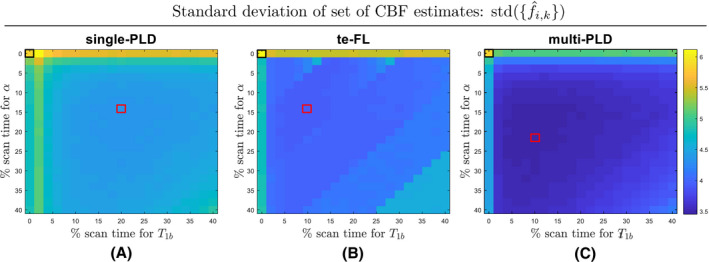
The standard deviation of the set of CBF estimates for 5‐minute combinations of a (A) single‐PLD (B) free‐lunch time‐encoded (te‐FL) and (C) equidistant multi‐PLD PCASL experiment with supporting experiments to estimate α and . The standard deviations linked to the single‐PLD, te‐FL, and multi‐PLD protocols without supporting measurements are highlighted with black boxes, while the protocols with the lowest standard deviation in each ASL modality are highlighted with a red box
For each ASL acquisition strategy, the standard deviation s reduced when allocating scan time for supporting measurements. The protocols with the lowest standard deviation are highlighted in red in Figure 2 for each ASL acquisition type. For these protocols, a relative variability of 8.6%, 8.0%, and 7.2% was found for single‐PLD, te‐FL, and multi‐PLD PCASL, respectively. Compared to the result of the single‐PLD protocol without supporting measurements shown above, this implies a reduction in relative variability of 26%, 33%, and 42% for single‐PLD, te‐FL, and multi‐PLD PCASL, respectively. Note that the standard deviation landscapes shown in Figure 2 are relatively flat. In other words, for all 3 ASL acquisition strategies, there is a rather wide range of scan time distributions that result in a similar CBF estimation variability as for the protocols highlighted in red.
Each standard deviation of the set of CBF estimates for each protocol shown in Figure 2 is the combined result of bias from different perfusion states and noise in the data. Each protocol suffers from both effects to a different degree, which is shown in more detail in Figure 3. Figure 3A visualizes the contrast between only acquiring ASL data and combining it with the measurement of α and by demonstrating the CBF estimation bias and precision for different underlying physiological perfusion states. It shows the trade‐off when sacrificing ASL scan time; a reduced spread in estimation bias comes at a cost of lower individual estimation precision. When the decision is made to perform supporting measurements, there is again a trade‐off between improving the estimation of α and and maintaining a sufficient SNR of the PCASL data (Figure 3B). On the one hand, when a very small percentage of time is used for supporting measurements, estimation of α and is very imprecise. On the other hand, when supporting measurements take up most of the scan time, the SNR of the ASL data is very low. Both extremes lead to lower CBF estimation precision, which is ultimately reflected in a higher variability. The optimal distribution of scan time lies in between these extreme cases.
Figure 3.

(A), A visualization of the trade‐off between the estimation precision on a voxel level and the spread in estimation bias on a population level. Each normalized distribution represents the fit to the histogram of CBF estimates originating from 100 data simulation repeats for a specific ground truth perfusion state . These fits were performed for estimates from 10 of the 1000 considered ground truth perfusion states, for the case of only single‐PLD data and the combination of single‐PLD data acquisition with supporting measurements with the lowest variability of CBF estimation in Figure 2A. (B), The average relative standard deviation for estimating α and is contrasted with the average inverse of the single‐PLD PCASL data SNR for the protocols represented on the diagonal in Figure 2A. For these protocols, the scan times for both supporting measurements are equal. The scan time shown on the x‐axis in (B) is the sum of both scan times. The SNR of single‐PLD PCASL data is defined as the ratio of the mean and standard deviation of the set of difference data repeats, where the number of repeats depends on the allocated ASL scan time
While the results in Figure 2 describe the main statistical entity of interest, that is, the CBF estimation variability, it provides no information about the overall mean of the set of CBF estimates of each protocol. Therefore, the distribution of the set of CBF estimates is showcased in Figure 4 for the 6 protocols highlighted in Figure 2.
Figure 4.
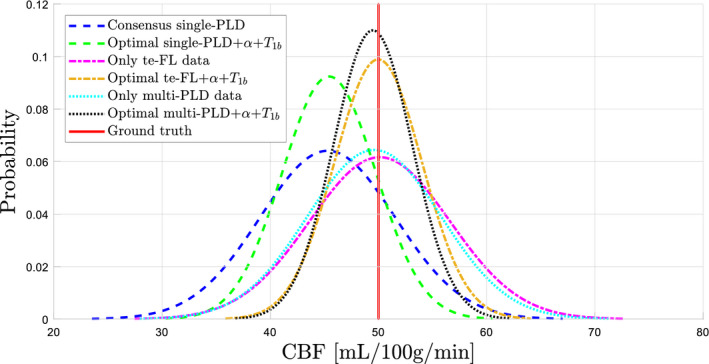
The normalized distribution of CBF estimates from the 6 protocols highlighted in Figure 2: the protocol with only single‐PLD PCASL data, only te‐FL PCASL data, and only multi‐PLD PCASL data, as well as the optimal protocol for each considered ASL modality
The results of the simulation sub‐studies, defined in Section 2.1.7, are summarized in Figure 5. In Figure 5A, CBF estimate distributions are shown when using the same model for data simulation as for quantification in a comparison to the distributions obtained from the main implementation of the simulation experiment. In terms of CBF estimation variability, a difference in the complexity of data simulation clearly has no significant effect. In terms of a bias offset, there is only a significant difference between both implementations of the simulation experiment for single‐PLD protocols. The results of the second sub‐experiment are summarized in Figure 5B. Having an offset bias in the estimation of α and from the supporting experiments has no effect on the CBF estimation variability compared to having unbiased supporting measurements. It only causes a fixed global bias in CBF estimation, consistent with the relation between α and on the one hand and CBF on the other hand in the quantification model, independent of the underlying perfusion state or noise in the data.
Figure 5.
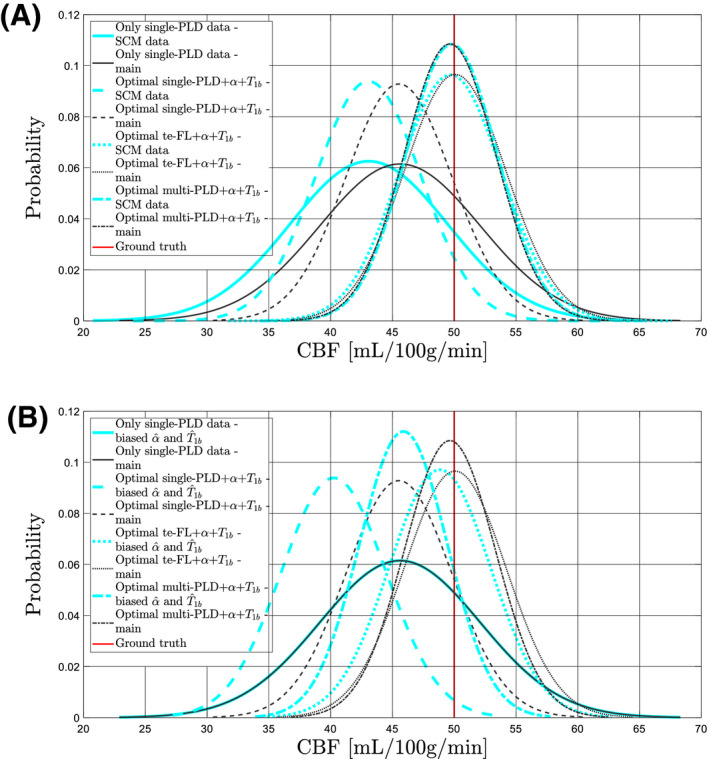
Results for 4 protocols are shown: the protocol with only single‐PLD PCASL data and the optimal protocol for each considered ASL modality. The black curves in subfigures (A) and (B) represent the normalized distributions of CBF estimates obtained from the main implementation of the simulation experiment with the realistic data simulation model. The cyan curves in subfigure (A) represent CBF estimate distributions for the exact same protocols, yet for data simulation using the single‐compartment model (SCM) as defined in Equation (5). In subfigure (B), the cyan curves represent CBF estimate distributions for the same protocols with an offset bias of 5% overestimation of both α and . Note there is no difference for the protocol with only single‐PLD PCASL data in (B), as no measurement of α and is performed in that protocol
3.2. Real data validation experiment
The distribution of the set of estimated CBF values, pooled over the considered population, for both quantification strategies is shown in Figure 6A. On a population level, there is a lower CBF estimation variability when using individual estimates, indicated by the standard deviation of the set of CBF estimates dropping from 21.0 mL/100 g/min when using a fixed value to 17.6 mL/100 g/min when using individually measured values. Note that, in contrast to the main simulation experiment, there are no ground truth CBF values to compare the estimated CBF values to and that those underlying ground truth CBF values differ in each considered voxel (ie, not fixed to 50 mL/100 g/min). Despite that, the standard deviation of the set of CBF estimates is still indicative of CBF estimation variability.
Figure 6.
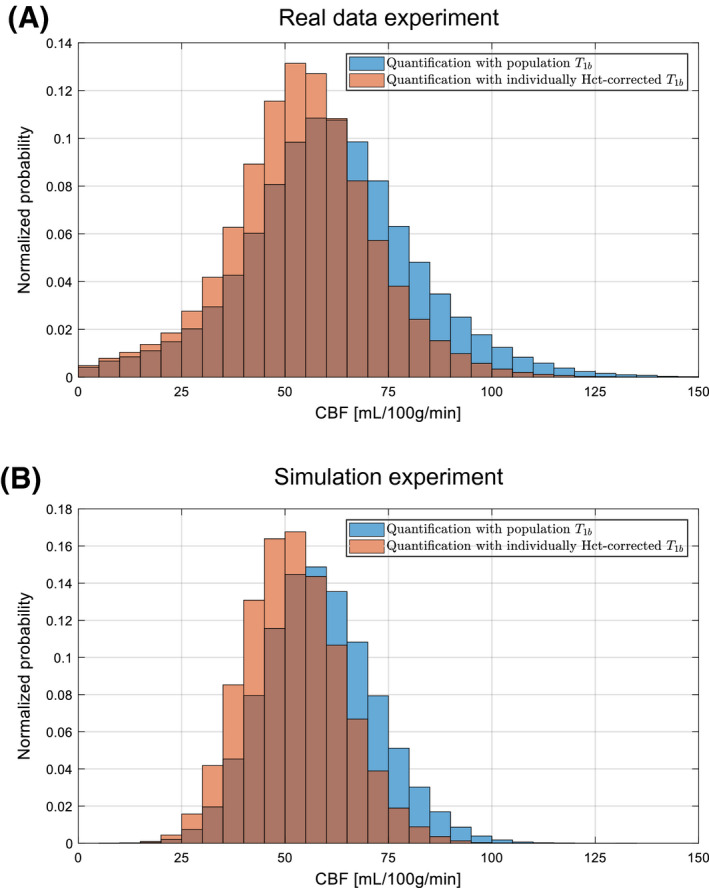
(A), Normalized distribution of the set of estimated GM CBF values, pooled over the considered population of 10 healthy volunteers, for quantification with a single population average for blood (blue) and with individual blood values (orange), estimated from a hematocrit measurement. (B), Normalized distribution of the set of estimated GM CBF values for the simulation experiment that closely mimicked the real data experiment
In Figure 6B, the CBF estimates are shown resulting from the modified simulation experiment, which mimics the real data experiment. There is a similar relative reduction in estimation variability. The absolute estimation variability is higher in the real data experiment, which is likely caused by partial volume effects, resulting in very low CBF estimates, and data outliers or remaining macrovascular signal, resulting in CBF overestimation. Such effects are not present in the simulation experiment. Both in real data and in simulations, there is a difference in the mean CBF value for both quantification methods. This can be attributed to the difference between the recommended quantification value for (ie, 1.65 seconds) and the mean of the estimated values in this specific population (ie, 1.75 seconds). Overall, the real data and simulation results, shown in Figure 6, clearly align.
4. DISCUSSION AND CONCLUSIONS
In this work, a range of 5‐minute MRI protocols was examined with respect to the CBF estimation variability for a multitude of physiological situations, as would be expected to be found in the general population. It was shown that there is a clear benefit in sacrificing some averages of PCASL for supporting measurements of the labeling efficiency α and the longitudinal relaxation time of blood . Combining these additional experiments with multi‐delay PCASL modalities instead of a single‐PLD PCASL scheme further reduced the estimation variability. The results presented above and discussed in this section are for a total scan time of 5 minutes. The simulation experiment was repeated for a total scan time of 2 and 10 minutes (results not shown), which resulted in the same general trends as described above regarding optimal scan time distribution and relative differences in CBF estimation variability between the 3 considered PCASL acquisition strategies.
The variability measures visualized in Figure 2 show that, compared to only acquiring PCASL data, it is beneficial to sacrifice part of the PCASL scan time for the measurement of α and . While optimal protocols were highlighted for each ASL acquisition strategy, many other protocols with different scan time distributions show comparable variabilities of CBF estimation. It is only when a supporting measurement is not performed or when very few ASL data are acquired that the CBF estimation variability significantly increases. The standard deviation landscape for the te‐FL PCASL acquisition strategy does, however, show some different behavior in the form of discrete jumps. This is mainly related to the temporal footprint of data acquisition of time‐encoded ASL, which is bound to repetitions of the entire set of Hadamard‐encoded images, while single‐ and multi‐PLD PCASL allow for more fine steps in allocating ASL scan time.
Comparing the results for the protocols without supporting measurements to the ones with supporting measurements for all 3 considered PCASL sampling strategies in Figure 4 allows to clearly isolate the benefit of using a percentage of the total scan time for estimation of α and . It is vital to emphasize that this benefit occurs on a population level. Estimating α and , compared to fixing it to a population average, reduces CBF estimation bias. On a population level, where α and can vary considerably, this leads to a reduced spread in CBF estimation bias (see Figure 3A). As a result, the CBF estimation variability on a population level decreases (see Figure 4). In short, reducing bias by performing the supporting measurements reduces the standard deviation of the total set of CBF estimates obtained from a large population, which might have seemed paradoxical at first. The priorities are different when considering a single individual. In a single diagnostic perfusion scan, is constant and α should not vary too much between different feeding arteries; estimating α and will only result in a global scaling of the CBF map, which for many diagnostic scans is not worth the accompanying loss in CBF estimation precision.
The optimal combinations of both multi‐delay PCASL modalities with supporting measurements outperform the optimal single‐PLD experiment in terms of CBF estimation variability (Figure 4). In fact, this is the case for most 5‐minute protocols (Figure 2). There are 2 main reasons. First, estimating the ATT alongside the CBF eliminates a source of bias, as not accounting for the ATT is known to lead to under‐ or overestimation. Second, for the considered prior distribution of the ATTs (see Table 1), both multi‐delay PCASL acquisition strategies sample the perfusion signal more optimally in terms of precise parameter estimation compared to the single‐PLD PCASL scheme. This statement is trivial for the te‐FL PCASL acquisition strategy, as the waiting period of the single‐PLD sequence is used to obtain extra data without affecting the temporal SNR of the data linked to the long labeling, that is, the perfusion block. 20 For the equidistant multi‐PLD sequence, the spread in PLDs guarantees sampling of the PCASL signal around its peak for most of the ATTs in the prior distribution. Moreover, the PLD of the recommended single‐PLD experiment is chosen to be longer than most ATTs that can be expected in the general population. Therefore, this PLD is much longer than the majority of ATTs from the considered distribution (see Table 1), resulting in an unnecessary large signal loss due to decay. Note that these statements are specifically in reference to CBF estimation variability. The qualitative perfusion map for a single subject obtained from the single‐PLD or from the first block of the te‐FL PCASL experiment will still have a higher SNR than the averaged difference maps obtained only from the longest PLDs of the multi‐PLD PCASL experiment, due to the difference in the number of repetitions.
Apart from a lower CBF estimation variability, quantification in multi‐delay PCASL methods clearly results in more accurate estimation of CBF on average compared to single‐delay PCASL protocols (Figure 4). This is caused by the difference in quantification model (Equation (4) and (5)). In multi‐delay methods, the ATT is taken into account and part of the longitudinal relaxation is assumed to be governed by the of tissue. Of course, this increased accuracy is a result of the way the simulation data were generated, which resembled the multi‐delay quantification model more than the single‐delay model (see also the study limitations). Furthermore, it is noteworthy that the mean of the set of CBF estimates for the optimal multi‐delay protocols almost coincides with the true underlying CBF value (Figure 4). This is not trivial, as PCASL data were simulated with a complex multi‐compartment perfusion model that includes dispersion effects, while CBF was quantified with a single‐compartment model. It is a clear indication of the value of the single‐compartment model (Equation (5)) as a valid approximation of more complex models with multiple compartments and dispersion effects.
Two sub‐studies of the main implementation of the simulation experiment were performed. First, PCASL data were simulated with the same model as used for quantification. As using this model for data simulation only results in a bias offset in quantification for the single‐PLD experiment (Figure 5A), reported differences in the CBF estimation variability between different protocols obtained from the main implementation of the simulation experiment can be attributed with confidence to the supporting measurements. In terms of bias offset, it is not surprising that there is no significant difference between both implementations of the simulation experiment for the multi‐PLD and te‐FL protocol, as the main implementation of the experiment with a mismatch between simulation model and quantification model already hardly showed a bias offset compared to the underlying ground truth CBF value. Remarkably, the single‐PLD quantification model (Equation (4)) estimates CBF more accurately when data were simulated with the more complicated model, compared to the single‐compartment model. Second, when an offset bias is introduced in the simulated supporting measurements, it results in an offset bias in the set of CBF estimates (Figure 5B). As there is no impact on the CBF estimation variability compared to unbiased supporting measurements, incorporating slightly biased supporting measurements would still be beneficial compared to only acquiring ASL data in terms of how comparable CBF estimates are between different subjects and/or different scan sessions.
The real data validation experiment showed a first indication of the potential benefit of supporting measurements in terms of decreasing the CBF estimation variability. However, it has multiple limitations compared to the main simulation experiments of this work. First, only the effect of measurements was studied, while simulation results indicate that measuring both and α will reduce CBF estimation variability more drastically (see Figure 2A). Second, only single‐PLD data were considered, while combining multi‐time‐point PCASL data with supporting measurements is expected to be more beneficial (see Figure 4). Third, was only estimated once in each subject. Repeated estimation of the of blood and the labeling efficiency from additional scans and repeated PCASL data acquisition would allow one to study the interplay of sacrificing ASL scan time and measurement variability within a fixed total acquisition time, as was studied in the main simulation experiments. Nonetheless, the close agreement between the results of the real data experiment and those of the simulation sub‐experiment, mimicking the real data experiment, supports the validity of the simulation experiments performed in this work.
There are several limitations to the simulation experiment performed in this study. First, the prior distributions of the respective parameters in the perfusion model used for data simulation play a central role. Each prior distribution represents the variability of a certain parameter in the considered population. Therefore, the importance of estimating α, and Δt is directly related to their underlying prior distribution. In this study, emphasis was put on carefully selecting prior distributions that match reported literature values in the general population, in order to maximize the confidence to extrapolate these results from simulation to real data. Optimal scan time distributions will be different when the underlying prior distributions of relevant parameters would be different, for example when more robust tagging techniques become mainstream or when dealing with specific patient populations. Note that in such cases, this simulation experiment should be rerun with adjusted parameter prior distributions to indicate the potential use of supporting measurements. However, it can still be expected that the general conclusion that some time should be attributed to support measurements will remain valid. Second, any data simulation model, regardless of its complexity, is an imperfect approximation of the underlying biophysical PCASL perfusion process. Nevertheless, in this study, a simulation model was used with the aspiration to match the biophysical reality as closely as possible. Ideally, these results need in vivo validation. Note that this would require a large subject group to sufficiently capture population variability. Furthermore, the analysis of the results would be challenging due to a lack of knowledge about the underlying ground truth parameter values. Third, the presented results are dependent on the parameter estimation method. In this study, parameter estimation from multi‐delay PCASL data was performed with a nonlinear least squares estimator. An alternative to this strategy is Bayesian inference, 33 , 34 which would also allow for the estimation of extra parameters with limited prior uncertainty alongside the CBF and ATT. However, it should be stressed that and α are not good candidates for estimation alongside the perfusion parameters. The of arterial blood can be considered as a global constant parameter throughout the brain. Estimating it separately in every voxel will result in local differences in that have no clear physical meaning. Regarding the labeling efficiency, it is impossible to estimate it alongside the CBF as they are not independently identifiable in the quantification model. Finally, the 3 ASL acquisition strategies selected in this study were selected pragmatically. The recommended single‐PLD implementation served as an evident benchmark. The time‐encoded free‐lunch PCASL protocol is a simple extension of the single‐PLD experiment and an equidistant version of the multi‐PLD PCASL experiment is the conventional implementation in most multi‐delay ASL studies. Estimation precision could be further increased for each of these 3 ASL modalities by means of experiment design optimization using Cramér‐Rao lower bound theory. 35 Nonetheless, the fact that it proves to be beneficial to sacrifice part of the ASL scan time for supporting measurements in 3 entirely different ASL sampling strategies (see Figure 4) strongly suggests that the merit of these supporting measurements is independent of the chosen sampling strategy. Indeed, it was shown that reducing estimation bias by means of supporting measurements is the driving force behind reducing the CBF estimation variability on a population level (see Figure 3A).
In conclusion, we demonstrated the benefit of sacrificing part of the ASL scan time for supporting measurements to estimate the labeling efficiency and the blood longitudinal relaxation time in terms of CBF estimation variability by means of a simulation experiment. When absolute quantification of CBF from PCASL data is required, such supporting experiments turn out to be indispensable. Furthermore, for the considered population statistics, multi‐time‐point PCASL methods seem to further improve CBF estimation reliability compared to the recommended single‐PLD PCASL acquisition strategy.
ACKNOWLEDGMENTS
PB is predoctoral fellow of the Research Foundation Flanders (FWO), Grant 1S69918N. JS and AJD gratefully acknowledge support of the European Space Agency (ESA) and BELSPO Prodex through the BrainDTI project. MJPvO acknowledges support from the EU (Horizon2020, CDS‐QUAMRI, Project number 634541), by the Dutch Heart Foundation and the Netherlands Organisation for Scientific Research (NWO), as part of their joint strategic research programme: “Earlier recognition of cardiovascular diseases” (project: Brain@Risk) and the Netherlands Organisation for Scientific Research (NWO) (VICI‐project; nr. 016.160.351).
APPENDIX A.
The dynamic ASL perfusion signal can be described mathematically as a system of modified Bloch equations, 36 , 37 or as a convolution of an arterial input function (AIF) and an impulse residue function (IRF). 23 , 27 For the purpose of this work, the latter approach is adopted as it allows for a higher level of complexity, and hence accuracy of data simulation. The IRF describes the ASL signal decay, and therefore, depends on the local T 1 relaxation of spins in the voxel. An IRF closely matching reality is given by the single‐pass approximation model with a venous contribution proposed by St. Lawrence et al, 23 which was extended with a microvascular arterial compartment for the current study:
| (A1) |
with , and the transit times through arterial, capillary, and venous space, respectively, , with , the distribution volume of tracer in the capillary space and PS the capillary permeability‐surface area product, , with f the CBF, and . The restricted exchange of water through the capillary wall is described by the blood‐to‐tissue water transit time .
The delivery of the labeled bolus to the destination voxel is described by the AIF. A realistic AIF incorporating dispersion effects using principles of fluid dynamics can be modeled as a convolution of a transport function with a rectangular bolus 21 , 22 :
| (A2) |
with α the labeling efficiency, w(t, τ) = Θ(τ−t) the bolus generated at the labeling site, where Θ(·) is the unit step function, and τ is the labeling duration, and with H(t) the total transport function, which depends on the local arterial transit time Δt and the center‐of‐vessel travel time , as defined in. 21 , 22
Throughout this work, a PCASL difference signal ΔS, acquired with a labeling duration at a time point , is simulated by a convolution of the IRF defined in Equation (A1) with the AIF defined in Equation (A2):
| (A3) |
with the equilibrium magnetization of arterial blood and n = 2 for single‐ or multi‐PLD PCASL or n = K for time‐encoded PCASL (te‐PCASL), with K the order of the Hadamard matrix coupled to the te‐PCASL acquisition scheme.
A vital part of realistic simulations is the incorporation of realistic noise. As label and control images are usually acquired at low spatial resolutions, resulting in high SNRs, it is reasonable to assume that their signal intensities are Gaussian distributed. 24 , 25 The resulting difference data will also follow a Gaussian distribution. Therefore, Gaussian distributed zero‐mean noise was added to PCASL difference signals generated with Equation (A3). An appropriate standard deviation for such additive Gaussian noise was determined based on a temporal SNR (tSNR) for 3D GRASE background‐suppressed single‐PLD PCASL data in GM reported by Vidorreta et al. 26 A single simulated PCASL difference data point could thereby be defined as
| (A4) |
with the additive noise, with for single‐ and multi‐PLD PCASL or for te‐PCASL data as it is the result of a linear combination of K images, instead of2 in the case of one PCASL signal in a single‐ or multi‐PLD sequence 38 . Ultimately, a PCASL difference dataset of N data points can be defined as acquired at time points and with labeling durations , where . Note that acquisition of multiple segments in a 3D readout leads to comparable noise averaging as acquisition of multiple averages.
Bladt P, van Osch MJP, Clement P, Achten E, Sijbers J, den Dekker AJ. Supporting measurements or more averages? How to quantify cerebral blood flow most reliably in 5 minutes by arterial spin labeling. Magn Reson Med. 2020;84:2523–2536. 10.1002/mrm.28314
REFERENCES
- 1. Alsop DC, Detre JA, Golay X, et al. Recommended implementation of arterial spin‐labeled perfusion MRI for clinical applications: a consensus of the ISMRM perfusion study group and the European consortium for ASL in dementia. Magn Reson Med. 2015;73:102‐116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Zhang K, Herzog H, Mauler J, et al. Comparison of cerebral blood flow acquired by simultaneous [15O]water positron emission tomography and arterial spin labeling magnetic resonance imaging. J Cereb Blood Flow Metab. 2014;34:1373‐1380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Heijtel D, Mutsaerts H, Bakker E, et al. Accuracy and precision of pseudo‐continuous arterial spin labeling perfusion during baseline and hypercapnia: a head‐to‐head comparison with 15O H2O positron emission tomography. NeuroImage. 2014;92:182‐192. [DOI] [PubMed] [Google Scholar]
- 4. Kilroy E, Apostolova L, Liu C, Yan L, Ringman J, Wang DJ. Reliability of two‐dimensional and three‐dimensional pseudo‐continuous arterial spin labeling perfusion MRI in elderly populations: comparison with 15O‐water positron emission tomography. J Magn Reson Imaging. 2014;39:931‐939. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. van Osch MJP, Teeuwisse WM, Chen Z, Suzuki Y, Helle M, Schmid S. Advances in arterial spin labelling MRI methods for measuring perfusion and collateral flow. J Cerebral Blood Flow Metabolism. 2018;38:1461‐1480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Lu H, Clingman C, Golay X, van Zijl PCM. Determining the longitudinal relaxation time (T 1) of blood at 3.0 Tesla. Magn Reson Med. 2004;52:679‐682. [DOI] [PubMed] [Google Scholar]
- 7. Hales PW, Kirkham FJ, Clark CA. A general model to calculate the spin‐lattice (T 1) relaxation time of blood, accounting for haematocrit, oxygen saturation and magnetic field strength. J Cereb Blood Flow Metab. 2016;36:370‐374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Li W, Liu P, Lu H, Strouse JJ, Zijl PCM, Qin Q. Fast measurement of blood T 1 in the human carotid artery at 3T: accuracy, precision, and reproducibility. Magn Reson Med. 2016;77:2296‐2302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Lindstrom TR, Koenig SH. Magnetic‐field‐dependent water proton spin‐lattice relaxation rates of hemoglobin solutions and whole blood. J Magn Reson (1969). 1974;15:344‐353. [Google Scholar]
- 10. Wu WC, Fernández‐Seara M, Detre JA, Wehrli FW, Wang J. A theoretical and experimental investigation of the tagging efficiency of pseudocontinuous arterial spin labeling. Magn Reson Med. 2007;58:1020‐1027. [DOI] [PubMed] [Google Scholar]
- 11. Dai W, Garvia D, de Bazelaire C, Alsop D. Continuous flow‐driven inversion for arterial spin labeling using pulsed radio frequency and gradient fields. Magn Reson Med. 2008;60:1488‐1497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Qiu M, Paul Maguire R, Arora J, et al. Arterial transit time effects in pulsed arterial spin labeling CBF mapping: insight from a PET and MR study in normal human subjects. Magn Reson Med. 2010;63:374‐384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Petersen ET, Mouridsen K, Golay X. The QUASAR reproducibility study, part II: results from a multi‐center arterial spin labeling test‐retest study. NeuroImage. 2010;49:104‐113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Chen Z, Zhang X, Yuan C, Zhao X, van Osch MJP. Measuring the labeling efficiency of pseudocontinuous arterial spin labeling. Magn Reson Med. 2017;77:1841‐1852. [DOI] [PubMed] [Google Scholar]
- 15. Aslan S, Xu F, Wang PL, et al. Estimation of labeling efficiency in pseudocontinuous arterial spin labeling. Magn Reson Med. 2010;63:765‐771. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Günther M, Valsala PI. A novel technique to improve the reliability of pseudo continuous arterial spin labeling In: University of Michigan International Workshop on Arterial Spin Labeling MRI: Technical Updates and Clinical Experience, Ann Arbor, Michigan, USA. 2019;abstract number: 9. [Google Scholar]
- 17. Gonzalez‐At JB, Alsop DC, Detre JA. Cerebral perfusion and arterial transit time changes during task activation determined with continuous arterial spin labeling. Magn Reson Med. 2000;43:739‐746. [DOI] [PubMed] [Google Scholar]
- 18. Kramme J, Gregori J, Diehl V, et al. Improving perfusion quantification in arterial spin labeling for delayed arrival times using optimized acquisition schemes. Z Med Phys. 2015;25:221‐229. [DOI] [PubMed] [Google Scholar]
- 19. Gunther M. Encoded continuous arterial spin labeling In: ISMRM Workshop on Cerebral Perfusion and Brain Function: Novel Techniques and Applications, Salvador da Bahia, Brazil. 2007;abstract number 3. [Google Scholar]
- 20. Teeuwisse WM, Schmid S, Ghariq E, Veer IM, van Osch MJP. Time‐encoded pseudocontinuous arterial spin labeling: basic properties and timing strategies for human applications. Magn Reson Med. 2014;72:1712‐1722. [DOI] [PubMed] [Google Scholar]
- 21. Gall P, Guether M, Kiselev V. Model of blood transport couples delay and dispersion and predicts ASL bolus measurements. In: Proceedings of the 18th Annual Meeting of ISMRM, Stockholm, Sweden: 2010;18:1736. [Google Scholar]
- 22. Kellner E, Gall P, Günther M, et al. Blood tracer kinetics in the arterial tree. PLOS ONE. 2014;9:1‐11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. St Lawrence K, Frank J, McLaughlin A. Effect of restricted water exchange on cerebral blood flow values calculated with arterial spin tagging: a theoretical investigation. Magn Reson Med. 2000;44:440‐449. [DOI] [PubMed] [Google Scholar]
- 24. Bouhrara M, Spencer RG. Fisher information and Cramér‐Rao lower bound for experimental design in parallel imaging. Magn Reson Med. 2018;79:3249‐3255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Aja‐Fernández S, Pieciak T, Vegas‐Sánchez‐Ferrero G. Spatially variant noise estimation in MRI: a homomorphic approach. Med Image Anal. 2015;20:184‐197. [DOI] [PubMed] [Google Scholar]
- 26. Vidorreta M, Wang Z, Rodríguez I, Pastor MA, Detre JA, Fernández‐Seara MA. Comparison of 2D and 3D single‐shot ASL perfusion fMRI sequences. NeuroImage. 2013;66:662‐671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Buxton RB, Frank LR, Wong EC, Siewert B, Warach S, Edelman RR. A general kinetic model for quantitative perfusion imaging with arterial spin labeling. Magn Reson Med. 1998;40:383‐396. [DOI] [PubMed] [Google Scholar]
- 28. Chen Y, Wang Z, Detre J. Impact of equilibrium magnetization of blood on ASL quantification. In: Proceedings of the 19th Annual Meeting of ISMRM, Montréal, Canada: 2011;19:300. [Google Scholar]
- 29. Bojorquez JZ, Bricq S, Acquitter C, Brunotte F, Walker PM, Lalande A. What are normal relaxation times of tissues at 3 T? Magn Reson Imaging. 2017;35:69‐80. [DOI] [PubMed] [Google Scholar]
- 30. Bladt P, den Dekker AJ, Clement P, Achten E, Sijbers J. The costs and benefits of estimating T 1 of tissue alongside cerebral blood flow and arterial transit time in pseudo‐continuous arterial spin labeling. NMR Biomed. 2019;e4182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Otsu N. A threshold selection method from gray‐level histograms. IEEE Trans Syst, Man, Cybernet. 1979;9:62‐66. [Google Scholar]
- 32. Fan AP, Jahanian H, Holdsworth SJ, Zaharchuk G. Comparison of cerebral blood flow measurement with [15O]‐water positron emission tomography and arterial spin labeling magnetic resonance imaging: a systematic review. J Cereb Blood Flow Metab. 2016;36:842‐861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Woolrich MW, Chiarelli P, Gallichan D, Perthen J, Liu TT. Bayesian inference of hemodynamic changes in functional arterial spin labeling data. Magn Reson Med. 2006;56:891‐906. [DOI] [PubMed] [Google Scholar]
- 34. Chappell MA, Groves AR, Whitcher B, Woolrich MW. Variational bayesian inference for a nonlinear forward model. IEEE Trans Signal Process. 2009;57:223‐236. [Google Scholar]
- 35. Woods JG, Chappell MA, Okell TW. A general framework for optimizing arterial spin labeling MRI experiments. Magn Reson Med. 2019;81:2474‐2488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Detre J, Leigh J, Williams D, Koretsky A. Perfusion imaging. Magn Reson Med. 1992;23:37‐45. [DOI] [PubMed] [Google Scholar]
- 37. Parkes LM, Tofts PS. Improved accuracy of human cerebral blood perfusion measurements using arterial spin labeling: Accounting for capillary water permeability. Magn Reson Med. 2002;48:27‐41. [DOI] [PubMed] [Google Scholar]
- 38. Dai W, Shankaranarayanan A,Alsop DC. Volumetric measurement of perfusion and arterial transit delay using hadamard encoded continuous arterial spin labeling. Magn Reson Med. 2013;69:1014‐1022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Jung Y, Wong EC, Liu TT. Multiphase pseudocontinuous arterial spin labeling (MP‐PCASL) for robust quantification of cerebral blood flow. Magn Reson Med. 2010;64:799‐810. [DOI] [PubMed] [Google Scholar]
- 40. Zhao L, Vidorreta M, Soman S, Detre JA, Alsop DC. Improving the robustness of pseudo‐continuous arterial spin labeling to off‐resonance and pulsatile flow velocity. Magn Reson Med. 2017;78:1342‐1351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Li W, Grgac K, Huang A, Yadav N, Qin Q, van Zijl PCM. Quantitative theory for the longitudinal relaxation time of blood water. Magn Reson Med. 2016;76:270‐281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. St Lawrence KS, Owen D, Wang DJJ. A two‐stage approach for measuring vascular water exchange and arterial transit time by diffusion‐weighted perfusion MRI. Magn Reson Med. 2012;67:1275‐1284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Herscovitch P, Raichle ME, Kilbourn MR, Welch MJ. Positron emission tomographic measurement of cerebral blood flow and permeability‐surface area product of water using [15O]water and [11C]butanol. J Cereb Blood Flow Metab. 1987;7:527‐542. [DOI] [PubMed] [Google Scholar]
- 44. Gregori J, Schuff N, Kern R, Günther M. T 2‐based arterial spin labeling measurements of blood to tissue water transfer in human brain. J Magn Reson Imaging. 2013;37:332‐342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Francis ST, Bowtell R, Gowland PA. Modeling and optimization of look‐locker spin labeling for measuring perfusion and transit time changes in activation studies taking into account arterial blood volume. Magn Reson Med. 2008;59:316‐325. [DOI] [PubMed] [Google Scholar]
- 46. Hua J, Qin Q, Pekar JJ, van Zijl PCM. Measurement of absolute arterial cerebral blood volume in human brain without using a contrast agent. NMR Biomed. 2011;24:1313‐1325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Li K, Zhu X, Hylton N, Jahng GH, Weiner MW, Schuff N. Four‐phase single‐capillary stepwise model for kinetics in arterial spin labeling MRI. Magn Reson Med. 2005;53:511‐518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Pawlik G, Rackl A, Bing RJ. Quantitative capillary topography and blood flow in the cerebral cortex of cats: an in vivo microscopic study. Brain Res. 1981;208:35‐58. [DOI] [PubMed] [Google Scholar]
- 49. Ma Y, Koo A, Kwan H, Cheng K. On‐line measurement of the dynamic velocity of erythrocytes in the cerebral microvessels in the rat. Microvascular Res. 1974;8:1‐13. [DOI] [PubMed] [Google Scholar]
- 50. Fenton BM, Zweifach BW.Microcirculatory model relating geometrical variation to changes in pressure and flow rate. Ann Biomed Eng. 1981;9:303‐321. [Google Scholar]


