Multi-GPU Immersed Boundary Method Hemodynamics Simulations

Abstract

Large-scale simulations of blood flow that resolve the 3D deformation of each comprising cell are increasingly popular owing to algorithmic developments in conjunction with advances in compute capability. Among different approaches for modeling cell-resolved hemodynamics, fluid structure interaction (FSI) algorithms based on the immersed boundary method are frequently employed for coupling separate solvers for the background fluid and the cells within one framework. GPUs can accelerate these simulations; however, both current pre-exascale and future exascale CPU-GPU heterogeneous systems face communication challenges critical to performance and scalability. We describe, to our knowledge, the largest distributed GPU-accelerated FSI simulations of high hematocrit cell-resolved flows with over 17 million red blood cells. We compare scaling on a fat node system with six GPUs per node and on a system with a single GPU per node. Through comparison between the CPU- and GPU-based implementations, we identify the costs of data movement in multiscale multi-grid FSI simulations on heterogeneous systems and show it to be the greatest performance bottleneck on the GPU.

1. Introduction

Within the last decade, cell-resolved simulations of 3D blood flow have provided new insights into important physiological phenomena such as sickle-cell anemia [1], malaria [2], and thrombosis [3]. Computational studies of cellular-scale events in large blood vessel networks necessitate simulations with clinically relevant resolutions and tractable times to solution. To achieve the dual objectives of clinical relevance and high performance requires both a massively parallel and efficient fluid structure interaction (FSI) solver. This approach requires optimizing both compute intensive routines and inter-process communication. Efficient use of multiple subsystems, such as processing units, memory, and interconnect is a challenging load balance problem for cell-scale blood flow simulations [4]. GPU-based approaches are increasingly popular for accelerating computation relative to CPU-based ones owing to their massive parallelism, greater peak floating point performance and memory bandwidth [5, 6, 7]. Previous GPU-accelerated FSI solvers have either been a hybrid CPU-GPU implementation [8, 9], limited to a single GPU [10, 11, 12], or focused on flows involving rigid or deformable bodies that are generally stationary [13, 11, 8]. Therefore, in this work we develop the first distributed GPU approach for simulating high hematocrit cell-resolved hemodynamics and present the communication strategy to accommodate distributed parallelization with multiple GPUs.

Achieving high performance on GPU-based architectures requires careful tuning of the simulation’s data movement and data access patterns to take advantage of the hardware. For distributed simulations, the immense throughput of GPUs relative to CPUs can lead to performance bottlenecks moving from the processing units to other subsystems such as the interconnects. Since many scientific applications face similar scaling challenges, supercomputer architectures have been trending towards fat nodes, with large compute and memory capacity per node, to limit application dependence on internode communication [14]. Such system characteristics are as important to performance of massively parallel simulations as the compute capabilities of the GPUs.

Regardless of the architecture, FSI codes focused on dynamic deformable bodies commonly utilize the immersed boundary method (IBM) to couple two separate solvers to model the fluid and structure components [15]. The main components of an IBM-based algorithm include the interpolation of the fluid velocity from Eulerian to Lagrangian grids, the determination of the force generated in each cell membrane in response to deformation, and the spreading of this force back to the Eulerian grid on which the fluid flow equations are subsequently solved [16, 17]. A popular approach for modeling fluid flow within an FSI algorithm is the lattice Boltzmann method (LBM) [18], which is well suited for parallelization [19, 20, 21, 22, 23] and GPU approaches [24, 25, 26, 27, 28]. The LBM is also representative of stencil neighborhood computations which are central to image processing, machine learning, and climate modeling [29]. The commonly employed finite element method (FEM) determines the cell forces due to deformation. Many FEM approaches provide high accuracy and stability at the expense of increased computation [30, 31, 32].

We perform simulations using HARVEY, a parallel hemodynamics solver for flows in complex vascular geometries [21]. In the present work we apply this to model 3D cell-resolved blood flow, where red blood cells (RBCs) are modeled with the FEM and coupled to an LBM fluid solver using the IBM. We extend our previous work on data motion in a CPU-based simulation [33] to develop and evaluate the performance of a CUDA GPU-based implementation that builds off of our GPU parallelized fluid-only solver [34]. Subsequent relative parallel efficiency and communication scaling are also evaluated.

In this study, we investigate performance on different GPU architectures in terms of simulation parameters such as hematocrit (volume fraction of RBCs) to evaluate the performance as a function of the amount of FSI, as well as delta function support size to modulate the communication volume. We also investigate in terms of hardware parameters such as host-device interconnects and HPC system architecture. This is augmented by an analysis of the scalability of our distributed, GPU-accelerated code with contextualization using our existing highly scalable CPU code [35]. For these purposes we show weak scaling results to evaluate how well our GPU-accelerated code can accommodate massively parallel hemodynamics simulations and whether there is a demonstrable benefit to GPU acceleration for FSI workloads.

Due to the differences in memory bandwidth between GPUs and CPUs we expect a benefit for memory bound operations with larger speedups for compute bound kernels. Three major kernels: the LBM, IBM interpolation, and IBM spreading have been shown to be memory bound [36, 37, 11] and therefore we expect a speedup proportional to the bandwidth differences between the CPUs and GPUs on the nodes of the particular systems we use in this work.

We use the same inter-node communication scheme for both the CPU and GPU code. Therefore, we expect that communication will constitute a larger proportion of the simulation time for the GPU simulations as the other computational aspects of the code would have already realized their respective speedups. Accordingly, communication and data movement optimizations will lead to greater speedup on GPU simulations than on the CPU. This is in contrast to our previous work which showed that different communication schemes modestly affect overall simulation time in CPU simulations [33].

In summary, the contributions of this paper are the following:

• The presentation of a fully GPU-accelerated FSI simulation with applications for cell-resolved hemodynamics.

• Comparison of performance, scaling behavior, and bottlenecks on thin node and pre-exascale fat node heterogeneous systems.

• Computational experiments showing that the processing power of GPUs leads to increased relative cost of communication versus CPU simulations.

• Demonstration of the superior scaling on fat-node versus thin-node systems due to the high relative cost of communication for GPU-accelerated FSI simulations.

Our analysis of the increasingly communication-bound performance for simulations where GPUs reduce computation time is relevant to a variety of applications targeting heterogeneous systems.

2. Methods

The immersed boundary method is used with HARVEY, a massively parallel computational fluid dynamics code, to perform the fluid structure interaction which couples the cell membrane forces determined using the finite element method to a fluid flow solver based on the lattice Boltzmann method [21, 38].

In the subsequent equations, we employ the convention of using lowerand upper-case letters for Eulerian and Lagrangian quantities, respectively.

2.1. Fluid mechanics using the lattice Boltzmann method

The lattice Boltzmann method provides a means of solving the Navier-Stokes equations which govern fluid-flow at the continuum-level [18]. With the LBM, the fluid is represented by a distribution of fictitious particles that evolves following the lattice Boltzmann equation:

$$f_i\left(x+c_i,t+1\right)=\left(1-\frac{1}{\tau }\right)f_i(x,t)+\frac{1}{\tau }{f}_i^{eq}(x,t)+h_i(x,t)$$ (1)

for distribution function f, lattice position x, timestep t, external force distribution h_i, equilibrium distribution $f_i^{eq}$, and relaxation time τ. Here we consider the timestep size (δt) and lattice spacing (δx) equal to unity. c_i is the discrete velocity of the i^th component of f, and we use a standard D3Q19 discretization where vectors point to 18 of the nearest-neighbor lattice positions, and one additional vector represents the rest velocity. We incorporate the external force field g(x, t) from the IBM in two steps in solving Equation 1; the equilibrium Maxwell-Boltzmann distribution is determined from the moments of the distribution function, and the force distribution h_i is determined from the external force g [39]. For the first step, the equilibrium distribution is determined from:

$$f_i^{eq}(x,t)={\omega }_i\rho \left(1+\frac{c_i\cdot v}{c_s^2}+\frac{vv:\left(c_i{c}_i-c_s^{2}I\right)}{2c_s^4}\right)$$ (2)

for the standard D3Q19 lattice weights ω_i and lattice speed of sound $c_s=\sqrt{\frac{1}{3}}$. The density ρ and momentum ρv, are the first two moments of the distribution function:

$$\rho =\sum _{i=1}^{19}{f}_i\rho v=\sum _{i=1}^{19}{c}_i{f}_i+\frac{1}{2}g.$$ (3)

For the second step, the force distribution h_i is determined from the external force g:

$$h_i=\left(1-\frac{1}{2\tau }\right){\omega }_i\left[\frac{c_i-v}{c_s^2}+\frac{c_i\cdot v}{c_s^4}{c}_i\right]\cdot g.$$ (4)

As discussed in [35], fluid points in the HARVEY LBM implementation are indirectly addressed, and an adjacency list for the LBM streaming operation is computed during setup. This addressing scheme is utilized to efficiently accommodate sparse geometries as are commonly encountered with complex vasculatures. The implementation used in the present work stores a single copy of the distribution function on the CPU (AA scheme [40]) and two copies, one read-only and the other for writing, on the GPU. Halfway bounceback boundary conditions [41] are employed. Other salient details about methods such as simulation initialization (i.e. mesh creation), load balancing, and additional data structures used can be found in our previous works [35, 38].

2.2. Finite element method for deformable cells

We model each deformable cell as a viscous fluid enclosed by an elastic membrane. The membrane is discretized by a triangular mesh generated by successively refining an icosahedron. Red blood cell membrane models commonly account for physical properties such as elasticity and resistance to bending, as well as the effects of surface viscosity [42]. In the present work, we model the membrane to be hyperelastic with resistance to shear and area dilation following the constitutive law of Skalak for the strain energy function W [43, 44]:

$$W=\frac{G}{4}\left(I_1^2+2I_1+2I_2+C{I}_2^2\right)$$ (5)

where G is the membrane shear elastic modulus, C is a constant related to the area dilation modulus, and I₁, I₂ are the strain invariants of the Green strain tensor. To model the membrane force in response to deformation, we use a common continuum-level FEM where loop elements are used as a subdivision surface [31, 45, 32]. This approach is more stable and extensible than those which assume a constant displacement gradient tensor of each element (e.g. [30]), although at the expense of increased computation on account of using 12 surrounding vertices to compute the strain on each triangular element.

2.3. Fluid structure interaction with the immersed boundary method

The immersed boundary method uses discrete delta functions δ to couple the FEM-based cell solver to the LBM fluid flow solver [16]. More specifically, these functions are formulated to transfer simulation data between the Lagrangian grid for the cells and the Eulerian lattice grid for the fluid flow. The IBM is implemented using three computational kernels that are called at each timestep: interpolation, membrane advection, and spreading. At each timestep, the velocity V of each Lagrangian vertex is interpolated from the bulk fluid velocity v defined on the Eulerian lattice x:

$$V(X,t)=\sum _{x}v\left(x,t\right)\delta \left(x-X\left(t\right)\right).$$ (6)

Using the vertex velocities, we then advect the cell membrane using the forward Euler method to update Lagrangian vertex positions X:

$$X\left(t+1\right)=X\left(t\right)+V\left(t\right),$$ (7)

With the updated positions of the Lagrangian vertices, the force generated in the membrane due to deformation between timesteps is determined using the FEM as previously described. These Lagrangian forces G are then coupled to the bulk fluid by spreading from vertex positions to surrounding Eulerian lattice grid points:

$$g\left(x,t\right)=\sum _{x}G\left(X,t\right)\delta \left(x-X\left(t\right)\right)$$ (8)

where g(x, t) is the external force used in Equation 4.

We use the symbol ϕ to denote the support of the delta function, which defines the interaction distance between Lagrangian and Eulerian grids for a particular cell membrane. The number of Eulerian grid points spanned by the discrete delta function in each direction gives the support size, and this function is evaluated at each lattice point within the support for each cell vertex. For support sizes of 3 and 4 this corresponds to 27 and 64 lattice points for each vertex. Different support sizes can affect the stability and accuracy to varying degrees depending on the application [16, 46]. Here we consider two delta functions corresponding to the aforementioned support sizes:

Delta function support ϕ = 3:

$${\delta }_i\left(r\right)=\{\begin{array}{ll}\frac{1}{3}\left(1+\sqrt{1-3r^2}\right)\hfill & \text{ if }r\le \frac{1}{2}\hfill \\ \frac{1}{6}\left(5-3r-\sqrt{-2+6r-3r^2}\right)\hfill & \text{ if }\frac{1}{2}<r\le \frac{3}{2}\hfill \\ 0\hfill & \text{ if }r>\frac{3}{2}\hfill \end{array}$$ (9)

Delta function support ϕ = 4:

$${\delta }_i\left(r\right)=\{\begin{array}{ll}\frac{1}{4}\left(1+\text{cos}\left(\frac{\pi }{2}r\right)\right)\hfill & \text{ if }r\le 2\hfill \\ 0\hfill & \text{ if }r>2\hfill \end{array}$$ (10)

where r is the distance between the vertex and lattice point in the support, and the i^th component of delta delineates the x, y, or z directions.

2.4. General parallelization framework

Domain decomposition spatially distributes the workload among tasks defined by rectangular cuboid bounding boxes. We assume the Lagrangian cell and Eulerian fluid domains to have coincident bounding boxes which partition the vascular geometry. We adopt the approach of [47] to establish the halo hierarchy underlying the inter-process communication scheme, with overlapping halos of adjacent task bounding boxes used to define neighbor relationships. Relative to a task, we refer to cell vertices and fluid lattice points as ‘owned’ if they are within the bounding box of the task, and ‘shared’ if not. Similar descriptions are used for cells based on the location of their geometric centroid. A representative example of bounding boxes overlaid with cells is given in Figure 1A.

Figure 1:

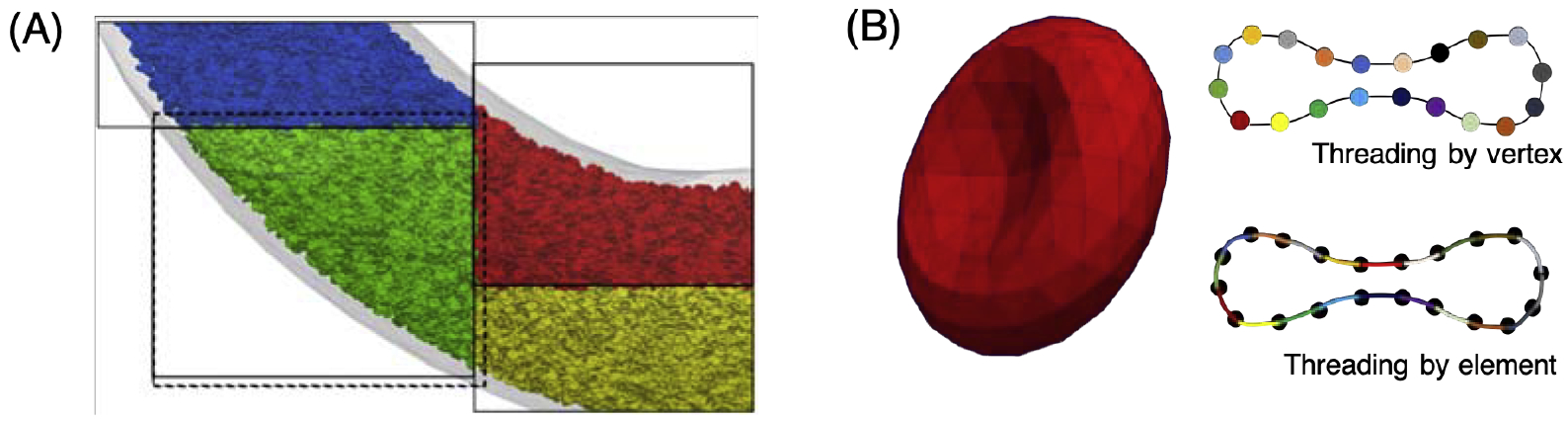
(A) Example of domain decomposition, with cells colored by the bounding box to which they belong. Dotted lines indicate halo data for the green task. (B) Lagrangian RBC mesh, and colors delineating GPU threading schemes for cell vertices and elements depending on the operation

Fluid halo:

Each task bounding box is encapsulated by a halo of fluid points, to achieve two separate ends. First, the LBM distribution components are communicated via an n point-wide halo, and are streamed at the next timestep into the bounding box. Second, the IBM interpolation is locally computed for all owned vertices on account of setting the halo width to $\lfloor \frac{\varphi }{2}\rceil$. For ϕ = 3 the fluid halo is one point wide since ${\delta }_i\left(\frac{3}{2}\right)=0$ in Equation 9, but has a width of two points for ϕ = 4.

Cell halo:

Calculations associated with the IBM are facilitated by means of a halo encapsulating the task bounding box. As described in [33], with our approach a complete copy of a shared cell in a halo is stored. The largest cell radius (r) anticipated in the simulation is used to set the width of this halo, which is defined as $\lfloor \frac{\varphi }{2}\rceil +r$. By defining it in this manner, all vertices that can potentially spread a force onto a task-owned fluid point are shared with the task.

GPU threading:

For the LBM portion of the GPU parallelized simulation, each MPI task launches a kernel with a one-to-one mapping of threads and its owned Eulerian lattice points. The indirectly addressed fluid data and associated data structures are stored in a structure of arrays (SoA) layout; in contrast to the array of structures (AoS) layout used in the CPU code. Previous work has shown that an SoA memory arrangement on GPUs enables contiguous memory accesses along each warp on the GPU to maximize throughput from the GPU main memory [11, 34]. The LBM collision and stream operations are undertaken at the same time in a fused kernel to reduce the number of reads and writes to main memory. We use the common AB scheme which requires a read from the A version of the LBM distribution data and a write to the B version of the LBM distribution so that un-updated data is not overwritten. A and B buffers are then swapped after the LBM update. A ‘push’ configuration is used which reads the pre-collision discrete particle at the fluid point described by a thread’s threadID and then writes the post-collision state to the fluid point’s 18 neighbors.

Similar to the fluid data layout, the cell data structures are aligned in an SoA format. Two different threading schemes are used for the cell computations. The interpolation, cell advection, and spreading routines are structured such that each thread handles one Lagrangian vertex. Vertex data for each cell is stored contiguously in device memory to improve locality. The aforementioned kernels are launched across all vertices for every cell which allows flexibility in tuning the blocksize for improved occupancy compared to restricting blocks to vertices in the same cell. Each thread accesses ϕ³ nearby Eulerian points for reading and writing during interpolation and spreading, respectively. Threads for the FEM routines operate on a triangular element to calculate the force it generates and then interpolate the force to its respective Lagrangian vertices according to the FEM shape functions. To reduce the data movement of the highly memory bound FEM kernels, threads perform redundant computations on adjacent triangles during loop subdivision. The alternative approach where threads operate on individual triangles has larger data movement costs since intermediate values are written to and later read from global memory.

The previously described immersed boundary and FEM GPU kernel launch schemes are depicted for a representative cell in Figure 1B. Atomic operations must be used for both the spreading and FEM kernels as multiple threads may write to the same Eulerian point or Lagrangian vertex [48, 12]. In the FEM kernel, adjacent elements simultaneously attempt to interpolate forces onto the same vertex. During immersed boundary spreading, multiple vertices could potentially have overlapping supports requiring the reduction of forces from multiple threads. Therefore, we use cudaAtomicAdd() to address these potential race conditions.

For MPI communication between GPUs, all relevant data must be transferred between the host and device both prior to and following data movement between nodes. See Figure 2 for a schematic of data transfers between host, device, and nodes. The amount of data transferred from device to host matches the amount of data transferred between MPI tasks. When launching kernels on multi-GPU jobs, working threads are only created for Lagrangian vertices or elements that ‘own’ a point thereby minimizing the amount of re-computation on shared halo data between tasks. Overall, the MPI parallelization scheme for the GPU code is largely the same as that of the CPU code as data is transferred into the format expected by the CPU communication data structures. This decision was made to simplify the codebase and avoid the complexity of maintaining multiple implementations of the communication framework.

Figure 2:

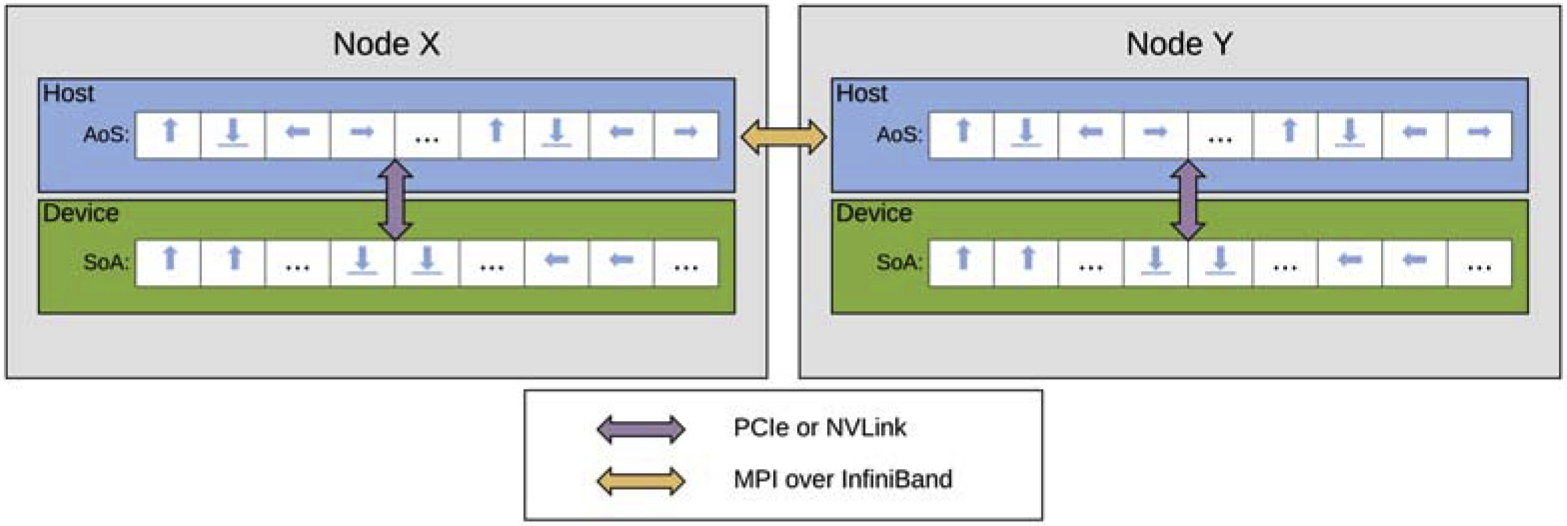
CPU-GPU and inter-node data movement. The small blue arrows represent particle distributions pointing in their respective discrete velocity directions, stored in an AoS layout and SoA layout on the host and device. For MPI communication, data moves between the host and device over PCIe or NVLink, denoted by the purple arrow. Inter-node data transfers are over InfiniBand, shown with the yellow arrow.

2.5. Communication schemes and fluid structure interaction workflow

The algorithm associated with the immersed boundary method coupling of the FEM cell solver to the LBM fluid solver is outlined in Algorithm 1. The initial setup, including placement of RBCs to reach the desired cell density, is first performed on the CPU and the initial simulation state data is migrated to the GPU. During each time step halo values are exchanged with neighbor processes, requiring both CPU-GPU and MPI data movement. The size of this LBM fluid halo is determined by the support used for the IBM functions. For example, a four point immersed boundary support requires a halo overlap of two points. Once updated halos are copied to the GPU, the GPU executes fluid flow and cell computations. The updated values in the halos of neighbors are then copied from the GPU to the CPU and communicated through MPI. Received halo values are copied to the GPU and the next iteration of the simulation loop proceeds.

The Lagrangian communication scheme for the cells is depicted in Figure 3. The IBM interpolation operation updates cell vertex positions which are local to an MPI task. These cell vertex positions are then communicated to the task which owns the cell centroid so that the cell position may be advected and force calculations performed. The FEM calculations are performed over all vertices of a cell by the task which owns the cell. Subsequently, vertex forces that will be spread to regions of another task are communicated so that each task locally performs the spreading operation.

Figure 3:

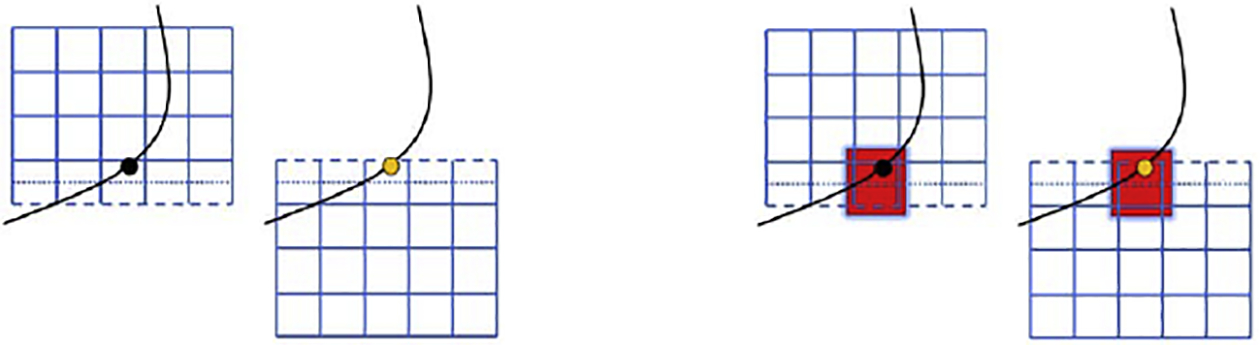
Lagrangian communication for the IBM spreading operation for ϕ = 2. First (left), the Lagrangian force is computed on the owned IBM vertex (black circle) by the upper task and communicated to the same vertex (yellow circle) on the lower task. Second (right), the IBM spreading operation (red box) is performed for this vertex by both tasks. Solid blue lines indicate fluid grid points owned by the task, dash blue line denotes fluid points on the halo, and the dotted line represents the boundary between tasks.

3. Results

3.1. Simulation setup

In the literature there are a variety of approaches for initially populating geometries with cells to achieve a dense suspension (e.g. [49], [50], [28]). With regard to blood flow, the suspension density is referred to as the hematocrit, which gives the volume fraction of red blood cells. Following the method described in [33], the present work uses an external library [51] to densely pack our geometry using periodic ‘tiles’. After the initial cell placement, a short start-up simulation is required as is the case with other approaches (e.g. [49]). We then randomly remove cells after the initial dense packing until the desired hematocrit is achieved.

Runs are conducted on two systems with differing architectures: the Duke Compute Cluster (DCC) and the Summit supercomputer at Oak Ridge National Laboratories. The DCC is a cluster with two Intel Broadwell Xeon E5–2699 v4 processors and one NVIDIA P100 GPU per node connected to the host via PCIe. There is a 7 GB/s Mellanox Infiniband interconnect. The Summit supercomputer is ranked the fastest supercomputer in the world as of November 2019 [52]. Each node has two IBM POWER9 22-core CPUs and 6 NVIDIA V100 GPUs. 150 GB/s bandwidth NVLink connects the CPU and each GPU on a socket while 50 GB/s NVLink connects all GPUs on a socket. Table 1 contains a summary of the system hardware. An important distinction is that Summit’s architecture centers on fat nodes with 6 GPUs and 6 times the total graphics memory of a DCC node with one GPU. This means for a given large problem size the DCC requires more nodes and inter-node communication—an important factor in scaling behavior. The DCC provides a relevant comparison to Summit as PCIe is the most common CPU-GPU interface and due to the high costs of fat node system architectures many HPC systems have few GPUs per node [53].

Table 1:

Summit and DCC Node Characteristics.

System	Summit	DCC
CPU	2X POWER9	2X Xeon E5–2699V4
Cores/CPU	21	22
Memory	512 GB	400GB
Memory Bandwidth	170 GB/s/CPU	76 GB/s/CPU
GPU	6X V100	1X P100
GPU Memory	16 GB/GPU HBM2	16 GB HBM2
GPU Memory Bandwidth	900 GB/s/GPU	732 GB/s
GPU-CPU Interface	NVLink 50 GB/s/GPU	32 GB/s
Interconnect	IB 25 GB/s	IB 7 GB/s

We investigate the single node and weak scaling performance of both the GPU and CPU implementations. Weak scaling experiments keep per node compute workload and memory requirements constant while increasing the simulation scale and node count. As it is often desirable to use available system resources, weak scaling provides insight into the performance of realistic simulation workloads for a given set of compute resources. In the single node performance study we examine a cubic geometry packed with red blood cells at 40% hematocrit, which is well within the range of volume fraction of red blood cells in healthy whole blood [54]. For weak scaling we consider progressively larger cubes with fluid points and red blood cell counts proportional to the number of nodes (see Table 2). A cubic geometry was chosen to specifically focus on the performance of the coupling algorithm and remove the influence of other factors such as load balancing. As exhibited by Figure 4, this method works for sparse, complex geometries such as vascular bifurcations.

Table 2:

Weak scaling input sizes on Summit (left) and DCC (right). Red blood cell counts are when hematocrit is 0.40. For simulations at lower hematocrit values the fluid grid is unchanged but the number of red blood cells decreases proportionately to the hematocrit.

Nodes	Fluid Grid	RBCs	Nodes	Fluid Grid	RBCs
1	5003	0.53M	1	3003	0.113M
2	6293	1.05M	2	3773	0.224M
…	…	…	4	3763	0.457M
32	15873	17M	8	6003	0.918M

Figure 4:

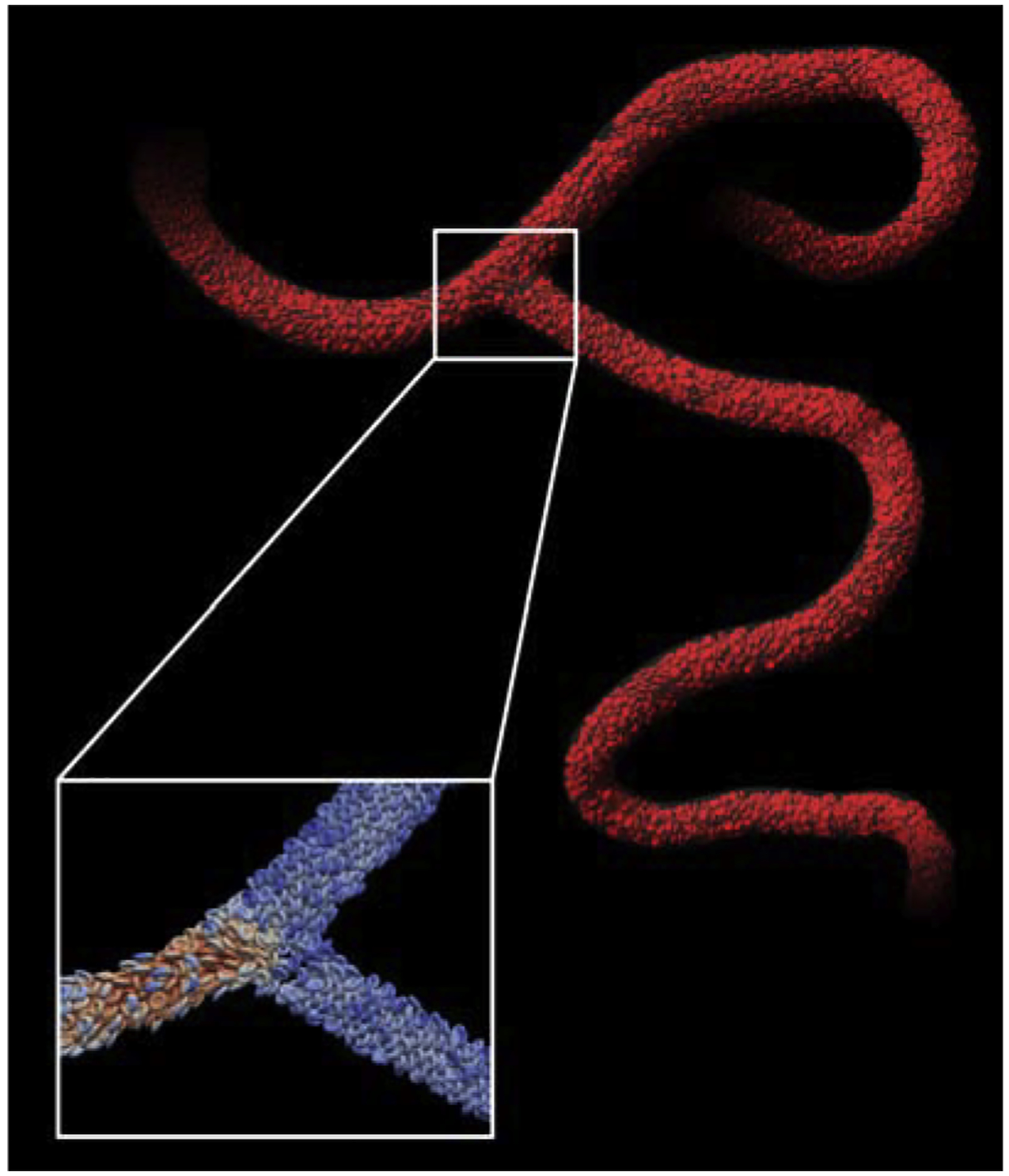
Red blood cells in a human cerebral vascular geometry simulated with HARVEY. Cells in the highlighted window are colored by vertex velocity.

For all measurements we display results for the launch configuration resulting in the best time to solution. On the DCC the GPU scheme uses a single task per node for the 1 node configuration and 4 tasks per node for the 2+ node configurations. The CPU scheme on the DCC uses 32 tasks per node with two OpenMP threads per rank. These aforementioned configurations on the DCC yielded the best performance in a preliminary performance study. On Summit the GPU scheme uses 16 tasks per node and the CPU scheme uses 32 tasks per node. While Summit has a total of 42 CPU cores and 6 GPUs per node, we observed better performance from 32 tasks per node (16 tasks on each CPU socket) on the CPU and 16 tasks per node for the GPU than when using a multiple of the number of CPU cores or GPUs. For this application power of two task counts result in better performance from improved load balancing and lower communication volume. Furthermore, the kernels are memory bound and the sustained memory bandwidth of the POWER9 CPU saturates once using 16 cores as measured by the STREAM benchmark [55, 56].

3.2. Single node performance

To isolate the performance costs of data movement over intra-node interfaces versus network interconnects, we investigate the absolute time that the GPU and CPU implementations spend in kernels and intra-node communication on Summit. An important distinction of the GPU implementation is that halo values are transferred over PCIe or NVLink between the host and device in addition to MPI requests between MPI tasks. In Figure 5 we see that for the same problem size the GPU implementation spends much less time in the kernels. This smaller absolute time in computationally intensive kernels is contrasted by an increase in the amount of time spent in communication as compared to the CPU version. While the GPU implementation is around 16–18 times faster overall, for the highest hematocrit simulations it spends 51.3% its runtime in data movement compared to 1.0% on the CPU implementation (51x difference). For lower hematocrit simulations where there is more communication compared to computation this effect is magnified with the GPU spending 50.1% of runtime in data movement and the CPU spending 0.7% (72x difference).

Figure 5:

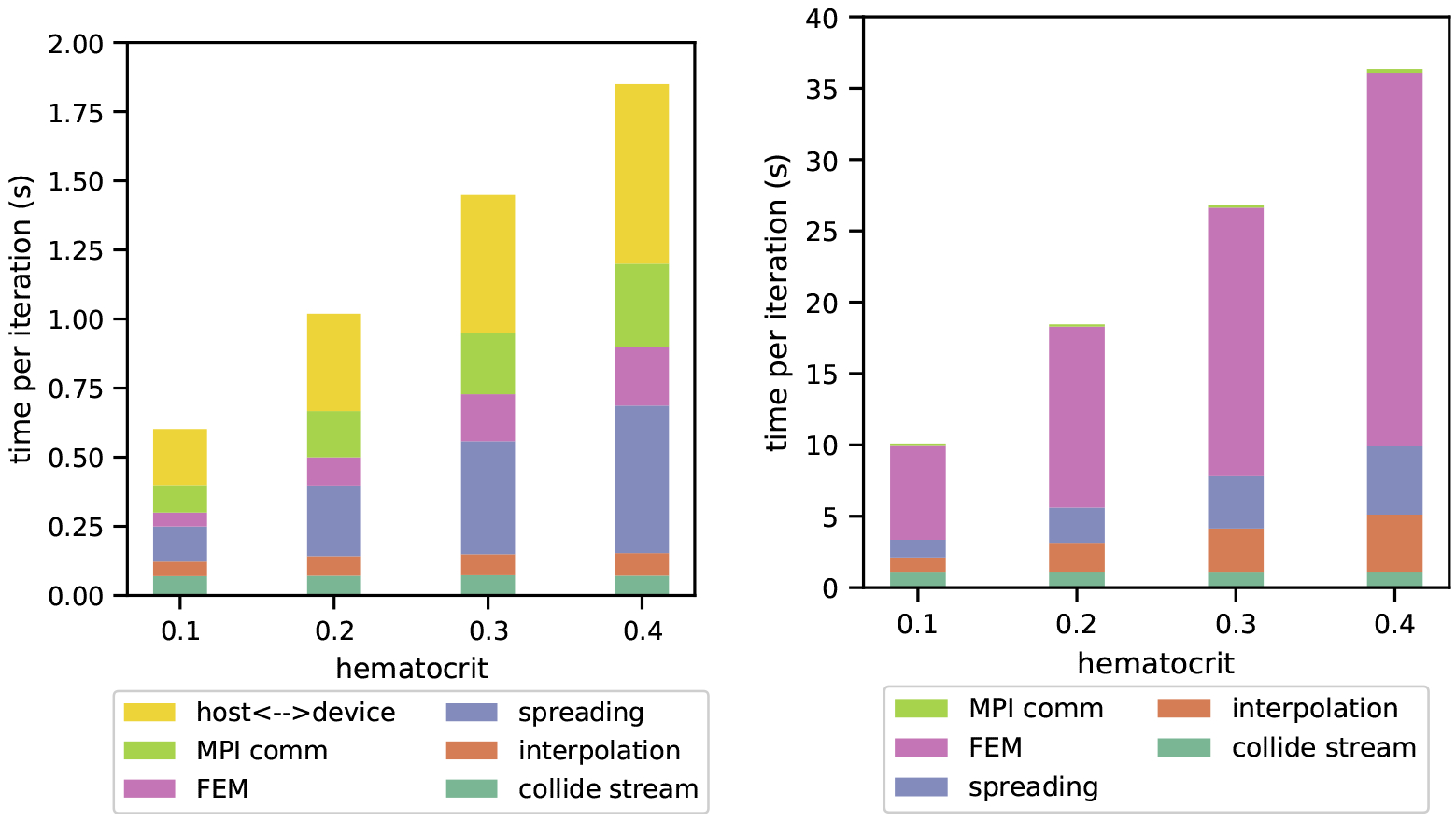
Single node performance analysis on Summit (P9 CPUs and V100 GPUs) with a support size ϕ = 4. On the left is the time per iteration for a GPU simulation and on the right is the time per iteration for a CPU simulation, both reported in seconds. Minor operations accounting for less than 1% of run time are omitted for clarity.

Unlike on the CPU, increased hematocrit on the GPU does not increase the time spent in different kernels uniformly. In particular, time spent in the relatively inexpensive interpolation function is nearly constant for all tested hematocrit levels. This is because differences in workload at different hematocrit values are insignificant compared to the overhead of launching the kernel. In contrast, both the CPU and GPU spend more time in the FEM and spreading kernels at increased hematocrit levels. These kernels have workloads large enough to mask launch overhead. On the GPU, the kernels for which the amount of time increases with hematocrit, such as FEM and spreading, are kernels with a large amount of atomic operations which limit the maximum achievable bandwidth. Moreover, the speedup over the CPU in individual kernels is 10x for spreading compared with 40x for interpolation at 0.40 hematocrit, showing that for similarly cache-optimized kernels the atomic operations have a stalling effect.

3.3. Multi-node performance

We perform a similar comparison of time spent in sections of the code when run on multiple nodes of Summit and the DCC, systems with differing network connectivity. Figure 6 shows the breakdown of time spent in different functions on 8 nodes of Summit and the DCC at 0.40 hematocrit and the domain sizes listed in Table 2. For the GPU implementation, over half of the run time is spent in data movement between MPI processes and between the CPU and GPU. On Summit we observe 55% of run time is spent overall in communication compared to 54% on the DCC. The percentages of run time spent in device-host transfers on Summit and the DCC are 29% and 35%, respectively. Thus, on Summit, MPI communication and device-host transfers make up similar proportions of run time while on the DCC more time is spent in device-host transfers. This difference is attributable to the greater bandwidth of the NVLinks on Summit compared to PCI Express on the DCC. Therefore, on Summit the largest bottleneck for our code is the node interlink while on DCC the largest bottleneck is the device-host interface.

Figure 6:

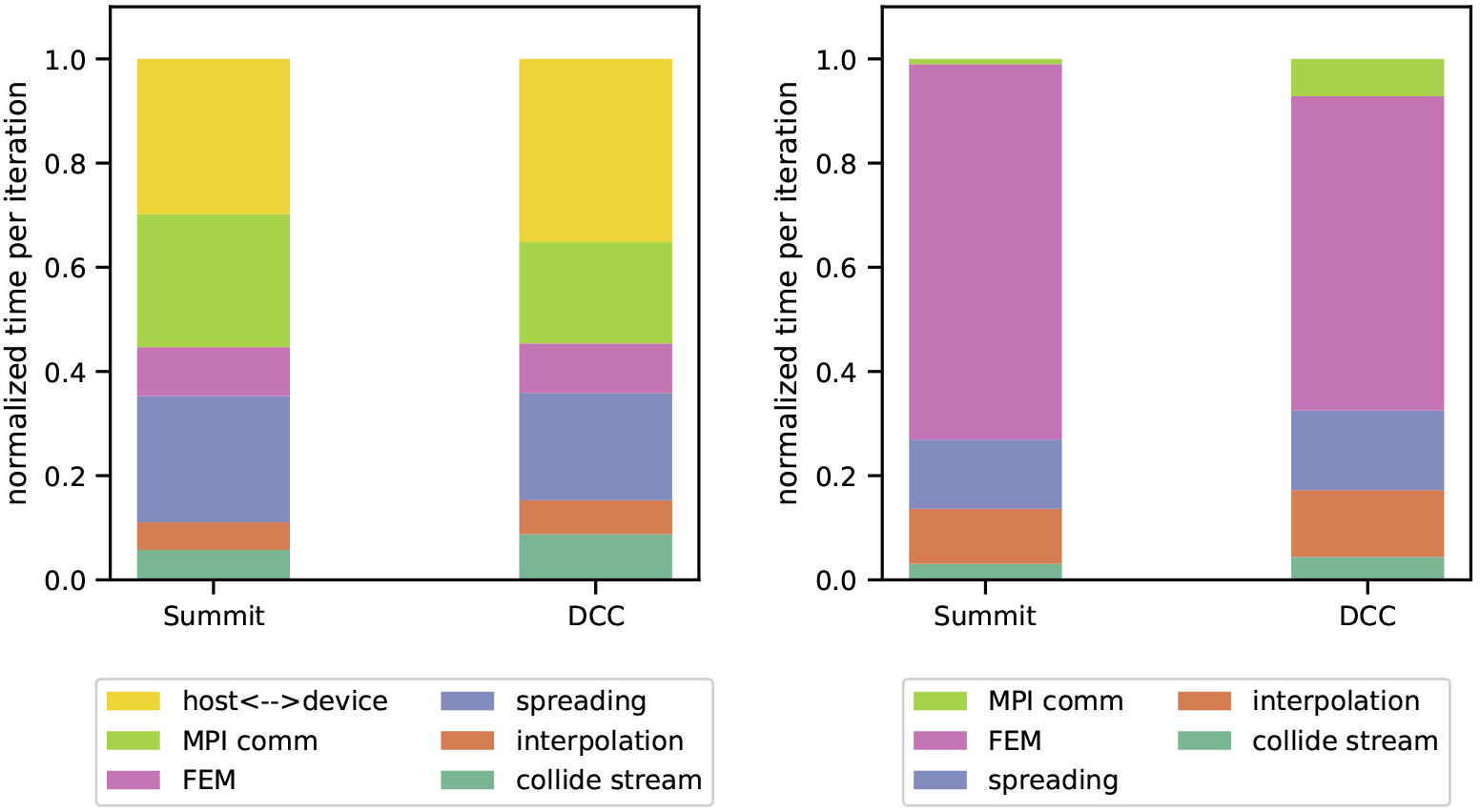
Distributed node performance analysis on Summit and the DCC on 8 nodes with GPU memory nearly full. These simulations have a support size ϕ = 4 and a hematocrit of 0.40. On the left are the normalized runtimes for GPU simulations and on the right are normalized runtimes for CPU simulations on each system. Minor operations accounting for less than 1% of run time are omitted for clarity.

In contrast, the CPU implementation spends only 1% of time in communication on Summit and 7% on the DCC, a difference mainly due to the larger problem size fitting on Summit nodes and correspondingly lower ratio of communication to processing work. On both systems the smaller proportion of time spent in communication shows that optimizations related to communication have less potential to reduce runtime for the CPU implementation than the GPU.

3.4. Weak scaling

As the purpose of a distributed memory parallelization scheme is to enable large-scale simulations which require multiple nodes, the scalability of a communication scheme is also important. We now consider the scalability of the full simulation, rather than the kernels and communication. Figure 7 shows weak scaling at 0.40 hematocrit for ϕ = 3 and 4. For weak scaling, we increase the problem size proportionally with the number of compute units, maintaining the same amount of work per node over successively larger node counts. To measure weak scaling efficiency, we normalize all runtimes by the runtime at the lowest task count. The input sizes for different node counts are summarized in Table 2. Simulations at the largest scales on Summit involve four billion fluid points and 17 million red blood cells.

Figure 7:

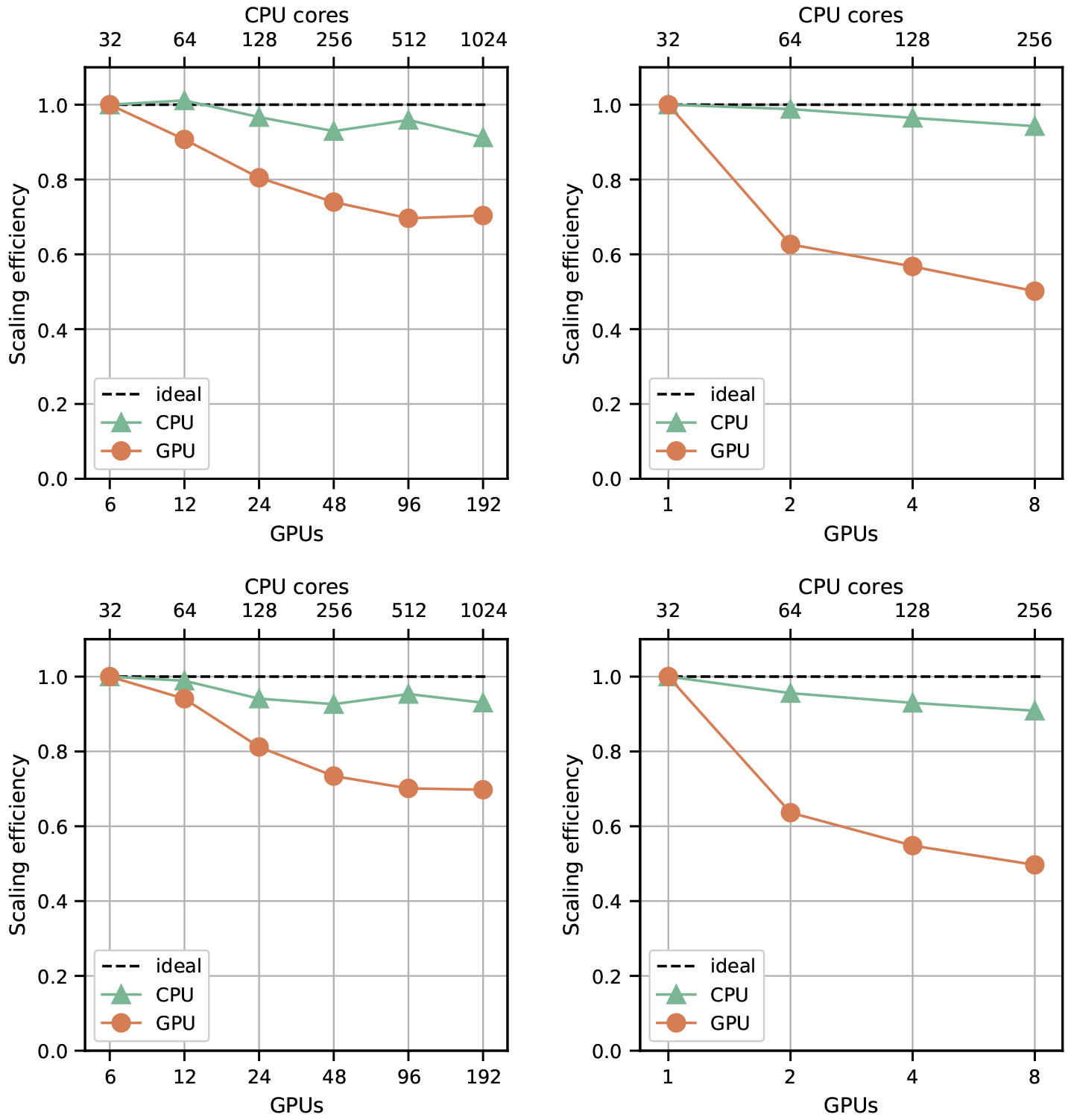
Weak scaling for Summit (V100 GPUs) on the left and the DCC (P100 GPUs) on the right. The top row represents runs with a support size of 4 and bottom row represents runs with a support size of 3.

The results in Figure 7 show support size to have a negligible effect on scaling behavior for both Summit and the DCC. The GPU implementation has lower scaling efficiency on both systems, as a larger percentage of time is spent in communication operations. The higher relative cost of communication leaves the GPU more vulnerable to scaling inefficiencies that also apply to the CPU code, but comprise a smaller portion of its run time. Weak scaling behavior on Summit is overall stronger than the DCC with a scaling efficiency at the highest tested node count of 0.7 compared to 0.5 on the DCC. Due to the larger GPU memory capacity per node on Summit and consequently the larger problem size per node, each node has proportionally less information to communicate over the InfiniBand interconnect when compared with the DCC weak scaling tests. These results highlight the benefits of a fat node system architecture in scaling GPU-based applications.

Next, we directly compared performance between our GPU and CPU implementations across the node counts and simulation cases used for the weak scaling experiments. On Summit the GPU is 13–18 times faster than the CPU as shown in Figure 8. These results are expected as the speedup is proportional to the system’s cumulative HBM to DRAM bandwidth ratios given that the code’s kernels are memory bound. The superior scaling efficiency on the CPU is due to the lower relative cost of communication. Portions of the code such as communication that are identical between GPU and CPU are not accelerated and have roughly equal absolute run time costs. However these portions of the code comprise a larger percentage of run time on the GPU and this higher relative cost affects scaling efficiency.

Figure 8:

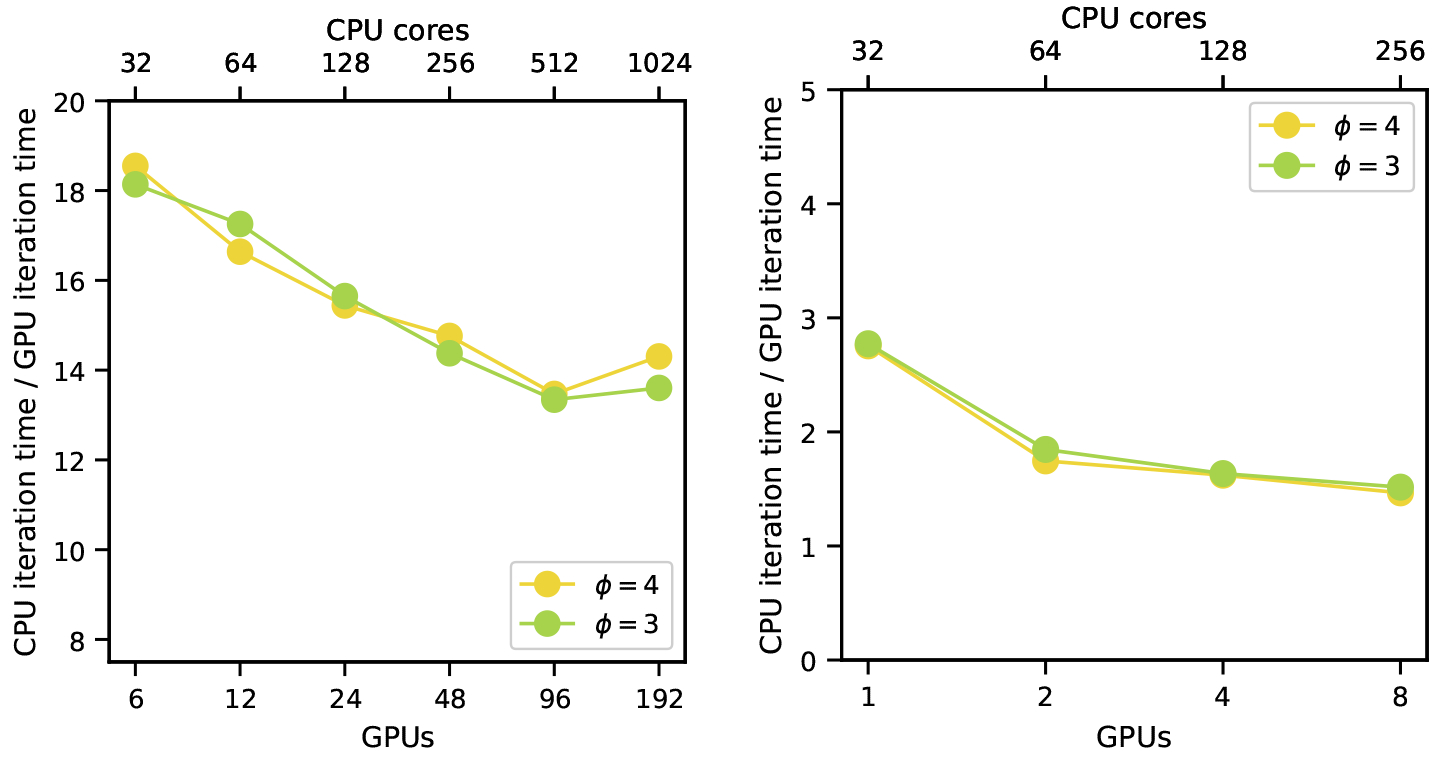
Weak scaling of runtime ratios between CPUs and GPUs for Summit (V100 GPUs) on the left and the DCC (P100 GPUs) on the right. Results for support sizes ϕ = 3 and 4 are shown.

3.5. Conclusion

In this paper we present the first massively parallel, fully GPU-accelerated, FSI solver for cell-resolved hemodynamics and analyze data movement in simulations of deformable red blood cell flow. We extend our previous work investigating the impacts of communication scheme choice, support size, and immersed body volume fraction for a CPU-based solver. We compare performance, scaling, and data movement costs of GPU and CPU implementations on two representative heterogeneous HPC systems. The intention of this work is to provide direction on parallelization options and communication costs for different hardware given an FSI hemodynamics model.

In our study, we find that the GPU implementation provides up to an 18x speedup over the CPU, but with less efficient weak scaling. The discrepancy in scaling efficiency is due to two factors. First, the use of a GPU necessitates halo data transfer with the CPU which requires additional data movement and competes for memory bandwidth with operations such as MPI requests. Second, since GPU execution of compute and memory intensive kernels requires a fraction of the time taken on the CPU, MPI communication of halos between time steps becomes a dominating factor in overall simulation time. During scaling tests, interconnect bandwidth and latency may suffer under increased workload and a greater number of neighbor MPI tasks residing off-node. For problems with a higher communication to computation work-load balance, such as simulations over a smaller domain or at lower hematocrit, the scaling efficiency further degrades. Such factors are important to consider when setting up not only FSI hemodynamic models, but a variety of communication intensive scientific applications to run on heterogeneous systems where problem sizes exceed GPU memory capacity. Programmers may obtain greater performance gains for GPU codes through optimizing communication or reducing memory usage due to the greater run time cost of communication for GPU codes.

We also highlight the relevance of these findings for memory and communication intensive stencil code, showing the merits of fat node systems through superior weak scaling on Summit compared to the DCC. As each Summit node has six times the graphics memory per node as the DCC, larger subdomains per node can be simulated thereby decreasing the ratio of internode communication to on-node computation. Further, we exhibited faster transfer of halos between the host and device on Summit due to the increased bandwidth and decreased latency of NVLink.

This study reveals several opportunities for future optimization of the GPU implementation. Atomic operations, such as those used in the IBM spreading and FEM kernels, use specialized hardware pipelines to modify main memory without interference from other threads; this serializes small reductions in the code and harms performance. In the future, we plan to reduce our reliance on atomic operations through the use of shared memory reductions across thread blocks which may contain the majority of the work for one cell. However, the greatest opportunity for speedup is from concurrent data transfers and kernel execution. Overlapping communication with kernel calls is a minor optimization on the CPU, but could significantly improve performance and scaling on the GPU due to the higher percentage of run time spent in data transfer. Moreover, on systems such as Summit that support GPU-GPU communication between MPI tasks, the CPU can be bypassed altogether to reduce halo exchange times.

Communication time for FSI codes is the leading target for future performance and scaling improvements. Though careful consideration must be given to optimizing data movement, our findings show the promise of current petascale and future exascale systems to substantially accelerate FSI simulations.

Highlights.

• First massively parallel fully GPU-accelerated FSI solver for blood flow simulations

• Compare performance, scaling, and data movement costs of GPU and CPU implementations on two representative heterogeneous HPC systems

• Provides direction on parallelization options and communication costs for hemodynamics models on different hardware

Biographies

Jeff Ames is a PhD candidate in the Department of Computer Science at Duke University.

Daniel F. Puleri is a PhD candidate at the Department of Biomedical Engineering at Duke University. He received his MS degree in Biomedical Engineering from Duke University and BS degree in Chemical and Biomolecular Engineering from the Georgia Institute of Technology. His current research activities focus on adhesive cancer cell modeling, high performance computing, and hemodynamics.

Peter Balogh received his Ph.D. in mechanical engineering from Rutgers University in 2018. He is currently a postdoctoral associate in the Department of Biomedical Engineering at Duke University. His research interests include computational fluid dynamics modeling of biological flows, numerical methods for complex fluid-structure interfaces, and code development for high performance computing. His current research is focused on modeling cancer cells and their transport through the circulatory system, and on investigating the remodeling of microvasculatures through comparisons with experiments.

John Gounley is a computational scientist in the Biomedical Science, Engineering, and Computing Group within the Computational Sciences and Engineering Division at Oak Ridge National Laboratory. He received a PhD in computational and applied mathematics from Old Dominion University in 2014. His research focuses on algorithms and scalability for biomedical simulations and data.

Erik Draeger is the Deputy Director of Application Development for the Exascale Computing Project, as well as the High Performance Computing group leader at the Center for Applied Scientific Computing (CASC) at Lawrence Livermore National Laboratory. He received a PhD in theoretical physics from the University of Illinois, Urbana-Champaign in 2001 and has over a decade of experience developing scientific applications to achieve maximum scalability and time to solution on next-generation architectures.

Amanda Randles is the Alfred Winborne and Victoria Stover Mordecai Assistant Professor of Biomedical Sciences at Duke University. She received her Ph.D. in Applied Physics and Master’s Degree in Computer Science from Harvard University. She obtained her B.A. in Computer Science and Physics from Duke University. Her research interests include high performance computing, scientific computing, computational fluid dynamics, and modeling biomedical phenomena.