Computation Through Neural Population Dynamics

Abstract

Significant experimental, computational, and theoretical work has identified rich structure within the coordinated activity of interconnected neural populations. An emerging challenge now is to uncover the nature of the associated computations, how they are implemented, and what role they play in driving behavior. We term this computation through neural population dynamics. If successful, this framework will reveal general motifs of neural population activity and quantitatively describe how neural population dynamics implement computations necessary for driving goal-directed behavior. Here, we start with a mathematical primer on dynamical systems theory and analytical tools necessary to apply this perspective to experimental data. Next, we highlight some recent discoveries resulting from successful application of dynamical systems. We focus on studies spanning motor control, timing, decision-making, and working memory. Finally, we briefly discuss promising recent lines of investigation and future directions for the computation through neural population dynamics framework.

1. INTRODUCTION

The human brain is composed of many billions of interconnected neurons and gives rise to our mental lives and behavior. Understanding how neurons take in information, process it, and produce behavior is the focus of considerable experimental, computational, and theoretical neuroscience research. In this review, we focus on how computations are performed by populations of neurons. Many insights have been gained in recent years, and the field is now ripe for substantial progress toward a more comprehensive understanding. This is due to a confluence of advances in large-scale neural measurements and perturbations, computational models, and theory (Paninski & Cunningham 2018).

A neuron’s inputs and cellular biophysics determine when it generates an action potential (Hodgkin & Huxley 1952). This is commonly summarized as a neuron’s action potential emission rate or firing rate [i.e., the firing rate x of neuron i at time t is x_i(t)]. This rate, especially in sensory areas, relates to various parameters [i.e., x_i(t) = r_i param₁(t), param₂(t), param₃(t), … where r is some function and param_i is a parameter such as the angle of a visual stimulus] (e.g., Hubel & Wiesel 1962).

While modeling individual neurons has provided foundational insights, in recent years there has been considerable interest in understanding how populations of neurons encode and process information (e.g., Georgopoulos et al. 1982, Saxena & Cunningham 2019), including the interaction between neurons (Cohen & Maunsell 2009, Mitchell et al. 2009). Most recently, models have embraced an even more general and potentially powerful conceptual framework that is central in engineering and physical sciences: a dynamical systems framework (e.g., Luenberger 1979, Shenoy et al. 2013). This approach has helped us to understand cortical responses that are dominated by intrinsic neural dynamics, as opposed to sensory input dynamics (Seely et al. 2016), and has been explored over the past 15 years in a variety of contexts (Briggman et al. 2005, 2006; Broome et al. 2006; Churchland et al. 2006c; Mazor & Laurent 2005; Rabinovich et al. 2008; Stopfer et al. 2003; Sussillo & Abbott 2009; Yu et al. 2005). In this framework, a neural population constitutes a dynamical system that, through its temporal evolution, performs a computation to, for example, generate and control movement (Churchland et al. 2006a, 2010, 2012; Pandarinath et al. 2018a,b; Shenoy et al. 2013; Williamson et al. 2019).

A prediction of this dynamical systems perspective is that dynamical features should be present in the neural population response. In its general and deterministic form, but setting aside synaptic plasticity and hidden neurons/states that can influence dynamics, a dynamical system can be expressed as

$$\frac{dx}{dt}=f(x(t),u(t)),$$ 1.

where x is now an N-dimensional (ND) vector describing the firing rates of all neurons recorded simultaneously, which we call the neural population state, and is evaluated around time t. The vector dx/dt is its temporal derivative, f is a potentially nonlinear function, and u is a vector describing an external input to the neural circuit (a U-dimensional vector). In this formulation, neural population responses reflect underlying dynamics resulting from the intracellular dynamics, circuitry connecting neurons to one another (captured by f), and inputs to the circuit (captured by u).

To help build intuition for what a dynamical feature might look like in a neural population response, let us consider a physical example that is low dimensional such as a pendulum (Figure 1a). A pendulum is a two-dimensional (2D) dynamical system whose state variables are position and velocity. The pendulum is shown in one of two initial states, which are the initial conditions of the pendulum dynamics. When the pendulum is released from its initial condition such that its equation of motion [x ≈ sin(x)] evolves through time, the initial conditions trace out two different position and velocity trajectories (Figure 1b). Plotting the state variables of position and velocity against each other in a 2D plot results in a state space plot (Figure 1c). The flow field shows what the pendulum would do if it started in any given position in its state space; thus, the state space plot yields a convenient summary of the overall dynamics.

Figure 1.

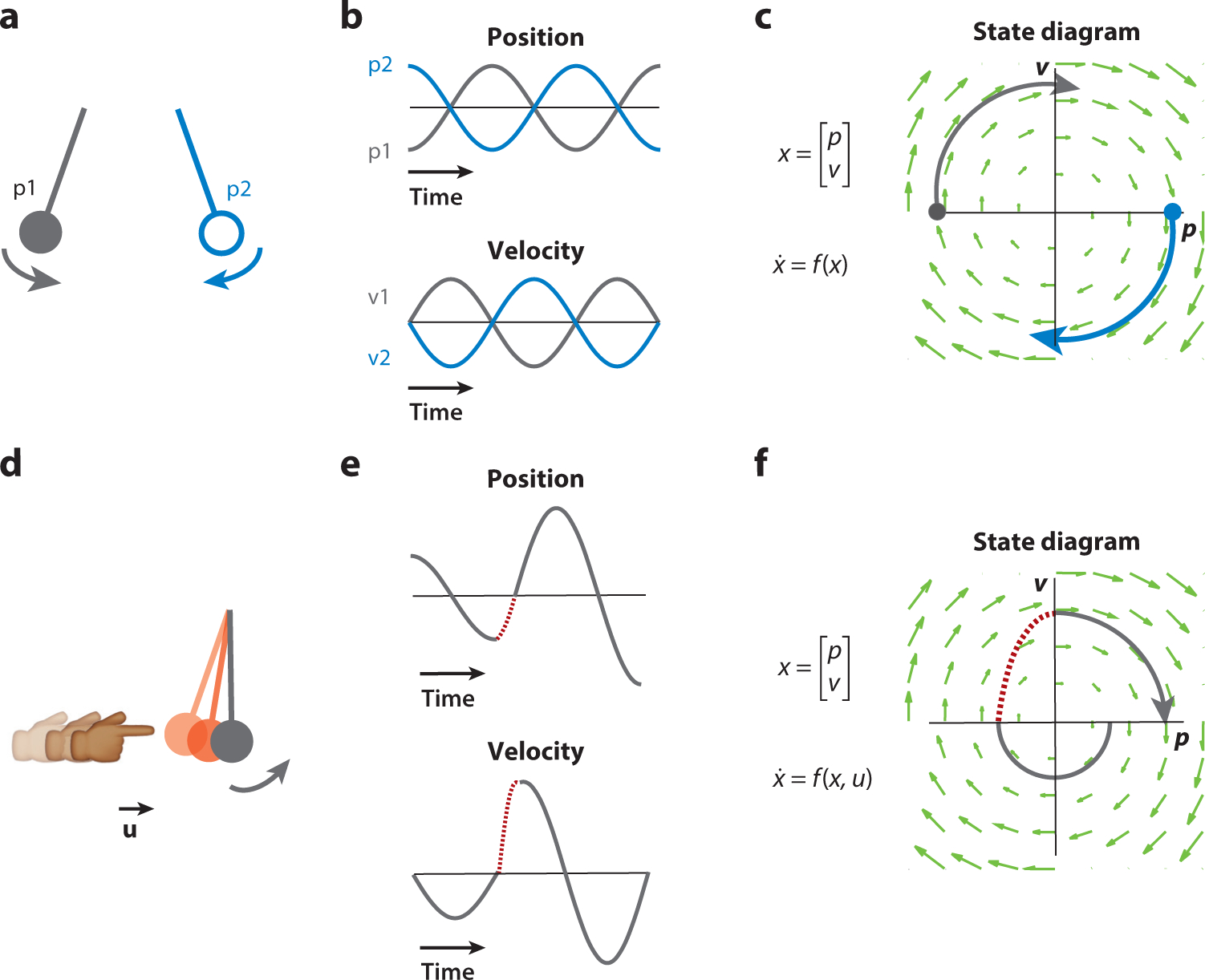
Example dynamics and population state of a frictionless pendulum. (a–c) A pendulum is a 2D dynamical system that has a simple relationship between the changes of the state of the pendulum (1D position and 1D velocity) and its current state. (a) Two example initial conditions are shown, p1 (gray; position is maximally negative and velocity is zero) and p2 (blue; position is maximally positive and velocity is zero). (b) As the pendulum moves through time, its state vector (position, top; velocity, bottom) is updated. (c) These trajectories can also be visualized by plotting one state variable against the other (position against velocity), beginning at the initial condition (circles) and moving along the flow field (green arrows), yielding the state space plot. The flow field shows the dynamical evolution of the pendulum for any set of initial conditions. (d–f) A pendulum with input perturbations. (d) One may perturb the pendulum during its motion, for example, by bumping it with a finger (brief period of the bumps appears in red). (e,f) This leads to a change in the pendulum state through time (red dashed lines) such that both the time series (e) and the state space trajectories (f) no longer follow the autonomous dynamics (as shown in panel e) while the input is active. After the perturbation is finished, the pendulum returns to its autonomous dynamics again (gray lines after red dashed lines). Figure adapted with permission from Pandarinath et al. (2018b).

We can elaborate on this example by considering the pendulum to also occasionally experience an external input [i.e., u(t) in Equation 1]. For example, we might briefly push it with our finger (Figure 1d). That perturbative input results in a change in the dynamical trajectory, shown in Figure 1e. When the dynamics are perturbed by pushing the pendulum, the autonomous dynamics are modified such that state trajectories (Figures 1e,f) no longer follow autonomous dynamics (Figure 1f). Thus, an input can modify the dynamics in a time-dependent way. This can be used in two ways in neural circuits: to add, for example, sensory input to a computation, or to contextualize a computation by changing the dynamical regime in which the circuit is operating. To summarize the pendulum example, the dynamical features are the initial conditions of the two trajectories (Figure 1a), the pendulum’s dynamical equation (shown in graphical form in Figure 1c and captured in the function f), and inputs that, for example, set the pendulum’s initial condition or briefly perturb its dynamics (Figure 1d).

Now let us return to a neural system, where if we have N neurons we can construct an ND neural population state by first counting spikes within some short time period (e.g., 10 ms), as in Figure 2a. We can then plot these spike counts in a state space plot, as shown in Figure 2a,b. Here, the vector of spike counts for neurons 1 through N (i.e., the neural population state) takes the place of position and velocity (i.e., physical states) from the pendulum example. We can similarly plot flow fields for these neural population dynamics, as shown in Figure 2c (in analogy to Figure 1c). The dynamics govern the evolution of the trajectory in state space; different initial conditions (i.e., starting states) lead to different trajectory evolutions (Figure 2d). Note that although we have described the neural population state in terms of binned spike counts, it is common to instead choose to work with the abstraction of continuous-valued underlying firing rates. These firing rates are a latent state, since they cannot be directly observed but rather must be inferred, typically through an inhomogeneous Poisson process over the observed spike counts.

Figure 2.

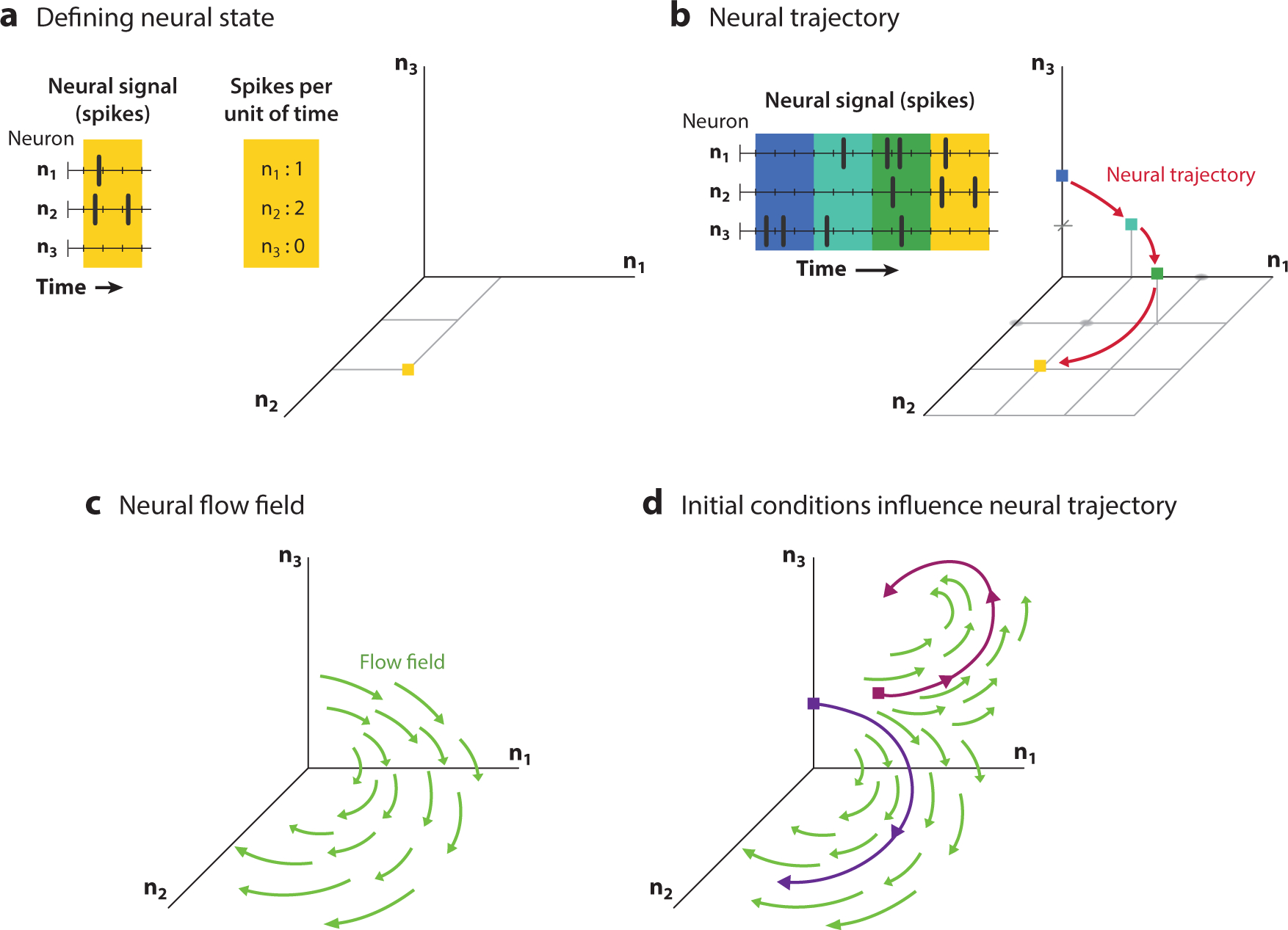
Neural population state and neural dynamics. (a) Three neurons spike through time (left), and these spikes are binned and counted (center). These spike counts are plotted in a three-dimensional state space (right) representing the three neurons (n₁, n₂, n₃), with a yellow square representing the state of the neural system at that time point. (b) Continued binning of spikes through time (left) leads to a neural population state that progresses in a sequence (blue, cyan, green, yellow), which is plotted in the neural state space plot (right) to yield an intuitive picture of the neural population dynamics. (c) The neural population dynamics can be represented by a flow field (green arrows) that describes how the neural population state evolves through time. (d) Two different neural trajectories (magenta and purple curves) can result from following the neural population dynamics from different initial conditions (magenta and purple squares).

Figure 2 describes a three-neuron population. However, most data sets involve many neurons, so we must contend with this additional complexity. In many areas of the brain, it is possible to reduce high-dimensional neural data (e.g., a hundred dimensions if measuring N= 100 neurons simultaneously) to lower-dimensional data (e.g., ten to twenty dimensions) without much loss in neural data variance captured (e.g., 5% variance lost) using a variety of different dimensionality reduction techniques (e.g., Cunningham & Yu 2014, Brunton et al. 2016, Kobak et al. 2016, Williams et al. 2018). While plotting only the first two or three dimensions (e.g., x₁ and x₂, whose dimensions capture the most and second-most data variance) ignores important data variance, the 2D to three-dimensional (3D) plot remains instructive, as it provides a sense of where the neural population state is and how it moves through time. However, we emphasize that any quantitative analysis of the population data should be done in a dimension high enough to explain all or nearly all of the neural variance.

The central question underlying many of the studies we review is how a neural circuit (captured by f) and its input (captured by u) create the population dynamics (depicted in Figure 2c,d; captured by Equation 1) that cause the neural population state to evolve through time to perform sensory, cognitive, or motor computations that result in perception, memory, and action. We term this general framework computation through neural population dynamics, or more succinctly, computation through dynamics (CTD).

2. COMPUTATION THROUGH NEURAL POPULATION DYNAMICS

Here we give an atypically lengthy mathematical introduction providing the series of concepts and procedures needed to better understand complex, high-dimensional neural systems. Readers familiar with these concepts may wish to skip to Section 3.

2.1. Deep Learning for Modeling Dynamical Systems

Deep learning (DL) is a catch-all phrase for a set of artificial neural network architectures along with supporting training algorithms, software libraries, and hardware platforms. DL is used to efficiently learn complex input-output relationships. In DL, a task is defined by a large training set of inputs and the desired outputs that should result from those inputs. To train a network, a loss function is defined relative to this training set, and that function is optimized by modifying the network parameters, typically via a gradient-descent algorithm. Successful optimization thus produces a network that solves the provided task.

For this review, we are primarily interested in using DL to model dynamical systems, i.e., f in Equation 1. The first approach is called data modeling, where we record the internal state of f [e.g., neural recordings represented by x(t)] and wish to identify f from those recordings. The second approach is task-based modeling, where we have a set of input-output pairs from a behavioral task (e.g., visually instructed arm reaches) and wish to identify a dynamical system, f, capable of transforming the input into the output. Both data modeling and task-based modeling are systems identification problems, and the DL approach to solving it is to use a parameterized dynamical system, called a recurrent neural network (RNN), denoted by

$$\frac{dx}{dt}=R_{\theta }(x(t),u(t)),$$ 2.

where R_θ is the RNN with parameters θ. Here the state variables, x(t), take on continuous values, and thus Equation 2 is often referred to as a rate network (as opposed to a spiking network). RNNs typically have an explicitly defined linear readout, expressed as

$$y(t)=Cx(t),$$ 3.

which states that the output, y(t), is a linear transformation of the state variables, x(t), through the readout matrix C. RNNs are universal approximators, which means they can approximate any f with high accuracy, whether f is defined by a large set of neural recordings or by task-based input-output pairs.

For example, imagine we wish to learn the dynamics of the pendulum, so f again is the equation of motion for the pendulum. To accomplish this, we collect a large set of initial conditions (the initial positions and velocities and a set of 2D inputs) and corresponding time series of the pendulum in operation (position and velocity state vectors through time) as training examples. We define the loss function to be mean squared error, averaged across time, of the RNN’s readouts y(t) relative to those measured positions and velocities. After training, R_θ should have dynamics such that y(t) very closely matches the measured position and velocity traces, and thus R_θ approximates f.

For neuroscientists, f is a biological neural circuit. This means f is likely expensive to sample, hard to run quickly, and challenging to run with novel inputs or under novel conditions. Furthermore, we do not know the precise equations and parameters for f, so a pure biophysical modeling approach is likely impractical. Training an RNN to learn f provides a model of the dynamics that can be simulated quickly, with novel inputs and conditions, and which has equations we can study as a proxy for f. This is true for either case where f models data or a task.

2.2. Understanding High-Dimensional Nonlinear Systems Via Learned Models

A key goal of systems neuroscience is to understand how neural computation gives rise to behavior, so it is not sufficient to simply learn data or task models that are inspired by experiments in neuroscience. We also want to understand how such models operate, which poses serious mathematical challenges, as the biological circuits (f) we study are usually nonlinear and high dimensional. Our approach to understanding f is to first model it, for example, with an RNN, and then study that model.

One ubiquitous approach is to ignore the nonlinearity of f and model the system with a linear dynamical system (LDS), L, defined as

$$\frac{dx}{dt}=L(x(t),u(t))=Ax(t)+Bu(t),$$ 4.

where A and B are matrices of learned parameters that map state and input, respectively, to the state update. Modeling f via an LDS is popular because linear models have a rich history of unreasonably good performance across many quantitative fields and because an LDS can be readily understood through well-established linear systems theory. An LDS can only have a few qualitatively different behaviors. It can exhibit decaying dynamics (Figure 3a), expansive dynamics (Figure 3b), oscillations (Figure 3d–f), or combinations of all of these dynamics in different dimensions (Figure 3c). An LDS can also have marginally stable dynamics if it is finely tuned. For example, an LDS can generate precisely balanced oscillations (Figure 3f) or act as a perfect integrator if an input to the system aligns with the integrating mode (Figure 3g). If one cannot precisely fine-tune the LDS, then the balance of the oscillator or quality of the integration degrades accordingly.

Figure 3.

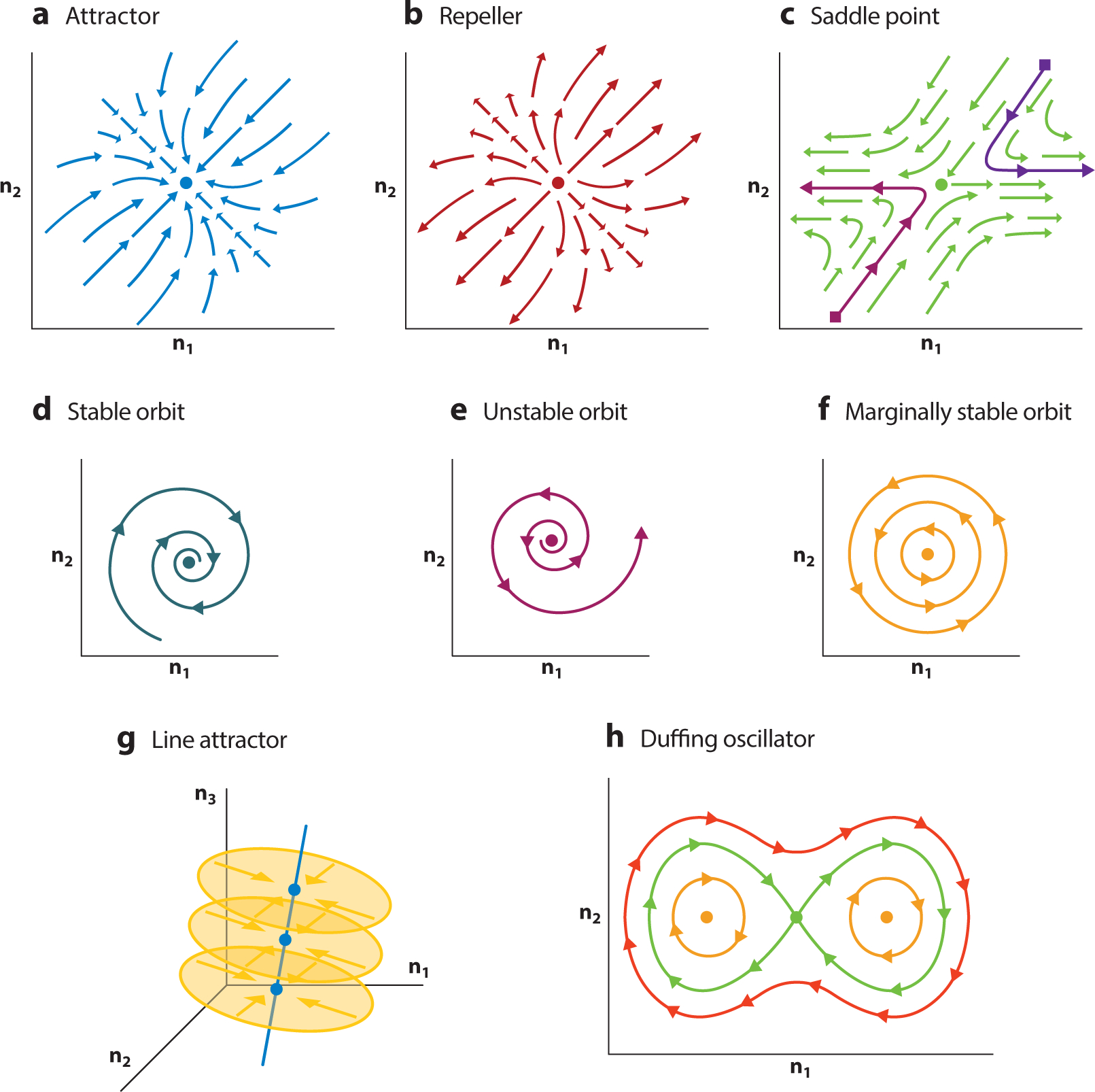
Linear dynamics and linear approximations of nonlinear systems around fixed points. (a–g) Examples of linearized dynamics around fixed points in a nonlinear system, showing fixed points (large dots) and flow fields (arrows). Panels show (a) an attractor, which is stable in all dimensions; (b) a repeller, which is unstable in all dimensions; and (c) a saddle point, which is a fixed point with both stable and unstable dimensions. Fixed points can have oscillatory dynamics that are both (d) stable and (e) unstable. Linear systems that are finely tuned may have marginally stable oscillations, which neither decay nor expand, or (f) exhibit line attractor dynamics, (g) which are stable (do not move) along the line attractor (blue line) but otherwise show stable attracting dynamics to the line attractor (yellow planes and arrows). (h) A nonlinear system such as a Duffing oscillator is well approximated by linear systems at the three fixed points: The two orange points are well approximated by oscillatory linear dynamics, while the green point is a saddle point, whose dynamics are well approximated by linear dynamics that are both stable and unstable. Note the flow fields given by the red line are not well approximated by linearization, highlighting a failure mode of linearization around fixed points in that good approximations tend to be local.

Linear systems are also useful for understanding RNNs. We do this by employing multiple LDSs, i.e., multiple linearizations of R_θ, tiling the RNN’s state space with LDSs. Each LDS is an approximately correct model of the RNN in its particular region of state space. This approach decomposes understanding nonlinear neural dynamics into three additional steps: identifying (a) where in state space to linearize, (b) the local LDSs, and (c) when to switch between these LDSs (e.g., Sussillo & Barak 2013). Through these linear approximations we understand R_θ, and through it f. Models that switch between multiple LDSs (SLDS) have a rich history and also may serve as stand-alone models of f (e.g., Linderman et al. 2017, Petreska et al. 2011).

The most natural place to linearize in state space is around a fixed point, which we denote with x*. For simplicity, we define fixed points while ignoring inputs, i.e., dx/dt = R_θ (x(t)), which again approximates dx/dt = f (x(t)). Fixed points are points in state space where repeated iteration of R_θ does not change the state, i.e., dx/dt = R_θ (x*(t)) = 0 (see Figure 3a). Fixed points are interesting for two reasons. First, stable fixed points are the simplest model of memory, as in Figure 3a or Figure 3d, since at those points the state is unchanged by repeated iteration of the dynamical equations, and perturbations away from the fixed points collapse back to the fixed points. Second, and more importantly for this review, the dynamics around fixed points are known to be approximately linear. The fixed points and corresponding linearizations of an RNN’s dynamics can be identified via numerical optimizations (Golub & Sussillo 2018, Sussillo & Barak 2013). Empirically, linearizing around fixed points is proving an effective means to interpret local dynamics of RNNs engaged in computation through neural population dynamics (Barak 2017).

Linearizing around fixed points yields LDSs of the form

$$\frac{d(\mathbf{\delta }x)}{dt}=A\left(x^{*}\right)\mathbf{\delta }x(t),$$ 5.

where δx(t) = x(t) − x*, which simply states that the linear system and state dynamics are now centered around the fixed point, x*. Furthermore, the linear dynamics, as expressed by the matrix A, are now a function of x* and are defined as the first derivative of R_θ with respect to x, evaluated at the fixed point, i.e., A(x*) = ∂R_θ /∂x(x*). If there are multiple fixed points in state space, typically one chooses to expand around the fixed point closest to the dynamics of interest. Both the utility and limitations of linearization for understanding a nonlinear system can be seen by considering the Duffing oscillator (Figure 3h).

In the general case, we must also consider the input u(t) and how to linearize around it as well. Accounting for inputs, we end up with the equation

$$\frac{d(\mathbf{\delta }x)}{dt}=A\left(x^{*},u^{*}\right)\mathbf{\delta }x(t)+B\left(x^{*},u^{*}\right)\mathbf{\delta }u(t),$$ 6.

where u* is the linearization point for the input and δu(t) = u(t) − u*. Careful choices of u* open up very interesting possibilities for studying contextual inputs and contextual dynamics. Contextual inputs are typically slowly varying inputs that are not considered input to the computation per se but rather shift the nature of the computation by changing the dynamics (Figure 4). The contextual input changes the dynamics by moving the average operating point in state space (A and B in Equation 6 are a function of u*). As a result, these contextual inputs can change both the recurrent dynamics and also the system response to other dimensions of the input (e.g., sensory input dimensions).

Figure 4.

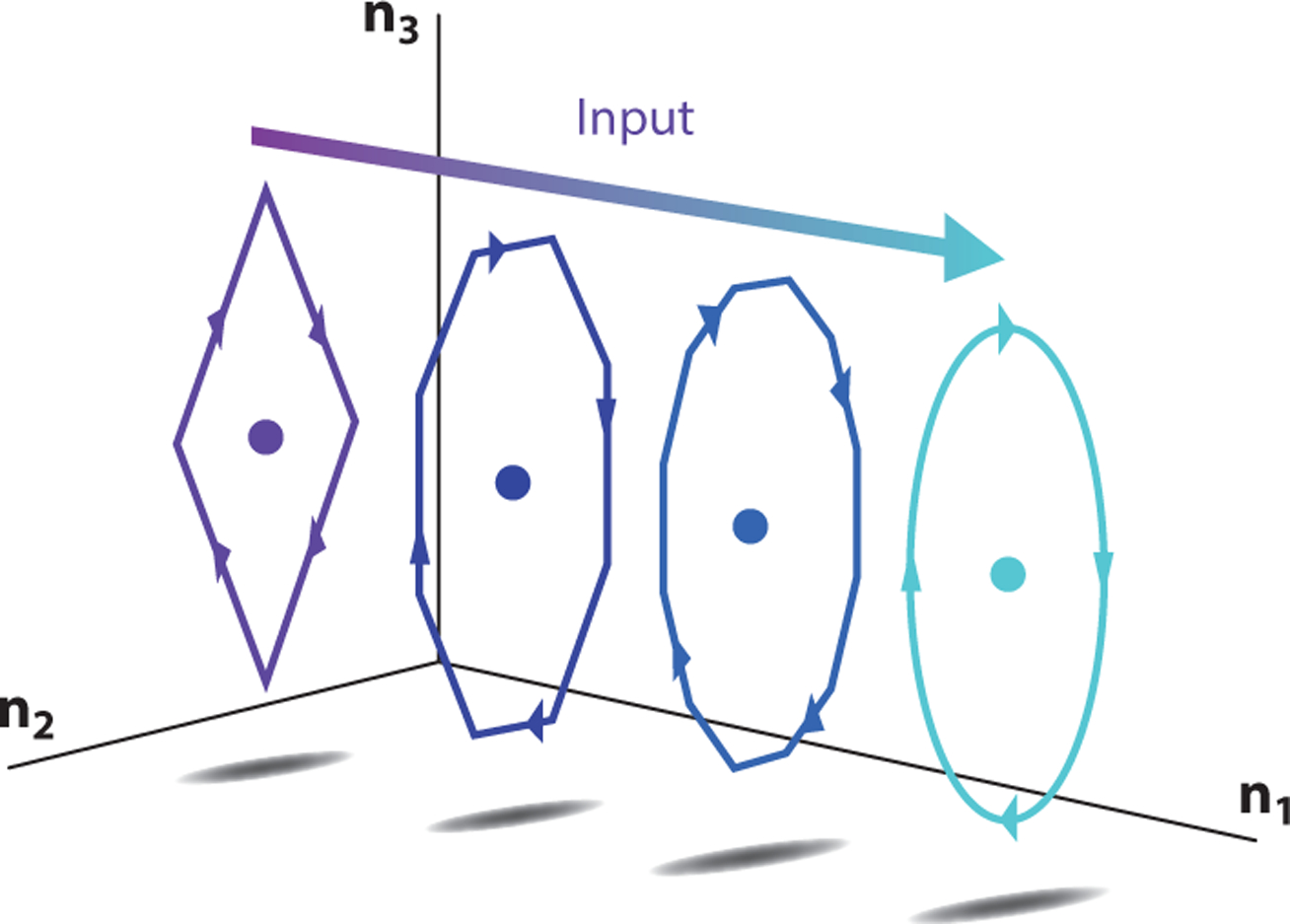
Contextual inputs. A static or slowly varying input can be viewed as contextualizing a nonlinear system such that it produces different dynamics under different values of the contextual input. In this diagram, increasing the value of a static input (from purple for small values to cyan for large values) moves the operating point of the nonlinear system (circles) such that the dynamics smoothly change from a diamond-like oscillation (purple arrows) to a circular oscillation (cyan arrows).

2.3. Linear Subspaces and Manifolds

Here we define three mathematical concepts that are relevant for dynamics in high-dimensional data, including neuroscientific data. See Figure 5 for illustrative examples.

Figure 5.

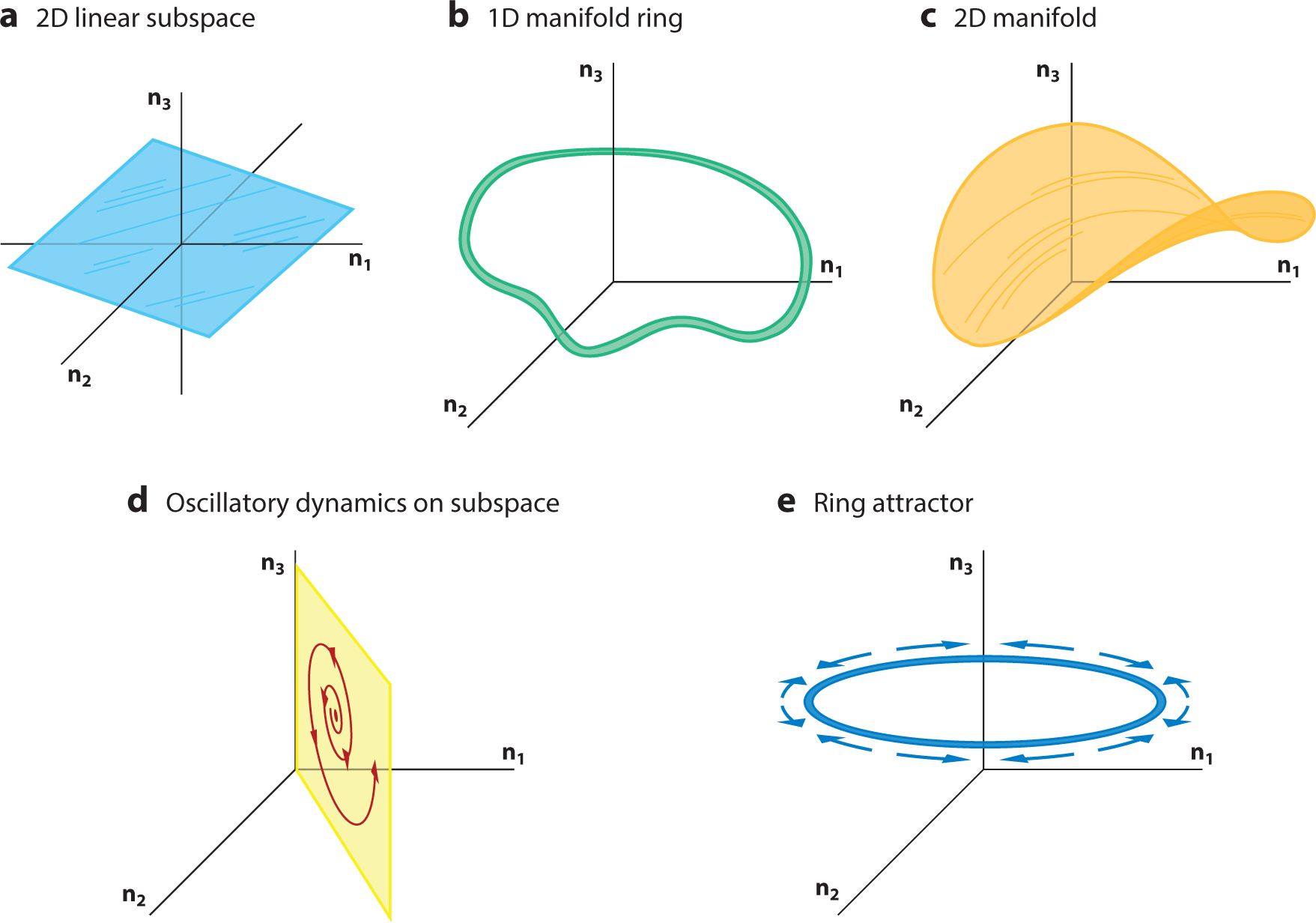
Subspaces and manifolds. (a) Two-dimensional (2D) linear subspace (blue) embedded in a three-dimensional (3D) space. (b) One-dimensional (1D) ring manifold (green) embedded in 3D space. (c) A smooth 2D manifold (orange) embedded in 3D space. (d,e) Dynamics may live in subspaces or on manifolds. (d) A 2D oscillation embedded in a 2D linear subspace, all of which is embedded in 3D space. (e) A ring attractor, which is a 1D manifold of stable fixed points (blue ring) embedded in 3D space. Inputs move the state along the ring attractor (blue arrows; note arrows here indicate the effect of inputs, not flow fields).

2.3.1. Linear subspace.

A linear subspace is a hyperplane that passes through the origin of a higher-dimensional space. For example, in 3D space, a 2D plane passing through the origin is a linear subspace (Figure 5a). Linear subspaces play a key role in dimensionality reduction, whereby measured ND neural states that empirically lie near a P-dimensional linear subspace (where P < N) are summarized and often denoised by a P-dimensional representation within the linear subspace (Cunningham & Yu 2014).

2.3.2. Null space.

The null space of a linear system is the space of all inputs to that system that result in a zero output. For a linear system defined by matrix A, an input vector x is in the null space of A if Ax = 0. A geometrical illustration is provided in Figure 6. In systems neuroscience, the communication from an upstream brain region to a downstream region can be modeled as a linear system, y = Ax, and the null space of that system is the set of upstream-region neural states, x, that do not directly contribute to the downstream-region activity (with neural states y). This concept has provided a neural population mechanism by which signals can be flexibly communicated within and across brain areas (Semedo et al. 2019); an example of this is how the motor cortex can prepare a movement without its preparatory activity causing premature movement (Kaufman et al. 2014).

Figure 6.

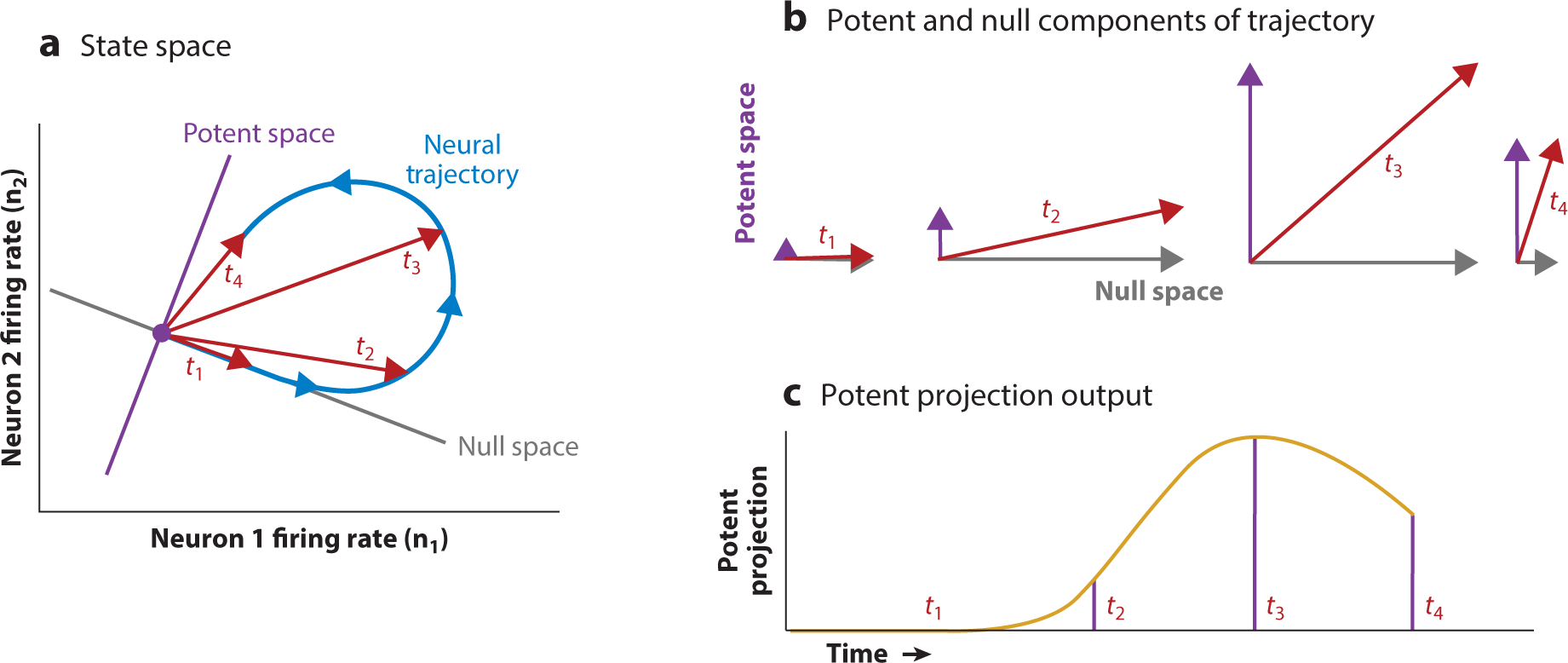
Null and potent subspaces. A state space can be divided up into nonoverlapping subspaces, called the potent and null (sub)spaces, where the potent space may be read out by a downstream area, while the null space is not read out. (a) A dynamical trajectory (blue arrows) in state space follows a looping dynamic from the origin back to the origin. While doing so, the trajectory has projections on the null space (gray line) and potent space (purple line). We focus on four points in time, t₁, t₂, t₃, and t₄ (red arrows). (b) The state space trajectory in panel a can be decomposed into its projections onto the potent and null spaces (shown for time points t₁, t₂, t₃, and t₄). (c) The projection of the state space trajectory onto the potent dimension through time (yellow line), highlighting its value at time points t₁, t₂, t₃, and t₄. There is a corresponding time series for the projection onto the null space (not shown), but this is not read out by a downstream area. Examples of this in systems neuroscience can be found in these references (Hennig et al. 2018, Kaufman et al. 2014, Perich et al. 2018, Semedo et al. 2019, Stavisky et al. 2017a).

2.3.3. Manifold.

A manifold, like a linear subspace, is a low-dimensional topological space embedded within a higher-dimensional space. Unlike a linear subspace, the more-general manifold can bend about as long as it remains linear when zoomed in on closely enough. For example, if we zoomed in closely enough on the one-dimensional (1D) ring manifold shown in Figure 5b, the curvature of the ring would disappear, and it would appear as a line. The same is true of the 2D manifold in Figure 5c, which is a warped plane embedded in a 3D space. Dynamical systems can generate states that are confined to manifolds. For example, in Figure 5d, an unstable oscillation is confined to a 2D plane within a 3D space. Another example is the ring attractor, a manifold of fixed points that lie along a 1D ring, whereby neural states move around the ring as a result of the system integrating inputs (Figure 5e). A number of neuroscientific studies have derived insights into neural systems by leveraging manifold structures identified from neurophysiological data (e.g., Chaudhuri et al. 2019, Kim et al. 2017, Sadtler et al. 2014; for a review, see Gallego et al. 2017).

3. DYNAMICAL SYSTEMS IN MOTOR CONTROL

Much of our understanding of the neural control of movement stems from the pioneering work of Evarts (Evarts 1964, 1968; Tanji & Evarts 1976), who recorded the activity of individual neurons from awake behaving monkeys and related it to muscle activation. Investigators have since employed other electrophysiological (single- and multielectrode arrays) and optical (calcium imaging and optogenetics) techniques to investigate neural correlates underlying behavior (e.g., Kalaska 2019, O’Shea et al. 2017). Early investigations, following work in primary visual cortex (V1) (Hubel & Wiesel 1962), attempted to characterize response properties of motor cortical neurons. There was success in correlating responses of individual neurons to task parameters (Georgopoulos et al. 1982, 1986, 1989). However, unlike V1, there was little consensus regarding what parameters motor cortical activity represented—some favored representation of higher-level movement parameters (e.g., end-effector velocity), while others favored the view that activity drove muscle activity more directly. Here we ask a different but related question: What principles guide generation of the observed time-varying patterns of motor cortical activity (Churchland et al. 2012, Shenoy et al. 2013)?

3.1. Motor Preparation: First Cog in a Dynamical Machine

One common experimental paradigm used in laboratory settings is the instructed-delay reaching task (Ames et al. 2014). The position of the animal’s arm in physical space controls the position of a cursor on a screen. Animals are trained to make rapid and accurate reaching arm movements as targets appear on the screen. Since movements are prepared before they are executed (Riehle & Requin 1989, Rosenbaum 1980, Wise 1985), this preparatory process is probed by requiring that animals wait a randomly distributed and experimentally controlled amount of time before initiating a reach. During this delay period, animals are cued to the target that they must ultimately reach to, and thus the measured neural activity is typically referred to as delay-period or preparatory activity. Previous work has shown that animals use this delay period to perform behaviorally relevant computations: More time to prepare reduces reaction times, and intracortical microstimulation during the delay period causes a reaction time penalty (Churchland & Shenoy 2007a, Churchland et al. 2006b). Furthermore, neural activity during the delay period is tuned to distance, direction, and speed, among other parameters (Churchland et al. 2006b; Even-Chen et al. 2019; Messier & Kalaska 1997, 1999; Santhanam et al. 2009; Yu et al. 2009). During this task, neural measurements are typically made in contralateral-to-arm primary motor (M1) and dorsal premotor cortex (PMd), though comparisons between ipsilateral and contralateral regions have also been investigated (Ames & Churchland 2019, Cisek et al. 2003).

From the CTD perspective, preparatory activity is viewed as an initial condition. It brings the population neural state to an initial value from which movement period activity evolves, governed by both the local dynamics of motor cortex as well as inputs from other brain regions. This predicts that different movements have different preparatory states, though different initial conditions can result in qualitatively similar movements (e.g., with different reaction times) (Churchland et al. 2006c, 2010, 2012; Michaels et al. 2016; Sussillo et al. 2015). Nonetheless, initial conditions closer to the optimal preparatory state have been shown to confer behavioral benefits, e.g., faster reaction times (Afshar et al. 2011, Ames et al. 2014). This initial condition hypothesis is an alternative to a representational hypothesis, which suggests that preparatory activity is a subthreshold version of movement-period activity. By itself, preparatory activity is not sufficient to trigger movement but could shorten time needed to rise above threshold and trigger movement, thus resulting in shorter reaction times (Bastian et al. 1998, 2003). At present, evidence appears to favor the initial condition hypothesis (Churchland et al. 2006c, Shenoy et al. 2013).

Other competing hypotheses argue preparatory activity is suppressive rather than facilitatory, i.e., it functions to inhibit movement (Wong et al. 2015), or that preparatory activity, while facilitatory, is not essential (Ames et al. 2014) or exhibits large variability (Michaels et al. 2015). In particular, Ames et al. (2014) showed that the preparatory state could be bypassed in trials with no delay period, though many aspects of the subsequent population response were conserved across both delay and nondelay contexts. Perfiliev et al. (2010) recently showed that using moving targets, in lieu of fixed ones, exhibited low latency reaches. Lara et al. (2018b) adapted this task design to test what aspects of preparatory activity are present in the absence of the delay period. To disambiguate whether the delay period is suppressive or preparatory, the authors also trained animals in a self-initiated reach context where animals were free to initiate movement at any point after target onset. Lara et al. concluded that delay period activity does indeed reflect a preparatory process that occurs even in the absence of a delay. However, this process need not be time-consuming; when necessary, it can rapidly set up an appropriate preparatory state prior to movement onset. These results dovetail with RNN models trained to produce muscle activity using preparatory activity as initial conditions (Hennequin et al. 2014, Sussillo et al. 2015). The dynamics in these models show surprising similarity to those measured in motor cortex of behaving animals. Recent results suggest that this same preparatory process can also be used during reach correction, for example, when a new reach target appears at a new location while moving toward an initial target (Ames et al. 2019). Finally, Inagaki et al. (2019) found that delay period neural activity in mouse anterior lateral motor cortex moves toward stable fixed points that correspond to movement directions. Critically, these fixed points are robust to optogenetic perturbation; occasionally activity hops to the other fixed point following perturbation, producing incorrect actions. This serves as a compelling demonstration that discrete attractor dynamics underlie delay period activity.

Since neurons are preferentially active during both preparation and movement, how does this activity avoid causing movement? Classic theories suggested that preparatory activity was subthreshold (Tanji & Evarts 1976) or gated (Cisek 2006). However, Churchland et al. (2010) showed there was limited correlation in preferred directions between preparation and movement, and Kaufman et al. (2010, 2013) analyzed neuron classes during preparation and did not find a bias toward inhibitory cells. The CTD framework provides a computational scheme that can explain this phenomenon through the concept of null spaces (Figure 6). If neural activity during preparation evolved along neural dimensions that were orthogonal to dimensions explored during movement, then preparatory activity would avoid causing movement prematurely. Kaufman et al. (2014) together with Elsayed et al. (2016) found evidence for such a mechanism in motor cortex: Output-potent dimensions presumably relay information to muscles and are preferentially active during movement, and output-null dimensions are preferentially active during preparation. Recently, Stavisky et al. (2017a) provided a test of the more general theory that orthogonal dimensions can be used for flexible computation by using a brain-computer interface (BCI) where the output dimensions could be experimentally controlled. They showed that sensory feedback relating to error signals is initially isolated in decoder-null rather than decoder-potent dimensions. Li et al. (2016) showed that following optogenetic perturbation, preparatory activity in mouse anterior lateral motor cortex was restored along behaviorally relevant neural dimensions but not along other noninformative dimensions (Druckmann & Chklovskii 2012, Li et al. 2016). Despite these studies, there may be constraints to the role that these output-null dimensions play (Hennig et al. 2018).

3.2. Dynamical Motifs During Movement

During arm movements, the largest component of the population response is condition-invariant and reflects the timing of movement. This component, termed the condition-independent signal (CIS), appears following the onset of the go cue and causes a substantial change in dynamics (Kaufman et al. 2016). Such a CIS has also been observed during reach-to-grasp movements (Rouse & Schieber 2018). While the precise role of the CIS is still not known, presumably following a well-timed input into motor cortex, it transitions the preparatory state to another region in neural state space. Functionally, the translation in state space releases the preparatory state from an attractor-like region to exhibit rotation-like dynamics (Churchland et al. 2012, Michaels et al. 2016, Pandarinath et al. 2015). These rotations, while only an approximation to the true nonlinear dynamics, explain a large fraction of variance. Recently, Stavisky et al. (2019) found rotatory dynamics that followed a condition-invariant component in hand/knob motor cortex of humans during speech, suggesting common dynamical principles underlying control of arm and speech articulators. The significance of these rotational dynamics is that they appear to correspond to neither purely representational parameters nor purely movement parameters. Rather, they can be interpreted as a basis set for building complex time-varying patterns, like those required for generating muscle activity. Recently, Sauerbrei et al. (2020) demonstrated that cortical pattern generation during dexterous movement requires continuous input for the thalamus. Thus, future work will need to disentangle the relative roles and contribution of inputs and local dynamics in cortical pattern generation.

As a sufficiency test for the rotations motif, Sussillo et al. (2015) trained RNNs to transform simple preparatory activity–like inputs into complex, spatiotemporally varying patterns of muscle activity. They found that when networks were optimized to be simple, the underlying solution was a low-dimensional oscillator that generated the necessary multiphasic patterns. This highlights an additional, perhaps underappreciated, aspect of using RNNs in systems neuroscience: hypothesis generation. While not done here, one could have performed this study even before that of Churchland et al. (2012) and committed to a quantitatively rigorous hypothesis.

The CTD framework was born out of the hope that relatively simple population-level phenomena might explain seemingly complex single-neuron responses (Churchland & Shenoy 2007b, Churchland et al. 2012, Shenoy et al. 2013). Dynamical models often succeed in this goal. For example, RNNs trained by Sussillo et al. (2015) reproduced both single-neuron responses and population-level features (e.g., rotational dynamics) despite not being fit to neural data. While it is possible to obtain rotation-like features from non-dynamical models [e.g., sequence-like responses (Lebedev et al. 2019)], such rotations are dissimilar from those observed empirically (Michaels et al. 2016). Perhaps more critically, the hypothesis of sequence-like responses does not account for single-neuron responses, which are typically multiphasic and/or peak at different times for different conditions (e.g., Churchland et al. 2012, figure 2). Given such complex responses, it is reasonable to ask whether the presence of apparently dynamical patterns (e.g., rotations) is inevitable at the population level. In fact, rotational dynamics are neither observed upstream in the supplementary motor area (SMA) (Lara et al. 2018a) nor downstream at the level of muscles. This is true even though complex and multiphasic responses are present in both situations. This highlights an emerging need: determining when population-level observations provide new information beyond single-neuron properties. A method for doing so was recently introduced (Elsayed & Cunningham 2017) and confirms that dynamical structure is not a byproduct of simpler features (e.g., temporal, neural, and condition correlations) within the data. Thus, dynamical models are appealing because training them to perform a hypothesized computation is often sufficient to naturally account for the dominant features of single-neuron and population-level responses.

Neural population responses exhibit a wide variety of patterns. Do all patterns directly guide movements, or are there patterns that only support driving the dynamics themselves? A recent study by Russo et al. (2018) found evidence for the latter. They started by exploring a general phenomenon of dynamical systems: Two very similar neural states can result in very different future behaviors, which is defined as high tangling. Russo et al. found evidence that a large portion of the response during motor generation was used for “untangling.” Untangling neural dynamics is potentially quite important, as even a small amount of noise in a highly tangled state space could radically change the future evolution of the dynamical system. Russo et al. suggested that additional dimensions of neural activity function to reduce tangling and have no further relationship to inputs and outputs of motor cortex. This was further supported by Hall et al. (2014), who found a consistent rotational structure in dominant neural dimensions during wrist movements; precise movement direction was only decodable from the lower-variance neural dimensions.

Russo et al. (2019) recently characterized another geometric property of the neural population response: divergence, i.e., two neural trajectories never follow the same path before diverging. Population activity in SMA, which keeps track of context (e.g., time), must be structured so as to robustly differentiate between actions that are the same now but will soon diverge. Russo et al. (2019) found that population activity in SMA was structured in a fashion to achieve this by keeping divergence low, whereas M1, which does not keep track of context, showed high divergence. They found that RNNs trained to track context naturally had low divergence independent of the exact solution chosen, and they showed a similar geometry to SMA (helical). In contrast, RNNs that were context naïve did not have low divergence, and their state space geometry resembled that of M1 (elliptical).

Taken together, the studies described thus far constitute the core concepts of CTD applied to cortical control of arm movements. In summary, (a) preparatory activity sets an initial condition to a neural dynamical system, where preparatory dimensions are approximately orthogonal to movement dimensions; (b) presumably a well-timed input from other brain regions gives rise to a CIS, which transitions the preparatory state to another region in neural state space; (c) rotational dynamics are observed in motor cortex, where a large part of the response during motor generation appears to serve to untangle and support driving the dynamics themselves; (d) movement begins; (e) sensory feedback is isolated in null-dimensions before influencing output-potent feedback corrections; and (f) these dynamics are largely stable across time for a given behavior (Chestek et al. 2007, Flint et al. 2016, Gallego et al. 2020).

3.3. Population Dynamics Underlying Motor Adaptation

To evaluate if and how the core principles change when behaviors are made more complex, we shift our focus from CTD applied to motor pattern generation to CTD applied to motor adaptation. We start by discussing error-driven learning, which has a rich history in human psychophysics (for a review, see Krakauer et al. 2019). Here we focus on two tasks: visuomotor rotation (VMR) adaptation and curl force-field (CF) adaptation. During VMR adaptation, when a subject moves her arm in space, the cursor movement is offset by an angle that is experimentally controlled (e.g., 45° counterclockwise). In order to adapt, subjects must learn to move their arm in the anti-VMR direction; for example, for a 45° counterclockwise VMR, they must move their arm in a 45° clockwise direction to cause the cursor to move directly to the target.

The CTD framework predicts that adaptation should largely affect preparatory dimensions, as setting a new initial condition is sufficient to overcome the VMR. For example, if a 45° counterclockwise rotation is applied, generating preparatory activity that corresponds to making a reach to a 45° clockwise target would produce the correct behavior. Such changes in preparatory activity must match the timescale of behavioral changes; in humans and monkeys, adaptation happens gradually over the course of several tens of trials. Vyas et al. (2018) found that preparatory states corresponding to making a reach to a particular target systematically rotated across trials to align with the anti-VMR direction in neural state space. The preparatory state on single trials was highly correlated with behavioral changes on those trials. Similar changes have also been observed for other visuomotor manipulations [e.g., gain adaptation (Stavisky et al. 2017b)]. A hallmark of motor adaptation is washout, i.e., once the visuomotor perturbation is removed, subjects make errors in the opposite direction, compared to learning. Vyas et al. exploited this fact to show that VMR learning can transfer between overt reaching and covert movement (i.e., cursor movement guided by BCIs) contexts. Their analyses revealed that the preparatory subspace is shared between both contexts, and thus changes that happen in one context persist across context changes. Moreover, covert movements and overt reaching engage a similar neural dynamical system, despite covert context requiring no muscle activity production.

Given this potentially critical role of preparatory activity during learning, Vyas et al. (2020) investigated the causal role between motor preparation and VMR adaptation. Vyas et al. found that disrupting the preparatory state via intracortical microstimulation did not affect stimulated trials. Instead, error (and thus learning) on subsequent trials was disrupted. Through a series of causal experiments, the authors concluded that preparatory activity interacts with the update computation of the trial-by-trial learning process to produce effects that are dose, brain-region, and temporally specific. Moreover, their results, consistent with Bayesian estimation theory, argued that the learning process reduces its learning rate, by virtue of lowering its sensitivity to error, when faced with uncertainty introduced via stimulation (Vyas et al. 2020, Wei & Körding 2009).

Another common task that has recently been investigated is CF adaptation. Here subjects are required to learn new arm dynamics as they experience large velocity-dependent forces in an experimenter-defined direction (Cherian et al. 2013, Thoroughman & Shadmehr 1999). Sheahan et al. (2016) developed a two-sequence task where planning and execution could be separated. They found that planning, and not execution, allowed human participants to learn two opposing CF perturbations that would otherwise interfere. The implication is that neural activity during motor preparation can function, at least partly, as a contextual input, which the motor system leverages to separate different movements. Perich et al. (2018) studied the neural correlates of CF learning in PMd and M1 and found a surprising degree of stability in the correlation structure (i.e., functional connectivity) both within and across areas. While activity changed systematically with adaptation in the null space (of the map from PMd to M1), surprisingly, the output potent map was preserved. This perhaps functions to preserve the communication link between PMd and M1 during learning, with the advantageous feature that it does not require dramatic changes to the pattern-generation circuitry. As shown by Stavisky et al. (2017a) for error processing, this result serves as yet another example of where orthogonal subspaces are a general computational motif, which the brain can exploit for flexible and parallel computation. Taken together, these studies open the door to applying the computation through dynamics framework to study the neural control of error-driven motor learning.

3.4. Implications of Manifold Structure on Learning

Many studies have reported that neural population dynamics tend to lie within a low-dimensional subspace (or manifold) embedded within the high-dimensional neural population state space (Cunningham & Yu 2014). In this section, we review studies developed to understand the implications of these manifolds on the flexibility of neural population dynamics. Causally attributing changes in neural population activity to changes in behavior is a notoriously difficult problem in systems neuroscience (Jazayeri & Afraz 2017, Otchy et al. 2015). BCIs have emerged as a powerful experimental paradigm for addressing this challenge (Golub et al. 2016). A BCI maps the activity of a set of recorded neurons into control signals, which are used to drive movements of a computer cursor (Shenoy & Carmena 2014). This setup is powerful for studying learning because the experimenter has complete knowledge of and ability to manipulate the mapping between neural activity and behavior (Athlaye et al. 2017, Chase et al. 2012, Jarosiewicz et al. 2008, Orsborn et al. 2014, Sakellaridi et al. 2019, Zhou et al. 2019).

Sadtler et al. (2014) leveraged this feature of the BCI paradigm in an experiment in which monkeys learned to make BCI cursor movements under various perturbations of this mapping. Each perturbation was designed relative to the linear subspace, termed the intrinsic manifold, that encompassed the movement-period M1 dynamics that animals generated when making nonperturbed BCI cursor movements. The key result was that animals could readily learn (within a few hours) perturbations that could be solved using neural dynamics that lie within the intrinsic manifold, but they could not as readily learn perturbations that required outside-manifold dynamics. Thus, these observed neural manifolds likely reflect intrinsic constraints of cortical circuits, perhaps governed by inherent network connectivity, which limits the regions of neural state space through which neural population dynamics may explore.

When learning did occur (within-manifold perturbations, WMPs), what was the guiding neural population mechanism? Given the constraint that neural population dynamics remain within the intrinsic manifold, each WMP prescribes a behaviorally optimal set of neural states that would most swiftly drive the cursor toward each target, while remaining within the intrinsic manifold and respecting physiological constraints on individual neuron firing rates. Golub et al. (2018) identified these optimal states and compared them to neural states generated by animals after learning. Interestingly, animals did not learn these optimal states but rather learned systematically according to an even more stringent constraint. The learned population dynamics predominantly visited neural states that were within animals’ prelearning neural repertoire, defined as the set of neural states produced during an initial block of nonperturbed trials in the BCI task. Although this neural repertoire remained fixed, through learning animals changed associations between the neural states in that repertoire and corresponding intended movements. This mechanism of learning by neural reassociation thus explained animals’ postlearning neural states as well as levels of behavioral performance attained.

Could animals have better learned the outside-manifold perturbations if given multiple days to do so? Oby et al. (2019) demonstrated that this was indeed the case. Here, learned neural population dynamics were shown to drive behavioral improvements due to them visiting new neural population states of two kinds: (a) within the prelearning manifold but outside the prelearning repertoire, and (b) entirely outside the prelearning manifold (and repertoire). Thus, there appear to be multiple learning mechanisms operating at different timescales. A fast-timescale mechanism reassociates existing neural states with new intended behaviors (Golub et al. 2018), and slower-timescale mechanisms drive out-of-repertoire and outside-manifold changes to the neural population dynamics (Oby et al. 2019).

How are these different mechanisms implemented? Changes to the observed M1 population dynamics could result from changing initial conditions in M1 (Figure 2d), changing the inputs received by M1 (Figure 4), or changing the network connectivity within M1. Measuring these types of changes in vivo poses tremendous technical challenges. However, as in previous examples discussed, important insight can be derived from RNN modeling approaches that follow the CTD framework. Wärnberg & Kumar (2019) showed that, using three different classes of RNN models, substantial out-of-repertoire and outside-manifold RNN dynamics [as observed by Oby et al. (2019)] required substantial changes to the RNNs’ synaptic weights. Within-repertoire changes (Golub et al. 2018) were possible with either changes to inputs or comparatively smaller changes to the synaptic weights.

4. DYNAMICAL SYSTEMS IN COGNITION

Animals display the ability to volitionally modulate their behavior in response to contextual cues, sensory feedback, or environmental changes. Here we highlight studies that have applied the CTD framework to investigate neural computations underlying such flexible executive control.

4.1. Motor Timing

We start by reviewing studies that focus on uncovering neural mechanisms underlying an animal’s ability to flexibly control their movement initiation and/or duration time (Mauk & Buonomano 2004, Remington et al. 2018a). An early model of motor timing described a rise-to-threshold mechanism (Jazayeri & Shadlen 2015, Killeen & Fetterman 1988, Meck 1996, Treisman 1963). This model was derived from evidence that neurons exhibited ramping activity, triggering movement when a threshold was reached (e.g., Romo & Schultz 1992). This is also consistent with a central clock model where neural circuits trigger movement once a fixed number of ticks have been accumulated.

Ramping signals are not the only mechanism by which neural circuits can keep track of time. Recent modeling work has proposed state-dependent networks, which inherently keep track of time as they are composed of units that have time-dependent biological properties, and thus evolving states of these networks encode the passage of time (Buonomano 2000, Buonomano & Maass 2009, Karmarkar & Buonomano 2007, Maass et al. 2002). In such models, temporally patterned stimuli are encoded as a whole rather than as individual interval components. Furthermore, states are expanded to include not only population firing rates but also instantaneous membrane potentials and synaptic strengths. Interval sensitivity is thus established as a nonlinear function of connectivity, short-term plasticity, and synaptic strength. Intriguingly, such models degrade if initial conditions have noise or are otherwise perturbed. Karmarkar & Buonomano (2007) demonstrated that this is indeed the case: In both models and human psychophysics, performance is disrupted when distractors are presented at random times.

Recent experimental evidence suggests that another strategy for flexible motor timing involves controlling the speed of neural state evolution. Such control is achieved by manipulating inputs and/or initial conditions of the dynamical system. Wang et al. (2018) studied animals performing a cue-set-go task where animals were provided a context cue at trial-onset that indicated the timing at which they had to initiate movement. Temporal profiles of the neural population response in dorsomedial frontal cortex (DMFC) were scaled according to the production time. Neural trajectories in a low-dimensional state space were structured such that different production times were associated with an adjustment of neural trajectory speed. Wang et al. hypothesized that this structure might be a consequence of thalamocortical inputs into DMFC. They found that thalamic neurons provided approximately tonic input into DMFC with activity level that was correlated with the set-go interval. This suggests that thalamic neurons can manipulate their tonic activity level in order to influence dynamics of DMFC, thus contextualizing dynamics of DMFC in order to control neural trajectory speed. They tested this prediction in models by training RNNs to perform the same task and found a similarity to measured electrophysiology; intervals of different durations corresponded to similar trajectories in state space moving at different speeds. In a related study, Egger et al. (2019) studied a 1-2-3-go task where animals had to estimate the time interval between 1–2 and 2–3 epochs before initiating a movement at the anticipated 3–4 epoch, labeled as 3-go. The authors found that the speed command was updated based on the error between the timing measured during the 2–3 epoch and the estimated timing derived from the simulated motor plan based on the 1–2 epoch. These results suggest that speed modulation in DMFC can be understood in terms of similar computational principles such as closed-loop feedback control (Egger et al. 2019).

Remington et al. (2018b) studied a ready-set-go task where animals estimated a time interval during the ready-set epoch and then, depending on a context cue, scaled their estimate by a gain factor of 1 or 1.5 before making a movement at the appropriate time during the set-go epoch. The authors found that neural trajectories in DMFC separated along two dimensions: one associated with gain and one with the interval. Within a single context, speed modulation during the set-go epoch was governed by selecting appropriate initial conditions in the ready-set epoch. Across contexts, there was a gain-dependent tonic input into DMFC, which resulted in two groups of isomorphic neural trajectories that separated along a dimension in state space. The authors provided further evidence for these findings by training distinct RNNs, one where the gain came in as a transient input, thus only affecting the initial condition, and one where the gain was a tonic input. RNNs with gain as a tonic (or contextual) input more faithfully matched electrophysiology.

4.2. Decision-Making and Working Memory

One of the first studies to incorporate electrophysiology from behaving monkeys in a decision-making task with sophisticated neural network modeling was performed by Mante et al. (2013). The authors recorded from prefrontal cortex as animals performed a context-dependent variant of a classic decision-making task. Animals observed randomly moving dots, with each dot randomly colored red or green. During the color context, animals had to ignore motion and report the dominant color of the dots. During the motion context, animals had to ignore color and report the dominant motion direction of the dots. Surprisingly, context dependence was neither due to irrelevant inputs being blocked nor due to the decision axis differing between contexts. Using RNN modeling, the authors found that the decision axis in their networks was a line attractor: a linear arrangement of stable fixed points with end points corresponding to converged decisions (Figure 3c). Moreover, inputs corresponding to the irrelevant context decayed quickly, whereas context-dependent inputs were longer lasting and caused desirable perturbations to neural trajectory evolution. Context dependence was not a result of traditional gating but rather of dynamics quenching activity along certain directions in state space, achieved via a contextually dependent state space shift.

Chaisangmongkon et al. (2017) also employed RNNs to study neural mechanisms underlying delayed match-to-category (DMC) tasks. Animals were tasked to report if a particular test stimulus was a categorical match to a previously presented sample stimulus; animals were pre-trained to differentiate between categories. The authors trained RNNs to perform DMC tasks and confirmed that behavior and neural activity strongly resembled that of animals performing the task (Freedman & Assad 2006, Swaminathan & Freedman 2012). RNN dynamics resembled slow and stable states connected by robust trajectory tunnels. During working memory, these tunnels functioned to force neural states to flow along two possible routes (corresponding to the sample categories), thus maintaining memory in a dynamic manner. Misclassification can thus be interpreted as noise pushing the state outside the correct tunnel and into the tunnel corresponding to the other category. By analyzing the state space geometry, Chaisangmongkon et al. found that RNNs solved the task by strategically navigating around attracting fixed points and unstable saddle points through slow and reliable transitions. That is, RNNs started with rest states, moving to those corresponding to sample categories, then to category working memory, then sample-test category combination, and finally to decision states. This study put forth the idea that delayed association in biological circuits can be performed using such transient dynamics. The study also serves as yet another example of how different regions of state space can subserve different computational roles (Churchland et al. 2012; Hennequin et al. 2014; Mante et al. 2013; Murakami & Mainen 2015; Rabinovich et al. 2001, 2008; Raposo et al. 2014). Other studies spanning working memory and its representations are reviewed in depth by Chaudhuri & Fiete (2016) and Miller et al. (2018).

A critical aspect of flexible decision-making involves integrating sensory evidence with prior information. Sohn et al. (2019) used a time-interval reproduction task and found evidence for Bayesian integration in neural circuits. Priors resembled low-dimensional curved manifolds across the population and warped underlying neural representations in a manner such that behavior was Bayes-optimal, i.e., responses were biased consistently with priors. The authors performed a causal test of the curved manifold hypothesis in models by perturbing RNN activity in a manner that revealed that curvature induced regression toward the mean of the prior. Such causal tests might be an important stopgap before similar perturbations can be performed in vivo.

In all of the studies reviewed thus far, RNNs are typically trained and optimized to perform a single task, which is certainly a poor approximation to biological networks that can solve many tasks. Yang et al. (2019) trained RNNs to perform 20 tasks commonly studied in systems neuroscience. The key discovery in this study was that RNNs developed compositionality of task representation, i.e., one task could be performed by recombining instructions for other tasks, and groups of neurons became specialized for specific cognitive processes. At least at a high level, this is a critical feature of biological systems. We believe future work along these lines will be critical, as biological neural circuits are rarely optimized to only perform single or a small handful of tasks. To aid in such efforts, Song et al. (2016) recently released a flexible framework for training RNNs for cognitive tasks. These authors have also made strides in developing models that do not simply rely on graded error signals to train RNNs. Animals, for example, often learn by being rewarded on a trial-by-trail basis, where elements of confidence, past performance, and value judgement are critical to the underlying computations, even if not apparent in the motor action. The authors developed a set of tools for reward-based training of RNNs, which match behavioral and electrophysiological recordings from an array of experimental paradigms and thus might serve as a powerful framework for studying value-based neural computations (Song et al. 2017).

5. CHALLENGES AND OPPORTUNITIES

The CTD framework has been successfully applied to study the effect of inputs, initial conditions, and neural population geometry on behavior. Many challenging questions, however, still remain unanswered. For example, what does the input-output structure look like for a particular brain region? Where do the inputs come from? How do they shape the local dynamics of that brain region? How does this organization inform the overall function of the circuit? While commendable progress has been made toward characterizing inputs (e.g., Wang et al. 2018), how activity from one brain region affects another (e.g., Semedo et al. 2019), or how population covariance structure changes across tasks (e.g., Gallego et al. 2018), further headway will likely require recording neural activity from many more of the brain regions involved in a given task. Fortunately, such progress is already underway. Advances in two-photon calcium imaging in larval zebrafish (Ahrens et al. 2012, Andalman et al. 2019, Naumann et al. 2016, Portugues et al. 2014), Drosophila (Kim et al. 2017), rodents (Allen et al. 2019, Chaudhuri et al. 2019, Stringer et al. 2019), and Caenorhabditis elegans (Kato et al. 2015, Nichols et al. 2017), as well as high channel count electrophysiology via NeuroPixels (e.g., Jun et al. 2017, Stringer et al. 2019, Trautmann et al. 2019), have enabled measuring and manipulating neural activity at unprecedented scale. We believe these technologies will present new opportunities to test the CTD framework.

The CTD framework makes strong predictions about neural dynamics under novel conditions. While many of these predictions expose themselves to falsification, it has been difficult to falsify them empirically. The challenge is nontrivial; testing CTD models requires a high degree of control over neural activity. The experimenter must be able to manipulate neural states arbitrarily in state space and then measure behavioral and neural consequences of such perturbations, as described by Shenoy (Adamantidis et al. 2015). Nonetheless, a burgeoning body of recent research on using optogenetics to spatiotemporally pattern neural activity in visual cortex has demonstrated that experimental control over population activity is indeed possible (e.g., Bashivan et al. 2019, Carrillo-Reid et al. 2019, Chettih & Harvey 2019, Marshel et al. 2019, Yang et al. 2018). Perhaps the time is fast approaching when such technology can interface with predictions made by CTD. In our view, this could potentially serve as a powerful and causal test of the CTD framework.

In closing, application of the CTD framework has uncovered several invariant motifs concealed behind complex neural population activity. Studying these motifs may help establish rigorous computational theories linking brain and behavior. We believe that meaningful progress in this branch of systems neuroscience likely requires three steps: (a) continued development of the CTD framework and other kinds of quantitative models that make empirically testable predictions, (b) further research into methodological approaches toward causal experiments, and (c) providing concrete strategies for updating models once new measurements are made.