Abstract
Evidence is accumulating that evolutionary changes are not only common during biological invasions but may also contribute directly to invasion success. The genomic basis of such changes is still largely unexplored. Yet, understanding the genomic response to invasion may help to predict the conditions under which invasiveness can be enhanced or suppressed. Here, we characterized the genome response of the spotted wing drosophila Drosophila suzukii during the worldwide invasion of this pest insect species, by conducting a genome-wide association study to identify genes involved in adaptive processes during invasion. Genomic data from 22 population samples were analyzed to detect genetic variants associated with the status (invasive versus native) of the sampled populations based on a newly developed statistic, we called C2, that contrasts allele frequencies corrected for population structure. We evaluated this new statistical framework using simulated data sets and implemented it in an upgraded version of the program BayPass. We identified a relatively small set of single-nucleotide polymorphisms that show a highly significant association with the invasive status of D. suzukii populations. In particular, two genes, RhoGEF64C and cpo, contained single-nucleotide polymorphisms significantly associated with the invasive status in the two separate main invasion routes of D. suzukii. Our methodological approaches can be applied to any other invasive species, and more generally to any evolutionary model for species characterized by nonequilibrium demographic conditions for which binary covariables of interest can be defined at the population level.
Keywords: biological invasions, Drosophila suzukii, GWAS, BayPass, Pool-Seq
Introduction
Managing and controlling introduced species require an understanding of the ecological and evolutionary processes that underlie invasions. Biological invasions are also of more general interest because they constitute natural experiments that allow investigation of evolutionary processes on contemporary timescales. Colonizers are known to experience differences in biotic interactions, climate, availability of resources, and disturbance regimes relative to populations in their native regions, often with opportunities for colonizers to evolve changes in resource allocation which favor their success (Balanya et al. 2006; Lee and Gelembiuk 2008; Dlugosch et al. 2015). Adaptive evolutionary shifts in response to novel selection regimes may therefore be central to initial establishment and spread of invasive species after introduction (Colautti and Barrett 2013; Colautti and Lau 2015). In agreement with this adaptive evolutionary shift hypothesis, experimental evidence is accumulating that evolutionary changes are not only common during invasions but also may contribute directly to invasion success (Ellstrand and Schierenbeck 2000; Lee 2002; Facon et al. 2011; Bock et al. 2015; Colautti and Lau 2015; Williams et al. 2016; Ochocki and Miller 2017). However, despite an increase in theoretical and empirical studies on the evolutionary biology of invasive species in the past decade, the genetic basis of evolutionary adaptations during invasions is still largely unexplored (Barrett 2015; Welles and Dlugosch 2018; Reznick et al. 2019).
The spotted wing drosophila, Drosophila suzukii, represents an attractive biological model to study invasion processes. This pest species, native to South East Asia, initially invaded North America and Europe, simultaneously in 2008, and subsequently La Réunion Island (Indian Ocean) and South America, in 2013. Unlike most Drosophilids, this species lays eggs in unripe fruits by means of its sclerotized ovipositor. In agricultural areas, it causes dramatic losses in fruit production, with a yearly cost exceeding one billion euros worldwide (Cini et al. 2012; Asplen et al. 2015). The rapid spreading of D. suzukii in United States and Europe suggests its remarkable ability to adapt or to acclimate to new environments and host plants. Using evolutionarily neutral molecular markers, Adrion et al. (2014) and Fraimout et al. (2017) finely deciphered the routes taken by D. suzukii in its invasion worldwide. Interestingly, both studies showed that North American (plus Brazil) and European (plus La Réunion Island) populations globally represent separate invasion routes, with different native source populations and multiple introduction events in both invaded regions (Fraimout et al. 2017). These two major and separate invasion pathways provide the opportunity to evaluate replicate evolutionary trajectories. Finally, D. suzukii is a good model species for finely interpreting genomic signals of interest due to the availability of genome assemblies for this species (Chiu et al. 2013; Ometto et al. 2013; Paris et al. 2020) along with the large amount of genomic and gene annotation resources available in its closely related model species D. melanogaster (Hoskins et al. 2015).
In this context, advances in high-throughput sequencing technologies together with population genomics statistical methods offer novel opportunities to disentangle responses to selection from other forms of evolution. These advances are thus expected to provide insights into the genomic changes that might have contributed to the success in a new environment (reviewed in Bock et al. 2015; Welles and Dlugosch 2018). Hence, comparing the structuring of genetic diversity on a whole-genome scale among invasive populations and their source populations might allow the characterization of the types of genetic variation involved in adaptation during invasion of new areas and their potential ecological functions. For example, Puzey and Vallejo-Marin (2014) used whole-genome resequencing data to scan for shifts in site frequency spectra to detect positive selection in introduced populations of monkey-flower (Mimulus guttatus). Regions putatively under selection were associated with flowering time and abiotic and biotic stress tolerance and included regions associated with a chromosomal inversion polymorphism between the native and introduced range.
Identifying loci underlying invasion success can be considered in the context of whole-genome scan for association with population-specific covariate. These approaches, also known as environmental association analysis (EAA), have received considerable attention in recent years (Coop et al. 2010; Frichot et al. 2013; de Villemereuil and Gaggiotti 2015; Gautier 2015). Most of the methodological developments have focused on properly accounting for the covariance structure among population allele frequencies that is due to the shared demographic history of the populations. This neutral covariance structure may indeed confound the relationship between the across population variation in allele frequencies and the covariates of interest (Coop et al. 2010; Frichot et al. 2013, 2015; Gautier 2015). Yet, defining relevant environmental characteristics or traits as proxy for invasion success remains challenging and might even be viewed as the key aim. Therefore, we propose to simply summarize invasion success into a binary variable corresponding to the population’s historical status (i.e., invasive or native) based on previous studies. By extension, functional annotation of the associated variants identified may provide insights into candidate traits underlying invasion success (Li et al. 2008; Estoup et al. 2016; Wu et al. 2019).
The Bayesian hierarchical model initially proposed by Coop et al. (2010), later extended in Gautier (2015) and implemented in the software BayPass, represents one of the most flexible and powerful frameworks to carry out EAA since it efficiently accounts for the correlation structure among allele frequencies in the sampled populations. Although association analyses may be carried out with categorical or binary covariables (see the example of Littorina population ecotypes in Gautier 2015), the assumed linear relationship with allele frequencies is not entirely satisfactory and may even be problematic when dealing with small data sets or if one wishes to disregard some populations.
In the present study, we developed a nonparametric counterpart for the association model implemented in BayPass (Gautier 2015). This new approach relies on a contrast statistic, we named C2, that compares the standardized population allele frequencies (i.e., the allele frequencies corrected for the population structure) between the two groups of populations specified by the binary covariable of interest. We evaluated the performance of this statistic on simulated data and used it to characterize the genome response of D. suzukii during its worldwide invasion. To that end, we generated Pool-Seq data (Gautier et al. 2013; Schlotterer et al. 2014) consisting of whole-genome sequences of pools of individual DNA (from n = 50 to n = 100 individuals per pool) representative of 22 worldwide populations sampled in both the invaded (n = 16 populations) and native (n = 6 populations) ranges of the species. We then estimated the C2 statistics associated with the invasive versus native status of the populations on a worldwide scale or considering separately each of the two invasion routes (European and American) as characterized by Fraimout et al. (2017). Our aim was to identify genomic regions and genes involved in adaptive processes underlying the invasion success of D. suzukii.
New Approaches
To identify single-nucleotide polymorphisms (SNPs) associated with a population-specific binary trait, such as the invasive versus native status of D. suzukii populations, we developed a new statistic, we called C2. The C2 statistic was designed to contrast SNP allele frequencies between the two groups of populations specified by the binary trait while accounting for the possibly complex evolutionary history of the different populations. Indeed, the shared population history is a major (neutral) contributor to allele frequency differentiation across populations (Bonhomme et al. 2010; Gunther and Coop 2013) that may confound association signals (Coop et al. 2010; Gautier 2015).
We here relied on the multivariate normal approximation introduced by Coop et al. (2010) and further extended by Gautier (2015) to model population allele frequencies and to define the C2 contrast statistic. More precisely, consider a sample made of J populations (each with a label ) that have been characterized for I biallelic SNPs (each with a label ), with the reference allele arbitrarily defined (e.g., by randomly drawing the ancestral or the derived state). Let αij represent the (unobserved) allele frequency of the reference allele at SNP i in population j. As previously defined and discussed (Coop et al. 2010; Gautier 2015), we introduced an instrumental allele frequency (for each SNP i and population j) taking values on the real line such that .
Following Coop et al. (2010) and Gautier (2015), a multivariate Gaussian (prior) distribution of the vector is then assumed for each SNP i:
| (1) |
where 1J is the all-one vector of length J; is the (scaled) covariance matrix of the population allele frequencies which captures information about their shared demographic history; and πi is the weighted mean frequency of the SNP i reference allele. If is used to build a tree or an admixture graph (Pickrell and Pritchard 2012), πi corresponds to the root allele frequency. We further define for each SNP i the vector of standardized (instrumental) allele frequencies in the J populations as:
| (2) |
where results from the Cholesky decomposition of Ω (i.e., ). The vector thus contains scaled allele frequencies that are corrected for both the population structure (summarized by ) and the across-population (e.g., ancestral) allele frequency (πi).
The C2 contrast statistic is then simply defined as the mean squared difference of the sum of standardized allele frequencies of the two groups of populations defined according to the binary trait modalities:
| (3) |
where is a vector of the trait values observed for each population j such that cj = 1 (respectively, ) if population j displays the first (respectively, second) trait modality. One may also define cj = 0 to exclude a given population j from the comparison. According to our model, the J elements of are independent and identically distributed as a standard Gaussian distribution under the null hypothesis of only neutral marker differentiation. The C2 statistic is thus expected to follow a distribution with one degree of freedom.
The estimation of the C2 statistic was here performed using the Markov-Chain Monte Carlo (MCMC) algorithm implemented in the BayPass software (Gautier 2015). Due to the hierarchical structure of the underlying Bayesian model, the SNP population allele frequencies (in the vectors ’s) tend to be pulled closer together (i.e., shrunk) because they share the same overarching prior multivariate Gaussian distribution (eq. 1) (see, e.g., Kruschke 2014, pp. 245–249, for a general presentation of shrinkage in Bayesian hierarchical models). This leads to a shrinkage of the estimated C2 posterior means and the estimates of the SNP-specific XtX differentiation statistic, as already noticed in Gautier (2015). The XtX is indeed defined as the variance of the standardized allele frequencies of the SNP across the populations () and is thus analogous to a SNP-specific FST that would account for the overall covariance structure of the population allele frequencies (Gunther and Coop 2013). As a matter of expedience, to ensure proper calibration of both the C2 and XtX estimates (see below), we decided to rescale the posterior means of the ’s as:
| (4) |
where is the posterior mean of and (respectively, ) is the mean (respectively, SD) of the I × J ’s ( usually). The following estimators of XtX and C2, denoted for each SNP i as and , respectively, were then obtained as:
| (5) |
Under the null hypothesis, and allowing one to rely on standard decision-making procedures, for example, based on P values or more preferably on q values to control for multiple-testing issues (Storey and Tibshirani 2003).
Results
Simulation-Based Evaluation of the Performance of Our Novel Statistical Framework
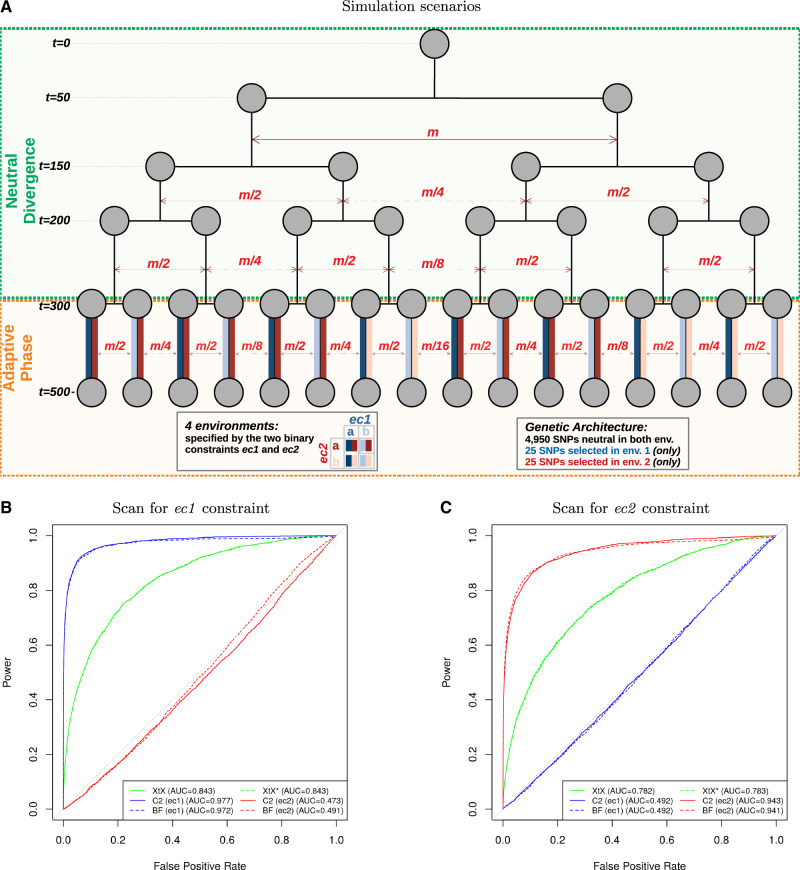
To evaluate the performances of the C2 contrast statistic for the identification of SNPs associated with binary population-specific covariables, we simulated 100 data sets under the evolutionary scenario depicted in figure 1A. This scenario was adapted from the so-called HsIMM model proposed by de Villemereuil et al. (2014) to deal with binary environmental constraints rather than environmental gradient. This scenario choice was motivated by the use of the same underlying HsIMM demographic history in previous studies to carry out in-depth evaluations of a wide range of popular methods for genome-wide selection scans and EAA in realistic situations (de Villemereuil et al. 2014; Gautier 2015). In these studies, the XtX statistic (for genome-wide selection scan approaches) and the Bayes Factor (BF) for EAA, as computed with BayPass, were found to be among the best performing approaches in their respective categories under various scenarios, including HsIMM. Each simulated data set consisted of 5,000 SNPs genotyped for 320 individuals belonging to 16 differentiated populations subjected to two different contrasting environmental constraints, denoted ec1 and ec2 in figure 1A. The ec1 constraint was aimed at mimicking adaptation of eight pairs of geographically differentiated populations to two different ecotypes (e.g., host plant) replicated in different geographic areas. Conversely, the ec2 might be viewed as replicated local adaptive constraints with a first type a specifying a large native area with several geographically differentiated populations (here six), and a second type b specifying invasive areas with differentiated populations originating from various regions of the native area (i.e., not related to the same extent to their contemporary native populations). It should be noted that the two ec1 types were evenly distributed in the population tree, whereas for ec2, the type b was overrepresented in ten populations (fig. 1A). During the adaptive phase, the fitness of individuals in the environment of their population of origin was determined by their genotypes at 25 SNPs for ec1 and 25 SNPs for ec2 constraints (hereafter referred to as ec1 and ec2 selected SNPs, respectively). Overall, the realized FST (Weir and Cockerham 1984) ranged from 0.110 to 0.122 (0.116 on an average) across the data sets, a level of differentiation similar to that observed in our worldwide D. suzukii sample (see below).
Fig. 1.
Evaluation of the performance of the C2 contrast statistic on simulated data and comparison with the BF for association and two XtX SNP-specific differentiation estimators. (A) Schematic representation of the demographic scenario used for the simulation. It consists of two successive phases: 1) a neutral divergence phase with migration (only some illustrative migration combinations being represented) leading to the differentiation of an ancestral population into 16 populations after four successive fission events (at generations t = 50, t = 150, t = 200, and t = 300) and 2) an adaptive phase (lasting 200 generations) during which individuals were subjected to selective pressures exerted by two environmental constraints (ec1 and ec2) each having two possible modalities (a or b) according to their population of origin (i.e., eight possible environments in total). Out of the 5,000 simulated SNPs, the fitness of individuals in the environment of their population of origin was determined by their genotypes at 25 SNPs for ec1 and 25 SNPs for ec2 constraints. In total, 100 data sets were simulated. (B and C) The ROC curves associated with the ec1 and ec2 C2 contrasts and the two corresponding BF for association are plotted together with those associated with the two XtX estimators (i.e., posterior mean estimator XtX, and the new calibrated estimator ). The FPRs associated with each statistic were obtained from the corresponding neutral SNP estimates combined over the 100 simulated data sets ( values in total). Similarly, the TPRs were estimated from either the n = 2,500 combined ec1 (B) or the ec2 (C) selected SNPs. ROC AUC values are given between parentheses.
We further estimated with BayPass (Gautier 2015) the C2 statistics for each ec1 or ec2 contrasting environmental constraints together with the corresponding BF as an alternative measure of the support for association representative of state-of-the-art EAA approaches. For comparison with standard genome-wide selection scan approaches, we also estimated the SNP XtX differentiation statistic, using both the posterior mean estimator (Gautier 2015) and the estimator described earlier. Note however that because selection scan approaches rely on (covariate-free) differentiation statistics (here, the XtX), they do not allow to distinguish among the outlier SNPs those responding to the ec1 constraint from those responding to the ec2 constraint.
Based on the status of each simulated SNP (i.e., neutral, and ec1 or ec2 selected) and combining results in the 100 simulated data sets, standard receiver-operating curves (ROCs) were computed (Grau et al. 2015) and plotted in figure 1B (respectively, fig. 1C) for the six statistics. This allowed comparing for various thresholds covering the range of variation of the different statistics, the power to detect ec1 (respectively, ec2) selected SNPs (i.e., the proportion of true positives among the corresponding selected SNPs) as a function of the false-positive rates (FPR, i.e., the proportion of positives among neutral SNPs). The C2 statistic was found to efficiently detect SNPs affected by ec1 and ec2 environmental constraints, the area under the ROC curve (AUC) being equal to 0.977 (fig. 1B) and 0.943 (fig. 1C), respectively. The unbalanced population representation of the two ec2 types had a limited impact on the performance of the C2 statistic to identify the underlying selected SNPs. In addition, the C2 statistics clearly discriminated the selected SNPs according to their underlying environmental constraint. In other words, no selection signal was identified by the C2 statistic computed for the ec2 (respectively, ec1) contrast on ec1 (respectively, ec2) selected SNPs, resulting in ROC AUC close to the value of 0.5 obtained with a random classifier.
The ROC curves displayed in figure 1B and C also revealed nearly identical performance of the C2 statistic and the BF. Accordingly, the correlation between both statistics was fairly high (Pearson’s r equal to 0.983 and 0.923 for ec1 and ec2, respectively). Yet, one practical advantage of the C2 statistic was its good calibration with respect to the null hypothesis of no association, the corresponding P values (assuming a distribution with 1 degree of freedom) being close to uniform (supplementary fig. S1, Supplementary Material online).
Similarly, the two XtX estimators were found highly correlated (Pearson’s r = 0.998) with almost confounded ROC curves, but only the was properly calibrated (supplementary fig. S2, Supplementary Material online). Their performances were however clearly worse than those obtained with the C2 (and BF) statistics. This was in part explained by their inability to discriminate between the two types of selected SNPs, that is, selected SNPs overly differentiated in ec2 generating false-positives in the identification of ec1 SNPs (fig. 1B) and vice versa. Accordingly, ROC AUC in figure 1B for the XtX were also smaller than in figure 1C, ec1 selected SNPs being more differentiated than those in ec2 due to the simulated design. Yet, the power of the XtX statistic to detect ec1 or ec2 selected SNPs remained substantially smaller than that of the corresponding C2 contrast statistics. For instance, at the 1% P-value significance threshold, the power to detect ec1 (respectively, ec2) selected SNPs was equal to 72.6% (respectively, 59.1%) with the C2 statistic and only 17.1% (respectively, 10.4%) with the estimator, even when considering for the latter, a unilateral test to only target overly differentiated SNPs. Note that, as expected from the good calibration of the statistic, similar results were obtained when considering empirical P-value thresholds computed from the distribution of the XtX statistics estimated from neutral SNPs.
Robustness of the Different Approaches to Demographic Events Typical of Biological Invasions
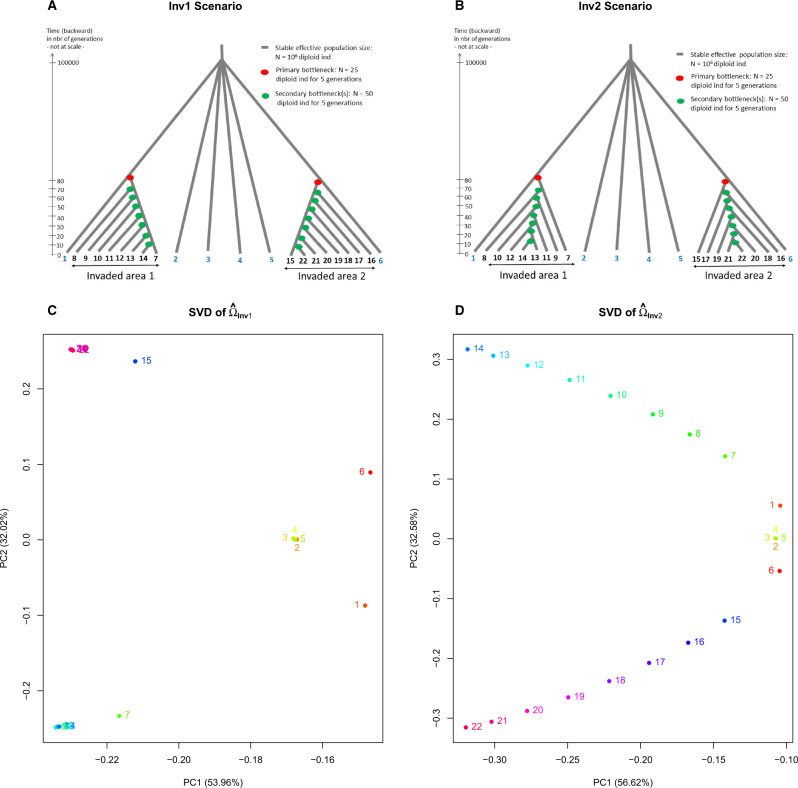
The HsIMM scenario used for the above simulations may imperfectly capture some characteristics of the demographic history of invasive species. Indeed, an invasion may be triggered by a relatively small number of colonizers leading to population bottlenecks (Estoup et al. 2016). Moreover, invasive species, particularly those with low dispersal capabilities (which is not the case of D. suzukii), may be prone to allele surfing, wherein a variant rises to high frequency by chance as the expansion wave advances due to repeated bottlenecks (Excoffier and Ray 2008). At the genomic level, such bottleneck events may lead to large but correlated random fluctuations of some variant frequencies in the invasive populations deriving from the founders of the primary introduction, up to the fixation of the same variant in all of them. To evaluate to which extent such demographic events may result in spurious signals of association of some variants with the invasive status of populations, we simulated data sets (with 165,020 and 152,321 evolutionary neutral SNPs, respectively) under two invasion scenarios: 1) the scenario Inv1 (fig. 2A) in which each invasive population of an area derived from the same primarily introduced population with a bottleneck occurring at different time in the past and 2) the scenario Inv2 (fig. 2B) in which the invasive populations of an area are successively founded one after the other with a bottleneck event at each foundation, a process likely to favor allele surfing during geographic range expansion. As for the D. suzukii case study detailed below, the two scenarios consisted of six native populations with a moderate level of genetic structuring (realized FST equal to 4.95% and 4.93%, respectively) and two groups of eight invasive populations, each group originating from one of the native populations and corresponding to a given invaded area. For the scenario Inv1, the chosen simulation parameters resulted in a realized FST within each group of 3.49% and 3.48% and an overall realized FST (among the 22 simulated native and invasive populations) of 9.60%. In the scenario Inv2, the succession of bottlenecks led to an increased level of differentiation among the invasive populations, compared with the scenario Inv1, with a realized FST within each of the two groups equal to 5.76% and 5.77% and an overall realized FST of 14.5%.
Fig. 2.
Description of the invasion scenarios Inv1 (A) and Inv2 (B) with values of the historical and demographical parameters used to simulated evolutionary neutral SNP data sets. The coordinates of the 22 populations on the first two axes of variation (following singular-value decomposition with the plot.omega function available in the BayPass package) of the scaled covariance matrix of allele frequencies (respectively, ) estimated using BayPass from the SNP data simulated under Inv1 (respectively, Inv2) are plotted in (C) (respectively, D).
We ran BayPass on the two data sets simulated under the invasion scenarios Inv1 and Inv2 to identify outlying differentiated SNPs (based on the statistic) and to evaluate the support for association of each SNP with the invasive population status (based on both the C2 statistic and the BF criterion). Three different association tests were used to compare the six native populations with: 1) all the 16 invasive populations ( and BF); 2) the eight invasive populations from the first group ( and BF); or 3) the eight invasive populations from the second group ( and BF). As shown in figure 2C and D, the estimated scaled covariance matrices provided an overall structuring of genetic diversity across the 22 simulated populations that was consistent with the simulated histories. The singular-value decomposition of the two matrices separated the populations according to their invasive or native origins in the first axis of variation, whereas the second axis separated the two groups of invasive populations. Under the Inv2 scenario, the successive bottlenecks at the origin of the different invasive populations also resulted in their clear separation on the first axis (fig. 2D). These results suggest that the shared population history may be globally well accounted for by the model. Accordingly, the distribution of the P values derived from the was close to uniform for the scenario Inv1 (supplementary fig. S3A, Supplementary Material online) as expected given that all the analyzed SNPs evolved neutrally. This resulted in a desired null FPR at both the 1% and the 5% q-value thresholds (table 1). Yet, for the Inv2 scenario, we observed an (undesirable) excess of small P values derived from the . However, this feature only resulted in an almost null FPR after correcting for multiple testing, the FPR being equal to only at the 5% q-value threshold (table 1).
Table 1.
Proportion of SNPs (FPR) Simulated under the Invasion Scenarios Inv1 (n = 165,020 SNPs) and Inv2 (n = 152,321 SNPs) Displaying Outlying Differentiation (based on the statistic) or Showing a Signal of Association with the Population Invasive Status (based on the BF criterion or the C2 statistic).
| Scenario Inv1 |
Scenario Inv2 |
|||
|---|---|---|---|---|
| All | G1 and G2 | All | G1 and G2 | |
| BF >20 (>15) | () | () | () | () |
| C 2 q value <0.01 (<0.05) | 0.0 (0.0) | 0.0 (0.0) | 0.0 (0.0) | () |
| q value <0.01 (<0.05) | 0.0 (0.0) | () | ||
Note.—Support for association was evaluated using the BayPass regression models (BF criterion) or the q value derived from the estimated contrast statistics C2 for the three different tests comparing the six native populations allele frequencies to: 1) all 16 invasive populations (“all”); 2) the eight invasive populations from the first group (“G1”); or 3) the eight invasive populations from the second group (“G2”) (supplementary fig. S3, Supplementary Material online). Results from the two latter tests were combined to compute FPRs (columns “G1 and G2” in the table). Note that the BF threshold of 20 dB (respectively, 15 dB) corresponds to decisive (respectively, very strong) evidence in favor of association according to the Jeffreys’ rule (Jeffreys 1961). To account for the bilateral nature of the underlying test (SNPs might be over or underdifferentiated if under directional or balancing selection), the P values derived from the statistic were computed as , where represents the cumulative density function of the distribution with J degrees of freedom (here J = 22).
Similar patterns were observed for the distribution of the P values derived from the different C2 statistics (supplementary fig. S3C and D, Supplementary Material online). Note that for the Inv1 scenario, we observed a smaller proportion of small C2P values than expected under uniform expectation that might originate from an imperfect deshrinking of the standardized allele frequencies. Overall, the FPR associated with the C2 statistics was null at the 1% q-value threshold for both the scenarios Inv1 and Inv2 except, for the latter, when considering and group-specific contrasts for which the FPR was equal to (table 1). At the stringent decisive evidence threshold of 20 dB (Jeffreys 1961) on BF, the FPR was always one order of magnitude higher ranging from to across the different analyses. This may result in a substantial amount of false-positives on (real) data sets of million SNPs.
Interestingly, supplementary figure S3E and F, Supplementary Material online, showed that the SNPs with the highest BF were clearly different from those with the highest C2 suggesting that C2 and BF may actually be sensitive to different confounding structuring of SNP genetic diversity. As detailed in supplementary table S1, Supplementary Material online, for the simulated data set Inv2, the median of the SNP-specific FST computed within all the invasive populations was equal to 0.12 across the 162 top SNPs (with a ), close to the median computed over all the simulated SNPs, but far lower than the median computed across the 74 top SNPs (with a derived P value ). Accordingly, the size of the allele frequency range within the invasive populations was larger for the top SNPs than for the top SNPs (0.745 against 0.450); but the reverse was observed within native populations. In addition, the average allele frequencies of the top SNPs were far smaller (median of 0.017) with a smaller range of variation (median of 0.070) when compared with top SNPs (median of 0.251) characterized by a wider range of variation (median of 0.215), whereas the same values computed over all the SNPs were intermediary between these two extremes. Overall, these results suggest that, in such invasion scenarios, the regression analysis based on BF may be more sensitive to neutral variants common in the native populations and displaying rather homogeneous allele frequencies within the invasive populations. In contrast, the C2 statistic appears more sensitive to variants rare in the native populations and raising to high allele frequencies with high heterogeneity in the invasive populations. Yet, correction for multiple testing on the C2 derived P value turned out to more efficiently control for FPRs than standard thresholds on the BF, and this for both simulated invasion scenarios.
Genome-Wide Scan for Association with Invasion Success in D. suzukii
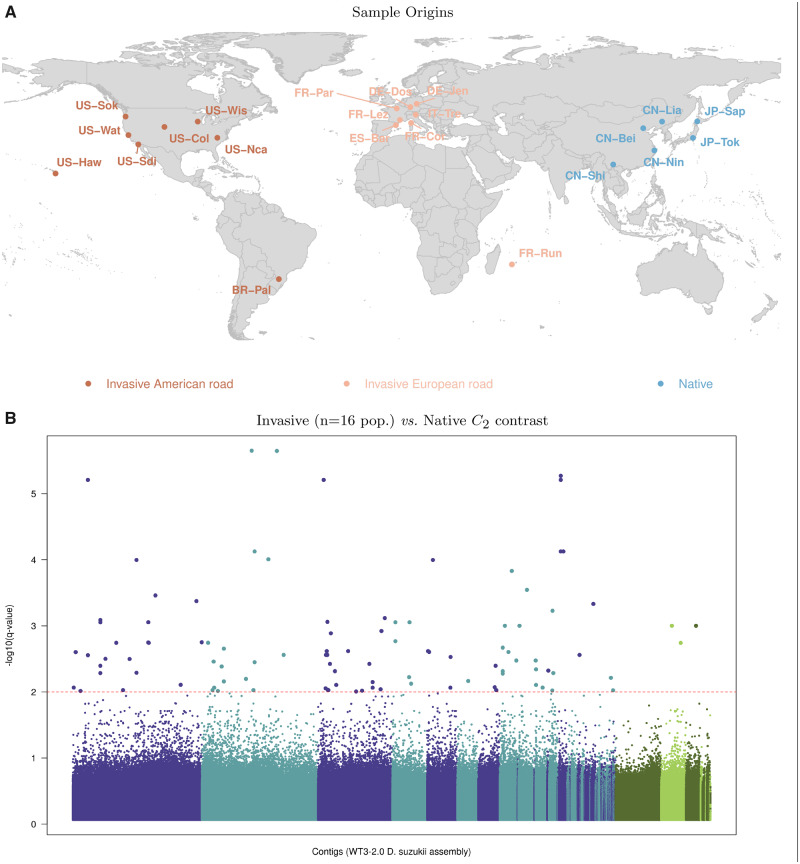
To identify genomic regions associated with the invasion success of D. suzukii, we carried out a genome scan, based on the C2 statistic, to contrast the patterns of genetic diversity among 22 populations originating from either the native (n = 6 populations) or invaded areas (n = 16 populations) (fig. 3A). To that end, we sequenced pools of 50–100 individuals representative of each population (supplementary table S2, Supplementary Material online) and mapped the resulting sequencing reads onto the newly released WT3-2.0 D. suzukii genome assembly (Paris et al. 2020). These Pool-Seq data allowed the characterization of 11,564,472 autosomal and 1,966,184 X-linked SNPs segregating in the 22 populations that were subsampled into 154 autosomal and 26 X-linked data sets (of ∼75,000 SNPs each) for further analyses.
Fig. 3.
Whole-genome scan for association with invasion success in Drosophila suzukii. (A) Geographic location of the 22 D. suzukii population samples genotyped using a pool-sequencing methodology. Population samples from the native range are in blue and those from the invaded range are in red (American invasion route) or light red (European invasion route) (Fraimout et al. 2017). See supplementary table S2, Supplementary Material online, for details on each population sample. (B) Manhattan plot of the SNP q values on a scale derived from the estimated C2 statistics for the native versus invasive status contrast of the 22 worldwide D. suzukii populations. SNPs are ordered by their position on their contig of origin displayed with alternating dark blue and light blue color when autosomal and dark green and light green when X-linked. The horizontal dashed line indicates the 1% q-value threshold (here corresponding to a P-value threshold of ) which gives the expected false-discovery rate, that is, the expected proportion of false-positives among the 110 SNPs (highlighted in the plot) above this threshold.
The overall differentiation was estimated using the recently developed FST estimator for Pool-Seq data (Hivert et al. 2018). It ranged from 8.86% to 9.02% (8.95% on an average) for the autosomal data sets and from 17.6% to 17.8% (17.8% on an average) for the X-chromosome data sets. Although a higher genetic differentiation is expected for the X-chromosome even under equal contribution of males and females to demography, the almost twice higher overall differentiation observed for the X chromosome compared with autosomes might have been accentuated by unbalanced sex ratio (e.g., polyandry), male-biased dispersal, or a higher impact of selection on the X-chromosome (Clemente et al. 2018). Inferring sex-specific demography was beyond the scope of the present study, but for our purposes, this finding justified to perform separate genome scans on autosomal and X-linked SNPs.
We ran BayPass on the different data sets to estimate, for every SNPs, the C2 statistic that contrasts the allele frequencies of native and invasive populations, while accounting for their shared population history as summarized in the scaled covariance matrix . Interestingly, the estimated matrices for autosomal and X-linked SNPs resulted in a similar structuring of the genetic diversity across the 22 populations (supplementary fig. S4, Supplementary Material online), which may rule out selective forces as the main driver of the differences of global differentiation levels observed between the two chromosome types. Note also that the representation of the two major axes of variation of (supplementary fig. S4, Supplementary Material online) resulted in a pattern intermediary between the ones obtained when analyzing the data simulated above under the invasion scenarios Inv1 and Inv2 (fig. 2). The distribution of the P values derived from the C2 statistics was well-behaved, being close to uniform for higher P values (supplementary fig. S5A, Supplementary Material online). To account for multiple-testing issues, we used the qvalue R package (Storey and Tibshirani 2003) to compute the individual SNP q values plotted in figure 3B.
A striking feature of the resulting Manhattan plot was the lack of clustering of SNPs with high q values which might be related to a small extent of linkage disequilibrium (LD) across the D. suzukii populations, as expected from their large effective populations sizes Fraimout et al. (2017). We identified 101 SNPs (including three X-linked) that were significant at the 1% q-value threshold (i.e., 1% of these 101 SNPs are expected to be false-positives). As a matter of comparison, we also estimated the BF for association of the (standardized) population allele frequencies with the native or invasive status of the population, that is, under a parametric regression model (Gautier 2015) (supplementary fig. S6A, Supplementary Material online). Out of the 101 significant SNPs previously identified, 80 displayed a BF >20 dB, the threshold for decisive evidence according to the Jeffreys’ rule (Jeffreys 1961). However, in total, 6,406 SNPs displayed a BF >20 dB probably due to an increase of false-positives at this threshold (see above simulations under invasion scenarios). We also compared the C2 statistic with the XtX measure of overall differentiation. The (two-sided) P values derived from the latter were also well behaved (supplementary fig. S5B, Supplementary Material online) and allowed the computation of q values to control for multiple testing. As shown in supplementary figure S6B, Supplementary Material online, at the same 1% q-value threshold for XtX, 71 out of the 101 C2 significant SNPs were significantly differentiated but they represented only a small proportion of the 35,546 significantly differentiated SNPs. This is not surprising since invasion success is obviously not the only selective constraint exerted on the 22 worldwide populations considered here.
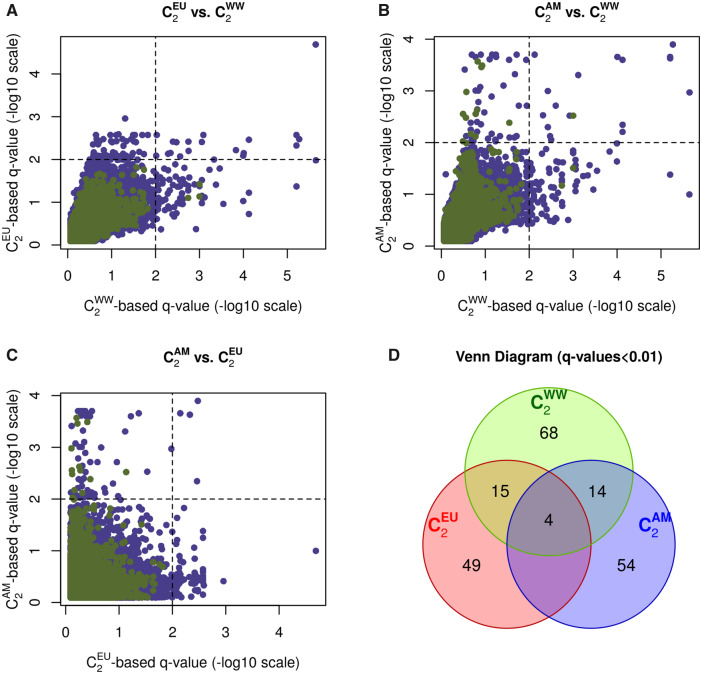
The North-American (plus Brazil) and European (plus La Réunion Island) populations globally represent separate invasion routes that can be considered as two independent invasion replicates (fig. 3A). Interestingly enough, this feature of historical invasion fits well with the overall pattern of structuring of genetic diversity inferred from the matrix estimated with our Pool-Seq data (see above and supplementary fig. S4, Supplementary Material online). To identify signals common or specific to each invasion routes, we estimated the C2 statistic associated with the invasive versus native status focusing either on the native and invasive populations of the European invasion route (), or native and invasive populations of the American invasion route (). Note that the two invasion routes were both represented by eight invasive populations, suggesting similar power for the two and statistics. As observed above, the distribution of P values derived from and were found well behaved (supplementary fig. S5C and D, Supplementary Material online, respectively) and hence q values to control for multiple testing could be confidently computed. The cross-comparisons of the C2 statistics considering the 22 worldwide populations (hereafter denoted ), the and the are plotted in figure 4A ( versus ), B ( versus ), and C ( versus ).
Fig. 4.
Pairwise comparison of the q values derived from the (native vs. invasive Drosophila suzuki populations of the European invasion route) versus the (native vs. worldwide invasive populations) statistics (A), the (native vs. invasive populations of the American invasion route) versus the statistic (B), and the versus the statistics (C). In (A), (B), and (C), the dashed vertical and horizontal lines indicate the 1% q-value threshold for the C2 derived q values. (D) Venn diagram of the number of SNPs significant at the 1% q values among the three contrast analyses ( and ). Values for the autosomal (X-linked) SNPs are plotted in purple (green).
In total, 204 SNPs (detailed in supplementary table S3, Supplementary Material online) were significant in at least one of the three contrasts at the 1% q-value threshold. The overlap among the three different sets of significant SNPs was summarized in the Venn diagram displayed in figure 4D. Among the 68 SNPs significant for the , 15 were also significant for and 49 were not significant in the other tests. Likewise, among the 72 SNPs found significant for the , 14 were also significant for and 54 were not significant in the other tests. Hence, the majority of the significant SNPs identified with either the or the contrasts might be viewed as specific to one of the two invasion routes, the signal being lost in the global worldwide comparison for a substantial proportion of them. This is presumably due to a reduced power resulting from the addition of noninformative populations when computing the statistic. Conversely, 68 SNPs found significant with were neither significant with nor contrasts. These SNPs might correspond to partially convergent signals among the two invasion routes (i.e., the informative populations are distributed among the two routes). Most interestingly, four SNPs were found significant at the 1% q-value threshold in the three contrast analyses ( and ) and might thus be viewed as strong candidates for association with the global worldwide invasion success of D. suzukii.
Annotation of Candidate SNPs
For annotation purposes, we relied on genomic resources available in D. melanogaster, a model species closely related to D. suzukii. More specifically, we extracted from the WT3-2.0 D. suzukii genome assembly 5-kb-long genomic sequences surrounding each of the 204 SNPs identified above and aligned them onto the dmel6 reference genome (Hoskins et al. 2015) using the BLAT algorithm implemented in the program pblat (Wang and Kong 2019). The gene annotation available from the UCSC genome browser (https://genome.ucsc.edu/, last accessed April 2020) allowed us to map 169 SNPs out of the 204 SNPs onto 130 different D. melanogaster genes, 145 SNPs lying within the gene sequences and 24 <2.5 kb apart (our predefined threshold; supplementary table S3, Supplementary Material online). Only one of the four SNPs significant for the three contrasts ( and ) could not be assigned to a D. melanogaster gene, because its derived 5-kb-long sequences aligned onto a D. melanogaster sequence located 10 kb away from the closest annotated gene.
Most of the 130 identified genes (80%) were represented by a single SNP, a feature in agreement with the visual lack of clustering of SNPs with strong signal already observed in the Manhattan plot (fig. 3B). It should be noticed that 14 of the 130 genes (∼11%) were long noncoding RNA. We however decided to focus on the 26 genes that were represented by at least two SNPs significant in one of the three contrast analyses; see table 2 for details. The significant SNPs underlying the different genes tended to be very close, spanning a few bp (span >1 kb for only five genes). In particular, we observed doublet variants (i.e., adjacent SNPs in complete LD) within three genes (cpo, ome, and lnc: CR45759).
Table 2.
Description of the 26 Orthologous Drosophila melanogaster Genes Represented by At Least Two of the 204 SNPs Found Significant for One of the Three Contrast Analyses, (6 native vs. 16 invasive populations), (six native vs. eight invasive populations of the European invasion route), and (six native vs. eight invasive populations of the American invasion route).
| Number of Significant SNPs |
|||||
|---|---|---|---|---|---|
| Drosophila melanogaster Gene (full name) | Position on dmel6 (in kb) | All C2 (dist. in bp) | |||
| Der-1 (Derlin-1) | chr2L:1,974–1,975 | 2 (236) | 1 | — | 1 |
| Gdi (GDP dissociation inhibitor) | chr2L:9,492–9,495 | 4 (342) | 4 | 4 | — |
| lncRNA:CR45693 (long noncoding RNA) | chr2L:14,51–14,512 | 2 (14) | 2 | 1 | — |
| Tpr2 (tetratricopeptide repeat protein 2) | chr2L:16,492–16,507 | 2 (8) | — | 2 | — |
| Ret (Ret oncogene) | chr2L:21,182–21,199 | 2 (70) | 2 | — | — |
| tou (toutatis) | chr2R:11,579–11,616 | 2 (18) | 1 | — | 2 |
| jeb (jelly belly) | chr2R:12,091–12,119 | 2 (14) | 2 | — | — |
| CG5065 | chr2R:16,608–16,625 | 2 (13) | — | 2 | — |
| bab2 (bric a brac 2) | chr3L:1,140–1,177 | 2 (11,189) | 1 | — | 1 |
| axo (axotactin) | chr3L:4,630–4,687 | 2 (25,886) | — | 1 | 1 |
| RhoGEF64C (ρ guanine nucl. exch. fact. at 64 °C) | chr3L:4,693–4,796 | 2 (8) | 2 | 1 | 1 |
| CG7509 | chr3L:4,803–4,805 | 2 (5) | — | 2 | — |
| Con (connectin) | chr3L:4,938–4,976 | 2 (616) | 1 | 1 | — |
| Ets65A (Ets at 65A) | chr3L:6,098–6,124 | 2 (27,998) | 1 | 1 | — |
| lncRNA:CR45759 (long noncoding RNA) | chr3L:6,787–6,787 | 4 (106) | — | — | 4 |
| ome (omega) | chr3L:14,673–14,748 | 2 (1) | 2 | — | — |
| sa (spermatocyte arrest) | chr3L:21,405–21,407 | 2 (61) | 1 | 1 | — |
| yellow-e (yellow-e) | chr3R:13,410–13,415 | 3 (33) | 3 | — | 1 |
| cv-c (crossveinless c) | chr3R:14,392–14,482 | 4 (2,737) | 1 | — | 3 |
| osa (osa) | chr3R:17,688–17,718 | 2 (29) | — | — | 2 |
| cpo (couch potato) | chr3R:17,944–18,016 | 3 (193) | 3 | 2 | 3 |
| Rh3 (rhodopsin 3) | chr3R:20,081–20,082 | 2 (5,709) | 2 | 1 | — |
| Ctl2 (choline transporter-like 2) | chr3R:29,123–29,128 | 2 (3) | — | — | 2 |
| Syt12 (synaptotagmin 12) | chrX:13,359–13,368 | 3 (65) | 1 | — | 2 |
| Ac13E (adenylyl cyclase 13E) | chrX:15,511–15,554 | 4 (19) | — | — | 4 |
| Axs (abnormal X segregation) | chrX:16,680–16,684 | 2 (11) | — | — | 2 |
Note.—The third column gives the overall number of significant SNPs (at the 1% q-value threshold) and their maximal spacing in bp (on the D. suzukii assembly). Columns 4–6 give the number of significant SNPs for each of the three contrast analyses.
Among these 26 candidate genes, 10 and 12 might be considered as specific to the European and American invasion routes, respectively, since they did not contain any SNP significant for the alternative contrasts. Only two genes contained SNPs significant in all three contrast analyses: RhoGEF64C with one SNP and cpo with two SNPs. Such convergent signals of association with invasive status in the two independent invasion routes were particularly convincing. The median allele frequencies (computed from raw read counts) for the reference allele underlying the corresponding RhoGEF64C significant SNP was 0.09 (from 0.00 to 0.44) in the native populations compared with 0.93 (from 0.90 to 0.98) and 0.87 (from 0.59 to 1.00) in the invasive populations of the European and American invasion routes, respectively (supplementary table S3, Supplementary Material online). Similarly, the two SNPs significant for the three contrast analyses in the cpo gene actually formed a doublet with a median reference allele frequency of 0.20 (from 0.02 to 0.33) in the native populations compared with 0.99 (from 0.91 to 1.00, excluding the outlying Hawaiian population) in the invasive populations of the European and American invasion routes, respectively (supplementary table S3, Supplementary Material online). Finally, for both the genes RhoGEF64C and cpo, all D. suzukii extended sequences underlying the corresponding SNPs aligned within potentially rapidly evolving intronic sequences. These sequences nevertheless displayed substantial similarities with other related Drosophila species, as shown in supplementary figure S7, Supplementary Material online, for the gene cpo.
Discussion
We characterized the genome response of D. suzukii during its worldwide invasion by conducting a genome-wide scan for association with the invasive or native status of the sampled populations. To that end, we relied on the newly developed C2 statistic that was aimed at identifying significant allele frequencies differences between two contrasting groups of populations while accounting for their overall correlation structure due to the shared population history. Our approach identified genomic regions and candidate genes most likely involved in adaptive processes underlying the invasion success of D. suzukii.
Overall, we found that a relatively small number of SNPs were significantly associated with the invasive status of D. suzukii populations. This may seem surprising since the binary trait under study (invasive versus native) is complex in the sense that numerous biological differences may characterize invasive and native populations. The invasion process itself, including the associated selective pressures and the genetic composition of the source populations, may actually differ depending on the considered invaded areas. Hence the small number of SNPs showing strong signals of association with the invasive status may stem from the integrative nature of our analysis over a large number of invasive populations from different invasion routes. The genomic features that may be identified under this evolutionary configuration are expected to correspond to major genetic changes instrumental to invasions shared by a majority of populations. Accordingly, it is worth noting that the independent contrast analyses of the two main invasion routes (i.e., the American and the European routes) point to substantially different subsets of SNPs significantly associated with the invasive status of the populations. This suggests that the source populations and some aspects of the invasion process differ in the two invaded areas. This could also reflect the presumably polygenic nature of the traits underlying invasion success since the evolutionary trajectories of complex traits may rely on different combinations of favorable genetic variants.
The availability of a high-quality genome assembly of D. suzukii (Paris et al. 2020) and a large amount of genomic resources for its sister model species D. melanogaster allowed identifying a set of genes associated with the invasive status of populations. A subset of those genes was associated with physiological functions and traits previously documented in D. melanogaster, but for most of them, functional and phenotypic studies turned out to be limited. Their putative role in explaining the invasion success thus remained largely elusive. To avoid too speculative interpretations (Pavlidis et al. 2012), we will not elaborate further on the candidate genes. Yet, we did notice that long noncoding RNAs represent >10% (14 out of 130) of our candidate genes, a feature which may underline a critical role of variants involved in gene regulation to promote short-term response to adaptive constraints during invasion. In addition, two genes RhoGEF64C and cpo contained SNPs that were found to be highly significantly associated with the invasive status in both the European and American invasion routes. Although the function of the RhoGEF64C gene has so far not been extensively studied, several functional and phenotypic studies in other Drosophila species identified genetic variation in the cpo gene associated with traits possibly important for invasion success. For instance, cpo genetic variation was found to contribute to natural variation in diapause in D. melanogaster populations of a North American cline and in populations from the more distantly related species Drosophila montana (Schmidt et al. 2008; Kankare et al. 2010). Moreover, indirect action of selection on diapause, by means of genetic correlations involving cpo genetic variation, was found on numerous other life-history traits in D. melanogaster (Schmidt et al. 2005; Schmidt and Paaby 2008). Specifically, compared with diapausing populations, nondiapausing populations had a shorter development time and higher early fecundity, but also lower rates of larval and adult survival and lower levels of cold resistance.
Both theoretical (Roughgarden 1971) and experimental (Mueller and Ayala 1981) evidence show that traits typical for colonization (i.e., the so-called r-traits; Charlesworth 1994), such as a nondiapausing phenotype, are selected when a population evolves in a new habitat with low densities and low levels of competition. Common garden studies are needed to assess potential differences in key life-history traits (including diapause induction and correlated traits) between native and invasive populations of D. suzukii and to evaluate to which extent these are related to the identified variants (including those within the cpo gene) differentiating the native and invasive populations of this species.
The C2 statistic we developed in the present study appears particularly well suited to search for association with population-specific binary traits. Apart from the invasive versus native status we studied in D. suzukii, numerous examples can be found where adaptive constraints may be formulated in terms of contrasting binary population features, including individual resistance or sensibility to pathogens or host-defense systems (Eoche-Bosy et al. 2017), high- versus low-altitude adaptation (Foll et al. 2014), ecotypes of origin (Westram et al. 2014; Roesti et al. 2015), or domesticated versus wild status (Alberto et al. 2018). In our simulation study using the HsIMM model, the power of the C2 statistic was similar to that of a standard BF obtained after assuming a linear relationship between the (standardized) population allele frequencies and their corresponding binary status. Yet, we found that the robustness of both statistics strongly differed according to the structuring of genetic diversity of the neutral variants. In the analyses of association with the invasion status of the neutral SNPs simulated under the two invasion scenarios we investigated, the BF was the highest for SNPs displaying homogeneous variant allele frequencies in the invasive populations and that were also common in all the populations. In this case, the assumed linear relationship of the population allele frequencies with their invasive or native group membership may result in significantly nonnull regression coefficients, whereas the difference of the mean allele frequencies of both groups (as measured after standardization by the C2 statistic) is not outlying. Conversely, the C2 contrast statistic was the highest for neutral variants that were rare in the native populations and for which allele frequencies were high on an average in the invasive populations, but still displayed high heterogeneity in invasive populations (hence the absence of linear relationship among populations with invasive or native group memberships). It should be noticed that these patterns were observable on raw allele frequencies since we simulated balanced population invasion histories. Because of the different behaviors of the BF criterion and the C2 statistic, combining both metrics may globally help reducing FPRs. Doing so may however substantially reduce power since the two metrics are similarly expected, at least to some extent, to be sensitive to different association signals at truly causal variants. We therefore chose to focus only on the C2 statistic to identify our candidate SNPs associated with invasive status in the D. suzukii populations.
It is worth stressing that C2 has several critical advantages over BF, as well as over any other decision criterion that may be derived from a parametric modeling. From a practical point of view, the C2 estimation does not require inclusion of any other model parameters making it more robust when dealing with data sets including a small number of populations (e.g., <8 populations), the later type of data sets often leading to unstable estimates of BF (unpublished results). In addition, it may easily be derived from only a subset of the populations under study (as we did here when computing the and contrasts specific to each of the two invasion routes), while using the complete design to capture more accurate information about the shared population history. Last, the calibration of the C2 under the null hypothesis represents an attractive property in the context of large data sets since it allows to deal with multiple-testing issues by controlling for false-discovery rate (Francois et al. 2016), via, for example, the estimation of q values (Storey and Tibshirani 2003).
To estimate the C2 statistic, we needed to correct allele frequencies for population structure. To that end, we relied on the Bayesian hierarchical model implemented in the software BayPass that has several valuable properties including 1) the accurate estimation of the scaled covariance matrix of population allele frequencies (), 2) the integration over the uncertainty of the across population allele frequencies (π parameter), and 3) the inclusion of additional layers of complexities such as the sampling of reads from (unobserved) allele counts in Pool-Seq data (Gautier 2015). However, as previously mentioned, the Bayesian hierarchical modeling results in shrinking the posterior means of the (lower level) model parameters (Kruschke 2014) and also related statistics such as, here, the C2 and XtX differentiation statistics. To ensure proper calibration of the two corresponding estimates, we hence needed to rely on the rescaled posterior means of the standardized allele frequencies. This empirical procedure proved efficient in providing well-behaved P values, while avoiding computationally intensive calibration procedure based on the analysis of pseudo-observed data sets simulated under the generative model (Gautier 2015). Still, this did not allow accounting for the uncertainty of the allele frequencies estimation (i.e., their full marginal distribution) and more importantly, it implicitly assumes exchangeability of SNPs both across the populations and along the genome. Such an assumption, which pertains to the null hypothesis of neutral differentiation only (and consequently of no association with binary population-specific covariable), might actually be viewed as conservative even in the presence of background LD across the populations, providing that a reasonably large number of SNPs is analyzed. Interestingly, the almost absence of clustering of associated SNPs we observed in the D. suzukii genome suggested a very limited extent of across-population LD, presumably resulting from large effective population sizes. This conversely led to a high mapping resolution. In practice, when dealing with large data sets, a subsampling strategy consisting in analyzing data sets thinned by marker position also allows further reduction of across-population LD (Gautier et al. 2018). Finally, it should be noticed that information from LD might be at least partially recovered by combining C2 or XtX derived P values into local scores (Fariello et al. 2017).
Other less computationally intensive (but less flexible and versatile) approaches may be considered to estimate the C2 statistic. For instance, the C2 statistic is closely related to the SB statistic recently proposed by Refoyo-Martinez et al. (2019) to identify footprints of selection in admixture graphs. However, although the C2 statistic relies on the full-scaled covariance matrix of population allele frequencies (), the SB statistic relies on a covariance matrix called F (Refoyo-Martinez et al. 2019) that specifies an a priori inferred admixture graph summarizing the history of the sampled populations. The covariance matrix F thus represents a simplified version of that may only partially capture the covariance structure of the population allele frequencies. In addition, to compute SB, the graph root allele frequencies are estimated as the average of allele frequencies across the sampled population, which might result in biased estimates, particularly when the graph is unbalanced. Deriving the matrix F from (Pickrell and Pritchard 2012) might actually allow interpreting C2 as a Bayesian counterpart of the SB statistic, thereby benefiting from the aforementioned advantages regarding the estimation of the parameters Ω and π and allowing proper analysis of Pool-Seq data.
Conclusion and Perspectives
Our genome-wide association approach allowed identifying genomic regions and genes most likely involved in adaptive processes underlying the invasion success of D. suzukii. The approach can be transposed to any other invasive species, and more generally to any species models for which binary traits of interest can be defined at the population level. The major advantage of our approach is that it does not require a preliminary, often extremely laborious, phenotypic characterization of the populations considered (e.g., using common garden experiments) in order to inform candidate traits for which genomic associations are sought. As a matter of fact, in our association study the populations analyzed are simply classified into two categories: invasive or native.
The functional and phenotypic interpretation of the signals obtained by our genome scan methods remains challenging. Such interpretation requires a good functional characterization of the genome of the studied species or, failing that, of a closely related species (i.e., D. melanogaster in our study). Following a strategy sometimes referred to as “reverse ecology” since it goes from gene(s) to phenotype(s) (Li et al. 2008), it is then necessary to test and validate via quantitative genetic experiments whether the inferred candidate traits show significant differences between native and invasive populations. The functional interpretation of the statistical association results can also benefit from experimental validation approaches based on techniques using RNA interference (RNA-silencing, e.g., Janitz et al. 2006) and/or genome editing approaches (Karageorgi et al. 2017) targeting the identified candidate variants. Hopefully, such a combination of statistical, molecular, and quantitative approaches will provide useful insights into the genomic and phenotypic responses to invasion, and by the same, will help better predict the conditions under which invasiveness can be enhanced or suppressed.
Materials and Methods
Simulation Study
We used computer simulations to evaluate the performance of the novel statistical framework described in New Approaches section. A first set of simulated data sets were generated under the SimuPOP environment (Peng and Kimmel 2005) using individual-based forward-in-time simulations implemented on a modified version of the code developed by de Villemereuil et al. (2014) for the so-called HsIMM-C demographic scenario. This corresponded to an highly structured isolation with migration demographic model (fig. 1A) that was divided in two successive periods: 1) a neutral divergence phase leading to the differentiation of an ancestral population into 16 populations after four successive fission events (at generations t = 50, t = 150, t = 200, and t = 300) and 2) an adaptive phase (lasting 200 generations) during which individuals of the 16 populations were subjected to selective pressures exerted by two environmental constraints (ec1 and ec2), each constraint having two possible modalities (a or b). We thus had a total of four possible environments in our simulation setting (fig. 1A).
All the simulated populations consisted of 500 diploid individuals reproducing under random-mating with nonoverlapping generations. From generation t = 150 (with four populations), the migration rate between two populations j and j′ was set to where p is the number of populations in the path connecting j to j' in the population tree. The migration rate between the two ancestral populations from generation t = 50 to t = 150 was set to m = 0.005. For illustration purposes, some of the migration edges were displayed in figure 1A.
Following de Villemereuil et al. (2014), a simulated genotyping data set consisted of 320 individuals (20 per populations) that were genotyped for 5,000 biallelic SNPs regularly spread along ten chromosomes of one Morgan length and with a frequency of 0.5 for the reference allele (randomly chosen) in the root population. Polygenic selection acting during the adaptive phase was simulated by choosing 50 randomly distributed SNPs (among the previous 5,000 ones) that influenced individual fitness according to either the ec1 or ec2 environmental constraints (with 25 SNPs for ec1 and 25 SNPs for ec2).
The fitness of each individual, given its genotype, can be defined at each generation. Let p(o) = j () denote the population of origin of individual o (), and (respectively, ) if the environmental constraint (k = 1, 2) of population j is of type a (respectively, b). Let further denote the local selective coefficient of SNP i such that if the SNP is neutral with respect to and otherwise. The fitness of each individual o (at each generation) given its genotypes at all the SNPs is then defined using a cumulative multiplicative fitness function as:
| (6) |
where is the genotype of individual o at marker i coded as the number of the reference allele (0, 1, or 2).
In a second time, we evaluated the robustness of the new C2 criterion as well as the BF statistic to the occurrence of bottleneck events, as the latter are expected (especially in the context of biological invasion) to strongly impact the genetic variation of populations within invaded areas and between invasive and native areas (Estoup et al. 2016). To this aim, we used the software DIYABC v2.1.0 (Cornuet et al. 2014) to simulate data sets composed of selectively neutral and independent SNP loci under two invasion scenarios depicted in figure 2. The two scenarios roughly mimic the situation of the worldwide D. suzukii invasion (Fraimout et al. 2017) by considering two invaded areas (with eight populations sampled in each area) with two independent primary bottlenecked introductions from two different native populations (among a set of six sampled native populations). The two scenarios differ by the relationships among the invasive populations within each invaded area: 1) in the scenario Inv1 each invasive population of an area derived from the same primarily introduced population with a bottleneck occurring at different time in the past and 2) in the scenario Inv2 the invasive populations of an area are successively founded one after the other with a bottleneck event at each foundation, a process likely to favor allele surfing during geographic range expansion (Excoffier and Ray 2008). A detailed description of the two invasion scenarios with values of the historical and demographical parameters used to simulate the two SNP data sets is provided in figure 2A and B. We used the “Simulate dataset + SNP option” of DIYABC v2.1.0 to generate autosomal SNP genotypes (n = 50 diploid individuals sampled per population) at 250,000 loci under both the scenarios Inv1 and Inv2, following the algorithm by Hudson (2002) which is equivalent to applying a default MAF threshold on the simulated data sets. As a matter of fact, each locus will be characterized by the presence of at least a single copy of a variant over all genes sampled from all studied populations (i.e., pooling all genes genotyped at the locus). We further applied a 1% MAF threshold on the simulated data sets (i.e., similar to that used on real data) before analyzing them using BayPass (hence a total of 165,020 and 152,321 SNPs analyzed with BayPass under the scenarios Inv1 and Inv2, respectively).
Sampling of D. suzukii Populations and DNA Extraction
Adult D. suzukii flies were sampled in the field at a total of 22 localities (hereafter termed sample sites) distributed throughout most of the native and invasive range of the species (fig. 3A and supplementary table S2, Supplementary Material online). Samples were collected between 2013 and 2016 using baited traps (with a vinegar–alcohol–sugar mixture) and sweep nets, and stored in ethanol. Only four of the 22 samples were composed of flies which directly emerged in the lab from fruits collected in the field (supplementary table S2, Supplementary Material online). Native Asian samples consisted of a total of six sample sites including four Chinese and two Japanese localities. Samples from the invasive range were collected in Hawaii (1 sample site), Continental US (6 sites), Brazil (1 site), Europe (7 sites), and the French island of La Réunion (1 site). The continental US (plus Brazil) and European (plus La Réunion Island) populations are representative of two separate invasion routes (the American and European routes, respectively), with different native source populations and multiple introduction events in both invaded areas (Fraimout et al. 2017; see supplementary table S2, Supplementary Material online).
Pool Sequencing
For each of the 22 sampling sites, the thoraxes of 50–100 representative adult flies (supplementary table S2, Supplementary Material online) were pooled for DNA extraction using the EZ-10 spin column genomic DNA minipreps kit (Bio Basic Inc.). Barcoded DNA PE libraries with insert size of ∼550 bp were further prepared using the Illumina Truseq DNA Library Preparation kit following manufacturer protocols using the 22 DNA pools samples. The DNA libraries were then validated on a DNA1000 chip on a Fragment Analyzer (Agilent) to determine size and quantified by qPCR using the Kapa library quantification kit to determine concentration. The cluster generation process was performed on cBot (Illumina) using the Paired-End Clustering kit (Illumina). Each pool DNA library was further paired-end sequenced on a HiSeq 2500 (Illumina) using the Sequence by Synthesis technique (providing 2×125 bp reads, respectively) with base calling achieved by the RTA software (Illumina). The Pool-Seq data were deposited in the Sequence Read Archive repository under the BioProject accession number PRJNA576997.
Raw paired-end reads were filtered using fastp 0.19.4 (Chen et al. 2018) run with default options to remove contaminant adapter sequences and trim for poor quality bases (i.e., with a phred-quality score <15). Read pairs with either one read with a proportion of low-quality bases over 40% or containing more than 5 N bases were removed. Filtered reads were then mapped onto the newly released WT3-2.0 D. suzukii genome assembly (Paris et al. 2020), using default options of the mem program from the bwa 0.7.17 software (Li and Durbin 2009; Li 2013). Read alignments with a mapping quality Phred-score <20 or PCR duplicates were further removed using the view (option -q 20) and markdup programs from the SAMtools 1.9 software Li et al. (2009), respectively.
Variant calling was then performed on the resulting mpileup file using VarScan mpileup2cns v2.3.4 (Koboldt et al. 2012) (options -min-coverage 50 -min-avg-qual 20 -min-var-freq 0.001 -variants-output-vcf 1). The resulting vcf file was processed with the vcf2pooldata function from the R package poolfstats v1.1 (Hivert et al. 2018) retaining only biallelic SNPs covered by >4 reads, <99.9th overall coverage percentile in each pool and with an overall MAF >0.01 (computed from read counts). In total, n = 11,564,472 SNPs (respectively, n = 1,966,184 SNPs) SNPs mapping to the autosomal contigs (respectively, X-chromosome contigs) were used for genome-wide association analysis. The median coverage per pool ranged from 58× to 88× and from 34× to 84× for autosomal and X chromosomes, respectively (supplementary table S2, Supplementary Material online). As previously described (Gautier et al. 2018), the autosomal and X-chromosome data sets were divided into subdata sets of ∼75,000 SNPs each (by taking one SNP every 154 SNPs and one SNPs every 26 SNPs along the underlying autosomal and X-chromosome contigs, respectively).
Genome Scan Analyses
All genome-wide scans were performed using an upgraded version (2.2) of BayPass (Gautier 2015) (available from http://www1.montpellier.inra.fr/CBGP/software/baypass/, last accessed April 2020), that includes the new C2 and XtX statistics estimated as described in New Approaches. We always used the BayPass core model with default options for the MCMC algorithm to obtain estimates of four items: 1) the scaled covariance matrix (); 2) the SNP-specific XtX overall differentiation statistic in the form of both , the posterior mean of XtX (Gautier 2015) and , our newly described calibrated estimator; 3) our novel C2 statistic in the form of the calibrated estimator described above; and 4) BF reported in deciban units (dB) as a measure of support for association with contrasts of each SNP based on a linear regression model (Coop et al. 2010; Gautier 2015). For BF, a value >15 dB (respectively, >20 dB) provides very strong (respectively, decisive) evidence in favor of association according to the Jeffreys’ rule (Jeffreys 1961).
For the D. suzukii data sets, we specified the pool haploid sample sizes, for either autosomes or the X-chromosome (supplementary table S2, Supplementary Material online), to activate the Pool-Seq mode of BayPass. The statistic for the contrast of the six native and 16 worldwide invasive populations was estimated jointly with the and statistics for the contrast of the six native and eight invasive populations of the European and American invasion routes, respectively. For these two latter estimates, this simply amounted to setting cj = 0 (see eq. 3) for all population j not considered in the corresponding contrast analysis. Finally, two additional independent runs (using option -seed) were performed to assess reproducibility of the MCMC estimates. We found a fairly high correlation across the different independent runs (Pearson’s r > 0.92 for autosomal and r > 0.87 and X-chromosome data) for the different estimators and thus only presented results from the first run. Similarly and for each chromosome type (i.e., autosomes or the X chromosome), a near perfect correlation of the posterior means of the estimated matrix elements was observed across independent runs as well as within each run across SNP subsamples, with the corresponding FMD distances (Gautier 2015) being always <0.4. We thus only reported results regarding the matrix that were obtained from a single randomly chosen subdata set analyzed in the first run.
Supplementary Material
Acknowledgments
We wish to thank our three anonymous reviewers for their very helpful and constructive comments. A.E., M.G., and L.O. acknowledge financial support from the National Research Fund ANR (France) through the project ANR-16-CE02-0015-01 (SWING), the Languedoc-Roussillon Region (France) through the European Union Program FEDER FSE IEJ 2014-2020 (project CPADROL), and the INRA Scientific Department SPE (AAP-SPE 2016 and 2018). MGX acknowledges financial support from France Génomique National infrastructure, funded as part of “Investissement d’avenir” program managed by Agence Nationale pour la Recherche (contract ANR-10-INBS-09). We are grateful to the genotoul bioinformatics platform Toulouse Midi-Pyrenees for providing computing resources, Nicolas Rode for useful discussions, and comments on a previous version of the article and Nicolas Ris, Jon Koch, Masahito Kimura, Simon Fellous, Vincent Debat, Marta Pascual, Ruth Hufbauer, Marindia Depra, Isabel Martinez, Pierre Girod, and Maxi Richmond for help in collecting some of the Drosophila suzukii samples.
References
- Adrion JR, Kousathanas A, Pascual M, Burrack HJ, Haddad NM, Bergland AO, Machado H, Sackton TB, Schlenke TA, Watada M, et al. 2014. Drosophila suzukii: the genetic footprint of a recent, worldwide invasion. Mol Biol Evol. 31(12):3148–3163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alberto FJ, Boyer F, Orozco-terWengel P, Streeter I, Servin B, de Villemereuil P, Benjelloun B, Librado P, Biscarini F, Colli L, et al. 2018. Convergent genomic signatures of domestication in sheep and goats. Nat Commun. 9(1):813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Asplen MK, Anfora G, Biondi A, Choi D-S, Chu D, Daane KM, Gibert P, Gutierrez AP, Hoelmer KA, Hutchison WD, et al. 2015. Invasion biology of spotted wing drosophila (Drosophila suzukii): a global perspective and future priorities. J Pest Sci. 88(3):469–494. [Google Scholar]
- Balanya J, Oller JM, Huey RB, Gilchrist GW, Serra L.. 2006. Global genetic change tracks global climate warming in Drosophila subobscura. Science 313(5794):1773–1775. [DOI] [PubMed] [Google Scholar]
- Barrett SCH. 2015. Foundations of invasion genetics: the Baker and Stebbins legacy. Mol Ecol. 24(9):1927–1941. [DOI] [PubMed] [Google Scholar]
- Bock DG, Caseys C, Cousens RD, Hahn MA, Heredia SM, Hubner S, Turner KG, Whitney KD, Rieseberg LH.. 2015. What we still don’t know about invasion genetics. Mol Ecol. 24(9):2277–2297. [DOI] [PubMed] [Google Scholar]
- Bonhomme M, Chevalet C, Servin B, Boitard S, Abdallah J, Blott S, Sancristobal M.. 2010. Detecting selection in population trees: the Lewontin and Krakauer test extended. Genetics 186(1):241–262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Charlesworth B. 1994. Evolution in age-structured populations. Cambridge studies in mathematical biology; 2nd ed. Cambridge: Cambridge University Press. [Google Scholar]
- Chen S, Zhou Y, Chen Y, Gu J.. 2018. Fastp: an ultra-fast all-in-one fastq preprocessor. Bioinformatics 34(17):i884–i890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chiu JC, Jiang X, Zhao L, Hamm CA, Cridland JM, Saelao P, Hamby KA, Lee EK, Kwok RS, Zhang G, et al. 2013. Genome of Drosophila suzukii, the spotted wing Drosophila. G3 (Bethesda) 3(12):2257–2271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cini A, Ioriatti C, Anfora G.. 2012. A review of the invasion of Drosophila suzukii in Europe and a draft research agenda for integrated pest management. Bull Insectol. 65:149–160. [Google Scholar]
- Clemente F, Gautier M, Vitalis R.. 2018. Inferring sex-specific demographic history from SNP data. PLoS Genet. 14(1):e1007191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Colautti RI, Barrett SCH.. 2013. Rapid adaptation to climate facilitates range expansion of an invasive plant. Science 342(6156):364–366. [DOI] [PubMed] [Google Scholar]
- Colautti RI, Lau JA.. 2015. Contemporary evolution during invasion: evidence for differentiation, natural selection, and local adaptation. Mol Ecol. 24(9):1999–2017. [DOI] [PubMed] [Google Scholar]
- Coop G, Witonsky D, Rienzo AD, Pritchard JK.. 2010. Using environmental correlations to identify loci underlying local adaptation. Genetics 185(4):1411–1423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cornuet J-M, Pudlo P, Veyssier J, Dehne-Garcia A, Gautier M, Leblois R, Marin J-M, Estoup A.. 2014. Diyabc v2.0: a software to make approximate Bayesian computation inferences about population history using single nucleotide polymorphism, DNA sequence and microsatellite data. Bioinformatics 30(8):1187–1189. [DOI] [PubMed] [Google Scholar]
- de Villemereuil P, Frichot E, Bazin E, Francois O, Gaggiotti OE.. 2014. Genome scan methods against more complex models: when and how much should we trust them? Mol Ecol. 23(8):2006–2019. [DOI] [PubMed] [Google Scholar]
- de Villemereuil P, Gaggiotti OE.. 2015. A new FST-based method to uncover local adaptation using environmental variables. Methods Ecol Evol. 6(11):1248–1258. [Google Scholar]
- Dlugosch KM, Anderson SR, Braasch J, Cang FA, Gillette HD.. 2015. The devil is in the details: genetic variation in introduced populations and its contributions to invasion. Mol Ecol. 24(9):2095–2111. [DOI] [PubMed] [Google Scholar]
- Ellstrand NC, Schierenbeck KA.. 2000. Hybridization as a stimulus for the evolution of invasiveness in plants? Proc Natl Acad Sci U S A. 97(13):7043–7050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eoche-Bosy D, Gautier M, Esquibet M, Legeai F, Bretaudeau A, Bouchez O, Fournet S, Grenier E, Montarry J.. 2017. Genome scans on experimentally evolved populations reveal candidate regions for adaptation to plant resistance in the potato cyst nematode Globodera pallida. Mol Ecol. 26(18):4700–4711. [DOI] [PubMed] [Google Scholar]
- Estoup A, Ravigne V, Hufbauer R, Vitalis R, Gautier M, Facon B.. 2016. Is there a genetic paradox of biological invasion? Annu Rev Ecol Evol Syst. 47(1):51–72. [Google Scholar]
- Excoffier L, Ray N.. 2008. Surfing during population expansions promotes genetic revolutions and structuration. Trends Ecol Evol. 23(7):347–351. [DOI] [PubMed] [Google Scholar]
- Facon B, Hufbauer RA, Tayeh A, Loiseau A, Lombaert E, Vitalis R, Guillemaud T, Lundgren JG, Estoup A.. 2011. Inbreeding depression is purged in the invasive insect Harmonia axyridis. Curr Biol. 21(5):424–427. [DOI] [PubMed] [Google Scholar]
- Fariello MI, Boitard S, Mercier S, Robelin D, Faraut T, Arnould C, Recoquillay J, Bouchez O, Salin G, Dehais P, et al. 2017. Accounting for linkage disequilibrium in genome scans for selection without individual genotypes: the local score approach. Mol Ecol. 26(14):3700–3714. [DOI] [PubMed] [Google Scholar]
- Foll M, Gaggiotti OE, Daub JT, Vatsiou A, Excoffier L.. 2014. Widespread signals of convergent adaptation to high altitude in Asia and America. Am J Hum Genet. 95(4):394–407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fraimout A, Debat V, Fellous S, Hufbauer RA, Foucaud J, Pudlo P, Marin J-M, Price DK, Cattel J, Chen X, et al. 2017. Deciphering the routes of invasion of Drosophila suzukii by means of ABC random forest. Mol Biol Evol. 34(4):980–996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Francois O, Martins H, Caye K, Schoville SD.. 2016. Controlling false discoveries in genome scans for selection. Mol Ecol. 25(2):454–469. [DOI] [PubMed] [Google Scholar]
- Frichot E, Schoville SD, Bouchard G, Francois O.. 2013. Testing for associations between loci and environmental gradients using latent factor mixed models. Mol Biol Evol. 30(7):1687–1699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frichot E, Schoville SD, de Villemereuil P, Gaggiotti OE, Francois O.. 2015. Detecting adaptive evolution based on association with ecological gradients: orientation matters. Heredity 115(1):22–28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gautier M. 2015. Genome-wide scan for adaptive divergence and association with population-specific covariates. Genetics 201(4):1555–1579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gautier M, Foucaud J, Gharbi K, Cezard T, Galan M, Loiseau A, Thomson M, Pudlo P, Kerdelhue C, Estoup A.. 2013. Estimation of population allele frequencies from next-generation sequencing data: pool-versus individual-based genotyping. Mol Ecol. 22(14):3766–3779. [DOI] [PubMed] [Google Scholar]
- Gautier M, Yamaguchi J, Foucaud J, Loiseau A, Ausset A, Facon B, Gschloessl B, Lagnel J, Loire E, Parrinello H, et al. 2018. The genomic basis of color pattern polymorphism in the Harlequin ladybird. Curr Biol. 28(20):3296–3302.e7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grau J, Grosse I, Keilwagen J.. 2015. PRROC: computing and visualizing precision-recall and receiver operating characteristic curves in r. Bioinformatics 31(15):2595–2597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gunther T, Coop G.. 2013. Robust identification of local adaptation from allele frequencies. Genetics 195(1):205–220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hivert V, Leblois R, Petit EJ, Gautier M, Vitalis R.. 2018. Measuring genetic differentiation from Pool-seq data. Genetics 210(1):315–330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoskins RA, Carlson JW, Wan KH, Park S, Mendez I, Galle SE, Booth BW, Pfeiffer BD, George RA, Svirskas R, et al. 2015. The release 6 reference sequence of the Drosophila melanogaster genome. Genome Res. 25(3):445–458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hudson RR. 2002. Generating samples under a Wright-Fisher neutral model of genetic variation. Bioinformatics 18(2):337–338. [DOI] [PubMed] [Google Scholar]
- Janitz M, Vanhecke D, Lehrach H.. 2006. High-throughput RNA interference in functional genomics. Berlin, Heidelberg (Germany: ): Springer Berlin Heidelberg; p. 97–104. [DOI] [PubMed] [Google Scholar]
- Jeffreys H. 1961. Theory of probability. 3rd ed.Oxford: Oxford University Press. [Google Scholar]
- Kankare M, Salminen T, Laiho A, Vesala L, Hoikkala A.. 2010. Changes in gene expression linked with adult reproductive diapause in a Northern malt fly species: a candidate gene microarray study. BMC Ecol. 10(1):3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karageorgi M, Bracker LB, Lebreton S, Minervino C, Cavey M, Siju KP, Kadow ICG, Gompel N, Prud’homme B.. 2017. Evolution of multiple sensory systems drives novel egg-laying behavior in the fruit pest Drosophila suzukii. Curr Biol. 27(6):847–853. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koboldt DC, Zhang Q, Larson DE, Shen D, McLellan MD, Lin L, Miller CA, Mardis ER, Ding L, Wilson RK.. 2012. Varscan 2: somatic mutation and copy number alteration discovery in cancer by exome sequencing. Genome Res. 22(3):568–576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kruschke J. 2014. Doing Bayesian data analysis. 2nd ed. A tutorial with R, JAGS, and Stan. Amsterdam: Academic Press. [Google Scholar]
- Lee CE. 2002. Evolutionary genetics of invasive species. Trends Ecol Evol. 17(8):386–391. [Google Scholar]
- Lee CE, Gelembiuk GW.. 2008. Evolutionary origins of invasive populations. Evol Appl. 1(3):427–448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H. 2013. Aligning sequence reads, clone sequences and assembly contigs with bwa-mem. arXiv, 1303.3997.
- Li H, Durbin R.. 2009. Fast and accurate short read alignment with Burrows-Wheeler transform. Bioinformatics 25(14):1754–1760. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H, Handsaker B, Wysoker A, Fennell T, Ruan J, Homer N, Marth G, Abecasis G, Durbin R, 1000 Genome Project Data Processing Subgroup. 2009. The sequence alignment/map format and Samtools. Bioinformatics 25(16):2078–2079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li YF, Costello JC, Holloway AK, Hahn MW.. 2008. “Reverse ecology” and the power of population genomics. Evolution 62(12):2984–2994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mueller LD, Ayala FJ.. 1981. Trade-off between r-selection and k-selection in Drosophila populations. Proc Natl Acad Sci U S A. 78(2):1303–1305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ochocki BM, Miller TEX.. 2017. Rapid evolution of dispersal ability makes biological invasions faster and more variable. Nat Commun. 8(1):14315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ometto L, Cestaro A, Ramasamy S, Grassi A, Revadi S, Siozios S, Moretto M, Fontana P, Varotto C, Pisani D, et al. 2013. Linking genomics and ecology to investigate the complex evolution of an invasive Drosophila pest. Genome Biol Evol. 5(4):745–757. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paris M, Boyer R, Jaenichen R, Wolf J, Karageorgi M, Green J, Cagnon M, Parinello H, Estoup A, Gautier M, et al. 2020. Near-chromosome level genome assembly of the fruit pest Drosophila suzukii using long-read sequencing. BiorXiv, 2020.01.02.892844. [DOI] [PMC free article] [PubMed]
- Pavlidis P, Jensen JD, Stephan W, Stamatakis A.. 2012. A critical assessment of storytelling: gene ontology categories and the importance of validating genomic scans. Mol Biol Evol. 29(10):3237–3248. [DOI] [PubMed] [Google Scholar]
- Peng B, Kimmel M.. 2005. simuPOP: a forward-time population genetics simulation environment. Bioinformatics 21(18):3686–3687. [DOI] [PubMed] [Google Scholar]
- Pickrell JK, Pritchard JK.. 2012. Inference of population splits and mixtures from genome-wide allele frequency data. PLoS Genet. 8(11):e1002967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Puzey J, Vallejo-Marin M.. 2014. Genomics of invasion: diversity and selection in introduced populations of monkeyflowers (Mimulus guttatus). Mol Ecol. 23(18):4472–4485. [DOI] [PubMed] [Google Scholar]
- Refoyo-Martinez A, da Fonseca RR, Halldórsdóttir K, Arnason E, Mailund T, Racimo F.. 2019. Identifying loci under positive selection in complex population histories. Genome Res. 29(9):1506–1520. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reznick DN, Losos J, Travis J.. 2019. From low to high gear: there has been a paradigm shift in our understanding of evolution. Ecol Lett. 22(2):233–244. [DOI] [PubMed] [Google Scholar]
- Roesti M, Kueng B, Moser D, Berner D.. 2015. The genomics of ecological vicariance in threespine stickleback fish. Nat Commun. 6(1):8767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roughgarden J. 1971. Density-dependent natural selection. Ecology 52(3):453–468. [Google Scholar]
- Schlotterer C, Tobler R, Kofler R, Nolte V.. 2014. Sequencing pools of individuals – mining genome-wide polymorphism data without big funding. Nat Rev Genet. 15(11):749–763. [DOI] [PubMed] [Google Scholar]
- Schmidt PS, Matzkin L, Ippolito M, Eanes WF.. 2005. Geographic variation in diapause incidence, life-history traits, and climatic adaptation in Drosophila melanogaster. Evolution 59(8):1721–1732. [PubMed] [Google Scholar]
- Schmidt PS, Paaby AB.. 2008. Reproductive diapause and life-history clines in North American populations of Drosophila melanogaster. Evolution 62(5):1204–1215. [DOI] [PubMed] [Google Scholar]
- Schmidt PS, Zhu C-T, Das J, Batavia M, Yang L, Eanes WF.. 2008. An amino acid polymorphism in the couch potato gene forms the basis for climatic adaptation in Drosophila melanogaster. Proc Natl Acad Sci U S A. 105(42):16207–16211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Storey JD, Tibshirani R.. 2003. Statistical significance for genomewide studies. Proc Natl Acad Sci U S A. 100(16):9440–9445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang M, Kong L.. 2019. pblat: a multithread blat algorithm speeding up aligning sequences to genomes. BMC Bioinformatics 20(1):28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weir BS, Cockerham CC.. 1984. Estimating f-statistics for the analysis of population structure. Evolution 38(6):1358–1370. [DOI] [PubMed] [Google Scholar]
- Welles S, Dlugosch K.. 2018. Population genomics of colonization and invasion. In: Rajora O, editor. Population Genomics. Cham City: Springer. p. 655–683.
- Westram AM, Galindo J, Rosenblad MA, Grahame JW, Panova M, Butlin RK.. 2014. Do the same genes underlie parallel phenotypic divergence in different littorina saxatilis populations? Mol Ecol. 23(18):4603–4616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williams JL, Kendall BE, Levine JM.. 2016. Rapid evolution accelerates plant population spread in fragmented experimental landscapes. Science 353(6298):482–485. [DOI] [PubMed] [Google Scholar]
- Wu N, Zhang S, Li X, Cao Y, Liu X, Wang Q, Liu Q, Liu H, Hu X, Zhou XJ, et al. 2019. Fall webworm genomes yield insights into rapid adaptation of invasive species. Nat Ecol Evol. 3(1):105–115. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.