An Improved Anticancer Drug-Response Prediction Based on an Ensemble Method Integrating Matrix Completion and Ridge Regression

Abstract

In this study, we proposed an ensemble learning method, simultaneously integrating a low-rank matrix completion model and a ridge regression model to predict anticancer drug response on cancer cell lines. The model was applied to two benchmark datasets, including the Cancer Cell Line Encyclopedia (CCLE) and the Genomics of Drug Sensitivity in Cancer (GDSC). As previous studies suggest, the dual-layer integrated cell line-drug network model was one of the best models by far and outperformed most state-of-the-art models. Thus, we performed a head-to-head comparison between the dual-layer integrated cell line-drug network model and our model by a 10-fold crossvalidation study. For the CCLE dataset, our model has a higher Pearson correlation coefficient between predicted and observed drug responses than that of the dual-layer integrated cell line-drug network model in 18 out of 23 drugs. For the GDSC dataset, our model is better in 26 out of 28 drugs in the phosphatidylinositol 3-kinase (PI3K) pathway and 26 out of 30 drugs in the extracellular signal-regulated kinase (ERK) signaling pathway, respectively. Based on the prediction results, we carried out two types of case studies, which further verified the effectiveness of the proposed model on the drug-response prediction. In addition, our model is more biologically interpretable than the compared method, since it explicitly outputs the genes involved in the prediction, which are enriched in functions, like transcription, Src homology 2/3 (SH2/3) domain, cell cycle, ATP binding, and zinc finger.

Graphical Abstract

This study proposed an ensemble learning method, simultaneously integrating a low-rank matrix completion model and a ridge regression model to predict anticancer drug response on cancer cell lines. The model was effectively applied to two benchmark datasets. It also explicitly outputs the genes involved in the prediction, which are enriched in functions.

Introduction

Due to its direct impact on the therapy of cancer patients, the accurate assessment of the anticancer drug response of an individual is essential for precision medicine. It has been reported that many genomic biomarkers are closely related to drug response, and patients sometimes benefit from these biomarkers in clinical trials.^1,2 However, human tissue samples are usually heterogeneous in cellular compositions,³ which makes it difficult to predict drug response at the tissue level. A compromised strategy is to study drug response at the cancer cell line level. During the past decade, many large-scale drug screenings have been performed on cultured human cancer cell line panels, including the National Cancer Institute (NCI)-60 study,⁴ connectivity map,⁵ Cancer Cell Line Encyclopedia (CCLE),⁶ Genomics of Drug Sensitivity in Cancer (GDSC) project,⁷ and more recently, Cancer Target Discovery and Development (CTD2) Project.^8,9

These large compendia of genomic and pharmacological data have provided a basis as well as an unprecedented opportunity to infer functional biomarkers associated with drug sensitivity. For example, Geeleher et al.¹⁰ studied variability in general levels of drug sensitivity in preclinical models to improve cancer biomarker discovery. By studying the expression patterns of 48 ATP-binding cassette (ABC) transporters on 60 cancer cell lines during the treatment of 1,429 anticancer drugs, Szakács et al.¹¹ confirmed the correlation between ABC transporter genes and the response of cytotoxic drugs in cancer cell lines. Through systematic analyses on 130 anticancer drugs and 639 human tumor cell lines, Garnett et al.⁷ identified several fusion genes, like EWS-FLI1, to be poly (ADP-ribose) polymerase (PARP) inhibitors. We applied a modified linear regression model to the CCLE data and identified several to hundreds of genes associated with the response of 24 anticancer drugs, respectively.¹² These findings emphasize the need for the use of molecular information to predict drug response and thus optimize personalized cancer therapy.

Provided with drug-response-associated genes, it is usually feasible to predict computationally the responses of cancer cell lines on anticancer drugs, which are often quantified by the activity area (the area above the fitted dose-response curve), IC₅₀ (the concentration of an anticancer drug to kill one-half inhibitory concentration of cancer cells), EC₅₀ (the concentration of an anticancer drug that gives half-maximal effective concentration cancer cell killing effect), or AUC (the area under the nonlinear dose-response curve).⁶ Generally speaking, a drug-response prediction problem mainly includes the sensitivity estimation of single compounds,⁶ sensitive or resistant prediction of either a particular drug class or a specific cancer type,¹³ and sensitivity prediction of a combination of several drugs.¹⁴ Among the three typical problems, single drug sensitivity prediction is the simplest, for which various computational methods have been developed recently. These methods primarily rely on regression, classification, heterogeneous network, multiple kernel learning, or ensemble/model selection. For example, Zhang et al.¹⁵ developed a dual-layer integrated cell line-drug network, consisting of both drug similarity network and cell line similarity network; verified the assumption that similar cell lines and similar drugs exhibit similar responses; and presented network-based models to estimate anticancer drug responses of cell lines.¹⁶ Based on this assumption, Liu et al.¹⁷ and Zhang et al.¹⁸ formulated a drug-response prediction as a recommender system problem, which was solved by two proposed techniques, respectively: the neighbor-based collaborative filtering with global effect removal method and the hybrid interpolation weighted collaborative filtering method; Wang et al.¹⁹ and Guan et al.²⁰ applied novel matrix factorizations with similar restrictions to infer anticancer drug response in cell lines. Despite the relative good-prediction performances of network or matrix factorization-based methods, most of them are uninterpretable in the sense that they provide very little information on what genes/biomarkers are associated with drug responses. In contrast, more interpretable models, like the Elastic-Net model used in the original CCLE paper, are usually poor in prediction accuracy. The readers are referred to Azuaje²¹ for a systematical summarization of key strategies, resources, techniques, challenges, and trends in this area.

In summary, recent progress in computational techniques has significantly improved anticancer drug-response prediction and contributed to preclinical drug screening.^22,23 However, highly accurate yet biologically interpretable models are still in demand. In this paper, we proposed an ensemble learning method, simultaneously integrating a low-rank matrix completion (MC) model and a ridge regression (RR) model, and applied it into two benchmark datasets, including CCLE and GDSC. Comparison with other methods suggests that our model achieves both high prediction accuracy and good biological interpretability simultaneously.

Results

Parameter Optimization

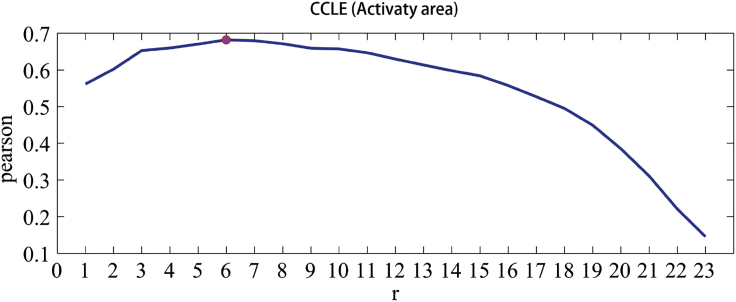
The MC model contains two parameters: ${\theta }_1$ and$r$. ${\theta }_1$ varied from 0 to 1 with an increment of 0.01, and $r$ varied with an increment of 1 from 1 to 24 for CCLE, 1 to 28 for phosphatidylinositol 3-kinase (PI3K) pathway, and 1 to 30 for extracellular signal-regulated kinase (ERK) signaling pathway, respectively. Figure 1 shows the trend of Pearson correlation coefficients (PCCs) between predicted and observed response values with an increase of $r$ for CCLE—first increases, then achieves it maximum at$r=6$, and decreases after that. Similar trends were observed for other two datasets (see Figure S1). The detail information about ${\theta }_1$ and $r$ in all three datasets was listed in Table S1.

Figure 1.

The Parameter $\mathit{r}$ Optimization for the MC Model in CCLE

The horizontal axis denotes the rank number, and the vertical axis denotes the Pearson correlation between predicted and observed response values.

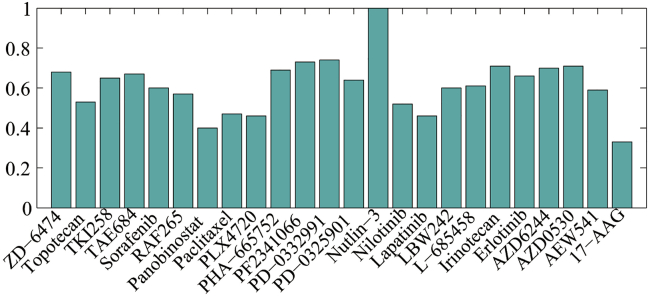
For the RR model, we selected $0.11\le \widehat{{\sigma }_k}\le 0.37$ for CCLE and $0.1\le \widehat{{\sigma }_k}\le 0.3$ for both the PI3K pathway and ERK signaling pathway. The detailed information about $\widehat{{\sigma }_k}$ for three datasets was shown in Tables S2A–S2C, respectively. ${\tau }_k$ ranged over [$\widehat{{\sigma }_k}-0.1$, $\widehat{{\sigma }_k}+0.1$] with an increment of 0.01, and ${\theta }_2$ ranged over [0, 2 × 10⁵] with an increment of 10. For the combination model, the weight parameter ${\beta }_k$ ranged over [0, 1], with an increment of 0.01. The detailed information about${\tau }_k$, ${\theta }_2$, and ${\beta }_k$ for three datasets was shown in Tables S3A–S3C, respectively. ${\beta }_k$ is greater than 0.5 for 79% of 24 drugs in CCLE, especially, ${\beta }_k=1$ for nutlin-3 (see Figure 2 for a more intuitive illustration). The results confirmed that the MC model plays a more important role than the RR model for most drugs in the combination model. Similar observations could be found in Figure S2: ${\beta }_k\ge 0.5$ for 61% of 28 drugs in PI3K and for 63% of 30 drugs in ERK, however ${\beta }_k=0.18$ for the drug FTI-277 in ERK, which illustrated a weak contribution of MC to the final prediction.

Figure 2.

The Weight Parameter β_k Optimization for the Combination Model in CCLE

Prediction Performance of the Proposed Models

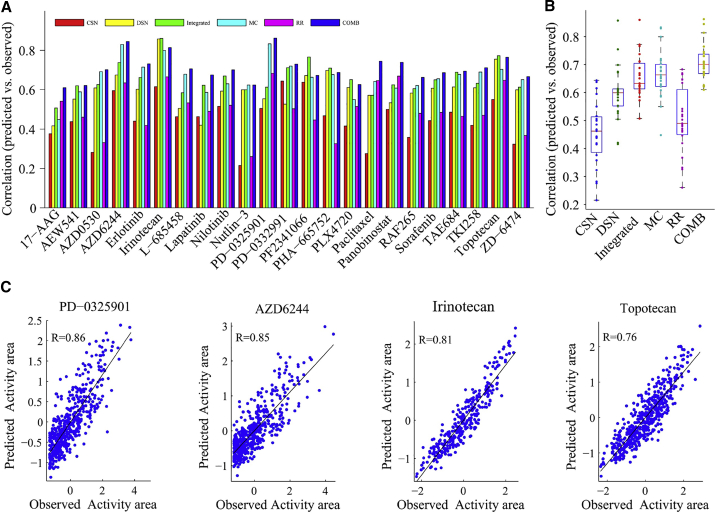
We first applied our models to the CCLE dataset. It has been reported that the prediction accuracy of the dual-layer integrated cell line-drug network model (abbreviated as the integrated model) is significantly higher than some models (cell line similarity network [CSN], drug similarity network [DSN], elastic net model, random forest, support vector regression, and prediction of drug response through an iterative sure independence screening [DISIS]).^15,24 Here, we compared CSN, DSN, and the integrated model, based on the PCC. Figure 3A showed the comparison for CCLE. As can be seen, the PCCs of 23 drugs obtained by the combination model are all higher than 0.6, 11 drugs higher than 0.7, and 3 drugs higher than 0.8 and superior to the integrated model for 78% of 23 drugs, especially the drug PD-0325901, in which its PCC reaches 0.86. In fact, the MC model alone is already superior to the compared models and got higher correlations than CSN, DSN, and the integrated model for 100%, 78%, and 52% drugs, respectively. Obviously, the combination model is superior to both MC and RR, which demonstrated that the correlations among drugs and the relationships between drug-response and gene-expression profiles are both important to prediction. For a better view, we exhibited an overall prediction comparison across 23 drugs (see Figure 3B) and also supplied scatterplots of four example drugs (see Figure 3C).

Figure 3.

Prediction Performance Analysis of the Combination Model in CCLE

(A) Bar graph showing the Pearson correlations between the predicted and observed activity areas of six different models for 24 drugs. CSN, based on the cell line similarity network; DSN, based on the drug similarity network; Integrated, based on the dual-layer integrated cell line-drug network model that integrates CSN and DSN; MC, based on the matrix completion model; RR, based on the ridge regression model; COMB, based on the MC-RR combination model. (B) Boxplot showing the Pearson correlation distributions of six models. (C) Scatterplots of observed and predicted responses for four example drugs using the combination model.

For two other datasets in GDSC, the combination model also exhibited good performance, superior to the integrated model for 93% of 28 drugs in PI3K and 87% of 30 drugs in ERK. Other comparison details for CSN and DSN were shown in Table 1. Notably, for the drug OSI-906, the combination model achieves 66% and 58% higher correlation than the integrated model in PI3K and ERK, respectively (see Figure S3). Meanwhile, the scatterplots (see Figure S4) of four example drugs from two datasets confirmed that the good performance of the combination model is not affected by a small number of outliers. In addition, the MC model is better than CSN, DSN, and the integrated model for about 90%, 90%, and 70% drugs in two datasets (see Table S4). The RR model is superior to CSN for the PI3K dataset but worse than DSN and significantly worse than the integrated model for all datasets (see Table S5). The boxplots (see Figure S5) showed the correlation comparison among six different models in two datasets, consistent with the above conclusions.

Table 1.

Prediction Comparison of the Combination Model with CSN, DSN, and the Integrated Models in Two Datasets (the Entry Is the Percentage of Drugs in the Dataset in Which the Correlations Are Higher Than That of the Compared Model)

Dataset	>CSN (%)	>DSN (%)	>Integrated (%)
PI3K	96	96	93
ERK	100	93	87

It is of note that there are other prediction models that consider various, additional information. For example, Stanfield et al.²⁵ integrated cell line mutation data and protein-protein interaction. HNMDRP, a heterogeneous network-based method, introduced cell line genomic profile, drug chemical structure, and drug-target and protein-protein interaction.²⁶ Due to the different data information, we here did not compare with them.

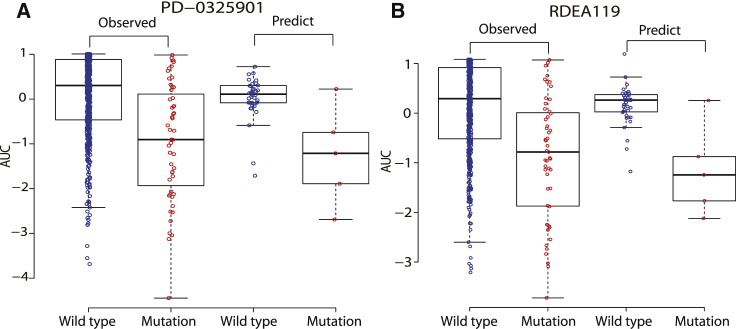
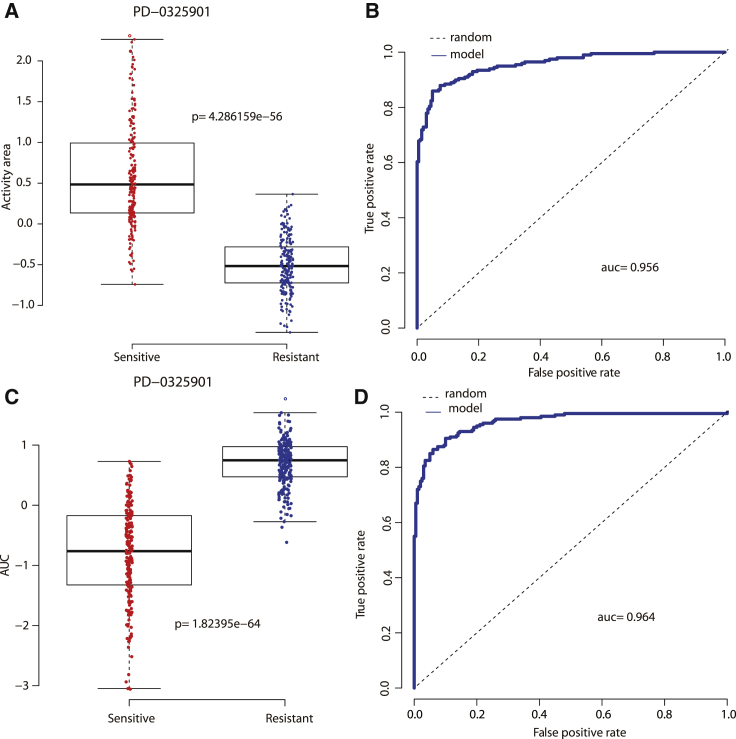
The common techniques to further test the predictive power of a model are to assess its reliability in identifying the estimation of missing data and to evaluate its ability in classifying cell lines sensitive or resistant to a specific drug. The estimation of missing data is considered to be reliable if they exhibit a consistent distribution pattern with that of observed data. Following this rule, we discussed two MEK inhibitors, PD-0325901 and RDEA119, in GDSC, for which about 7% response values are missing across all cell lines. We utilized p value to illustrate “consistent pattern” statistically. As is shown in Figure 4, the observed response values of wild cell lines are significantly higher than that of BRAF mutant cell lines when treated with both PD-0325901 (p = 7.75e−07) and RDEA119 (p = 6.39e−07). Consistently, the predicted (missing) response values of wild cell lines are also significantly higher than that of BRAF mutant cell lines when treated with both PD-0325901 (p = 0.04841) and RDEA119 (p = 0.02999). In summary, BRAF mutant cell lines are more sensitive to MEK inhibitors than wild cell lines, which is in agreement with published literature.15, 16, 17 In addition, with the use of a similar method in Wei et al.,¹⁶ Dong et al.,²⁷ and Staunton et al.,²⁸ we ranked cell lines for each drug according to the observed response values. Specifically, we referred to the top 200 cell lines as “sensitive,” the bottom 200 cell lines as “resistant,” and the remaining cell lines as “intermediate,” which were removed from our analysis. Based on this criterion, we discussed that the cell line is sensitive or resistant to a specific drug based on the predicted response values of the combination model and obtained better results than our previous study.¹⁶ Figure 5 illustrated the desired cell line-type recognition to the example drug PD-0325901 in two datasets, with accuracy = 0.885, AUC = 0.956 (the area under the receiver operating characteristic [ROC] curve), and p = 4.286159e−56 in CCLE, and accuracy = 0.9, AUC = 0.964, and p = 1.82395e−64 in GDSC. The detailed cell line type to PD-0325901 in CCLE, identified by the combination model, was listed in Table S6. We found that many non-small cell lung carcinoma (NSCLC) cell lines (such as A549, CAL12T, NCIH1299, NCIH23) and NRAS mutant cell lines (such as CHP212, IPC298, SKMEL2, HUT78, HDMYZ, SKNAS, TT2609C02, HEC151, HT1080, NCIH1299, KMM1) are more sensitive to PD-0325901, in agreement with the previous studies.^6,29 It is well known that activating mutations in NRAS are top predictors of sensitivity for the MEK inhibitor PD-0325901.²

Figure 4.

Consistent Drug-Response Patterns between Predicted (Missing) and Observed (Existing) Data for the BRAF Mutant and Wild Cell Lines When Treated with Two MEK Inhibitors in GDSC

(A) The responses of the BRAF mutant and wild cell lines to PD-0325901. (B) The responses of the BRAF mutant and wild cell lines to RDEA119.

Figure 5.

The Results of Cell Line-Type Recognition (Sensitive or Resistant) to an Example Drug PD-0325901, Respectively, in Two Datasets

(A) Boxplot of type recognition for PD-0325901 in CCLE. (B) ROC curve of type recognition for PD-0325901 in CCLE. (C) Boxplot of type recognition for PD-0325901 in GDSC. (D) ROC curve of type recognition for PD-0325901 in GDSC.

Drug-Response-Associated Genes and Their Function Enrichment Analyses

We assembled the top 1,000 genes for each drug in three datasets based on the RR model (see Table S7). Interestingly, many of the selected genes are well-known drug-sensitivity biomarkers. For example, NQO1, in which its expression produces a high-potency intermediate (17-AAGH2), was identified as the top-most predictive feature for the response of the heat shock protein 90 (HSP90) inhibitor 17-AAG. This finding is consistent with other literature.^6,7,30,31 SPRY2, which encodes a regular of MAPK output, was also verified as the top predictive feature for the MEK inhibitors PD-0325901 and AZD6244.^2,6,7 SLFN11—with the top-most features of two DNA topoisomerase I inhibitors, irinotecan and topotecan—was also known to be associated with the sensitivity of two drugs.⁶ In addition, SLFN11 was observed to be associated with the response of microtubule-stabilizing agent paclitaxel, which is cytotoxic, as are irinotecan and topotecan. It was suggested that topoisomerase I inhibitors and microtubule-stabilizing agents might offer an effective treatment option for some cancer type. There were other top predictors, including ERBB2 and HGF, for the epidermal growth factor receptor (EGFR)/HER2 inhibitor lapatinib^6,7,32 and mesenchymal-epithelial transition (MET)/anaplastic lymphoma kinase (ALK) inhibitor PF-2341066.^6,33 Top genes IGF1R, EGFR, and MDM2 have been demonstrated to be associated with the response of the IGF-1R inhibitor AEW541,^6,34 EGFR inhibitor erlotinib,^6,35 and MDM2 inhibitor nutlin-3,^6,36 respectively. Notably, PTEN expression was significantly correlated with 13 drug sensitivities in CCLE, which indicated that PTEN expression might inform the therapeutic selectivity of many anticancer drugs.

Besides the aforementioned gene features, we also detected many other drug-response-related genes not mentioned in Barretina et al.⁶ but that played significant roles in our RR model. For example, BCL11A, a transcriptional repressor that inhibits expression of fetal globin genes in adults and a potential therapeutic target for the treatment of globinopathies,³⁷ was related to 6 drug responses in CCLE. BCL11B, closely correlated to BCL11A, was also a common valuable feature gene for 4 drugs. FAM19A1, belonging to a novel secreted family with conserved cysteine residues and restricted expression in the brain,³⁸ was identified as the top predictor for the gamma-secretase inhibitor L-685458 and MDM2 inhibitor nutlin-3. DPEP3, encoding a membrane-bound glycoprotein from the family of dipeptidases involved in hydrolytic metabolism of various dipeptides, made the highest contributions to the sensitivities of multi-kinase inhibitors sorafenib and TKI258. ENPP6, highly expressed in liver sinusoidal endothelial cells and developing oligodendrocytes,³⁹ was verified as the top predictor for IGF-1R inhibitor AEW541, ALK inhibitor TAE684, and multi-kinase inhibitor TKI258. PPIA, a key target for treating APOE4-mediated neurovascular injury and the resulting neuronal dysfunction and degeneration,⁴⁰ not only had the top 2 features for histone deacetylase (HDAC) inhibitor panobinostat and DNA topoisomerase I inhibitor irinotecan but also closely associated with 5 drug responses in CCLE, which indicated that PPIA might be involved in some fundamental mechanisms of the multi-drug targeting process. APOL4, which may play a role in lipid exchange and transport throughout the body, as well as in reverse cholesterol transport from peripheral cells to the liver, also exhibited substantial connections with the sensitivity of vascular endothelial growth factor receptor (VEGFR) and EGFR inhibitor ZD-6474, Abl inhibitor nilotinib, and Src and Abl inhibitor AZD0530. All of these prioritized genes could act as candidate biomarkers of drug sensitivity and might ultimately be useful for the deployment of targeted therapies in cancer.

We also performed function enrichment analyses of drug-response-associated genes by the Database for Annotation, Visualization and Integrated Discovery (DAVID) tools⁴¹ (https://david.ncifcrf.gov/home.jsp) and listed the terms with Benjamini false discovery rate (FDR) less than 0.05 in Table S8. The word cloud plot of the 186 functions existing in at least 2 drugs in CCLE was drawn in Figure 6. Clearly, many functions have a close relationship with cancers. For example, “transcription” and “transcription regulation” were the two most significant terms and enriched in 11 drugs, respectively. It has been reported that changes in certain genes during transcription play an important role in cancer development.⁴² “mRNA processing” and “SH2” (Src homology 2) domain were the second most enriched terms. The mechanisms of 3′ end mRNA processing and of its regulation are highly relevant both in biology and in medicine.⁴³ SH2 domain, a structurally conserved protein domain, is important to the treatment of breast cancer.⁴⁴ Besides the gene functions mentioned above, “RNA binding” and “zinc” also deserve attention. Alterations in the expression and function of RNA-binding proteins amplify the effects of cancer driver genes, accelerate tumor progression, and promote aggressiveness.⁴⁵ Zinc supplementation should have beneficial effects on cancer by decreasing angiogenesis and induction of inflammatory cytokines while increasing apoptosis in cancer cells.⁴⁶

Figure 6.

The Word Cloud Plot of 186 Functional Annotations Occurring in at Least 2 out of 24 Drugs in CCLE

The word cloud plots of the enriched gene functions for two other datasets were shown in Figure S6. As an example, the term “kinase” was enriched in multiple drugs. It has been discovered that receptor tyrosine kinases (RTKs) play key roles in growth, metabolism, adhesion, motility, death, and oncogenesis;⁴⁷ protein kinases are critical in many cellular processes;⁴⁸ and the Src family of protein tyrosine kinases is also related with oncogenesis, proliferation, and survival.⁴⁹ In addition, several other top enriched gene functions have also been verified to associate with cancers, such as ATP binding, which plays a role in human breast cancer drug resistance;⁵⁰ cell membrane, an adjuvant in cancer therapy;⁵¹ nucleotide binding, contributing to cancer cell radioresistance;⁵² cell junction molecules, which are diagnostic and prognostic markers;⁵³ and SH3 domain, a potential target for anticancer drug design.⁵⁴ In a word, these results showed that the drug-response-related genes prioritized by the RR model indeed are involved in various biological activities of carcinomas.

Discussion

The aim of this study is to utilize gene-expression profiles of cell lines and observed cell line-drug responses to predict known/unknown anticancer drug sensitivities. To our best knowledge, it is the first time to model the drug-response prediction as a combination of MC and RR, for which MC is superior in prediction sensitivity, whereas RR presents biological interpretable results. As expected, the combination model outperforms a popular integrated model in three tested data. To improve the prediction performance further, one direction is to introduce more drug-response-associated features, for example, the information of chemical structure of drugs and the genomic information of cell lines, including gene mutation and copy variation number.^27,55 The other possible direction is to incorporate more efficient mathematical models. The performance of an ensemble method usually increases with the number of predictors. However, it is out of the scope of this study.

Based on the RR model, we consistently found many important drug-response-associated genes. For example, SLFN11 is one of the top genes inferred by our model, which has been demonstrated to be topoisomerase inhibitors.⁶ Furthermore, functional analyses prioritized transcription, SH2/3 domain, “cell cycle,” “ATP binding,” and “zinc finger” as top functions enriched in drug-response-associated genes, which is also consistent with previous literature. However, the finding that AHR expression is strongly correlated with sensitivity of the MEK inhibitor PD-0325901 in Barretina et al.⁶ was not observed in our work. It might be caused by the different feature selection methods. To enhance the identification of strong biomarkers of the RR model, further attention should be paid on gene screening. In addition, as we all know, many genes function corporately. Thus, it might be better to add this information by adopting a group feature-based model, like group lasso.

Finally, we compared prediction results of 19 common drugs in PI3K and ERK signaling pathways based on AUC (see Figure S7). Most drugs have different correlations between predicted and observed response values in two pathways under three models. The disagreements are mainly from three aspects, including different cell line-drug-response matrices, different sample groups of 10-fold crossvalidation, and different final screened genes corresponding to two pathways. It is interesting that the disagreements derived by the combination model are the lowest, which indicates, to a certain degree, that the combination model usually produces a more stable prediction.

Materials and Methods

Datasets

The CCLE⁶ and GDSC⁷ projects provide two most important publicly available resources for investigating the anticancer drug response in which drug responses of several hundred cancer cell lines, together with their genomic and transcriptomic information, including gene expression, mutation, and copy number variation, were profiled. For CCLE (https://portals.broadinstitute.org/ccle), there are 491 cancer cell lines with both drug-response profiles of 24 anticancer drugs (measured by the activity area, the more sensitive cell lines will get higher activity areas to a drug) and expression profiles of 18,900 genes available. Specifically, the cell line-drug-response information can be formulated as a matrix of size 491 × 24 (11,784 entries) with row representing cell lines and column representing drugs, among which 424 (3.6%) are missing values. For GDSC (release-5.0; https://www.cancerrxgene.org), there are 655 cancer cell lines with both responses of 140 drugs (measured by AUC, the more sensitive cell lines will get lower AUC values to a drug) and expression profiles of 12,072 genes available. The drug-response profile can be formulated as a matrix of size 655 × 140 (91,700 entries), among which 18,029 (19.66%) are missing. Our data and software are publicly available at https://zenodo.org/record/1325121#.W2IiA1i0Xcs.

The MC Model

MC is a traditional mathematical model that has been applied in many fields, such as influenza antigenic cartography^56,57 and microRNA (miRNA)-disease association.^58,59 The aim of MC is to impute the missing entries in an incomplete matrix by taking the advantages of the relationships among row vectors and column vectors. Thus, the anticancer drug-response prediction can be formulated as the MC problem. We first replaced all missing values in the observed cell line-drug-response matrix with 0, and then standardized each column by Z scores to derive the normalized matrix denoted by $\mathbf{M}={\left[M_{ik}\right]}_{m\times p}$, where$m$ is the number of cell lines, and $p$ is the number of drugs. Let $E=\left\{\left(i,k\right)|M_{ik}\ne 0,i\in \left[m\right],k\in \left[p\right]\right\}$, here $\left[m\right]=\left\{1,2,\cdots ,m\right\}$ and$\left[p\right]=\left\{1,2,\cdots ,p\right\}$, and let $\mathbf{Z}={\left[Z_{ik}\right]}_{m\times p}$ denote the underlying cell line-drug-response matrix. Then we could use the following optimization problem to estimate the drug-response matrix,

$$\begin{array}{c}\min \frac{1}{2}\sum _{\left(i,k\right)\in E}{(Z_{ik}-M_{ik})}^2+{\theta }_{1}G\left(\mathbf{Z}\right)\\ s.t.\mathbf{Z}=U_{m\times r}{\text{Σ}}_{r\times r}{\left(V_{p\times r}\right)}^{\text{T}}\end{array}$$ (1)

where ${\theta }_1$ is a model parameter. Similar to previous studies,^56,57 the regularization function is$G\left(\mathbf{Z}\right)=\sum _{i=1}^{m}g\left(\frac{\parallel U^i{\parallel }^2}{3\alpha r}\right)+\sum _{k=1}^{p}g\left(\frac{\parallel V^i{\parallel }^2}{3\alpha r}\right)$, where$g\left(z\right)=e^{{(z-1)}^2}-1$ when $z\ge 1$, and $g\left(z\right)=0$otherwise. $U^i\left(V^i\right)$ denotes the $i$^th row of $U\left(V\right)$, and$\text{α}=\max (m,p)$.

We utilized the alternating gradient descend (AGD) algorithm⁵⁶ to solve the problem (Equation 1) by the following steps.

• (1)Trimming: randomly assign some observed values to 0s from a row (column) in $\mathbf{M}$ when the row (column) contains more than $\left(2\left|E\right|/m\right)\left(2\left|E\right|/p\right)$ observed values, and denote the resulted matrix by ${\mathbf{M}}^{\left(0\right)}.$
• (2)Initialization: do singular value decomposition ${\mathbf{M}}^{\left(0\right)}=U\text{Σ}{V}^T$. Set $U^{\left(0\right)}=U_0\text{∗}\sqrt{m}$ and $V^{\left(0\right)}=V_0\text{∗}\sqrt{m}$, where $U_0$ and $V_0$ are the first $r$ columns of $U$ and $V,$ respectively.
• (3)Iteration:

• (a) Fix $U^{\left(k\right)}$ and $V^{\left(k\right)}$, and calculate the matrix ${\text{Σ}}_{r\times r}$ to minimize the squared error

$$\frac{1}{2}\sum _{\left(i,k\right)\in E}{(Z_{ik}-M_{ik})}^2$$

• (b)Set $U^{\left(k+1\right)}=U^{\left(k\right)}+t\ast {\nabla }_{U^{\left(k\right)}}$ and $V^{\left(k+1\right)}=V^{\left(k\right)}+t\ast {\nabla }_{V^{\left(k\right)}}$.
• (c)Repeat (a) and (b) until they converge or reach predetermined iteration times.

$$\mathrm{H}\mathrm{e}\mathrm{r}\mathrm{e},\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{o}\mathrm{s}\mathrm{e}U=\left[\begin{array}{ccc}{a}_{11}& \cdots & a_{1r}\\ ⋮& \ddots & ⋮\\ a_{m1}& \cdots & a_{mr}\end{array}\right]\mathrm{a}\mathrm{n}\mathrm{d}V=\left[\begin{array}{ccc}{b}_{11}& \cdots & b_{1r}\\ ⋮& \ddots & ⋮\\ b_{p1}& \cdots & b_{pr}\end{array}\right]$$

Then,

$${\nabla }_U=\left({\left(U\text{Σ}{V}^{\text{T}}\right)}^E-\mathbf{M}\right)V{\text{Σ}}^{\text{T}}+U{Q}_U+{\theta }_1\frac{4}{3\alpha r}{U}_{\nabla }$$

$${\nabla }_V={\left({\left(U\text{Σ}{V}^{\text{T}}\right)}^E-\mathbf{M}\right)}^{\text{T}}U\text{Σ}+V{Q}_V+{\theta }_1\frac{4}{3\alpha r}{V}_{\nabla }$$

$$\text{where}{\text{Q}}_U=\frac{1}{m}{U}^{\text{T}}\left(\mathbf{M}-{\left(U\text{Σ}{V}^{\text{T}}\right)}^E\right)V{\text{Σ}}^{\text{T}},{\text{Q}}_V=\frac{1}{p}{V}^{\text{T}}{\left(\mathbf{M}-{\left(U\text{Σ}{V}^{\text{T}}\right)}^E\right)}^{\text{T}}U\text{Σ}$$

$$U_{\nabla }=\left[\begin{array}{ccc}{a}_{11}{e}^{{(\frac{a_{11}^2+\cdots +a_{1r}^2}{3\alpha r}-1)}^2}(\frac{a_{11}^2+\cdots +a_{1r}^2}{3\alpha r}-1)& \cdots & a_{1r}{e}^{{(\frac{a_{11}^2+\cdots +a_{1r}^2}{3\alpha r}-1)}^2}(\frac{a_{11}^2+\cdots +a_{1r}^2}{3\alpha r}-1)\\ ⋮& \ddots & ⋮\\ a_{m1}{e}^{{(\frac{a_{m1}^2+\cdots +a_{mr}^2}{3\alpha r}-1)}^2}(\frac{a_{m1}^2+\cdots +a_{mr}^2}{3\alpha r}-1)& \cdots & a_{mr}{e}^{{(\frac{a_{m1}^2+\cdots +a_{mr}^2}{3\alpha r}-1)}^2}(\frac{a_{m1}^2+\cdots +a_{mr}^2}{3\alpha r}-1)\end{array}\right]$$

$$V_{\nabla }=\left[\begin{array}{ccc}{b}_{11}{e}^{{(\frac{b_{11}^2+\cdots +b_{1r}^2}{3\alpha r}-1)}^2}(\frac{b_{11}^2+\cdots +b_{1r}^2}{3\alpha r}-1)& \cdots & b_{1r}{e}^{{(\frac{b_{11}^2+\cdots +b_{1r}^2}{3\alpha r}-1)}^2}(\frac{b_{11}^2+\cdots +b_{1r}^2}{3\alpha r}-1)\\ ⋮& \ddots & ⋮\\ b_{p1}{e}^{{(\frac{b_{p1}^2+\cdots +b_{pr}^2}{3\alpha r}-1)}^2}(\frac{b_{p1}^2+\cdots +b_{pr}^2}{3\alpha r}-1)& \cdots & b_{pr}{e}^{{(\frac{b_{p1}^2+\cdots +b_{pr}^2}{3\alpha r}-1)}^2}(\frac{b_{p1}^2+\cdots +b_{pr}^2}{3\alpha r}-1)\end{array}\right]$$

The RR Model

It has been suggested that regression models, such as elastic net and RR, tend to exhibit good and robust performance in different settings.^60,61 Here, we applied RR to predict drug responses by assuming a linear relationship between the gene-expression profiles of cell lines and drug responses. However, the number of genes is much larger than that of cell lines in our data. To avoid overfitting, for each drug, we need to filter out unimportant genes.

Let $\mathbf{X}={\left[X_{ij}\right]}_{m\times n}$ denote the cell line-gene-expression matrix, where $n$ is the number of genes. Let ${\mathbf{M}}_k$ be the $k\text{th}$ column of $\mathbf{M}(1\le k\le p)$. We then divided ${\mathbf{M}}_k$ into ten nonoverlapping groups randomly with almost the same size and selected nine groups as the training set and the remaining group as the test set. Without loss of generality, we selected the $q$th group as the test set and the other 9 groups as the training set. With the deletion of all zeros in the training set, we obtained the resulting vector ${\mathbf{M}}_k^{\left(q\right)}$. Meanwhile, we deleted gene-expression values of corresponding cell lines, normalized the remaining gene-expression values by Z score, and obtained the matrix ${\mathbf{X}}^{\left(q\right)}$. Let ${\mathbf{X}}_j^{\left(q\right)}$ be the $j$th column of ${\mathbf{X}}^{\left(q\right)}$, $j=1,\cdots ,n.$ We computed PCCs $\rho$, such that the size of the set ${\text{Ω}}_{{\sigma }_k^{\left(q\right)}}=\left\{j\right|j\in \left[n\right]\text{ and }\left|\rho \left({\mathbf{X}}_j^{\left(q\right)},{\mathbf{M}}_k^{\left(q\right)}\right)\right|\ge {\sigma }_k^{\left(q\right)}\}$ is close to the number of cell lines as much as possible. We set ${\sigma }_k=\text{min}${${\sigma }_k^{\left(q\right)},q=1,\cdots ,10$}, and repeated the above procedure 10 times. The minimum value of the 10 ${\sigma }_k$s was referred to as $\widehat{{\sigma }_k}$. Under the help of $\widehat{{\sigma }_k}$, we could use the above training sets to find ${\tau }_k$ easily (satisfying that the size of the set ${\text{Ω}}_{{\tau }_k}=\left\{j\right|j\in \left[n\right]\text{ and }\left|\rho \left({\mathbf{X}}_j^{\left(q\right)},{\mathbf{M}}_k^{\left(q\right)}\right)\right|\ge {\tau }_k\}$ is close to the number of cell lines as much as possible) and to train the RR model by minimizing the following formula:

$$\frac{1}{2}\sum _{i\in {\text{E}}_k}{(\sum _{j\in {\text{Ω}}_{{\tau }_k}}{\text{X}}_{ij}{\text{λ}}_{jk}^{{\tau }_k}-{\text{M}}_{ik})}^2+{\theta }_2\sum _{j\in {\text{Ω}}_{{\tau }_k}}{\left({\text{λ}}_{jk}^{{\tau }_k}\right)}^2$$ (Equation 2)

Here, ${\text{E}}_k=\left\{i\right|i\in \left[m\right]{\text{ and M}}_{ik}\ne 0\}$, ${\text{λ}}_{jk}^{{\tau }_k}$ are RR estimators, and ${\text{θ}}_2$ is a penalty factor for reducing the number of effective features associated with drug responses. Finally, we used the test sets to determine the optimal parameters in the formula (Equation 2).

Let $\mathbf{\tau }=\left[{\tau }_1,\cdots ,{\tau }_k,\cdots ,{\tau }_p\right]$, and ${\mathbf{\lambda }}^{\mathbf{\tau }}={\left[{\text{λ}}_{jk}\right]}_{n\times p}$, ${\text{λ}}_{jk}={\text{λ}}_{jk}^{{\tau }_k}$ if $j\in {\text{Ω}}_{{\tau }_k}$, otherwise ${\text{λ}}_{jk}=0$. Then, the predicted cell line-drug-response matrix $\mathbf{Y}$ under $\mathbf{\tau }$ can be formulated as $\mathbf{Y}=\mathbf{X}{\mathbf{\lambda }}^{\mathbf{\tau }}$.

The MC-RR Combination Model

Ensemble learning usually achieves better predicting accuracy than single predictors and thus is promising in prediction.^15,62, 63, 64 It is reasonable to combine the MC and RR models since the former emphasizes relationships among drugs and deals with all drugs simultaneously, whereas the latter takes advantage of the close relationship between drug-response and gene-expression profiles and tackles each drug separately. We combined two models as follows:

$${\hat{\mathbf{M}}}_k={\beta }_k{\mathbf{Z}}_k+(1-{\beta }_k){\mathbf{Y}}_k,1\le k\le p$$ (Equation 3)

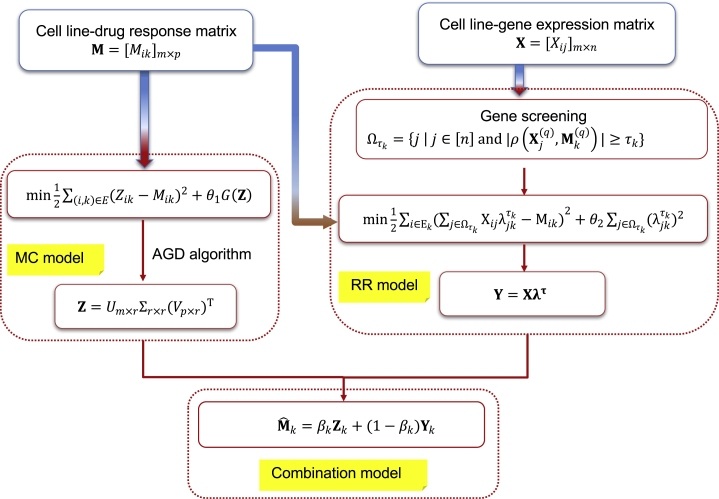
where ${\hat{\mathbf{M}}}_k$ is the $k\text{th}$ column of the prediction matrix $\hat{\mathbf{M}}$ of the combination model; ${\mathbf{Z}}_k$ and ${\mathbf{Y}}_k$, respectively, denote the $k\text{th}$ column of the MC-prediction matrix $\mathbf{Z}$ and RR-prediction matrix $\mathbf{Y}$; and ${\beta }_k$ is a weight parameter. Figure 7 showed the workflow of the MC-RR combination model.

Figure 7.

The Workflow of the MC-RR Combination Model

Crossvalidation and Evaluation Criteria

We conducted 10-fold crossvalidation to evaluate the performance of models and determine model parameters. Observed values in $\mathbf{M}$ were divided into 10 groups randomly with almost the same size. One group was taken as the testing set and the rest as the training set each time. The operation was repeated 10 runs, such that each value in $\mathbf{M}$ was predicted once, and PCCs between predicted and observed values in $\mathbf{M}$ were calculated. It is of noting that the MC model was performed on the whole$\mathbf{M}$ with all of the drugs simultaneously, but the RR model and the combination model were applied to each drug separately. Hence, to each drug, we restricted the grouping of training and testing sets to train a separate model in each run and required model parameters to be equal for all 10 runs to avoid overfitting. The whole crossvalidation was run 10 times, the average PCC was used to measure the performance of models, and the optimal parameters were determined by maximizing the average PCC.

Author Contributions

J.Y. and Y.L. conceived the concept of the work and designed the experiments. C.L. and D.W. performed the literature search and experiments. C.L., F.R., and Y.L. completed theoretical derivation. J.X. and L.H. collected and analyzed the data. D.W., J.L., and G.T. conducted case studies. Y.L., J.Y., and C.L. wrote the paper. All authors have approved the manuscript.

Conflicts of Interest

The authors declare no competing interests.