Life History Effects on Neutral Diversity Levels of Autosomes and Sex Chromosomes

Understanding the determinants of neutral diversity patterns on autosomes and sex chromosomes provides a bedrock for our interpretation of population genetic data...

Abstract

Understanding the determinants of neutral diversity patterns on autosomes and sex chromosomes provides a bedrock for the interpretation of population genetic data; in particular, differences between the two informs our understanding of sex-specific demographic and mutation processes. While sex-specific age-structure and variation in reproductive success have long been known to affect neutral diversity, theoretical descriptions of these effects were complicated and lacking in generality, stymying attempts to relate diversity patterns of species with their life history. Here, we derive general yet simple expressions for these effects. In particular, we show that life history effects on X-to-autosome ratios of pairwise diversity levels (X:A diversity ratios) depend only on the male-to-female ratios of mutation rates, generation times, and reproductive variances. Our results reveal that changing the male-to-female ratio of generation times has opposite effects on X:A ratios of diversity and divergence. They also explain how sex-specific life histories modulate the response of X:A diversity ratios to changes in population size. More generally, they clarify that sex-specific life history—generation times in particular—should have marked effects on X:A diversity ratios in many taxa and enable further investigation of these effects.

ELUCIDATING the forces that shape neutral diversity patterns has been a major obsession of modern population genetics (Crow and Kimura 1970; Gillespie 2004; Charlesworth and Charlesworth 2010) and a main driver of inferences from population genetic data (e.g., International HapMap Consortium 2003; Myers et al. 2005; McVicker et al. 2009; Li and Durbin 2011). Contrasting relative neutral diversity levels on the X and autosomes is particularly interesting in this regard, as this contrast provides a unique setting for testing our understanding of the effects of these evolutionary forces. All else being equal, the ratio of genetic diversity levels on X and autosomes should mirror the ratio of their numbers in the population and thus equal 3/4. However, autosomes spend an equal number of generations in diploid form in both sexes, whereas the X spends twice as many generations in diploid form in females than in haploid form in males. As a result, X-to-autosome (X:A) diversity ratios can also be shaped by sex differences in life history and mutation processes [which are sexually dimorphic in many species (Hedrick 2007)], as well as by differences between X and autosomes in the effects of demographic history and selection at linked sites. Here, we focus on life history effects (as well as their interactions with demographic history), setting aside selection at linked sites, whose effects have been studied extensively (Charlesworth et al. 1987; Haldane 1924; Hammer et al. 2010; Charlesworth 2012). We focus on the X throughout, but similar arguments apply to neutral diversity on sex chromosomes more generally.

While the effects of sex-specific age-structures on neutral diversity have been modeled for decades (Felsenstein 1971), these effects have been underappreciated in empirical studies of X:A diversity ratios. Notably, in many species, generation times differ substantially between sexes (De Magalhães et al. 2007), with likely implications for the diversity levels of X compared to autosomes. Indeed, parental ages are among the strongest known modifiers of mutation rates, and of the degree of male mutation bias (α), in mammals (Crow 2006; Sayres et al. 2011; Segurel et al. 2014; Jónsson et al. 2017; Gao et al. 2019). Additionally, longer male than female generation times increase the numbers of generations that occur on the X relative to autosomes per unit time, influencing rates of divergence on the X relative to autosomes on a phylogenetic branch of fixed length (Amster and Sella 2016). By the same token, we would expect sex-specific generation times to affect diversity ratios: for a given absolute time (in years) to the most recent common ancestor (MRCA) of alleles at X or autosome linked loci, sex differences in generation times will lead to different numbers of generations on the X and autosomal lineages. In the case of diversity, however, this effect cannot be considered in isolation, as the coalescence process (and thus the distributions of times to the MRCAs on the X and autosomes) will also be affected by sex-specific generation times, and, perhaps, by sex specific age structure more generally (Charlesworth 2001).

The effects of age structure on the effective population size were first described by Felsenstein (1971) in a haploid model, and later extended for the X and autosomes by others (e.g., Hill 1972; Johnson 1977; Emigh and Pollak 1979; Pollak 1990; Charlesworth 1994; Charlesworth 2001). Felsenstein assumed a haploid population, in which $M_i$ individuals survive to age i, and a proportion $p_i$ of newborns descend from parents of age i. He relied on identity by decent considerations to show that

$$N_e=\frac{G{M}_1}{1+{\displaystyle {\sum }_i{q}_{i+1}^2\left(M_1/M_{i+1}-M_1/M_i\right)}},$$ (1)

where $q_i={\displaystyle \sum _{j\ge i}{p}_j},$ and $G={\displaystyle \sum _{i}i\cdot p_i}$ is the expected generation time. While this result, its extensions to X and autosomes (Hill 1972; Johnson 1977; Emigh and Pollak 1979; Pollak 1990; Charlesworth 1994), and generalizations incorporating reproductive variance (Charlesworth 2001), provide valuable insights, they depend on a full parametrization of the age structure of the population. The dependence on so many parameters limits our understanding of the general effects of age structure on neutral diversity. Hill and Pollak derived alternative expressions for the $N_e$ of autosomes (Hill 1972) and of the X (Pollak 1990). For autosomes, for example, Hill showed that

$$\frac{1}{N_e^A}=\frac{2+{\sigma }_{MM}^2+2\left({\gamma }_M/{\gamma }_F\right)\text{Cov}\left(mm,mf\right)+{\left({\gamma }_M/{\gamma }_F\right)}^2{\sigma }_{MF}^2}{16M_1\cdot {\gamma }_M\cdot G_A}+\frac{2+{\sigma }_{FF}^2+2\left({\gamma }_F/{\gamma }_M\right)\text{Cov}\left(fm,ff\right)+{\left({\gamma }_F/{\gamma }_M\right)}^2{\sigma }_{FM}^2}{16M_1\cdot {\gamma }_F\cdot G_A},$$ (2)

where ${\sigma }_{st}^2$ is the variance in the number of descendants of sex $t$ that parents of sex $s$ have throughout their life, $\text{Cov}\left(sm,sf\right)$ is the covariance between the numbers of male $\left(sm\right)$ and female $\left(sf\right)$ descendants of parents of sex s throughout their life, ${\gamma }_s$ is the proportion of newborns of sex s, and $G_A$ is the sex-averaged generation time. While Hill and Pollak’s expressions rely on fewer parameters, they are still quite complicated, again limiting our understanding of the effects of age structure. In both cases, the underlying parameters are also difficult to measure in nature, making it hard to relate the theoretical results with observed X:A diversity ratios. In contrast, the effects of a sex-specific age-structure on X:A ratios of neutral substitutions between species depend only on the male-to-female ratio of generation times (Charlesworth 1994; Amster and Sella 2016), making them easy to understand and to test against phylogenetic observations (Amster and Sella 2016).

Unlike sex-specific age structure, differences in reproductive variance between males and females, i.e., variance in the number of offspring produced throughout life, on X:A diversity ratios have been considered by many empirical studies [e.g., (Charlesworth 2001; Hammer et al. 2008)]. Reproductive variance can arise from age-structure per se, i.e., from stochastic differences in age at death, age-specific fecundity, and sampling variance in the number of offspring. It can also arise from endogenous differences among individuals (due to environmental, social, or genetic causes). For example, many species are known to be highly polygynous, i.e., a minority of males sire offspring with multiple females, resulting in a higher reproductive variance in males than in females. We consider such variation in male fecundity to be endogenous. Since the X spends twice as many generations in females than in males, higher male reproductive variance decreases coalescence rates on the X relative to on autosomes, and, thus, increases the X:A diversity ratio. Both theoretical and empirical studies suggest that this effect can be substantial (e.g., Charlesworth 2001; Hammer et al. 2008).

From a theoretical standpoint, the effects of endogenous variation in reproductive success take simple forms when they are studied in isolation, i.e., without interactions with age structure. Notably, Wright (Wright 1939, 1986) derived a simple expression for the effective population size of diploid populations with endogenous reproductive variance and nonoverlapping generations, i.e., without age-structure (see below); we present a straightforward generalization of their expression for the X (also see below). Since then, several studies have incorporated reproductive variance into models with age structure, under the assumption that the age structure and reproductive variance are completely or partially independent (e.g., Sagitov and Jagers 2005; Pollak 2011). This assumption does not account for known correlations between ages of reproduction, reproductive success, and longevity: for example, between the age of first reproduction and longevity (Westendorp and Kirkwood 1998; Pettay et al. 2005), or between reproductive success and longevity (Westendorp and Kirkwood 1998; Thomas et al. 2000). A couple of studies considered more general models combining reproductive variance and age structure, but their analyses relied on simulations with particular parameter choices (Evans and Charlesworth 2013) or they resulted in complicated analytical results (Charlesworth 2001), with even more parameters than those with age-structure alone.

Our goal here is to understand how sex-specific age structure and variation in reproductive success affect neutral diversity levels on the X and autosomes in a general setting. Importantly, we aim to derive simple expressions for these dependencies, in terms of parameters that are straightforward to measure, so that the models can be related to and tested against observed diversity levels on the X and autosomes. To achieve these goals, we build on the coalescent treatment of age-structured populations (Orive 1993; Sagitov and Jagers 2005; Pollak 2011). We define the effective population size, $N_e$, in terms of the expected coalescence time of a pair of neutral alleles (i.e., we use this expectation for haploids and half that for diploids), but note that other definitions used in cited work are equivalent to ours under the models considered.

Data availability

The authors state that all data necessary for confirming the conclusions presented in the manuscript are represented fully within the manuscript. Supplemental material available at figshare: https://doi.org/10.25386/genetics.12440075.

Results

The haploid case

The model:

To illustrate how we treat the coalescence process in an age-structured population, we first consider the haploid model proposed by Felsenstein (1971). We assume a haploid, panmictic population of constant size that is divided into age classes of 1 year (for convenience). We denote the number of individuals of age $a_{max}\ge a\ge 1$ by $M_a$, where $M_a$ is assumed to be constant, $M_{a+1}\le M_a$ due to mortality, and $M_a=0$ for ages $a>a_{max}$ (see Table 1 for a summary of notations). We further assume that each of the $M_1$ newborns is independently chosen to descend from a random parent: the ages of the parents are chosen from a distribution $A={\left(p_a\right)}_{a=1}^{a_{max}}$ with expectation G (the generation time), and the specific parent is chosen with uniform probability within the age class (endogenous reproductive variance is considered below).

Table 1. Notation for the haploid model.

Notation	Definition
$p_a$	Probability that a newborn descends from a parent of age a
$M_a$	Number of individuals of age a
$G$	Expected generation time
$M$	Effective age-class size
$\overrightarrow{r}={\left(r_a\right)}_{a=1}^{a_{max}}$	Relative reproductive success, where $r_a$ is the relative reproductive success at age a
$W_{i,j}$	Expected value of $r_i\cdot r_j$ conditioned on survival to age j ($j\ge i$)
$W$	Weighted average of $W_{i,j}$
$V$	Reproductive variance

Effective population size:

This model was solved by Sagitov and Jagers (2005) in a coalescent framework, and here we provide an intuitive account of the solution (see SI Section 1 for a rigorous derivation).

We consider the rate of coalescence for a sample of two alleles. To this end, we trace their lineages backward in time in steps of the same size in which we measure age (e.g., years). When we trace the lineage of a single allele backward in time, the age of the individuals that carry it, a, forms a Markov chain, with stationary distribution ${\mathit{ϵ}}_a$. As we would expect from intuition, the stationary probability of being carried by a newborn is ${\mathit{ϵ}}_1=1/G.$ More generally, ${\mathit{ϵ}}_a={\displaystyle \sum _{j\ge a}{p}_j/G}$ (Sagitov and Jagers 2005), where, intuitively, the term $p_j/G$ represents the probability that the allele was carried by a newborn $j-a+1$ years ago (with probability $1/G$) who inherited it from a parent of age j (with probability $p_j$). When we trace the lineages of two alleles backward in time, a coalescence can occur in age class $a$ in two possible routes. In the first, both alleles would be in newborns in the previous time step (with stationary probability ${\mathit{ϵ}}_1^2$), descending from age class a (with probability $p_a^2$) from the same parent (with probability $1/M_a$). In the second, only one of the alleles would be in a newborn in the previous time step and the other would be in the ${\left(a+1\right)}^{th}$ age class (with stationary probability $2\cdot {\mathit{ϵ}}_1\cdot {\mathit{ϵ}}_{a+1}$), and the first allele would descend from the second the next step backward in time (with probability $p_a/M_a$). This second route also requires that $a<a_{max}$ (which is handled by defining ${\mathit{ϵ}}_{a_{max}+1}=0$). Thus, the stationary probability of coalescence per year in age class a is

$$\frac{{\left({\mathit{ϵ}}_1\cdot p_a\right)}^2}{M_a}+2{\mathit{ϵ}}_1{\mathit{ϵ}}_{a+1}\frac{p_a}{M_a}\text{ .}$$ (3)

The probability of coalescence per generation and corresponding effective population size follow. Multiplying the probabilities per age class per year by the generation time, summing them over age classes, and rearranging terms, we find that

$$\frac{1}{N_e}=\frac{1}{G}{\displaystyle \sum _a\frac{w_a}{M_a}},$$ (4)

where $w_a=p_a^2+2{\displaystyle \sum _{j>a}{p}_a{p}_j}.$ In SI Section 1.3, we show that deviations from the stationary age distribution have negligible effects on coalescence rates, and thus that this approximation—and by analogy, those in the rest of the paper—conform with standard theory in neglecting effects that are smaller than an order of $1/N_e$ (Hudson 1990). Note that the (a, j)-term in $w_a$ is proportional to the probability that the coalescence in age class a occurs in an individual that gave birth to a newborn carrying one of the alleles at age a and a newborn carrying the other allele at age j. The $w_a$ terms add up to 1, allowing us to define the effective age class size, M, as the weighted harmonic mean

$$\frac{1}{M}={\displaystyle \sum _a\frac{w_a}{M_a}}.$$ (5)

The effective population size can then be viewed as the product of the effective age-class size and the effective number of age-classes, which is simply the expected generation time G, i.e.,

$$N_e= G\cdot M.$$ (6)

In SI Section 1.5, we show that Equation 6 is equivalent to Felsenstein’s formula (Equation 1). The definition of the effective age-class size as a harmonic mean simplifies this formula and provides an intuition for the effect of age-structure on $N_e$.

Reproductive variance:

Next, we extend the model to incorporate endogenous reproductive variance. To this end, we assume that each newborn is assigned a random vector $\overrightarrow{r}$ (from a distribution that is a parameter of the model) describing its age-dependent, relative reproductive success, such that its probability of being chosen as a parent among the individuals of age class a is $r_a/M_a$ (thus, $r_a$ corresponds to the expected, rather than realized, reproductive success of the individual at age a). We further assume that the proportion of individuals with a given vector $\overrightarrow{r}$ that reach age a, $f_a\left(\overrightarrow{r}\right),$ can vary with age, in effect allowing for dependencies between expected reproductive success and longevity. In SI Section 1.7, we detail why our results also apply to models that incorporate dependencies between realized reproductive success and longevity, such as the one proposed by Evans and Charlesworth (Evans and Charlesworth 2013). Our results thus apply to quite general interactions between reproductive success and age structure, including those that have been observed (see Introduction).

The extended model can be solved along the same lines we described above (see SI Section 1.2). Specifically, the coalescence rate per generation for a sample of two alleles and corresponding effective population size take a similar form:

$$\frac{1}{N_e}=\frac{1}{G}{\displaystyle \sum _a\frac{w_a}{M_a}},$$ (7)

but in this case

$$w_a=p_a^2{W}_{a,a}+2{\displaystyle \sum _{j>a}{p}_a{p}_j{W}_{a,j}},$$ (8)

where $W_{a,j}\equiv E_{\overrightarrow{r}}\left(r_a\cdot r_j\text{|individual reaches age}\ge j\right)$ for $j\ge a.$ As in the simpler case, the (a, j)-term in $w_a$ is proportional to the probability that coalescence in age class a occurs in an individual that gave birth to a newborn carrying one of the alleles at age a and a newborn carrying the other allele at age j; but in this case, the coefficients $W_{a,j},$ and their weighted sums $w_a$, incorporate the effect of endogenous reproductive variance. In contrast to the simpler case, the $w_a$ terms do not necessarily add up to 1. We therefore introduce a normalization by $W={\displaystyle \sum _a{w}_a},$ and define the effective age class size as

$$\frac{1}{M}=\frac{1}{G}{\displaystyle \sum _a\frac{w_a/W}{M_a}}.$$ (9)

In these terms, the effective population size takes the form

$$N_e=G\cdot M/W.$$ (10)

Recasting in terms of reproductive variance:

To provide further intuition, we first consider the special case in which relative reproductive success is independent of age and of mortality rates. Namely, each newborn is assigned a scalar relative reproductive success r at birth, such that its probability of being chosen as a parent among the individuals of age class a is $r/M_a$; the distribution of r values then has expectation 1 (by construction). We denote its variance by $V_r$ ($V_r=0$ when there is no endogenous reproductive variance). In this case, the coalescence rates in any given age class are increased by a factor $1+V_r,$ and therefore the effective population size is

$$N_e= \frac{1}{1+V_r}G\cdot M.$$ (11)

Thus, $W=1+V_r$, which can be interpreted as the reproductive variance caused by the Poisson sampling of parents, which contributes 1, and by the endogenous reproductive variance, which contributes $V_r.$ In turn, the contribution of age-structure to reproductive variance is reflected in the term $G\cdot M.$

The results of the general model can also be recast in terms of the reproductive variance. First consider a haploid Wright–Fisher process (i.e., with nonoverlapping generations) with endogenous reproductive variance, modeled similarly to the example considered above. In this case, Wright (1939, 1986) showed that the effective population size is

$$N_e= N/V,$$ (12)

where $N$ is the census population size and $V=1+V_r$ is the reproductive variance (strictly speaking, Wright derived an equivalent result for a diploid hermaphrodite model). Second, in the case with age-structure but without endogenous reproductive variance, Hill (1972) showed that the effective population size can also be written as

$$N_e=G\cdot M_1/V,$$ (13)

where $G\cdot M_1$ is the number of newborns per generation, and $V$ is the reproductive variance introduced by age structure. Comparing Equations 6, 10, and 13, we see that this variance can be expressed as $V=M_1/M$ $\left(\ge 1\right).$ This expression makes intuitive sense, as $V$ defined in this way would be the reproductive variance in the case considered by Wright, if individuals in the next generation were randomly chosen from a reproductive pool including only $M$ out of $M_1$ individuals in the previous one. In SI Section 1.4, we show that Equation 13 also holds for general models with age-structure and endogenous reproductive variance. In this case, the reproductive variance is

$$V=\left(M_1/M\right)\cdot W,$$ (14)

where the first term in this product, $M_1/M,$ is the variance introduced by stochasticity in birth and mortality, and the second term, $W,$ reflects the contribution of endogenous reproductive variance.

In summary, Equation 13 implies that all the effects of age-structure and endogenous reproductive variance (and any dependence between them) on the effective population size can be summarized in terms of the generation time, $G,$ the number of newborns per year, $M_1,$ and the reproductive variance, $V.$ In principle this equation applies to Y or W chromosomes, although in practice the effects of selection at linked loci are likely to dominate diversity levels on such chromosomes. Equation 13 also shows that, along with the reproductive variance, it is the number of newborns per generation, $G\cdot M_1,$ rather than the census population size, $N={\displaystyle \sum _a{M}_a},$ that determines the effective population size in age-structured populations. One implication is that (in the model with endogenous reproductive variance) $G\cdot M_1$ is an upper bound on $N_e$ whereas $N$ is not (see SI Section 1.6).

Stochastic fluctuations in population size and continuous time:

Here, and below, we assume that the sizes of age classes are constant but we expect our results to hold under moderate, stochastic fluctuations in these sizes (e.g., due to sampling variance). To see why, consider the effects of relaxing the assumption of a constant population size in a model without age structure and with nonoverlapping generations. Assume, for example, that the population size in any given generation, $N\prime ,$ is described by a zero-truncated Poisson distribution with a constant mean $N,$ reflecting stochastic fluctuations with a constant carrying capacity. The coalescence rate in such a model would be $E\left(1/(N^{\prime }\right)\cong E\left(1/\left(N^{\prime }+1\right)\right)=\left(1-exp\left(-N\right)\right)/N\cong 1/N$ (neglecting effects that are smaller than an order of $1/N),$ thus illustrating that stochastic fluctuations in population size have a negligible effect on $N_e.$ By the same token, we would expect our approximations to hold under moderate, stochastic fluctuations in the sizes of age classes when the population size is sufficiently large.

We also assume discrete time steps, but expect our approximations to apply to models in continuous time. Indeed, consider a model of a population of size $N,$ in which individuals have a constant lifespan of 1 year. If we measure time in discrete units of $1/n$-th of a year then we have $n$ age classes, corresponding to ages $a=1,\dots n$, with $M_a=N/n$ and $p_a= M_a/N=1/n$, and a generation time of $G=\left(n+1\right)/2.$ From Equations 5 and 6 we find that $M=N/n$ and $N_e=\frac{n+1}{2n}N.$ When $n=1,$ this model becomes the standard Wright–Fisher model with nonoverlapping generations, in which $N_e=N.$ In the continuous time limit $\left(n\to \mathrm{\infty }\right),$ $N_e=N/2.$ In other words, in continuous time, the effective population size is reduced to half of the census size [as is the case in the Moran model, in which each death/birth happens at a distinct time (Ewens 2004)]. Importantly, as we increase $n,$ the effective population size changes smoothly and converges quickly, suggesting that our results (e.g., Equations 13 and 18) remain intact in models in continuous time.

X and autosomes

The diploid model with two sexes is more elaborate, but it is defined and solved along the same lines that we have described for the haploid model. Notably, in the diploid case, we allow for age-dependent mortality, fecundity, and endogenous reproductive variance to differ between the sexes. We also accommodate X and autosomal modes of inheritance (i.e., X-linked alleles in males always descend from females, whereas in all other cases alleles are equally likely to descend from males or females). In SI Section 2.3, we solve this model for the stationary distributions of sex and age and corresponding coalescence rates, by extending Pollak’s results for age-structured populations with two sexes (Pollak 2011) to account for endogenous reproductive variance.

Here, we describe the two formulations for the effective population sizes on the X and autosomes (defined as half the inverse of the coalescence rates) relying on the intuition gained from the haploid model. By analogy with the haploid case (Equation 10), we can express the effective population sizes on the X and autosomes in terms of their respective effective sizes of age-classes. First, we define the basic quantities ($G,$ $W,$ and $M$) for each sex as in the haploid case. Second, we define these quantities for the X and autosomes as the appropriate averages over their values in males and females (Table 2). Formulated in this way, the effective population size for the X and autosomes take the form

$$N_e^X=\frac{3}{4}\cdot \frac{2G_X{M}_X}{W_X}\text{and}{N}_e^A=\frac{2G_A{M}_A}{W_A}.$$ (15)

We note that the factor of 2, which is absent in the haploid case (Equation 10), does not arise from diploidy, which is accounted for by the definition of $N_e$ in the diploid case. Rather, it arises from doubling the effective number of age classes when there are two sexes (i.e., $2G$ instead of $G$ classes in the haploid case), which doubles the expected coalescence time (because for a pair of alleles to coalescence, they must be in an individual of a given age and sex; see SI Section 2.3).

Table 2. Notation for the diploid model with two sexes.

Notation	Definition
$M_1$	Number of newborns (of both sexes) per-year
${\gamma }_M,{\gamma }_F$	Proportion of male and female newborns
$G_F, G_M$	Expected generation times in females and males
$G_X=\frac{1}{3}{G}_M+\frac{2}{3}{G}_F,$ $G_A=\frac{1}{2}{G}_M+\frac{1}{2}{G}_F$	Expected generation times for X and autosomes
$W_F,W_M$	Expected endogenous reproductive success factors in males and females
$W_X=\frac{1}{3}{W}_M+\frac{2}{3}{W}_F,$ $W_A=\frac{1}{2}{W}_M+\frac{1}{2}{W}_F$	Expected endogenous reproductive success factors for X and autosomes
$M_F,M_A$	Effective sizes of age classes in males and females
$1/M_X=\frac{1}{3}\cdot \left(W_M/W_X\right)/M_M+\frac{2}{3}\cdot \left(W_F/W_X\right)/M_F,$ $1/M_A=\frac{1}{2}\cdot \left(W_M/W_A\right)/M_M+\frac{1}{2}\cdot \left(W_F/W_A\right)/M_{\mathit{F}}$	Effective sizes of age classes for X and autosomes
$V_M, V_F$	Reproductive variance of males and females
$V_X=\frac{1}{3}{V}_M+\frac{2}{3}{V}_F,$ $V_A=\frac{1}{2}{V}_M+\frac{1}{2}{V}_F$	Reproductive variance for X and autosomes
${\mu }_M, {\mu }_F$	Expected mutation rate per generation in males and females
${\mu }_X=\frac{1}{3}{\mu }_M+\frac{2}{3}{\mu }_F,$ ${\mu }_A=\frac{1}{2}{\mu }_M+\frac{1}{2}{\mu }_F$	Average mutation rate on the X and autosomes
$f\left(x\right)=\left(2x+4\right)/\left(3x+3\right)$	Function relating male-to-female ratios and X:A ratios

All quantities in males and females are defined as in the haploid model (Table 1). All quantities for X and autosomes, other than effective age-class sizes, are arithmetic averages over sexes, weighted by the proportion of generations that X and autosomes spend in each sex. The effective age-class sizes are harmonic averages over sexes, weighted by the relative endogenous reproductive success factors, $W,$ in each sex

We can also express the effective population sizes on the X and autosomes in terms of the number of newborns per generation and the reproductive variances (by analogy with Equation 13 for the haploid case). To this end, we first generalize Wright’s result for the effects of endogenous reproductive variance with nonoverlapping generations [Equation 12; (Wright 1939, 1986)] to the X and autosomes. We assume that the population consists of $N_F$ females and $N_M$ males, with a total population size of $N\equiv N_M+N_F,$ and denote the proportion of each sex by ${\gamma }_s\equiv N_s/N,$ where $s=F, M.$ Under this model

$$N_e^A=\frac{2N}{\frac{1}{2}\left({\gamma }_M{V}_M+{\gamma }_F/{\gamma }_M \right)+\frac{1}{2}\left({\gamma }_F{V}_F+{\gamma }_M/{\gamma }_F\right)}\text{and}{N}_e^X=\frac{3}{4}\cdot \frac{2N}{\frac{1}{3}\left({\gamma }_M{V}_M+{\gamma }_F/{\gamma }_M \right)+\frac{2}{3}\left({\gamma }_F{V}_F+ {\gamma }_M/{\gamma }_F\right)}\text{,}$$ (16)

where $V_F$ and $V_M$ are the reproductive variances in females and males, respectively (SI Section 2.4). With an equal sex ratio at birth (i.e., ${\gamma }_M={\gamma }_F=1/2$), these expressions reduce to

$$N_e^A=\frac{2N}{\frac{1}{2}\left(2+V_A\right)}\text{and}{N}_e^X=\frac{3}{4}\cdot \frac{2N}{\frac{1}{2}\left(2+V_X\right)},$$ (17)

where $V_A$ and $V_X$ are the reproductive variance on the X and autosomes, respectively (Table 2). When there is no endogenous reproductive variance and $V_X=V_A=2,$ the (Poisson) sampling variance in a panmictic sexually reproducing population, Equation 17 reduces to the results for the standard Wright–Fisher model, $N_e^A=N$ and $N_e^X=\frac{3}{4}N.$ Equations 16 and 17 differ from the analogous Equation 12 for the haploid case in a couple of ways. In SI Section 2.6 we provide some intuition for these differences by recasting the effective population sizes on X and autosomes in terms of allelic rather than individual reproductive variances. Doing so makes the analogy between the haploid and diploid formulas apparent.

By analogy with the haploid case (Equation 13), the expressions with general age-structure and endogenous reproductive variances follow from replacing the population size by the number of newborns per generation:

$$N_e^A=\frac{2G_A{M}_1}{\frac{1}{2}\left({\gamma }_M{V}_M+{\gamma }_F/{\gamma }_M \right)+\frac{1}{2}\left({\gamma }_F{V}_F+{\gamma }_M/{\gamma }_F\right)}\text{and}{N}_e^X=\frac{3}{4}\cdot \frac{2G_X{M}_1}{\frac{1}{3}\left({\gamma }_M{V}_M+{\gamma }_F/{\gamma }_M \right)+\frac{2}{3}\left({\gamma }_F{V}_F+ {\gamma }_M/{\gamma }_F\right)},$$ (18)

where in this case, the variances $V_M$ and $V_F$ also include the effects of age-structure, $M_1$ is the number of newborns of both sexes per year, and the proportions of each sex, ${\gamma }_F$ and ${\gamma }_M,$ are defined with respect to the numbers of newborns rather than individuals (SI Section 2.4). In fact, Equation 18 remains valid when the parameters $M_1,$ ${\gamma }_F$ and ${\gamma }_M$, and $V_M$ and $V_F$ are defined for the individuals of sex $s$ who survive to age $a_s,$ as long as $a_s$ precedes reproductive age (because removing all individuals that do not reach $a_s$ from the model does not affect the coalescent). For example, we can take $a_s$ to be the reproductive age of sex $s,$ $M_1$ the number of individuals (of both sexes) that survive to reproductive age per year, ${\gamma }_S$ the proportion of individuals among them of sex $s,$ and $V_s$ the reproductive variance of a random individual of sex $s$ that survive to reproductive age.

The expressions in Equation 18 are considerably simpler than the results of previous work [see SI Section 2.5 for a detailed discussion of the relationship of our results to those of Hill (1972) and Pollak (1990)]. In particular, they are given in terms of fewer parameters, which can be measured more readily in extant populations, especially given the flexibility to measure parameters at any age preceding reproductive age (e.g., circumventing difficulties of accounting for infant mortality). Moreover, Equation 18 demonstrates that the behavior under a general model of age-structure and endogenous reproductive variance is well approximated by the standard coalescence process (with nonoverlapping generations and no endogenous reproductive variance) using the appropriate effective population sizes (Equation 18) and units for time (i.e., using generation times on the X and autosomes, $G_X$ and $G_A$, respectively, to describe the coalescence process in years) (see SI Sections 1.2 and 1.3).

Diversity levels on X and autosomes:

With expressions for the effective population sizes in hand, we turn to diversity levels. We allow for mutation rates to vary with sex and age [as they do in many taxa; (Segurel et al. 2014)], with their per generation rates in females, ${\mu }_F,$ and in males, ${\mu }_M,$ defined as expectations over parental ages. The mutation rates per generation on the X, ${\mu }_X,$ and autosome, ${\mu }_A,$ are defined by the appropriate averages over their values in males and females (Table 2). The expected heterozygosity on X and autosomes then follow from the standard forms:

$$E\left({\pi }_A\right)=4N_e^A{\mu }_{A}andE\left({\pi }_X\right)=4N_e^X{\mu }_X$$ (19)

(Charlesworth and Charlesworth 2010). Note that these expressions are usually derived assuming that the genealogical and mutational processes are independent (Hudson 1990). This assumption is violated here, because both the coalescence and mutation rates depend on the ages along a lineage. In SI Section 3, we show that the standard forms hold nonetheless.

We can now combine our results to derive expressions for X:A ratios of effective population sizes and pairwise diversity levels (i.e., heterozygosities). From Equation 18, with some rearrangement of terms, the ratio of effective populations sizes is

$$\frac{N_e^X}{N_e^A}=\frac{3}{4}\cdot \frac{f\left(G_M/G_F\right)}{f\left(\frac{{\gamma }_M{V}_M+{\gamma }_F/{\gamma }_M}{{\gamma }_F{V}_F+{\gamma }_M/{\gamma }_F}\right)},$$ (20)

and, from Equation 19, the ratio of expected heterozygosities is

$$\frac{E\left({\pi }_X\right)}{E\left({\pi }_A\right)}=\frac{3}{4}\cdot \frac{f\left({\mu }_M/{\mu }_F\right)\cdot f\left(G_M/G_F\right)}{f\left(\frac{{\gamma }_M{V}_M+{\gamma }_F/{\gamma }_M}{{\gamma }_F{V}_F+{\gamma }_M/{\gamma }_F}\right)},$$ (21)

where $f\left(x\right)=\frac{2x+4}{3x+3}$ (f is defined such that, given a sex dependent parameter $C,$ whose values on the X and autosomes are weighted arithmetic averages over sexes, i.e., $C_X=\frac{1}{3}{C}_M+\frac{2}{3}{C}_F$ and $C_A=\frac{1}{2}{C}_M+\frac{1}{2}{C}_F,$ its X:A ratio is given by $C_X/C_A=f\left(C_M/C_F\right)$).

When mutation rates, age structures, and endogenous reproductive variances are identical in both sexes, Equation 21 reduces to the naïve neutral expectation of 3/4. When they vary between sexes, Equation 21 shows that, even if many parameters are required to model life history, mutational and life history effects on the ratio reduce to the effects of the male-to-female ratios of mutation rates $\left(\alpha ={\mu }_M/{\mu }_F\right),$ generation times $\left(G_M/G_F\right),$ and reproductive variances [more precisely,$\left({\gamma }_M{V}_M+{\gamma }_F/{\gamma }_M\right)/\left({\gamma }_F{V}_F+{\gamma }_M/{\gamma }_F\right)$]. Importantly, Equations 20 and 21 are much simpler and more general than previous results, and are expressed terms of sex ratios of parameters that are considerably easier to measure in extant populations.

Discussion

Having a general yet simple expression for mutational and life history effects on the X:A diversity ratio allows us to draw several implications. First, it allows us to generalize previous bounds on the effects of each. Notably, we see that the multiplicative effect of the male-to-female ratios of mutation rates and generation times is bound between 2/3 and 4/3 [see Miyata et al. (1987) for the mutational bound alone], and the effect of the male-to-female ratio of reproductive variances is bound between 3/4 and 3/2 (see Charlesworth 2001). Considering these factors jointly, X:A diversity ratios are bound between 1/4 and 2, a wider range than appreciated previously (note that these bounds apply only under a constant population size; see below). The functional dependence on the three male-to-female ratios also suggests that changes in them will have the greatest impact when they are small (because $\left|f’\left(x\right)\right|$ declines with $x$). As the male-to-female ratios on the right hand side of Equation 21 are male biased (i.e., >1) in many taxa (Fenner 2005; Dixson 2009; Sayres and Makova 2011), we would expect differences in them among populations or closely related species to result in larger differences in X:A ratios when they are ∼1, and to have much smaller effects if far from 1.

Second, our results clarify the differential effects of life history on X:A ratios of diversity and divergence. More precisely, we consider not divergence but the number of substitutions that accumulate on the X and autosomes on a lineage since a species split (i.e., ignoring multiple hits and the contribution of ancestral polymorphism), denoted $K_X$ and $K_A,$ respectively. The equivalent expression to Equation 21 for the ratio of substitutions is

$$\frac{E\left(K_X\right)}{E\left(K_A\right)}=\frac{f\left({\mu }_M/{\mu }_F\right)}{f\left(G_M/G_F\right)}$$ (22)

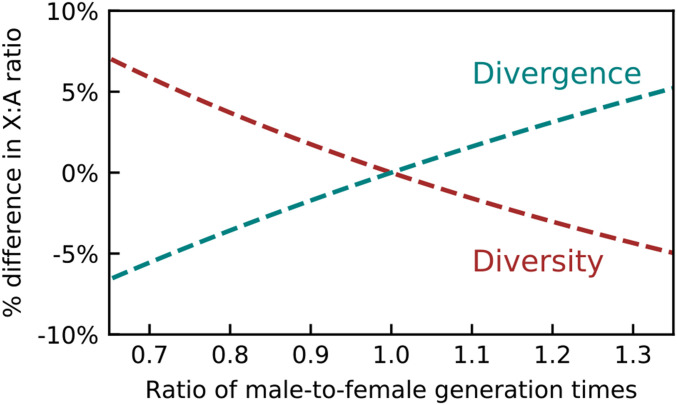
(Charlesworth 1994; Amster and Sella 2016). Thus, male mutation bias, $\alpha ={\mu }_M/{\mu }_F,$ has the same effect on ratios of diversity and substitutions. In contrast, reproductive variances and the sex ratio at birth affect only the diversity ratio because they affect the relative rates of coalescence, and, thus, the relative lengths of lineages on the X and autosomes; for the substitutions ratio, this length is set by the species’ split time. Interestingly, the male-to-female ratio of generation times $\left(G_M/G_F\right)$ has opposite effects on diversity and substitutions ratios (Figure 1). These opposing effects arise because generation times affect not only the relative number of generations on X compared to autosomes, which affects both diversity and substitutions ratios, but also relative coalescence rates, which affects only the diversity ratio.

Figure 1.

The male-to-female ratio of generation times $\left(G_M/G_F\right)$ has opposite effects on X:A ratios of diversity levels and substitutions.

Third, we can rely on the results for a constant population size to study how changes in population size and life history over time jointly affect X:A diversity ratios. Changes in population size are known to affect patterns of genetic variation in general [this signal underpins modern demographic inference, e.g., Li and Durbin (2011)], and X:A diversity ratios in particular (Hey and Harris 1999; Wall et al. 2002; Pool and Nielsen 2007). Having shown that life history also dramatically affects X:A ratios, it is natural to ask how these effects act jointly. In SI Section 4, we extend our model to incorporate these effects. We assume that population size and sex-specific life histories and mutation rates are piecewise-constant in n time intervals, where the i-th interval moving backward from the present is $\left(T_{i-1},T_i\right)$, and $0=T_0<T_1<\dots <T_n=\mathrm{\infty }.$ We show that the expected heterozygosity on autosomes at the present is well approximated by the recursion

$${\pi }_A\left(T_{i-1}\right)=\left(1-\text{exp}\left(-\frac{T_i-T_{i-i}}{2G_A^i{N}_e^{A,i}}\right)\right)\cdot 4N_e^{A,i}{\mu }_A^i+\text{exp}\left(-\frac{T_i-T_{i-i}}{2G_A^i{N}_e^{A,i}}\right)\cdot {\pi }_A\left(T_i\right),$$ (23)

where ${\pi }_A\left(T_{n-1}\right)=4N_e^{A,n}{\mu }_A^n,$ and heterozygosity on the X follows a similar recursion (Eqs. S136 and S137). The ratio $N_e^{X,i}/N_e^{A,i}$ in any given interval i follows from the effects of the male-to-female ratios of generation times and reproductive variances in a constant population size (Equation 20). These recursions can be solved for ${\pi }_A$ and ${\pi }_X$ at the present and for their values at any time in the past (i.e., by substituting $t$ for $T_0$ in the recursions). In SI Section 4.3, we further describe how standard coalescence simulators can be used to incorporate the effects of sex- and time-dependent mutation rates, reproductive variances and age structure.

To illustrate how life history modulates the effects of changes in population size on the X:A diversity ratio, we consider a simple scenario, in which the autosomal population size drops from $N_A$ to $k\cdot N_A$ at time $t=0$, where here we consider $t$ to be increasing forward in time. We further assume that male-to-female ratios of generation times, reproductive variances, and mutation rates are constant, and set the ratio of mutation rates to $\alpha =1$ to isolate genealogical effects. Under these assumptions, the equilibrium X:A diversity ratio, which is also the ratio at times $t<0$, is $F\equiv \frac{3}{4}\cdot \frac{f\left(G_M/G_F\right)}{f\left(\frac{{\gamma }_M{V}_M+{\gamma }_F/{\gamma }_M}{{\gamma }_F{V}_F+{\gamma }_M/{\gamma }_F}\right)}$ (with $\alpha \ne 1$, $F$ is further multiplied by $f\left(\alpha \right)$). Solving the recursions (Equation 23 and S137), we find that the diversity ratio at times $t\ge 0$ is

$$\frac{E\left({\pi }_X\left(t\right)\right)}{E\left({\pi }_A\left(t\right)\right)}=F\cdot \frac{k+\left(1-k\right)\text{exp}\left(- \frac{t}{F\cdot 2G_x\cdot k{N}_A}\right)}{k+\left(1-k\right)\text{exp}\left(- \frac{t}{2G_A\cdot k{N}_A}\right)},$$ (24)

which converges to the equilibrium ratio $F$ in the long run (i.e., when $t\gg G_A\cdot k\cdot N_A$).

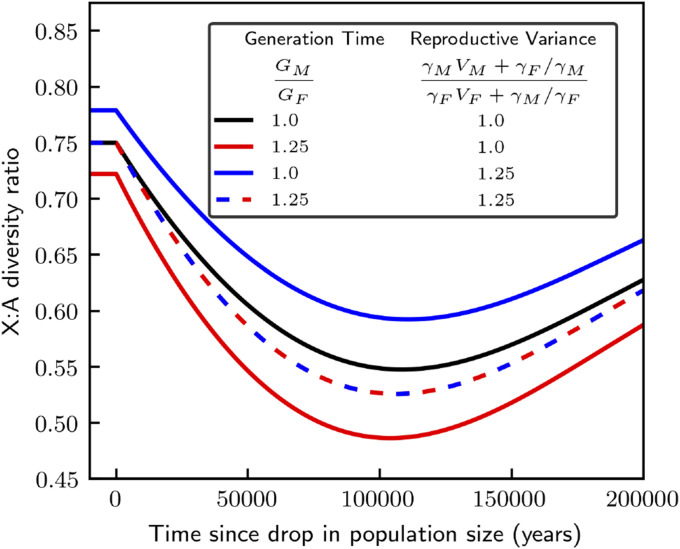
This example illustrates how life history modulates the transient response of the X:A diversity ratio to changes in population size (Figure 2). Without sex-specific life histories, i.e., when $F=3/4$ and $G\equiv G_X=G_A,$ Equation 24 reduces to the expression derived by Pool and Nielsen (2007). As they show, higher coalescence rate on the X compared to autosomes result in faster equilibration of X-linked diversity levels to the new population size, with exponential rate ${\left[3/4\cdot \left(2G\cdot k{N}_A\right)\right]}^{-1}$ compared to ${\left[2G\cdot k{N}_A\right]}^{-1},$ and, thus, in a transient reduction of the X:A diversity ratio (black curve in Figure 2). A higher male reproductive variance weakens the difference between X and autosome (blue curve in Figure 2), because it causes coalescence rates (and thus rates of equilibration) to be more similar on the X and autosomes, decreasing equilibration rates on the X by a factors of $f\left(\frac{{\gamma }_M{V}_M+{\gamma }_F/{\gamma }_M}{{\gamma }_F{V}_F+{\gamma }_M/{\gamma }_F}\right).$ On the other hand, a longer male generation time enhances the difference between X and autosomes in two ways (red curve in Figure 2): it increases coalescence rates and thus equilibration rates per generation on the X compared to autosomes (by a factor of$1/f\left(G_M/G_F\right)$), and it also decreases the relative number of generations that elapsed since the drop in population size on the X compared autosomes (by another factor of ${\left[G_X/G_A\right]}^{-1}=1/f\left(G_M/G_F\right)$). More generally, sex-specific life history modulates the effects of changes in population size on X:A diversity ratios in two ways: one is by changing the relative X:A coalescence time scale of the response in generations; the other is by changing the relative X:A generation times, and thus the relative rate of response of X vs. autosome per unit time (in years).

Figure 2.

Sex-specific life histories modulate the responses to a change in population size on the X and autosomes. We consider a scenario in which the autosomal population size dropped from $N_A=10,000$ to $N_A=1000$ at time $t=0,$ and show the response of the X:A diversity ratio afterward. We assume an autosomal generation time of 30 years, a sex-ratio of mutation rates of $\alpha =1,$ with the reproductive variances and generation times ratios specified in the legend.

Fourth, our results indicate that age-structure likely has underappreciated and non-negligible effects on the genetic diversity of X (or Z) and autosomes in many species. Notably, sex-specific generation times are the strongest known modifier of mutation rates (Crow 2006; Kong et al. 2012; Segurel et al. 2014), and, as we show, their genealogical effects on divergence and diversity on autosomes and sex chromosomes can also be substantial. Our results can therefore help to interpret observed diversity ratios in many species, given estimates for life history trait values. In particular, in a parallel paper (Amster et al. 2020), we take such an approach to show that after accounting for the differential effects of linked selection on the X and autosomes, the joint effects of changes in life history and population size can fully explain the variation in X:A diversity ratios across human populations.