Multi-trait Genome-Wide Analyses of the Brain Imaging Phenotypes in UK Biobank

Wu introduced a new method termed aMAT for multi-trait analysis of any number of traits. The author conducted extensive simulations, confirming that aMAT yields well-controlled Type I error....

Abstract

Many genetic variants identified in genome-wide association studies (GWAS) are associated with multiple, sometimes seemingly unrelated, traits. This motivates multi-trait association analyses, which have successfully identified novel associated loci for many complex diseases. While appealing, most existing methods focus on analyzing a relatively small number of traits, and may yield inflated Type 1 error rates when a large number of traits need to be analyzed jointly. As deep phenotyping data are becoming rapidly available, we develop a novel method, referred to as aMAT (adaptive multi-trait association test), for multi-trait analysis of any number of traits. We applied aMAT to GWAS summary statistics for a set of 58 volumetric imaging derived phenotypes from the UK Biobank. aMAT had a genomic inflation factor of 1.04, indicating the Type 1 error rate was well controlled. More important, aMAT identified 24 distinct risk loci, 13 of which were ignored by standard GWAS. In comparison, the competing methods either had a suspicious genomic inflation factor or identified much fewer risk loci. Finally, four additional sets of traits have been analyzed and provided similar conclusions.

GENOME-wide association studies (GWAS), which analyze one trait at a time, have identified thousands of genetic variants associated with an impressive number of complex traits and diseases (Buniello et al. 2018). However, the identified genetic variants explain only a small proportion of the overall heritability of complex traits, leaving most of the heritability unexplained (Manolio et al. 2009). On the other hand, many genetic variants are associated with multiple, sometimes seemingly unrelated, traits (Solovieff et al. 2013). This motivates multi-trait association tests (Conneely and Boehnke 2007; Yang and Wang 2012; He et al. 2013; Kim et al. 2015; Zhu et al. 2015; Guo and Wu 2018) that detect associations between genetic variants and multiple traits by jointly analyzing these traits, increasing statistical power, explaining missing heritability, and enhancing biological interpretations.

As deep phenotyping data from epidemiological studies and electronic health records are becoming rapidly available (Bycroft et al. 2018; Elliott et al. 2018), they create an exciting opportunity to analyze a large number of traits jointly, which may lead to a better understanding of the genetic component of complex traits. For example, GWAS of 3144 brain image-derived phenotypes have been carried out to provide insights into the genetic architecture of brain structure and function (Elliott et al. 2018). Perhaps because deep phenotyping data emerged recently, most existing multi-trait methods have been developed for analyzing a relatively small number of (i.e., <10) traits. It is unclear whether existing multi-trait association testing methods can handle any number of traits.

In this work, we develop a novel computationally efficient multi-trait association testing method, termed adaptive multi-trait association test (aMAT). Compared with many existing methods, aMAT has two compelling features that make it potentially useful in many settings. First, aMAT yields well-controlled Type l error rate when analyzing any number of traits (e.g., hundreds). This is achieved by taking into account the potential singularity of the trait correlation matrix. In contrast, many competing methods yield incorrect Type l error rates. Second, aMAT maintains high statistical power (usually more powerful than competing methods) over a wide range of scenarios. Because the association pattern varies between genetic variants, the most optimal test will also vary and is an unknown prior. To maintain high power, aMAT first constructs a class of test such that hopefully one of them may have good power for a given scenario and then combines the testing results data-adaptively. Through simulations, we demonstrate these two compelling features. Additionally, by analyzing several brain image-derived phenotypes GWAS summary results jointly, we demonstrate that our approach can reproducibly identify additional associated genetic variants that have been ignored by several existing methods and standard GWAS. These newly identified genetic variants provide additional biological insights into brain structure.

Materials and Methods

Overview of aMAT

We build upon previous works (Pan et al. 2014; Bulik-Sullivan et al. 2015a,b; Sun and Lin 2019) to develop a novel multi-trait association test for jointly testing the association between a single genetic variant and any number of (i.e., potentially hundreds) traits. We use one SNP for illustration, and the same method can be applied to all SNPs across the genome. Suppose we have its Z scores across p traits of interest, $\mathit{Z}=\left(Z_1,Z_2,\dots ,Z_p\right)\prime .$ Under the null hypothesis H₀ that there is no association between the SNP and any trait of interest, $\mathit{Z}$ follows a multivariate normal distribution (Kim et al. 2015; Zhu et al. 2015; Guo and Wu 2018) with mean zero and trait correlation matrix R, i.e., $\mathit{Z}\sim N\left(0,\mathit{R}\right)$.

aMAT involves three steps. First, we apply linkage disequilibrium (LD) score regression (LDSC) (Bulik-Sullivan et al. 2015a,b) to obtain an estimate of the trait correlation matrix, denoted by $\widehat{\mathit{R}}$ (Guo and Wu 2018; Turley et al. 2018). Second, we construct a class of multi-trait association tests (MATs) such that, hopefully, each of them will be powerful under a certain scenario. To deal with potential (near) singularity problem of $\widehat{\mathit{R}}$, we calculate a modified pseudoinverse of $\widehat{\mathit{R}}$, denoted by ${\widehat{\mathit{R}}}_{\gamma }^{+}$. The test statistics of MAT(γ) is defined as:

$$T_{\text{MAT}\left(\gamma \right)}=\mathit{Z}\prime {\widehat{\mathit{R}}}_{\gamma }^{+}\mathit{Z}.$$

Third, because the uniformly most powerful test does not exist, and the optimal value of γ is data-dependent and unknown, we propose adaptive MAT (aMAT) to combine the results from a class of MAT tests:

$$T_{\text{aMAT}}=\underset{\gamma \in \text{Γ}}{\text{min}}{p}_{\text{MAT}\left(\gamma \right)},$$

where $p_{\text{MAT}\left(\gamma \right)}$ is the P-value of the MAT$\left(\gamma \right)$ test and the default setting of Γ is $\text{Γ}=\left\{1,10,30,50\right\}$. In the end, we apply a Gaussian copula approximation to calculate the P-value of aMAT efficiently.

Details of aMAT

Suppose we have Z score across p traits of interest for a SNP, $\mathit{Z}=\left(Z_1,Z_2,\dots ,Z_p\right)\prime .$ Let $\mathit{\beta }=\left({\beta }_1,\dots ,{\beta }_p\right)\prime$ be the true marginal effect sizes for these p traits. Note that Z score can be calculated by $Z_j={\widehat{\beta }}_j/{\text{SE}}_j,$ where ${\widehat{\beta }}_j$ is the estimated effect size for trait j and SE_j is its standard deviation. We are interested in testing whether the SNP is associated with any trait of interest, i.e., $H_0:\mathit{\beta }=0$ vs $H_1:{\beta }_j\ne 0$ for at least one $j\in \left\{1,2,\dots ,p\right\}.$ Of note, testing multi-trait effect $\left(H_0:\mathit{\beta }=0\right)$ is different from testing cross phenotype or pleiotropy effect (Solovieff et al. 2013), where the null hypothesis is, at most one of the β_j, $j=1,\dots ,p$, is nonzero. Under the null hypothesis $H_0:\mathit{\beta }=0$, Z asymptotically follows a multivariate normal distribution with mean zero and correlation matrix R, i.e., $\mathit{Z}\sim N\left(0,\mathit{R}\right)$ (Kim et al. 2015; Zhu et al. 2015; Guo and Wu 2018). We construct aMAT by the following three steps: (1) estimating the trait correlation matrix R; (2) constructing a class of MATs; (3) and constructing aMAT to maintain high power across a wide range of scenarios.

Estimating the trait correlation matrix $\mathbb{R}$

Following others (Guo and Wu 2018; Turley et al. 2018), aMAT applies LDSC (Bulik-Sullivan et al. 2015a,b) to obtain an estimate of R, denoted by $\widehat{\mathit{R}}$. Specifically, we apply the bivariate LDSC (Bulik-Sullivan et al. 2015b) to estimate the off-diagonal elements and the univariate LDSC (Bulik-Sullivan et al. 2015a) to estimate the diagonal elements of R. Because R is the same for all the SNPs across the genome under the null, R needs to be estimated only once.

By applying LDSC, aMAT considers estimation error, including population stratification, cryptic relatedness, unknown sample overlap, and technical artifacts (Turley et al. 2018). As demonstrated by others (Guo and Wu 2018), LDSC provides a more accurate estimate of R than a commonly used approach that estimates R by sample correlation of genome-wide Z scores for each pair of traits (Kim et al. 2015; Zhu et al. 2015).

Constructing a class of MATs

Because the underlying association pattern is unknown, we construct a class of MATs and hopefully each of them would be powerful for a given scenario.

Many existing methods involve the inverse of the estimated trait correlation matrix $\widehat{\mathit{R}}$. We observe that $\widehat{\mathit{R}}$ is often near singular when the number of traits is large, leading to incorrect Type l error rates. To address this, we propose using a modified pseudoinverse approach. Specifically, we first apply the singular value decomposition (SVD) to $\widehat{\mathit{R}}$ as $\widehat{\mathit{R}}=\mathit{U}\Sigma \mathit{U}\prime$, where U is a p × p orthogonal matrix and Σ is a p × p diagonal matrix that contains the descending ordered singular values σ_i of $\widehat{\mathit{R}}$ on its diagonal. We next calculate a modified pseudoinverse of $\widehat{\mathit{R}}$ by

$${\widehat{\mathit{R}}}_{\gamma }^{+}=\mathit{U}{\displaystyle {\sum }_{\gamma }^{\mathit{+}}\mathit{U}\prime },$$

where ${\Sigma }_{\gamma }^{+}$ is formed from Σ by taking the reciprocal of the largest k singular values ${\sigma }_1,\dots ,{\sigma }_k,$ and setting all other elements to zero, where k is the largest integer that satisfies ${\sigma }_1/{\sigma }_k<\gamma .$ This is analogous to the principal components analysis, which restricts the analysis to top k axes of the largest variation. Next, we construct a class of multi-trait association tests (MATs) as:

$$T_{\text{MAT}\left(\gamma \right)}=\mathit{Z}\prime {\widehat{\mathit{R}}}_{\gamma }^{+}\mathit{Z}.$$

Of note, $T_{\text{MAT}\left(\gamma \right)}$ follows a chi-squared distribution ${\chi }_k^2$ with k degrees of freedom under the null, and the P-value of MAT(γ) can be calculated analytically. MAT(γ) covers many existing tests as special cases. For example, MAT(1) equals to a principal component (PC)-based association test called ET (Guo and Wu 2018). MAT(50) equals to chi-squared test approximately when the estimated trait correlation matrix $\widehat{\mathit{R}}$ is not near singular.

Constructing aMAT

Because the association pattern varies between SNPs, the most optimal test will also vary and is an unknown prior. For example, MAT(1) achieves high power when the first PC captures the majority association signals across the p traits. In contrast, when most PCs have weak signals, MAT(1) will lose power and MAT with larger γ will be more powerful. To maintain high power over a wide range of scenarios, we propose aMAT, a test that uses the smallest P-value from a class of MATs as the test statistics:

$$T_{\text{aMAT}}=\underset{\gamma \in \text{Γ}}{\text{min}}{p}_{\text{MAT}\left(\gamma \right)},$$

where $p_{\text{MAT}\left(\gamma \right)}$ is the P-value of the MAT$\left(\gamma \right)$ test, and a sensible default choice of $\text{Γ}$ is $\text{Γ}=\left\{1,10,30,50\right\}.$. Similar test statistics have been widely used in gene-level association tests (Pan et al. 2014; Sun and Lin 2019), pathway-based analysis (Kwak and Pan 2015), and microbiome association analysis (Wu et al. 2016).

To calculate the P-value of aMAT analytically, we apply a Gaussian copula approximation method, which has been used successfully in gene-level association tests (Sun and Lin 2019). Specifically, the Gaussian copula approximation-based method involves the following two steps. First, we estimate the correlation matrix Ω of a set of MAT(γ)s $\left[\gamma \in \text{Γ}\right]$ test statistics via the parametric bootstrap. Specifically, we first simulate a new Z score vector Z^null under the null by a multivariate normal distribution with mean zero and estimated trait correlation matrix $\widehat{\mathit{R}}$. Next, we apply a class of MATs to the simulated Z score Z^null and obtain their P-values. Under the null hypothesis, the P-values of MATs are uniformly distributed, and thus their inverse-normal transformed values $\left(q_{\gamma }={\text{Φ}}^{-1}\left(1-p_{\text{MAT}\left(\gamma \right)}\right)\right)$ follow a multivariate normal distribution with mean zero and covariance Ω. We repeat this procedure B (e.g., 10,000) times and then estimate Ω by the sample correlation matrix of q_γ, denoted by $\widehat{\Omega }$. Because the null distribution for each SNP remains the same, this step only needs to be implemented once for the whole genome.

Second, we apply a Gaussian copula approximation for the joint distribution of q_γ for $\gamma \in \text{Γ}$. Specifically, the P-value of aMAT $\left(p_{\text{aMAT}}\right)$ can be calculated as

$$\begin{array}{l}{p}_{\text{aMAT}}\\ =1-{\text{Φ}}_M\left[{\left\{{\text{Φ}}^{-1}\left(1-T_{\text{aMAT}}\right),\dots ,{\text{Φ}}^{-1}\left(1-T_{\text{aMAT}}\right)\right\}}_{\left|\text{Γ}\right|\times 1};\widehat{\Omega }\right],\end{array}$$

where ${\text{Φ}}_M$ denotes joint distribution function of a multivariate normal distribution and $\left|\text{Γ}\right|$ is the size of Γ.

Simulations

To speed up and simplify computations, we directly generated Z scores from its asymptotic normal distribution, $N\left(\text{Δ},\mathit{R}\right).$ This simulation procedure has been widely used by others (Guo and Wu 2018; Turley et al. 2018). The estimated trait correlation matrix of brain image-derived phenotypes (IDPs) (Elliott et al. 2018) was used as the true trait correlation matrix R such that the simulation settings are similar to real applications. We mainly considered two scenarios: (1) the trait matrix for the set of 58 volumetric IDPs, denoted by Volume; and (2) the trait matrix for the set of 472 structural magnetic resonance imaging (MRI)-related IDPs derived by Freesurfer, denoted by Freesurfer. To evaluate the impact of estimation error on R, two simulation settings were considered. First, we assumed R is known and conducted tests with R. Second, we assumed R is unknown and conducted tests with the estimated trait correlation matrix $\widehat{\mathit{R}}\left(s\right).$ Specifically, similar to Turley et al. 2018, independent normal noise with mean zero and variance s was added to each element of the matrix R to simulate $\widehat{\mathit{R}}\left(s\right).$ Based on our real data applications, the sampling variance was roughly 5 × 10⁻⁵. Thus we varied s from 10⁻⁵ to 10⁻⁴ to evaluate the impact of the estimation error on R.

We simulated 500 million or 1 billion Z score vectors under the null $\left(\text{Δ}=0\right)$ to evaluate Type l error rates with different significance level α and simulated $10,000$ Z score vectors under the alternative $\left(\text{Δ}\ne 0\right)$ to evaluate statistical power at the genome-wide significance level 5 × 10⁻⁸. Under the alternative, a wide range of scenarios were considered. For example, similar to Guo and Wu (2018), we generated $\text{Δ}={\displaystyle {\sum }_{j=1}^{k}c{\sigma }_j{u}_j},$ where u_j is the singular vector of the trait correlation matrix R, σ_j is the jth singular value of R, c is the effect size, and k is the largest integer that satisfies ${\sigma }_1/{\sigma }_k<\gamma .$ We varied γ and c to simulate different scenarios. We also considered other situations such as $\text{Δ}=c{u}_j$ and $\text{Δ}=c.$ To save space, most simulation results were relegated to the supplementary material.

We compared aMAT with the following popular tests: (1) the sum of Z score vector (${\displaystyle {\sum }_{j=1}^p{Z}_j};$ denoted as SUM) (He et al. 2013); (2) the sum of squared Z score vector (${\displaystyle {\sum }_{j=1}^p{Z}_j^2};$ denoted as SSU) (Pan 2009; Yang and Wang 2012); (3) a standard chi-squared test; (4) a modified chi-squared test called Hom (Zhu et al. 2015) that is powerful for the homogeneous effect situation; and (5) a PC-based association test (Guo and Wu 2018), which equals MAT(1). For chi-squared tests, we applied the generalized inverse. When the trait correlation matrix is near singular (our focus here), two popular tests Het (Zhu et al. 2015) and AT (Guo and Wu 2018) had numerical issues, failing to provide p-values and thus having been ignored in our comparisons. The minP test (Conneely and Boehnke 2007), a method that takes the minimum marginal p-values across p traits as the test statistics, is highly conservative and time-consuming when p is large, and, thus, has only been briefly discussed.

Analysis of UK Biobank brain imaging GWAS summary data

We reanalyzed GWAS summary results of IDPs with up to 8428 individuals (Elliott et al. 2018) in UK Biobank to gain additional insights into the genetic architecture of brain imaging. Specifically, we conducted multi-trait association tests to detect genetic associations for five sets of highly related IDPs with up to 472 IDPs per set. These five sets were determined by Elliott et al. (2018), covering a wide range of the IDP classes with significant trait correlations in each grouping. To be concrete, we focused on the set of 58 brain volumetric measures (Elliott et al. 2018) and briefly discussed the results of additional four IDP sets.

Data preprocess and multi-trait association tests:

We removed variants that were either nonbiallelic or strand ambiguous (SNPs with A/T or C/G alleles) and analyzed the remaining 9,971,805 SNPs. LDSC was applied to estimate the trait correlation matrix. For each set of IDPs, we applied aMAT with the default setting $\left(\text{Γ}=\left\{1,10,30,50\right\}\right)$ and many competing methods, including SUM, SSU, MAT(1) (equals ET), Chi-squared, and Hom tests to test the overall association between a SNP and a predefined IDP set.

Result analyses:

We used the genomic inflation factor to evaluate the empirical Type l error rates. The genomic inflation factor is defined as the ratio of the median of the observed test statistic to the expected median, which quantifies the extent of inflation and false positive rate. An ideal genomic inflation factor is 1. However, because of the polygenic nature of GWAS signals, a genomic inflation factor is usually slightly larger than 1. However, a genomic inflation factor >1.2 or even 1.5 shows an indication of inflated Type l error rates, and a genomic inflation factor <0.9 shows evidence for conservative Type l error rates.

In addition, we used Functional Mapping and Annotation (FUMA) (Watanabe et al. 2017) v1.3.4c to identify independent genomic risk loci and lead SNPs in significant loci. Via FUMA, we further obtained the functional consequences for these SNPs by matching SNPs to many functional annotation databases, including CADD scores (Kircher et al. 2014), REgulomeDB scores (Boyle et al. 2012), chromatin states (Ernst and Kellis 2012; Kundaje et al. 2015), and ANNOVAR categories (Wang et al. 2010). For lead SNPs identified by aMAT, replication was tested by an independent dataset obtained from ENIGMA consortium (Hibar et al. 2015). Specifically, we applied aMAT to the GWAS summary statistics of seven brain subcortical volumetric IDPs, including the volume of mean putamen, the volume of mean thalamus, the volume of mean pallidum, the volume of mean caudate, intracranial volume, the volume of mean amygdala, and the volume of mean accumbens. Then, the replication rate was evaluated by the two-tailed binomial test. In the end, we filtered genome-wide significant SNPs identified by aMAT based on their functional annotations, and then mapped them to genes by the following three strategies (via FUMA): positional mapping, eQTL mapping, and chromatin interaction mapping.

Data availability

The author states that all data necessary for confirming the conclusions presented in the article are represented fully within the article. The UK Biobank summary data are available in the http://big.stats.ox.ac.uk. The LDSC software and its required LD scores are available in the https://github.com/bulik/ldsc. The validation data from NIGMA Consortium can be obtained from http://enigma.ini.usc.edu/research/download-enigma-gwas-results/. The software for our proposed method aMAT is available at https://github.com/ChongWuLab/aMAT. Supplementary files are available at https://figshare.com/articles/aMAT_supplementary/9764519.

Results

aMAT yields well-controlled Type 1 error rates

Table 1 shows the Type l error rates of different multi-trait methods with the Freesurfer trait correlation matrix. Our proposed methods MAT and aMAT yielded well-controlled Type l error rates at different significance levels α. Of note, the Freesurfer set contained 472 IDPs, and 27 eigenvalue values of the trait correlation matrix were <0.01 (Supplemental Material, Figure S1). As expected, chi-squared and Hom tests yielded inflated Type l error rates because corresponding test statistics involve the inverse of a near singular correlation matrix. Also, SSU yielded inflated Type l error rates. All methods except SSU yielded well-controlled Type l error rates under simulations with the Volume trait correlation matrix and thus were relegated to the Supplementary materials (Table S1).

Table 1. Type l error rates of different methods with the Freesurfer trait correlation matrix.

α	5 × 102	1 × 102	1 × 104	1 × 106	5 × 107	5 × 108
SUM	5.0 × 10−2	1.0 × 10−2	1.0 × 10−4	9.7 × 10−7	5.2 × 10−7	4.5 × 10−8
SSU	4.6 × 10−2	1.0 × 10−2	1.8 × 10−4	3.5 × 10−6a	2.0 × 10−6a	2.7 × 10−7a
Chi-squared	4.7 ×10−2	1.0 × 10−2	1.7 × 10−4a	4.3 × 10−6a	2.6 × 10−6	4.9 × 10−7a
Hom	5.6 × 10−1a	4.5 × 10−1a	2.5 × 10−1a	1.5 × 10−1a	1.4 × 10−1a	1.1 × 10−1a
MAT(1)	5.0 × 10−2	1.0 × 10−2	1.0 ×10−4	9.8 ×10−7	4.8 ×10−7	4.8 ×10−8
MAT(10)	5.0 × 10−2	1.0 × 10−2	1.0 ×10−4	1.0 × 10−6	4.9 ×10−7	4.5 × 10−8
MAT(30)	5.0 × 10−2	1.0 × 10−2	1.0 ×10−4	1.0 × 10−6	5.2 × 10−7	5.4 × 10−8
MAT(50)	5.0 × 10−2	1.0 × 10−2	9.9 × 10−5	9.6 × 10−7	4.4 × 10−7	4.6 × 10−8
aMAT	4.7 × 10−2	9.4 × 10−3	9.5 × 10−5	1.1 × 10−6	5.5 × 10−7	4.7 × 10−8

We simulated 1 billion (1 × 10⁹) replications under the null and estimated Type l error rates as the proportions of P-values less than significance level α.

^aInflated Type l error rates.

aMAT offers robust statistical power

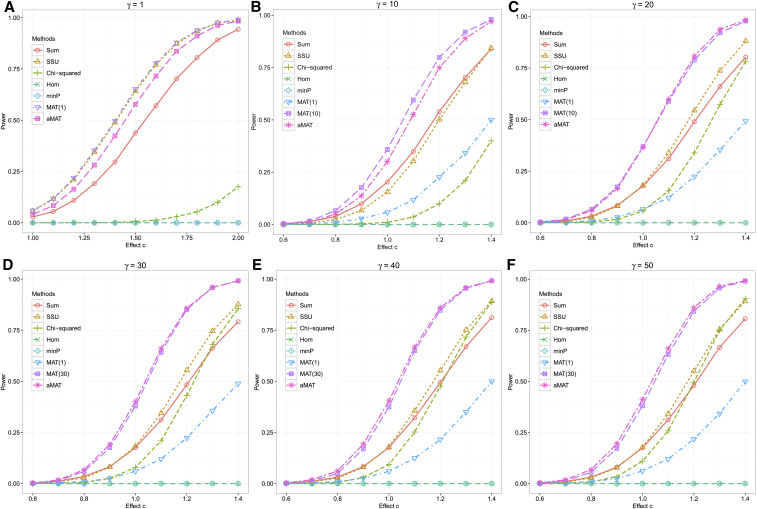
Figure 1 shows the empirical power of different methods with the true Volume trait correlation matrix R. When the first PC was informative, as expected, the MAT(1) performed best. However, MAT(1) was sensitive to the signal distribution and yielded much lower power when the top PC has weak or no signal (Figure S2). The minP test was highly conservative, and the power was almost zero for the situations we considered. The Hom test (Zhu et al. 2015) was known to be powerful for the homogeneous effect situation, but the power was close to zero when many principal components were informative (Figure 1). SUM and SSU tests ignored the relationships among traits and thus were less powerful than MAT tests. Because there is no uniformly optimal test for a composite alternative $H_1:\mathit{\beta }\ne 0$, different MATs achieved high power under different scenarios. However, aMAT maintained high power across a wide range of scenarios by combining the results from a class of MAT tests.

Figure 1.

Empirical power comparison with true Volume trait correlation matrix. Under the alternative, we generated $\text{Δ}={\displaystyle {\sum }_{j=1}^{k}c{\sigma }_j{u}_j}$, where u_j is the jth singular vector of the Volume trait correlation matrix R, σ_j is the jth singular value, c is the effect size, and k is the largest integer that satisfies ${\sigma }_1/{\sigma }_k<\gamma$. Empirical power was estimated as the proportions of p-values less than the significance level 5 × 10⁻⁸.

We considered several additional settings, including varying the way of selecting informative singular vectors and generating Δ, the trait correlation matrix [including five traits, 25 traits, Volume (58 traits), Area (206 traits), Thickness (208 traits), and Freesurf (472 traits)], and the generating distribution for Δ (Figures S3–S13). We show that aMAT achieved high statistical power under all simulations considered. In contrast, competing methods that achieved high power under a few specific situations could lose power substantially under several other situations.

aMAT is robust to the estimation error of the trait correlation matrix

In the previous two subsections, we assumed the trait correlation matrix R was known. However, R is unknown and has to be estimated. To evaluate the impact of estimation error on R, we simulated Z score vectors from its asymptotic normal distribution $N\left(\text{Δ},\mathit{R}\right)$ and compared different testing methods with the estimated trait correlation matrix $\widehat{\mathit{R}}\left(s\right)$, which was constructed by adding independent normal noise with mean zero and variance s to each element of R.

Table 2 shows the Type l error rates of different methods with the estimated Volume trait correlation matrix $\widehat{\mathit{R}}\left({10}^{-4}\right)$. Both MAT and aMAT yielded well-controlled Type l error rates. In comparison, both chi-squared and Hom tests yielded inflated Type l error rates even though they had controlled (slightly conservative) Type l error rates with the true Volume trait correlation matrix R (Table S1). This is because both chi-squared and Hom test statistics involve the inverse of the estimated trait correlation matrix $\widehat{\mathit{R}}\left(s\right)$ and small estimation error could lead to a large deviation.

Table 2. Type l error rates for different methods with the estimated Volume trait correlation matrix $\widehat{\mathit{R}}\left({\text{10}}^{-\text{4}}\right)$.

α	0.05	0.01	1 × 104	1 × 106	5 × 107	5 × 108
SUM	5.0 × 10−2	1.0 × 10−2	1.0 × 10−4	1.0 × 10−6	5.0 × 10−7	4.7 × 10−8
SSU	4.6 × 10−2	1.0 × 10−2	1.9 × 10−4	4.1 × 10−6	2.4 × 10−6	3.9 × 10−7
Chi-squared	6.4 × 10−2	2.8 × 10−2	1.1 × 10−2	7.4 × 10−3	7.1 × 10−3	6.2 × 10−3
Hom	1.7 × 10−1	9.9 × 10−2	5.0 × 10−2	3.6 × 10−2	3.4 × 10−2	3.1 × 10−2
MAT(1)	5.0 × 10−2	1.0 × 10−2	1.0 × 10−4	1.0 × 10−6	5.2 × 10−7	4.9 × 10−8
MAT(10)	5.0 × 10−2	1.0 × 10−2	9.9 × 10−5	1.0 × 10−6	5.0 × 10−7	5.7 × 10−8
MAT(30)	5.0 × 10−2	1.0 × 10−2	1.0 × 10−4	1.0 × 10−6	5.2 × 10−7	4.5 × 10−8
MAT(50)	5.0 × 10−2	1.0 × 10−2	9.9 × 10−5	1.0 × 10−6	5.0 × 10−7	4.5 × 10−8
aMAT	4.7 × 10−2	9.4 × 10−3	9.9 × 10−5	1.2 × 10−6	6.4 × 10−7	4.7 × 10−8

We simulated 500 million (5 × 10⁸) replications with true Volume trait correlation matrix R under the null and constructed test statistics with $\widehat{\mathit{R}}\left({10}^{-4}\right)$. Type 1 error rates were estimated as the proportions of P-values less than significance level α.

We next evaluated the impact of estimation errors on the statistical power. Figure 2 shows that the empirical power of MATs and aMAT with either true (R) or estimated $\left(\widehat{\mathit{R}\left({10}^{-4}\right)}\right)$ trait correlation matrix were almost the same, indicating estimation errors had little impact on the power of MATs and aMAT.

Figure 2.

Empirical power comparison between true and estimated Volume trait correlation matrix. Under the alternative, we generated $\text{Δ}={\displaystyle {\sum }_{j=1}^{k}c{\sigma }_j{u}_j}$, where u_j is the singular vector of the true Volume correlation matrix R, c is the effect size and k is the largest integer that satisfies ${\sigma }_1/{\sigma }_k<\gamma$. We simulated 10,000 replications with R and constructed test statistics with $\widehat{\mathit{R}}\left({10}^{-4}\right)$. We further estimated empirical power as the proportions of P-values less than significance level 5 × 10⁻⁸. MAT(1), MAT(10), MAT(30), MAT(50), aMAT represent the results with $\widehat{\mathit{R}}\left({10}^{-4}\right)$, while MAT(1)-t, MAT(10)-t, MAT(30)-t, MAT(50)-t, aMAT-t represent the results with R.

In the end, we considered several additional settings with different s (s = 10⁻⁵ or s = 5 × 10⁻⁵) and/or with the estimated Freesurf trait correlation matrix. The results were similar to those in Table 2 and Figure 2, thus were relegated to the Supplementary material (Figures S14–S18 and Tables S2–S6).

aMAT identifies novel risk loci for brain volumetric measures

To demonstrate aMAT’s effectiveness in real multi-trait association studies, we performed a multi-stage study for a set of 58 volumetric IDPs—a set defined by (Elliott et al. 2018). In the discovery stage, we applied aMAT to the GWAS data of UK Biobank (Elliott et al. 2018). aMAT had a genomic inflation factor of 1.04 (Figure S19), indicating well-controlled type l error rates. In total, aMAT identified 801 significant SNPs (with P < 5 × 10⁻⁸), 453 of which were ignored by standard GWAS for any IDP at the 5 × 10⁻⁸ genome-wide significance level. These 801 GWAS variants were represented by 28 lead SNPs, located in 24 distinct risk loci (Figure 3 and Table 3). Among these 28 lead SNPs, 13 (46.4%) were ignored by any individual IDP tests at the 5 × 10⁻⁸ genome-wide significance level.

Figure 3.

Multi-trait analysis for the Volume set. Manhattan plot displays the association results of aMAT per variant ordered by their genomic position on the x axis and showing the strength with the $-{\text{log}}_{10}\left(p\right)$ on the y axis.

Table 3. Summary statistics of significantly associated regions identified by aMAT in the multi-trait analysis of a set of volume related IDPs.

Locus	SNP	CHR	BP	A1	A2	MAF	aMAT P	Nearest Gene
1	rs72688340	1	47,983,839	G	A	0.171	2.5 × 10−9	AL356458.1
2	rs6665134	1	180,949,628	C	A	0.401	1.7 × 10−10	STX6
3	rs476557	1	215,140,251	A	C	0.475	4.3 × 10−8	RP11-323K10.1
4	rs1504	2	37,066,018	T	G	0.447	1.4 × 10−8	AC007382.1
5	rs13070564	3	190,629,975	G	T	0.383	8.8 × 10−13	GMNC
6	rs10031823	4	103,125,031	T	C	0.395	1.3 × 10−8	SLC39A8
6	rs34333163	4	103,283,117	A	G	0.075	4.4 × 10−16	SLC39A8
7	rs1922930	6	1,364,691	A	C	0.118	3.8 × 10−8	RP4-668J24.2
8	rs77126132	7	54,966,738	G	A	0.089	1.8 × 10−8	SNORA73
9	rs2707521	7	120,940,436	C	T	0.377		CPED1
10	rs2974298	8	42,376,477	T	C	0.493	2.5 × 10−9	SLC20A2
11	rs10217651	9	118,923,652	A	G	0.386	1.7 × 10−14	PAPPA
11	rs35565319	9	119,065,043	C	T	0.072	6.7 × 10−16	PAPPA
11	rs7030607	9	119,245,183	G	A	0.36	6.7 × 10−9	ASTN2
12	rs12783517	10	21,878,407	C	T	0.299	1.3 × 10−8	MLLT10
13	rs4962692	10	126,424,823	G	A	0.414	2.7 × 10−10	FAM53B
14	rs1187159	11	92,009,792	T	C	0.413	5.1 × 10−11	NDUFB11P1
15	rs73123652	12	65,874,956	T	C	0.106	1.1 × 10−12	MSRB3
16	rs4301837	12	102,336,310	T	C	0.496	6.9 × 10−9	DRAM1
16	rs17797222	12	102,913,946	A	G	0.224	3.6 × 10−13	RP11-210L7.1
17	rs12146713	12	106,476,805	T	C	0.093	3.2 × 10−9	NUAK1
18	rs77956314	12	117,323,367	T	C	0.083	1.2 × 10−9	HRK
19	rs10129414	14	56,193,272	G	A	0.438	2.0 × 10−9	RP11-813I20.2
20	rs2464469	15	58,362,025	G	A	0.412	2.1 × 10−13	ALDH1A2
21	rs13330163	16	70,660,243	A	G	0.453	3.0 × 10−12	IL34
22	rs12920553	16	87,227,046	G	T	0.418	3.5 × 10−10	C16orf95
23	rs6121038	20	30,254,773	T	G	0.291	5.2 × 10−10	BCL2L1
24	rs1004764	22	38,474,852	G	A	0.377	4.2 × 10−9	SLC16A8

Independent lead SNPs are defined by $r^2<0.1$ and distinct loci are >250 kb apart. SNP, CHR, BP, A1, A2 are the lead SNP, chromosome, position, reference allele, and alternate allele, respectively. The MAF is the minor allele frequency and obtained from the 1000 genomes reference panel (Phase 3). aMAT P is the P-value for the aMAT test. SNPs in bold correspond to the novel SNPs that were ignored by standard GWAS for any IDP at the genome-wide significance level 5 × 10⁻⁸.

Next, we replicated our findings in an independent dataset obtained from the ENIGMA consortium (Hibar et al. 2015), which contains GWAS summary statistics of seven subcortical volumes in up to 13,171 subjects. Although the seven brain subcortical volumetric IDPs reported in the ENIGMA consortium represent only a subset of the volumetric IDPs we analyzed before, the replication rate was high. Out of the 24 distinct risk loci, four (rs73123652, rs77956314, rs10129414, and rs1187159) were successfully replicated (two-tailed binomial test $P=6.25\times {10}^{-30}$) under the genome-wide significance threshold $\left(P<5\times {10}^{-8}\right)$. The numbers of replicated SNPs rose to 13 under a relaxed cutoff of 0.05 (two-tailed binomial test $P=2.24\times {10}^{-10}$).

To link the identified variants to functional annotation, we applied FUMA (Watanabe et al. 2017). First, functional annotation of all genome-wide significant SNPs (n = 772, excluding those not available in FUMA database) showed that significant SNPs were mostly (90.8%) located in intronic/intergenic areas (Figure 4B and Table S7). Those relevant SNPs were also enriched for chromatin states 4 (33.2%) and 5 (40.0%), indicating effects on active transcription (Figure 4A). More important, six SNPs were exonic nonsynonymous, which lead to probably deleterious changes in the sequence of the encoded protein (Table S8). Five genome-wide significant SNPs (rs10507144, rs3789362, rs4646626, rs6680541, and rs2845871) had a high observed probability of a deleterious variant effect [CADD score (Kircher et al. 2014) ≥ 20]. Overall, these results suggest that most associated SNPs are located in noncoding regions despite some nonsynonymous variants having been found.

Figure 4.

Functional annotation and implications of aMAT results. (A, B) Distribution of (A) functional effects and (B) minimum chromatin state across 127 tissue/cell types for variants in aMAT identified genomic risk loci. (C) Zoomed-in Circos plot of chromosome 20. Circos plots show implicated genes by either chromatin interaction (colored orange) or eQTLs (colored green) or both (colored red). The dark blue areas are genomic risk loci identified by aMAT. Chromatin interactions and eQTL associations are colored orange and green, respectively. The most outer layer shows a Manhattan plot, displaying $-{\text{log}}_{10}\left(p\right)$ for SNPs with P < 0.05. (D) Venn diagram of number of linked genes by three different strategies.

Second, we linked the associated variants to genes via the three gene-mapping strategies used in FUMA. Figure 4D shows the Venn diagram of the number of mapped genes by three mapping strategies. Positional, eQTL, and chromatin interaction gene mapping strategies linked SNPs to 54, 50, and 76 genes, respectively. This resulted in 133 unique mapped genes (Table S9), 13 of which were identified by all three mapping strategies (Table S10). The locus (rs6121038) on chromosome 20 is particularly notable. Many genes in this locus (including FOXS1, MYLK2, TPX2, BCL2L1, and COX412) might interact physically or through eQTL, as indicated by chromatin interaction data in the mesenchymal stem cell line (Figure 4C). Therefore, those genes might affect volumetric IDPs via a similar biological mechanism. Six genes (STX6, EGFR, SMIM19, METTL10, LEMD3, and MYLK2) are of particular interest as they are implicated via eQTL mapping with brain-related tissues. By searching the GWAS Catalog (Buniello et al. 2018), we found that three out of six (METTL10, LEMD3, and MYLK2) were reported to be associated with volumetric IDPs. For example, METTL10 was associated with mean platelet volume (Astle et al. 2016), total hippocampal volume (Van der Meer et al. 2018), and dentate gyrus granule cell layer volume (Van der Meer et al. 2018). STX6 was identified by all three mapping strategies and contained a significant SNP (rs3789362) with CADD score >20. STX6 was reported to be associated with progressive supranuclear palsy (PSP) (Höglinger et al. 2011; Chen et al. 2018) and the volume of many brain regions (including cerebellum, thalamus, putamen, pallidum, hippocampus, and brainstem) were significantly reduced in PSP compared to control subjects (Messina et al. 2011). Future studies might thus consider the potential role of STX6 in PSP.

Third, the identified genes were enriched in many GWAS Catalog reported volumetric gene sets, including dentate gyrus granule cell layer volume $\left(P=1.46\times {10}^{-13}\right),$ hippocampal subfield CA4 volume $\left(P=1.46\times {10}^{-13}\right),$ and hippocampal subfield CA3 volume $\left(P=5.96\times {10}^{-12}\right)$ (Figure S20). We further performed gene-set analysis for tissue expression and biological pathways via FUMA. Two related tissues (brain cerebellar hemisphere and brain cerebellum) were nominally associated with the volumetric IDPs set when correcting only for the number of tissues being tested (Figure S21).

In summary, for brain volumetric measures, aMAT identified several novel and replicable risk loci that have been ignored by standard GWAS analysis. Via FUMA, we found most associated SNPs are located in noncoding regions, and the mapped genes are enriched in volumetric-related gene sets. These newly identified SNPs/loci not only showcase the power of our proposed approach but also provide novel insights into the genetic basis of brain volumetric measures. By linking the associated variants to genes, we offered a shortlist of genes (such as STX6, EGFR, and SMIM19) that warrant further investigation.

aMAT identifies novel risk loci for four additional IDP sets

We further applied aMAT to four additional IDP sets, which were defined by Elliott et al. (2018) and represented many IDP classes with significant trait correlations in each grouping (Figure 5). These sets include 206 region area-related IDPs (denoted by Area), 208 region thickness-related IDPs (denoted by Thickness), 472 structural MRI-related IDPs constructed by Freesurfer (denoted by Freesurfer), and 138 T1 ROI-related IDPs (denoted by ROIs). In total, we identified 84 independent risk loci and 97 lead SNPs, 59 of which were ignored by any individual IDP tests at the genome-wide significance level (Table 4, Figures S22–S25, and Tables S11–S14).

Figure 5.

The estimated trait correlation matrix for different sets of IDPs. The left was for T1 FAST region of interests (ROIs) set, which contained 138 IDPs, and the right was for Freesurf set, which contained 472 IDPs. Note that the trait correlation estimated here was the correlation of the raw phenotypes conditional on the covariates (e.g., confoundings), which was different from the raw trait correlation provided by Elliott et al. (2018).

Table 4. Summary statistics of aMAT for analyzing four additional IDP sets.

	IDPs	Sig SNPs	Loci	Lead SNPs	Novel SNPs
Area	206	2264	25	28	19
Thickness	208	39	2	2	0
Freesurf	472	2820	23	29	15
ROIs	138	2721	34	38	25

IDPs, Sig SNPs, Loci, Lead SNPs are the number of IDPs in the set, number of genome-wide significant SNPs identified by aMAT, number of independent risk loci, number of lead SNPs in the identified risk loci, respectively. Novel SNPs is the number of lead SNPs that were ignored by any individual GWAS at genome-wide significance level (5 × 10⁻⁸).

aMAT performs better than competing methods in real data applications

We compared aMAT to many competing methods. First, aMAT had a good genomic inflation factor in general (from 0.967 to 1.097) (Table S15). In comparison, the chi-squared and Hom tests had unstable genomic inflation factors. For example, the chi-squared test had a genomic inflation factor of 0.338 for analyzing the Volume IDP set, while the Hom test had a genomic inflation factor of 3.102 for analyzing the Freesurf IDP set, and 0.755 for analyzing the Area IDP set. SUM had a good genomic inflation factor, and SSU had a slightly inflated genomic inflation factor (between 1.186 and 1.250). These results are in line with our simulation results.

Next, we compared the statistical power of different tests that have a good genomic inflation factor. Figure S26 shows the Venn diagram for the numbers of significant SNPs and associated loci identified by the tests at the 5 × 10⁻⁸ genome-wide significance level for analyzing the Volume IDP set. aMAT, MAT(50), MAT(1), and SUM identified 801, 671, 3, and 25 significant SNPs, respectively. More important, aMAT, MAT(50), MAT(1), and SUM detected 453, 347, 0, and 18 significant and novel SNPs, respectively; a significant and novel SNP is defined as the genome-wide significant SNP but not detected by any individual GWAS analysis at the 5 × 10⁻⁸ genome-wide significance level. We further compared the results at the risk region level; a risk region is defined by LDetect (Berisa and Pickrell 2016). aMAT detected 23 risk regions, while MAT(1) and SUM identified 1 and 3 risk regions, respectively. Of note, each test detected some risk regions that have been ignored by other tests. For example, aMAT and SUM tests identified five and three risk regions that were ignored by other methods, respectively. This illustrates that each test can be more powerful than the others under certain genetic architectures. For analyzing other IDP sets, we obtained similar results (Figures S27–S30).

Discussion

We have introduced aMAT, a multi-trait association test, to conduct jointly analysis of any number of traits. Through simulations and real data analyses, we demonstrated that aMAT could yield well-controlled Type l error rates and achieve high statistical power across a wide range of scenarios. To our knowledge, this is the very first method that is designed to deal with multi-trait analysis of any number of traits. As deep phenotyping data are becoming rapidly available and popular, we expect that aMAT will serve as a useful tool to better understand the genetic architecture of complex traits. As an illustration, we applied aMAT to the Volume set (of 58 volumetric IDPs) and identified 28 lead SNPs located in 24 distinct risk loci, 13 of which were missed by any individual IDP tests at the genome-wide significance level 5 × 10⁻⁸. These identified lead SNPs were well replicated by an independent dataset (Hibar et al. 2015).

aMAT is a computationally efficient method since P-values can be calculated analytically. We further improved the computational efficiency by precalculating the distribution under the null, which remains the same for all SNPs. For example, by a parallel computing strategy with 100 cores in a standard server (each core has 4 GB memory), aMAT completed calculating p-values for multi-trait analysis of volumetric set in 2.2 min (∼9.97 million SNPs in total, Table S16). Of note, because aMAT involves combining results from different tests, it is excepted that aMAT is slightly slower than competing methods. To facilitate data analysis for both statistical and clinical investigators, we have implemented our proposed method aMAT into open-source software.

aMAT is a general framework and can be easily extended to incorporate other multi-trait methods such as MTAG (Turley et al. 2018), N-GWAMA (Baselmans et al. 2019), and HIPO (Qi and Chatterjee 2018). Specifically, we can treat any other powerful multi-trait test as an individual MTA test and then apply aMAT to combine their results to further improve the power. However, since most multi-trait methods are originally designed for analyzing a few phenotypes jointly and ignore the potential singularity problems of the trait correlation matrix, some minor adaptions and strict evaluations are needed. Thus, we leave it to our future work. More importantly, we view aMAT to be complementary (rather than superior) to standard GWAS. This is because standard GWAS focus on a single trait and may identify several risk loci that have been ignored by aMAT.

We conclude with two limitations of our proposed method aMAT. First, the optimal choice of Γ is unknown. Of note, the default setting $\text{Γ}=\left\{1,10,30,50\right\}$ performs well in both simulations and real data analyses. We further evaluated several different choices of Γ and found that aMAT results were robust to the choice of Γ in many simulation settings (Figure S31). However, there is no theoretical guarantee for our default choice of Γ. Second, aMAT applies LDSC to estimate the trait correlation matrix, and, therefore, inherits both benefits and limitations from LDSC. For example, aMAT applies the univariate LDSC to estimate the diagonal elements of the trait correlation matrix, and univariate LDSC is known to be biased for a trait with high (SNP) heritability (de Vlaming et al. 2017). We leave these interesting topics for future work.