Social distancing merely stabilized COVID‐19 in the United States

Abstract

Social distancing measures have been imposed across the United States in order to stem the spread of COVID‐19. We quantify the reduction in the doubling rate, by state, that is associated with this intervention. Using the earlier of K‐12 school closures and restaurant closures, by state, to define the start of the intervention, and considering daily confirmed cases through April 23, 2020, we find that social distancing is associated with a statistically‐significant ( p < 0.01) reduction in the doubling rate for all states except for Nebraska, North Dakota, and South Dakota, when controlling for false discovery, with the doubling rate averaged across the states falling from 0.302 (0.285, 0.320) days ⁻¹ to 0.010 (−0.007, 0.028) days ⁻¹ . However, we do not find that social distancing has made the spread subcritical. Instead, social distancing has merely stabilized the spread of the disease. We provide an illustration of our findings for each state, including estimates of the effective reproduction number, R, both with and without social distancing. We also discuss the policy implications of our findings.

1. INTRODUCTION

Over one million Americans are confirmed to have contracted SARS‐CoV‐2, the virus that causes COVID‐19, as of April 28, 2020 (New York Times Github repository, 2020). Efforts to stem the spread of the disease have resulted in unprecedented societal disruptions (Akay & Akay, 2020; Akiyama, Spaulding, & Rich, 2020; Chen, Coura‐Filho, & Rehder, 2020; Fauci, Lane, & Redfield, 2020; Gallagher & Schleyer, 2020; Gandhi, Havlir, & Yokoe 2020; Gandhi, Del Rio, & Lynch, 2020; Gates, 2020). These efforts have largely taken the form of mandated or recommended social distancing measures by state and local governments. These social distancing measures incur substantial economic cost (Ashworth, Finnoff, Newbold, Shogren, & Thunstrom, 2020; Greenstone & Nigam, 2020). At the same time, their efficacy in reducing the spread of the disease is presumed but not well understood.

Around mid‐March, the 50 states and the District of Columbia independently imposed a similar suite of social distancing measures at nearly the same time. These measures appear to have caused a substantial, albeit delayed, and change to the spread of the virus (e.g., Figure 1). By separately analysing the spread of the virus before and after these interventions, appropriately correcting for delays in their effect, one can test and quantify their effectiveness.

FIGURE 1.

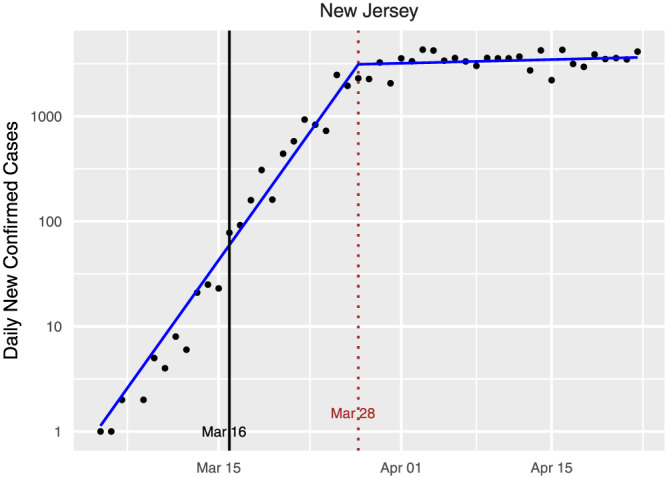
New confirmed cases of COVID‐19 by day for New Jersey, along with the fitted model from our learned‐delay analysis. Under our definition, New Jersey began social distancing on March 16, and a clear changepoint is observed around 12 days later. A 12‐day delay between infection and a confirmed test is consistent with other states and with the independent estimate in Appendix C1. Note that the number of new cases per day appears to have merely plateaued as a result of the intervention. We call this the standard plot for New Jersey. Standard plots for all states and the District of Columbia are available in Appendix B

1.1. Contributions and findings

Using an interrupted time series analysis of the confirmed case counts, we estimate the doubling rate of the spread across the different states in the United States both before and after the imposition of widespread social distancing measures (hereafter, the “intervention”). Compensating for the delay between infection and confirmed diagnosis is a central component of the analysis. We find that in all states except Nebraska, North Dakota, and South Dakota, the intervention is associated with a statistically‐significant decrease in the doubling rate of the spread. The average of the pre‐intervention doubling‐rate point estimates across the states was 0.302 days⁻¹ , meaning that the number of new infections per day was doubling every 3.31 days. Post‐intervention, the average fell to 0.010 days⁻¹ , meaning that the number of infections was still increasing, but required about 100 days to double. We are not able to conclude that any of the states made the spread subcritical (i.e., obtained a negative doubling rate) through the interventions, although some have negative point estimates of the post‐intervention doubling rate. Thus, while this study finds substantial evidence that social distancing interventions reduce the transmission rate of SARS‐CoV‐2, it also suggests that these measures are insufficient to make the spread subcritical. That is, social distancing has largely plateaued, but not decreased, the number of infected individuals. The policy implications of this finding are discussed in Section 5.

As part of the analysis, we estimate the average delay between infection and confirmed diagnosis using two different methods. These give estimates of 11.5 and 12 days, respectively, which are consistent with an estimate obtained by combining estimates from the literature on the length of the incubation period and the time between symptom onset and a positive test, as described in Appendix C1.

1.2. Related work

Estimating the doubling rate of a disease like COVID‐19 is related to the problem of estimating the mean number of “descendants” in a Galton‐Walton branching process (Athreya & Ney, 1972). Classical methods (Harris, 1948; Schuhmacher, Sturm, & Zähle, 2016) for that problem assume a time‐invariant distribution over the number of descendants, which differs from the changepoint method used here. More recently, an approach for estimating the number of people infected by individual patients with an infectious disease, not merely the average over this group, has been reported (Wallinga & Teunis, 2004). By considering when specific patients were known to be infected, this gives an estimate of the infection rate over time. This assumes a closed system, however, in which there are no external infections beyond the first. Later workers (Bettencourt & Ribeiro, 2008) noted that this method requires a large number of samples and proposed a Bayesian alternative requiring less data. A recent extension of the latter approach has been applied to COVID‐19 tracking in the United States (Systrom, 2020). That method (and the accompanying dashboard (Systrom, 2020)) does not account for interventions, so it does not provide separate pre‐ and post‐intervention estimates of the parameters, which are necessary for determining the efficacy of the intervention. Intervention‐aware methods, such as those considered here, also provide more accurate real‐time estimates by separating data coming from different regimes. The concern that the Bettencourt and Ribeiro estimator would be slow to reflect interventions has already been raised (Systrom, 2020).

The closest work to the present paper also examines the spread of COVID‐19 in the United States using an interrupted time series analysis with the goal of quantifying the effect of social distancing (Siedner et al., 2020). It finds the impact of social distancing to be relatively modest, increasing the doubling time from 3.3 days to 5.0 days. It implicitly assumes the average time between infection and a confirmed test, which we call the confirmed case delay, to be 4 days. It also relies on data only up to (and including) March 30. Our estimates place the confirmed case delay at around 12 days, so that the effects of the interventions would not appear until late March. By allowing for a 12‐day delay and using data up to and including April 23, we conclude that social distancing interventions are associated with a much larger reduction in the spread of the disease. Studies using Bayesian methods and event‐study regressions have yielded findings that are inline with those of this work (Courtemanche, Garuccio, Le, Pinkston, & Yelowitz, 2020; Dehning et al., 2020).

Interrupted time series (ITS) analysis, which is the primary statistical method used in this work, is a quasi‐experimental study design that has been used to evaluate the effectiveness of policy changes on longitudinal data in public health (Bernal, Cummins, & Gasparrini, 2017; Penfold & Zhang, 2013; Slavova et al., 2018), social sciences (McDowall, McCleary, & Bartos, 2019), and other disciplines.

2. DATA

We have used multiple independent data sources for the various analyses reported in the paper. State‐level cases and death counts were obtained from the New York Times (NYT) Github repository (New York Times Github repository, 2020). These data include only lab‐confirmed cases of COVID‐19 reported by a federal, state, territorial, or local government agency. Thus, it does not count cases that are probable but not confirmed. As only a small set of states are reporting probable cases (e.g., Ohio, Wyoming, and Idaho) starting after April 14, 2020, we rely on confirmed cases in order to be consistent across states.

We have used K‐12 school (Education Week, 2020) and restaurant (Wida, 2020) closures as indicators of interventions. These were chosen because they represent the first widely disruptive social distancing measures that were imposed. If a school closure was announced in the evening, we consider it as applying on the next day. If a closure was announced on a weekend, we used the first weekday for which schools were closed. The earlier of restaurant closing and school closing is defined as the intervention date for each state (Table B4). Taking the earlier of the two reduces the likelihood of anticipatory behaviour.

For the analysis in Appendix C1 on the confirmed case delay, we use data on COVID‐19 cases by illness onset recorded by the CDC (2020). We reference data on testing in New York State in Section 6. These data were obtained from the COVID Tracking Project (2020).

3. METHODOLOGY

We focus on estimating the doubling rate, β , measured in inverse days, of new infections across the 50 states and the District of Columbia 1, both before and after the intervention. We assume that during each period, the number of new infections per day is expressed as

$$2^{\alpha +\beta ·n+W_n}$$ (1)

where n is a discrete time index, α is a constant, and {W _n } is a mean‐zero Gaussian noise process. The parameters α and β are assumed to vary both with the intervention and across states. Other than the change at the intervention, we assume that β is constant over time within a state. This is tantamount to modelling the spread of the disease as a branching process (Athreya & Ney, 1972), which is appropriate if the time horizon is sufficiently short that the fraction of susceptible individuals is approximately constant. When working with branching‐process models of infectious diseases, it is common to consider the expected number of new infections caused by a single infected individual; in epidemiology, this is called the effective reproduction number, R. If R  > 1, then the number of infected individuals grows exponentially, and we say the process is supercritical. If R < 1, it contracts exponentially, and we say the process is subcritical. If R = 1, we call the process critical. One can compute R from the doubling rate β and the distribution of the serial interval using the Lotka‐Euler equation (Dublin & Lotka, 1925; Feller, 1941). For any serial interval distribution, this transformation maps positive β values to superunity R values and negative β values to subunity R values. We focus on the doubling rate, rather than R, because it can be more directly estimated from the time series of confirmed cases and because it is more useful for making short‐term predictions about confirmed case counts and hospital loads. One can obtain a simple upper bound on R in terms of β and the mean serial interval μ by applying Jensen's inequality to the Lotka‐Euler equation (Wallinga & Lipsitch, 2007),

$$R\le 2^{\mu \beta }.$$ (2)

Prior work has estimated μ at 4 days for COVID‐19 (Du et al., 2020; Nishiura, Lintona, & Akhmetzhanova, 2020). All of the doubling‐rate estimates in this paper can be translated to estimated upper bounds on R using this inequality, although the resulting bounds are less certain than the underlying estimates of β due to the exponentiation and uncertainty about μ . 2

Considering each state in isolation, we estimate the doubling rate before and after the intervention as follows. Let C _n denote the number of new confirmed cases on day n, where the index n = 1 refers to the first day after March 1 for which the state records at least two consecutive days of positive confirmed cases. This convention is designed to appropriately handle states with one very early case (e.g., Washington) followed by many days of zero cases. We model C _n as proportional to a delayed version of the quantity in (1):

$$C_{n+N}=\theta ·2^{\alpha +\beta ·n+W_n}$$

where 0 < θ ≤ 1 represents the fraction of newly infected people that are confirmed to have the disease; note that θ can be absorbed into α for the purposes of modelling C _n . We apply the transformation

$$Y_n={\log }_2(1+C_n).$$ (3)

Including the effect of the intervention (but ignoring the effect of the add‐one transformation to C _n ), we model {Y _n } as

$$Y_{n+N}=\alpha +{\beta }_0·n+({\beta }_1-{\beta }_0)·(n-d)·\mathbf{1}(n>d)+W_n,$$ (4)

where 1(·) is the standard indicator function and {W _n } satisfies

$$W_n=\gamma ·W_{n-1}+Z_n,$$ (5)

where {Z _n } is an independent and identically distributed (i.i.d.) Gaussian sequence with mean zero and variance σ ² , making {W _n } a first‐order autoregressive [AR(1)] Gaussian process. The parameter d represents the state‐specific intervention date defined in the previous section. Thus, d is known but state‐dependent. The quantity N, which we call the confirmed case delay, represents the average time (in days) between when someone is infected with SARS‐CoV‐2 and when they are confirmed to have COVID‐19 and included in the published counts. We assume that N is integer‐valued. The parameters β ₀ and β ₁ are the doubling rates before and after, respectively, the intervention. The unknown parameters in the model are

$$\alpha ,{\beta }_0,{\beta }_1,N,\gamma ,{\sigma }^2.$$

We are particularly interested in β ₀ , β ₁ , and N.

For each of the states, we fit the model using two approaches, which differ primarily in how they handle the confirmed case delay, N. The first, which we call the learned‐delay approach, fits N to the data on par with the other parameters in the model. This is tantamount to finding a changepoint in the {Y _n } time series for which there is a significant difference between the doubling rates. The difference between the changepoint epoch and d then forms a point estimate of N. For this purpose, we use an algorithm that declines to identify a changepoint (effectively setting β ₁ = β ₀ ) if there is insufficient evidence of a change (Fearnhead, Maidstone, & Letchford, 2019). For states with a detected changepoint, we then obtain a point estimate of N in addition to the other parameters, which can vary by state. This approach assumes γ = 0, so that the errors are taken to be i.i.d.

The second approach, which we call fixed‐delay, takes the confirmed case delay to be N = 12 for all states. This choice can be justified as follows. First, 11.5 is the median estimate of N across the states obtained by the learned‐delay method (See Figure 3). Second, estimating the confirmed case delay from a separate analysis of CDC data gives a point estimate 12 days, as described in Appendix C1. The fixed‐delay method does not require that γ = 0; that is, it allows for {W _n } to be AR(1). For both methods, the unknown parameters are estimated via maximum likelihood. The code for both methods is available, along with copies of the datasets used and the scripts needed to produce the figures in the paper (Wagner et al., 2020).

FIGURE 3.

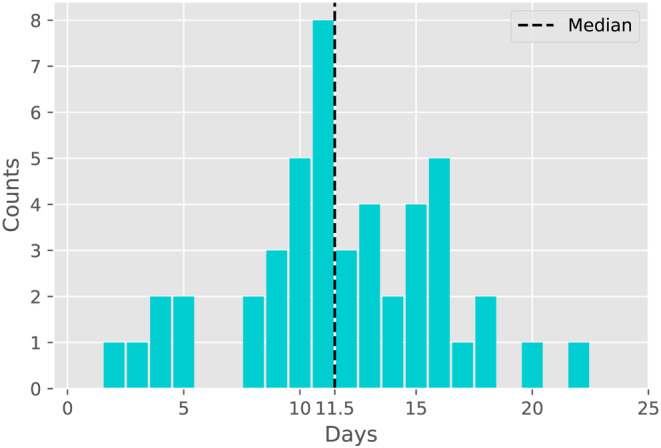
Histogram of point estimates of the confirmed case delay N given in Figure 2

4. RESULTS

Tables B1 and B2 in Appendix B show the results of the learned‐delay model and fixed‐delay model, respectively. Figure 5 compiles all of the findings from both models.

FIGURE 5.

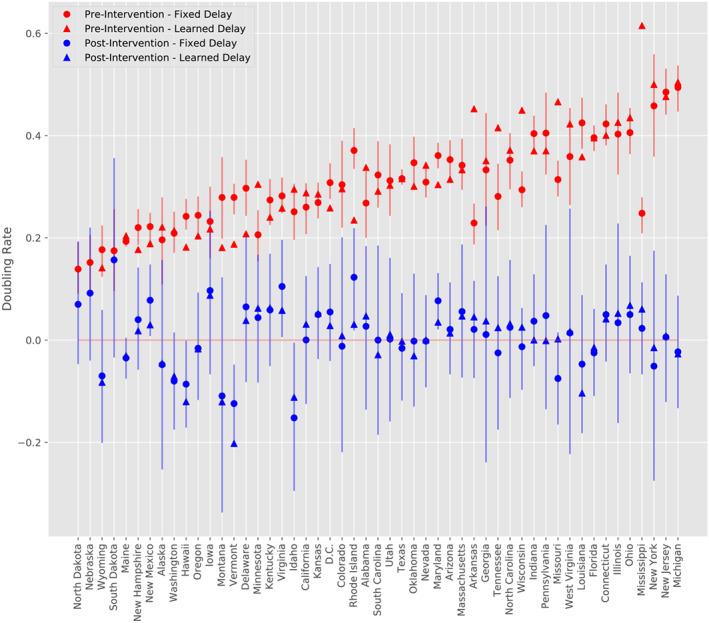
Doubling rate estimates for all states pre‐ and post‐intervention under the learned‐delay and fixed‐delay models. States are in increasing order with respect to the mean of the pre‐intervention doubling rates under the two models. Vertical segments depict approximate 95% confidence intervals for the fixed‐delay model estimates using the t distribution, standard error of slopes, and degrees of freedom obtained from the fixed‐delay model

Table B1 includes the estimates of the confirmed case delay, N, for those states for which a changepoint is detected by the learned‐delay model. This column of the table is plotted in Figure 2, and a histogram is provided in Figure 3. The median is 11.5 days, which supports the choice used in the fixed‐delay model, as noted earlier. The model declines to declare a changepoint for three states, whose standard plots are shown in Figure 4. For such states, this model does not find evidence of the efficacy of the social distancing measures imposed. For Nebraska in particular, the intervention occurred quite late (April 3), so it is possible that the change is simply not observed in the available data. It should also be noted that these states had some of the lowest pre‐intervention doubling rates, according to Figure 5.

FIGURE 2.

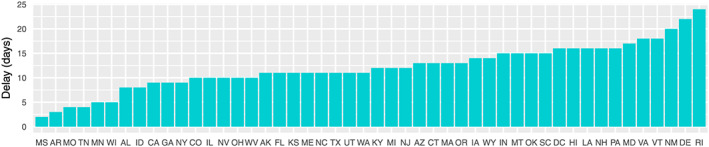
Time between the defined intervention and identified changepoint. This forms an estimate of the confirmed case delay N for each state. Three states (Nebraska, North Dakota, and South Dakota) do not have significant changepoints and are not included

FIGURE 4.

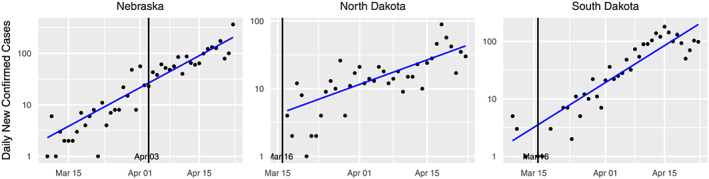
Confirmed case counts for states without a detected changepoint. The vertical black line indicates the intervention date for each state

Standard plots (showing the fitted learned‐delay model) for each state are provided in Figures B1, B2, B3, B4 in Appendix B. As exemplars, we consider three states that were among the first in the United States to have confirmed cases, namely, New York, California, and Washington. These states have large numbers of confirmed cases, making the data from these states of higher quality. Since the number of deaths is at least an order of magnitude lower than the number of cases, for most states, the former is too noisy to be of much use. For these states, however, it provides a useful comparison with the confirmed case counts.

The results of our analysis for these three states are shown in Figure 6. For all three states, we see two regimes for the growth rate for both the confirmed cases and deaths data. The growth rate begins in a supercritical state indicating exponential growth. The growth rate then decreases substantially, presumably indicating that the intervention is making an impact, albeit with a delayed effect. However, we note that the number of confirmed cases and deaths does not rapidly decline after the change for California and New York, whereas the Washington plot appears to show a decrease in both cases and deaths as a result of the intervention.

FIGURE 6.

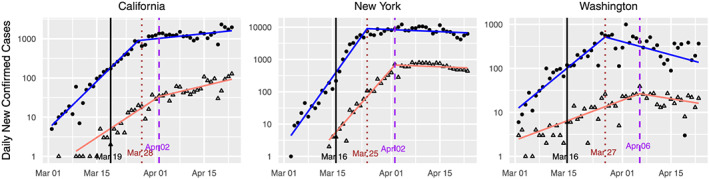
Standard plots for California, New York, and Washington State, augmented with data on confirmed deaths. The vertical black line indicates the intervention date for each state. The sloped lines indicate the fitted values from the learned‐delay method applied to the confirmed case data (blue) and the confirmed deaths data (red)

To determine the significance level of this finding, we turn to the fixed‐delay model, which provides approximate 95% confidence intervals for the doubling rates and their difference (see Table B2) using the Student's t distribution to account for the small sample size. It also provides approximate p values against the null hypotheses that β ₁ ≥ 0, β ₀ ≤ 0, and β ₁ ≥ β ₀ . We utilize a one‐sided t test for both cases, with a significance level of 0.05. A one‐sided test is appropriate since we hypothesize the pre‐intervention period should show signs of rapid growth in the number of cases, and after the intervention, there should be a significant decrease in the doubling rate. We find that the intervention is associated with a statistically‐significant decrease in the doubling rate ( p < 0.01) for all states, even after controlling for false discovery rates using the Benjamini‐Hochberg procedure (Benjamini & Hochberg, 1995), except for Nebraska, South Dakota, and North Dakota. When controlling for false discovery, we are not able to conclude that any of the states have achieved a negative β ₁ ; Washington comes the closest with respect to statistical significance. Recall that Nebraska, South Dakota, and North Dakota are also the states for which the learned‐delay method does not find a significant changepoint.

The point estimates across the ensemble of states also show a substantial reduction in the doubling rate associated with the intervention, with the post‐intervention doubling rate being close to critical. The pre‐intervention doubling‐rate averaged across all states is 0.302 (0.285,0.320) days ⁻¹ . Post‐intervention, it is 0.010 (− 0.007,0.028) days ⁻¹ , the difference being −0.292 (−0.296, −0.288) days ⁻¹ . Using Equation (2), these estimates translate to estimated upper bounds on R pre‐ and post‐intervention of 2.310 and 1.028, respectively, or a 55% reduction in contact between contagious and susceptible individuals. It should be emphasized, however, that there is a considerable variation in these values among the states, and the R induced from the average doubling rate is distinct from the average of the induced R values. Estimated bounds on R for each state are provided in Table B3 and Figure 7.

FIGURE 7.

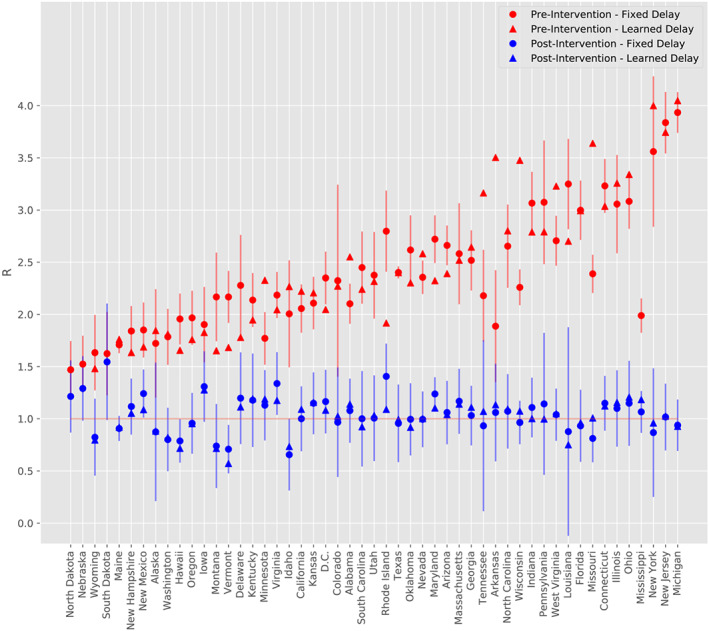
Estimated R for all states pre‐intervention and post‐intervention under the learned‐delay and fixed‐delay models. States are in increasing order with respect to the mean of pre‐intervention doubling‐rate point estimates under the fixed‐delay and learned‐delay models. Vertical segments depict approximate 95% confidence intervals for the estimated R using the Delta method and standard error estimates of slopes from the fixed‐delay model, conditional on the estimate μ = 4 days. The pre‐intervention estimate of R in the learned‐delay model for Mississippi (5.50) is not shown

Thus, while this study finds social distancing measures to be effective at reducing the spread of SARS‐CoV‐2, it does not find conclusive evidence that they have pushed the spread into the subcritical ( β ₁ < 0) regime. Across the ensemble of states, the post‐intervention slopes are in fact quite close to zero. The mean slope of the point estimates is 0.010 days ⁻¹ , as noted earlier, with 31 of the states having a post‐intervention doubling rate between −0.05 and 0.05 days ⁻¹ , which corresponds to a doubling or halving time exceeding 20 days. This indicates that the pandemic across many regions plateaued, rather than contracted, post‐intervention, with each infected individual infecting nearly one other individual on average ( R = 1). In those locations, COVID‐19 under social distancing provides a naturally occurring example of a near‐critical branching process (Athreya & Ney, 1972), and the observed plateau should be contrasted with the symmetrical apex that is presumed in some predictive models (IHME COVID‐19 health service utilization forecasting team, 2020).

For the fixed‐delay method, we conducted a sensitivity analysis on the order of the autoregressive noise process and found that allowing for higher order dependence did not significantly improve the fit. For each state, we conducted a Ljung‐Box test for up to 7 lags on the residuals of our fixed‐delay model, and after adjusting for multiple testing using an FDR procedure (Benjamini & Hochberg, 1995), none of the states showed evidence of higher order autocorrelation. We also tested for residual normality using Kolmogorov‐Smirnov test and also found that after adjusting for multiple testing, none of the states showed statistically‐significant deviations from normality.

5. POLICY IMPLICATIONS

This study finds that the social distancing measures enacted in the United States are associated with a significant decrease in the doubling rate of COVID‐19 infections. Indeed, the exponential growth that was observed pre‐intervention was stabilized with the intervention. The study thus provides support for the use of social distancing measures. The study also points to the importance of timeliness when imposing such measures. Roughly speaking, the number of daily new cases was doubling every 3 days pre‐intervention and became constant with the intervention. As such, we expect that intervening just 3 days earlier would have halved the number of daily new cases post‐intervention.

Given the substantial social and economic costs of such measures, there is interest in the question of when they should be relaxed. As of late April, some states have already begun this process with Georgia allowing certain businesses, such as gyms and barbershops, to reopen (Hagemann & Booker, 2020). In fact, Alabama, Florida, Georgia, Mississippi, South Carolina, and Tennessee announced a coordinated attempt to reopen (Dixon, 2020; McArdle, 2020). Standard plots for these states are shown in Figure 8.

FIGURE 8.

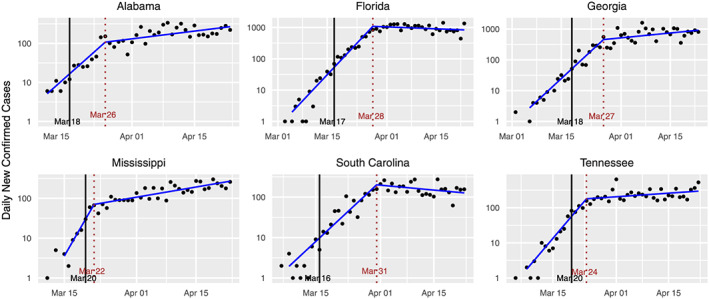
Standard plots for several states proposing an imminent relaxation of social distancing measures as of April 26

Since a systematic relaxation of social distancing will presumably increase the doubling rate, from a public health perspective, it is advisable to relax such measures only when there is evidence that the spread has become subcritical. Among negative doubling rates, those that are farther from zero (i.e., are larger in absolute value) allow for more relaxation of social distancing measures without the spread returning to supercriticality.

We see that the curves for these states appear similar to those for the early states in Figure 6. In particular, we see a substantial change in the growth rate occurring some days after the intervention, but the spread does not appear to have become subcritical, with the exception of South Carolina and possibly Florida. This study finds that other states, such as Idaho, Vermont, Montana, Washington, and Hawaii have a stronger basis for relaxing social distancing at this time.

The lack of clear subcriticality among the post‐intervention doubling rates suggests that existing social distancing measures will need to remain in place for some time. On the other hand, it is possible that a subset of the existing social distancing measures are responsible for the observed reductions in the doubling rate. If this is the case, then the remaining measures could be relaxed with no harmful effect. Also, any additional measures taken, such as contract tracing or the use of masks, will tend to reduce the doubling rate further. Finally, in the absence of a change in interventions, the doubling rate will tend to decrease over time as the population of susceptible individuals decreases.

6. LIMITATIONS OF THE ANALYSIS

Our analysis relies on the number of confirmed cases of COVID‐19 reported by federal, state, territorial, and local authorities. Beyond the delay between infection and confirmation, which was discussed earlier, this statistic likely underestimates the number of actual cases, and it could be subject to selection bias. We note, however, that if the confirmed case counts reflect a constant fraction θ of the actual number of cases, as assumed in our model, then this undercount will not materially affect the estimation of the doubling rate β since θ · C _n and C _n grow at the same exponential rate. Likewise, the doubling rates in different subpopulations cannot diverge so long as those subpopulations are sufficiently connected, making sampling bias less of a concern.

Of greater concern is variability in the availability of tests, as temporal variation in testing could affect the estimates of the doubling rate. New York State, for instance, saw a rapid increase in the number of daily tests followed by a plateauing around March 19, as shown in Figure 9. This approximately coincides with the detected changepoint in the number of confirmed cases by the learned‐delay method. It is possible that for some states, the abrupt change that we detect in confirmed cases does not reflect an actual change in the spread of disease but only a change in detection capabilities.

FIGURE 9.

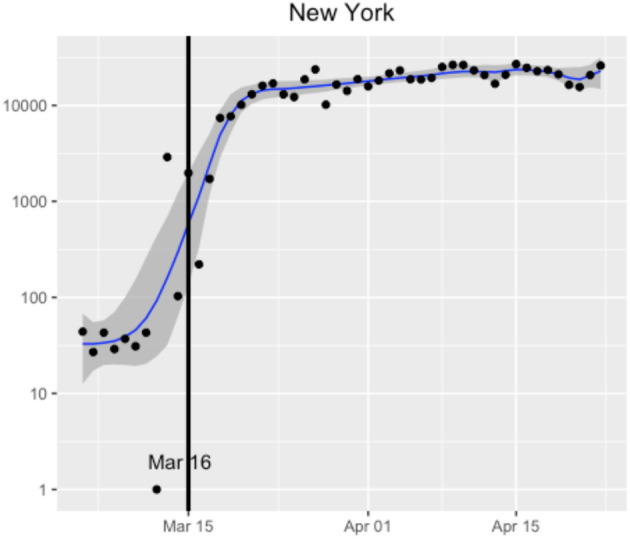
The daily number of tests in New York State. The vertical black line indicates the intervention date. The blue line indicates a smoothed trend estimated by the dynamic shrinkage model (Kowal, Matteson, & Ruppert, 2019), with corresponding dark grey (credible) bands reflecting variability in the trend estimate

Controlling for this effect is challenging because the data on the number of tests are subject to additional types of errors. States vary in whether their test counts report the number of distinct people tested or the number of tests performed and whether they represent the number of tests taken or completed. Data on the number of tests is also not available for all of the states for the time interval considered here, as some states initially reported only confirmed cases.

One could potentially rely on the number of deaths attributed to COVID‐19 instead of the number of confirmed cases. This approach is subject to four complications, however. First, the mean time between infection and death is presumably longer than the time between infection and confirmed diagnosis. Second, the number of deaths is a noisier signal because the number of deaths is lower than the number of confirmed cases, often by an order of magnitude, as noted earlier. Third, improvements in treatment could decrease the infection fatality rate over time, causing a decrease in recorded deaths that is independent of social distancing measures. Finally, some states have not been performing COVID‐19 tests post‐mortem. In this case, any reported COVID‐19 death would have been already reported as a confirmed case and would not reveal new information about the number of infections.

Mitigating this concern, we note that for New York, the number of tests plateaued slightly before the number of cases did. We also note that data on deaths and hospitalizations, while lower in quality than the number of confirmed cases, are broadly consistent with the findings based on the confirmed case count alone. Notably, we do not see pronounced increases or decreases in deaths or hospitalizations post‐intervention for states in which the estimated doubling rate post‐intervention is near zero. We also do not see a saturation in the fraction of positive tests, which would indicate an uncaptured exponential increase in the number of actual COVID‐19 patients. Finally, several states have continued to see supercritical growth post‐intervention.

Another limitation of our analysis is that it treats states separately and thereby ignores the influence that neighbouring states have on one another. Nor does it capitalize on the potential similarity among the model parameters for similar states. We also assume an unchanging reservoir of susceptible individuals; an SIR‐type model (e.g., Martcheva, 2015) is appropriate when the fraction of the population that is exposed to the virus varies over the period under study. Our analysis assumes a single changepoint when the first large‐scale social distancing measures are imposed. It cannot distinguish among the relative benefits of different interventions imposed around the same time. It also does not account for anticipatory behavioural changes that could have preceded the formal imposition of interventions. Several factors, for which this study does not control, could have contributed to differing doubling rates between the pre‐ and post‐intervention periods, separate from the social distancing measures considered here. These include improvements in treatment, changes in the weather, and the adoption of mask‐wearing. An analysis that controls for these effects would be valuable, as would one that used mobility data instead of state policies as the input. Subsequent analyses may require additional changepoints as states relax, and possibly reimpose, social distancing measures, however. The confirmed case delay could also vary over time as a result of changing testing protocols.

APPENDIX A. AN INDEPENDENT ESTIMATE OF THE CONFIRMED CASE DELAY

A.1.

The quantity N is the sum of the mean incubation time and the mean time between symptom onset and confirmed diagnosis. Various works have estimated the mean incubation time to be 5 days (Backer, Klinkenberg, & Wallinga, 2020; Lauer et al., 2020; Li et al., 2020). We focus here on estimating the time between symptom onset and confirmed diagnosis.

We estimate this quantity using data from the CDC (2020). The CDC reports COVID‐19 cases in the United States by date of illness onset from January 12, 2020, to April 15, 2020, as well as by date of confirmed diagnosis (Figure A1, top). The CDC warns that estimates are not accurate after April 5, 2020, due to difficulty in accurately determining illness onset after community spread began.

FIGURE A1.

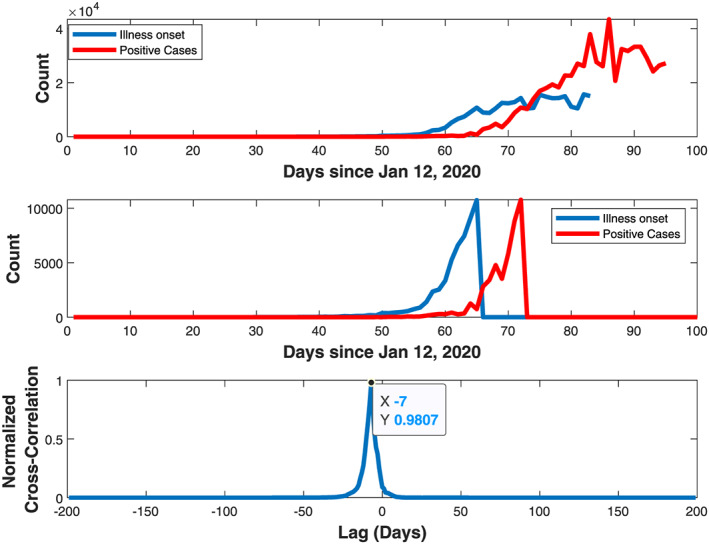
Estimation of confirmed case delay via cross‐correlation between illness‐onset and positive case confirmation time series

We truncate the time series so that both end when their respective cumulative counts reach 10, 000 (Figure A1, middle). The lag between illness onset and case confirmation is determined using a normalized cross‐correlation operation (Figure A1, bottom). The lag is estimated to be 7 days. When added to the incubation time, this results in a total time of 12 days from exposure to confirmed test, which essentially coincides with the estimate of 11.5 days obtained in the body of the paper. An earlier work estimated the mean time from symptom onset to confirmed test to be 4.8 days (Pellis et al., 2020), which translates to a point estimate of N of about 10 days.

APPENDIX B. PARAMETER ESTIMATES AND STANDARD PLOTS FOR ALL STATES

B.1.

TABLE B1.

Results from the learned‐delay model

State	Intervention date	Change date	N	β 0	β 1	β 1 − β 0
Alabama	03‐18	03‐26	8	0.338	0.047	−0.291
Alaska	03‐16	03‐27	11	0.221	−0.045	−0.266
Arizona	03‐16	03‐29	13	0.314	0.014	−0.301
Arkansas	03‐17	03‐20	3	0.452	0.045	−0.407
California	03‐19	03‐28	9	0.288	0.031	−0.257
Colorado	03‐17	03‐27	10	0.296	0.008	−0.287
Connecticut	03‐16	03‐29	13	0.4	0.041	−0.359
Delaware	03‐16	04‐07	22	0.208	0.038	−0.169
D.C.	03‐16	04‐01	16	0.258	0.028	−0.23
Florida	03‐17	03‐28	11	0.395	−0.015	−0.41
Georgia	03‐18	03‐27	9	0.351	0.037	−0.313
Hawaii	03‐16	04‐01	16	0.182	−0.12	−0.302
Idaho	03‐23	03‐31	8	0.295	−0.112	−0.407
Illinois	03‐16	03‐26	10	0.426	0.052	−0.374
Indiana	03‐16	03‐31	15	0.37	0.0	−0.37
Iowa	03‐17	03‐31	14	0.217	0.088	−0.129
Kansas	03‐17	03‐28	11	0.285	0.052	−0.233
Kentucky	03‐16	03‐28	12	0.24	0.063	−0.177
Louisiana	03‐16	04‐01	16	0.358	−0.104	−0.462
Maine	03‐18	03‐29	11	0.204	−0.031	−0.234
Maryland	03‐16	04‐02	17	0.304	0.035	−0.269
Massachusetts	03‐17	03‐30	13	0.333	0.047	−0.286
Michigan	03‐16	03‐28	12	0.504	−0.027	−0.531
Minnesota	03‐17	03‐22	5	0.305	0.062	−0.242
Mississippi	03‐20	03‐22	2	0.615	0.06	−0.555
Missouri	03‐23	03‐27	4	0.466	0.002	−0.464
Montana	03‐16	03‐31	15	0.181	−0.121	−0.302
Nebraska	04‐03	N/A	N/A	0.147	0.147	N/A
Nevada	03‐16	03‐26	10	0.342	0.0	−0.342
New Hampshire	03‐16	04‐01	16	0.177	0.018	−0.159
New Jersey	03‐16	03‐28	12	0.476	0.008	−0.468
New Mexico	03‐16	04‐05	20	0.189	0.03	−0.159
New York	03‐16	03‐25	9	0.5	−0.015	−0.515
North Carolina	03‐16	03‐27	11	0.371	0.032	−0.34
North Dakota	03‐16	N/A	N/A	0.086	0.086	N/A
Ohio	03‐15	03‐25	10	0.435	0.068	−0.367
Oklahoma	03‐17	04‐01	15	0.301	−0.031	−0.332
Oregon	03‐16	03‐29	13	0.204	−0.017	−0.221
Pennsylvania	03‐16	04‐01	16	0.37	−0.001	−0.371
Rhode Island	03‐16	04‐09	24	0.235	0.031	−0.204
South Carolina	03‐16	03‐31	15	0.291	−0.029	−0.32
South Dakota	03‐16	N/A	N/A	0.153	0.153	N/A
Tennessee	03‐20	03‐24	4	0.415	0.024	−0.391
Texas	03‐21	04‐01	11	0.316	−0.003	−0.318
Utah	03‐16	03‐27	11	0.303	0.011	−0.292
Vermont	03‐17	04‐04	18	0.188	−0.202	−0.39
Virginia	03‐16	04‐03	18	0.258	0.058	−0.2
Washington	03‐16	03‐27	11	0.214	−0.071	−0.285
West Virginia	03‐16	03‐26	10	0.423	0.017	−0.406
Wisconsin	03‐17	03‐22	5	0.449	0.025	−0.424
Wyoming	03‐19	04‐02	14	0.141	−0.082	−0.224

Note: The confirmed case delay N is quoted in days. All β parameters are quoted in days ⁻¹ . All dates are in calendar year 2020.

TABLE B2.

Results from the fixed‐delay model with one‐sided t test and approximate 95% CIs for pre‐ and post‐intervention slopes and their difference

State	β 0	95% CI	β 1	95% CI	β 1 − β 0	95% CI
Alabama	0.268***	(0.22, 0.32)	0.027	(−0.09, 0.15)	−0.241***	(−0.31, −0.17)
Alaska	0.196***	(0.14, 0.25)	−0.048	(−0.18, 0.08)	−0.243***	(−0.32, −0.17)
Arizona	0.353***	(0.3, 0.4)	0.021	(−0.11, 0.15)	−0.332***	(−0.41, −0.25)
Arkansas	0.229***	(0.15, 0.31)	0.021	(−0.17, 0.22)	−0.208***	(−0.33, −0.09)
California	0.26***	(0.25, 0.27)	0	(−0.04, 0.04)	−0.26***	(−0.29, −0.23)
Colorado	0.304***	(0.27, 0.34)	−0.012	(−0.11, 0.09)	−0.316***	(−0.38, −0.25)
Connecticut	0.423***	(0.39, 0.45)	0.05	(−0.02, 0.12)	−0.373***	(−0.42, −0.33)
Delaware	0.297***	(0.21, 0.38)	0.065	(−0.14, 0.27)	−0.232***	(−0.36, −0.11)
D.C.	0.308***	(0.27, 0.35)	0.055	(−0.04, 0.15)	−0.253***	(−0.31, −0.2)
Florida	0.396***	(0.37, 0.43)	−0.025	(−0.11, 0.06)	−0.42***	(−0.47, −0.37)
Georgia	0.333***	(0.29, 0.37)	0.011	(−0.09, 0.12)	−0.321***	(−0.39, −0.25)
Hawaii	0.242***	(0.17, 0.31)	−0.086	(−0.25, 0.07)	−0.328***	(−0.42, −0.23)
Idaho	0.251***	(0.17, 0.33)	−0.152	(−0.38, 0.08)	−0.402***	(−0.56, −0.25)
Illinois	0.403***	(0.37, 0.43)	0.034	(−0.04, 0.11)	−0.369***	(−0.42, −0.32)
Indiana	0.404***	(0.35, 0.46)	0.037	(−0.11, 0.18)	−0.367***	(−0.46, −0.28)
Iowa	0.232***	(0.18, 0.28)	0.097	(−0.03, 0.22)	−0.134***	(−0.21, −0.05)
Kansas	0.269***	(0.22, 0.31)	0.05	(−0.06, 0.16)	−0.219***	(−0.29, −0.15)
Kentucky	0.274***	(0.24, 0.31)	0.059	(−0.04, 0.15)	−0.215***	(−0.27, −0.16)
Louisiana	0.425***	(0.37, 0.48)	−0.047	(−0.19, 0.1)	−0.472***	(−0.56, −0.38)
Maine	0.193***	(0.14, 0.24)	−0.035	(−0.16, 0.09)	−0.227***	(−0.31, −0.15)
Maryland	0.361***	(0.33, 0.4)	0.077	(−0.01, 0.17)	−0.284***	(−0.34, −0.23)
Massachusetts	0.342***	(0.31, 0.38)	0.056	(−0.04, 0.15)	−0.286***	(−0.35, −0.22)
Michigan	0.494***	(0.41, 0.58)	−0.023	(−0.23, 0.19)	−0.518***	(−0.64, −0.39)
Minnesota	0.206***	(0.17, 0.25)	0.044	(−0.06, 0.14)	−0.162***	(−0.22, −0.1)
Mississippi	0.248***	(0.18, 0.31)	0.023	(−0.14, 0.18)	−0.225***	(−0.32, −0.13)
Missouri	0.314***	(0.25, 0.38)	−0.075	(−0.26, 0.11)	−0.389***	(−0.52, −0.26)
Montana	0.279***	(0.21, 0.35)	−0.109	(−0.27, 0.05)	−0.388***	(−0.48, −0.3)
Nebraska	0.152***	(0.14, 0.17)	0.092	(−0.01, 0.2)	−0.06	(−0.16, 0.04)
Nevada	0.309***	(0.26, 0.36)	−0.002	(−0.13, 0.13)	−0.311***	(−0.39, −0.23)
New Hampshire	0.22***	(0.19, 0.25)	0.04	(−0.05, 0.13)	−0.18***	(−0.24, −0.12)
New Jersey	0.485***	(0.46, 0.51)	0.006	(−0.05, 0.06)	−0.478***	(−0.52, −0.44)
New Mexico	0.222***	(0.18, 0.26)	0.078	(−0.01, 0.17)	−0.144***	(−0.2, −0.09)
New York	0.458***	(0.41, 0.51)	−0.051	(−0.18, 0.08)	−0.509***	(−0.6, −0.42)
North Carolina	0.352***	(0.31, 0.39)	0.025	(−0.07, 0.12)	−0.327***	(−0.39, −0.27)
North Dakota	0.139***	(0.03, 0.25)	0.07	(−0.18, 0.32)	−0.07	(−0.21, 0.07)
Ohio	0.406***	(0.34, 0.47)	0.05	(−0.1, 0.2)	−0.357***	(−0.45, −0.27)
Oklahoma	0.347***	(0.29, 0.4)	−0.002	(−0.14, 0.13)	−0.348***	(−0.43, −0.27)
Oregon	0.244***	(0.21, 0.28)	−0.016	(−0.1, 0.06)	−0.259***	(−0.31, −0.21)
Pennsylvania	0.405***	(0.37, 0.44)	0.048	(−0.04, 0.14)	−0.357***	(−0.42, −0.3)
Rhode Island	0.371***	(0.29, 0.45)	0.123	(−0.06, 0.3)	−0.247***	(−0.35, −0.15)
South Carolina	0.323***	(0.29, 0.36)	0	(−0.09, 0.09)	−0.323***	(−0.38, −0.27)
South Dakota	0.175***	(0.08, 0.27)	0.157	(−0.08, 0.4)	−0.017	(−0.16, 0.13)
Tennessee	0.281***	(0.23, 0.33)	−0.025	(−0.16, 0.11)	−0.306***	(−0.4, −0.22)
Texas	0.316***	(0.29, 0.34)	−0.016	(−0.1, 0.07)	−0.333***	(−0.4, −0.27)
Utah	0.312***	(0.27, 0.35)	0.002	(−0.09, 0.1)	−0.31***	(−0.37, −0.25)
Vermont	0.279***	(0.2, 0.36)	−0.124	(−0.32, 0.07)	−0.403***	(−0.52, −0.29)
Virginia	0.282***	(0.24, 0.33)	0.105	(−0.01, 0.22)	−0.177***	(−0.25, −0.11)
Washington	0.209***	(0.17, 0.24)	−0.08	(−0.17, 0.01)	−0.289***	(−0.35, −0.23)
West Virginia	0.359***	(0.26, 0.46)	0.014	(−0.21, 0.24)	−0.345***	(−0.47, −0.22)
Wisconsin	0.294***	(0.25, 0.34)	−0.013	(−0.14, 0.11)	−0.307***	(−0.38, −0.23)
Wyoming	0.177***	(0.13, 0.22)	−0.07	(−0.18, 0.04)	−0.248***	(−0.32, −0.18)

Note: All β quantities and their CIs are quoted in days ⁻¹ .

^∗ p < 0.1 for corresponding one‐sided p values.

^∗∗ p < 0.05 for corresponding one‐sided p values.

^{∗ ∗ ∗} p < 0.01 for corresponding one‐sided p values.

TABLE B3.

Estimated upper bound on R from the learned‐delay (LD) and fixed‐delay (FD) models

State	Pre‐intervention R (LD)	Post‐intervention R (LD)	Pre‐intervention R (FD)	Post‐intervention R (FD)
Alabama	2.55	1.14	2.1	1.08
Alaska	1.84	0.88	1.72	0.88
Arizona	2.39	1.04	2.66	1.06
Arkansas	3.5	1.13	1.89	1.06
California	2.22	1.09	2.06	1.0
Colorado	2.27	1.02	2.32	0.97
Connecticut	3.04	1.12	3.23	1.15
Delaware	1.78	1.11	2.28	1.2
D.C.	2.05	1.08	2.35	1.16
Florida	2.99	0.96	3.0	0.93
Georgia	2.64	1.11	2.52	1.03
Hawaii	1.66	0.72	1.96	0.79
Idaho	2.27	0.73	2.01	0.66
Illinois	3.26	1.16	3.06	1.1
Indiana	2.79	1.0	3.07	1.11
Iowa	1.83	1.28	1.9	1.31
Kansas	2.21	1.16	2.11	1.15
Kentucky	1.95	1.19	2.14	1.18
Louisiana	2.7	0.75	3.25	0.88
Maine	1.76	0.92	1.71	0.91
Maryland	2.32	1.1	2.72	1.24
Massachusetts	2.52	1.14	2.58	1.17
Michigan	4.05	0.93	3.93	0.94
Minnesota	2.33	1.19	1.77	1.13
Mississippi	5.5	1.18	1.99	1.07
Missouri	3.64	1.01	2.39	0.81
Montana	1.65	0.72	2.17	0.74
Nebraska	N/A	N/A	1.52	1.29
Nevada	2.58	1.0	2.36	0.99
New Hampshire	1.63	1.05	1.84	1.12
New Jersey	3.74	1.02	3.84	1.02
New Mexico	1.69	1.09	1.85	1.24
New York	4.0	0.96	3.56	0.87
North Carolina	2.8	1.09	2.65	1.07
North Dakota	N/A	N/A	1.47	1.21
Ohio	3.34	1.21	3.08	1.15
Oklahoma	2.3	0.92	2.62	0.99
Oregon	1.76	0.95	1.97	0.96
Pennsylvania	2.79	1.0	3.07	1.14
Rhode Island	1.92	1.09	2.8	1.41
South Carolina	2.24	0.92	2.45	1.0
South Dakota	N/A	N/A	1.62	1.55
Tennessee	3.16	1.07	2.18	0.93
Texas	2.4	0.99	2.4	0.96
Utah	2.32	1.03	2.38	1.01
Vermont	1.68	0.57	2.17	0.71
Virginia	2.04	1.17	2.19	1.34
Washington	1.81	0.82	1.79	0.8
West Virginia	3.23	1.05	2.71	1.04
Wisconsin	3.48	1.07	2.26	0.96
Wyoming	1.48	0.8	1.63	0.82

TABLE B4.

Intervention date by state

State	K‐12 school closure	Restaurant closure	Intervention date	Start date
Alabama	03‐18	03‐19	03‐18	03‐13
Alaska	03‐16	03‐18	03‐16	03‐16
Arizona	03‐16	03‐20	03‐16	03‐06
Arkansas	03‐17	03‐20	03‐17	03‐11
California	03‐19	03‐19	03‐19	03‐01
Colorado	03‐23	03‐17	03‐17	03‐05
Connecticut	03‐17	03‐16	03‐16	03‐08
Delaware	03‐16	03‐16	03‐16	03‐11
D.C.	03‐16	03‐16	03‐16	03‐14
Florida	03‐17	03‐20	03‐17	03‐05
Georgia	03‐18	04‐03	03‐18	03‐06
Hawaii	03‐16	03‐17	03‐16	03‐14
Idaho	03‐23	03‐25	03‐23	03‐13
Illinois	03‐17	03‐16	03‐16	03‐05
Indiana	03‐19	03‐16	03‐16	03‐08
Iowa	04‐02	03‐17	03‐17	03‐08
Kansas	03‐17	03‐20	03‐17	03‐12
Kentucky	03‐16	03‐16	03‐16	03‐08
Louisiana	03‐16	03‐17	03‐16	03‐09
Maine	04‐02	03‐18	03‐18	03‐12
Maryland	03‐16	03‐16	03‐16	03‐08
Massachusetts	03‐17	03‐17	03‐17	03‐05
Michigan	03‐16	03‐16	03‐16	03‐12
Minnesota	03‐18	03‐17	03‐17	03‐10
Mississippi	03‐20	03‐24	03‐20	03‐15
Missouri	03‐23	03‐23	03‐23	03‐12
Montana	03‐16	03‐20	03‐16	03‐13
Nebraska	04‐03	04‐03	04‐03	03‐10
Nevada	03‐16	03‐21	03‐16	03‐11
New Hampshire	03‐16	03‐16	03‐16	03‐02
New Jersey	03‐18	03‐16	03‐16	03‐04
New Mexico	03‐16	03‐19	03‐16	03‐11
New York	03‐18	03‐16	03‐16	03‐03
North Carolina	03‐16	03‐17	03‐16	03‐11
North Dakota	03‐16	03‐20	03‐16	03‐17
Ohio	03‐16	03‐15	03‐15	03‐11
Oklahoma	03‐17	04‐01	03‐17	03‐13
Oregon	03‐16	03‐17	03‐16	03‐07
Pennsylvania	03‐16	03‐19	03‐16	03‐06
Rhode Island	03‐16	03‐17	03‐16	03‐16
South Carolina	03‐16	03‐18	03‐16	03‐08
South Dakota	03‐16		03‐16	03‐10
Tennessee	03‐20	03‐23	03‐20	03‐08
Texas	03‐23	03‐21	03‐21	03‐04
Utah	03‐16	03‐19	03‐16	03‐10
Vermont	03‐18	03‐17	03‐17	03‐14
Virginia	03‐16	03‐25	03‐16	03‐07
Washington	03‐17	03‐16	03‐16	03‐01
West Virginia	03‐16	03‐18	03‐16	03‐17
Wisconsin	03‐19	03‐17	03‐17	03‐09
Wyoming	03‐19	03‐19	03‐19	03‐13

Note: The intervention date is defined to be the earlier of the K‐12 closure date and the restaurant closure date. The start date is the first day after March 1 for which there are two consecutive days of new cases. All dates are in calendar year 2020.

FIGURE B1.

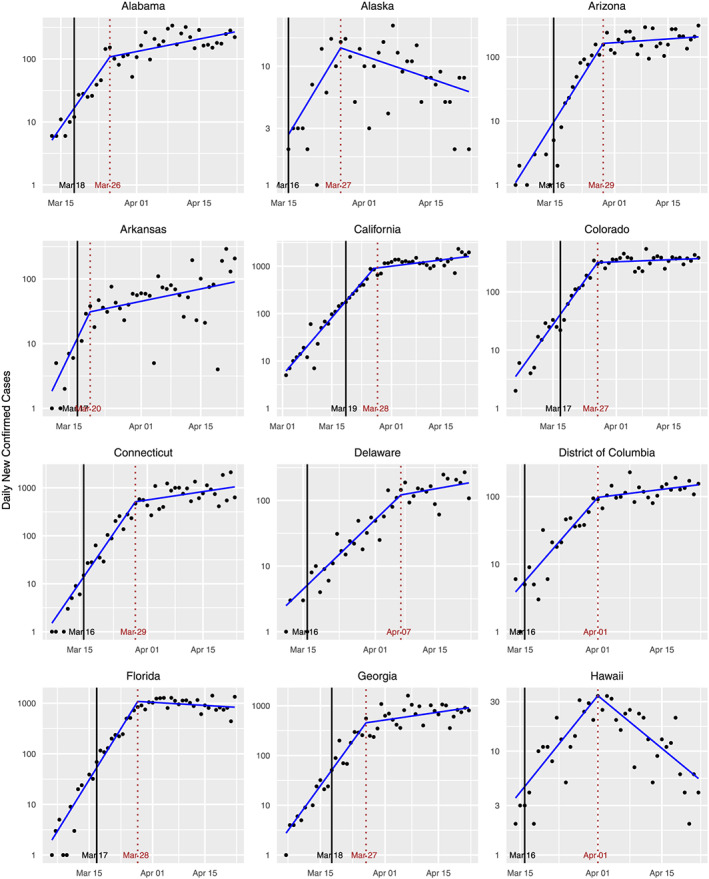
Standard plots for various states

FIGURE B2.

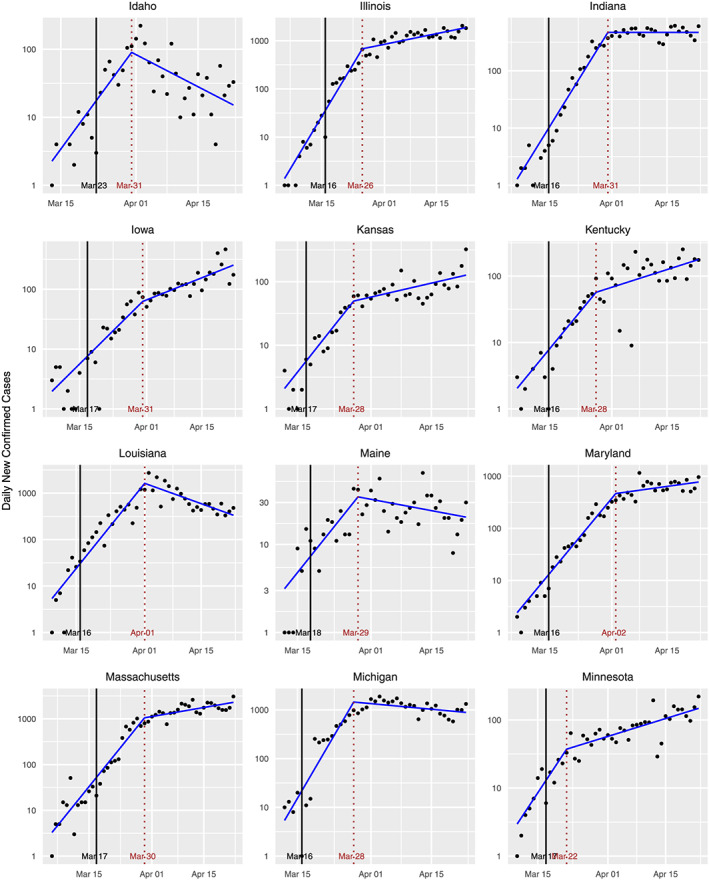
Standard plots for various states

FIGURE B3.

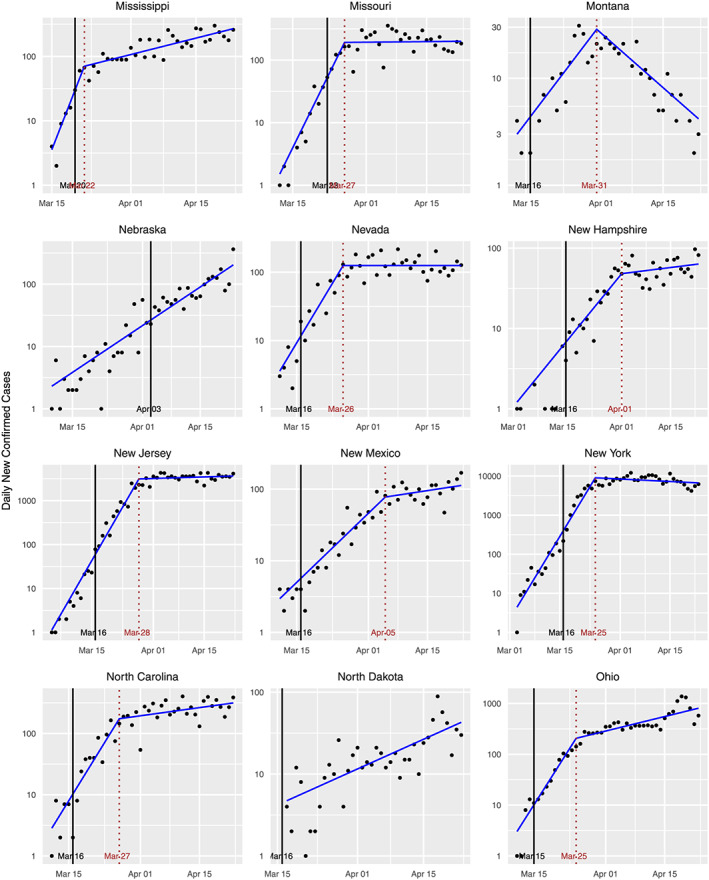
Standard plots for various states

FIGURE B4.

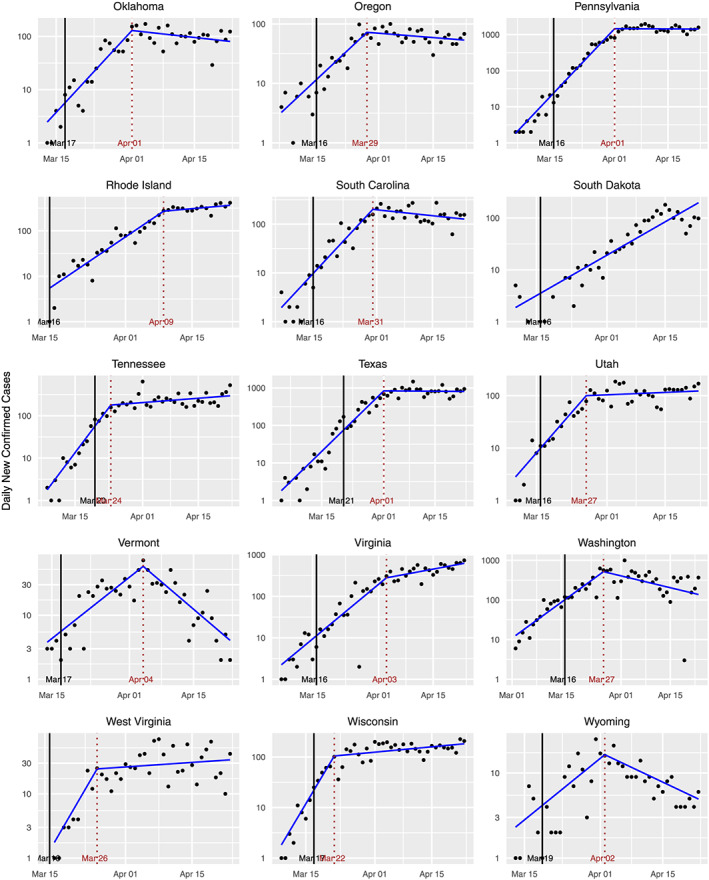
Standard plots for various states

Wagner AB, Hill EL Ryan SE, et al. Social distancing merely stabilized COVID‐19 in the United States. Stat. 2020;9:e302. 10.1002/sta4.302

DATA AVAILABILITY STATEMENT

The data that support the findings of this study are openly available from the New York Times Repository on Coronavirus (Covid‐19) Data in the United States, available at https://github.com/nytimes/covid‐19‐data, from the CDC's ‘Previous U.S. COVID‐19 Case Data’, available at https://www.cdc.gov/coronavirus/2019‐ncov/cases‐updates/previouscases.html, and from the COVID Tracking Project (https://covidtracking.com).