Soft Tissue Artifact Causes Underestimation of Hip Joint Kinematics and Kinetics in a Rigid-Body Musculoskeletal Model

Abstract

Rigid body musculoskeletal models have been applied to study kinematics, moments, muscle forces, and joint reaction forces in the hip. Most often, models are driven with segment motions calculated through optical tracking of markers adhered to the skin. One limitation of optical tracking is soft tissue artifact (STA), which occurs due to motion of the skin surface relative to the underlying skeleton. The purpose of this study was to quantify differences in musculoskeletal model outputs when tracking body segment positions with skin markers as compared to bony landmarks measured by direct imaging of bone motion with dual fluoroscopy (DF). Eleven asymptomatic participants with normally developed hip anatomy were imaged with DF during level treadmill walking at a self-selected speed. Hip joint kinematics and kinetics were generated using inverse kinematics, inverse dynamics, static optimization and joint reaction force analysis. The effect of STA was assessed by comparing the difference in estimates from simulations based on skin marker positions (SM) versus virtual markers on bony landmarks from DF. While patterns were similar, STA caused underestimation of kinematics, range of motion (ROM), moments, and reaction forces at the hip, including flexion-extension ROM, maximum internal rotation joint moment and peak joint reaction force magnitude. Still, kinetic differences were relatively small, and thus they may not be relevant nor clinically meaningful.

1. Introduction

Forces within the human body dictate development, homeostasis, pathology, and repair (Guilak et al., 2004). Non-invasive, in-vivo measurement of joint moments as well as muscle and joint reaction forces is currently impossible. Musculoskeletal models are an attractive alternative to experimental studies of cadaveric tissue, as they can estimate internal forces and moments from external measurements of body positions, inertial parameters, and ground reaction forces (Ku et al., 2015). Most often, body positions are derived from measurements of markers adhered to the skin’s surface. While this methodology provides relatively fast estimates of human movement, markers adhered to the skin surface move relative to the underlying skeleton that they are meant to track, a phenomenon known as soft tissue artifact (STA) (Cereatti et al., 2017; Leardini et al., 2005; Peters et al., 2010). Accordingly, STA may influence model outputs, which include joint kinematics, joint moments, muscle activation/forces and joint reaction forces.

The extent to which STA affects musculoskeletal model estimates for the hip joint remains unclear due to the paucity of dynamic in-vivo measurement techniques that do not suffer from STA. Previous studies have incorporated synthetic STA into computational simulations (Lamberto et al., 2017; Myers et al., 2015). While this approach permits systematic evaluation of STA, it lacks an experimental reference standard. Pins implanted into bone address this issue by providing direct measurements of bone motion (Benoit et al., 2015; Camomilla et al., 2015); however, in addition to being invasive, bone pins may interfere with natural soft tissue movement between the skin surface and the underlying skeleton.

High-speed dual fluoroscopy (DF) quantifies joint kinematics with sub-millimeter and sub-degree accuracy via registration of volumetric imaging data with X-ray images. One of the salient advantages of DF is that is does not suffer from STA since bone motion is visualized directly. Previously, our group validated DF to less than one millimeter and one degree bias and precision in the hip during large range of motion movements (i.e. clinical exams) (Kapron et al., 2014). This technique has also been applied to study biomechanics of the knee (Bey et al., 2008), ankle (Roach et al., 2016), and shoulder (Bey et al., 2006; Zhu et al., 2012).

The purpose of this study was to quantify differences in musculoskeletal model outputs of joint kinematics, joint moments, muscle activation/forces and joint reaction forces when tracking body segment positions with skin markers as compared to bony landmarks measured by direct imaging of bone motion with DF. We recently used DF to measure STA of the pelvis and femur during dynamic activities in the gait laboratory and found that skin markers significantly underestimated angles and range of motion of the hip joint (Fiorentino et al., 2017). Thus, we hypothesized that musculoskeletal model estimates of peak hip joint mechanics metrics would be reduced for skin marker measurements as compared to dual fluoroscopy.

2. Methods

2.1. Participants and Walking Speed

Eighteen participants signed informed consent to enroll in this study that was approved by University of Utah’s Institutional Review Board (IRB). Seven participants were excluded based on morphological findings of structural hip disease visible on an anterior-posterior plain film radiograph. Eleven participants (N=11) (six male) were imaged with skin marker motion capture and DF; these participants were included in our previous study, which quantified STA of the pelvic and femoral body segments (Fiorentino et al., 2017). Participant characteristics were as follows (mean (standard deviation, SD)): aged 23.2 (2.2) years, height 173.3 (10.4) cm, mass 63.8 (10.9) kg, body-mass index (BMI) 21.1 (1.9) kg/m². The side to be imaged was chosen to provide relative balance between the number of left and right hips (six right). Participants walked on an instrumented, dual belt treadmill (Bertec Corporation, Columbus, OH, USA) at their self-selected speed, determined by a timed walk test off the treadmill (mean ± SD speed: 1.3 ± 0.1 m/s) (Fiorentino et al., 2016a).

2.2. Skin Marker Motion Capture

Retroreflective spherical markers (14 mm diameter) were placed on the lower limb to track the positions of the foot, tibia, femur, pelvis and torso (Table 1) (Figure 1) (Fiorentino et al., 2016a). Marker positions were captured at 100 Hz with a 10-camera optical motion capture system (Vicon Motion Systems, Oxford, UK) running Vicon Nexus software (v1.8.5). Marker trajectories were reconstructed and gap-filled with Nexus (Fiorentino et al., 2016a).

Table 1.

Skin Marker Locations

Body	Anatomical Location (Number of Markers at Location)
Torso	Acromioclavicular joint (2)
	Lower back (cluster of 4)
Pelvis	Anterior aspect of ASIS (2)
	Posterior aspect of PSIS (2)
	Lateral aspect of iliac crest (2)
Femur	Lateral aspect of greater trochanter (1, ipsilateral side only)
	Mediala and lateral epicondyles (2)
	Lateral femur, halfway between GRT and knee (cluster of 4)
Tibia	Lateral tibia, at the largest cross section (cluster of 4)
	Mediala and lateral malleoli (2)
Foot	Posterior surface of calcaneus (1)
	Dorsal aspect of 2nd proximal phalanx (1)
	Dorsal aspect of 5th proximal phalanx (1)

^aMedial markers were only necessary for model calibration and were removed prior to dynamic acquisition; ASIS = anterior superior iliac spine, PSIS = posterior superior iliac spine, GRT = greater trochanter.

Fig. 1.

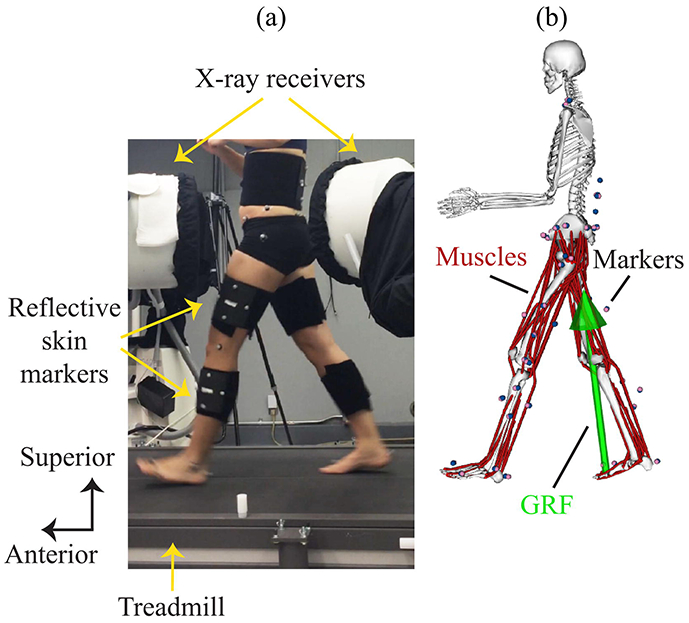
Experimental setup in gait laboratory and OpenSim model. (a) Participants walked on a dual belt instrumented treadmill while being imaged simultaneously using high-speed dual fluoroscopy (i.e. X-rays) and an optical motion capture system that measured the position of retroreflective markers adhered to the skin. (b) An OpenSim musculoskeletal model contained model markers (pink) that tracked experimental positions of skin markers (blue). Simulations used the marker positions, ground reaction forces (GRF), and model parameters as input to calculate joint moments, muscle activations, muscle forces and joint reaction forces.

2.3. Dual Fluoroscopy and Model-based Tracking

The custom DF system (Radiological Imaging Services, Hamburg, PA, USA) and model-based tracking (MBT) were previously described in detail (Kapron et al., 2014). DF images were recorded at 100 Hz using high-speed cameras focused on the output phosphor window of the image intensifiers (Figure 1). Three-dimensional (3D) motion was quantified from DF images via MBT (Bey et al., 2006). The MBT software semi-automatically aligned projections from computed tomography (CT) bone models with DF images from the gait laboratory (Kapron et al., 2014). The MBT solutions transformed bony landmarks that were semi-automatically identified on the CT bone surface into the DF reference frame using previously described methods (Kapron et al., 2014). Bony landmark locations, hereafter referred to as “virtual DF markers,” were then transformed into the laboratory reference frame of the optical motion capture system (Fiorentino et al., 2016b).

2.4. Post-processing

Skin marker and virtual DF marker trajectories were combined in MATLAB (v9.1, The Mathworks, Inc., Natick, MA, USA). All trajectories were filtered using a low-pass, bi-directional, 4th order Butterworth filter with cutoff frequency of 6 Hz (Kapron et al., 2014). Ground reaction forces (GRF) and center of pressure (CoP) locations were filtered using a low-pass, bi-directional, 4th order critically-damped filter with cutoff frequency of 12 Hz based on a residual analysis (Winter, 2009). All cutoff frequencies were adjusted for multiple passes (Robertson and Dowling, 2003). Due to fluctuations in treadmill speed (Sloot et al., 2015) and relatively large errors in CoP locations at initial foot contact and push off, CoP locations were placed under the heel and toe markers at 0.1 s after foot contact and before push off, respectively. Processing and export from MATLAB utilized code from the Biomechanical Toolkit (Barre and Armand, 2014).

2.5. Musculoskeletal Model

A previously described and publicly available rigid-body musculoskeletal model was used (Rajagopal et al., 2016). This musculoskeletal model has been shown to predict muscle activity in good agreement with electromyography data during walking and running; moment arms of muscles crossing the hip, knee and ankle also compared well with experimental values from the literature (Rajagopal et al., 2016). All 14 degrees of freedom in the upper limb and four in the ankle (bilateral subtalar and metatarsophalangeal joints) were fixed, leaving 19 degrees of freedom in the model. Hill-type muscle models (Zajac, 1989) were used to represent 80 muscle-tendon units in the lower limb (Millard et al., 2013). Muscle-tendon parameters were derived from previous studies of 21 cadaver specimens (Ward et al., 2009) and 24 young healthy adults (Handsfield et al., 2014). Subject-specific models were created by scaling the anthropometric dimensions of the default model to the dimensions of the participant during a static, standing trial. The Scale Tool in OpenSim software (v3.3) (Delp et al., 2007) was used to determine scale factors for each body segment by matching the location of model markers placed at anatomical locations in the generic model to corresponding experimental marker locations during the static trial. To improve the geometric accuracy of the model, virtual DF marker locations, rather than skin markers, were used to scale the pelvis and femur segments for all models. All lower limb segments were scaled according to OpenSim guidelines (OpenSimVideos, 2017), which included scale factors that were calculated to match a model marker at the hip joint center with the experimental marker at the center of the femoral head. Model markers were placed at post-scaling experimental locations to calculate the errors associated with STA during dynamic motion.

2.6. Gait Simulations

Custom MATLAB code was used to create OpenSim setup files and run tools using OpenSim’s Application Programming Interface. The Inverse Kinematics (IK) Tool was used to find the degrees of freedom of the model that minimized the error between model marker locations and experimental marker locations. All marker weights on the pelvis were set to one due to comparable mean STA values (range 1.3 – 1.7 cm) from our previous study (Fiorentino et al., 2017). For the femur, however, the greater trochanter marker was eliminated from the current analysis due to large STA measurements, and the thigh markers and knee marker were given equal weight of one due to their similar mean STA values (2.3 cm and 2.4 cm, respectively) in our previous study (Fiorentino et al., 2017). Two IK simulations were performed for each participant. The first, hereafter simply referred to as “DF-IK,” set the IK marker weights to zero for skin markers on the DF-imaged femur and pelvis. The second, termed “SM-IK,” set the IK marker weights to zero for DF virtual markers on the DF-imaged femur and pelvis. All other marker weights were set to one. Note that the only difference between the models was the markers used to track the pelvis and femur motion; all segment lengths, inertial properties, joint centers, etc., were identical. Joint angles were low-pass filtered in OpenSim with a cutoff frequency of 6 Hz.

Detailed descriptions for IK and the remaining analyses are available in OpenSim’s online documentation (http://simtk-confluence.stanford.edu:8080/display/OpenSim/OpenSim+Documentation). The remaining analyses were performed separately for DF-IK and SM-IK solutions. Joint moments were calculated using the Inverse Dynamics (ID) Tool, which used the IK solutions and ground reaction force measurements as inputs. Individual muscle activation levels and muscle-tendon unit forces were determined using Static Optimization (SO) Analysis within the Analyze Tool. All muscles were included in the SO Analysis. While solving for joint moments, static optimization minimized total muscle activation squared and was constrained by muscle force-length-velocity properties. Weak ideal actuators were added to all model degrees of freedom except for those at the hip to improve the robustness and stability of SO (Skalshoi et al., 2015). Muscle activations were limited to 0.9 (out of 1.0 maximum) since activations should be less than this for walking at self-selected speed (Lenaerts et al., 2008). For simulations during which muscle activation reached 0.9, the participant’s maximum muscle force was iteratively scaled in 1% increments. Hip joint reaction forces (JRF) were calculated as the femur force on the pelvis in the reference frame of the pelvis. JRF were calculated using Joint Reaction Analysis within the Analyze Tool (Steele et al., 2012).

2.7. Model Outputs and Errors

Model outputs were time-normalized to the gait cycle between successive foot strikes of the ipsilateral limb that was imaged with DF. Marker errors were calculated as the root-mean-square (RMS) difference between experimental marker positions relative to model marker positions. Results were generated only for the side that was imaged with DF and only for muscles that crossed the hip joint. Range of motion (ROM) was calculated from the raw joint angle data as the range of joint angles in each anatomical direction. All kinetic model outputs were normalized to account for between-participant differences in body size. Joint moments were normalized by body mass (Nm/kg), and muscle forces and joint reaction forces were normalized by body weight (BW). The DF-IK results served as the reference (i.e. SM-IK – DF-IK), as this technique does not suffer from STA.

2.8. Statistics

Results were reported as mean (lower and upper limit of 95% confidence interval, CI) unless otherwise noted. One gait cycle for each participant was analyzed. Statistical analyses were conducted in MATLAB. Differences between model outputs from DF-IK and the SM-IK were assessed using a paired t-test or Wilcoxon sign-rank test, depending on the outcome of an Anderson-Darling test for normality (Anderson and Darling, 1954). For tests in multiple anatomical directions or over many muscles, p values were adjusted for multiplicity using the Holm step-down procedure (Ludbrook, 1998) prior to determining significance. Significance was set at p<0.05. If significant, unadjusted p-values were reported.

3. Results

Significant differences were observed between DF-IK and SM-IK for model marker errors, peak joint angles, ROM, peak joint moment, peak muscle activation, peak muscle force, and peak joint reaction force (Table 2). Model marker RMS errors were larger for IK solutions based on SM-IK (11.2 (10.3 12.1) mm) compared to DF-IK (10.6 (9.9 11.3) mm) (p=.007). Joint angle profiles were qualitatively similar between SM-IK and DF-IK simulations (Figure 2a-c). Peak flexion angle was smaller for the SM-IK relative to DF-IK simulations (22.9 (20.5 25.2) deg vs. 26.6 (23.9 29.2) deg, respectively) (p<.001), as was peak internal rotation angle (4.9 (1.8 8.1) deg vs. 6.4 (3.1 9.8) deg, respectively) (p=.03) and peak external rotation angle (6.4 (2.9 9.9) deg vs. 8.3 (5.0 11.6) deg, respectively) (p=0.01). ROM was smaller for SM-IK than DF-IK for all rotational directions: flexion-extension (42.2 (38.7 45.7) deg vs. 45.7 (41.9 49.5) deg, respectively) (p<.001), adduction-abduction (11.8 (9.4 14.3) deg vs. 12.6 (10.3 14.9) deg, respectively) (p<.05) and internal-external rotation (11.4 (9.4 13.3) deg vs. 14.8 (12.8 16.8) deg, respectively) (p<.001) (Figure 2d).

Table 2.

Summary of Metrics That Differed between SM-IK and DF-IK Simulations

Metrica	Direction or Muscle	SM Models – DF Modelsb,c,d
Marker RMS Error	Euclidean Distance	0.6 (0.1 1.0) mm
Peak Joint Angle	Flexion	−3.7 (−4.4 –3.0) deg
	Internal Rotation	−1.5 (−2.5 –0.5) deg
	External Rotation	1.9 (0.9 2.9) deg
Range of Motion	Flexion-Extension	−3.6 (−4.5 –2.6) deg
	Adduction-Abduction	−0.8 (−1.4 –0.1) deg
	Internal-External Rotation	−3.4 (−4.3 –2.5) deg
Peak Joint Moment	Internal Rotation	−0.01 (−0.02 –0.01) Nm/kg
	External Rotation	0.01 (0.00 0.01) Nm/kg
Peak Muscle Activation	Biceps Femoris Long Head	0.01 (0.01 0.02) out of 1
	Semimembranosus	0.02 (0.01 0.03) out of 1
	Semitendinosus	0.01 (0.01 0.02) out of 1
	Gluteus Medius	−0.02 (−0.03 –0.01) out of 1
	Sartorius	−0.01 (−0.02 –0.01) out of 1
	Tensor Fasciae Latae	−0.02 (−0.03 –0.01) out of 1
Peak Muscle Force	Adductor Brevis	0.02 (0.01 0.02) BW
	Semitendinosus	0.00 (0.00 0.01) BW
	Sartorius	−0.00 (−0.01 –0.00) BW
Peak Joint Reaction Force	Anterior	−0.2 (−0.2 –0.1) BW
	Superior	−0.1 (−0.2 –0.1) BW
	Magnitude	−0.2 (−0.3 –0.1) BW

^aAll metrics were measured for the hip joint

^bOnly metrics that exhibited a significant difference between SM and DF Models are reported

^cData were tested for normality prior to statistical testing

^dDifferences are listed as mean (lower 95% upper 95% confidence interval)

Fig. 2.

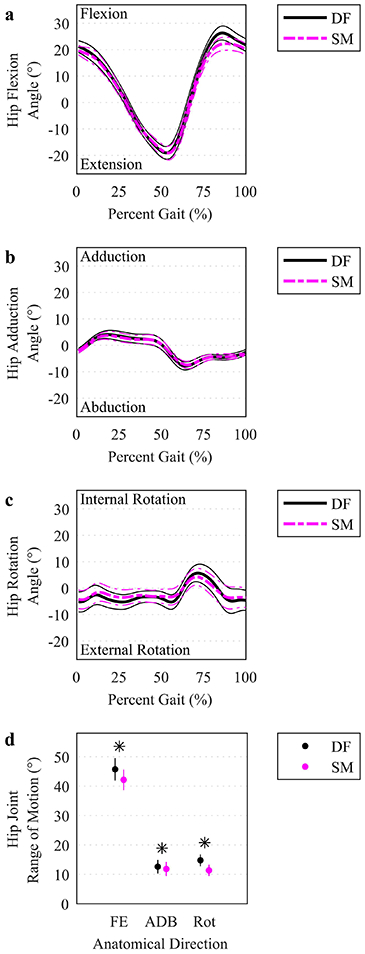
Hip joint angles and range of motion. (a-c) The mean (thicker lines) and ± 95% CI (thinner lines) hip joint angles were plotted for DF (solid, darker lines) and SM (lighter, dashed lines) IK solutions over the time-normalized gait cycle. Percent gait starts at foot contact (0%) for the ipsilateral imaged hip and ends at the next foot contact (100%). (d) Range of motion in each anatomical direction was plotted at the mean (circles) with a vertical line representing ± 95% CI. An asterisk indicates a significant difference between DF and SM using a paired t test (p<.05). FE: flexion/extension. ADB: adduction/abduction. Rot: internal/external rotation.

Joint moment curves varied similarly for SM-IK and DF-IK (Figure 3a-c). However, peak rotation moments were smaller for SM-IK than DF-IK for internal rotation (0.15 (0.13 0.17) Nm/kg vs. 0.16 (0.15 0.18) Nm/kg, respectively) (p=.01) and external rotation (−0.12 (−0.10 −0.13) Nm/kg vs. −0.12 (−0.11 −0.14) Nm/kg, respectively) (p=.04) (Figure 3d).

Fig. 3.

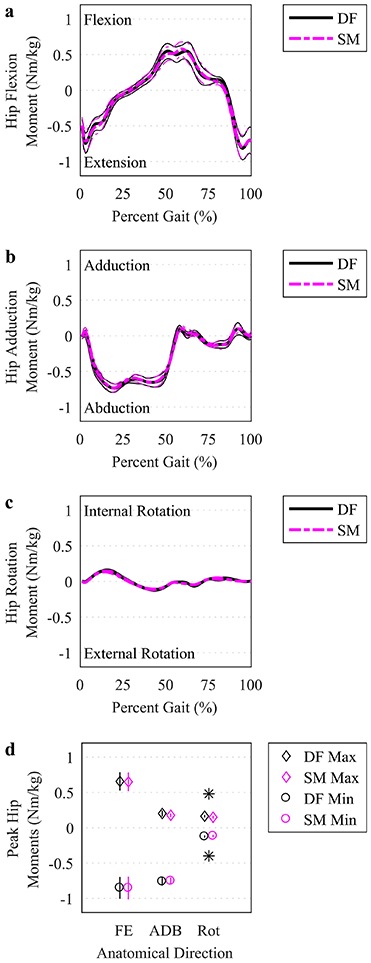
Hip joint moments. (a-c) The mean (thicker lines) and ± 95% CI (thinner lines) hip joint moments were plotted for simulations based on DF (solid, darker lines) and SM (lighter, dashed lines) IK solutions over the time-normalized gait cycle. (d) Peak moments (maximum and minimum) in each anatomical direction were plotted at the mean (symbols, see legend) with a vertical line representing ± 95% CI. An asterisk indicates a significant difference between DF and SM using a paired t test (p<.05). FE: flexion/extension. ADB: adduction/abduction. Rot: internal/external rotation.

Muscle activations (Figure 4a-c) and forces (Figure 5a-c) varied similarly over the gait cycle for SM-IK and DF-IK. Six muscles exhibited different maximum muscle activation between the DF-IK and SM-IK (Figure 4d)—the biceps femoris long head, semimembranosus and semitendinosus had higher maximum activations for SM-IK, and the gluteus medius, sartorius and tensor fasciae latae had lower maximum activations for SM-IK. Three muscles exhibited different maximum muscle forces between the DF-IK and SM-IK (Figure 5d)—the adductor brevis and semitendinosus had higher maximum forces in the SM-IK simulations, while the sartorius had lower maximum force in the SM-IK simulations. Model residual forces did not differ between the SM-IK and DF-IK simulations (Fx: 0.06 (0.05 0.08) BW vs. 0.07 (0.06 0.09) BW, Fy: 0.10 (0.09 0.12) BW vs. 0.10 (0.09 0.12) BW, Fz: SM: 0.06 (0.04 0.07) BW vs. DF: 0.06 (0.04 0.07) BW), nor did model residual moments (Mx: 0.27 (0.23 0.32) Nm/kg vs. 0.29 (0.24 0.34) Nm/kg, My: 0.15 (0.13 0.18) Nm/kg vs. DF: 0.15 (0.13 0.18) Nm/kg, Mz: 0.48 (0.42 0.53) Nm/kg vs. DF: 0.48 (0.43 0.54) Nm/kg).

Fig. 4.

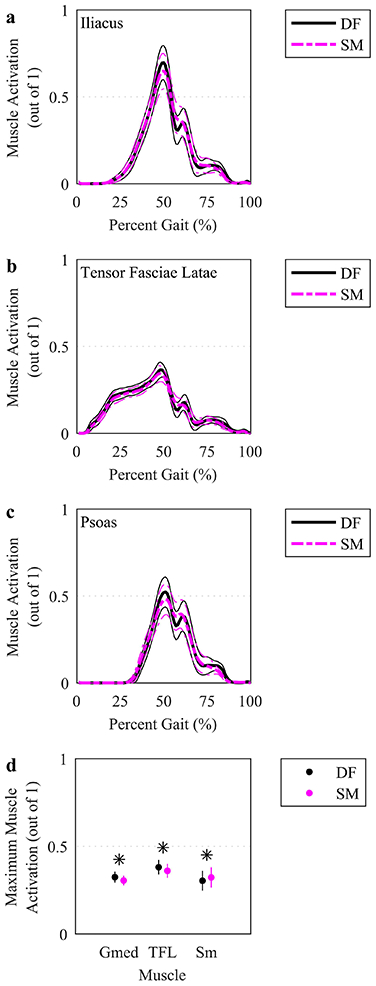
Simulated activations for select muscles. (a-c) The mean (thicker lines) and ± 95% CI (thinner lines) muscle activations were plotted for simulations based on DF (solid, darker lines) and SM (lighter, dashed lines) IK solutions over the time-normalized gait cycle. The three muscles with the highest time-integral of muscle activation were plotted. (d) Maximum muscle activations were plotted at the mean (circles) with a vertical line representing ± 95% CI across participants. The three muscles with the highest activation and a significant difference using a paired t test, indicated by an asterisk (p<.05), between DF and SM were plotted. AL: adductor longus. Gmed: gluteus medius. TFL: tensor fasciae latae. Sm: semimembranosus.

Fig. 5.

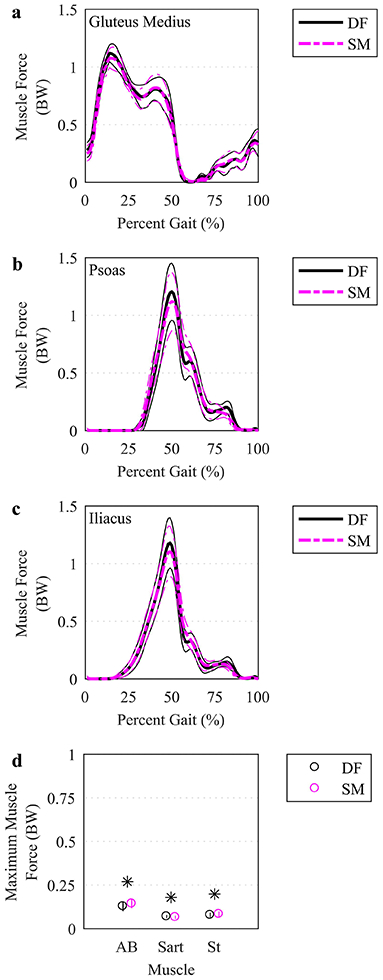
Simulated forces for select muscles. (a-c) The mean (thicker lines) and ± 95% CI (thinner lines) muscle forces were plotted for simulations based on DF (solid, darker lines) and SM (lighter, dashed lines) IK solutions over the time-normalized gait cycle. The three muscles with the largest time-integral of muscle force were plotted. (d) Maximum muscle forces were plotted at the mean (circles) with a vertical line representing ± 95% CI. Only the muscles with a significant difference using a paired t test, indicated by an asterisk (p<.05), between DF and SM were plotted. BW: body weight. AB: adductor brevis. Sart: Sartorius. Il: iliacus. St: semitendinosus.

Hip joint reaction force curves appeared qualitatively similar between DF-IK and SM-IK (Figure 6a-c). However, the maximum hip JRF was smaller in the anterior-posterior direction for SM-IK (2.2 (1.7 2.7) BW) relative to DF-IK (2.4 (1.9 2.9) BW) (p=.01), the superior-inferior direction for SM-IK (3.3 (3.1 3.6) BW) relative to DF-IK (3.5 (3.2 3.7) BW) (p=.01). The net resultant hip JRF was also smaller in the SM-IK (4.0 (3.5 4.5) BW) compared to the DF-IK (4.2 (3.7 4.7) BW) (p=.01) (Figure 6d).

Fig. 6.

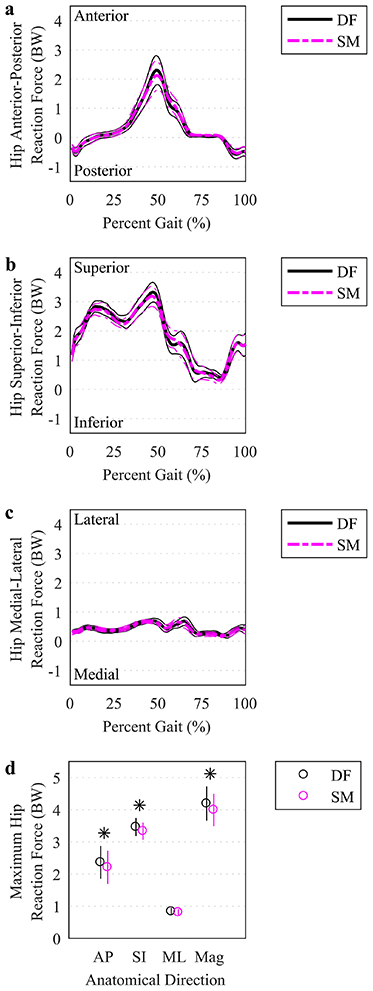
Hip joint reaction forces. (a-c) The mean (thicker lines) and ± 95% CI (thinner lines) hip joint reaction forces were plotted for simulations based on DF (solid, darker lines) and SM (lighter, dashed lines) IK solutions over the time-normalized gait cycle. (d) Maximum hip reaction forces in each anatomical direction, as well as the resultant force magnitude, were plotted at the mean (circles) with a vertical line representing ± 95% CI. An asterisk indicates a significant difference between DF and SM using a paired t test (p<.05). BW: body weight. AP: anterior-posterior. SI: superior-inferior. ML: medial-lateral. Mag: magnitude.

4. Discussion

The purpose of this study was to determine the extent to which soft tissue artifact affects biomechanical predictions provided by a musculoskeletal model. We tracked hip joint motion using traditional retroreflective skin markers and high-speed dual fluoroscopy, the latter of which does not suffer from STA. We found good qualitative agreement between kinematic and kinetic metrics over the time-normalized gait cycle, but peak hip joint angles, range of motion, and peak kinetic variables differed between simulations based on SM compared to simulations based on DF. Peak joint angles, ROM, peak joint moments and maximum joint reaction forces generated by SM motion underestimated those generated by DF, thus confirming our hypothesis.

To our knowledge, the current study was the first to use musculoskeletal models for assessing STA’s impact on hip joint kinematics and kinetics during dynamic motion using measurements from a reference standard. Two other studies measured hip STA, but these investigations analyzed quasi-static motion (i.e. multiple static positions) (Camomilla et al., 2017a; Hara et al., 2014). Previous studies of joints have almost exclusively focused on reducing errors in kinematics (Benoit et al., 2015; Bonci et al., 2014; Camomilla et al., 2015; Clement et al., 2015; Potvin et al., 2017). Theoretically, reducing kinematic errors improves the accuracy of model predictions derived using experimentally acquired joint angles and translations; this notion is indirectly supported by our findings, which demonstrated that differences in kinematics between SM and DF resulted in an underestimation of kinetic variables.

A previous study that employed a Monte Carlo simulation analysis of joint kinematics-dependent STA reached the same conclusion as our study: overall patterns of kinematics and kinetics were relatively unaffected by STA; however, analysts studying gait should exercise caution when interpreting extrema from musculoskeletal model simulations based on skin markers (Lamberto et al., 2017). In the current study we only found a small difference of 0.2 BW in the magnitude of the hip joint reaction force when comparing SM-IK and DF-IK models. Interestingly, Lamberto et al. (2017) found that hip contact forces were much more affected by STA, with maximum contact forces varying by 1.5-1.8 BW. Differences in the methodological approach between our study and that published by Lamberto et al. likely explain discrepancies in joint reaction force results. Notably, we used experimental dual fluoroscopy kinematics to calculate STA, whereas Lamberto et al. employed a Monte Carlo analysis based on perturbation of marker positions. Lamberto et al. also evaluated differences in joint reaction forces over a large range (5th to 95th variation of outcome variable of interest) whereas we reported differences between measurements from skin markers and dual fluoroscopy.

While each of the metrics studied exhibited at least one significant difference, some statistically significant results were of relatively low magnitude, and thus may not be relevant nor clinically meaningful. A previous review of the literature concluded that a number of methodological factors affect joint moments in clinical gait analysis (Camomilla et al., 2017b). However, the magnitude at which a significant difference becomes clinically relevant will depend on the study population as well as the research question. An option for studies involving children is to calculate the gait deviation index for kinetic variables (GDI-Kinetic) (Rozumalski and Schwartz, 2011). While the GDI-Kinetic takes into account features of the raw kinetic data and combinations of features, a previous study in 18 healthy pediatric participants found that deviations in hip abduction moment of greater magnitude than in our study did not meet the threshold for clinical significance (Kiernan et al., 2015), suggesting that the differences we estimated herein would not be considered clinically relevant.

In the current study, statistical testing found a significant difference between model outputs when tracking hip motion using skin markers as opposed to DF bony landmarks. It should be noted however, that the effects of STA on model outputs may be dissimilar between different participant populations when one population is more adversely affected by STA. For example, a recent study showed that STA was higher in participants with a larger BMI (Camomilla et al., 2017a); therefore, future studies might expect differential effects of STA on model outputs when comparing groups with dissimilar BMIs. In addition, STA from errors in identifying anatomical landmarks will affect the model scaling process and thus joint kinetics, which a previous study found to influence knee joint contact forces by 1.44 BW (Lund et al., 2015).

Other factors besides STA can influence results derived from musculoskeletal models. Modeling parameters, such as bony landmark positions, maximum muscle tension and musculotendon geometry, have been shown to induce moderate effects on model estimates of joint angles, joint moments and muscle/joint contact forces (Carbone et al., 2012; Valente et al., 2014). Even choice of the model itself can lead to substantially different predictions (Wagner et al., 2013). Furthermore, the current study only investigated one marker set. It is possible that different marker sets would change the magnitude of STA, which in turn could increase or decrease the error in range of motion, peak moments, and maximum hip joint reaction forces. Furthermore, changing the weights of individual markers—which was not performed in this study—as part of inverse kinematics solution may exert a significant effect on kinetic variables of interest, and that effect may depend on the study population. The method for calculation of joint kinematics may have an effect on kinetic results as well, though a study that reported a normative database of hip biomechanics using direct kinematics calculation found similar waveforms and magnitudes as the current study (Bennett et al., 2018). Last, the foot COP location was placed under the heel at foot strike and under the toe at push off; the extent to which this correction affected results was not assessed.

While the DF and model-based tracking technique yields submillimeter and subdegree bias and precision, the CT scan and DF imaging expose participants to ionizing radiation. The total effective dose equivalent (TEDE) was 10.72 mSv, which corresponds to more than four years of the world wide average of natural background radiation (United Nations Scientific Committee on the Effects of Atomic Radiation, 2008) and roughly 20% of the TEDE a worker is permitted to receive in a year (Nuclear Regulatory Commission, 1991).

The data presented herein motivates the need for future work to minimize model errors when estimating hip joint mechanics from musculoskeletal models. Previous publications showed that the effects of STA on knee joint kinematic errors can be reduced (Camomilla et al., 2015; Clement et al., 2015; Potvin et al., 2017), and future studies of hip joint mechanics should aim to limit the effects of STA on musculoskeletal model outputs.