DIFFEOMORPHIC SMOOTHING FOR RETINOTOPIC MAPPING

Abstract

Retinotopic mapping, the mapping of visual input on the retina to cortical neurons, is an important topic in vision science. Typically, cortical neurons are related to visual input on the retina using functional magnetic resonance imaging (fMRI) of cortical responses to slowly moving visual stimuli on the retina. Although it is well known from neurophysiology studies that retinotopic mapping is locally diffeomorphic (i.e., smooth, differentiable, and invertible) within each local area, the retinotopic maps from fMRI are often not diffeomorphic, especially near the fovea, because of the low signal-noise ratio of fMRI. The aim of this study is to develop and solve a mathematical model that produces diffeomorphic retinotopic mapping from fMRI data. Specifically, we adopt a geometry concept, the Beltrami coefficient, as the tool to define diffeomorphism, and model the problem in an optimization framework. Efficient numerical methods are proposed to solve the model. Experimental results with both synthetic and real retinotopy data demonstrate that the proposed method is superior to conventional smoothing methods.

1. INTRODUCTION

Almost half of the human cerebral cortex is dedicated to visual processing. Identifying and analyzing visual areas of the human brain is an extremely important topic in vision science and neurobiology [1]. Retinotopic mapping via functional magnetic resonance imaging (fMRI) provides a noninvasive way of defining the location and size of receptive filed of populations of visual neurons on the retina [2]. Typically, cortical neurons are related to visual input on the retina using fMRI of cortical responses to slowly moving visual stimuli on the retina. The visual stimulus is carefully designed so that the stimulus pattern is unique with respect to each retinal location [3, 4]. By recording and analyzing the fMRI signals at each cortical location, one can decode the best retinal visual input coordinate that generates such fMRI signals [2, 5]. Previous studies have revealed that much of the visual cortex is organized into visual regions (e.g., V1, V2) with a retinotopic map in each region [6]. It is well known from neurophysiology studies that retinotopic mapping is topology preserving (i.e., local neighborhood relationships are maintained) and diffeomorphic (i.e., smooth, differentiable, and invertible) within each visual area [7, 8]. However, the decoded visual coordinates from fMRI retinotopic mapping studies are not guaranteed to be diffeomorphic or topological preserving. One reason is the signal-noise ratio and spatial resolution of fMRI signals are low. Another reason is that the decoding process largely deciphers the fMRI signal point by point without considering the local smoothness, although Gaussian spatial smoother has been applied to fMRI signal processing [9].

Some have conducted spatial smoothing on retinotopic maps to perform automatic delineation of visual regions [10, 7]. However, the smoothing is applied to the visual coordinates one dimension at a time, e.g., the x and y visual coordinates separately. There is no guarantee of diffeomorphism. Another promising approach is registering the noisy retinotopic maps to a diffeomorphic template and assigning the template retinotopic coordinates after registration [11]. It relies on diffeomorphic registration of two surfaces, which is not easy to achieve. Even if the registration issue can be solved, how to define the right template will remain a big problem.

Can we pursuit a spatial smoother specifically designed for retinotopic mapping which generates new diffeomorphic visual coordinate close to the raw coordinate? It is easy (e.g., use Euclidean distance) to measure coordinate changes during the smoothing process, the crucial question is how to define, quantify, and ensure the diffeomorphic condition.

In this work, we adopt the Beltrami coefficient to quantify the diffeomorphism as it also quantifies angle deviation. The reason we care angle deviation is that previous work shows retinotopic mappings preserve angles to a considerable extent [12, 13]. We further model the smoothing process as an optimization procedure with diffeomorphic constraints and elaborate the numerical steps to solve the optimization problem. We tested our algorithm on a synthetic dataset and a real dataset. The synthetic data is generated using an ideal retinotopic mapping model (ground truth) with added noise. The application of our proposed method to the synthetic data generates diffeomorphic results without any big deviations, while other methods violate the condition. The real dataset is the Human Connectome Project 7T retinotopy (HCP) data [14]. We also achieved diffeomorphic retinotopic mapping. In addition, we obtained Beltrami coefficients that quantify angle distortions for each subject. Our method guarantees diffeomorphic results and minimizes the angle distortion, two important conditions for a valid retinotopic mapping research.

2. PROBLEM RESTATEMENT

We restate the problem in a biological intuitive and mathematically rigorous way. Assume there is a light spot on point $v=\left(v^{(1)},v^{(2)}\right)\in {ℝ}^2$ in the visual field, as shown in Fig. 1. After the visual system’s perception, propagation, and dispensation, the light spot will eventually active a population of neurons. The main purpose of retinotopic mapping is to find the center v and the extent $\sigma \in {ℝ}^{+}$ of its receptive field on the retina, for each point $P=(X,Y,Z)\in {ℝ}^3$ on visual cortex.

Fig. 1.

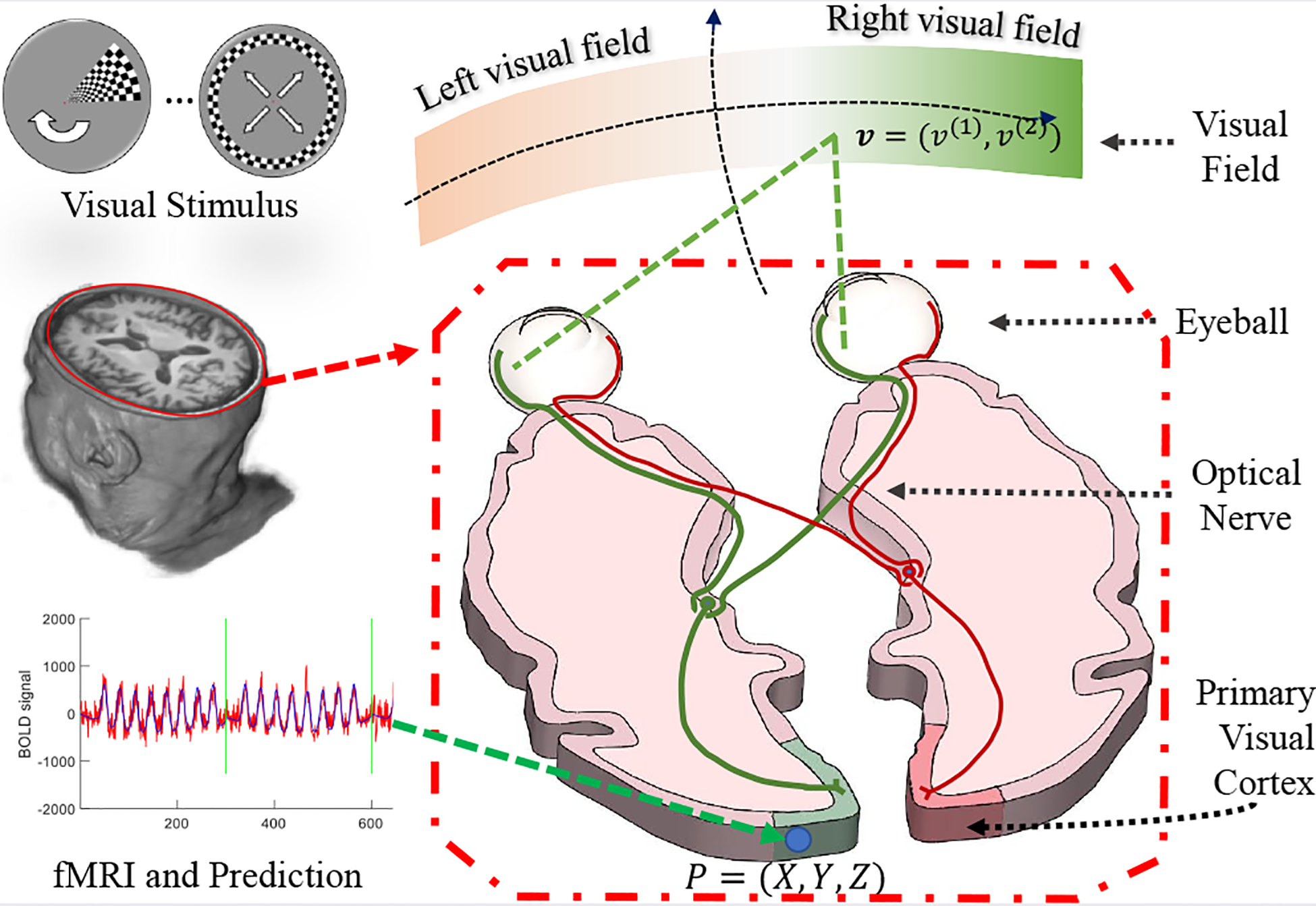
Illustration of visual system to the visual cortex.

fMRI provides a noninvasive way to determine v and σ for P, based on the following procedure. (1) Design a stimulus time sequence s (t; v), such that the stimulus sequence is unique for every visual coordinate, i.e., s (t; v₁) ≠ s (t; v₂), ∀ v₁ ≠ v₂; (2) Present the stimulus sequence to an individual and record the fMRI signals from the visual cortex; (3) For each fMRI time sequence on a cortical location, y (t; P), determine the corresponding receptive field, including its center location v and its size σ on the retina, that most-likely generated the fMRI signals. Specifically, given the neurons’ spatial response r (v′; v, σ) (a predefined model depicts neural response around v) and the hemodynamic function h (t) (a model of the time course of neural activation to a stimulus), the predicted fMRI signal can be written as:

$$\widehat{y}(v,\sigma )=\beta \left(\int r\left(v\prime ;v,\sigma \right)s\left(t,v\prime \right)dv\prime \right)*h(t)$$ (1)

where, β is a coefficient that converts the units of response to the unit of fMRI activation. Then the parameters v and σ are given by minimizing the prediction error,

$$(v,\sigma )=\mathit{\text{arg}}\underset{{}_{(v,\sigma )}}{\mathit{\text{min}}}|\widehat{y}(v,\sigma )-y(P){|}^2.$$ (2)

The retinotopic mapping of the entire visual cortex is obtained when (v, σ) is solved for every point on the cortical surface. Previous work has shown that nearby visual cortex will share nearby visual coordinates, i.e., topology preserving [15, 11, 16]. The notion retinotopic mapping preserves topology means that, if f is the retinotopic mapping, f : P ↦ v, then a neighboring point P′ of P, will have visual coordinate v′ close to v. That is, f is diffeomorphic in the domain of cortical surface.

Unfortunately, due to the low signal-noise ratio of fMRI, f is not guaranteed to be diffeomorphic. We propose a diffeomorphic smoothing on f, such that the new mapping $\widehat{f}:P\mapsto \widehat{v}$ is diffeomorphic and $\widehat{v}$ is close to v. We adopt the Beltrami coefficient [17] to quantify the diffeomorphism,

$${\mu }_f=\frac{(E-G+2iF)}{(E+G+2\sqrt{EG-F^2})},$$ (3)

where $g(\widehat{v})=\left(\begin{array}{cc}E(\widehat{v})& F(\widehat{v})\\ F(\widehat{v})& G(\widehat{v})\end{array}\right)$ is the metric tensor. If ∣μ_f∣< 1 then f is diffeomorphic. Furthermore, the bigger ∣μ_f∣ is, the larger angle deviation is. Therefore, the diffeomorphism defined in this way also provides a measure of angle deviation. We aim to find $\widehat{v}=\widehat{f}(P)$, such that,

$$\widehat{v}=\mathit{\text{arg}}\underset{\widehat{v}}{\mathit{\text{min}}}\int |v-\widehat{v}{|}^{2}ds,\text{ s}\mathrm{.t}|{\mu }_f|<1$$ (4)

3. MODEL AND METHOD

3.1. Model in Discrete

In practice, cortical surface S is usually not an analytical function but consists of a bunch of vertices V_S and triangular faces F_S, i.e. S = (F_S, V_S). Similarly, visual space can also be discretized. Instead of taking another discretization, it is beneficial to take the same discretization as S. Then, the remaining problem is to find a visual coordinate v_i for every vertex P_i ∈ V_S.

It is easier to discuss and solve problems on 2D instead of the original 3D cortical surface. Since diffeomorphism is transitive (If f and c are both diffeomorphic function, then the composite function f ○ c is also diffeomorphic), we can compute a conformal mapping (diffeomorphic and angle preserving) from the occipital region of the cortex to a parametric disk [18] to simplify the problem to 2D. As shown in Fig. 2. the gray colored region is mapped to the unit disk by $c:P\mapsto u,u=\left(u^{(1)},u^2\right)\in {ℝ}^2$. Although conformal mapping is angle preserving, it introduces distance distortion. To reduce the distortion, we cut a geodesic disk patch: pick a point on the cortical surface that corresponds to the fovea as the center point, then we calculate the geodesic distances from all cortical position to the center point [19] and only keep the portion of cortical surface whose geodesic distance to the center point is within a certain value. If we can solve $f_c=f○c^{-1}:u\in {ℝ}^2\mapsto v\in {ℝ}^2$ with constraint $|{\mu }_{f_c}|<1$, then we can obtain diffeomorphic retinotopic mapping by f = f_c ○ c. Accordingly, we simplify Eq. (4) to,

$${\widehat{f}}_c=\mathit{\text{arg}}\underset{f_c}{\mathit{\text{min}}}\int {\left|f_c-{\widehat{f}}_c\right|}^{2}du,\text{ s}\mathrm{.t}|{\mu }_f|<1$$ (5)

To solve Eq. (5) in discrete, we form the energy as,

$$E=\sum _i{\left|F_i-{\widehat{F}}_i\right|}^2+{\lambda }_1{|{\mu }_i|}^2+{\lambda }_2{\left|\nabla {\widehat{F}}_i\right|}^2$$ (6)

where F_i = f_c (u_i) is the raw result from Eq. (2), ${\widehat{F}}_i$ is to be solved, ${\mu }_i={\mu }_{f_c}\left(u_i\right)$ is the Beltrami coefficient at u_i, λ₁ and λ₂ are constants. Compared to Eq. (5), gradient of $\widehat{F}$, $\nabla {\widehat{F}}_i$, is introduced to increase smoothness, and ∣μ_i∣² is used to reduce non-diffeomorphism as well as angle distortion.

Fig. 2.

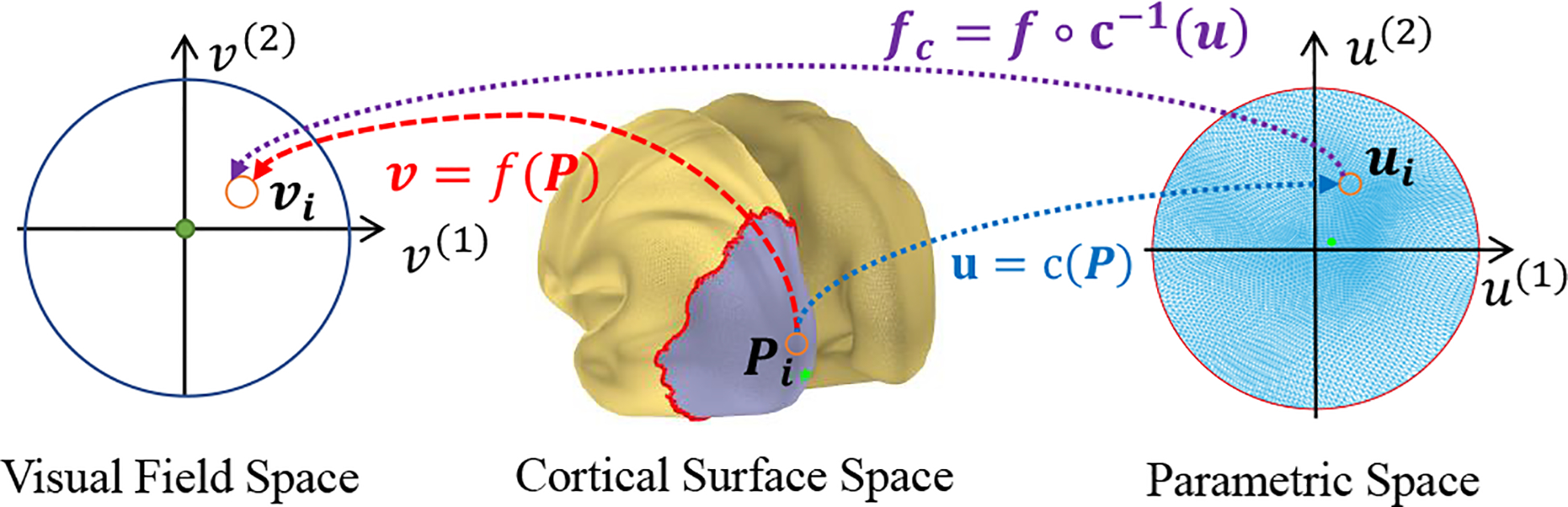
Illustration of several spaces and relations between them.

3.2. Numerical Method

Unfortunately, it is hard to minimize the energy in Eq. (6) directly, as it mixes the Beltrami coefficient and the mapping function together. The solution is to alternatively solv with respect to function and Beltrami coefficient in separate steps. Unavoidably, we need tools to convert the mapping function and Beltrami coefficient back and forth.

3.2.1. Beltrami Coefficient

Since we have a parametric coordinate u for the cortical surface S, the definition, Eq. (3), can be simplified to,

$${\mu }_f=\left(\frac{\partial f}{\partial u^{(1)}}+i\frac{\partial f}{\partial u^{(2)}}\right)/\left(\frac{\partial f}{\partial u^{(1)}}-i\frac{\partial f}{\partial u^{(2)}}\right).$$ (7)

Given the explicit form of function f(u), we can compute μ_f according to Eq. (7). In the discrete case, f_c is interpreted linearly on each triangle. As shown in Fig. 3(a), for u within the triangle Δu_iu_j u_k, f_c (u) = α_iv_i + α_jv_j + α_kv_k, where v_i = f_c (u_i), v_j = f_c (u_j), and v_k = f_c (u_k). The coefficients α_i, α_j, and α_k are called barycentric coefficients. Specifically, α_i (similarly for α_j and α_k) is the area portion of triangle Δuu_ju_k to Δu_iu_ju_k, i.e. α_i = Area (Δuu_ju_k) /Area (Δu_iu_ju_k). Now we can compute the Beltrami coefficient ${\mu }_f{}_{{}_c}$ according to Eq. (7). It is easy to see that ${\mu }_f{}_{{}_c}$ is a constant for each triangle.

Fig. 3.

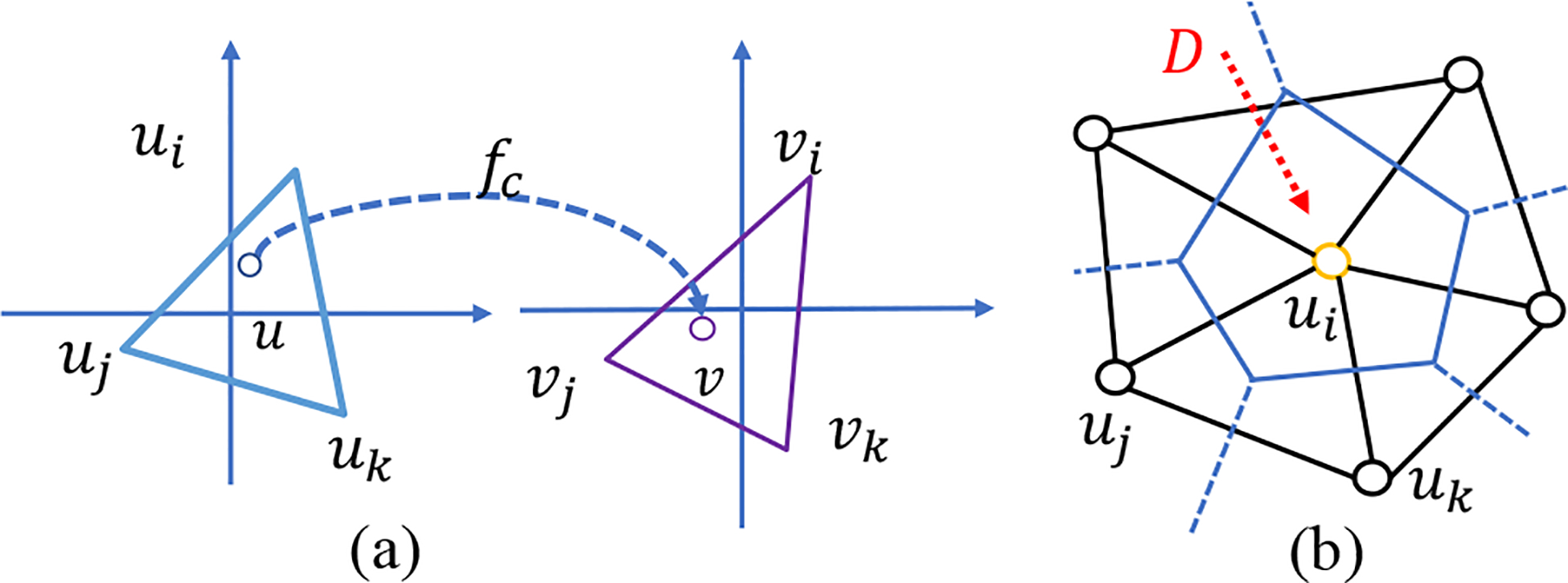
(a) Illustration of approximate the mapping in discrete. (b) The divergence approximation on the vertex ring.

3.2.2. Linear Beltrami Solver (LBS)

We briefly introduce the LBS to recovery function f = (f⁽¹⁾, f⁽²⁾) for the given Beltrami coefficient μ = ρ + iτ .It was first introduced in [20, 21]. According to the definition in Eq. (7), we have,

$$\left(\frac{\partial f}{\partial u^{(1)}}+i\frac{\partial f}{\partial u^{(2)}}\right)/\left(\frac{\partial f}{\partial u^{(1)}}-i\frac{\partial f}{\partial u^{(2)}}\right)=\rho +i\tau .$$ (8)

After re-organizing Eq. (8) and eliminating f⁽²⁾, we derive,

$$\nabla \cdot A\nabla f^{(1)}=0,$$ (9)

where $A=\left(\begin{array}{ll}{\alpha }_1\hfill & {\alpha }_2\hfill \\ {\alpha }_2\hfill & {\alpha }_3\hfill \end{array}\right),{\alpha }_1=\frac{{(\rho -1)}^2+{\tau }^2}{1-{\rho }^2-{\tau }^2},{\alpha }_2=\frac{-2\tau }{1-{\rho }^2-{\tau }^2}$ and ${\alpha }_3=\frac{1+2\rho +{\rho }^2+{\tau }^2}{1-{\rho }^2-{\tau }^2}$, ∇f⁽¹⁾ = (∂f⁽¹⁾/∂u⁽¹⁾ + ∂f⁽¹⁾/∂u⁽²⁾), and the divergence ∇ on vector G = A∇f⁽¹⁾ = (G⁽¹⁾, G⁽²⁾) is defined as ∇ · G = ∂G⁽¹⁾/∂u⁽¹⁾ + ∂G⁽²⁾/∂u⁽²⁾. By solving the partial equation Eq. (9) with certain boundary conditions, we can solve f⁽¹⁾. Similarly, f⁽²⁾ can be solved.

In the discrete case, the function is linearly interpreted on each triangle. The gradient of f, ∇f (u), can be written out. For the divergence on vector G, ∇ · G, it is approximated on the dual cell of each vertex (a cell consisted of circumcenters of neighboring triangles). As shown in Fig. 3(b), consider the vertex u_i with its neighbors N(u_i), the divergence on vector G is approximated by,

$$\nabla \cdot G=\frac{1}{\left|D\right|}{\int }_{\partial D}Gds=\frac{1}{\left|D\right|}\sum _{T_j\in N\left(u_i\right)}{G}_{T_j}\cdot \left(u_k-u_j\right)$$ (10)

Applying the approximations, we have a linear equation for each f_i together with its neighboring vertices, according to Eq. (9). Finally, we can solve f efficiently by collecting all the equations and write them in a matrix form.

3.2.3. Laplacian Smoothing and Chopping

Now we can convert between the function and Beltrami coefficient. Our purpose is to make a smooth result. We apply the smooth operation on the function and Beltrami coefficient by the Laplacian smoothing. For instance, to get a smooth Beltrami coefficient v, we solve the following,

$$v=\mathit{\text{arg}}\underset{{}_v}{\mathit{\text{min}}}\int |\nabla v{|}^2+\lambda |v-\mu {|}^{2}ds$$ (11)

where λ is a constant. Eq. (11) can be efficiently solved by its Euler-Lagrange equation (−∇ · ∇ + 2λI) ν = 2λμ.

Although we penalize the non-diffeomorphism in Eq. (6), if there is a consistent point whose ∣μ∣ > 1, it breaks the diffeomorphic result. To avoid this situation, we shrink ν′ = ν/ ∣ν∣, if ∣ν∣ > 1. This process is called Chop.

3.2.4. Algorithm

The overall smoothing process is summarized in Alg. 1.

4. RESULTS

4.1. Synthetic Data

We first evaluate the performance of the algorithm on synthetic data. The ground truth mapping is given by,

$$u^{(1)}+i{u}^{(2)}=\mathrm{\text{log}}\left(v^{(1)}+i{v}^{(2)}\right)$$ (12)

We choose log function as it is a good approximation of the retinotopic mapping from visual space to the flattened cortical surface, introduced by Schwartz [12]. As shown in Fig. 4(a), the visual domain is mapped to the parametric space Fig. 4(b). We also show the mapping with a small amount of noise in Fig. 4(c) and a large amount of noise in Fig. 4(d). We apply several smoothing methods on the synthetic mapping data in both small and big noise cases including Average Smoothing, Median Smoothing, and Laplacian Smoothing [22]. The result for the big noisy case is shown in Fig. 5. All of them are spatial smoothing procedures. Average Smoothing takes the average around each neighborhood. Median Smoothing takes the median value of each neighborhood. Laplacian smoothing is the so-called “Perfect Smoothing”. Except for the proposed method, all smoothing procedures process the coordinates u⁽¹⁾ and u⁽²⁾ separately. We list the performance metric of all the methods in Table 1.

Fig. 4.

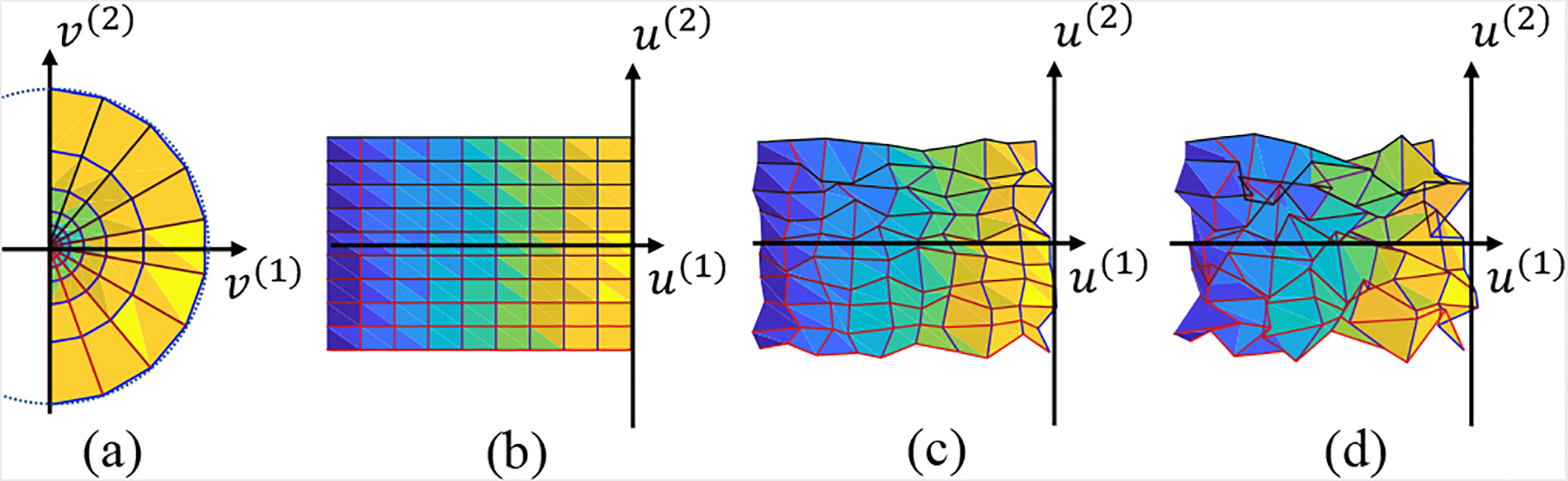
Function domain, its mapping result and mapping results with noise: (a) mapping domain on the visual field; (b) mapping result without noise; (c) mapping result with weak noise under Peak Signal-Noise Ratio (PSNR) is 20 dB; (d) mapping result with strong noise (PSNR = 10 dB).

Fig. 5.

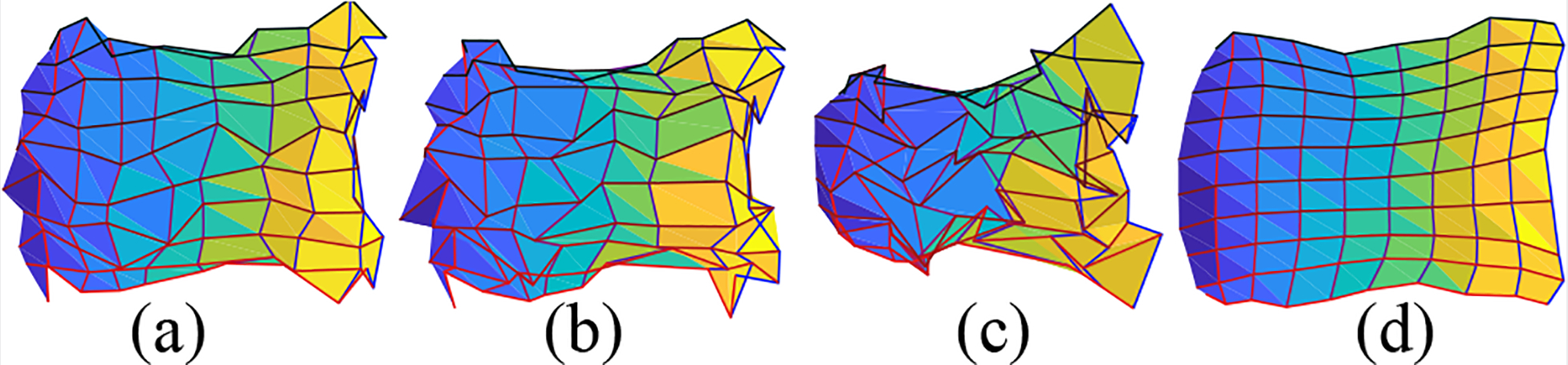
Smoothing results for map with big noise: (a) average smoothing; (b) median smoothing; (c) Laplacian smoothing; (d) the proposed smoothing.

Table 1.

Comparing different smoothing methods by four metrics, mean value deviation of function, the max of the function deviation, and the number of overlapped triangles (non-diffeomorphic triangles). Value deviation means error to the ground truth. For cells with two values like “A/B”, “A” is the result for the map with a small added noise (PSNR = 20 dB); while “B” is the result for the map with a big added noise (PSNR = 10 dB).

Method	Value Deviation		# Flipped Triangles
	Mean	Max
Before Smoothing	0.25/0.40	0.64/1.05	19/56
Average Smoothing	0.18/0.24	0.62/0.77	3/8
Median Smoothing	0.22/0.28	0.69/0.83	2/24
Laplacian Smoothing	0.23/0.36	0.66/0.92	11/43
Proposed	0.19/0.22	0.65/0.75	0/0

We found that (1) all the smoothing methods helped reduce the noise, and reduce flipped triangles (i.e. triangle violates the topology preserving condition); (2) with a small amount of added noise, the topology violation problem is not severe, average smoothing can also achieve almost diffeomorphic results; (3) however, with a large amount of added noise, only our method can achieve diffeomorphic result.

4.2. HCP Data

With 7-Tesla MRI systems, the signal-to-noise ratio of retinotopic mapping has been dramatically improved. Still, the mapping is noisy and non-diffeomorphic. We apply our smoother on data from a 7T MRI system. The details of the dataset can be found in [14]. Because we only interested in smoothing, we took publicly available data of the decoded retinotopic coordinate for each cortical vertex of five subjects [23], and evaluate the performance of our method. The total number of flipped triangles for raw data is 1313, for the average, median, and Laplacian methods are 1289, 1312, and 1337, respectively. Proposed method has no flip triangles.

For a more persuasive and intuitive comparison, Fig. 6 shows the retinotopic mapping of the left hemisphere of the a subject, and the smoothed results of different methods. The original mapping is not diffeomorphic. Although all smoothing methods improved the smoothness, only our method can generate diffeomorphic result, especially near the fovea.

Fig. 6.

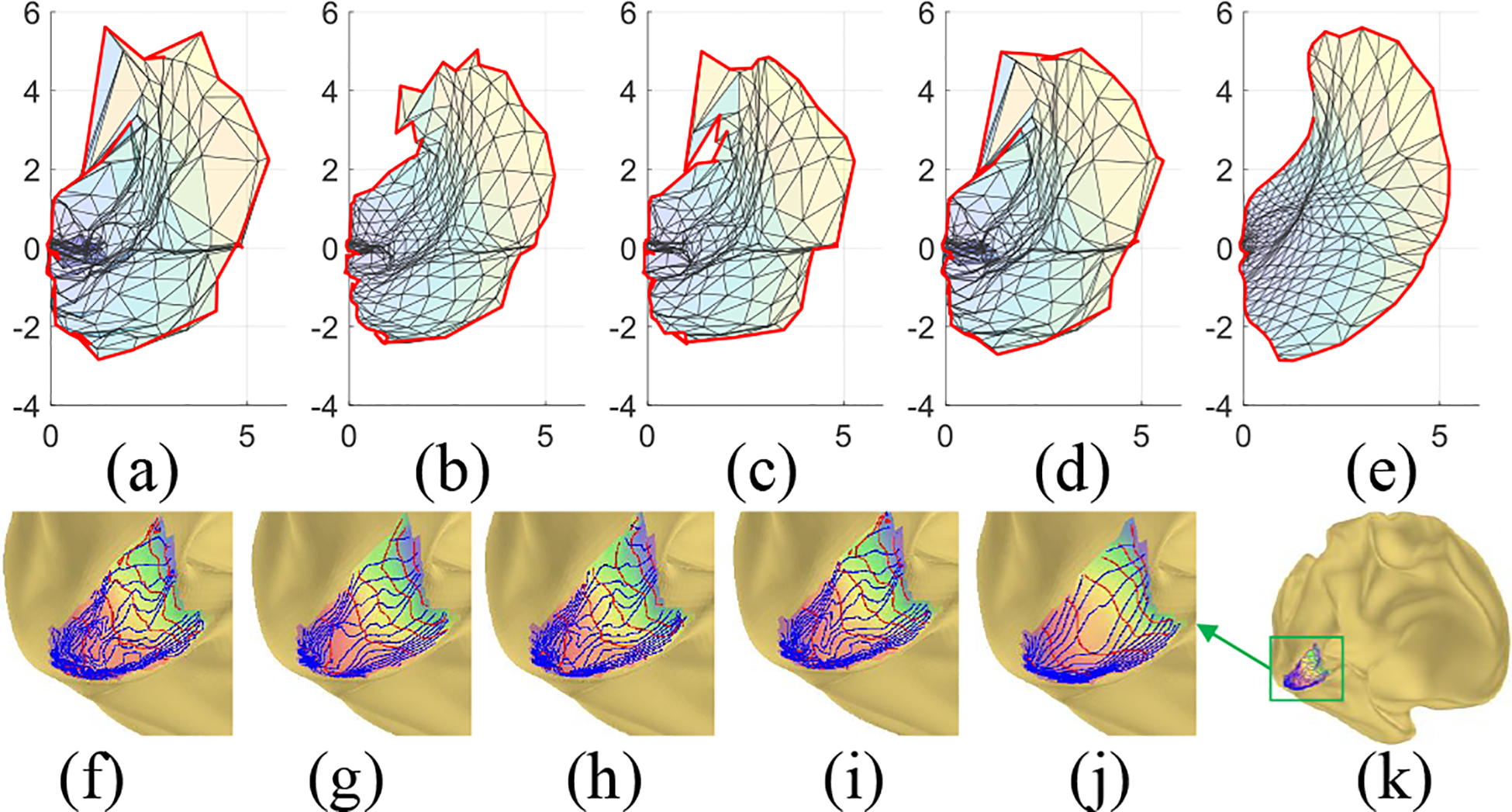
A subject’s left retinotopic mapping: (a) raw retinotopic mapping; (b)-(e) smoothing results of average, median, Laplacian, and proposed smoothing methods; (f) the raw mapping on cortical surface; (g)-(j) smoothing results on inflated surface of each method, in the same order of (b)-(e); (k) The left inflated cortex.

5. CONCLUSION AND FUTURE WORK

We adopted Beltrami coefficient to quantify diffeomorphism of retinotopic mapping and formed a mathematical model to generate diffeomorphic maps. The proposed smoother guarantees diffeomorphism and minimizes angle distortion. In future, we will (1) apply the method to the data from all subjects of the HCP cohort, and provide reliable angle distortion measures; (2) use the Beltrami coefficient to improve coregistrations of noisy retinotopic maps.