Intercellular communication controls agonist-induced calcium oscillations independently of gap junctions in smooth muscle cells

Extracellular matrix rigidity regulates how smooth muscle cells perceive contractile agonist concentration.

Abstract

In this study, we report the existence of a communication system among human smooth muscle cells that uses mechanical forces to frequency modulate long-range calcium waves. An important consequence of this mechanical signaling is that changes in stiffness of the underlying extracellular matrix can interfere with the frequency modulation of Ca²⁺ waves, causing smooth muscle cells from healthy human donors to falsely perceive a much higher agonist dose than they actually received. This aberrant sensing of contractile agonist dose on stiffer matrices is completely absent in isolated smooth muscle cells, although the isolated cells can sense matrix rigidity. We show that the intercellular communication that enables this collective Ca²⁺ response in smooth muscle cells does not involve transport across gap junctions or extracellular diffusion of signaling molecules. Instead, our data support a collective model in which mechanical signaling among smooth muscle cells regulates their response to contractile agonists.

INTRODUCTION

Excessive constriction of hollow, tubular transport organs including the airways and the vasculature is a common pathophysiological feature of widespread diseases like asthma and hypertension. The vessel/airway wall undergoes pathological changes in the smooth muscle and in the extracellular matrix (ECM) that surrounds and supports the cells with the onset of disease (1, 2). The search for mechanisms that underlie the development of these diseases and the search for novel therapies have largely focused on the smooth muscle cells (SMCs), as they are the primary effectors of constriction (3). Pathological changes in the ECM, on the other hand, have not received much attention (1, 4). More recent studies show that changes in the ECM can affect organ function at the very early stages and can even precede the thickening of the muscle layer (5). Perhaps, mechanobiological interactions between healthy SMCs and an altered ECM are playing a more critical role in the pathogenesis and progression of diseases like asthma and hypertension than is currently appreciated. In this study, we examined how changes in the matrix stiffness can affect how SMCs sense the dose of an applied agonist.

Agonist-induced Ca²⁺ oscillations and long-range Ca²⁺ waves are critical mechanisms that regulate vital parameters such as blood pressure and airway resistance (6, 7). Binding of a muscle agonist, like histamine or acetylcholine, to a surface receptor on the SMC and the subsequent rise in cytosolic Ca²⁺ concentration, is the universal trigger for force generation in the smooth muscle (8). Agonist exposure induces Ca²⁺ oscillations in SMCs that propagate as waves within the smooth muscle layer (9). These agonist-induced Ca²⁺ oscillations serve two critical functions in the smooth muscle. (i) The concentration/dose of agonist detected by the surface receptors is transduced into the frequency of Ca²⁺ oscillations, with a higher concentration of muscle agonist resulting in a higher frequency of Ca²⁺ oscillations, which can then be detected by downstream Ca²⁺ sensors and translated into a dose-dependent increase in smooth muscle contractility (6, 10). (ii) Agonist-induced Ca²⁺ oscillations propagate as waves around the circumference of the organ and enable the synchronized contractions of SMCs necessary to constrict the airway/blood vessels (9). At present, little is known about the role of extracellular mechanical factors such as ECM stiffness in regulating agonist-induced Ca²⁺ oscillations and Ca²⁺ waves that can move across an SMC ensemble.

In this study, we report a collective phenomenon in clusters of human airway SMCs, where ECM stiffness alters the intercellular communication between cells in an SMC ensemble, causing increased Ca²⁺ oscillation frequencies and synchronized Ca²⁺ oscillations. This altered Ca²⁺ response results in a relative force increase by SMCs on stiff substrates. We examined intercellular transport of Ca²⁺ in SMC cells, and we show that contrary to current dogma, the physical mechanism that enables intercellular Ca²⁺ waves does not involve molecular transport across gap junctions or paracrine signaling through extracellular diffusion. Rather, this phenomenon appears to be driven by force-transfer among cells in the cluster. The collective response of SMCs to agonist could be a mechanism by which matrix remodeling can drive disease progression in asthma and hypertension.

RESULTS

Matrix stiffness alters the Ca²⁺ response to agonist in multicellular clusters of SMCs but not in isolated cells

Modeling the SMC layer in 2D using micropatterning

To study the role of altered matrix stiffness on the frequency of Ca²⁺ oscillations, we used micropatterning to create a two-dimensional (2D) approximation of the organization of SMCs seen in lung slices (Fig. 1A and fig. S1A). The substrate that we use is NuSil (11), an optically clear, nonporous polydimethylsiloxane (PDMS) substrate whose Young’s modulus, E, can be varied in the range of 0.3 to 70 kPa (11). On the basis of the measurements of ECM stiffness in healthy human airways, we set the ECM stiffness of healthy human airways to E = 0.3 kPa (12). This matches the ECM stiffness of small airways (inner diameter, <3 mm), which are known to collapse in asthma (13). With the onset of airway remodeling, collagen is deposited in the airways and the stiffness of the ECM increases (1). A substrate stiffness of E = 13 kPa was used to mimic remodeled ECM. These ECM stiffness values are also representative of the two distinct regimes of mechanosensing seen in all adherent cells (14, 15). Using a Ca²⁺ sensitive fluorescent dye (Fluo4-AM), we imaged and quantified the time period of Ca²⁺ oscillations in these smooth muscle (SM) rings plated on soft and stiff ECM. Images were recorded at a rate of 1 per second for 5 min following exposure to 10⁻⁵ M histamine. On soft ECM (E = 0.3 kPa), exposure to histamine resulted in Ca²⁺ oscillations with a mean time period of 43.64 ± 1.45 s (N = 4, Fig. 1E). When the substrate stiffness was increased to E = 13 kPa, the same dose of agonist induced significantly faster oscillations with a mean time period of 22.79 ± 2.42 s (N = 4; t test, P < 0.001; Fig. 1E). Therefore, at the same dose of agonist, stiff substrates resulted in a doubling of the cytosolic Ca²⁺ oscillation frequency in healthy SMCs.

Fig. 1. Effect of matrix stiffness on agonist-induced Ca²⁺ oscillations in SMCs.

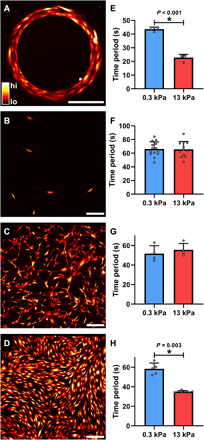
(A) To study the role of altered matrix stiffness on the time period of agonist-induced Ca²⁺ oscillations, we micropatterned a 2D approximation of the in situ organization of SMCs. Cells were also cultured on nonpatterned surfaces in three different densities: (B) isolated, (C) sparse, and (D) confluent. The colors in Fig. 1 (A to D) correspond to cytosolic [Ca²⁺] concentrations as indicated by the color bar in Fig. 1A. Scale bars, 200 μm. (E) Increasing matrix stiffness from 0.3 to 13 kPa caused a significant decrease in Ca²⁺ oscillation period in SMC rings (t test, P < 0.001; N = 4 each). (F and G) The periods of SMC Ca²⁺ oscillations were not affected by matrix stiffness in both isolated (soft, N = 14; stiff, N = 12) and sparse (N = 4 each) conditions (t test, P = 0.93 and P = 0.481, respectively). (H) Confluent cells behaved like those patterned in a ring, with cells plated on stiff matrix exhibiting significantly faster Ca²⁺ oscillations in response to 10⁻⁵ M histamine compared to those on a soft matrix (soft, N = 5; stiff, N = 7; Mann-Whitney rank sum test, P = 0.003). These results demonstrate that matrix stiffness can modulate the agonist-induced Ca²⁺ response of confluent SMCs but not that of isolated cells.

Interactions between ECM and isolated cells are insufficient to explain altered Ca²⁺ response

To explain the role of matrix stiffness in regulating the Ca²⁺ response to a low dose of agonist, we first hypothesized that this phenomenon was linked to cell-matrix interactions at the level of the individual cell. With increased matrix stiffness, SMCs develop higher cytoskeletal prestress (15), opening stretch-activated Ca²⁺ channels (16) and potentially increasing the Ca²⁺ flux into the cell. To test this hypothesis, we cultured human airway SMCs at a low density such that individual cells were isolated, spaced at least 100 μm from each other (Fig. 1B and fig. S1B). We first measured baseline traction (pre-agonist) stress exerted by these isolated cells on the substrate to confirm that the baseline traction was significantly higher in isolated cells cultured on stiff, with a mean traction stress of 15.95 ± 5.02 Pa (N = 21), versus isolated cells cultured on soft substrates, with a mean traction stress of 6.98 ± 1.68 Pa (N = 16). The corresponding median stresses were 6.89 Pa on soft matrix and 16.00 Pa on stiff substrate (Mann-Whitney rank sum test, P < 0.001). We then exposed these isolated SMCs to 10⁻⁵ M histamine and measured the time period of Ca²⁺ oscillations. Contrary to our expectations, ECM stiffness had no impact on the Ca²⁺ response of isolated SMCs to 10⁻⁵ M histamine (Fig. 1F). Cells cultured on the soft substrate had a mean period of 66.11 ± 10.55 s (N = 14), and those on the stiff matrix had a mean period of 65.73 ± 11.48 s (N = 12), which was not statistically significantly different (t test, P = 0.930). Therefore, despite the higher levels of prestress in individual cells, ECM stiffening has no impact on the agonist-induced Ca²⁺ frequency of isolated cells.

SMCs sense matrix as a collective and alter their Ca²⁺ response to agonist

To further probe this phenomenon, starting with the isolated SMCs (Fig. 1B), we increased the seeding density (Fig. 1C and fig. S1C) until we had a confluent cluster of SMCs (Fig. 1D and fig. S1D). At each seeding density, we measured the time period of Ca²⁺ oscillations for SMCs adhering to soft (E = 0.3 kPa) and stiff (E = 13 kPa) substrates in response to 10⁻⁵ M histamine (Fig. 1, F to H). Sparsely seeded cells (Fig. 1G) responded similarly to isolated cells (Fig. 1F), exhibiting no statistically significant difference between the agonist-induced Ca²⁺ oscillations on soft and stiff matrix (t test, P = 0.481). The mean time period of oscillations of sparse SMCs on the soft substrate was 51.74 ± 8.11 s (N = 4) and 55.63 ± 6.48 s (N = 4) on the stiff substrate (Fig. 1G). Confluent cells behaved like those patterned in a ring, with cells plated on stiffer substrate exhibiting a significantly higher frequency of Ca²⁺ oscillations in response to 10⁻⁵ M histamine. Confluent SMCs on soft matrix had a mean time period of 58.36 ± 5.89 s (N = 5), and the same healthy, confluent cells on stiff matrix had a mean period of 35.03 ± 1.03 s (N = 7, Fig. 1H). The corresponding median time periods were 58.87 s on soft matrix and 35.11 s on stiff matrix (Mann-Whitney rank sum test, P = 0.003). These results suggest the existence of a collective phenomenon in SMCs, where clusters of confluent SMCs alter their agonist-induced Ca²⁺ oscillations in response to changes in matrix stiffness, while isolated cells do not. In fig. S2, we include additional measurements made on two intermediate stiffnesses, E = 0.6 kPa, E = 3 kPa, and glass (E→∞). These experiments confirm that Ca²⁺ oscillations resulting from exposure to 10⁻⁵ M histamine are unaffected by ECM stiffness in isolated SMCs, whereas in confluent cells, the same dose of agonist can evoke a significantly different Ca²⁺ response in SMCs depending on the stiffness of the underlying matrix. This finding is extremely important in all smooth muscle pathologies because all downstream Ca²⁺-dependent molecular processes rely on Ca²⁺ oscillations to perceive the external concentration of contractile agonist detected by the G protein–coupled receptors on the cell surface. Here, we show that the combination of confluence and ECM stiffness can alter how cells perceive contractile agonist.

Matrix stiffening synchronizes Ca²⁺ oscillations within a multicellular SMC cluster

We next explored the nature of intercellular communication underlying the collective agonist-induced Ca²⁺ response in SMCs. To do this, we first analyzed the time series of histamine-induced Ca²⁺ oscillations for signs of interactions among the different SMCs within a confluent cluster. After correcting for drift due to photobleaching of the fluorophore, we calculated the cross-correlation coefficient (ρ_i,j ϵ [−1,1]) of the Ca²⁺ oscillations occurring in the ith cell and the jth cell in the cluster for all the cells in a cluster. The measured values of ρ_i,j in a typical SMC cluster is depicted in Fig. 2A as a representative 24 × 24 matrix, with the extreme values ρ_i,j → 1 (pink) indicating that the Ca²⁺ levels in the ith and jth cell rise and fall perfectly in sync with each other (perfectly correlated) (Fig. 2B), ρ_i,j → −1 (green) indicating that when the Ca²⁺ levels in ith cell rises, the Ca²⁺ levels in the jth cell falls and vice versa (anti-correlated), and ρ_i,j → 0 (white) indicating that no correlation in the Ca²⁺ oscillations occurs in ith and jth cells (Fig. 2B). To avoid the effects of histamine diffusion, the first 60 s immediately after application of histamine was not considered in the correlation calculation. Histograms of ρ_i,j measured in isolated SMCs and confluent clusters of SMCs cultured on soft and stiff matrices are shown in Fig. 2 (C and D), respectively. Isolated SMCs (Fig. 2C) did not exhibit correlated Ca²⁺ oscillations, with a mean ρ of zero, regardless of whether they were cultured on soft (0.01 ± 0.06, N = 5) or stiff (0.03 ± 0.06, N = 4) substrates. However, for cells in a confluent cluster, matrix stiffening caused a statistically significant shift in ρ toward positive correlation (Fig. 2D). The mean ρ for confluent clusters on soft matrices was 0.03 ± 0.04, N = 4, versus on stiff matrices, ρ increased to 0.26 ± 0.10, N = 5. A two-way analysis of variance (ANOVA) test with confluence and ECM stiffness as independent factors showed a significant interaction between confluence and ECM stiffness (P = 0.007). Post hoc pairwise comparisons using the Holm-Sidak test showed a significant difference in the pairwise correlations in confluent clusters due to ECM stiffness (P < 0.001). In the isolated cells, there was no statistical difference in the pairwise correlations due to ECM stiffness (P = 0.733). We also did not observe any systematic relationship between the pairwise correlation in Ca²⁺ oscillations and the distance between the SMCs.

Fig. 2. Effect of matrix stiffness and confluence on the correlated nature of Ca²⁺ oscillations.

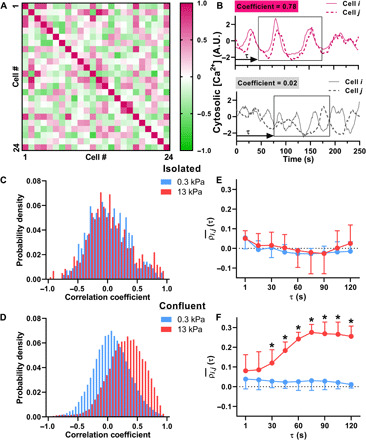
(A) The cross-correlation coefficients (ρ_i,j) range in values from 1 (positively correlated, pink) to 0 (uncorrelated, white) to −1 (negatively correlated, green), as shown in a representative 24 × 24 cell matrix. (B) Examples of Ca²⁺ oscillations measured in two cells with high pairwise correlation (ρ = 0.78) and low pairwise correlation (ρ = 0.02). A.U., arbitrary units. (C) In isolated cells, the Ca²⁺ oscillations were generally uncorrelated with a probability density function centered around zero. ECM stiffness did not affect pairwise correlations in isolated SMCs (soft, N = 5; stiff, N = 4; P = 0.733, two-way ANOVA). (D) In confluent cells, there is a statistically significant increase in ρ, indicating that the Ca²⁺ oscillations were more synchronized on stiffer ECM (soft, N = 4; stiff, N = 5; two-way ANOVA, P = 0.007). (E and F) To evaluate the time it takes after agonist addition for Ca²⁺ oscillations to become synchronized, we calculated ρ_i,j(τ) within a 120-s moving window. (E) ρ_i,j(τ) in isolated cells does not change over time (soft, N = 5; stiff, N = 4; P = 0.274) or with stiffness (P = 0.303) (two-way ANOVA). (F) However, in confluent cells on stiff matrix, ρ_i,j(τ) shows a significant increase after 30 s (soft, N = 4; stiff, N = 5) (two-way ANOVA, P < 0.001). Error bars indicate SD.

Next, we investigated the time it takes after the addition of histamine for the Ca²⁺ oscillations to synchronize. To do this, we repeated the previous calculation of cross-correlations, but instead of using the entire time series, we used a time window of 120 s starting at t = 60 s after addition of histamine and repeated the ρ_i,j calculation for the Ca²⁺ time series within this 120 s window for all cells in the cluster. The time window was then shifted in increments of 15 s over the rest of the 5-min time frame over which we measured Ca²⁺ oscillations. The average through time, ρ_i,j(τ), of cross-correlation coefficients is shown between all isolated cells (Fig. 2E) and between all confluent cells (Fig. 2F) on either soft (blue) or stiff (red) matrix. A two-way ANOVA with time after addition of histamine and ECM stiffness as the two independent factors shows no difference due to stiffness (P = 0.303) or time (P = 0.274) in isolated cells. However, in confluent cells on stiff ECM, the correlation coefficients gradually increase over time, for about 1 min, which matches the time course for force generation in airway SMCs (17). In conjunction with our findings from the previous section, these results demonstrate that the combination of a stiff matrix and confluent clusters of cells not only leads to faster Ca²⁺ oscillations but also causes histamine-induced Ca²⁺ oscillations to synchronize across the cells in the cluster.

Gap junctions do not play a role in regulating the collective Ca²⁺ response of SMC clusters

The most well-studied long-range communication mechanism in multicellular systems is the intercellular waves of Ca²⁺ that are capable of propagating over distances much longer than a cell length through a regenerative Ca²⁺-induced Ca²⁺ release mechanism (18). This mode of communication is mediated through two critical pathways: (i) gap junction channels, which connect the cytoplasm of neighboring cells and allow the transport of signaling molecules from one cell to its neighbor, and (ii) extracellular diffusion of a signaling molecule like adenosine 5′-triphosphate (ATP), which can diffuse and bind to purinergic receptors on neighboring cells, causing Ca²⁺ release in these cells (19).

Transport through gap junctions is unaffected by ECM stiffness

We first fluorescently labeled gap junctions by staining for connexin-43 (Cx43). The expression of Cx43 (red) for confluent clusters of SMCs on soft and stiff substrates is shown in Fig. 3 (A and B), respectively. The actin filaments (green) and the nucleus (blue) are also labeled. From these images, we quantified the number of gap junctions per cell for confluent cells plated on soft and stiff substrates. There was no significant difference between Cx43 expression on soft and stiff substrates from N = 5 independent samples per stiffness, each containing approximately 35 cell measurements (t test, P = 0.977) (Fig. 3C). Next, we tested whether ECM stiffness induced a change in the efficiency of transport through gap junctions. To this end, we used a commonly used technique to quantitatively assess the efficiency of transport through gap junctions called gap-FRAP (fluorescent recovery after photobleaching) (20). Briefly, a confluent layer of SMCs was incubated with membrane-permeable calcein-AM. Upon entering the cell, the acetyl methyl ester bond was hydrolyzed by intracellular esterases, trapping the hydrophilic calcein molecule within the cell (Fig. 3D, column 1). The calcein in one cell selected at random was then bleached using a high-intensity laser (Fig. 3D, column 2). The bleached calcein molecules and the unbleached calcein molecules in neighboring cells diffuse through gap junctions, leading to a recovery in fluorescence (Fig. 3D, column 3). The kinetics and extent of recovery in fluorescence in the bleached cell reflect the efficiency of transport across gap junctions via diffusion. A typical recovery curve is shown in Fig. 3E, where F₀, F_b, and F_r indicate the fluorescence intensity in the target cell at baseline, after bleaching, and after recovery. To quantify the extent of recovery, we calculated the mobile fraction, Γ, given by

$$\mathrm{\Gamma }=\frac{F_{\mathrm{r}}-F_{\mathrm{b}}}{F_0-F_{\mathrm{b}}}\times 100\%$$ (1)

for confluent SMCs cultured on soft and stiff matrices (N = 16 and 18 independent trials, respectively). We found no difference in the mobile fraction due to ECM stiffness. SMCs on soft matrix had a mean mobile fraction, Γ, of 42.19 ± 10.50%, and those on stiff matrix had a Γ of 40.05 ± 9.18% (t test, P = 0.532) (Fig. 3F). We also did not observe any statistically significant difference in the rate of recovery in fluorescence k_r, which was calculated by fitting an exponential function F(t) = F_b + F_r(1 − e^−krt) to the recovery curve. On soft ECM, k_r was 0.01 ± 0.02 (N = 16), and on stiff ECM, k_r was 0.01 ± 0.05 (N = 18). There was no statistical difference in the rate of recovery due to ECM stiffness (t test, P = 0.55).

Fig. 3. Effect of matrix stiffness on intercellular communication via gap junctions.

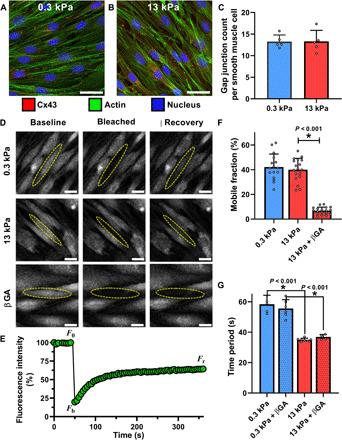
Confluent SMCs on soft (A) and stiff (B) matrix were stained for the gap junction protein Cx43, actin, and the nucleus. (C) Gap junctions were counted for each SMC in individual frames on soft (N = 5) and stiff (N = 5) matrix, represented by the mean and SD of these measurements, and we found no statistical difference due to matrix stiffening (t test, P = 0.977). (D) Diffusion through gap junctions was quantified by bleaching a small fluorescent molecule within a cell and measuring signal recovery due to intercellular diffusion, a technique called gap-FRAP. (E) A representative recovery curve for one cell shows a recovery of ~40% its initial fluorescence. These values were used to calculate mobile fraction, a measure of diffusion efficiency through gap junctions. (F) Matrix stiffness had no effect on mobile fraction (t test; soft, N = 16; stiff, N = 18; P = 0.532). The gap junction blocker βGA significantly reduced the recovery (D) and mobile fraction (F) (N = 18, Mann-Whitney rank sum test). (G) Despite blocking gap junctions with βGA, there was no effect on Ca²⁺ oscillation periods in confluent cells on either soft (N = 6) or stiff (N = 4) matrix (two-way ANOVA, P = 0.784 treatment within stiffness). Scale bars, 30 μm.

Blocking gap junctions does not affect agonist-induced Ca²⁺ oscillations

To further explore the role of gap junctions in the collective response of the SMCs to agonist, we used 30 μM of 18β-glycyrrhetinic acid (βGA) to block transport across gap junctions. βGA causes dephosphorylation of connexins and disassembly of gap junctions (21). We first used gap-FRAP to verify that a 30 μM dose of βGA was sufficient to completely block transport across gap junctions. The mobile fraction, Γ, measured in a confluent layer of SMCs after application of 30 μM βGA dropped significantly from a mean of 40.05 ± 9.18% to 6.84 ± 2.89% (N = 18, with corresponding medians of 40.41 and 7.02%, respectively; Mann-Whitney rank sum test, P < 0.001) (Fig. 3F). This recovery is similar to the 7.89% recovery that we measured in an isolated cell. Similar minimal recovery has been noted in the literature (22), indicating that transport across gap junctions was blocked. After 30 min of incubation with 30 μM dose of βGA, we measured histamine-induced Ca²⁺ oscillations in confluent clusters of SMCs. Unexpectedly, we found that blocking gap junctional transport had no impact on the histamine-induced Ca²⁺ oscillation periods in multicellular clusters of SMCs, regardless of the stiffness of the ECM (soft, N = 6; stiff, N = 4) (Fig. 3G). A two-way ANOVA with treatment (βGA) and ECM stiffness as the two independent factors showed no difference in the time period of histamine-induced Ca²⁺ oscillations due to treatment (P = 0.784) for a given stiffness. Post hoc pairwise comparisons with the Holm-Sidak method showed that the Ca²⁺ oscillations remained significantly faster on the stiff matrix (P < 0.001) even after blocking gap junctions.

Mechanical force transfer among cells regulates the collective Ca²⁺ response of SMC clusters

Ca²⁺ wave propagation follows the contractile axis of the SMCs

Next, we considered extracellular diffusion of signaling molecules, such as ATP, as a possible mode of intercellular communication that enables the collective Ca²⁺ response of SMC clusters on stiff matrices (18). To do this, we measured the direction in which the Ca²⁺ wave propagates from one cell to the next in SMC clusters cultured on stiff substrates. If we select a cell in an SMC cluster, a wave that passes through it will appear as a localized increase in Ca²⁺ in the cell, which is followed by a localized increase in Ca²⁺ in one of its neighbors. We reasoned that if the intercellular Ca²⁺ transport was being enabled by extracellular diffusion of signaling molecules, then the resulting Ca²⁺ wave should have an equal chance of moving in all directions (isotropic). We split the direction of propagation of the Ca²⁺ wave from an SMC into two directions: a direction parallel to the contractile axis of the SMC and a direction perpendicular to the contractile axis of the SMC. For the cell labeled 1 shown in Fig. 4A (insets), cells 2 and 4 were considered parallel to cell 1’s contractile axis and cells 3 and 5 were considered perpendicular to cell 1’s contractile axis. We calculated the conditional probability for a localized increase in Ca²⁺ in one cell to be followed by a localized increase in a parallel neighbor versus its perpendicular neighbor. This conditional probability quantifies the isotropy in Ca²⁺ wave propagation with respect to the contractile axis of the SMC, with equal probability (0.5) in parallel and perpendicular direction indicating isotropy in Ca²⁺ wave propagation. Instead, we found that there was an 80.5 ± 7.53% chance for the Ca²⁺ wave to follow the contractile axis of the SMC (Fig. 4B; N = 10; t test, P < 0.001). The high probability of the Ca²⁺ wave to follow the contractile axis of the SMCs rules out extracellular diffusion as the dominant mechanism for intercellular communication in our experiments.

Fig. 4. Role of mechanical force in Ca²⁺ wave propagation through multicellular ensembles of SMCs.

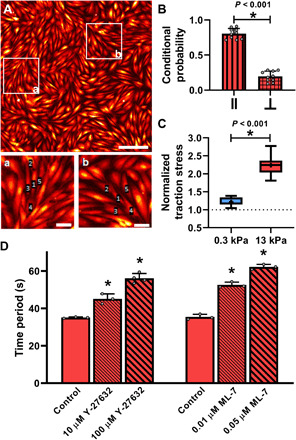
(A) SMCs in confluent layers form organized clusters of cells, with certain cells aligned end-to-end along their contractile axis (parallel), and others branching off at an angle (perpendicular). Scale bars, 250 μm. Insets (a) and (b) show cells 2 and 4 parallel to the contractile axis of cell 1, whereas cells 3 and 5 are perpendicular. Inset scale bars, 50 μm. The conditional probability for a localized increase in Ca²⁺ in cell 1 to be followed by an increase in a parallel or perpendicular neighbor is plotted in (B) with mean and SD. Ca²⁺ waves were statistically more likely to propagate along the contractile axis (t test, N = 10). (C) Histamine caused a significantly greater increase in traction stress in confluent cells on stiff matrix (N = 21) rather than on soft matrix (N = 12, t test). (D) The faster agonist-induced Ca²⁺ oscillations on stiff ECM were systematically abrogated in a dose-dependent manner by preincubating the SMCs with the ROCK inhibitor Y-27632 for 1 hour before histamine exposure (N = 3 and 4; P < 0.001, one-way ANOVA). Identical results can be obtained with MLCK inhibition by preincubating with increasing doses of ML-7 for 5 min (N = 3 each; P < 0.001, one-way ANOVA).

Mechanical force transfer between SMCs regulates their Ca²⁺ response

Thus far, we have ruled out transport through gap junctions and extracellular diffusion, the two widely accepted mechanisms responsible for intercellular communication in confluent cell clusters using Ca²⁺ waves (18). The propensity of Ca²⁺ waves to follow the direction of the contractile axis of the SMC suggested force transfer between neighboring SMCs as a potential mechanism that regulates the collective Ca²⁺ response of SMC clusters. To quantify SMC forces in our confluent clusters, we used Fourier transform traction force microscopy (23) to measure the traction stress generated by cells exposed to 10⁻⁵ M histamine. Traction stress is the force exerted by the cell normalized by the cross-sectional area over which the force acts. Before agonist stimulation, mean traction stresses for isolated cells were 6.98 ± 1.68 Pa on soft (N = 16) and 15.95 ± 5.02 Pa on stiff (N = 21) substrates, and 13.56 ± 1.56 Pa on soft (N = 12) and 14.26 ± 1.89 Pa on stiff (N = 21) substrates for confluent cells. We found that histamine had generated a normalized traction (post-histamine traction stress/pre-histamine traction stress) of 1.22 ± 0.11 in confluent cells on soft substrates (N = 12). On stiffer matrix, a confluent cluster of SMCs from the same healthy donor and passage generated normalized force of 2.24 ± 0.26 (N = 21) (Fig. 4C). There was a statistically significant difference (P < 0.001, t test) between the force generated on soft and stiff substrates in response to the same dose of agonist. To test the possibility that higher force transfer among cells on stiff substrates was responsible for this collective phenomenon, we experimentally measured the effect of reducing muscle force on Ca²⁺ oscillations with two independent inhibitors of force generation: (i) Rho-associated kinase (ROCK) inhibitor, Y-27632, which reduces SMC force by inhibiting myosin light chain phosphorylation and by removing the inhibitory effect of ROCK on the activity of myosin light chain phosphatase, and (ii) myosin light chain kinase (MLCK) inhibitor, ML-7, which reduces force by inhibiting myosin light chain phosphorylation. Confluent SMC clusters on E = 13 kPa matrix were pretreated with increasing doses of either Y-27632 for 1 hour before histamine exposure or increasing doses of ML-7 for 5 min before histamine exposure (Fig. 4D). We found that increasing the concentration of Y-27632 from 10 μM (N = 3) to 100 μM (N = 4) abolished the stiffness-induced reduction in time period of Ca²⁺ oscillations in a dose-dependent manner (one-way ANOVA with treatment as the independent variable, P < 0.001). Similarly, increasing the dose of ML-7 from 0.01 to 0.05 μM also abolished the stiffness-induced reduction in time period of Ca²⁺ oscillations in a dose-dependent manner (one-way ANOVA, P < 0.001). With both these inhibitors, the higher concentration resulted in histamine-induced Ca²⁺ oscillation periods on stiff matrices that were not statistically different from the histamine-induced Ca²⁺ oscillation periods on soft matrices. These results demonstrate that the exaggerated histamine-induced Ca²⁺ response due to matrix stiffening can be systematically and completely abrogated by reducing mechanical forces in the multicellular ensemble.

Confining the SMCs to a line reduces the variability in Ca²⁺ oscillation periods

Comparing the alignment of SMCs in Fig. 1 (B to D) and Fig. 4A, we observed that with the onset of confluence, SMCs naturally tend to organize themselves into spatial clusters of aligned cells. To test the effect of SMC alignment on the higher frequency of Ca²⁺ oscillation on stiff substrates, we compared the time period of Ca²⁺ oscillations in confluent SMC clusters to the time period of Ca²⁺ oscillations in SMC clusters micropatterned in a line 1000 μm long and 15 μm wide (~1 cell wide and ~10 cell length long) (Fig. 5A and fig. S1E). The idea here was to eliminate the possibility of intercellular communication occurring perpendicular to the contractile axis in confluent clusters through mechanisms that are less likely to be influenced by force. We found that while the mean time period of oscillations was nearly identical in both confluent SMC clusters and lines of SMCs, the probability of cells with a higher time period of Ca²⁺ oscillations decreases when SMCs are aligned (Fig. 5B). An F test shows a significant decrease in the variability of the time period distribution when the cells are aligned in a line (soft, N = 8; stiff, N = 6; P < 0.001). This result is consistent with the idea that higher Ca²⁺ frequencies are being driven by force transfer along the contractile axis.

Fig. 5. Effect of confining SMCs in a line using micropatterning.

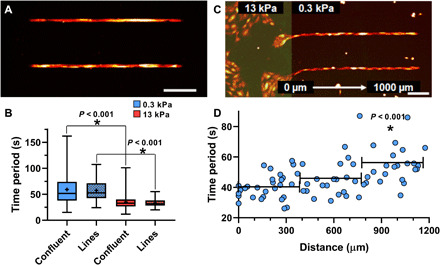
(A) When SMCs were patterned in lines, (B) the probability of finding SMCs with high time periods decreased and the variance of the time periods from aligned cells was significantly smaller than confluent cells (F test, P < 0.001). Matrix stiffness still affected the oscillation period (soft, N = 8; stiff, N = 6; Mann-Whitney rank sum test). To probe the limits of the SMC cluster’s collective matrix sensing abilities, we simulated localized ECM stiffening by (C) patterning SMCs in lines spanning a dual-stiffness PDMS substrate (E = 13 kPa highlighted in green, left, and E = 0.3 kPa, right). (D) The Ca²⁺ oscillation time period of cells along lines is plotted as a function of the distance from the stiff matrix. Binning cells in 400-μm intervals, only those over 800 μm from stiff matrix had different Ca²⁺ oscillation time periods from cells directly in contact (t test, N = 4). Scale bars, 250 μm.

The effect of localized ECM stiffening can be sensed by SMCs over long distances

ECM remodeling in airways and blood vessels often occurs as spatially localized processes. How does this pathological change in the ECM spread? Current theories require cells to migrate into the region of stiffer ECM for them to sense the altered matrix and respond by excessive secretion of matrix proteins, thereby creating a positive feedback loop that leads to more ECM remodeling (24). However, given the collective nature of ECM stiffness sensing in SMC clusters, it may be possible for SMCs located far away from the site of ECM remodeling to detect this localized change, although these SMCs are not physically in contact with the stiff ECM. To test this hypothesis and to quantify the distance over which a localized increase in ECM stiffness would be felt by an ensemble of SMCs, we created a dual-stiffness substrate (Fig. 5C), where the region marked in green has Young’s modulus of 13 kPa and the region in black has Young’s modulus of 0.3 kPa. We then patterned SMCs in a line starting from the stiff region and extending into the soft region. Cells on soft and stiff ECM were simultaneously exposed to 10⁻⁵ M histamine, and we measured the time period of Ca²⁺ oscillations in SMCs on the soft ECM for 5 min. The change in Ca²⁺ oscillation time period was not sudden as one moved from the stiff to the soft ECM (Fig. 5D). Rather, the mean time period increased at a slow rate of 1.83 s/100 μm. We grouped the cells by distance from the edge into 400-μm bins and statistically tested the difference in the time period of Ca²⁺ oscillations between each bin and cells in physical contact with the stiff substrate. We found that there was no statistically significant difference between histamine-induced Ca²⁺ oscillations for cells on stiff substrates and cells up to 800 μm (approximately 8 cell lengths) away from the edge (N = 4; Mann-Whitney rank sum test, P = 0.140). Cells beyond 800 μm had significantly different time periods (N = 4; t test, P < 0.001). This result demonstrates that spatially localized alterations in the ECM can be detected by SMCs far from the site of ECM remodeling, suggesting that ECM pathology can spread through the organ much faster than currently believed.

DISCUSSION

Increased stiffness of the ECM that surrounds and supports cells in tissue is associated with a number of disease conditions ranging from cancer and fibrosis (25) to cardiovascular (26), lung (1), eye (27), and age-related diseases (28). Traditionally, pathological alterations in the ECM were thought to be the consequence of disease progression. However, it is now becoming increasingly apparent in many diseases that matrix stiffening precedes disease development and could, therefore, contribute to disease progression (5, 29). Recognizing the importance of ECM remodeling, clinical trials were undertaken to restore the healthy, homeostatic state of the ECM (30). These early efforts were unsuccessful (31) and attention has now turned to understanding and targeting the mechanisms by which cells perceive and respond to changes in the ECM (29).

Here, we demonstrate a collective phenomenon in SMCs in which matrix stiffness alters the intercellular communication between cells in an ensemble resulting in elevated contractility at low doses of agonist. We show that this collective mechanosensing phenomenon is enabled by crosstalk among cells using Ca²⁺ waves (18). A common mechanism of communication involves the molecular transport of Ca²⁺ and inositol trisphosphate (IP₃) across gap junctions. However, our measurements showed no tendency for molecular transport through gap junctions to differ depending on ECM stiffness. We blocked transport through gap junctions using βGA (32) and confirmed that the dose we used was sufficient to completely disrupt molecular transport across gap junctions. Contrary to our expectations based on current models (18), blocking transport through gap junctions had no impact on the collective agonist response of SMCs to ECM stiffening. There was no change in the Ca²⁺ oscillation for SMCs on soft and stiff substrates after βGA treatment. Following a recent finding that mechanical forces can synchronize contraction of cardiac myocytes in the developing heart independent of gap junctions (32), we tested whether ECM stiffening led to a switch in the mode of communication between cells from molecular signaling through gap junctions to mechanical force–based signaling.

Ca²⁺ waves can travel distances far greater than a cell length because Ca²⁺ waves regenerate in each cell by “calcium-induced calcium release” from the endoplasmic reticulum (ER). In the most widely accepted theory of long-range Ca²⁺ transport, Ca²⁺ release from the ER is enabled by a messenger molecule, IP₃, which diffuses faster than Ca²⁺ and activates the receptors on the ER, so when the Ca²⁺ wave arrives, it can release more Ca²⁺. This theory had its basis in measurements of IP₃ diffusivity in the Xenopus extract model of the cytoplasm (33), which put the diffusivity of IP₃ at 400 μm²/s and that of Ca²⁺ at 40 μm²/s. However, more recent measurements made in human cells show that IP₃ diffuses at a slower rate than Ca²⁺ (34). Our finding that molecular diffusion through gap junctions is not necessary to sustain Ca²⁺ waves in SMC clusters is consistent with the challenge to the dogma of Ca²⁺ wave propagation through gap junctions.

In contrast to Ca²⁺ wave propagation in other cell types, measurements in confluent SMC clusters (Fig. 4, A and B) show that Ca²⁺ waves follow the direction of the contractile axis of the SMCs. Further, reducing the SMC force in our experiments with two independently acting muscle relaxants slowed the Ca²⁺ oscillations and intercellular Ca²⁺ waves (Fig. 4D), suggesting that mechanical force transfer from one cell to its neighbor enables the intercellular Ca²⁺ transport. Can force transfer between cells also serve as a mechanism that amplifies and modulates the frequency of oscillations as the Ca²⁺ wave moves from cell-to-cell? The mechanisms that underlie the findings of the present study can be understood in light of previous works by Felix et al. (35) and Tanaka et al. (36) who show that forces applied to a cell membrane cause phosphatidylinositol 4,5-bisphosphate (PIP₂) to be hydrolyzed, resulting in an increase in cytosolic IP₃ concentration. This would mean that for every SMC cell within a confluent cluster, there are two ways by which IP₃ can be released into the cytosol: (i) from agonist binding to G protein–coupled receptors on the cell surface and (ii) from IP₃ generated by a contracting SMC pulling on its neighbor causing IP₃ release in the neighboring cell (35, 36). This additional method of IP₃ release only exists for cells in a confluent cluster. Further, we have previously shown that force transfer between SMCs increases eightfold with matrix stiffening (12). Such a force-based IP₃ release mechanism can explain how SMC clusters alter their agonist-induced Ca²⁺ oscillations in a matrix stiffness–dependent manner while isolated cells, which lack the second source of IP₃, do not.

Dysfunction in the smooth muscle has long been thought to be responsible for the exaggerated narrowing of transport organs in diseases like asthma, hypertension, and Crohn’s disease. Asthma is an example of a disease where remodeling of the ECM is well characterized (1), but its effects are not considered in therapy or drug development. Asthmatics can be free of inflammation and have spirometry and respiratory mechanics within the range of healthy individuals up until they are exposed to a smooth muscle agonist at which point airways in an asthmatic will hyperconstrict (37). This exaggerated response of the airway is currently thought to result from the sensitization of force-generating pathways in the SMC due to prolonged exposure to inflammatory agents. Here, we demonstrate that the fault may instead lie in changes in ECM stiffness that can regulate how SMCs perceive agonist dose. To assess the overall magnitude and potential physiological impact of the observed effect, we measured the Ca²⁺ response to different doses of histamine at two different stiffnesses (fig. S3). The data show that if the ECM stiffness of small airways (inner diameter, <3 mm) in a healthy human lung with E = 0.3 kPa (12) were to remodel and become stiff (E = 13 kPa), healthy airway SMCs would now respond to a dose of 10⁻⁵ M histamine as though they received 10⁻³ M histamine (two-log-dose higher concentration). We also demonstrate that the corresponding agonist-induced force is also substantially higher (Fig. 4C).

There are several confounding factors to consider as one extrapolates these findings at the length scale of cells to the length scale of the airway/lung. These confounding factors include but are not limited to the following. (i) Connectivity among SMCs within the airway: To constrict an airway, SMCs need to connect with each other to form a percolating force transfer path that winds around the circumference of the airway and generates a force sufficient to narrow the airway lumen. These physical connections between cells can occur through direct cell-cell (cadherin-based contacts) or cell-ECM (focal adhesion) connections, which are, in turn, dependent on mechanical forces (12). (ii) Transmural pressure: The mechanical load presented by the ECM, which will vary depending on the size of the airway and the transmural pressure. (iii) Additional confounding factors: Surface tension, airway tone, parenchymal tethering forces, etc., will also play a role in dictating the degree to which airway lumen narrows in response to smooth muscle activation by inhaled agonist. Experimentally validating these results in lung tissue will require the development of new technology to alter ECM stiffness of airways. With careful calibration, it might be possible to adapt methods from tissue engineering like ultraviolet (UV)–induced cross-linking of collagen to study the effects of ECM stiffening in situ in precision-cut lung slices.

At first glance, it appears contradictory that stretch decreases airway smooth muscle force (38). Yet, stretch has also been shown to trigger a rise in cytosolic Ca²⁺ (39). The key to this apparent paradox may be found in the single stretch experiments of Krishnan et al. (40) as well as computational models of the effect of stretch on muscle force (15). These studies show that the decline in force occurs almost instantly upon stretching and is related to rupture events in the cytoskeleton. The recovery, however, is slow and occurs at a time scale of the order of hundreds of seconds in human smooth muscle. When a cell is being subjected to cyclic stretch (such as the length oscillations), the cell is attempting to recover its original prestress that it lost immediately after the onset of stretch. To regain prestress, myosin activity is required, and this necessitates higher Ca²⁺ levels.

ECM remodeling in airways and blood vessels often occurs as spatially localized processes. We also show that a spatially localized change in the ECM might be sufficient for exaggerated force generation in SMCs far away from the site of ECM remodeling. Consequently, the effects of ECM remodeling may manifest much earlier in disease progression than currently believed. Our findings are relevant to finding previously unidentified pathways by which ECM remodeling can be the primary driver of disease and for ongoing efforts to develop new drugs that target mechanosensory pathways (29). For airway smooth muscle, and asthma, in particular, these results show that the current treatment regimen may need to shift to new paradigms that target matrix remodeling and mechanosensory pathways for a more lasting cure.

MATERIALS AND METHODS

Fabrication of optically clear substrates of tunable stiffness

NuSil is an optically clear, biologically inert PDMS substrate with Young’s modulus tunable in the range from 0.3 to 70 kPa (11). Equal parts of NuSil gel-8100 parts A and B (NuSil, Carpinteria, CA, USA) were mixed with various amounts of the cross-linking compound of Sylgard 184 (Dow Corning, Midland, MI, USA) to adjust substrate stiffness. A cross-linker volume 0.36% of the combined parts A and B volume was added for substrates with Young’s modulus E = 13 kPa, and no cross-linker was added to the 1:1 A:B mixture for substrates with Young’s modulus E = 0.3 kPa. After mixing, the substrate was spin-coated onto 30-mm-diameter, #1.5 glass coverslips for 50 s to produce a 100-μm-thick layer. They settled on a level surface at room temperature for 1 hour before curing at 60°C overnight. These cured substrates on coverslips were secured in sterile 40-mm Bioptech dishes (Biological Optical Technologies, Butler, PA, USA) to be used for cell culture.

Matrix protein coating

To coat the entire silicone substrate with protein, a volume of 0.1% gelatin solution was added and incubated at room temperature in the biosafety cabinet for 1 hour. To create protein patterns, we used the Alvéole’s PRIMO optical module and the Leonardo software, a UV-based, contactless photopatterning system (Alvéole, Paris, France). The substrate surface was first coated with poly-l-lysine (PLL) (500 μg/ml; Sigma-Aldrich, St. Louis, MO, USA) for 1 hour at room temperature. The substrate was washed with phosphate-buffered saline (PBS) and 10 mM 4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid (HEPES) buffer adjusted to pH 8.0 and then incubated with methoxy polyethylene glycol-Succinimidyl Valerate (mPEG-SVA) (50 mg/ml; Laysan Bio Inc., Arab, AL, USA) at room temperature for 1 hour and washed with PBS once more. The PRIMO system was calibrated using fluorescent highlighter on an identical substrate. The PBS was replaced by (4-benzoylbenzyl) trimethylammonium chloride (PLPP) (14.5 mg/ml; Alvéole, Paris, France), and then the desired pattern, previously created with graphic software, was illuminated with UV light focused on the substrate surface for 30 s. Patterned surfaces were washed again with PBS and then incubated with 0.1% gelatin for 1 hour at room temperature. The substrate was washed and maintained hydrated in PBS at 4°C overnight.

Human airway SMC culture

Primary human airway SMCs were acquired through the Gift of Hope Foundation (via J. Solway, University of Chicago) and through the American Type Culture Collection (https://www.atcc.org). Both these sources are public and pertinent medical information about the donor was relayed to us, but all donor identifiers are removed. The donor remains anonymous and cannot be identified directly or through identifiers linked to the subjects, meeting National Institutes of Health (NIH) guidelines. In this study, we used four healthy human donors with no history of asthma: two male, ages 59 and 34, and two female, ages 18 and 82. This study was carried out in accordance with the guidelines and regulations approved by the Institutional Biosafety Committee at Northeastern University. Cells were grown under standard culture conditions of 37°C and 5% CO₂ and used by P6 for all experiments. Culture medium: Cells were cultured in 10% fetal bovine serum, Dulbecco’s modified Eagle’s medium/F12 (Fisher Scientific), 1× penicillin/streptomycin (Fisher Scientific), 1× MEM nonessential amino acid solution (Sigma-Aldrich), and amphotericin B (25 μg/liter; Sigma-Aldrich). Before any measurements, the growth medium was switched to serum-free medium for at least 24 hours. The serum-free medium was composed of Ham’s F-12 medium (Sigma-Aldrich), 1× penicillin/streptomycin, amphotericin B (50 μg/liter), 1× glutamine (Fisher Scientific), 1.7 mM CaCl₂ 2H₂O, 1× Insulin-Transferrin-Selenium Growth Supplement (Corning Life Sciences, Tewksbury, MA), and 12 mM NaOH. Both patterned and nonpatterned gelatin-coated substrates were UV-sterilized for 1 hour and then incubated at 37°C for 1 hour before seeding human airway SMCs, passages 3 to 6. For patterned substrates, cells were seeded in Bioptech dishes at 10⁴ cells per cm² and incubated for 10 min in 10% serum medium to allow cells to adhere to patterns. Next, the dishes were washed with PBS to remove excess cells and then filled with 10% serum medium and incubated for 6 to 24 hours. For nonpatterned substrates, cells were seeded at the desired density and then incubated in 10% serum medium for 6 to 24 hours. After this time, medium was replaced with serum-free medium and incubated for at least 24 hours before measurements. For isolated cells, the seeding density was 10² cells per cm². For sparse cells, the seeding density was 10³ cells per cm². For confluent cells, the seeding density was 10⁴ cells per cm².

Fluorescent imaging of Ca²⁺

Serum-starved airway SMCs were loaded with a fluorescent cytosolic Ca²⁺ indicator to record changes in [Ca²⁺]. FLIPR Ca²⁺ 6 (Molecular Devices, San Jose, CA, USA) was used for all Ca²⁺ measurements except Fig. 1A and fig. S1A, where we used Fluo4-AM (Sigma-Aldrich, St. Louis, MO, USA). The commonly used Fluo4-AM is prone to photobleaching, and the measured Ca²⁺ traces must be bleach-corrected before measurements of the time period. FLIPR Ca²⁺ 6, on the other hand, did not photobleach even after 30 min of continuous imaging at 1 Hz. Fluo4-AM was prepared according to the manufacturer’s standards. Cells were loaded with 0.2 μM Fluo4-AM solution, diluted in Hanks’ balanced salt solution (HBSS), and incubated at room temperature for 1 hour. Next, the cells were washed with HBSS and incubated in the dark in HBSS for an additional 30 min. The cells were washed once more before imaging. FLIPR Ca²⁺ 6 was also prepared according to the manufacturer’s standards. Cells were incubated with a 1:1 solution of FLIPR Ca²⁺ 6 and serum-free medium at 37°C and 5% CO₂ for 2 hours before imaging. Both Ca²⁺ indicators use acetoxymethyl esters to pass through the cell membrane, which are then hydrolyzed by cytosolic esterases, trapping the fluorescent dye inside the cell. Cells were imaged with a Leica DMi8 inverted microscope, a Leica DFC6000 camera (Leica, Wetzlar, Germany), and a Lumencor Sola SEII LED light source (Lumencor, Beaverton, OR, USA). A fluorescein isothiocyanate (FITC) filter cube (excitation, 480/40 nm; emission, 527/50 nm) was used to image the fluorescent dye. Fluorescent intensity increases with increasing cytosolic [Ca²⁺]. Sixteen-bit images were recorded at 1 Hz for 1 min before agonist addition and for at least 5 min after 10⁻⁵ M histamine exposure. To analyze data, each image sequence was loaded in Fiji ImageJ, and regions of interest (ROIs) were hand-selected in the cytoplasm of each cell to obtain mean grayscale intensities over the area of the ROI for each frame in time. A custom MATLAB (MathWorks, Natick, MA, USA) code was written to process the data and measure mean Ca²⁺ oscillation periods. This code measured mean Ca²⁺ oscillation periods by finding peaks in the time series data above a certain prominence and taking the mean of the time between all sequential peaks (fig. S4).

Cell traction force measurements

The base NuSil substrates were coated with a layer of fluorescent beads as fiducial markers for traction force microscopy. A 5% solution of 0.2-μm-diameter red fluorescent carboxylate-modified microspheres (FluoSpheres, Invitrogen, Carlsbad, CA, USA) in PBS was vortexed for 10 s. Solution (2 ml) was added to each substrate in a Bioptech dish and left at room temperature for 1 hour to allow the beads to adhere. The bead solution was poured off, substrates were washed three times with PBS, and then PBS was poured off. NuSil solution was prepared as described before, with the appropriate amount of cross-linker to match the stiffness of the base substrate. NuSil was spin-coated onto the newly bead-coated base substrate at 2500 rpm to create a 1-μm-thick layer and seal the beads. These substrates rested on a flat surface for 1 hour before curing overnight at 60°C. Substrates were protein-coated and seeded with cells as before. After a 24-hour incubation in serum-free medium, the SMC tractions were recorded by imaging the fluorescent beads with a 20×/0.55 dry objective and the Leica DMi8 microscope in an environmental chamber maintained humidified at 37°C. Images were taken at baseline, after a 15-min incubation with 10⁻⁵ M histamine, and after cells were removed using RLT Lysis Buffer (Qiagen, Hilden, Germany). Using these images, cellular forces were calculated with a custom MATLAB (MathWorks, Natick, MA, USA) software program using Fourier traction force microscopy (23).

Fluorescent labeling of Cx43/actin/nuclei

Cells were fluorescently labeled for Cx43 and filamentous actin (F-actin). Cells were fixed in 4% paraformaldehyde in PBS at room temperature for 10 min. Then, cells were permeabilized with 100% ethanol for 10 min at 20°C. Following permeabilization, cells were blocked using 1× PBS containing 0.1% Tween 20, 1% bovine serum albumin (BSA), and glycine (22.52 mg/ml) for 30 min at room temperature. Next, cells were stained for Cx43 (ab11370; Abcam, Cambridge, UK) at a dilution of 1:200 in 1× PBS containing 1% BSA for 1 hour at 37°C. Secondary antibody labeling and phalloidin staining were done simultaneously at dilutions of 1:200 and 1:40, respectively, using Alexa Fluor 594 (ab150080; Abcam, Cambridge, UK) and Alexa Fluor 488 Phalloidin (A12379; Invitrogen, Carlsbad, CA, USA). Last, cells were labeled with NucBlue (Fisher Scientific, Waltham, MA, USA) to label cell nuclei. Images were acquired using a 63×/1.4 oil-immersion objective (Leica, Wetzlar, Germany).

The gap-FRAP assay

Gap-FRAP is an experimental technique that has been established as an effective method of observing gap junctional communication of small fluorescent molecules between adjacent cells (22). SMCs were cultured on NuSil gels of E = 0.3 kPa and E = 13 kPa until confluence was achieved and then serum-starved for at least 24 hours before the experiment. Cells were loaded with 1 μM calcein-AM solution diluted in warmed 1× PBS solution and incubated at 37°C and 5% CO₂ for 15 min. Calcein-AM is a cell-permeable dye that is hydrolyzed into fluorescent calcein by cytoplasmic esterases upon entry through cell membrane and has been shown to permeate through gap junctions due to its low molecular size (622 Da) (20). After dye incubation, samples were washed with warm 1× PBS solution and returned to serum-free medium for experiments. FRAP was performed using a Zeiss confocal laser scanning microscope system equipped with a 20×/0.8 objective and a 488-nm argon laser. Fluorescence data were captured using ZEN 2012 SP5 imaging software (Zeiss, Oberkochen, Germany). Samples were placed in an incubation chamber maintaining 37°C during experiments to preserve cell viability during imaging. Before photobleaching, a manual ROI was drawn around the border of a target cell visibly connected to adjacent cells. Whole cells were selected for photobleaching to ensure that fluorescence recovery could only be attributed to the diffusion of calcein from adjacent cells. Laser power was adjusted to 1%, and images were acquired every 5 s for 50 s using scan speed 12 (pixel dwell, 0.42 μs) to provide baseline fluorescence measurements. After baseline scans were acquired, the laser power was adjusted to 100% and cells were bleached to at least 20% of their initial fluorescence using scan speed 2 (pixel dwell, 40 μs). Following the bleaching step, fluorescence recovery images were collected every 5 s for approximately 5 min at 1% laser power. The images from gap-FRAP experiments were analyzed using Fiji ImageJ software. First, baseline fluorescence intensities from the target cell were averaged over the first 10 frames captured to establish a reference value for fluorescence recovery. Next, fluorescence intensities were measured during the recovery period and divided by the average baseline intensity to normalize the data. To account for any photobleaching occurring during the recovery period, fluorescence intensities were collected from a region at the edge of the field of view. These values were used to adjust the intensity of the target cell over time to account for fluorescence degradation due to repeated scanning of the microscopic field, because the edge region was not affected directly during the bleaching step. The normalized fluorescence values of the bleached cell during recovery were plotted as a function of time. To compare fluorescence recovery across multiple sample groups, the mobile fraction of fluorescent molecules was calculated. Mobile fraction (Γ) measures the fraction of fluorescent molecules that contribute to recovery of fluorescence in bleached cells and is calculated with Eq. 1, where F₀, F_b, and F_r indicate the fluorescence intensity in the cell being bleached at baseline, after bleaching, and after recovery, respectively (Fig. 3E).

Gap junction blocker experiments

Gap junctions between confluent SMCs were blocked with βGA (Sigma-Aldrich, St. Louis, MO, USA). Confluent SMCs on soft (E = 0.3 kPa) and stiff (E = 13 kPa) substrates were incubated with 30 μM βGA at 37°C and 5% CO₂ for 30 min. Although βGA is a common gap junction blocker, it has been reported to affect cell viability at higher concentrations (21). We used gap-FRAP to find the lowest possible dose of βGA that still blocked gap junctions between confluent cells, which we used here in our experiments. This treatment was used in conjunction with the Ca²⁺ imaging protocol to investigate the role of gap junctional diffusion in agonist-induced Ca²⁺ oscillations.

Force-inhibitor experiments

SMC contractile force was reduced with two separate inhibitors of force: Y-27632 (Sigma-Aldrich, St. Louis, MO, USA), a specific inhibitor of ROCK, and ML-7 (Sigma-Aldrich, St. Louis, MO, USA), a selective inhibitor of MLCK. Confluent SMCs on soft (0.3 kPa) and stiff (13 kPa) substrates were preincubated with 10 or 100 μM Y-27632 for 1 hour or 0.01 or 0.05 μM ML-7 for 5 min, in tandem with the 2-hour FLIPR Ca²⁺ 6 indicator incubation, before experiments. Ca²⁺ imaging and 10⁻⁵ M histamine addition were added as previously described.

Data presentation and statistical testing

Throughout the manuscript, we represent data as the average of N independent trials. The error bars indicate SD over independent trials. The individual data points are shown in all bar plots. Each data point is, in turn, the average of measurements made over multiple cells within one trial. SigmaStat (Systat Software, San Jose, CA) was used to perform statistical tests. Two-way ANOVAs followed by post hoc pairwise comparisons were used to test for significant differences in datasets, which were influenced by two independent factors. One-way ANOVAs followed by post hoc pairwise comparisons were used to test for significant differences in datasets of three or more groups, which were influenced by one independent factor. Pairwise comparisons used the t test when the data were normally distributed. Otherwise, the Mann-Whitney rank sum test was used to compare the median values. The specific tests used, the number of samples, and the P value are described along with the corresponding results. A P value of 0.05 was used as the threshold for a statistically significant difference between datasets.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/32/eaba1149/DC1

View/request a protocol for this paper from Bio-protocol.