The global subseafloor biosphere subsists under extreme and widespread energy limitation.
Abstract
Microbial cells buried in subseafloor sediments comprise a substantial portion of Earth’s biosphere and control global biogeochemical cycles; however, the rate at which they use energy (i.e., power) is virtually unknown. Here, we quantify organic matter degradation and calculate the power utilization of microbial cells throughout Earth’s Quaternary-age subseafloor sediments. Aerobic respiration, sulfate reduction, and methanogenesis mediate 6.9, 64.5, and 28.6% of global subseafloor organic matter degradation, respectively. The total power utilization of the subseafloor sediment biosphere is 37.3 gigawatts, less than 0.1% of the power produced in the marine photic zone. Aerobic heterotrophs use the largest share of global power (54.5%) with a median power utilization of 2.23 × 10−18 watts per cell, while sulfate reducers and methanogens use 1.08 × 10−19 and 1.50 × 10−20 watts per cell, respectively. Most subseafloor cells subsist at energy fluxes lower than have previously been shown to support life, calling into question the power limit to life.
INTRODUCTION
Marine sediments harbor a vast number of microorganisms across a wide range of depositional settings (1). These microorganisms have been shown to survive for extraordinarily long periods of time (2). Contrary to life at Earth’s surface, subsurface organisms are severely energy limited (3). Many of these sediment-dwelling microbes are novel and uncultured (4, 5) and survive under extreme energy limitation for millennia, thus calling into question the limit for life (2, 6). They are also responsible for degrading Earth’s largest pool of organic C (7), exerting a major control on global climate and biogeochemical cycles (8). The availability of energy to microorganisms in subseafloor sediments varies considerably from one environment to another (9) and imposes limits on their rates of activity, as well as their survival (3, 10). However, outside of measurements from specific sites (11–13) and laboratory experiments (14), the rate of energy utilization, i.e., power, of subseafloor life is not well known. Therefore, questions pertaining to microbial activity levels, community assembly, adaptive evolution, and even the lower power limit to life remain unanswered (3, 15, 16). Here, we quantify the power utilization for all microorganisms contained in subseafloor sediments that were deposited during the past 2.59 million years (i.e., the Quaternary period). A bioenergetic ecosystem model was developed and implemented on a 0.25° × 0.25° resolution global grid. Our model calculates the volumetric distribution, rate, and thermodynamic properties of particulate organic carbon (POC) degradation, as well as the global distribution of cells and electron acceptors, in Quaternary-age subseafloor sediments. On this basis, we calculate, in three dimensions, the cell-specific power of microbial life in the global marine sediment habitat.
RESULTS AND DISCUSSION
Metabolism and organic carbon degradation in global marine sediments
We designate POC degraded in oxic sediments to be mediated by O2, POC degraded in the sulfate-reducing zone to be mediated by SO42−, and attribute POC degraded beneath the sulfate-methane transition to methanogenesis (reactions 1 to 3; table S1). The thickness and depth of Holocene- and Pleistocene-aged sediments, as well as the depth of oxygen penetration and the depth of the sulfate-methane transition, are highly variable across the seafloor (fig. S1). Oxic sediments are mostly restricted to deep-water abyssal zones (fig. S2). Together, we estimate that 2.7% of the Quaternary subseafloor sediment volume is oxic and that it contains 6.80 × 103 Pg of organic C (4.6% of Quaternary subseafloor sediment POC). Our mechanistically derived estimate for the global mass of organic carbon in oxic marine sediment (6.80 × 103 Pg of C) is very closely aligned with an independent empirically derived estimate (6.7 × 103 to 16.0 × 103 Pg of C) (17). Sulfate-reducing and methanogenic sediments are more widespread (33.0 and 64.3% of sediment volume, respectively), particularly underlying shallow-water shelf and margin settings, and in deeper and thicker sedimentary layers (fig. S2). We calculate that sulfate-reducing sediments contain 8.31 × 104 Pg of organic C (56.9% of Quaternary subseafloor sediment POC) and methanogenic sediments contain 5.63 × 104 Pg of organic C (38.5% of Quaternary subseafloor sediment POC). We find that rates of POC degradation are mostly reflective of the volumetric POC distribution across subseafloor sediments. The majority of POC degradation in Quaternary sediments globally is mediated by sulfate reduction (64.5%; 0.171 Pg of C year−1). We calculate that oxic sediments mediate 6.9% of global subseafloor POC degradation (0.018 Pg of C year−1), while methanogenic sediments mediate 28.6% (0.076 Pg of C year−1) (Fig. 1). Our results underpin the understanding that sulfate plays a major role in the global degradation of organic C in marine sediments (18–20), while simultaneously verifying the importance of methanogenesis (21).
Fig. 1. Volumetric distribution and flux of sediment, cells, organic carbon, and energy across major marine sediment catabolic zones in global Quaternary subseafloor sediment.
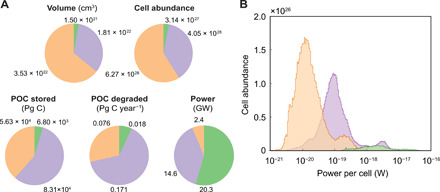
(A) The proportion of total sediment volume (cubic centimeters), number of microbial cells, POC stored (petagrams of C) and degraded (petagrams of C per year), and power used (gigawatts) in each catabolic zone in Quaternary sediment. (B) Frequency distribution of cell-specific power utilization in Quaternary-age sediment. Green denotes oxic, lilac signifies sulfate-reducing, and orange represents methanogenic sediment.
Power utilization in global marine sediments
The flux of energy, i.e., power, that is supplied to and used by microorganisms is calculated using the rates of POC degradation combined with the Gibbs energies of O2, SO42−, and CH4-mediated catabolism under representative in situ conditions (tables S1 and S2). The combined total power used by all microorganisms in subseafloor sediment is 37.3 GW. This is equivalent to only 0.08% of the power produced photosynthetically in the marine photic zone (22, 23). Microbial power utilization is the highest, per cubic centimeter of sediment, in shallow coastal settings (up to 10−9 W cm−3), and it is uniformly low (~10−14 W cm−3) in the oldest Pleistocene sediments (2.59 million years) (fig. S2). High power (per cubic centimeter) in sediments underlying northern high latitudes and Southeast Asian shelves can be attributed to high concentrations of reactive POC (fig. S3) that degrade relatively rapidly.
Notably, we find that O2-mediated POC degradation constitutes the major power source in subseafloor sediments (20.3 GW; 54.5% of global subseafloor power), despite oxic sediment comprising a minor fraction of total sediment volume and POC. Microorganisms in sulfate-reducing sediment use 14.6 GW of power globally (39.1% of the global total), while microorganisms in methanogenic sediments use only 2.4 GW, equivalent to only 6.4% of the global subseafloor power utilization. The dichotomy between both the volume and amount of POC stored within each sedimentary layer and the power realized by POC degradation for each catabolic strategy underscores the need to consider not only POC concentrations and other geochemical constituents but also the rate and energetics of major catabolic pathways occurring in the subseafloor biosphere.
Cell-specific power utilization
The power per individual microbial cell is calculated by dividing the total power used by the number of microorganisms present in a sedimentary horizon. Our results confirm that subseafloor sediment microorganisms are characterized by extreme and widespread energy limitation. We calculate that 84.0% of microorganisms subsist at an energy flux less than the lowest previously calculated estimate of the basal power limit to life for natural settings [1.9 × 10−19 W per cell (13)]. The median rate of microbial energy utilization in Quaternary-age marine sediments, i.e., cell-specific power, is 3.32 × 10−20 W per cell, which is more than two orders of magnitude lower than the lowest experimentally derived maintenance power for microorganisms (24) and five orders of magnitude lower than the lowest culture-based estimates of maintenance power (25).
Stepwise decreases in microbial power utilization largely follow the redox state of the sediment (Fig. 1). The delineation of microbial power utilization according to catabolic zones is consistent with a continuous decrease in reactivity and degradation rate of organic matter with increasing sediment depth and sediment age (26). Microorganisms situated within oxic sediments exhibit the highest power per cell, with a median power utilization of 2.23 × 10−18 W per cell. This is broadly consistent with field data–derived estimates of the maintenance power of microorganisms from oxygen-bearing sediments [5.30 × 10−18 W per cell (6)]. The power utilization of microorganisms situated in anoxic sediments is generally lower than that in oxic sediments (27, 28). This is clearly reflected by our data: We find that cell-specific power in anoxic sediments is one to two orders of magnitude lower than that in oxic sediments, with a median power utilization of 1.08 × 10−19 and 1.50 × 10−20 W per cell in sulfate-reducing and methanogenic sediments, respectively. Globally, we find that extremely few cells (<0.02%) subsist at less than 1 zW (10−21 W), substantiating a theoretically posed “minimum decay prevention power” for microbial life (13).
Distinct high- and low-power zones arise according to catabolic strategy and geography (Fig. 2). It can be shown that the somewhat multimodal distribution of cellular power utilization (Fig. 1) arises from log-normal distributions within each domain (i.e., shelf, margin, and abyssal settings) (fig. S4). Microorganisms contained in continental shelf sediments, particularly in northern high latitudes and near Southeast Asia, use comparatively higher power than elsewhere (Fig. 2). This highlights that sediment POC with relatively short depositional pathways (i.e., situated in shallow water, <200 m) is tilted toward higher reactivity (fig. S3) (29) and supports microorganisms at a higher activity state (Fig. 2). High cell-specific power is also prevalent in oxic sediments underlying the ocean rises of the East and Central Pacific, the Southwest and Southeast Indian Ridges, and the Mid-Atlantic Ridge (2000 to 3000 m). These regions are characterized by low cell abundance (1, 2), where microorganisms are sustained for millennia with extremely low mortality (2, 30) on ancient POC (17), but via a highly exergonic terminal electron transfer step (table S2). Sulfate-reducing sediments underlie many of the major ocean basins (>4000-m water depth), including the North Pacific, North Atlantic, Argentine, Canary, Angola, Cape, Southwest Pacific, and Mid–Indian Ocean basins. These sediments contain cells using very little power (<10−20 W per cell). Methanogenesis, which is prevalent in shallow-water sediments near continental land masses, is shown to provide even less power to individual organisms (10−21 to 10−20 W per cell). These extremely low-power settings, largely in deeper and thicker sedimentary layers underlying shallow-water shelf and margin settings, are typically characterized by high rates of mortality among subseafloor microbial communities (31). Nevertheless, the sustained presence of microbes, even in deeper, low-power sedimentary layers, indicates that at least a fraction of the microbial population are capable of surviving at powers far lower than has been calculated for any natural environment previously (13).
Fig. 2. Cell-specific power utilization across major marine sediment catabolic zones.
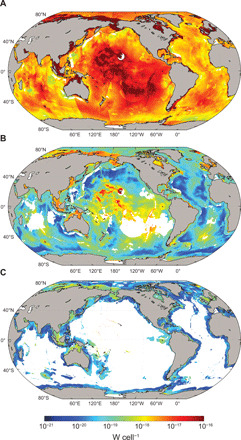
Power per cell (watts) calculated on a global scale and depth-integrated for the (A) oxic, (B) sulfate-reducing, and (C) methanogenic sedimentary layers. White areas denote absence of the corresponding catabolic zone.
Uncertainty in our calculations arises from (i) the rate of POC degradation, (ii) the Gibbs energy of the reaction, and (iii) the number of cells carrying out the reaction. Uncertainty is evaluated for each of these factors (i to iii) individually and concurrently (i.e., together) (see Supplementary Text). The reactivity of POC deposited onto the seafloor and its evolution during burial are accounted for by a set of adjustable parameters (see Materials and Methods) using a theoretically and empirically well-established reactive continuum modeling approach, validated using a large body of carefully dated organic matter and pore water depth profiles, rate measurements, isotopic signatures, and authigenic mineral distributions from a wide range of marine settings across contrasting depositional environments and temporal scales. We prescribe parameter values that are consistent with decades of observations, laboratory experiments, and modeling, in which the decrease in organic matter reactivity with increasing sediment depth and age, as well as from continental to abyssal environments, is widely observed (29). Nevertheless, to address the uncertainty in our results associated with (i) POC degradation rates, we evaluate a range of simulations encapsulating all possible variability in the reactivity of POC deposited onto the seafloor and its evolution during burial, constrained by a global parameter compilation (see Supplementary Text). To address the uncertainty associated with variability in (ii) the Gibbs energy arising from spatial heterogeneities in the concentrations of reactants and products, we run additional simulations, where the concentrations of the reactants and products are varied over realistic ranges to represent high-energy and low-energy scenarios. The calculation of power per cell also relies on an estimate of the number of cells carrying out the reaction, for which we use the best available spatially resolved global model for subseafloor biomass distribution (1) and simplify the reaction network to account for the most pertinent biogeochemical processes and the major catabolic pathways of POC oxidation. A large body of evidence suggests that the vast majority of microorganisms in subseafloor sediments are involved in the degradation of organic matter and overwhelmingly hold the genetic potential to degrade organic molecules, especially in organic-rich, coastal, and/or anoxic settings (see Supplementary Text). Nevertheless, to account for uncertainty in (iii) the number of microbial cells present in the sediment and carrying out the metabolism prescribed to a certain redox zone, we carry out additional simulations where cell abundance is varied by up to 50%. These factors (i to iii), tested individually and simultaneously, produce relatively minor deviations in the median-per-cell power (1.42 × 10−20 to 10.20 × 10−20 W per cell; see Supplementary Text). Under all tested scenarios, the percentage of microorganisms subsisting at less than 1.9 × 10−19 W per cell is at least 65.7%—underscoring the highly energy-limited nature of microbial life in subseafloor sediments.
Quantifying the energy turnover of the subseafloor biosphere is critical to determining the cell-specific minimum power requirement for life, as well as to predict the habitable boundaries of life on Earth. This study advances previous knowledge of the abundance, distribution, and activity of microorganisms in the subsurface (1, 32, 33) by providing the catabolic rates and specific activities of these microorganisms on a global scale. Considering that a small number of cells use a disproportionately large fraction of the total energy in marine sediments, we find that extraordinarily low power is a characteristic of almost all subseafloor sediment–hosted life. We report energy fluxes that fall short of previously calculated cell maintenance requirements for natural settings, verifying the overwhelmingly low-power nature of the deep biosphere (10). Considering that cells are subsisting at or near basal maintenance power requirements (13), it is unlikely that growth (i.e., cellular division), and by extension evolution, can be sustained widely throughout subseafloor sediments, validating what has shown to be the case for specific sites (15). The prevalence of dormant and nongrowing microorganisms, however, affords a survival advantage permitting ecological coexistence (34) and maintenance of biodiversity (35) in subseafloor sediments. Overall, our data represent evidence for widespread energy limitation in the marine subsurface, and that the overwhelming majority of subseafloor sediment microorganisms may subsist at close to the power limit for life.
MATERIALS AND METHODS
Experimental design
Here, we present and apply a new bioenergetic modeling approach that is used to quantify the distribution and rate of POC degradation, as well as the global distribution of cells, electron acceptors, and the thermodynamic properties of POC degradation. On this basis, we calculate the cell-specific power (i.e., energy per unit time per individual microbial cell), P (watts) according to
| (1) |
where r denotes the rate of reaction (grams of C degraded per cubic centimeter per second), ΔGr (joules per gram of C) represents the Gibbs energy of the reaction, and Y (cells per cubic centimeter) is the number of microbial cells carrying out the reaction. The modeling framework is implemented on a 0.25° × 0.25° resolution global grid using the following global datasets and models.
Reaction-transport model
We use a one-dimensional reaction-transport model (RTM) to calculate the distribution and degradation rate of POC in subseafloor sediments throughout the Quaternary period, following the approach described in (36). Similar to Wallmann et al. (37), constant boundary conditions and parameters are used to characterize the Holocene (0 to 11,700 years old) and Pleistocene (11,700 years old to 2.59 million years old) depositional environments.
The one-dimensional conservation equation for POC in porous media is given by (38–39)
| (2) |
where POC (grams of C per cubic centimeter dry sediment) is the concentration of POC, t refers to time, Db (square centimeters per year) stands for the bioturbation coefficient, ω (centimeters per year) represents the sedimentation rate, and RPOC (grams of C per cubic centimeter per year) denotes the rate of organic matter degradation. The porosity, Φ, of marine sediments in the shelf, margin, and abyss domains was calculated as a function of depth, z (meters), assuming steady-state compaction, according to (40)
| (3) |
where Φ0 denotes the porosity at the sediment-water interface (SWI) and c0 (per meter) stands for the compaction length scale, which characterizes how a given sediment type will compact under its own weight.
Quaternary sediments are divided into three layers: Holocene bioturbated [top 10 cm (39)], nonbioturbated Holocene (<11,700 years), and Pleistocene (<2.59 million years). Sediment mixing was assumed to be constant over the bioturbated layer and nonexistent immediately below it. The rate of organic matter degradation, RPOC, was described using a reactive continuum model (RCM). The RCM assumes a continuous yet dynamic distribution of organic compounds comprising a range of reactivities and reproducing the often-observed decrease in apparent POC reactivity with increasing sediment depth (and thus age) (41). Within the RCM, RPOC is given by
| (4) |
where om(k,t) represents a probability density function that determines the concentration of organic matter having a degradability between k and k + dk at time t, with k being analogous to a reaction rate constant. The initial distribution or organic compounds [om(k,0)] cannot be inferred by observations and may take different mathematical forms. We use a gamma function (36, 41–43), assuming first-order degradation kinetics, whereby the initial (t = 0) distribution of om over k is given by
| (5) |
where POC0 is the initial organic matter content (at the SWI), Γ is the gamma function, a (years) is the average lifetime of the reactive components of the POC, and ν is a dimensionless parameter determining the shape of the distribution near k = 0. Assuming steady-state conditions (∂POC/∂t = 0) and a known organic C content at the sediment water interface, POC0, the change in the POC concentration as a function of depth, POC(z), is given by (41)
| (6) |
where age(z) refers to the age of the sediment layer at depth z. Following the approaches described in (36, 44), we use a multi-G approximation of the RCM for the bioturbated sediment. Within the bioturbated zone, POC is represented by 500 distinct fractions that are degraded according to a first-order organic matter degradation rate law with a degradation rate constant, ki
| (7) |
where
| (8) |
The initial proportion of total organic matter in fraction i, Fi, as well as its respective reactivity, ki, can be determined through the initial probability density function that determines the concentration of organic matter having a degradability between k and k + dk at time 0 (Eq. 4). The initial fraction of total POC characterized by a distinct reactivity k is given by
| (9) |
The initial fraction of POC within the reactivity range between 0 and k, i.e., having a reactivity ≤k, is then given by integrating Eq. 9, assuming a, ν, and k > 0
| (10) |
where Γ(ν,a∙k) denotes the inverse gamma function.
In the bioturbated sediment, the RCM is approximated by dividing the reactivity range k = [10−15, 10(−log(a) + 2)] into 500 equal reactivity bins, kj, thus ensuring a comprehensive approximation of the gamma function defined by the respective a and ν values. The initial fraction, Fi, of total POC within the reactivity bin kj−1 and kj (and thus with reactivity ki = kj−1 + (kj − kj−1)/2) in the 500G model can then be calculated as
| (11) |
The most reactive fraction, F500, with reactivity k500 = 10−log(a) + 2 year−1 is calculated on the basis of the upper incomplete gamma function
| (12) |
The derived rate constants are used in Eq. 2 by expressing RPOC according to Eq. 7 to determine POC concentrations and degradation rates in the Holocene bioturbated layer (<10 cm). Assuming steady-state conditions, the general solution of Eq. 2 for each organic matter fraction i is given by
| (13) |
where
| (14) |
| (15) |
and
| (16) |
The integration constants Ai and Bi are defined by the chosen boundary conditions. Here, we apply a known POC concentration at the sediment-water interface [POC(0) = POC0] and assume continuity (equal flux and concentration) across the bottom of the bioturbated layer, i.e.
| (17) |
Below the Holocene bioturbated zone, the values of age(z) that are required to evaluate Eq. 6 are calculated using burial rates, ω(z), porosity depth profiles, Φ(z), and the apparent age of organic matter at the lower limit of the Holocene bioturbated zone, agezbio. By inserting POCbio and agezbio into Eq. 6 for POC(z) and age(z), respectively, agezbio can be solved
| (18) |
Assuming an exponentially decreasing porosity, Eq. 2, and steady-state compaction, the burial velocity, ω, at depth z is then [e.g., (38)]
| (19) |
where ω0 corresponds to the burial velocity at the SWI. The age of a given sediment layer at depth z below the Holocene bioturbated zone, age(z), is given by [e.g., (38)]
| (20) |
Substituting Eq. 19 into Eq. 20 results in
| (21) |
which, upon integration, leads to
| (22) |
The age of POC below the Holocene bioturbated zone is thus given by
| (23) |
The depth distribution of organic matter in marine sediments deposited since the beginning of the Quaternary period can thus be calculated with knowledge of the sedimentation rate, level of bioturbation, porosity structure, bulk organic matter concentration at the SWI, and the distribution of organic compounds across the reactivity range at the sediment-water interface.
Total POC budget
The fraction of total POC preserved in a layer of sediment that accumulated over a given time interval, , is given as the ratio of the total amount of POC stored in the ith sediment layer [i = Holocene bioturbated (0 to zbio), Holocene nonbioturbated (zbio to zholo), and Pleistocene (zholo to zpleis)], (grams of C per square centimeter), and the total steady-state input of POC to that respective layer, , (grams of C per square centimeter)
| (24) |
where
| (25) |
and
| (26) |
The amount of POC degraded in the ith layer, , is given by
| (27) |
Two different global datasets (0.25° × 0.25°) of values for ω, the sedimentation rate, are used: one for Holocene bioturbated and Holocene sediments and the other for Pleistocene sediments.
Parameters and forcings
The concentration of Holocene and Pleistocene POC at the sediment-water interface, POC0, and sedimentation rates, ω, are constrained according to (37), which used data from (45, 46) and an algorithm that correlates water depth and sedimentation rate (47). Following (36), the bioturbation coefficient is calculated as a function of water depth based on a compilation of empirical data collected in (48). Its values range spatially from 0.59 to 27 cm2 year−1, decreasing in magnitude as water depth increases. It is constant throughout the depth of Holocene bioturbated zone and immediately drops to zero beneath it. Values of Φ0 and c0 are chosen to describe the shelf, margin, and abyss based on sediments that are representative of these domains (see table S3) (49). We partitioned the ocean floor into shelf, margin, and abyss domains to specify values for some of the model parameters (fig. S5 and table S3). We choose a constant ν parameter of 0.125 for all three sediment domains, which is characteristic of fresh organic matter and based on observations that the ν parameter values do not vary much between sites (29, 41). We link values of the a parameter with sedimentation rates, based on global observations (29, 41). This approach accounts for order-of-magnitude changes in a due to factors that control organic matter transit times from its source to deposition. These parameters thus reflect typically observed RCM parameter variability across various depositional environments. Uncertainties arising from parameter values are addressed in Supplementary Text.
Global reaction network and catabolic strategy
We designate all sediments shallower than the maximum O2 penetration depth as oxic. To map O2 penetration depth in marine sediments on a global scale (fig. S1), we combine (i) global datasets of oxygen concentrations in marine sediments and (ii) previous modeling results (2). First, we use a global dataset of oxygen concentrations and corresponding water depths (table S4) to formulate a regression model [R2 = 0.64; based on (50)]. This model is extrapolated over the entire ocean floor. For data in columns 81 to 91 (table S4), oxygen penetration depth was determined following the methods described in (51). Second, we superimpose (onto our global map) the results from a modeling study (2), which designated regions of the seafloor where O2 is known to penetrate through all sedimentary layers to basement rock. We define the sulfate reduction zone as the horizon between the maximum O2 penetration depth and the depth of the sulfate-methane transition. We use data from (52) to map the global sulfate-methane transition depth onto our 0.25° × 0.25° global grid. The reaction zones designated within our model are based on the best available published datasets and include not only global compilations of marine sediment core data (50, 52) but also global models (2, 52). Data from the numerous core samples (n = 1704) documenting the distribution of sulfate-reducing and methanogenic sediments included in our study are available via (52) and the International Ocean Discovery Program. We designate POC degraded in oxic sediments to be mediated by O2, POC degraded in the sulfate-reducing zone to be mediated by SO42−, and prescribe POC degraded beneath the sulfate-methane transition to methanogenesis (reactions 1 to 3; table S1), thus simplifying the reaction network to account for the most pertinent biogeochemical process, based on widely accepted modeling and experimental studies (18, 21, 53). Although other oxidants are used by microorganisms for degrading organic matter in marine sediments, such as nitrate, and metal oxides, these have been shown to be quantitatively unimportant metabolic pathways on a global scale (29, 44, 54–56)—mainly because of their low concentration compared to SO42−, the additional consumption of Fe and Mn oxides in a range of rapid secondary redox reactions (57), and the rapid exchange of O2 in shallow sediment. O2, SO42−, and CH4-mediated POC degradation are considered here because the vast majority of marine sedimentary organic carbon is degraded via these pathways (18, 21, 54). Energy may also be provided by fermentation, although its importance is not well known. We use acetate (CH3COO−) as a proxy for POC. To undertake a study of this scale, such an assumption is essential, since the identity of the thousands of organic molecules consumed by microorganisms in natural settings is spatially disparate and is rarely known. Acetate is a fair choice of molecule, being a regular constituent of marine sediment pore water (26). Fractional changes in Gibbs energies associated with the choice of organic compound do not meaningfully affect our results (see “Uncertainty” section in Supplementary Text). In addition, the Gibbs energies of organic matter degradation are, on a per-electron basis, much more sensitive to the identity of the electron acceptor than that of the organic compound (58, 59). By focusing on the oxidant, we are capturing the first-order energetic differences of organic matter degradation in different environmental settings.
Gibbs energy calculations
The amount of energy available from the oxidation of organic matter by aerobic, sulfate-reducing, and methanogenic pathways is calculated on the basis of the Gibbs energy function
| (28) |
where ΔGr0 and Qr refer to the standard molal Gibbs energy and the reaction quotient of the indicated reaction, respectively, R represents the gas constant, and T denotes temperature in kelvin. Values of ΔGr0 were calculated using the revised Helgeson-Kirkham-Flowers equations of state (60–62), the SUPCRT92 software package (63), and thermodynamic data taken from (64–68). Individual values of Qr are calculated for each reaction using
| (29) |
where ai stands for the activity of the ith species and vi corresponds to the stoichiometric coefficient of the ith species in the reaction of interest. Activity of the ith species is calculated according to
| (30) |
where mi and γi denote the molality and individual activity coefficient of the ith species, respectively. Values of γi are computed as a function of temperature and ionic strength using an extended version of the Debye-Hückel equation (69).
We have selected specific sets of representative conditions that are used to calculate Gibbs energies of each reaction (table S2). We define reactions at 5°C and 100 bars of pressure. For aerobic heterotrophy, we base our calculations on chemical data from oxic South Pacific Gyre sediments (2). For sulfate-reducing and methanogenic sediments, we use chemical data from anoxic Limfjorden and Peru Margin sediments (9, 70). To address the uncertainty in our results arising from spatial variability of these conditions, we ran additional simulations, where the concentrations of the reactants and products were varied to represent high-energy and low-energy scenarios (see Supplementary Text).
Cell abundance
Global subseafloor cell abundance was estimated on the basis of a power law formulation from (1)
| (31) |
where Y (cells per cubic centimeter) is cell abundance, z (meters) denotes the depth below the seafloor, and b and m are parameters based on mean sedimentation rate and distance from landmasses greater than 105 km2. b and m were interpolated onto our 0.25° × 0.25° global grid based on data provided in (1). Cell concentration in the uppermost bioturbated layer (Yzbio, 0 to 10 cm) was uniformly described, following (1), as
| (32) |
Global totals
We quantified total subseafloor sedimentary volume, POC degradation, and cell abundance by integrating across specific sediment depth and age horizons and by summing across the global grid representing the entire ocean floor.
Supplementary Material
Acknowledgments
We thank R. Glud (University of Southern Denmark) and F. Wenzhöfer (Alfred Wegener Institute, Bremerhaven) for providing oxygen penetration data and for discussion related to the approach and D. Hüelse for discussion. We also thank J. Kallmeyer (German Research Centre for Geosciences, GFZ) and R. Pockalny (University of Rhode Island) for sharing published datasets on cell abundance and oxygen in global sediments. We also thank the anonymous reviewers of the manuscript, who provided many helpful comments and suggestions. Funding: This research was supported by the NSF-sponsored Center for Dark Energy Biosphere Investigations (C-DEBI, OCE-0939564), the Deep Carbon Observatory [the Deep Life Modelling and Visualization (DLMV) and Deep Energy programs], the NASA Astrobiology Institute–Life Underground (NAI-LU, NNA13AA92A), the NASA Astrobiology Program under the Joint NASA-NSF Ideas Lab on the “Origins of Life” (NSF Solicitation 16-570), the Alexander von Humboldt Foundation, a NERC grant (NE/T010967/1), the European Union Horizon 2020 research and innovation program under the Marie Skłodowska-Curie grant agreement no. 643052 (C-CASCADES), and the USC Zumberge Fund Individual Grant Program. This is C-DEBI contribution 534. Author contributions: J.A.B. designed the study with contributions from D.E.L. and J.P.A. D.E.L., J.A.B., S.A., E.B., and A.W.D. designed and implemented the RTM. M.E. assisted with defining the sulfate-methane transition depth. J.A.B. performed additional calculations, analyzed data, and wrote the manuscript with significant contributions from all co-authors. Competing interests: The authors declare that they have no competing interests. Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials. Additional data related to this paper are available on https://www.bco-dmo.org/project/776336.
SUPPLEMENTARY MATERIALS
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/32/eaba0697/DC1
REFERENCES AND NOTES
- 1.Kallmeyer J., Pockalny R., Adhikari R. R., Smith D. C., D’Hondt S., Global distribution of microbial abundance and biomass in subseafloor sediment. Proc. Natl. Acad. Sci. U.S.A. 109, 16213–16216 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.D’Hondt S., Inagaki F., Zarikian C. A., Abrams L. J., Dubois N., Engelhardt T., Evans H., Ferdelman T., Gribsholt B., Harris R. N., Hoppie B. W., Hyun J.-H., Kallmeyer J., Kim J., Lynch J. E., McKinley C. C., Mitsunobu S., Morono Y., Murray R. W., Pockalny R., Sauvage J., Shimono T., Shiraishi F., Smith D. C., Smith-Duque C. E., Spivack A. J., Steinsbu B. O., Suzuki Y., Szpak M., Toffin L., Uramoto G., Yamaguchi Y. T., Zhang G.-l., Zhang X.-H., Ziebis W., Presence of oxygen and aerobic communities from sea floor to basement in deep-sea sediments. Nat. Geosci. 8, 299–304 (2015). [Google Scholar]
- 3.Jørgensen B. B., Marshall I. P. G., Slow microbial life in the seabed. Ann. Rev. Mar. Sci. 8, 311–332 (2016). [DOI] [PubMed] [Google Scholar]
- 4.Lloyd K. G., Schreiber L., Petersen D. G., Kjeldsen K. U., Lever M. A., Steen A. D., Stepanauskas R., Richter M., Kleindienst S., Lenk S., Schramm A., Jørgensen B. B., Predominant archaea in marine sediments degrade detrital proteins. Nature 496, 215–218 (2013). [DOI] [PubMed] [Google Scholar]
- 5.Lipp J. S., Morono Y., Inagaki F., Hinrichs K.-U., Significant contribution of Archaea to extant biomass in marine subsurface sediments. Nature 454, 991–994 (2008). [DOI] [PubMed] [Google Scholar]
- 6.Røy H., Kallmeyer J., Adhikari R. R., Pockalny R., Jørgensen B. B., D’Hondt S., Aerobic microbial respiration in 86-million-year-old deep-sea red clay. Science 336, 922–925 (2012). [DOI] [PubMed] [Google Scholar]
- 7.Parkes R. J., Cragg B., Roussel E., Webster G., Weightman A., Sass H., A review of prokaryotic populations and processes in sub-seafloor sediments, including biosphere:geosphere interactions. Mar. Geol. 352, 409–425 (2014). [Google Scholar]
- 8.Rothman D. H., Atmospheric carbon dioxide levels for the last 500 million years. Proc. Natl. Acad. Sci. U.S.A. 99, 4167–4171 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.D’Hondt S., Jørgensen B. B., Miller D. J., Batzke A., Blake R., Cragg B. A., Cypionka H., Dickens G. R., Ferdelman T., Hinrichs K.-U., Holm N. G., Mitterer R., Spivack A., Wang G., Bekins B., Engelen B., Ford K., Gettemy G., Rutherford S. D., Sass H., Skilbeck C. G., Aiello I. W., Guèrin G., House C. H., Inagaki F., Meister P., Naehr T., Niitsuma S., Parkes R. J., Schippers A., Smith D. C., Teske A., Wiegel J., Padilla C. N., Acosta J. L. S., Distributions of microbial activities in deep subseafloor sediments. Science 306, 2216–2221 (2004). [DOI] [PubMed] [Google Scholar]
- 10.Jørgensen B. B., D’Hondt S., A starving majority deep beneath the seafloor. Science 314, 932–934 (2006). [DOI] [PubMed] [Google Scholar]
- 11.Trembath-Reichert E., Morono Y., Ijiri A., Hoshino T., Dawson K. S., Inagaki F., Orphan V. J., Methyl-compound use and slow growth characterize microbial life in 2-km-deep subseafloor coal and shale beds. Proc. Natl. Acad. Sci. U.S.A. 114, E9206–E9215 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Inagaki F., Hinrichs K.-U., Kubo Y., Bowles M. W., Heuer V. B., Hong W.-L., Hoshino T., Ijiri A., Imachi H., Ito M., Kaneko M., Lever M. A., Lin Y.-S., Methé B. A., Morita S., Morono Y., Tanikawa W., Bihan M., Bowden S. A., Elvert M., Glombitza C., Gross D., Harrington G. J., Hori T., Li K., Limmer D., Liu C.-H., Murayama M., Ohkouchi N., Ono S., Park Y.-S., Phillips S. C., Prieto-Mollar X., Purkey M., Riedinger N., Sanada Y., Sauvage J., Snyder G., Susilawati R., Takano Y., Tasumi E., Terada T., Tomaru H., Trembath-Reichert E., Wang D. T., Yamada Y., Exploring deep microbial life in coal-bearing sediment down to ~2.5 km below the ocean floor. Science 349, 420–424 (2015). [DOI] [PubMed] [Google Scholar]
- 13.LaRowe D. E., Amend J. P., Power limits for microbial life. Front. Microbiol. 6, 718 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Morono Y., Terada T., Nishizawa M., Ito M., Hillion F., Takahata N., Sano Y., Inagaki F., Carbon and nitrogen assimilation in deep subseafloor microbial cells. Proc. Natl. Acad. Sci. U.S.A. 108, 18295–18300 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Starnawski P., Bataillon T., Ettema T. J. G., Jochum L. M., Schreiber L., Chen X., Lever M. A., Polz M. F., Jørgensen B. B., Schramm A., Kjeldsen K. U., Microbial community assembly and evolution in subseafloor sediment. Proc. Natl. Acad. Sci. U.S.A. 114, 2940–2945 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Orsi W. D., Edgcomb V. P., Christman G. D., Biddle J. F., Gene expression in the deep biosphere. Nature 499, 205–208 (2013). [DOI] [PubMed] [Google Scholar]
- 17.Estes E. R., Pockalny R., D’Hondt S., Inagaki F., Morono Y., Murray R. W., Nordlund D., Spivack A. J., Wankel S. D., Xiao N., Hansel C. M., Persistent organic matter in oxic subseafloor sediment. Nat. Geosci. 12, 126–131 (2019). [Google Scholar]
- 18.D. Canfield, E. Kristensen, B. Thamdrup, Advances in Marine Biology: Aquatic Geomicrobiology (Academic Press, 2005). [DOI] [PubMed] [Google Scholar]
- 19.Jørgensen B. B., Mineralization of organic matter in the sea bed—The role of sulphate reduction. Nature 296, 643–645 (1982). [Google Scholar]
- 20.Tromp T. K., Van Cappellen P., Key R. M., A global model for the early diagenesis of organic carbon and organic phosphorus in marine sediments. Geochim. Cosmochim. Acta 59, 1259–1284 (1995). [Google Scholar]
- 21.B. B. Jørgensen, S. Kasten, Sulfur cycling and methane oxidation, in Marine Geochemistry, H. D. Schulz, M. Zabel, Eds. (Springer Berlin Heidelberg, 2006), pp. 271–309. [Google Scholar]
- 22.Nealson K. H., Conrad P. G., Life: Past, present and future. Philos. Trans. R. Soc. Lond. B Biol. Sci. 354, 1923–1939 (1999). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Field C. B., Behrenfeld M. J., Randerson J. T., Falkowski P., Primary production of the biosphere: Integrating terrestrial and oceanic components. Science 281, 237–240 (1998). [DOI] [PubMed] [Google Scholar]
- 24.Marschall E., Jogler M., Henßge U., Overmann J., Large-scale distribution and activity patterns of an extremely low-light-adapted population of green sulfur bacteria in the Black Sea. Environ. Microbiol. 12, 1348–1362 (2010). [DOI] [PubMed] [Google Scholar]
- 25.Tijhuis L., Van Loosdrecht M. C., Heijnen J. J., A thermodynamically based correlation for maintenance Gibbs energy requirements in aerobic and anaerobic chemotrophic growth. Biotechnol. Bioeng. 42, 509–519 (1993). [DOI] [PubMed] [Google Scholar]
- 26.Beulig F., Røy H., Glombitza C., Jørgensen B. B., Control on rate and pathway of anaerobic organic carbon degradation in the seabed. Proc. Natl. Acad. Sci. U.S.A. 115, 367–372 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.McCollom T. M., Amend J. P., A thermodynamic assessment of energy requirements for biomass synthesis by chemolithoautotrophic micro-organisms in oxic and anoxic environments. Geobiology 3, 135–144 (2005). [Google Scholar]
- 28.Lever M. A., Rogers K. L., Lloyd K. G., Overmann J., Schink B., Thauer R. K., Hoehler T. M., Jørgensen B. B., Life under extreme energy limitation: A synthesis of laboratory- and field-based investigations. FEMS Microbiol. Rev. 39, 688–728 (2015). [DOI] [PubMed] [Google Scholar]
- 29.Arndt S., Jørgensen B. B., La Rowe D. E., Middelburg J. J., Pancost R. D., Regnier P., Quantifying the degradation of organic matter in marine sediments: A review and synthesis. Earth Sci. Rev. 123, 53–86 (2013). [Google Scholar]
- 30.Bradley J. A., Amend J. P., LaRowe D. E., Necromass as a limited source of energy for microorganisms in marine sediments. J. Geophys. Res. Biogeosci. 123, 577–590 (2018). [Google Scholar]
- 31.Braun S., Mhatre S. S., Jaussi M., Røy H., Kjeldsen K. U., Pearce C., Seidenkrantz M.-S., Jørgensen B. B., Lomstein B. A., Microbial turnover times in the deep seabed studied by amino acid racemization modelling. Sci. Rep. 7, 5680 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Bar-On Y. M., Phillips R., Milo R., The biomass distribution on Earth. Proc. Natl. Acad. Sci. U.S.A. 115, 6506–6511 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Magnabosco C., Lin L.-H., Dong H., Bomberg M., Ghiorse W., Stan-Lotter H., Pedersen K., Kieft T. L., van Heerden E., Onstott T. C., The biomass and biodiversity of the continental subsurface. Nat. Geosci. 11, 707–717 (2018). [Google Scholar]
- 34.Jones S. E., Lennon J. T., Dormancy contributes to the maintenance of microbial diversity. Proc. Natl. Acad. Sci. U.S.A. 107, 5881–5886 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Lennon J. T., Jones S. E., Microbial seed banks: The ecological and evolutionary implications of dormancy. Nat. Rev. Microbiol. 9, 119–130 (2011). [DOI] [PubMed] [Google Scholar]
- 36.LaRowe D. E., Arndt S., Bradley J. A., Burwicz E., Dale A. W., Amend J. P., Organic carbon and microbial activity in marine sediments on a global scale throughout the Quaternary. Geochimica et Cosmochimica Acta 10.1016/j.gca.2020.07.017(2020). [Google Scholar]
- 37.Wallmann K., Pinero E., Burwicz E., Haeckel M., Hensen C., Dale A., Ruepke L., The global inventory of methane hydrate in marine sediments: A theoretical approach. Energies 5, 2449–2498 (2012). [Google Scholar]
- 38.R. A. Berner, Early diagenesis: A theoretical approach, in Princeton Series in Geochemistry (Princeton Univ. Press, 1980). [Google Scholar]
- 39.B. P. Boudreau, Diagenetic Models and Their Implementation: Modelling Transport and Reactions in Aquatic Sediments (Springer, 1997), vol. 171. [Google Scholar]
- 40.Athy L. F., Density, porosity, and compaction of sedimentary rocks. Am. Assoc. Pet. Geol. Bull. 14, 1–24 (1930). [Google Scholar]
- 41.Boudreau B. P., Ruddick B. R., On a reactive continuum representation of organic matter diagenesis. Am. J. Sci. 291, 507–538 (1991). [Google Scholar]
- 42.Aris R., Prolegomena to the rational analysis of systems of chemical reactions II. Some addenda. Arch. Ration. Mech. Anal. 27, 356–364 (1968). [Google Scholar]
- 43.Ho T. C., Aris R., On apparent second-order kinetics. AIChE J. 33, 1050–1051 (1987). [Google Scholar]
- 44.Dale A. W., Nickelsen L., Scholz F., Hensen C., Oschlies A., Wallmann K., A revised global estimate of dissolved iron fluxes from marine sediments. Global Biogeochem. Cycles 29, 691–707 (2015). [Google Scholar]
- 45.Seiter K., Hensen C., Schröter J., Zabel M., Organic carbon content in surface sediments—Defining regional provinces. Deep Sea Res. Part I Oceanogr. Res. Pap. 51, 2001–2026 (2004). [Google Scholar]
- 46.Romankevich E. A., Vetrov A. A., Peresypkin V. I., Organic matter of the World Ocean. Russ. Geol. Geophys. 50, 299–307 (2009). [Google Scholar]
- 47.Burwicz E. B., Rüpke L. H., Wallmann K., Estimation of the global amount of submarine gas hydrates formed via microbial methane formation based on numerical reaction-transport modeling and a novel parameterization of Holocene sedimentation. Geochim. Cosmochim. Acta 75, 4562–4576 (2011). [Google Scholar]
- 48.Middelburg J. J., Soetaert K., Herman P. M. J., Empirical relationships for use in global diagenetic models. Deep Sea Res. Part I Oceanogr. Res. Pap. 44, 327–344 (1997). [Google Scholar]
- 49.T. Hantschel, A. I. Kauerauf, Fundamentals of Basin and Petroleum Systems Modeling (Springer-Verlag, 2009). [Google Scholar]
- 50.Glud R. N., Oxygen dynamics of marine sediments. Mar. Biol. Res. 4, 243–289 (2008). [Google Scholar]
- 51.Glud R. N., Gundersen J. K., Holby O., Benthic in situ respiration in the upwelling area off central Chile. Mar. Ecol. Prog. Ser. 186, 9–18 (1999). [Google Scholar]
- 52.Egger M., Riedinger N., Mogollón J. M., Jørgensen B. B., Global diffusive fluxes of methane in marine sediments. Nat. Geosci. 11, 421–425 (2018). [Google Scholar]
- 53.Hülse D., Arndt S., Daines S., Regnier P., Ridgwell A., OMEN-SED 1.0: A novel, numerically efficient organic matter sediment diagenesis module for coupling to Earth system models. Geosci. Model Dev. 11, 2649–2689 (2018). [Google Scholar]
- 54.Thullner M., Dale A. W., Regnier P., Global-scale quantification of mineralization pathways in marine sediments: A reaction-transport modeling approach. Geochem. Geophys. Geosyst. 10, Q10012 (2009). [Google Scholar]
- 55.Parkes R. J., Webster G., Cragg B. A., Weightman A. J., Newberry C. J., Ferdelman T. G., Kallmeyer J., Jørgensen B. B., Aiello I. W., Fry J. C., Deep sub-seafloor prokaryotes stimulated at interfaces over geological time. Nature 436, 390–394 (2005). [DOI] [PubMed] [Google Scholar]
- 56.Middelburg J. J., Levin L. A., Coastal hypoxia and sediment biogeochemistry. Biogeosciences 6, 1273–1293 (2009). [Google Scholar]
- 57.Van Cappellen P., Wang Y., Cycling of iron and manganese in surface sediments: A general theory for the coupled transport and reaction of carbon, oxygen, nitrogen, sulfur, iron, and manganese. Am. J. Sci. 296, 197–243 (1996). [Google Scholar]
- 58.LaRowe D. E., Van Cappellen P., Degradation of natural organic matter: A thermodynamic analysis. Geochim. Cosmochim. Acta 75, 2030–2042 (2011). [Google Scholar]
- 59.LaRowe D. E., Amend J. P., Catabolic rates, population sizes and doubling/replacement times of microorganisms in natural settings. Am. J. Sci. 315, 167–203 (2015). [Google Scholar]
- 60.Helgeson H. C., Kirkham D. H., Flowers G. C., Theoretical prediction of the thermodynamic behavior of aqueous electrolytes by high pressures and temperatures: IV. Calculation of activity coefficients, osmotic coefficients, and apparent molal and standard and relative partial molal properties to 600°C and 5 kb. Am. J. Sci. 281, 1249–1516 (1981). [Google Scholar]
- 61.Tanger J. C. IV, Helgeson H. C., Calculation of the thermodynamic and transport properties of aqueous species at high pressures and temperatures: Revised equations of state for the standard partial molal properties of ions and electrolytes. Am. J. Sci. 288, 19–98 (1988). [Google Scholar]
- 62.Shock E. L., Oelkers E. H., Johnson J. W., Sverjensky D. A., Helgeson H. C., Calculation of the thermodynamic properties of aqueous species at high pressures and temperatures. Effective electrostatic radii, dissociation constants and standard partial molal properties to 1000 °C and 5 kbar. J. Chem. Soc. Faraday Trans. 88, 803–826 (1992). [Google Scholar]
- 63.Johnson J. W., Oelkers E. H., Helgeson H. C., SUPCRT92: A software package for calculating the standard molal thermodynamic properties of minerals, gases, aqueous species, and reactions from 1 to 5000 bar and 0 to 1000°C. Comput. Geosci. 18, 899–947 (1992). [Google Scholar]
- 64.Shock E. L., Helgeson H. C., Calculation of the thermodynamic and transport properties of aqueous species at high pressures and temperatures: Correlation algorithms for ionic species and equation of state predictions to 5 kb and 1000°C. Geochim. Cosmochim. Acta 52, 2009–2036 (1988). [Google Scholar]
- 65.Shock E. L., Helgeson H. C., Sverjensky D. A., Calculation of the thermodynamic and transport properties of aqueous species at high pressures and temperatures: Standard partial molal properties of inorganic neutral species. Geochim. Cosmochim. Acta 53, 2157–2183 (1989). [Google Scholar]
- 66.Shock E. L., Helgeson H. C., Calculation of the thermodynamic and transport properties of aqueous species at high pressures and temperatures: Standard partial molal properties of organic species. Geochim. Cosmochim. Acta 54, 915–945 (1990). [Google Scholar]
- 67.Sverjensky D. A., Shock E. L., Helgeson H. C., Prediction of the thermodynamic properties of aqueous metal complexes to 1000°C and 5 kb. Geochim. Cosmochim. Acta 61, 1359–1412 (1997). [DOI] [PubMed] [Google Scholar]
- 68.Schulte M. D., Shock E. L., Wood R. H., The temperature dependence of the standard-state thermodynamic properties of aqueous nonelectrolytes. Geochim. Cosmochim. Acta 65, 3919–3930 (2001). [Google Scholar]
- 69.Helgeson H. C., Thermodynamics of hydrothermal systems at elevated temperatures and pressures. Am. J. Sci. 267, 729–804 (1969). [Google Scholar]
- 70.Jørgensen B. B., Parkes R. J., Role of sulfate reduction and methane production by organic carbon degradation in eutrophic fjord sediments (Limfjorden, Denmark). Limnol. Oceanogr. 55, 1338–1352 (2010). [Google Scholar]
- 71.A. Vion, L. Menot, Continental margins between 140m and 3500m depth (2009).
- 72.Steen A. D., Crits-Christoph A., Carini P., De Angelis K. M., Fierer N., Lloyd K. G., Thrash J. C., High proportions of bacteria and archaea across most biomes remain uncultured. ISME J. 13, 3126–3130 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Zinke L. A., Glombitza C., Bird J. T., Røy H., Jørgensen B. B., Lloyd K. G., Amend J. P., Reese B. K., Microbial organic matter degradation potential in Baltic Sea sediments influenced by depositional conditions and in situ geochemistry. Appl. Environ. Microbiol. 85, e02164-18 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Orsi W. D., Richards T. A., Francis W. R., Predicted microbial secretomes and their target substrates in marine sediment. Nat. Microbiol. 3, 32–37 (2018). [DOI] [PubMed] [Google Scholar]
- 75.Baker B. J., Lazar C. S., Teske A. P., Dick G. J., Genomic resolution of linkages in carbon, nitrogen, and sulfur cycling among widespread estuary sediment bacteria. Microbiome 3, 14 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Marshall I. P. G., Karst S. M., Nielsen P. H., Jørgensen B. B., Metagenomes from deep Baltic Sea sediments reveal how past and present environmental conditions determine microbial community composition. Mar. Genomics 37, 58–68 (2018). [DOI] [PubMed] [Google Scholar]
- 77.Zinke L. A., Mullis M. M., Bird J. T., Marshall I. P. G., Jørgensen B. B., Lloyd K. G., Amend J. P., Reese B. K., Thriving or surviving? Evaluating active microbial guilds in Baltic Sea sediment. Environ. Microbiol. Rep. 9, 528–536 (2017). [DOI] [PubMed] [Google Scholar]
- 78.Orsi W. D., Ecology and evolution of seafloor and subseafloor microbial communities. Nat. Rev. Microbiol. 16, 671–683 (2018). [DOI] [PubMed] [Google Scholar]
- 79.Biddle J. F., Lipp J. S., Lever M. A., Lloyd K. G., Sørensen K. B., Anderson R., Fredricks H. F., Elvert M., Kelly T. J., Schrag D. P., Sogin M. L., Brenchley J. E., Teske A., House C. H., Hinrichs K.-U., Heterotrophic Archaea dominate sedimentary subsurface ecosystems off Peru. Proc. Natl. Acad. Sci. U.S.A. 103, 3846–3851 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Ruff S. E., Biddle J. F., Teske A. P., Knittel K., Boetius A., Ramette A., Global dispersion and local diversification of the methane seep microbiome. Proc. Natl. Acad. Sci. U.S.A. 112, 4015–4020 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Reese B. K., Zinke L. A., Sobol M. S., La Rowe D. E., Orcutt B. N., Zhang X., Jaekel U., Wang F., Dittmar T., Defforey D., Tully B., Paytan A., Sylvan J. B., Amend J. P., Edwards K. J., Girguis P., Nitrogen cycling of active bacteria within oligotrophic sediment of the mid-atlantic ridge flank. Geomicrobiol. J. 35, 468–483 (2018). [Google Scholar]
- 82.Tully B. J., Heidelberg J. F., Potential mechanisms for microbial energy acquisition in oxic deep- sea sediments. Appl. Environ. Microbiol. 82, 4232–4243 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Durbin A., Teske A., Microbial diversity and stratification of South Pacific abyssal marine sediments. Environ. Microbiol. 13, 3219–3234 (2011). [DOI] [PubMed] [Google Scholar]
- 84.Chun J., Oren A., Ventosa A., Christensen H., Arahal D. R., da Costa M. S., Rooney A. P., Yi H., Xu X.-W., De Meyer S., Trujillo M. E., Proposed minimal standards for the use of genome data for the taxonomy of prokaryotes. Int. J. Syst. Evol. Microbiol. 68, 461–466 (2018). [DOI] [PubMed] [Google Scholar]
- 85.Tkacz A., Hortala M., Poole P. S., Absolute quantitation of microbiota abundance in environmental samples. Microbiome 6, 110 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Myers C. L., Barrett D. R., Hibbs M. A., Huttenhower C., Troyanskaya O. G., Finding function: Evaluation methods for functional genomic data. BMC Genomics 7, 187 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Janda J. M., Abbott S. L., 16S rRNA gene sequencing for bacterial identification in the diagnostic laboratory: Pluses, perils, and pitfalls. J. Clin. Microbiol. 45, 2761–2764 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Nealson K. H., Sediment bacteria: Who’s there, what are they doing, and what’s new? Annu. Rev. Earth Planet. Sci. 25, 403–434 (1997). [DOI] [PubMed] [Google Scholar]
- 89.Arnosti C., Bell C., Moorhead D. L., Sinsabaugh R. L., Steen A. D., Stromberger M., Wallenstein M., Weintraub M. N., Extracellular enzymes in terrestrial, freshwater, and marine environments: Perspectives on system variability and common research needs. Biogeochemistry 117, 5–21 (2014). [Google Scholar]
- 90.Lloyd K. G., Steen A. D., Ladau J., Yin J., Crosby L., Phylogenetically novel uncultured microbial cells dominate Earth microbiomes. mSystems 3, e00055-18 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Burdige D. J., Gardner K. G., Molecular weight distribution of dissolved organic carbon in marine sediment pore waters. Mar. Chem. 62, 45–64 (1998). [Google Scholar]
- 92.Fox C. A., Abdulla H. A., Burdige D. J., Lewicki J. P., Komada T., Composition of dissolved organic matter in pore waters of anoxic marine sediments analyzed by 1H nuclear magnetic resonance spectroscopy. Front. Mar. Sci. 5, 172 (2018). [Google Scholar]
- 93.LaRowe D. E., Burwicz E., Arndt S., Dale A. W., Amend J. P., Temperature and volume of global marine sediments. Geology 45, 275–278 (2017). [Google Scholar]
- 94.Mogollón J. M., Dale A. W., Fossing H., Regnier P., Timescales for the development of methanogenesis and free gas layers in recently-deposited sediments of Arkona Basin (Baltic Sea). Biogeosciences 9, 1915–1933 (2012). [Google Scholar]
- 95.Wallmann K., Aloisi G., Haeckel M., Obzhirov A., Pavlova G., Tishchenko P., Kinetics of organic matter degradation, microbial methane generation, and gas hydrate formation in anoxic marine sediments. Geochim. Cosmochim. Acta 70, 3905–3927 (2006). [Google Scholar]
- 96.Middelburg J. J., A simple rate model for organic matter decomposition in marine sediments. Geochim. Cosmochim. Acta 53, 1577–1581 (1989). [Google Scholar]
- 97.Westrich J. T., Berner R. A., The role of sedimentary organic-matter in bacterial sulfate reduction: The G Model Tested. Limnol. Oceanogr. 29, 236–249 (1984). [Google Scholar]
- 98.Marquardt M., Hensen C., Piñero E., Wallmann K., Haeckel M., A transfer function for the prediction of gas hydrate inventories in marine sediments. Biogeosciences 7, 2925–2941 (2010). [Google Scholar]
- 99.Glud R. N., Gundersen J. K., Jørgensen B. B., Revsbech N. P., Schulz H. D., Diffusive and total oxygen uptake of deep-sea sediments in the eastern South Atlantic Ocean: In situ and laboratory measurements. Deep Sea Res. Part I Oceanogr. Res. Pap. 41, 1767–1788 (1994). [Google Scholar]
- 100.Glud R. N., Gundersen J. K., Røy H., Jørgensen B. B., Seasonal dynamics of benthic O2 uptake in a semienclosed bay: Importance of diffusion and faunal activity. Limnol. Oceanogr. 48, 1265–1276 (2003). [Google Scholar]
- 101.Glud R. N., Holby O., Hoffmann F., Canfield D., Benthic mineralization and exchange in Arctic sediments (Svalbard, Norway). Mar. Ecol. Prog. Ser. 173, 237–251 (1998). [Google Scholar]
- 102.Wenzhöfer F., Holby O., Kohls O., Deep penetrating benthic oxygen profiles measured in situ by oxygen optodes. Deep Sea Res. Part I Oceanogr. Res. Pap. 48, 1741–1755 (2001). [Google Scholar]
- 103.Wenzhöfer F., Adler M., Kohls O., Hensen C., Strotmann B., Boehme S., Schulz H. D., Calcite dissolution driven by benthic mineralization in the deep-sea: In situ measurements of Ca2+, pH, pCO2 and O2. Geochim. Cosmochim. Acta 65, 2677–2690 (2001). [Google Scholar]
- 104.Jahnke R. A., Emerson S. R., Reimers C. E., Schuffert J., Ruttenberg K., Archer D., Benthic recycling of biogenic debris in the eastern tropical Atlantic Ocean. Geochim. Cosmochim. Acta 53, 2947–2960 (1989). [Google Scholar]
- 105.Wenzhöfer F., Glud R. N., Benthic carbon mineralization in the Atlantic: A synthesis based on in situ data from the last decade. Deep Sea Res. Part I Oceanogr. Res. Pap. 49, 1255–1279 (2002). [Google Scholar]
- 106.Witte U., Aberle N., Sand M., Wenzhöfer F., Rapid response of a deep-sea benthic community to POM enrichment: An in situ experimental study. Mar. Ecol. Prog. Ser. 251, 27–36 (2003). [Google Scholar]
- 107.Witte U., Wenzhöfer F., Sommer S., Boetius A., Heinz P., Aberle N., Sand M., Cremer A., Abraham W.-R., Jørgensen B. B., Pfannkuche O., In situ experimental evidence of the fate of a phytodetritus pulse at the abyssal sea floor. Nature 424, 763–766 (2003). [DOI] [PubMed] [Google Scholar]
- 108.Black K. S., Fones G. R., Peppe O. C., Kennedy H. A., Bentaleb I., An autonomous benthic lander:: Preliminary observations from the UK BENBO thematic programme. Cont. Shelf Res. 21, 859–877 (2001). [Google Scholar]
- 109.Glud R. N., Stahl H., Berg P., Wenzhöfer F., Oguri K., Kitazato H., In situ microscale variation in distribution and consumption of 2: A case study from a deep ocean margin sediment (Sagami Bay, Japan). Limnol. Oceanogr. 54, 1–12 (2009). [Google Scholar]
- 110.Giordani P., Helder W., Koning E., Miserocchi S., Danovaro R., Malaguti A., Gradients of benthic–pelagic coupling and carbon budgets in the Adriatic and Northern Ionian Sea. J. Mar. Syst. 33–34, 365–387 (2002). [Google Scholar]
- 111.Lansard B., Rabouille C., Denis L., Grenz C., In situ oxygen uptake rates by coastal sediments under the influence of the Rhône River (NW Mediterranean Sea). Cont. Shelf Res. 28, 1501–1510 (2008). [Google Scholar]
- 112.Lansard B., Rabouille C., Denis L., Grenz C., Benthic remineralization at the land–ocean interface: A case study of the Rhône River (NW Mediterranean Sea). Estuar. Coast. Shelf Sci. 81, 544–554 (2009). [Google Scholar]
- 113.Sachs O., Sauter E. J., Schlüter M., van der Loeff M. M. R., Jerosch K., Holby O., Benthic organic carbon flux and oxygen penetration reflect different plankton provinces in the Southern Ocean. Deep Sea Res. Part I Oceanogr. Res. Pap. 56, 1319–1335 (2009). [Google Scholar]
- 114.Canfield D. E., Jørgensen B. B., Fossing H., Glud R., Gundersen J., Ramsing N. B., Thamdrup B., Hansen J. W., Nielsen L. P., Hall P. O. J., Pathways of organic carbon oxidation in three continental margin sediments. Mar. Geol. 113, 27–40 (1993). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/32/eaba0697/DC1


