Designing a Study of Correlates of Risk for Ebola Vaccination

Abstract

The recombinant vesicular stomatitis virus (rVSV) Ebola vaccine was shown to be very efficacious in a novel ring vaccination trial in Guinea. However, no correlates of vaccine protection have been established for Ebola vaccines. Several Ebola vaccine candidates are available, but conducting randomized trials of additional candidates in outbreaks is difficult. Establishing correlates of vaccine protection is essential. Here we explore power and sample-size calculations to evaluate potential correlates of risk during an Ebola vaccination campaign in an outbreak. The method requires that a blood draw be made at a predetermined time after vaccination. The statistical analysis estimates the relative risk of the Ebola endpoint occurring from after the blood draw through to the end of follow-up, contrasting vaccine recipients with different values of the immune response marker. The analysis can be done assuming a trichotomous or continuous marker. Under certain assumptions, at an overall vaccine efficacy of 75%, 50 Ebola endpoints in the vaccinees provided good power. At an overall vaccine efficacy of 90%, 20 Ebola endpoints gave good power. Power was highest when more vaccinees were in the high- and low-responder groups versus the middle group and when vaccine efficacy differed the most between the high- and low-responder groups.

Abbreviations

CoR

correlate of risk

DRC

Democratic Republic of the Congo

rVSV

recombinant vesicular stomatitis virus

VE

vaccine efficacy

On August 1, 2018, the Ministry of Health of the Democratic Republic of the Congo (DRC) declared a new outbreak of Ebola virus disease in North Kivu Province in eastern DRC. This was just days after the Ministry of Health of the DRC had on July 24, 2018, declared an outbreak in the western part of the DRC from May–July 2018 over (1). That had been the first large outbreak since the Ebola virus disease outbreak in West Africa in 2014. Ring vaccination using the Merck recombinant vesicular stomatitis virus (rVSV)–Zaire Ebola virus (ZEBOV)-GP vaccine was implemented in May 2018. In ring vaccination, the contacts and the contacts of contacts of confirmed cases are vaccinated. Health-care workers and front-line workers, such as people working on safe burials, were also vaccinated. In the new outbreak, ring vaccination and vaccination of health-care workers and front-line workers were implemented once again. However, the situation on the ground has made containment of the outbreak more difficult. As of October 3, 2019, there were 3,201 Ebola cases (3,087 confirmed) with 2,139 deaths (2,025 confirmed), and since August 8, 2018, 232,275 people had been vaccinated (2).

The rVSV Ebola vaccine was shown to be very efficacious in a novel ring vaccination trial in Guinea (3). The point estimate of vaccine efficacy (VE) was 100% with a lower 95% confidence bound of 70%. Over 3,300 people were vaccinated in the May–July 2018 outbreak in DRC, with no Ebola cases reported in vaccinated individuals. The WHO supports acceleration of new Ebola interventions in Africa—in particular, the development of additional candidate vaccines (4). However, because one vaccine has already been shown to be highly efficacious, it is difficult due to ethical considerations in an outbreak in high-risk populations to do a randomized trial. To guide vaccine candidates through licensure, it would be helpful to establish immune correlates of risk (CoRs) and correlates of protection. Aside from possibly using animal challenge models, such a study must occur in an outbreak where vaccine breakthrough events could happen. A report pointed out that getting VE estimates from the Guinea ring-vaccination trial was complex (5), making another case for the usefulness of studying correlates of protection.

Here we explore sample size calculations for a study of potential immune CoRs during an Ebola vaccination campaign in an outbreak. We apply previously developed methods for power calculations (6) for assessing CoRs from VE trials or prospective cohort studies to the Ebola vaccine setting. Under a number of assumptions, the methods can be applied in outbreaks with no placebo group. We considered power and sample size calculations and discuss the feasibility of conducting such a study.

METHODS

The methods are based on the power and sample-size calculations for assessing CoR in clinical efficacy trials developed by Gilbert et al. (6). A CoR is an immune response biomarker that correlates with the clinical endpoint within a cohort such as the per-protocol vaccinated group in a VE trial (7). This method to establish CoRs relies on the VE varying as a function of the potential immune correlate(s), with VE being higher in those individuals with a measured marker value indicating a stronger immune response and VE being lower in those with a measured marker value indicating a weaker immune response. The approach in Gilbert et al. (6) specifies an overall treatment efficacy and biomarker-specific treatment efficacies as input parameters, making transparent in the power calculations the link between the CoR effect size in the vaccine arm and the corresponding difference in biomarker-specific treatment efficacies. The approach also accounts for the component of interindividual variability of the biomarker that is not biologically relevant.

The approach is based on a case-control sampling plan for assessing a CoR in vaccine recipients. It is assumed that a blood sample is drawn, ideally from everyone but possibly from a sample of individuals, at some prespecified time after vaccination. It could be that several blood draws are planned, including before vaccination at baseline (visit 0). At a minimum, 1 blood draw at a prespecified interval after the last vaccine dose, say visit 1, is drawn and stored. It is good if the time point also has maximum interindividual variability (subtracting out measurement error variability) in the immune response measures. A “visit-1 marker” could be defined using any data collected up to visit 1, so it could refer to a fold-rise titer since baseline (visit 0), a commonly studied marker. Then, after the follow-up period, or at the end of the outbreak, the immune assay(s) are performed on all cases that occurred after the prespecified marker measurement. Controls are sampled from those individuals who complete follow-up free of the Ebola endpoint. It is also important to assess visit-1 individual-

level signatures—that is, to build models that give the best individual-level classification of whether a vaccine recipient experiences the Ebola endpoint, called individual-level signatures of risk. This can be accomplished using machine learning (8).

CoRs and individual-level signatures in vaccinees are not of direct interest in themselves. We really seek correlates of VE and/or partially valid surrogate endpoints of Ebola disease, which are 2 types of correlates of protection. Correlates of VE and surrogate endpoints cannot be directly assessed without a placebo/control group. What value is there in CoR/signature assessment in a vaccine group alone?

Identified strong CoRs and signatures in a vaccine group are still very useful, because they might be reasonably hypothesized to also be correlates of VE and/or partially valid surrogate endpoints. Here we illustrate how a CoR in vaccinees translates to a correlate of VE. Suppose that we have a measured biomarker denoted by x. A correlate of VE is a visit-1 (V1) marker with variability of VE(x) in x defined (see equation bellow) where the V1 marker is the immune response value if assigned to the vaccine group. Notice that the denominator is not identifiable because it is based on those in the placebo group who would have had a value x of the immune response if they had been vaccinated, which they were not.

The analysis of CoRs/signatures studies the numerator of VE(x) with a strong CoR defined by the numerator strongly varying in x. The following assumption implies that a CoR is also a correlate of VE: After controlling for the baseline prognostic factors of Ebola disease that are included in the analysis, the placebo-group Ebola risk (denominator) does not vary in x as strongly as the vaccine-group risk (numerator).

The stronger the CoR in vaccinees, the greater the credibility of this assumption. However, this assumption is not testable, and the denominator is not estimable from the study. Here we present power calculations for a CoR under this assumption that allows it to be interpreted as a correlate of VE.

The statistical analysis estimates relative risk of the Ebola endpoint occurring from after visit 1 through to the end of the follow-up time, contrasting vaccine recipients with different values of the immune response marker. The analysis can be done assuming a continuous marker or a trichotomous marker. The overall VE is defined to be the average VE among all vaccinees, whereby some subgroups could have lower or higher VE than the overall VE. Henceforth we use “marker” to mean an immune response marker defined by visit 1.

Factors that influence the ability to discover and characterize CoRs:

• Number of Ebola endpoint cases between visit 1 and the specified follow-up period with visit-1 immune response markers measured;

• Level of overall (average) VE after visit 1;

• Strength of the association of the visit-1 marker in vaccine recipients with the Ebola endpoint and with VE;

• Biologically relevant dynamic range/intervaccinee variability of the visit-1 marker(s); and

• Precision of the assay for measuring the functionally relevant immune response ().

Noise sources include technical assay measurement error and intervaccinee variability in the timing of sampling of immune response markers relative to the immunizations. The parameter is the fraction of the variability of the measured biomarker that is potentially biologically relevant for protection and is specified to reflect the quality of the biomarker. It is a function of the true variability of the biomarker and variability due to measurement error. A equal to 1 indicates there is no measurement error, just true error. If 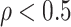, likely the biomarker would be a poor correlate.

The rVSV Ebola vaccine requires just 1 dose. For the rVSV Ebola vaccine, a good visit-1 time point seems to be between 14 and 28 days, when most rVSV Ebola vaccinees had seroconverted in a phase I trial (9). During the ring vaccination trial in Guinea, no case occurred in the arm randomized to immediate vaccination more than 10 days after vaccination (3). Day 21 could be a good choice.

Trichotomous efficacy and biomarkers

This approach assumes that each of the vaccinated individuals is in one of 3 latent/unknown baseline subgroups according to whether they have low, medium, or high categorical immune response marker(s). Trichotomous efficacy also assumes that vaccinated individuals can be divided into 3 subgroups according to their level of VE.

For a trichotomous biomarker, the CoR effect size is defined as the relative risk of disease in the high-response group compared with the risk of disease in the low-response group. A value of 1 for the CoR effect size means there is no difference in the risk in the 2 groups—the VE in each subgroup is the same, so there is no power. A smaller value of the CoR effect size yields a larger difference in the VE in the high response-group compared with the low-response group and gives higher power.

For estimation in the trichotomous scenario, one approach fits a logistic regression model that accounts for the case-control sampling, with input variables the high-versus-low immune response indicator and baseline prognostic covariates, and averages over the fitted value covariate-specific conditional risks for each of the high- and low-response subgroups to estimate the covariate-adjusted high-versus-low relative risk or odds ratio. A confidence interval and P value are obtained by the delta method. One could also use case-control sampling-adjusted logistic regression without the averaging, for simplicity. However, this latter approach does not estimate the same parameter as the former approach, and the former parameter is typically of interest.

We assess a CoR in the vaccine arm by testing 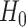: Risk(Low) Risk(High) versus 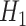: Risk(Low) 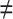Risk(High). We use a 1-sided 0.025-level Wald test from the 2-phase logistic regression model accounting for the sampling design (10).

The power calculations are interpreted assuming that VE is relative to a hypothetical placebo group. To interpret the CoR as a correlate of VE, the risk in the unvaccinated is assumed to be the same for all unvaccinated. Calculations are done under the following simplifying assumptions:

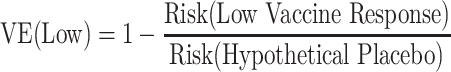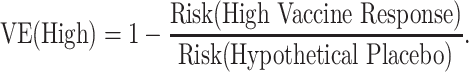For example, VE(High) = 85% means that vaccinees with a “high” immune response have a 85% reduced rate of the Ebola endpoint during follow-up compared with what would be expected had they not been vaccinated. A VE(Low) = 10% means that vaccinees with a “low” immune response have a 10% reduced rate of the Ebola endpoint during follow-up compared with what would be expected had they not been vaccinated. The overall VE is a weighted average of the VEs in the 3 subgroups.

For the trichotomous marker power calculations, 5 input parameters must be specified, where these 5 parameters determine 2 other parameters mathematically. The 5 input parameters are: 1) overall VE for disease events after visit 1; 2) a range of VE low-response subgroup values; 3) a range of VE medium-response subgroup values; 4) the fraction of vaccine recipients in the low-response subgroup; and 5) the fraction of vaccine recipients in the high-response subgroup. From these input values, the fraction of vaccine recipients in the medium-response group and the range of VE high values are mathematically determined.

In the present work, the VE in the middle VE group is assumed to equal the overall VE. Thus for a fixed overall VE, the VE in the middle VE group is also fixed. The VE varies over a range only in the low-response subgroup and the high-response subgroup. All calculations are done assuming that VE is not below zero (i.e., harmful) for any vaccine recipient or subgroup defined by x continuous or trichotomous. There would be nothing wrong with doing calculations setting VE(Low) = −50%, say, but we are choosing a scenario to study wherein the vaccine does not harm any marker-defined subgroups. For the rVSV Ebola vaccine, this assumption implies that being vaccinated does not make one more susceptible to Ebola virus disease.

Continuous marker

An immune response could also be a continuous marker. We present this briefly here, with further details in Gilbert et al. (6). For a continuous marker, we are interested in estimating the relative risk (RR) as it varies over values of

the marker, denoted by x (see equation above) where V1 is visit 1. A common approach to estimate the relative risk for a rare event setting is to use a logistic regression model designed to handle the case-control sampling of the markers (10). We assess a CoR in vaccinees by testing 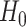: Risk(x) Risk for all x versus Risk(x) varies in x. We use a 1-sided 0.025-level Wald test (10).

We can study a normally distributed quantitative marker with a lower limit of quantification subgroup. For example, for an overall VE = 75%, the lowest 20th percentile of responses might be assumed to have VE = 0%. Calculations assume that there is a hypothetical placebo group that would have a specified risk of the Ebola endpoint. We assume that Risk(Placebo with V1 marker = x) = Risk (Hypothetical Placebo), where the first risk is for people who got placebo but would have had a V1 marker value of x if assigned to the vaccine group. In other words, we assume that any advantage of the V1 marker comes through the vaccine and is not some latent property of people related to how they would have responded to the vaccine if taken. Calculations are then done under the simplifying assumption that VE(x) 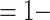Risk(x Vaccine)/Risk(Hypothetical Placebo).

The calculations presented here can be done with the open-source R (R Foundation for Statistical Computing, Vienna, Austria) package CoRpower (11). It is available on CRAN at https://cran.r-project.org/package=CoRpower.

RESULTS

In this section, we present power calculations for CoR analysis in vaccine recipients, with interpretation of the results in terms of correlates of VE under the assumptions described above. Table 1 summarizes the projected number of cases and controls available and the required number of vaccinees with blood storage for the CoRs analysis of vaccine recipients assuming either an 8% or 0.8% Ebola attack rate in the hypothetical placebo group and either a 75% or 90% overall VE. An 8% Ebola attack rate in the hypothetical placebo group corresponds to a 2% or 0.8% attack rate in the vaccine group at an overall VE of 75% or 90%. A 0.8% Ebola attack rate in the hypothetical placebo group corresponds to a 0.2% or 0.08% attack rate in the vaccine group at an overall VE of 75% or 90%. In the current Ebola outbreak, the attack rate in the unvaccinated individuals in the rings was estimated to be 0.656% (12), so 0.8% is a close approximation. At an attack rate of 8%, we assumed a total sample size of n = 500, 1,000, or 2,500 vaccine recipients with blood storage at baseline and visit 1. At an attack rate of 0.8%, we assumed a total sample size of n = 5,000, 10,000, or 25,000 vaccine recipients with blood storage at baseline and visit 1. At an assumed overall 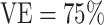, we present power calculations assuming blood was stored on enough vaccinees to produce 10, 20, or 50 cases. The power calculations for overall 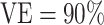did not converge when the number of vaccinees with blood stored produced only 8 expected cases; thus, results for overall 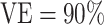are presented only for 20 expected cases.

Table 1.

Projected Number of Cases and Controls and Number of Vaccine Recipients With Blood Storage for Correlates of Risk Analysis

No. of Vaccine Recipients With Baseline, Visit-1 Blood Storage		Assumed Overall VE %	Expected No. of Ebola Endpoint Cases With Immunological Data	No. of Uninfected Vaccinee Controls (5:1 Ratio)	Total No. With Immunological Data
AR a   = 8%	AR a  = 0.8%
500	5,000	75	10	50	60
1,000	1,000	75	20	100	120
2,500	25,000	75	50	250	300
2,500	25,000	90	20	100	120

Abbreviations: AR, attack rate; VE, vaccine efficacy.

^a Attack rate in the hypothetical placebo group.

The cases are those who develop Ebola disease after visit 1 during the follow-up period. The controls are those who complete the follow-up period without experiencing Ebola. After observing the cases and controls, immunological assays would be conducted on the selected (visit 1 and possibly baseline) case-control samples. We included all cases, that is, vaccinees with the Ebola endpoint, in the analysis. We randomly sampled controls, defined as vaccinees free of the Ebola endpoint at the end of follow-up, drawing a 5:1 control:case ratio. Simulations have shown that a ratio of controls to cases of 5:1 is 86% as efficient as using the full cohort (13). Then we calculated power for a visit-1 CoR for Ebola endpoints after visit 1.

Figure 1 shows the effect on power at overall VE = 75% of varying the fractions of vaccinees with low and high VE at precision level 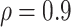when the number of vaccinees with blood storage produces 50 cases. The correlate of VE is denoted as the correlate of protection (CoP) in the figures. The power calculations were done using 1,000 simulated data sets, thus the lines are not smooth. The x-axis gives the assumed values of VE high, VE medium, and VE low as they are varied together. On the left, VE high = VE medium = VE low = 75% and power is 0%. On the right, the difference in the vaccine efficacies is most extreme, with VE high = 96%, VE medium = 75%, and VE low = 0%. The results illustrate that power is greater when greater fractions of vaccinees are split into the low and high VE bins and when the difference in VE high and VE low is greater. With 70% of vaccinees at VE high, and 20% of vaccinees at VE low, power of 80% is achieved when VE high is >83% and VE low is <50%. However, with only 40% of vaccinees at VE high and 10% of vaccinees at VE low, VE high must be greater than 86% and VE low must be less than 38% to achieve 80% power. Power is greater if the precision level ρ is >0.9 and lower if ρ is <0.9.

Figure 1.

Simulated power for a planned study to detect a 3-level correlate of protection (CoP) in vaccinees at overall vaccine efficacy (VE) = 0.75 with a trichotomous marker by fractions of vaccinees with low VE and high VE (1-sided 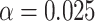). There are 250 controls and 50 cases; controls:cases = 5:1. The percentage with low value of immune marker = percentage with low VE; the percentage with high value of immune marker = percentage with high VE; precision .

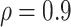Figure 2 shows how power varies with the number of cases produced in vaccinees with blood storage at overall VE = 75% when 70% of the vaccinees are in the VE high group and 20% of the vaccinees are in the VE low group, the most powerful split in Figure 1. Power falls off quickly as the number of cases in vaccinees with blood storage drops. With just 10 cases in vaccinees with blood storage, the difference in VE high and VE low must be extreme to achieve 80% power.

Figure 2.

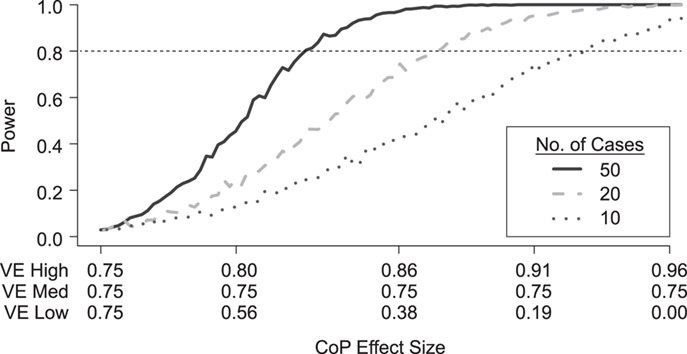
Simulated power for a planned study to detect a 3-level correlate of protection (CoP) in vaccinees at overall vaccine efficacy (VE) = 0.75 with a trichotomous marker by number of cases with blood storage (1-sided 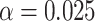); 50, 20, and 10 cases; controls:cases = 5:1. 20% of vaccine recipients have low response and VE low. 70% of vaccine recipients have high response and VE high; precision .

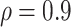Figure 3 shows the effect on power at overall VE = 90% of varying the fractions of vaccinees with low and high VE at precision level 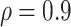. On the left side of the graph, VE high = VE medium = VE low = 90% and power is 0. On the right side the VE high = 98.5% and VE low = 30%, the most extreme values allowed at this high overall VE. Similar to the conditions at overall VE = 75%, the results illustrate that power is greater when greater fractions of vaccinees are split into the low and high VE bins. However, at this very high overall VE, the fractions that can be in the VE low group as well as at what the lowest VE can be are limited by the assumption that VE is not negative. Here the fraction in the VE low group varies between 5% and 12%, and the fraction in the VE high group varies between 60% and 80%. The VE in the VE low group only goes down to 30%. Power is greater than 80% if about 70%–80% of vaccinees are in the VE high group with VE high > 94% and 10%–12% of vaccinees are in the low VE group with VE low < 60%.

Figure 3.

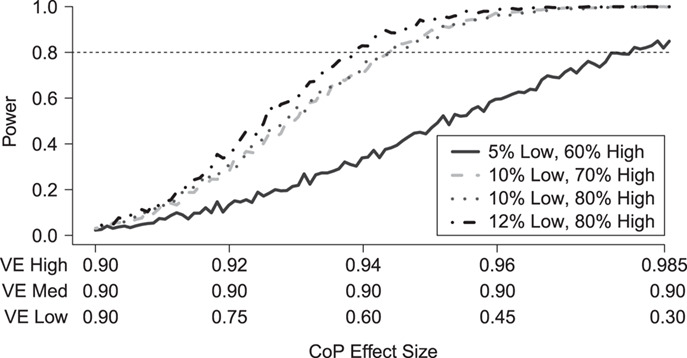
Simulated power for a planned study to detect a 3-level correlate of protection (CoP) in vaccinees at overall vaccine efficacy (VE) = 0.90 with a trichotomous marker by fractions of vaccinees with low VE and high VE (1-sided 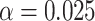). There are 100 controls and 20 cases; controls:cases = 5:1. The percent with low value of immune marker = percent with low VE; the percent with high value of immune marker = percent with high VE; precision .

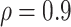Table 2 presents a summary of the limits on VE(High) and VE(Low) when power achieves 80% at different splits among the percentage in the low VE subgroup and high VE subgroup when overall VE = 75% and precision level 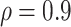. The scenarios with 10 cases and 50 controls or 20 cases with 100 controls are considered analogous to Figure 1, which assumes 50 cases and 250 controls. Power achieves 80% at less extreme values of VE(High) and VE(Low) when greater fractions are split into the low and high bins. Power is greater if precision level ρ is >0.9 and lower if ρ is <0.9.

Table 2.

Limits on Vaccine Efficacy (High) and Vaccine Efficacy (Low) When Power Achieves 80% at Different Splits in Percentages in the Low Vaccine Efficacy and High Vaccine Efficacy Subgroups^a

		No. of Cases = 10; No. of Controls = 50		No. of Cases = 20; No. of Controls = 100
% With Low VE	% With High VE	Min VE(High)%	Max VE(Low)%	Min VE(High)%	Max VE(Low)%
10	40	–b	–b	>94	<9
15	50	>95	0	>90	<24
15	60	>95	<5	>89	<26
20	70	>93	<13	>87	<34

Abbreviation: VE, vaccine efficacy.

^a Overall VE = 75%; precision 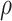= 0.9.

^b Does not achieve 80% power for any VE(High) and VE(Low).

DISCUSSION

We have shown that at an overall VE = 75%, 50 Ebola endpoints in the vaccinees provided good power under certain assumptions. At an overall VE = 90%, 20 Ebola endpoints gave good power under certain assumptions. Several lessons have been learned by examining the power to detect CoRs of an Ebola vaccine such as the rVSV Ebola vaccine (Figure 4). First, power depends markedly on the strength of the association of the visit-1 marker with the Ebola disease endpoint and requires that relatively large fractions of vaccine recipients be at the extreme ends of the immune response. The WHO published preliminary efficacy estimates of the rVSV-Ebola vaccine in the ring vaccination campaign in North Kivu Province in April 2019 (12). The estimated VE in the rings was 97.5% (95% confidence interval: 95.8, 98.5). With this very high VE, the potential variability in the VE for different levels of the CoR could potentially be very limited, and thus the power might be even lower than simulated here. Second, power depends markedly on the number of vaccine recipients with blood storage. Third, with a highly efficacious vaccine, the number of breakthrough cases in vaccinees could be low. Thus the number of vaccinees for whom blood storage is needed could be very high. This is especially true when the correlates analysis would consider multiple markers and might need to build in multiplicity correction or training/validation sets, and a larger number of vaccinees would need blood storage. Fourth, power drops off rapidly with decreasing 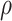. In general, it is prudent to allow only immune response markers in a primary correlates study that are known to have a high signal-to-noise ratio to ensure near maximal power and other reliability properties, and 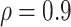is one reasonable benchmark for a qualifying marker. We recommend including only markers with enough qualification or validation.

Figure 4.

Lessons learned from designing a study of correlates of risk of Ebola vaccine.

Although not illustrated in these results, it is important in the analysis to adjust for variables related to exposure to infection. The reason it is important is that we aim for the CoRs to have interpretation in terms of differential biological susceptibility to the outcome, not differential exposure to the outcome. This is important for arguing that a strong CoR is likely also a correlate of protection.

The strength of the association of the visit-1 marker with the Ebola disease endpoint might be partially controlled. If there are animal challenge correlates-of-protection studies, then one could favor down-selecting immune response markers that showed strong associations with the outcome in the challenge trials. One can use external or previous clinical trials studying immunogenicity of a vaccine candidate and down-select immune response markers that have the widest biologically relevant dynamic range. Given the numerous immunogenicity studies of current Ebola vaccine candidates, this might be an option. Further, regarding a sampling design point, if there is knowledge of which individuals are expected to have low or high immune-response marker values, then one might oversample individuals based on the predicted extremes to increase power. In practice, however, this would likely be difficult.

To interpret a CoR as a correlate of VE, in this analysis, we assumed that after controlling for the baseline prognostic factors of Ebola disease that are included in the analysis, the hypothetical placebo-group Ebola risk does not vary in the value of the biomarker as strongly as the vaccine-group Ebola risk. If most of the hypothetical placebo group had not been exposed to Ebola previously, then this could be a plausible assumption. Also, the stronger the CoR in vaccinees, the greater the credibility of this assumption. However, this assumption is not testable.

The attack rate in the vaccinated could be influenced by indirect effects of ring vaccination. That is, exposure could actually be much lower than if no one had been vaccinated, so the attack rate in the vaccinees might be correspondingly lower; thus, a greater number of stored blood samples would be needed to produce 20 vaccinated cases. The assumption about the hypothetical attack in the absence of vaccination must take this into account.

One complication is that the controls are those who complete the follow-up period without experiencing Ebola. The follow-up period would likely be through to the end of the epidemic or possibly when transmission locally has been eliminated. Different outbreaks will have different follow-up periods. The controls for a case from any outbreak would likely need to come from the same outbreak, with additional control in the analysis for exposure variables. The consequences of having different follow-up periods in different outbreaks require further thought.

Another consideration is planning to understand how breakthrough cases correspond to the ramping up of the immune response after vaccination. In the ring vaccine trial in Guinea, there were cases in vaccinated people up to 6 days after they were vaccinated, and in the current DRC outbreak there were cases up to 9 days after they were vaccinated. If early samples from these people had been obtained after vaccination, we would know their biomarker levels as they ramped up around the time they became an early case. This could provide important information about correlates. Going forward, it might be useful to have 1 or more early postvaccination samples from individuals.

Having more than one Ebola vaccine available for future outbreaks is essential. Implementing CoR studies for Ebola vaccines is a public health priority. With a highly efficacious vaccine available, gathering the necessary information will be a challenge. If the number of cases accrued in vaccinated individuals is not high enough to reach statistical significance in one outbreak, the study could be conducted over multiple outbreaks. It might be useful to establish and improve surveillance and biobank systems that store blood samples from many thousands of Ebola-vaccinated individuals, such that when epidemics occur the biobank could be accessed to enable correlates studies. Ebola is now being viewed as a disease that will return again and again, so we should take a long-term perspective on planning to accrue the information needed to aid licensure of Ebola vaccines. Combining results across outbreaks will be important.