Abstract

Protein dynamics on various time scales from femtoseconds to milliseconds impacts biological function by driving proteins to conformations conducive to ligand binding and creating functional states in enzyme catalysis. Neutron vibrational spectroscopy carried out by measuring inelastic neutron scattering from protein molecules in combination with molecular simulations has the unique ability of detecting and visualizing changes in the picosecond protein vibrational dynamics due to ligand binding. Here we present neutron vibrational spectra of a homodimeric pyridoxal 5′-phosphate-dependent enzyme, aspartate aminotransferase, obtained from the open internal aldimine and closed external aldimine conformational states. We observe that in the external aldimine state the protein structure stiffens relative to the internal aldimine state, indicating rigidified vibrational dynamics on the picosecond time scale in the low-frequency regime of 5–50 cm–1. Our molecular dynamics simulations indicate substantial changes in the picosecond dynamics of the enzyme secondary structure elements upon substrate binding, with the largest contributions from just two helices and the β-sheet.
Introduction
Living systems are very dynamic on all levels, from the whole multicellular organism to a single cell and down to the level of individual biomacromolecules. If one could watch a cell in “action” on the molecular level, the motions of the constituent biomacromolecules might seem chaotic, but these motions are in fact highly orchestrated and regulated by internal and external stimuli to maintain homeostasis. In condensed phase systems, many motions of biomacromolecules are coupled, from the molecular vibrations to diffusion. Over the years, the motions of biomacromolecules, including low-frequency conformational dynamics, have captivated the interest of many scientists in an effort to gain insight into the physical forces that drive a specific biological function.1,2 The motions of macromolecular assemblies span more than 18 orders of magnitude in time, electronic transitions occur in attoseconds (EHz), bond vibrations occur in low femtoseconds (PHz), collective vibrations of protein secondary structure in picoseconds (low THz), protein domains can move on the nano-to-millisecond time scale (GHz–KHz), and cellular organization occurs in seconds to days (Table 1). The motions of atoms within molecules are coupled in time, and as correlations increase, the more collective a particular dynamical process becomes. Many collective motions in biomacromolecules have been identified to induce allosteric signaling, mechanical work, and many other important biological functions.3−5
Table 1. Physical Events, Phenomena, and Their Associated Time Scales and Frequencies.
| event | physical phenomena | time scale, s | frequency | wavenumber, cm–1 |
|---|---|---|---|---|
| electron–proton pairing | weak force gauge Boson | 10–18 (as) | EHz | |
| electronic transition | UV/vis absorption | 10–16–10–15 (as—hundreds of as) | EHz–PHz | >4000 |
| bond vibration | IR absorption | 10–15–10–14 (fs—tens of fs) | PHz–high THz | 4000–100 |
| protein vibrational dynamics | 10–13–10–12 (hundreds of fs–ps) | low THz—sub-THz | 50–15 | |
| protein breathing modes | 10–12–10–11 (ps—tens of ps) | sub-THz | 15–1 | |
| internal conversion microwave absorption | bond rotations/translations | 10–14–10–10 (tens of fs—hundreds of ps) | high THz–GHz | 1000–100 |
| domain motion | protein conformational dynamics | 10–9–10–6 (ns−μs) | GHz–MHz | 0.03–0.03 × 10–3 |
| ligand/substrate binding | induced fit | 10–8–10–3 (hundreds of μs–ms) | GHz–KHz | 0.03–0.03 × 10–6 |
In biomacromolecules, domain motions are linked to solvent diffusion and therefore occur at relatively low frequencies. The frequency of domain transitioning from an open to a closed conformation is in the GHz-to-MHz range, and the two states are separated by an energy barrier on the order of several kT (Boltzmann constant times the absolute temperature). Such low-frequency, high-amplitude cooperative collective motions drive biomacromolecules between what is typically a relatively small number of possibly functional conformational states having distinct three-dimensional structures. Associated with the low-frequency domain motions are higher-frequency (low THz) small-amplitude fluctuations around the average structure, exploring a large ensemble of closely related conformations (Table 1). These motions include variations in nonbonded contacts associated with the secondary structure that can promote both strain and stability within conformations.6−8 Therefore, it is commonly recognized that conformational sampling, or dynamics, of proteins is interwoven into their functional abilities and is crucial for many biological processes on various time scales.
Enzymatic catalysis is thought to be strongly influenced by protein dynamics.9,10 Enzymes accelerate rates of chemical reactions by substantially altering and lowering transition-state energies to control metabolism, signaling, and energy transduction and maintaining genetic information. The ability of enzymes to accelerate the rates of chemical reactions by many orders of magnitude, compared to that of the same uncatalyzed reactions in aqueous solvent,11 permits cells to carry out many functions on the biologically relevant time scales at physiological conditions. Researchers have proposed that enzyme conformational dynamics plays a major role in the rate acceleration of chemical reactions, thus directly contributing to the catalytic power of enzymes.12 Warshel and colleagues13−15 define dynamical effects to when (a) the transmission factor for the transition-state crossing is small, (b) there are non-Boltzmann coherent motions, (c) large deviations from the transition-state theory are apparent, and (d) the coupling modes in the enzyme do not follow the Boltzmann distribution. Recent studies suggest that the constraints implemented by Warshel and colleagues might be too restrictive.1 For example, adenylate kinase (Adk), which catalyzes the reversible conversion of adenosine triphosphate (ATP) and adenosine monophosphate (AMP) molecules into two ADP molecules, has been subjected to extensive experimental studies to analyze possible dynamical effects that contribute to catalysis. Using NMR relaxation experiments, Kern and co-workers provided evidence that the opening of the nucleotide lids is the rate-limiting step for the overall turnover of Adk,1,16 suggesting that there are catalytically important collective domain motions in Adk. In contrast, molecular simulation studies on Adk concluded that there is no significant dynamical coupling between the chemical and conformational trajectories,15 indicating that atomic motions do not directly enhance the reaction rate. Similarly, conformational changes in the propyl cis–trans isomerase cyclophilin A have been suggested to influence the overall turnover rate.17 Conversely, for many enzymes, it has been shown that the pre-organization of the active site and electrostatic contributions from amino acid residues located near and far from the catalytic site are the major phenomena that stabilize the transition state and increase the rate of the chemical reaction.18 It is important to note that the motions of domains and secondary structure elements in enzymes are important for how the protein functions as a catalyst, but these motions should not necessarily be directly coupled to chemical catalysis. Thus, the role of dynamical contribution to enzymatic catalysis is an important topic of ongoing research and debate.19
Inelastic neutron scattering (INS) is a vibrational spectroscopy technique that uses cold-thermal neutrons (0.001–1 eV) to gain or lose resonance energy during scattering, comparable to infrared Raman spectroscopy. Cold and thermal neutrons have an energy distribution that matches the vibrational and conformational dynamics of biomacromolecules in the condensed phase, which allows coupling of neutrons to different types of molecular motions to study the biomacromolecular function in a broad range of time scales (fs–ns) using various neutron scattering techniques.20−26 INS measurements are used to probe macromolecular dynamics in a broad frequency range, from a few wavenumbers (3 cm–1, 0.1 THz) to a few thousand wavenumbers (2000 cm–1, 60 THz), by exploiting the incoherent scattering of hydrogen in a sample.27−29 Using INS, vibrational molecular motions of proteins can be probed by detecting the energy transfer of the neutrons to/from the biomacromolecule after they interact with the biological sample.30,31 The vibrational nature of the molecular motions in the frequency regime of ∼5–100 cm–1 (0.15–3 THz) overlays the inelastic scattering (Boson) peak located in this same realm.27,28,32−34
Here, we used INS to detect, analyze, and compare vibrations of the secondary structure elements (i.e., helices, β-sheets, loops) within lyophilized D2O-hydrated powders of aspartate aminotransferase (AAT) enzyme on the picosecond time scale corresponding to the vibrational frequency range of 5–50 cm–1 (6.6–0.66 ps or 0.15–1.5 THz). AAT is responsible for sequestering and transferring ammonia from aspartic acid to α-ketoglutarate in the forward reaction and from glutamate to oxaloacetate in the reverse, where directionality is governed by mass action and comparable barrier heights. AAT is a homodimeric enzyme in which each monomer has a large domain that contains a lysine in a solvent-exposed active site linked by a Schiff base to a pyridoxal 5′-phosphate (PLP) cofactor (internal aldimine) and small domain, which closes over the active site when the substrate binds. During the forward transferase reaction, the open-state AAT–PLP internal aldimine binds aspartate, the small domain closes, and the cofactor switches to AAT–PLP−α-Asp external aldimine (Scheme 1 and Figure 1). While in the closed state, a 1,3-proton shift initiates hydrolysis of the external aldimine. The small domain then opens to release oxaloacetate, with the ammonia sequestered in the active site as pyridoxamine. The inhibitor 2-methyl aspartate (2-MeAsp) blocks the 1,3-proton shift, trapping the enzyme in the closed conformation external aldimine form. The INS spectra of the open state (internal aldimine) and closed state (external aldimine) were compared to quantify dynamical changes occurring in AAT due to substrate binding on the molecular level. We performed molecular dynamics (MD) simulations by constructing models that (a) closely match the experimentally measured hydrated powder samples and (b) take advantage of our recently published neutron structures of AAT.35 We observed that the binding of 2-MeAsp, a competitive inhibitor, to AAT causes reduction of the inelastic scattering peak height on the INS spectra in the 10–50 cm–1 frequency range, indicating stiffening of the protein’s secondary structure elements, affecting their picosecond vibrational dynamics. MD simulations produced the same trend for the computed INS spectra, demonstrating rigidification within the picosecond protein vibrations range, and provided evidence of the reduced vibrational density of states (VDOS) in the external aldimine state compared to that in the internal aldimine state. We were able to discern that changes in the vibrational dynamics of two helices and the β-sheet accounted for ∼40% of the overall change in protein vibrations in this time regime. Our findings demonstrate that, in the closed conformational state of the external aldimine, the vibrational frequencies of the picosecond motions of the helices and the β-sheet shift to higher energies, where the observed dynamical stiffening can be seen in the INS spectra and MD simulations.
Scheme 1. Chemical Diagrams of Pyridoxal 5′-Phosphate Cofactor (PLP), Internal Aldimine Produced by the Reaction with the AAT Catalytic Lys Residue, and External Aldimine Formed after the Internal Aldimine Reacts with the α-Methyl Aspartic Acid (2-CH3-Asp) Substrate Analogue.
Protonation states in the internal and external aldimine states correspond to the observed hydrogen atom positions in our previously reported neutron structure (PDB ID 5VJZ). Hydrogen bonds are shown as dashed lines, as observed in the neutron structure.
Figure 1.

Structural alignment of the internal aldimine (cyan) and external aldimine (dark pink) states of AAT. Internal aldimine (yellow carbon atoms) and external aldimine (green carbon atoms) are each shown within one of the monomers in a ball-and-stick representation, colored by the atom type.
Materials and Methods
Sample Preparation
The protein expression and purification were conducted in the same manner as described previously.36 After the hydrogenated protein was purified and concentrated to ∼10 mg/mL, the protein was dialyzed overnight at 4 °C twice in the buffer made with D2O containing 10 mM NH4OAc, pD = 7.5, and 0.1 mM PLP. For the internal aldimine sample, the protein was frozen at −80 °C after dialysis. For the external aldimine sample, 3.0 mg of 2-MeAsp (20 mM after mixing) was added to 3 mL of protein (∼10 mg/mL, 0.2 mM) after dialysis and then quickly mixed and placed to −80 °C. In this sample, there is about 100 times more hydrogen in the protein than that introduced by 2-MeAsp; therefore, the inelastic neutron scattering signal would be dominated by the protein. The frozen protein samples were lyophilized for 48 h. The volatile NH4OAc evaporates during the lyophilization step. The samples (∼30 mg each) were then rehydrated to 30% w/w each with pure D2O vapor in a glovebox and then placed in aluminum foil pouches.
Inelastic Neutron Scattering
The two protein samples were loaded in vanadium sample holders, and the INS spectra were measured at 120 K for ∼12 h each using the VISION neutron spectrometer located at the Spallation Neutron Source (SNS), Oak Ridge National Laboratory. VISION is an indirect-geometry spectrometer optimized for an improved signal-to-noise ratio to measure molecular vibrations over a broad energy range (−2–1000 meV) but does not allow for Q resolution. Therefore, VDOS cannot be directly calculated from the experimental data. The momentum transfer Q is a function of the energy transfer,37 and for the energy range of interest in this study, Q ranges from 1 to 4 Å–1. The energy resolution of the instrument is about 1.5% of the energy transfer. Neutron scattering from an empty sample holder was also measured under the same conditions, and the resulting spectrum was subtracted as background from the protein INS spectra. For VISION, vanadium sample holders are used for the E–Q range of interest as polycrystalline aluminum produces similar background as vanadium after orientational averaging and Brillouin zone integration. The INS spectra for the two samples were normalized by the total measurement time (proton charge) and the elastic neutron scattering peak.
To determine the contribution of vibrational dynamics to substrate binding with INS, some assumptions and approximations must be considered. To obtain sufficient signal-to-noise and minimize the scattering from the solvent, the protein sample must be prepared by freeze-drying the hydrogenated protein and rehydrated with D2O to a degree of 30% w/w. It is also important to estimate the contribution of coherent scattering from D in D2O to the overall signal from the samples to ensure that the scattering signal is indeed dominated by the incoherent scattering of hydrogen within the protein. We calculate that there is ∼1.3 mmol of D in D2O and ∼2.2 mmol of H in the protein; then, the total signal from D in D2O measures ∼5% of the total signal from H in protein. If we assume that the hydration levels in the two samples differed by as much as several percent, such differences would contribute negligibly to the D2O neutron scattering signals and thus to the observed differences in the signal between the samples. Therefore, the dynamic structure factor can be assumed to be incoherent, dominated by the motions of the protein, and the differences in neutron scattering signals between the two samples come from altered vibrational motions in proteins and not from differences in the hydration levels. In addition, the incoherent scattering is the self-correlations of atoms in space and time, allowing the structure factor to be a sum over atoms.
Previously, VDOS of trehalose-coated myoglobin were determined to be very similar at both 100 K and 300 K.22 Above the glass-transition temperature, anharmonic motions along with overdamping of the low-energy modes will result in quasi-elastic scattering, which is beyond the resolution of the VISION instrument. Importantly, previous molecular dynamics simulations have shown that the vibrational modes in proteins are effectively harmonic (∼99%) at 300 K.38 The experiment is conducted below the glass-transition temperature (∼180–200 K). Specifically, the experiment is conducted at 120 K to ensure harmonic motions of the atoms, allowing simpler data interpretation.
Solution Molecular Dynamics
For the classical molecular dynamics (MD) simulation, the models were adapted from the recent AAT neutron structure.35 Restrained by crystal contacts, this structure has one internal aldimine monomer and one external aldimine monomer within the dimeric AAT. Simplified models for MD simulations were generated by superimposition, the internal aldimine monomer replacing the external aldimine monomer to create a ligand-free dimer and vice versa for the ligand-bound dimer. Molecular mechanics force field parameters were generated as previously described.12 In short, the antechamber module assisted in assigning atom types from the General AMBER Force Field,39,40 and the program R.E.D41 was used to compute the atomic partial charges by the restrained electrostatic potential (RESP) charge fitting procedure.
The MD models were generated with the leap module of AMBER16 using the ff14SB force field to describe the protein.40 The system was further solvated in a cubic box of TIP3P water with a 20 Å length between the protein and the nearest face of the solvent box, while also retaining the crystallographic water positions.42 Each system was then minimized using 1000 steps of steepest descent algorithm, followed by 250 steps of conjugate gradient. A cutoff of 8 Å for real-space nonbonded interactions was applied, and the particle mesh Ewald method was used to compute the long-range electrostatic interactions.43 Periodic boundary conditions were applied for each system. The SHAKE algorithm was applied to constrain all bonds to hydrogen, allowing a 2 fs integration step to be used.44 A three-step equilibration procedure was used. First, the system was heated from 0 to 300 K over 500 ps using Langevin dynamics with a collision frequency of 1 ps–1. All heavy atoms of the protein, internal, and external aldimines were restrained with a harmonic potential of 5 kcal mol–1 Å–2. Second, a 500 ps simulation at a constant pressure (1 atm) with isotropic scaling was carried out with heavy-atom restraints. Finally, a 500 ps equilibration step, in which only the Cα atoms were restrained, was run. After the equilibration, the system was subjected to 40 ns unrestrained production MD in an NPT ensemble. Coordinates were saved every 10 ps for data analysis. Throughout the simulation, the AAT models exhibited moderate backbone RMSD fluctuations (<2.5 Å), indicating that the systems were stable over this time scale.
Powder Molecular Dynamics
To generate protein powder models, three dimeric AAT molecules with internal or external aldimines in their active sites containing a 7.0 Å solvent shell were randomly oriented. Additional water molecules were added to ensure that the hydration level was the same as in the samples used for the experimental INS data collection, 30% w/w. The protein powder models were generated with the leap module of AMBER16 using the ff14SB force field to describe the protein, and a periodic box was set to enclose all atoms at the edge of the cubic box.40 Each protein powder model was minimized using 1000 steps of steepest descent algorithm, followed by 250 steps of conjugate gradient. A similar protocol as in the solution MD simulations was used for the nonbonding interactions and equilibration. However, to mimic the INS experiment, the protein powder model was first equilibrated using the NVT ensemble (300 K) for 1 ns. The second equilibration step involved a 1 ns simulation at a constant pressure (1 atm) with isotropic scaling. Each system was then cooled to 120 K using 20 K intervals over 1 ns for each simulation. Once the system reached 120 K, a 2 ns simulation at a constant temperature (120 K) was conducted. After the system was equilibrated, three 50 ps production simulations using a 1 fs integration step were performed for data analysis. The positions of the atoms were saved every 1 fs throughout the production simulations.
Analysis of Protein Powder MD Simulations
To analyze
the MD simulations of the protein powder models, each of the three
50 ps production simulations was used to compute the averaged VDOS
and INS spectra. All computations were performed using Python scripts
written in-house. Starting from the position (xn) and velocity  of each atom, the mean-squared displacement
(eq 1.1) and the velocity
autocorrelation function (eq 1.2) were computed
of each atom, the mean-squared displacement
(eq 1.1) and the velocity
autocorrelation function (eq 1.2) were computed
| 1.1 |
| 1.2 |
The velocity autocorrelation function (C(t)) is essentially the self-correlation of each atom in time. A damping function (eq 1.3) was applied to the velocity autocorrelation function to smooth out the numerical artifact resulting from finite-time truncations
| 1.3 |
By applying a Fourier transformation of the velocity autocorrelation function, the power spectrum of the VDOS (g(ω)) can be obtained (eq 1.4), which describes the number of vibrational modes per interval of energy and directly contributes to the INS signal (eq 1.5)
| 1.4 |
| 1.5 |
where
| 1.6 |
and
| 1.7 |
In eq 1.5, g(ω) is the VDOS, q is the scattering vector, σi is the incoherent scattering cross section of atom i, and m is the mass of atom i. In eq 1.6, kBT is the Boltzmann constant times the temperature the simulation was conducted at.
Using the above equations, the incoherent INS spectra can be directly computed. Specifically, by iterating over the number of atoms and the frequency range, while also accounting for the incoherent scattering cross section of each atom, the incoherent INS spectra were computed (eq 1.5). It is important to note that the MD simulations were conducted in H2O (TIP3P water model). However, when accounting for the contribution of the solvent in the INS spectra calculation, the incoherent scattering cross section for deuterium was substituted for the hydrogen atoms of water. In addition, the VDOS in the INS spectra calculations were normalized by setting the integral of g(ω) equal to one.
For the comparison of the absolute VDOS (eq 1.8) of the internal and external aldimine states, g(ω) was normalized so that the integral is equal to the number of vibrational degrees of freedom (3N – 6) of the protein minus the hydrogen constraints (NC)
| 1.8 |
To identify and quantify changes in the vibrational dynamics of each protein secondary structure element (α-helices and β-sheets), we first considered the relative changes in the partial VDOS of each element (eqs 1.9 and 1.10)
| 1.9 |
| 1.10 |
where α1:α2 is the selected range of atoms within each structural element. The partial vibrational densities of states (VDOS) (g(ω)p) were integrated over the 0–60 cm–1 frequency range (ω1 – ω2), where significant differences were observed in the INS spectra and VDOS from MD simulations for internal and external aldimine states of AAT. Next, we calculated the absolute contribution (eq 1.11) of each element VDOS changes to the overall VDOS of the protein
| 1.11 |
Here, the absolute partial VDOS (gabs) are normalized to the vibrational degrees of freedom minus the hydrogen constraints for an individual structural element and then weighted to the overall VDOS of the entire protein.
Results
INS Spectra of the Picosecond Vibrational Dynamics Indicate That the AAT External Aldimine State Is Stiffer than the Internal Aldimine State
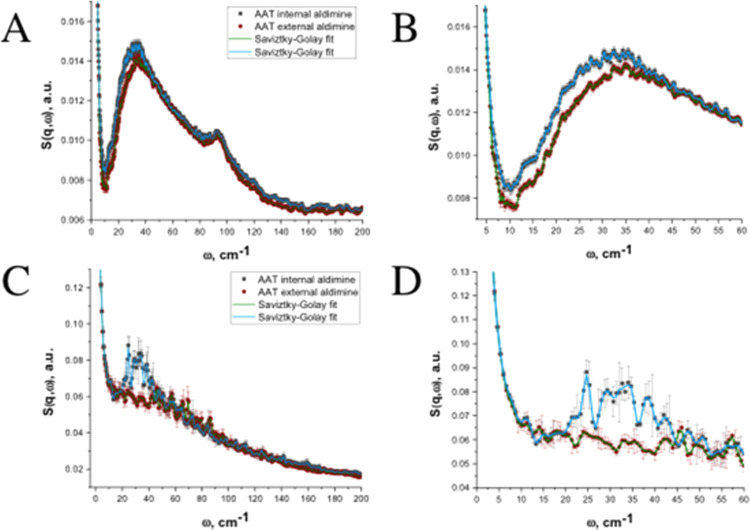
The INS vibrational spectra of both the internal and external aldimine states overlay the broad boson peak, which spans the frequency range of ∼10–150 cm–1 (0.3–4.5 THz) and is a characteristic of amorphous materials (Figure 2A). The exact origin of the boson peak from the amorphous material is still a fundamental question in the field of physics.45 The boson peak contains a signal resulting from acoustic modes arising from interparticle phonons and intraparticle molecular vibrations in a sample, in our case, perhaps, local ordering within the amorphous AAT. A peak at ∼95 cm–1 in the inelastic spectra shown in Figure 2A is the instrument artifact. We observed that the external aldimine state has a significantly lower signal indicated by the reduced dynamic structure factors, S(q,ω), in the frequency range of 10–50 cm–1 compared to the internal aldimine state. The reduced amplitude of this inelastic peak is indicative of fewer vibrations in this energy range in the enzyme’s closed state, making AAT stiffer in the external aldimine state (Figure 2A). In this low-frequency range (Figure 2B), the vibrations are more collective, which can be related to the breathing-like character (5–15 cm–1) of the enzyme and collective small-amplitude vibrational motions of the secondary structure elements, such as helices, β-sheets, and loops, in the picosecond regime (15–50 cm–1).2,27,28 It is important to note that higher-energy modes (e.g., rotations of side chains) were also observed but were not the focus of this study. The higher-energy (>100 cm–1) peak assignments were not considered and are not discussed further. The vibrations at energies above 100 cm–1 correspond to localized motions of individual amino acid residues, such as rotations of their side chains. Our INS picosecond vibrational dynamics spectra show that AAT is stiffer in the external aldimine state. MD simulations were used to model the changes in AAT dynamics caused by the substrate analogue binding and to quantitate the vibrational motions responsible for the observed dynamical changes on the molecular level.
Figure 2.
INS spectra. (A, B) are the experimental spectra. (C, D) are the computed spectra from MD simulations. Gray denotes the internal aldimine (open state) and red denotes the external aldimine (closed state) of AAT. The light blue and green lines are Savitzky–Golay smoothing trends (five-point third-order polynomial).
MD Simulations Indicate That Picosecond Dynamics Destabilizes the AAT External Aldimine State Relative to the Internal Aldimine State
To perform a quantitative assessment of the observations made with the INS spectroscopy, we carried out MD simulations of the internal and external aldimine states of AAT in the modeled powder state. Critical to the success of the MD simulations is the construction of hydrated powder models such that (1) the experimental conditions are appropriately mimicked and (2) the simulations are run within a reasonable amount of time. Therefore, the MD models contained three randomly oriented physiological AAT dimers hydrated to the same level as measured in the samples used in the INS experiments (30% w/w). Each AAT dimer was constructed using our published neutron structures of the internal and external aldimine states. These models contain accurate positions of hydrogen atoms, ensuring that the electrical charges are distributed correctly throughout the enzyme molecules. In the computed INS spectra generated from the MD simulations of such protein powder models, the characteristic boson peak is significantly less pronounced on a relative scale for both states (Figure 2C), as expected.6 The signal in the INS spectra is in arbitrary units and is related to the amount of material. In the experimental INS spectra, the internal aldimine has a significantly larger signal in the frequency range of 20–50 cm–1 compared to the external aldimine state (Figure 2A,B), indicative of more vibrational motions in the open state of AAT. This difference can be computed and is consistent with the internal aldimine being less rigid than the external aldimine (Figure 2C,D). These results justified additional analysis to discern the protein vibrational dynamics of AAT.
The INS spectra provide a qualitative measure of the differences between vibrational modes within a discrete energy range of the open and the closed states of AAT. A more direct approach for determining the magnitude of vibrational modes is to compute the absolute vibrational density of states (VDOS). The INS signal is directly related to the VDOS (eq 1.5 in Materials and Methods) of the system, and the VDOS is computed from MD simulations of the protein powder models using the power spectrum of the velocity autocorrelation function. The computed absolute VDOS of the internal and external aldimine (Figure 3) are reflective of the experimental INS spectra. Specifically, the VDOS of the open internal aldimine state have more low-energy vibrational modes in the frequency range of ∼20–50 cm–1. As the substrate analogue binds to AAT, forming the external aldimine, the protein rigidifies. It is important to note that the low-frequency modes that are present in the internal aldimine do not vanish once the substrate analogue binds, but rather shift to a higher frequency (Figure 4). As the external aldimine forms and small domain closes, many additional protein–protein and protein–substrate interactions are formed, perhaps contributing to shifting some vibrational motions to higher frequencies.
Figure 3.

Vibrational density of states of the AAT enzyme. The dark gray squares correspond to the internal aldimine (open-state) VDOS and the red spheres are for the external aldimine (closed-state) VDOS. The light blue and green lines are Savitzky–Golay smoothing trends (five-point third-order polynomial).
Figure 4.
Difference (external aldimine–internal aldimine) in the vibrational density of states plotted in the range of 0–100 cm–1. The red dashed line is a Savitzky–Golay smoothing (20-point second-order polynomial) to show the overall trend.
For structural biologists and biochemists, there is a focus on identifying changes in the secondary structure between individual states of a protein. Comparing both the relative and absolute VDOS of each structural element allows a more thorough approach to assess the magnitude of the change in the vibrational dynamics between the open and closed states of AAT. To establish which secondary structure components (elements) contribute to the overall and relative change in dynamics, the partial VDOS of each α-helix, β-sheet, and the catalytic loop (C-loop), which contains the catalytic residue (Lys258), were computed. It is important to note that the motions of each structural element can be coupled with neighboring and even more distant elements. However, the partial VDOS calculation provides quantitative information regarding the contribution to the change in vibrational modes of each structural element.
For each structural element, the relative change in their individual VDOS is positive except for helix 12 in the small domain (Table 2). A positive change in VDOS occurs when the specific structural element has more vibrational modes in the low-energy regime (1–50 cm–1) for the internal aldimine compared to that for the external aldimine state. Many of the α-helices and the β-sheet have a significant (>10%) relative change in their VDOS (Table 2 and Figure 5). As the substrate binds forming the closed-state external aldimine, not only does the small domain rigidify but the picosecond vibrational dynamics also indicates that virtually all of the protein is stiffer. When comparing the absolute partial VDOS changes (Table 3), the β-sheet, helix 6, and helix 11 have the most significant contributions to the absolute difference in the total VDOS. Helix 6 is on the outer edge of the large domain, while the β-sheet spans the large domain (Figure 6). Helix 11 transverses from the large domain to the small domain in AAT, acting like a protein hinge. In fact, it can be clearly seen in Figure 1 that helix 11 is bent in the open internal aldimine state but becomes virtually linear in the external aldimine state.
Table 2. Relative Changes in VDOS of the Secondary Structure Elements Integrated in the 0–60 cm–1 Frequency Range between the Internal and External Aldimine States of AATa.
| structural elements | relative VDOS change, % |
|---|---|
| helix 1 | 9.0 |
| helix 2 | 18.3 |
| helix 3 | 17.9 |
| β sheet | 19.6 |
| helix 4 | 14.9 |
| helix 5 | 15.7 |
| helix 6 | 17.8 |
| helix 7 | 17.7 |
| helix 8 | 14.8 |
| helix 9 | 9.1 |
| helix 10 | 2.0 |
| helix 11 | 14 |
| helix 12 | –8b |
| helix 13 | 8.8 |
| C-loop | 9.1 |
The negative value for the percent VDOS change for helix 12 indicates more vibrations (i.e., softened dynamics) for this helix in the external aldimine state relative to the internal aldimine state, which is opposite to the overall trend in the case of the other AAT secondary structure elements.
Figure 5.

Partial vibrational density of states (g(ω)p) of the β-sheet (A) and helices 6 (B) and 11 (C) in the AAT enzyme. The dark gray squares correspond to the internal aldimine (open-state) VDOS and the red spheres are for the external aldimine (closed-state) VDOS. The light blue and green lines are Savitzky–Golay smoothing trends (five-point third-order polynomial).
Table 3. Absolute Contributions of the Changes in VDOS of the Secondary Structure Elements to the Total Change in VDOS between the Internal and External Aldimine States of AATa.
| structural elements | absolute contribution, % |
|---|---|
| helix 1 | 2.5 |
| helix 2 | 4.6 |
| helix 3 | 4.6 |
| β sheet | 14.2 |
| helix 4 | 4.3 |
| helix 5 | 2.8 |
| helix 6 | 10.8 |
| helix 7 | 5.7 |
| helix 8 | 5.4 |
| helix 9 | 8.3 |
| helix 10 | 4.5 |
| helix 11 | 14.3 |
| helix 12 | –2.9 |
| helix 13 | 7.7 |
| C-loop | 4.5 |
| total | 88.8 |
Figure 6.
Secondary structural elements of AAT. The β-sheet and C-loop are colored magenta and blue, respectively. α-Helices 6 and 11 whose VDOS changes make the largest contribution to the changes in the vibrational dynamics of AAT are colored red and green, respectively. The external aldimine and catalytic Lys258 are shown in ball-and-stick. The other AAT monomer is grayed out for clarity.
We observed that changes in the INS spectra and VDOS between the open and closed states of AAT in the powder form are comparable. Also, a comparison of the motions of the atoms in the powder and solution models shows that the change in root-mean-square fluctuations (RMSFs) follows the same trend going from the internal aldimine to the external aldimine states. In the external aldimine state, the RMSFs of the atoms are significantly smaller throughout the enzyme in both the solution and powder models independent of the temperature (Figure 7). The magnitude of the RMSF between the powder and solution models is justifiably significantly different. This large difference in the magnitude of the RMSF is due to the temperature of the MD simulation. The temperature of the solution MD simulation was conducted at 300 K, while the protein powder MD simulation was conducted at 120 K. However, the regions and the trend of RMSF changes between the internal and external aldimine states are consistent between the solution and powder models (Figure 7), providing evidence that motions of atoms are not drastically different between the solution and powder forms of AAT.
Figure 7.

RMSF of the atoms in the solution (A, B) and powder (C, D) MD simulations performed at 300 and 120 K, respectively. A and C are for the internal aldimine (open state), while B and D are for the external aldimine (close state). Warm colors (red-to-yellow) are high RMSF, whereas cool colors (green-to-blue) are low RMSF. It is important to note that the powder and solution models are on different scales but are consistent between the internal and external aldimine states.
Discussion
Numerous X-ray crystallographic structures have demonstrated that protein association with a ligand generally leads to structural stabilization, reduced flexibility, and rigidification of proteins because ligand binding is often accompanied by a large conformational change that results in a more compact protein molecule. This is clearly demonstrated in the case of AAT—upon substrate analogue binding, the small domain moves toward the large domain and closes over the active site (Figure 1), resulting in lower atomic B-factors and a better-defined electron density for parts of the small domain.35 According to the hierarchical model of motions, the overall reduction in protein dynamics should span broad time scales, from picosecond vibrational motions to the slow microsecond-to-millisecond collective domain motions. The stiffened structure has fast vibrations that contribute to the slower large conformational changes.1,46 In contrast, reduction in slow conformational dynamics due to ligand binding should not necessarily lead to enhancement of the fast vibrational motions.
Protein flexibility observed in the low-frequency regime (<50 cm–1) corresponds to the collective vibrational modes of the secondary structure elements;2,6−8 it can either increase or decrease upon ligand binding, and there are no general rules to predict whether such picosecond vibrational dynamics would stiffen or soften in the complex. More rigid protein vibrations would contribute unfavorably to the ligand binding free energy, acting to destabilize the complex, whereas softening of the vibrational dynamics would provide a favorable stabilizing free-energy component for ligand binding.47−49 Previous INS,23,50,51 anisotropic THz microscopy,51 optical Kerr-effect spectroscopy,52 and NMR47,49,53 measurements and molecular simulations53,54 performed on several proteins have demonstrated that ligands exert a significant effect on the protein vibrations, altering fast vibrational dynamics and making the proteins either more rigid or more flexible on the picosecond time scale. Decreased vibrational dynamics was detected in complexes of lysozyme with chitotriose,51,52 cytochrome P450cam with camphor,53 and human acetylcholinesterase with organophosphorus nerve agent soman.50 Conversely, in complexes of dihydrofolate reductase with clinical drug methotrexate23 and mouse major urinary protein47 with the pheromone, the proteins softened. The change in the vibrational free energy upon complex formation was calculated for the dihydrofolate reductase/methotrexate complex, where the increase of breathing-like vibrations in the enzyme complex contributed −4.1 kcal/mol to the stability of the complex. Interestingly, the entropic contribution was favorable of −6.0 kcal/mol, compensated by the unfavorable enthalpic term of +1.9 kcal/mol. The entropic terms were calculated for lysozyme49 and mouse major urinary protein47 complexes to be of +6.7 kcal/mol (unfavorable) and −12 kcal/mol (favorable), respectively.
We calculated that the additional vibrational motions that are present in the open conformation of the AAT internal aldimine state in the 20–50 cm–1 frequency range are mostly due to extra vibrations within helices 6 and 11 and the core β-sheet that may be coupled with the motions of the large and small domains (Table 3). As stated above, large collective motions of domains are coupled to the solvent. However, the role of solvent or the changes in solvent-accessible surface area in relation to the changes in low-energy vibrations cannot be decoupled. Here, we report the net change in the frequency of protein vibrations between the open and closed states of AAT, which can be influenced by changes in solvent–protein interactions and changes in the internal nonbonded protein–protein interactions.
The formation of the external aldimine shifts these vibrational motions of the enzyme secondary structure elements to higher frequencies, effectively destabilizing the external aldimine state (Figure 4), which would be a similar effect of chitotriose on lysozyme49 and an opposite effect of methotrexate on dihydrofolate reductase.23 It is interesting, yet perhaps counterintuitive, that the secondary structure elements having the largest positional shifts when the small domain closes over the active site upon the formation of the external aldimine are helices 1, 12, and 13 (Figures 1 and 6). Changes in the picosecond vibrations of the latter helices contribute significantly less to the total changes in the AAT vibrational dynamics than those of helices 6, 11, and the β-sheet, with helix 12 becoming dynamically softer instead of stiffer (Tables 2 and 3). According to Warshel’s criteria, such a change in the picosecond vibrational dynamics occurring in an enzyme intermediate complex would not be considered a dynamical effect on catalysis as such dynamics does not drive the system toward the transition state.13,14 However, what we observe with the INS experiments and detect in the MD simulations of AAT is a clear effect of altered vibration dynamics on the stability of a stationary point (i.e., of an enzyme intermediate) along the enzyme-catalyzed chemical transformation.
We hypothesize that the destabilization of the external aldimine state may be beneficial for catalysis. For an enzyme to convert substrate to product without additional energy, the overall potential energy must remain the same, which is accomplished by shifting vibrational tension between protein regions. Stiffening of the picosecond vibrational motions in the closed conformation of the external aldimine state would increase the free energy of the complex. Moreover, rigidifying the external aldimine state may help keep the scissile Cα-H bond in the proper alignment, which ensures strong σ → π* hyperconjugation with the PLP π-system that contributes ∼1012 orders of magnitude to the rate enhancement of the Cα-H bond cleavage.55 If our hypothesis is correct, the picosecond vibrational dynamics that destabilizes the PLP–Asp external aldimine intermediate and hyperconjugation that promotes the 1,3-proton shift work in unison to promote this reaction step. Due to limitations in both INS and MD, the quantification and direct relationship between protein dynamics and catalysis are undefined. Specifically, the loss of q resolution on the VISION instrument affects the ability to compute the experimental vibrational free energy. The MD presented here samples the open internal aldimine and closed external aldimine intermediate states; no conclusion can be made on the entire space of the free-energy surface that encompasses the rate-limiting portion of the AAT-catalyzed transamination reaction. More rigorous statistical assessment, extended sampling, and relation to solution dynamics of powder MD models are needed to obtain the possible relationship of protein dynamics and catalysis. Current efforts are focused on developing a more direct approach to gain insights into the influences of protein dynamics. Regardless, what we observe with the INS experiments and detect in the MD simulations of AAT is a clear effect of altered quantifiable vibrational dynamics upon substrate binding.
Acknowledgments
Research at ORNL’s Spallation Neutron Source (VISION beamline) was sponsored by the Scientific User Facilities Division, Office of Basic Energy Sciences, U.S. Department of Energy (DOE-BES). The D2O used in this research was supplied by the United States Department of Energy Office of Science by the Isotope Program in the Office of Nuclear Physics. The Office of Biological and Environmental Research supported research at the Oak Ridge National Laboratory’s Center for Structural Molecular Biology (CSMB) involving protein expression and purification, using facilities supported by the Scientific User Facilities Division, Office of Basic Energy Sciences, U.S. Department of Energy. The authors specially thank Rhonda Moody of the User Labs and Sample Support at the Spallation Neutron Source for her technical support during sample preparation for neutron scattering experiments. S.D., Y.C., L.L.D., and A.K. were supported by the U.S. Department of Energy’s (DOE) Office of Basic Energy Sciences.
Author Present Address
∥ Schrödinger, Inc., 120 West 45th Street, New York, New York 10036, United States.
Author Contributions
S.D., T.C.M., and A.K. conceived and coordinated the study. S.D., O.G., T.C.M. and K.L.W. carried out protein expression and purification. S.D., O.G., and A.K. prepared samples for neutron scattering. Y.C. and L.L.D. collected inelastic neutron scattering data. S.D., Y.C., and L.L.D. performed computational analysis. The manuscript was written through the contributions of all authors. All authors have given approval to the final version of the manuscript.
The authors declare no competing financial interest.
References
- Henzler-Wildman K.; Kern D. Dynamic personalities of proteins. Nature 2007, 450, 964–972. 10.1038/nature06522. [DOI] [PubMed] [Google Scholar]
- Chou K.-C. Low-frequency collective motion in biomacromolecules and its biological functions. Biophys. Chem. 1988, 30, 3–48. 10.1016/0301-4622(88)85002-6. [DOI] [PubMed] [Google Scholar]
- Yun M.; Zhang X.; Park C. G.; Park H. W.; Endow S. A. A structural pathway for activation of the kinesin motor ATPase. EMBO J. 2001, 20, 2611–2618. 10.1093/emboj/20.11.2611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kosztin I.; Bruinsma R.; O’Lague P.; Schulten K. Mechanical force generation by G proteins. Proc. Natl. Acad. Sci. U.S.A. 2002, 99, 3575–3580. 10.1073/pnas.052209199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peracchi A.; Bettati S.; Mozzarelli A.; Rossi G. L.; Miles E. W.; Dunn M. F. Allosteric Regulation of Tryptophan Synthase: Effects of pH, Temperature, and α-Subunit Ligands on the Equilibrium Distribution of Pyridoxal 5′-Phosphate– l-Serine Intermediates. Biochemistry 1996, 35, 1872–1880. 10.1021/bi951889c. [DOI] [PubMed] [Google Scholar]
- Kurkal-Siebert V.; Smith J. C. Low-temperature dynamics: a simulation analysis of interprotein vibrations and the Boson peak at 150K. J. Am. Chem. Soc. 2006, 128, 2356–2364. 10.1021/ja055962q. [DOI] [PubMed] [Google Scholar]
- Nickels J. D.; Perticaroli S.; O’Neill H.; Zhang Q.; Ehlers G.; Sokolov A. P. Coherent neutron scattering and collective dynamics in the protein, GFP. Biophys. J. 2013, 105, 2182–2187. 10.1016/j.bpj.2013.09.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perticaroli S.; Nickels J. D.; Ehlers G.; O’Neill H.; Zhang Q.; Sokolov A. P. Secondary structure and rigidity in model proteins. Soft Matter 2013, 9, 9548–9556. 10.1039/c3sm50807b. [DOI] [PubMed] [Google Scholar]
- Schramm V. L.Introduction: Principles of Enzymatic Catalysis; ACS Publications, 2006. [Google Scholar]
- Dynamics in Enzyme Catalysis, Topics in Current Chemistry; Klinman J.; Hammes-Schiffer S., Eds.; Springer, 2013; Vol. 337, pp 1–212.23539379 [Google Scholar]
- Wolfenden R.; Snider M. J. The depth of chemical time and the power of enzymes as catalysts. Acc. Chem. Res. 2001, 34, 938–945. 10.1021/ar000058i. [DOI] [PubMed] [Google Scholar]
- Hay S.; Scrutton N. S. Good vibrations in enzyme-catalyzed reactions. Nat. Chem. 2012, 4, 161–168. 10.1038/nchem.1223. [DOI] [PubMed] [Google Scholar]
- Kamerlin S. C.; Warshel A. At the dawn of the 21st century: Is dynamics the missing link for understanding enzyme catalysis?. Proteins 2010, 78, 1339–1375. 10.1002/prot.22654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warshel A.; Bora R. P. Perspective: Defining and quantifying the role of dynamics in enzyme catalysis. J. Chem. Phys. 2016, 144, 180901 10.1063/1.4947037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pisliakov A. V.; Cao J.; Kamerlin S. C.; Warshel A. Enzyme millisecond conformational dynamics do not catalyze the chemical step. Proc. Natl. Acad. Sci. U. S. A. 2009, 106, 17359 10.1073/pnas.0909150106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolf-Watz M.; Thai V.; Henzler-Wildman K.; Hadjipavlou G.; Eisenmesser E. Z.; Kern D. Linkage between dynamics and catalysis in a thermophilic-mesophilic enzyme pair. Nat. Struct. Mol. Biol. 2004, 11, 945. 10.1038/nsmb821. [DOI] [PubMed] [Google Scholar]
- Eisenmesser E. Z.; Millet O.; Labeikovsky W.; Korzhnev D. M.; Wolf-Watz M.; Bosco D. A.; Skalicky J. J.; Kay L. E.; Kern D. Intrinsic dynamics of an enzyme underlies catalysis. Nature 2005, 438, 117–121. 10.1038/nature04105. [DOI] [PubMed] [Google Scholar]
- Warshel A. Electrostatic origin of the catalytic power of enzymes and the role of preorganized active sites. J. Biol. Chem. 1998, 273, 27035–27038. 10.1074/jbc.273.42.27035. [DOI] [PubMed] [Google Scholar]
- Harijan R. K.; Zoi I.; Antoniou D.; Schwartz S. D.; Schramm V. L. Inverse enzyme isotope effects in human purine nucleoside phosphorylase with heavy asparagine labels. Proc. Natl. Acad. Sci. U.S.A. 2018, 201805416 10.1073/pnas.1805416115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anunciado D. B.; Nyugen V. P.; Hurst G. B.; Doktycz M. J.; Urban V.; Langan P.; Mamontov E.; O’Neill H. In Vivo Protein Dynamics on the Nanometer Length Scale and Nanosecond Time Scale. J. Phys. Chem. Lett. 2017, 8, 1899–1904. 10.1021/acs.jpclett.7b00399. [DOI] [PubMed] [Google Scholar]
- Seeger P. A.; Daemen L. L.; Larese J. Z. Resolution of VISION, a crystal-analyzer spectrometer. Nucl. Instrum. Methods Phys. Res., Sect. A 2009, 604, 719–728. 10.1016/j.nima.2009.03.204. [DOI] [Google Scholar]
- Cordone L.; Ferrand M.; Vitrano E.; Zaccai G. Harmonic behavior of trehalose-coated carbon-monoxy-myoglobin at high temperature. Biophys. J. 1999, 76, 1043–1047. 10.1016/S0006-3495(99)77269-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balog E.; Becker T.; Oettl M.; Lechner R.; Daniel R.; Finney J.; Smith J. C. Direct determination of vibrational density of states change on ligand binding to a protein. Phys. Rev. Lett. 2004, 93, 028103 10.1103/PhysRevLett.93.028103. [DOI] [PubMed] [Google Scholar]
- Jacrot B.; Cusack S.; Dianoux A. J.; Engelman D. M. Inelastic neutron scattering analysis of hexakinase dynamics and its modification on binding of glucose. Nature 1982, 300, 84–86. 10.1038/300084a0. [DOI] [PubMed] [Google Scholar]
- Cusack S.; Doster W. Temperature dependence of the low frequency dynamics of myoglobin. Biophys. J. 1990, 58, 243–251. 10.1016/S0006-3495(90)82369-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diehl M.; Doster W.; Petry W.; Schober H. Water-coupled low-frequency modes of myoglobin and lysozyme observed by inelastic neutron scattering. Biophys. J. 1997, 73, 2726 10.1016/S0006-3495(97)78301-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith J.; Cusack S.; Pezzeca U.; Brooks B.; Karplus M. Inelastic neutron scattering analysis of low frequency motion in proteins: a normal mode study of the bovine pancreatic trypsin inhibitor. J. Chem. Phys. 1986, 85, 3636–3654. 10.1063/1.450935. [DOI] [Google Scholar]
- Kneller G. R. Inelastic neutron scattering from damped collective vibrations of macromolecules. Chem. Phys. 2000, 261, 1–24. 10.1016/S0301-0104(00)00223-8. [DOI] [Google Scholar]
- Squires G. L.Introduction to the Theory of Thermal Neutron Scattering; Cambridge University Press, 2012. [Google Scholar]
- Cusack S.; Smith J.; Finney J.; Tidor B.; Karplus M. Inelastic neutron scattering analysis of picosecond internal protein dynamics. Comparison of harmonic theory with experiment. J. Mol. Biol. 1988, 202, 903–908. 10.1016/0022-2836(88)90566-9. [DOI] [PubMed] [Google Scholar]
- Doster W.; Cusack S.; Petry W. Dynamical transition of myoglobin revealed by inelastic scattering. Nature 1989, 337, 754–756. 10.1038/337754a0. [DOI] [PubMed] [Google Scholar]
- Doster W.; Cusack S.; Petry W. Dynamic instability of liquidlike motions in a globular protein observed by inelastic neutron scattering. Phys. Rev. Lett. 1990, 65, 1080–1083. 10.1103/PhysRevLett.65.1080. [DOI] [PubMed] [Google Scholar]
- Orecchini A.; Paciaroni A.; Bizzarri A. R.; Cannistraro S. Low-frequency vibrational anolmalies in β-lactoglobulin: contribution of different hydrogen classes revealed by inelastic neutron scattering. J. Phys. Chem. B 2001, 105, 12150–12156. 10.1021/jp0114889. [DOI] [Google Scholar]
- Pieper J.; Irrgang K.-D.; Renger G.; Lechner R. E. Density of vibrational states of the light-harvesting complex II of green plants studied by inelastic neutron scattering. J. Phys. Chem. B 2004, 108, 10556–10565. 10.1021/jp049341f. [DOI] [Google Scholar]
- Dajnowicz S. J.; Parks R. C.; Blakeley J. M.; Keen M. P.; Weiss D. A.; Gerlits K. L.; Kovalevsky O.; Mueser A.; Timothy C. Direct visualization of critical hydrogen atoms in a pyridoxal 5′-phosphate. Nat. Commun. 2017, 8, 995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dajnowicz S.; Parks J. M.; Hu X.; Gesler K.; Kovalevsky A. Y.; Mueser T. C. Direct evidence that an extended hydrogen-bonding network influences activation of pyridoxal 5′-phosphate in aspartate aminotransferase. J. Biol. Chem. 2017, 292, 5970–5980. 10.1074/jbc.M116.774588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitchell P. C. H.; Parker S. F.; Ramirez-Cuesta A. J.; Tomkinson J.. Vibrational Spectroscopy with Neutrons, with Applications in Chemistry, Biology, Materials Science and Catalysis; World Scientific: Singapore, 2005. [Google Scholar]
- Kitao A.; Hayward S.; Go N. Energy landscape of a native protein: Jumping-among-minima model. Proteins 1998, 33, 496–517. . [DOI] [PubMed] [Google Scholar]
- Wang J.; Wolf R. M.; Caldwell J. W.; Kollman P. A.; Case D. A. Development and testing of a general amber force field. J. Comput. Chem. 2004, 25, 1157–1174. 10.1002/jcc.20035. [DOI] [PubMed] [Google Scholar]
- Case D. A.; C D. S.; Cheatham T. E.; Darden T. A. III; Duke R. E.; Giese T. J.; Gohlke H.; Goetz A. W.; Greene D.; Homeyer N.; Izadi S.; Kovalenko A.; Lee T. S.; LeGrand S.; Li P.; Lin C.; Liu J.; Luchko T.; Luo R.; Mermelstein D.; Merz K. M.; Monard G.; Nguyen H.; Omelyan I.; Onufriev A.; Pan F.; Qi R.; Roe D. R.; Roitberg A.; Sagui C.; Simmerling C. L.; Botello-Smith W. M.; Swails J.; Walker R. C.; Wang J.; Wolf R. M.; Wu X.; Xiao L.; York D. M.; Kollman P. A.. AMBER; University of California: San Francisco, 2016. [Google Scholar]
- Dupradeau F.-Y.; Pigache A.; Zaffran T.; Savineau C.; Lelong R.; Grivel N.; Lelong D.; Rosanski W.; Cieplak P. The REd. Tools: Advances in RESP and ESP charge derivation and force field library building. Phys. Chem. Chem. Phys. 2010, 12, 7821–7839. 10.1039/c0cp00111b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jorgensen W. L.; Chandrasekhar J.; Madura J. D.; Impey R. W.; Klein M. L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. 10.1063/1.445869. [DOI] [Google Scholar]
- Darden T.; York D.; Pedersen L. Particle mesh Ewald: An N·log (N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. 10.1063/1.464397. [DOI] [Google Scholar]
- Ryckaert J.-P.; Ciccotti G.; Berendsen H. J. Numerical integration of the cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. J. Comput. Phys. 1977, 23, 327–341. 10.1016/0021-9991(77)90098-5. [DOI] [Google Scholar]
- Zorn R. The boson peak demystified?. Physics 2011, 4, 44. 10.1103/Physics.4.44. [DOI] [Google Scholar]
- Henzler-Wildman K.; Lei M.; Thai V.; Kerns S. J.; Karplus M.; Kern D. A hierarchy of time scales in protein dynamics is linked to enzyme catalysis. Nature 2007, 450, 913–918. 10.1038/nature06407. [DOI] [PubMed] [Google Scholar]
- Zidek L.; Novotny M. V.; Stone M. J. Increased protein backbone conformational entropy upon hydrophobic ligand binding. Nat. Struct. Biol. 1999, 6, 1118–1121. 10.1038/70057. [DOI] [PubMed] [Google Scholar]
- Fischer S.; Smith J. C.; Verma C. S. Dissecting the vibrational entropy change on protein/ligand binding: burial of a water molecule in bovine pancreatic trypsin inhibitor. J. Phys. Chem. B 2001, 105, 8050–8055. 10.1021/jp0120920. [DOI] [Google Scholar]
- Moorman V. R.; Valentine K. G.; Wand A. J. The dynamical response of hen egg white lysozyme to the binding of a carbohydrate ligand. Protein Sci. 2012, 21, 1066–1073. 10.1002/pro.2092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peters J.; Martinez N.; Trovaslet M.; Scannapieco K.; Koza M. M.; Masson P.; Nachon F. Dynamics of human acetylcholinesterase bound to non-covalent and covalent inhibitors shedding light on changes to the water network structure. Phys. Chem. Chem. Phys. 2016, 18, 12992–13001. 10.1039/C6CP00280C. [DOI] [PubMed] [Google Scholar]
- Niessen K. A.; Xu M.; Paciaroni A.; Orecchini A.; Snell E. H.; Markelz A. G. Moving in the right direction: protein vibrational steering function. Biophys. J. 2017, 112, 933–942. 10.1016/j.bpj.2016.12.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turton D. A.; Senn H. M.; Harwood T.; Lapthorn A. J.; Ellis E. M.; Wynne K. Teraherz underdamped vibrational motion governs protein-ligand binding in solution. Nat. Commun. 2014, 5, 3999 10.1038/ncomms4999. [DOI] [PubMed] [Google Scholar]
- Miao Y.; Yi Z.; Cantrell C.; Glass D. C.; Baudry J.; Jain N.; Smith J. C. Coupled flexibility change in cytochrome P450cam substrate binding determined by neutron scattering, NMR, and molecular dynamics simulation. Biophys. J. 2012, 103, 2167–2176. 10.1016/j.bpj.2012.10.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balog E.; Perahia D.; Smith J. C.; Merzel F. Vibrational softening of a protein on ligand binding. J. Phys. Chem. B 2011, 115, 6811–6817. 10.1021/jp108493g. [DOI] [PubMed] [Google Scholar]
- Dajnowicz S.; Parks J. M.; Hu X.; Kovalevsky A. Y.; Mueser T. C. Hyperconjugation promotes catalysis in a pyridoxal-5′-phosphate-dependent enzyme. ACS Catal. 2018, 8, 6733–6737. 10.1021/acscatal.8b01911. [DOI] [Google Scholar]