Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2020 Jul 24;5(30):19268–19276. doi: 10.1021/acsomega.0c02825

On the Second Explosion Limits of Hydrogen, Methane, Ethane, and Propane

Jie Liu †,*, Ruiguang Yu †, Biao Ma †, Chenglong Tang ‡,*
PMCID: PMC7409258  PMID: 32775930

Abstract

graphic file with name ao0c02825_0015.jpg

In this work, we have first investigated the explosion limit behaviors from hydrogen to propane through numerical simulations and validated with the available experimental data. The shape of the explosion limit curves and the possible turning points (P1–2, T1–2), first to second limit transition, and (P2–3, T2–3), second to third limit transition that bound the second explosion limit as a function of the fuel carbon number, have been examined. Results show that with an increase of methane mole fraction in the hydrogen/methane system, the upper turning point (P1–2, T1–2) remains almost unchanged and the lower transition point (P2–3, T2–3) rotates counterclockwise around (P1–2, T1–2). With a further increase of carbon number, (P1–2, T1–2) moves to the lower-pressure and -temperature region and (P2–3, T2–3) gradually moves to the lower-pressure and higher-temperature region. The slope of the second explosion limit is inversely proportional to the carbon number, kPT = 0.0069 – 0.005/(Xc – 0.7), approximately. Second, a sensitivity analysis has been conducted to study the elementary reaction on the second explosion limits. The results show that the chain branching and termination reactions governing the explosion limit of hydrogen have a little effect on the second explosion limit of methane. The C2H5O2H decomposition to form OH radicals is dominant in controlling the nonmonotonic behavior of the second explosion limit of C2H6. The second explosion limit behavior of propane is governed by three sets of reactions in the low-temperature oxidation process.

1. Introduction

Flammable gases widely exist in petroleum, coal, chemical, metallurgy, textile, medicine, and other industries. Under certain conditions, the combustible mixture will explode in the processes of transportation, storage, mining, and utilization, resulting in a huge loss of life and property. Therefore, the phenomenon of explosion has always been concerned by researchers owing to the explosion characteristics,1 minimum ignition energy,2 and flammability characteristics.3 The explosion limits of a homogeneous fuel/oxidizer mixture that separates the explosive and nonexplosive regions are dominated by the competition of the radical producing and removing reactions, the result of which is pressure- and temperature-dependent.4 As such, the explosion limit is typically characterized in the pressure–temperature parameter space and can be described by the pressure as a complex function of the system temperature. As a prominent example, the explosion limit of the H2–O2 mixture presents a Z-shaped curve, which consists of two turning points. The nonexplosion to explosion transition boundary divides the pressure vs temperature curve into the first, second, and third explosion limits under the low-, medium-, and high-pressure conditions, respectively.5 The first and third explosion limits are controlled by the competitive mechanism of the chain branching reactions and the diffusion mechanism of active radicals to the wall (chain termination step), while the second limit relies primarily on the competition between chain termination and branching reactions.4 Semenov et al. studied the first explosion limit and found that the elimination of H radicals is more important than that of O and OH radicals when determining this limit.6 However, Glassman pointed out that at low pressures, the elimination of OH and H radicals was equally critical to the first explosion limit.7 When the pressure is sufficiently high, the reaction between HO2 and H2 produces H2O2, which subsequently decomposes to two OH radicals and increases system reactivity. When this lumped channel overtakes the wall destruction mechanism of HO2, explosion happens again, and this critical pressure is the so-called third explosion limit.8 Recently, Sánchez observed that the third explosion limit can be well predicted by five HO2- and H2O2-involving reactions.9

The second explosion limit presents a significantly different characteristic compared with the first and third explosion limits. The appearance of the second explosion limit makes the explosion limit curve change from monotonic to nonmonotonic.10 In particular, the second explosion limit of hydrogen is peculiar in that as the pressure is further increased inside the peninsular of the explosion regime, the mixture becomes nonexplosive. The second limit is the control limit of purified chemical kinetics, i.e., the free radical formation reaction competes with the termination reaction of the free radicals.11 Moreover, as the three-body termination reaction H + O2 + M = HO2 + M is pressure-sensitive, it will override the most effective chain branching reaction to generate the second explosion limit when the H2/O2 system moves from a lower pressure to a higher pressure under a constant temperature. The appearance of the second explosion limit of hydrogen then demonstrates that the reactivity of the system in the medium-pressure region is reduced.

Plenty of studies on H2/O2 systems have clearly recognized the three explosion limits and the corresponding controlling mechanisms for each limit. For explosion limits of larger molecules, however, only limited investigations have been conducted. Specifically, Liang et al. have investigated the hydrogen addition effect on the explosion limits of CO/O2 mixtures and showed that the explosion curve changed from a C-shape to Z-shape with minute quantities of hydrogen addition, and the most severe change appeared in the second explosion limit region.12 Subsequently, they investigated the CH4/O2 system and showed that the addition of 5% of H2 also changed the monotonic explosion curve to the nonmonotonic Z-shaped one.13 The presence of inert gas in the system did not affect the shape of the explosion limit curve but only shifted the explosion limit curve to higher temperatures.14 Because propane occupies the position between lower and higher hydrocarbons, at very early times, Newitt and Thornes15 experimentally measured the ignition temperature of propane/oxygen in a closed homogeneous reactor with varying pressures. They showed that at lower and higher pressures, the ignition temperature decreased with increasing pressure, while at intermediate pressures, the ignition temperature increased with increasing pressure, which was consistent with the widely recognized negative temperature coefficient (NTC) behavior caused by the formation of cool flame. At the same time, low-temperature combustion is accompanied by a cool flame, which not only affects the safety of the engine but also plays an important role in the combustion technology of the advanced engine.16 Furthermore, the typical negative temperature coefficient (NTC) behavior was reported for larger alkanes.17 Recently, Yu et al. first investigated the effect of equivalence ratio and N2 addition on the explosion limit of propane.18 After that, Liu et al. investigated the effect of O3 addition on the cool flame region of the explosion limit of propane.19

The objectives of the present work are the following. Because only Newitt and Thornes reported the experimentally measured explosion temperature as a function of system pressure though that was decades ago and only propane was investigated. As such, our first objective is to use several well-recognized kinetic mechanisms that have been widely used in the combustion chemistry community to numerically investigate the explosion limit behaviors from hydrogen to propane with gradually increasing the carbon number in the system. The shape of the explosion limit curve and the possible turning point shift as a function of the fuel carbon number will be examined. We note that the classic Z-shaped explosion limit curve has been widely recognized for the hydrogen/oxygen system, while fewer investigations for larger molecules have been reported. We also note that the second explosion limit depends on the competition between the chain branching and termination reactions, which may be complex and demands more investigations. As such, we will emphasize on the second explosion limit. Second, because the detailed mechanisms contain hundreds of chain branching and termination reactions, a sensitivity analysis will be conducted to find out the most important elementary reactions that control the second explosion limits of all of the C0–C3 alkane/oxygen systems. This can be realized by tuning the rate constant of each elementary reaction and accessing the response of the explosion limit curve, and by doing this, the sensitive reactions that affect the second explosion limit behaviors will be selected. These sensitive reactions will be subsequently removed individually from the mechanism, and the predictions from the mechanism without including these reactions will be compared with the original one to identify the controlling elementary reactions for the second explosion limit behaviors. In the following, we will specify our numerical method and the criterion of the explosion limit. Then, we will show our numerically calculated explosion limit curves using the validated kinetic mechanisms, followed by the effect of the dominant elementary reactions on the nonmonotonic second explosion limit curves.

2. Numerical Approach Method

The explosion limits of C0–C3 alkanes are calculated using the SENKIN code.20 An explosion is identified if the system temperature increases by 50 K compared with the initial temperature within 10 s under certain pressure conditions, as recommended in ref (5). The initial calculated pressure is ranged from 3.5 to 3.2 × 107 Pa, which covers the working range of the common combustion devices, and the explosion temperature searching range is 350–2500 K. Other criteria like an average pressure increase rate of 3%/ms can be found for the determination of the cool flame ignition.21

Three different detailed chemical kinetic models are used in this study, which are the comprehensive iso-octane combustion model (KAUST),22 Aramco 2.0 model,23 and methane/propane oxidation model24 from the National University of Ireland Galway (NUIG). As the KAUST and Aramco 2.0 models include larger hydrocarbon molecules, only the C3 subset species and related reactions are used in this study. Diffusion of the carriers to the chamber wall is assumed to be much faster than wall absorption since only a small amount of the carriers that reach the wall are absorbed.5 Moreover, concentrations of the carriers at the wall are assumed to be the same as those in the gas phase such that a zero-dimensional reactive system with a volume V and surface area S is assured.

The carriers are destroyed at the wall according to the reactions,

H, O, OH, HO2, H2O2, HCO 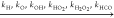Inline graphic wall destruction, with the corresponding reaction rate per unit volume kH, kO, kOH, kHO2, kH2O2, and kHCO given by

2. 1

where v̅ = (8kBT/πm)1/2 is the average velocity of the thermal motion of the carriers at temperature T, m is the molar mass, and kB is the Boltzmann constant. The sticking coefficient ε measures the destruction efficiency in the collision with the wall, and usually, ε ≈ 10–5 to 10–2 is selected for quartz.5 As the reaction vessel used in the Newitt and Thornes experiment is made of transparent silica, the sticking coefficient is taken as 10–3 in this study.

3. Results and Discussion

3.1. Kinetic Model Validation and the Boundary of the Second Explosion Limit

To begin with, the simulation results of the explosion limits for hydrogen and propane with different kinetic mechanisms are presented in Figure 1. Experimental data from Lewis and von Elbe for the hydrogen/oxygen system4 and from Newitt and Thornes for the propane/oxygen system15 are also used to validate these kinetic models. For stoichiometric hydrogen/oxygen, as shown in Figure 1a, all of the kinetic models reproduce the experimentally observed “Z-shaped” explosion limit curve in the pressure and temperature parameter space. The second explosion limit is bounded by two turning points, (P1–2, T1–2) and (P2–3, T2–3). The turning point (P1–2, T1–2) indicates the thermodynamic state that separates the first and second limits, and the point (P2–3, T2–3) indicates the turning from the second limit to the third limit. On the first and the third explosion limit curves, the pressure decreases with an increase of temperature, indicating that at higher temperatures, explosion can be triggered with lower reactant concentrations. On the second explosion limit curve, the pressure increases with an increase of temperature, indicating that the explosion will be triggered with higher reactant concentrations. Additionally, all of the three kinetic models show excellent agreement with the experimental measurement from Lewis, including the prediction of the position and the two turning points that bound the second explosion limit.

Figure 1.

Figure 1

Open in a new tab

Comparison of the calculation and experimental explosion limits of hydrogen (a) and propane (b); the experiment data of the H2 are taken from ref (4), and the experiment data of C3H8 are taken from ref (15).

The explosion limits for equimolecular propane/oxygen mixture are shown in Figure 1b, and experiments from Newitt and Thornes show that the curve is “S-shaped”. All of the three models qualitatively captured the explosion limit curve, although the turning point predictions deviate slightly from the measurements. Compared with the kinetic models of Aramco 2.0 and KAUST, the methane/propane model shows better agreement between the predicted and measured turning points. Additionally, similar to that of hydrogen, on both the first and third explosion limit curves, the explosion pressure increases at lower temperatures, and on the second explosion limit curve, pressure increases at higher temperatures. However, the turning point pressure from the first to the second explosion limit P1–2 is higher than that from the second to the third explosion limit P2–3, and the turning point temperature T1–2 is higher than T2–3, which is different from the hydrogen/oxygen system shown in Figure 1a. This phenomenon is consistent with the negative temperature coefficient (NTC) characteristics for typical hydrocarbons. Because of its good performance for the explosion limit curve prediction, the methane/propane model (C1/C3)24 is then selected for the following calculations of the C0–C3 alkane/oxygen system.

To further verify the prediction ability of the methane/propane mechanism, the comparison between the calculated and experimental explosion limits of methane and ethane are shown in Figure 2. It can be seen that the overall trend of the calculated results and the experimental results is in good agreement, and the position of the second explosion limit is also very close.

Figure 2.

Figure 2

Open in a new tab

Comparison of the calculated and experimental explosion limits of methane and ethane; the experimental data are taken from ref (25).

3.2. Second Explosion Limit Dependence on Carbon Number

Since both the first and third explosion limits have been well-recognized and reasonably interpreted by previous investigations,6−9 we will then focus on the second explosion limit and see how it changes the Z-curve explosion limit behavior of the hydrogen/oxygen system to the S-curve behavior of the propane/oxygen system by gradually increasing the carbon number of the fuel. In each calculation, a stoichiometric fuel/O2 mixture is used.

3.2.1. From C0 to C1

Figure 3 shows the explosion limit curves of the H2/CH4/O2 system with increasing methane substitution (XC1, the mole fraction of methane in the H2/methane fuel blends). As can be seen that the upper turning point (P2–3 = 0.86 bar, T2–3 = 825.8 K) remains almost unchanged with an increase of CH4 substitution, indicating that increasing the carbon number has a weak influence on the second to the third explosion limit transition. However, with an increase of XC1, the transition point for the first to the second explosion limit (P1–2, T1–2) gradually moves to the higher-pressure and -temperature region, i.e., (0.012 bar, 712.9 K), (0.014 bar, 753.2 K), and (0.017 bar, 794 K), respectively, for XC1 = 20, 40, and 60%. As such, the second limit rotates counterclockwise around the upper turning point and the explosion region is narrowed. In addition, with an increase of XC1, the positive slope of the second explosion limit curve significantly increases to an infinitely large value at XC1 ≈ 20%. Then, the slope (kPT, defined in Section 3.3) transits to a negative value and the magnitude of the slope decreases with further increasing XC1. As a consequence, the explosion curve transits from nonmonotonic (pure H2) to monotonic (pure CH4), and the turning point that separates the three explosion limits cannot be determined clearly such that the second explosion limit vanishes. In this case, we define a pseudo-(P1–2, T1–2) for a higher XC1 (>0.8) system by extrapolating the well-defined turning point (P1–2, T1–2) for a lower XC1 (0–0.6) system to higher XC1 cases. In this way, we can clearly see the trend of the second limit behavior, which can be quantified by the value of kPT.

Figure 3.

Figure 3

Open in a new tab

Effect of methane addition on the second explosion limit of hydrogen.

3.2.2. From C1 to C2

Figure 4 shows the explosion limit curves of the CH4/C2H6/O2 system with increasing ethane substitution (XC2, the mole fraction of methane in the CH4/C2H6 fuel blends). For the methane/oxygen system, the explosion pressure exhibits a monotonic decrease with an increase of temperature in the whole examined region. For XC2 < 10%, no obvious turning points show up on the whole explosion limit curve, and with an increase of XC2, the explosion pressure for temperatures higher than 700 K does not change much, while for lower temperatures, the explosion pressure decreases. For XC2 > 10%, the increased carbon number results in the presence of two turning points and bound a period of an almost horizontal line. As such, the second explosion limit is retrieved. On the second explosion limit curve, the pressures for different XC2 systems all show weak dependence on temperature. However, the turning point for the first to the second limit (P1–2, T1–2) gradually moves to higher temperatures, while the turning point for the second to the third limit transition (P2–3, T2–3) moves to a lower-temperature region, resulting in an expanded second limit region. Because for XC2 larger than 10% the two turning points can be well defined, we also extrapolate the bound pressure and temperature on the second explosion limit to lower XC2 cases such that we also get two pseudoturning points for lower XC2 cases. It is noted that for the pure CH4/O2 system (XC1 = 1 for H2/CH4 or XC2 = 0 for CH4/C2H6 fuel blends), there is no second explosion limit. As such, the pseudoturning points obtained by extrapolating XC2 from 1 to 0 in CH4/C2H6 in Figure 4 do not show the pseudoturning points in Figure 3, which is obtained by extrapolating XC1 from 0 to 1. It seems that the second limit curve also rotates counterclockwise with an increase of carbon number XC2.

Figure 4.

Figure 4

Open in a new tab

Effect of ethane addition on the second explosion limit of methane.

3.2.3. From C2 to C3

Figure 5 shows the explosion limit curves of the C2H6/C3H8/O2 system with increasing propane substitution (XC3, the mole fraction of propane in the C2H6/C3H8 fuel blends). It is seen that for all different XC3 cases, the explosion limit curve is “S”-shaped, and with an increase of XC3, nonmonotonic S-shaped behavior of the curve becomes more severe and the second explosion limit shifts to lower pressures. In addition, the transition point temperature T1–2 gradually moves to a higher-temperature region, while the transition point temperature for the second to the third explosion limit T2–3 gradually moves to a lower-temperature region, indicating an extended second explosion limit. Furthermore, the reduction extent of P2–3 is comparable to that of P1–2 for small XC3 cases, and a more obvious decrease of P2–3 is observed when XC3 is larger than 0.1. From ethane to propane, it seems that the second limit curve again rotates counterclockwise with an increase of carbon number XC3.

Figure 5.

Figure 5

Open in a new tab

Effect of propane addition on the second explosion limit of ethane.

3.2.4. Overall Trend of the Second Limit Slope Versus Carbon Number

With an increase of carbon number, the second explosion limit curves all rotate counterclockwise, as shown in Figures 3–5. To more clearly present the effect of carbon number on the second explosion limit, the slope of the quasi-linear relationship between the logarithmic pressure and temperature is derived, as in eq 2.

3.2.4. 2

where P1–2 and P2–3 are the pressures of the turning points and T1–2 and T2–3 are the temperatures of the turning points.

Figure 6 shows the kPT as a function of the carbon number. Carbon number ranges of [0, 1], [1, 2], and [2, 3], respectively, represent fuel mixtures of H2/CH4 (0 ≤ XC1 ≤ 1.0), CH4/C2H6 (0 ≤ XC2 ≤ 1.0), and C2H6/C3H8 (0 ≤ XC3 ≤ 1.0).

Figure 6.

Figure 6

Open in a new tab

Trends of the slopes of the second explosion limit from C0 to C3.

It is seen that with an increase of carbon number, the slope variations can be divided into two regions. Pure hydrogen has a positive slope, further increasing XC1 initially weakly and then significantly increasing the slope to an infinitely large value at XC1 ≈ 0.7 (carbon number ≈ 0.7). Then, the slope just changes from positive infinity to negative infinity and the magnitude gradually decreases. As the carbon number further increases, the slope magnitude gradually decreases to zero at the carbon number around 1.5 (XC2 ≈ 0.5). Further increasing the carbon number only weakly increases the slope with a positive sign. The dependence of the slope of the second explosion limit on the carbon number can be expressed as the following function

3.2.4. 3

It is shown from Figure 6 that the slope calculated by this fit function agrees well with the slope calculated from the explosion limit curve. Therefore, the slope of the second explosion limit is inversely proportional to the carbon number.

3.3. Controlling Elementary Reactions for the Second Explosion Limit

We note that the second explosion limit is controlled by the competition between the chain branching and termination reactions.4,11 For the carbon number lower than 0.70, chain termination reactions dominate the second explosion limit because the transition temperature T2–3 is larger than T1–2, resulting in a nonexplosion peninsular, as shown in Figure 3. With an increase of carbon number, T1–2 gradually increases and approaches T2–3. As such, the nonexplosive peninsular region gradually narrows, indicating that the chain termination reactions become weaker compared to the chain branching reactions. When the carbon number is increased to around 0.70, T1–2 equals T2–3, the nonexplosive peninsular vanishes, and the roles of the chain termination reactions and the chain branching reactions are comparable. For the carbon number higher than 0.70, T1–2 is always larger than T2–3, indicating that the chain branching reactions become dominant in controlling the second explosion limit. Additionally, since the kinetics of different fuel systems inherently contain different chain termination and chain branching reactions, we will then examine further what are those elementary reactions (either chain branching or termination) that dominate the second explosion limit.

To realize this goal, a two-step approach is adopted. First, to find the key reactions controlling the second explosion limit behavior for C0–C3 alkane molecules, the sensitivity analysis is conducted by perturbing the rate constant of each elementary reaction and comparing the corresponding explosion limit curve with the original one. In each sensitivity calculation, the pre-exponential factor of the rate constant is reduced by 90% for each individual reaction. The explosion limit curve calculated by the modified mechanism will be compared with that calculated by the original mechanism. The reactions that have an obvious effect on the explosion curves will be retained in the reduced mechanism. As the key reactions related to the explosion limit of pure hydrogen have been studied extensively in previous research, the sensitivity analysis with respect to hydrogen is not performed in this study.12,14 Instead, a nine-reaction mechanism is directly used as the reduced mechanism of hydrogen, where the reaction rate constants and the thermal parameters are all taken from the methane/propane model.24

The sensitivity analysis shows that a total number of 30 reactions should be retained to reproduce the explosion limit of methane calculated by the detailed mechanism. In addition, the explosion limit of C2H6 can be well reproduced with 77 reactions based on the sensitivity analysis. Furthermore, to maintain the accuracy of the explosion limit calculations, a total number of 194 reactions are kept in the reduced mechanism for C3H8. The explosion limits of the stoichiometric hydrogen/oxygen, methane/oxygen, ethane/oxygen, and propane/oxygen mixtures calculated by the detailed and reduced mechanisms are compared in Figure 7. It is shown that the shape and position of the explosion limits calculated by the detailed mechanism can be well reproduced by the reduced mechanisms with 9, 30, 77, and 194 reactions for hydrogen, methane, ethane, and propane, respectively.

Figure 7.

Figure 7

Open in a new tab

Comparison of the calculation explosion limits of H2, CH4, C2H6, and C3H8 with the detailed and reduced mechanism.

Second, we remove the most sensitive elementary reactions in the reduced mechanism one at a time and compare the correspondingly calculated second explosion limit with the original reduced model. By doing this, the elementary reactions that affect the second explosion limit most will be found out. The criterion is to see whether the complete explosion limit curve will lose its nonmonotonic behavior for hydrogen, ethane, or propane. In the following, we apply these two steps toward hydrogen, methane, ethane, and propane systems, respectively.

3.3.1. Toward H2 and CH4

We first compare the explosion limit curves calculated by the reduced mechanism (black solid line) and the mechanism with reducing the rate constant of H + O2 ⇔ O + OH (red dash) and H + O2 + M ⇔ HO2 + M (blue dot) by 90%, as shown in Figure 8a. Other elementary reactions that have much weaker effects are not shown. This comparison indicates that the third-body termination reaction H + O2 + M ⇔ HO2 + M and the chain branching reaction H + O2 ⇔ O + H are the most sensitive in determining the explosion limit for hydrogen. For methane, as shown in Figure 8b, the explosion limit curve is monotonic and these two reactions have almost no effect on the explosion limit curve.

Figure 8.

Figure 8

Open in a new tab

Sensitivities of the chain termination and branching reactions on the explosion limits of hydrogen (a) and methane (b).

For the second step, the explosion limits of hydrogen and methane are calculated without including the termination reaction (H + O2 + M ⇔ HO2 + M) or the branching reaction (H + O2 ⇔ O + OH) in the reduced mechanisms, as shown in Figure 9. It is obvious that the explosion limit curve of hydrogen will lose its nonmonotonic characteristics when the termination reaction is excluded in the reduced mechanisms and the reactivity of the system is significantly improved, as shown in Figure 9a. In addition, when the branching reaction is not included in the reaction mechanism, the reactivity of the hydrogen/oxygen mixture reduces significantly as the explosion limit moves toward a high-temperature region. However, there is only a very small shift for the methane explosion limit without including the termination or branching reaction in the reduced mechanism, as shown in Figure 9b. So, the dominated chemical kinetics of these two fuels on the explosion limit is inconsistent.

Figure 9.

Figure 9

Open in a new tab

Effect of the chain and termination reaction on the second explosion limits of hydrogen (a) and methane (b).

The main reactions with larger sensitivity on the explosion limit of methane are given in Figure 10. The oxidation of methane is initiated by CH4 + O2 = CH3 + HO2, from which the methyl and OH radicals will be generated. After the radical pool is formed, the most sensitive methane-related reactions are CH4 + OH ⇔ CH3 + H2O and CH4 + HO2 ⇔ CH3 + H2O2. The reaction of methyl (CH3) with hydroperoxyl (HO2) is important as the concentrations of both radicals are very high during the oxidation process of methane. The reaction path can be a chain-propagating reaction CH3 + HO2 = CH3O + OH or a termination reaction CH3 + HO2 = CH4 + O2. The reaction of the formyl radical is considered important for flame speed predictions. For explosion limit calculations, the formyl decomposition reaction HCO + M = H + CO + M and the reaction with molecular oxygen HCO + O2 = CO + HO2 are both important. The formyl radical is generated from CH2O reacted with OH and CH3. Also, CH2O radicals are produced from CH3 and CH3O in their reaction with molecular oxygen. The reactions involving methyl, methoxy, and methylperoxy have a significant effect on the explosion limit of methane. This means that for the methane oxidation process the reactive free radicals are mainly generated through the C1 subset reactions, which are very important in reproducing the correct kinetic behavior. As the explosion limit was no longer dominated by the chain termination reaction, the explosion limit has no nonmonotonic characteristics compared with the explosion limit of hydrogen.

Figure 10.

Figure 10

Open in a new tab

Main reactions with larger sensitivity on the explosion limit of methane.

3.3.2. Toward C2H6

By the same approach, we have first found the seven elementary reactions exhibiting the largest sensitivity with respect to the explosion limit of C2H6, as shown in Figure 11. Similar to the methane case, the branching reaction H + O2 ⇔ O + H also has almost no effect on the explosion limit. However, the H2O2 decomposition reaction obviously affects the first explosion limit. We note that after the radical pool is formed, ethane is mainly consumed through H-abstraction by H or HO2, instead of by O2. The ethylperoxy radical C2H5O2 is largely produced by the addition of molecular oxygen to the ethyl radical due to the long lifetime of RO2• radicals, which is the most important species for ethane oxidation.26 The ethylperoxy radical can further abstract a hydrogen atom from ethane to generate C2H5O2H through C2H62 + C2H5O2 ⇔ C2H5 + C2H5O2H. The cleavage of the weak O–O bond of C2H5O2H leads to a chain branching reaction C2H5O2H ⇔ C2H5O + OH.27 As the rate of the C2H5O2H generation reaction reduces, the length of the second explosion limit reduces and P1–2 and P2–3 both increase. The reduction of the reaction rate of C2H5O2H ⇔ C2H5O + OH will shorten the length of the second explosion limit, while P1–2 is almost not changed. Under low-pressure conditions, C2H5O2H is largely decomposed to C2H4 + HO2. With the reduction of the rate of C2H5O2H decomposition, both P1–2 and P2–3 are reduced obviously. For the ethane system, the hydroperoxyethyl species C2H4O2H is unimportant for the explosion limit of ethane because only a negligibly small amount of C2H5O2 undergoes the isomerization process.26

Figure 11.

Figure 11

Open in a new tab

Reactions exhibiting the largest sensitivities with respect to the explosion limit of C2H6.

Figure 12 shows that when C2H5O2H ⇔ C2H5O + OH is removed in the mechanism, the calculated explosion limit changes drastically and becomes monotonic. In addition, removing C2H6 + C2H5O2 ⇔ C2H5 + C2H5O2H will significantly shorten the length of the second explosion limit and the second limit is shifted to higher pressures. The C2H5O2H decomposition to form the OH radical is dominant in controlling the nonmonotonic behavior of the second explosion limit of C2H6.

Figure 12.

Figure 12

Open in a new tab

Dominant reactions for the explosion limit behaviors of C2H6.

3.3.3. Toward C3H8

As the carbon number increases, more reaction channels become to affect the explosion limit curve,28 and the determination of the dominant reaction for the second explosion limit of C3H8 is more complex since more fuel-specific reactions are affecting the explosion limit behavior. Figure 13 shows that the most sensitive reactions do not affect the general nonmonotonic explosion limit behavior but only shift the two turning points. H-abstraction from propane by OH and HO2 produces two isomers. n-Propyl (n-C3H7) and iso-propyl (i-C3H7) are generated by OH,29 and i-C3H7 is produced through hydrogen abstraction by the HO2 radical. Then, the addition of produced propyl radicals to molecular oxygen forms propylperoxyl radicals (C3H7O2), which then undergo the isomerization process to generate the propylhydroperoxyl radical C3H6OOH. The propylhydroperoxyl radical can decompose to C3H6 + HO2 or react with molecular oxygen to form C3H6OOHO2. The formed C3H6OOHO2 will decompose to c3ket + OH. Thereafter, the decomposition of c3ket will generate a second OH radical. These reactions have also been recognized to be responsible for the NTC behavior of the larger hydrocarbons.30

Figure 13.

Figure 13

Open in a new tab

Most sensitive reactions and their effect on the explosion limit behaviors of C3H8 (a, b).

Figure 14 further shows the comparison between the calculated explosion limits with removing the three types of reaction groups and the calculations with the original mechanism. First, if the reaction path of the molecular oxygen addition to propylhydroperoxyl radical (the second O2 addition) is cut off, which is used to block the formation of the twice OH radical generation in the chain branching path, the second explosion limit changes to almost a horizontal line instead of the nonmonotonic curve. Second, the second explosion limit still appears as a line with a small inclined angle when the second OH release reactions (the c3ket decomposition reactions) are deleted from the mechanism. This is because the first OH release reactions are still working. Third, when the reactions of the molecular oxygen addition and the decomposition of C3H6OOH are both excluded from the mechanism, a quasi-monotonic explosion limit curve is achieved. This means that C3H6OOH undergoes the decomposition reaction when the molecular oxygen addition reaction path is blocked, which will generate the C3H6 radical. The C3H6 subset reactions will give an explosion limit similar to that of C2H6. From the above analysis, it is concluded that the second explosion limit behavior of propane is governed by the three sets of reactions, as presented in Figure 14.

Figure 14.

Figure 14

Open in a new tab

Dominant reactions for the second explosion limit of C3H8.

4. Conclusions

In this study, the explosion limits of the typical C0–C3 alkanes are analyzed computationally and theoretically. The critical path of the reaction influencing the second explosion limit is found. The key elementary reactions affecting the explosion limit of C0–C3 alkanes are obtained.

The second explosion limit of pure hydrogen has a positive slope, further increasing XC1 initially weakly then significantly increases the slope to an infinitely large value at XC1 ≈ 0.7. Then, the slope just changes from positive infinity to negative infinity and the magnitude gradually decreases. As the carbon number further increases, the slope magnitude gradually decreases to zero at the carbon number around 1.5. Further increasing the carbon number only weakly increases the slope with a positive sign. The dependence of the slope of the second explosion limit on the carbon number can be expressed using an inverse proportional function.

The termination reaction H + O2 + M ⇔ HO2 + M and the chain branching reaction H + O2 ⇔ O + H, which are the key reactions in determining the explosion limit of C0, have a very small effect on the explosion limit of C1–C3. The nonmonotonic characteristic of the C2 explosion limit is controlled by the chain propagation reaction C2H5O2H ⇔ C2H5O + OH. The NTC behavior in the explosion limit of C3 is governed by the low-temperature reactions of C3H8, which will generate two OH radicals and significantly improve the reactivity of the system.

Acknowledgments

This study is supported by the International Science and Technology Cooperation of China (No. 2019YFE0100200) and the National Natural Science Foundation of China (No. 51406007). The authors gratefully acknowledge the valuable discussion with Prof. John Griffiths from the University of Leeds.

The authors declare no competing financial interest.

References

  1. Su B.; Luo Z.; Wang T.; Yan K.; Cheng F.; Deng J. Coupling Analysis of the Flame Emission Spectra and Explosion Characteristics of CH4/C2H6/Air Mixtures. Energy Fuels 2020, 34, 920–928. 10.1021/acs.energyfuels.9b03242. [DOI] [Google Scholar]
  2. Ajrash M. J.; Zanganeh J.; Moghtaderi B. Influences of the Initial Ignition Energy on Methane Explosion in a Flame Deflagration Tube. Energy Fuels 2017, 31, 6422–6434. 10.1021/acs.energyfuels.6b03375. [DOI] [Google Scholar]
  3. Huang L.; Wang Y.; Yang Z.; Wang Q.; Pei S.; Zhang L.; Ren S. Flammability and Explosion Characteristics of Methane in Oxygen-Reduced Air and Its Application in Air Injection IOR Process. Energy Fuels 2019, 33, 11850–11860. 10.1021/acs.energyfuels.9b02489. [DOI] [Google Scholar]
  4. Lewis B.; von Elbe G.. Combustion; Flames; and Explosions of Gases, 2nd ed.; Academic Press: New York, 1961. [Google Scholar]
  5. Wang X.; Law C. K. An analysis of the explosion limits of hydrogen-oxygen mixtures. J. Chem. Phys. 2013, 138, 134305 10.1063/1.4798459. [DOI] [PubMed] [Google Scholar]
  6. Semenov N. N.Some Problems in Chemical Kinetics and Reactivity; Princeton University: New Jersey, 1959. [Google Scholar]
  7. Glassman I.; Yetter R. A.. Combustion, 4th ed.; Elsevier: New York, 2008. [Google Scholar]
  8. Azatyan A. A.; Andrianova Z. S.; Ivanova A. N. Role of the HO2 radical in hydrogen oxidation at the third self-ignition limit. Kinet. Catal. 2010, 51, 337–347. 10.1134/S002315841003002X. [DOI] [Google Scholar]
  9. Sánchez A. L.; Fernández-Tarrazo E.; Williams F. A. The chemistry involved in the third explosion limit of H2–O2 mixtures. Combust. Flame 2014, 161, 111–117. 10.1016/j.combustflame.2013.07.013. [DOI] [Google Scholar]
  10. Law C. K.Combustion Physics; Cambridge University Press, 2006. [Google Scholar]
  11. Sher E.; Sher I.; Bar-Kohany T. Another view of the upper and intermediate explosion limits of H2-O2 system. Int. J. Hydrogen Energy 2013, 38, 14912–14914. 10.1016/j.ijhydene.2013.08.143. [DOI] [Google Scholar]
  12. Liang W.; Liu J.; Law C. K. On explosion limits of H2/CO/O2 mixtures. Combust. Flame 2017, 179, 130–137. 10.1016/j.combustflame.2017.01.024. [DOI] [Google Scholar]
  13. Liang W.; Liu Z.; Law C. K. Explosion limits of H2/CH4/O2 mixtures: Analyticity and dominant kinetics. Proc. Combust. Inst. 2018, 37, 1–8. 10.1016/j.proci.2018.07.059. [DOI] [Google Scholar]
  14. Liu J.; Wang J.; Zhang N.; et al. On the explosion limit of syngas with CO2 and H2O additions. Int. J. Hydrogen Energy 2018, 43, 3317–3329. 10.1016/j.ijhydene.2017.12.176. [DOI] [Google Scholar]
  15. Newitt D. M.; Thornes L. S. The Oxidation of Propane. Part I. The Products of the Slow Oxidation at Atmospheric and at Reduced Pressures. J. Chem. Soc. 1937, 1656–1665. 10.1039/jr9370001656. [DOI] [Google Scholar]
  16. Wang Z.; Gou X.; Zhong C. Experimental and Kinetic Study on the Cool Flame Characteristics of Dimethyl Ether. Energy Fuels 2019, 33, 9205–9214. 10.1021/acs.energyfuels.9b01711. [DOI] [Google Scholar]
  17. Liu C.; Zhang Y.; Xiong D.; et al. Flammability and Propagation Dynamics of Planar Freely Propagating Dimethyl Ether Premixed Flame. ACS Omega 2020, 5, 10965–10976. 10.1021/acsomega.0c00792. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Yu R.; Liu J.; Ma B. The dependence of NTC behavior on the equivalence ratio and nitrogen fraction in cool flame region. Fuel 2020, 271, 117623 10.1016/j.fuel.2020.117623. [DOI] [Google Scholar]
  19. Liu Jie.; Yu R.; Ma B. Effect of Ozone Addition on the Cool Flame and Negative Temperature Coefficient Regions of Propane-Oxygen Mixtures. ACS Omega 2020, 5, 16448–16454. 10.1021/acsomega.0c00725. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Lutz A. E.; Kee R. J.; Miller J. A.. SENKIN: A FORTRAN Program For Predicting Homogeneous Gas Phase Chemical Kinetics with Sensitivity Analysis, No. SAND-87-8248; Sandia National Laboratories: Livermore, CA, 1988; 87–8248.
  21. Guo J.; Peng W.; Zhang S.; Lei J.; Jing J.; Xiao R.; Tang S. Comprehensive Comparison of the Combustion Behavior for Low-Temperature Combustion of n-Nonane. ACS Omega 2020, 5, 4924–4936. 10.1021/acsomega.9b03786. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Atef N.; Kukkadapu G.; Mohamed S. Y.; et al. A comprehensive iso-octane combustion model with improved thermochemistry and chemical kinetics. Combust. Flame 2017, 178, 111–134. 10.1016/j.combustflame.2016.12.029. [DOI] [Google Scholar]
  23. Li Y.; Zhou C. W.; Somers K. P.; et al. The Oxidation of 2-Butene: A High Pressure Ignition Delay, Kinetic Modeling Study and Reactivity Comparison with Isobutene and 1-Butene. Proc. Combust. Inst. 2017, 36, 403–411. 10.1016/j.proci.2016.05.052. [DOI] [Google Scholar]
  24. Petersen E. L.; Kalitan D. M.; Simmons S.; et al. Methane/Propane Oxidation at High Pressures: Experimental and Detailed Chemical Kinetic Modelling. Proc. Combust. Inst. 2007, 31, 447–454. 10.1016/j.proci.2006.08.034. [DOI] [Google Scholar]
  25. Townend D. T. A.; Chamberlain E. A. C. The influence of pressure on the spontaneous ignition of inflammable gas-air mixtures – IV-methane-, ethane-, and propane-air mixtures. Proc. R. Soc. London, Ser. A 1936, 154, 95–112. 10.1098/rspa.1936.0039. [DOI] [Google Scholar]
  26. Hashemi H.; Jacobsen J. G.; Rasmussen C. T.; et al. High-pressure oxidation of ethane. Combust. Flame 2017, 182, 150–166. 10.1016/j.combustflame.2017.03.028. [DOI] [Google Scholar]
  27. Naik C. V.; Dean A. M. Detailed kinetic modeling of ethane oxidation. Combust. Flame 2006, 145, 16–37. 10.1016/j.combustflame.2005.12.006. [DOI] [Google Scholar]
  28. Bai S.; Davis M. J.; Sivaramakrishnan R.; et al. A chemical pathway perspective on the kinetics of low-temperature ignition of propane. Combust. Flame 2019, 202, 154–178. 10.1016/j.combustflame.2019.01.006. [DOI] [Google Scholar]
  29. Hashemi H.; Christensen J. M.; Harding L. B.; et al. High-pressure oxidation of propane. Proc. Combust. Inst. 2019, 37, 461–468. 10.1016/j.proci.2018.07.009. [DOI] [Google Scholar]
  30. Ji W.; Zhao P.; He T.; et al. On the controlling mechanism of the upper turnover states in the NTC regime. Combust. Flame 2016, 164, 294–302. 10.1016/j.combustflame.2015.11.028. [DOI] [Google Scholar]

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES