COVID-19 indoor exposure levels: An analysis of foot traffic scenarios within an academic building

Abstract

Minimizing all aspects of COVID-19 exposure is a high priority as universities prepare to reopen. One of those aspects includes developing protocols for interior spaces such as academic buildings. This paper applies mathematical modeling to investigate different virus exposure levels due to traffic patterns within academic buildings. The assumption used are: 1) Risk of infection is a product of exposure rate and time and 2) the exposure rate decreases with distance. One-way vs. two-way pedestrian traffic scenarios within hallways were modeled and analyzed for various configurations. The underlying assumption that a small exposure to a large number of people is similar to a large exposure to a few people is the driver to minimize exposures levels in all aspects. The analysis indicates that minimizing the time spent in passing between classes is the driving factor in minimizing risk, and one-way traffic may increase the time required to pass between classes. While the case presented is limited, the modeled approaches are intended to provoke future research that can be extended and applied to larger populations to help provide decision makers with more rigorous tools to shape future policies regarding traffic flow within buildings.

Highlights

• •This paper analyzes foot traffic scenarios within an academic building.
• •A case model allows comparison of one-way vs. two-way indoor traffic.
• •This case can provoke further study of COVID-19 exposure levels within buildings.

1. Introduction

In the near future, as university administrators prepare for the return of students to physical campuses, developing protocols for interior spaces in academic classroom buildings will be a necessity. One of several challenges to be addressed involves factoring in social distancing guidelines as applied to building features that are typically designed with minimal distance, such as corridors. While universities may follow some of the same social distancing policies several workplaces are adopting, including one-way traffic in corridors, scientific evidence regarding most ideal foot traffic scenarios within buildings is lacking.

The literature includes limited studies analyzing the impacts of a virus within indoor environments. Most of the existing studies focus on medical spaces such as hospitals and dental offices (Fiorillo et al., 2020; Yen et al., 2020). Other research has included analysis of exposure levels within correctional facilities (Barnert et al., 2020; Irvine et al., 2020) or aboard cruise ships (Liu et al., 2020; Mizumoto and Chowell, 2020). A few works that have investigated virus impacts within confined indoor environments such as workplaces or schools have taken a broad-brush approach and reviewed evidence of social distancing impacts (Ahmed et al., 2018).Others raised questions about public space design through a larger lens that included outdoor spaces such as sidewalks, streets, and public transportation (Honey-Roses et al., 2020).

Studies with a narrower focus have examined the physics of airborne droplets and airflow patterns (Mittal et al., 2020; Robinson et al., 2012). Dietz et al., 2020 modeled the spatial connectivity of microbes within a confined space, factoring in ventilation and humidity, while Fiorillo et al., 2020 studied surface contacts. Two papers focus on modeling exposure within confined spaces, specifically looking at scenarios of pedestrian exposure within a building. The goal of one of those two studies, Ronchi and Lovreglio (2020), was to offer an occupant exposure model that can be combined with crowd modeling to help develop metrics for risk assessments. The other paper, Goscé et al. (2014) earlier analytical modeling of disease spread, used a corridor scenario to study the dependence of contact rate on crowd behavior. Their findings suggested that infection rate “at a population scale has an analytically tractable non-linear dependency on crowd density” (p. 1).

Big box retailers have implemented foot traffic protocols within their stores that restrict pedestrian traffic to a one way direction within aisles. Such an approach is based not on scientific study but on conjecture. When developing protocols directing foot traffic within buildings, it is preferable to consider the results of mathematical study. Traffic flow in classroom buildings is somewhat unique in that there are short periods of congestion followed by long periods of limited traffic flow. The simple case model offered here is intended to establish a baseline to compare one-way vs, two-way traffic within classroom buildings and can provoke further study of exposure levels within buildings on a larger scale. This study applies mathematical analysis to investigate both one-way and two-way pedestrian traffic patterns within an academic building.

2. Methods

This analysis draws on the rules of thumb used by the Health Physics community that have been developed over the past century (Cember and Johnson, 2009). Specifically, risk is dependent on the factors of time, distance, and shielding, and the exposure rate falls off as a function of 1/r².

2.1. Assumptions

This study relies on multiple assumptions. The fundamental assumption is that the longer the time spent near an infected person, the more the risk is increased. Further, a long exposure at a distance can have a comparable risk as does a short exposure at a close distance. Also, subjects are complying with proper social distancing rules such as the WHO-recommendation of six-foot separation when possible and the wearing of face coverings. An additional assumption underlying this case is that no additional shielding is used and that the masks are not N95 medical masks. Finally, exposure rate α (risk per unit time) is normalized at six feet from a point source for comparison purposes, i.e. Risk = α ∗ t where $\alpha =\frac{6^2}{x^2}$ per unit time is the exposure rate and x is the distance between subjects, therefore Risk per unit time at 6 ft = $\frac{6^2}{6^2}$ = 1.

3. Two student case

Before looking at a congested case it will be helpful to consider the simplest case of only two students in a hallway.

This section uses modeling of one-way and two-way pedestrian traffic within a one-dimensional corridor for the case of two students. This case is depicted in Fig. 1 , which shows the four configurations analyzed; one-way 6, 10 and 15 ft separation and the two-way configuration where the distance is changing with time. From those insights, this study is designed to inform understanding that could later be applied to larger populations within more crowded scenarios.

Fig. 1.

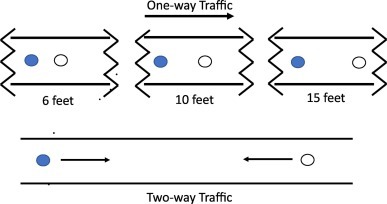
One dimensional traffic.

3.1. One-way pedestrian traffic

For the unidirectional scenario, individuals are assumed to walk at a constant rate V and the distance to the exit is L. Therefore, the transit time is given by t = L/V. Individuals are also assumed to maintain a separation of 6, 10, and 15 ft. while exiting. Since risk = exposure rate ∗time we get the risk levels presented in Table 1 (remembering that the exposure rate at 6 ft. is defined as 1 and we assume that the exposure rate is a function of $\frac{1}{r^2}$).

Table 1.

One-way indoor pedestrian traffic.

Separation	Exposure rate	Risk (t = 10)
6 ft	1	10
10 ft	0.36	3.6
15 ft	0.16	1.6

3.2. Two-way pedestrian traffic

Applying the above assumptions, the equation for two-way pedestrian traffic is:

$$R=2{\int }_0^t\mathit{Exposure\; rate}\mathit{dt}+1\ast 12/V.$$

Since Exposure rate = α

$$R=2{\int }_0^t\alpha \mathit{dt}+1\ast 12/V$$ (1)

The first term on the right-hand side of this equation (2∫₀ ^t α dt) represents the Risk accumulated while the subjects approach each other (the integral is multiplied by 2 to account for the exposure as the two subjects move away from each other), and the second term (1∗12/V) represents the Risk accumulated while the subjects are within the WHO-recommended guideline of 6 ft from each other.

The equation for the distance between subjects, x, is represented as

$$x=L-V\ast t\to t=\frac{L-x}{V}\to \mathit{dt}=\frac{-1}{V}\mathit{dx}\text{and when}\mathrm{t}=0,x=L,$$

when $x=6,t=\frac{L-6}{V.}$therefore

$$R=2{\int }_L^6\frac{-36}{V{x}^2}\mathit{dx}=2\ast \frac{36}{V}\left[\frac{1}{6}-\frac{1}{L}\right]+1\ast 12/V$$ (2)

For two-way traffic let's assume L = 50 and V = 5 (transit time of 10), then the risk (as calculated from Eq. (2)) is 4.5 or equivalent to a 9 ft. separation condition for one-way traffic. This one- dimensional two student analysis shows that the Risk may not be reduced when using one-way traffic patterns in classroom buildings. For the case analyzed here, the one-way traffic with 6-ft separation (R = 10) yielded a higher risk than the two-way case (R = 4.5). It should be noted that this analysis only provides the relative risk between the different cases studied and should only be used to compare one case to another and should not be considered a measure of the absolute risk.

4. Infinite line of students

Juxtaposed to the two student case is an infinite line of students. Here we use this analysis to determine the effect of a crowded hallway during a transit period.

4.1. One-way pedestrian traffic

Consider an infinite line of students, walking along the hall, all properly socially spaced at 6 ft apart. Thus, an individual has someone 6 ft ahead and 6 ft behind, 12 ft ahead and 12 ft behind, etc. If risk is proportional to time of exposure divided by distance squared, an individual's risk per time is

$$2\alpha \sum _{j=1}^{\infty }\frac{1}{{\left(6j\right)}^2}=\frac{\alpha {\pi }^2}{108}\cong 0.0914\alpha =3.29,$$

where we have normalized to risk per time as 1 at a distance of 6 ft.

Therefore, the risk per unit time to an individual in an infinite line with 6-ft spacing is 0.0914 α. To determine the risk for one-way traffic, simply multiply by the time spent in transit.

4.2. Two-way pedestrian traffic

Now consider another similar line of students, but walking the other direction in the hall, with 4 ft between the two lines; this is a case where the physical dimensions of the hallway do not allow for a 6-ft separation. The distance between these students and the above-cited individual waking in the opposite direction is changing with time. Applying the assumption that both lines of pedestrians are walking at 1 ft per unit of time, and considering all distances relative to some particular individual, the distances are

$$\sqrt{4^2+{\left(6k-2t\right)}^2}$$

thus, the risk per time is

$$\alpha \sum _{-\infty }^{\infty }\frac{1}{16+{\left(6k-2t\right)}^2}=\alpha \frac{cosh\left(\frac{2\pi }{3}\right)\pi sinh\left(\frac{2\pi }{3}\right)}{24{\left(cosh\left(\frac{2\pi }{3}\right)\right)}^2-24{\left(cos\left(\frac{\mathit{\pi t}}{3}\right)\right)}^2}.$$

This is 3-periodic, so when integrated from t = 0 to 3 the model arrives at

$$\left(sinh\left(\frac{2\pi }{3}\right)\pi \left(\sqrt{2cosh\left(\frac{4\pi }{3}\right)-2}+2\sqrt{cosh{\left(\frac{2\pi }{3}\right)}^2-1}\right)\right)/\left(16\sqrt{cosh{\left(\frac{2\pi }{3}\right)}^2-1}\sqrt{2cosh\left(\frac{4\pi }{3}\right)-2}\right)$$

Or, ≅0.3927α. The risk from pedestrians traveling in the same direction over a period of 3 time units is ≅3 ∙ (0.0914α) = 0.2742α. Thus, the total risk is 2.432 times as high for two-way traffic as for one-way, for the same amount of time. It is worth noting that if the hallway parameters are changed and widened to allow two lines of traffic to be 6 ft apart, the risk from pedestrians going the opposite way is 0.2672α, which is slightly less than from those going the same way.

However, one-way traffic requires individuals to travel a longer distance. Assume a 120 ft long building, with three classrooms. This building has doors at 20, 60, and 100 ft along the hall, and a door at each end. In this case one way traffic would require individuals to walk the full length of the hall, so 120 time units. Taking the shortest path (possible only with two-way traffic) would be the same for those in the middle room, but only 40 time units for those in the two ends. If all pedestrians are required to leave by the same door, with one direction of traffic on a different floor which has the same arrangement of classrooms, the one-way traffic time of travel would be 240 units. The two-way travel times would be 40, 120, and 200 for each floor.

5. Discussion/conclusion

As pandemic response protocols are being developed on university campuses, student foot traffic within academic buildings is one of many factors to consider. While big box retailers have chartered a path of restricting pedestrian traffic flow in store aisles to be unidirectional, there is no evidence that this pattern is preferable or universally applicable to all indoor scenarios. The analysis presented in this paper of one-way and two-way foot traffic scenarios within building corridors can be used to evaluate different pedestrian traffic patterns in an academic building setting. The strategy of restricting foot traffic in building corridors to be unidirectional, although it reduces the exposure per unit time, often increases the time spent in the hall, more than canceling out the reduction.

The simple one-dimensional case of two students shows one-way traffic separation would have to be increased by 50% (9 ft. vs 6 ft) to produce the same relative risk as two-way traffic. This is caused by the students staying in relatively close contact when traveling in the same direction, while the distance between students traveling in opposite directions changes with time. When considering an infinite line of students, the width of the hallway, or ability of the traffic to properly social distance becomes important. For the two-way scenario analyzed, a 4 ft. separation yielded a higher risk per unit time than the one-way scenario, while a 6 ft. separation yielded a slightly lower risk per unit time. This section of the analysis is based on risk per unit time which means that the overall magnitude of the relative risk is dependent on the time spent in passing. This result suggests that the time spent in passing is more important than the traffic flow patterns when trying to minimize risk.

From these scenarios we draw two fundamental conclusions:

• 1)narrow hallways should be considered for one-way traffic, while wide hallways should be considered for two-way traffic

and

• 2)the time spent in passing through a hallway should be minimized.

This study is in agreement with Goscé et al.'s (2014) study indicating that crowd density plays a major factor. Practical application of this study's results includes the suggestion that for students passing between classes, a staggered schedule can be used to lower the crowd density. Also, extending the time between classes would allow for an exit period where the students would leave the building followed by an entrance period when the students would enter.

While this study is limited to focusing on student traffic within academic buildings, the conclusions offered may have application when considering pedestrian traffic inside of other settings including retail stores. Typically, pathways within retain stores do not lend themselves to proper social distancing and the traffic does not flow at a constant rate. Through further research, these factors within each environment should be analyzed and used to inform policies designating traffic flow patterns.