Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Jul 15;124(33):7093–7101. doi: 10.1021/acs.jpcb.0c05229

Mechanisms of Airborne Infection via Evaporating and Sedimenting Droplets Produced by Speaking

Roland R Netz 1
PMCID: PMC7409921  PMID: 32668904

Abstract

graphic file with name jp0c05229_0007.jpg

For estimating the infection risk from virus-containing airborne droplets, it is crucial to consider the interplay of all relevant physical-chemical effects that affect droplet evaporation and sedimentation times. For droplet radii in the range 70 nm < R < 60 μm, evaporation can be described in the stagnant-flow approximation and is diffusion-limited. Analytical equations are presented for the droplet evaporation rate, the time-dependent droplet size, and the sedimentation time, including evaporation cooling and solute osmotic-pressure effects. Evaporation makes the time for initially large droplets to sediment much longer and thus significantly increases the viral air load. Using recent estimates for SARS-CoV-2 concentrations in sputum and droplet production rates while speaking, a single infected person that constantly speaks without a mouth cover produces a total steady-state air load of more than 104 virions at a given time. In a midsize closed room, this leads to a viral inhalation frequency of at least 2.5 per minute. Low relative humidity, as encountered in airliners and inside buildings in the winter, accelerates evaporation and thus keeps initially larger droplets suspended in air. Typical air-exchange rates decrease the viral air load from droplets with an initial radius larger than 20 μm only moderately.

1. Introduction

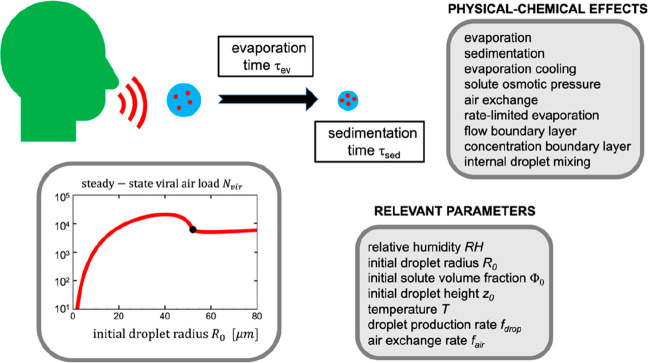
For understanding airborne viral infection pathways, the sedimentation properties of saliva droplets that contain nonvolatile solutes and are subject to gravitational force, evaporation, and evaporation cooling are crucial. The typical considered droplet radii are less than 5 μm, because such droplets stay floating in air for many minutes even in the absence of evaporation. Aspects of this problem have been treated in previous experimental and theoretical works.1−13 Based on empirical expressions for the radius dependence of droplet evaporation and sedimentation times, Wells suggested that droplets with a radius smaller than 50 μm completely evaporate before falling to the ground and stay sedimenting as so-called droplet nuclei for a long time.2 In a seminal contribution, Duguid studied droplet sizes produced by humans sneezing, coughing, and speaking from microscopic analysis of marks left on slides and found droplet radii between 1 and 500 μm.3 In fact, 95% of all particles had radii below 50 μm, and most final droplet radii were around 5 μm. Later studies basically confirmed these results and showed that, in addition, many droplets are produced in the submicron radius range during coughing and speaking.14−19 In a few studies, multimodal droplet size distributions were found,20,21 which has been rationalized in terms of distinct physiological droplet production mechanisms. In other studies, it was shown that the number of droplets produced while speaking depends on the voice loudness22 and that droplet production while exhaling is the product of complex fluid fragmentation processes.23 Recently, a much more sensitive method, time-resolved laser-light scattering, showed that far more droplets are produced than could be detected previously,24,25 which demonstrates that the measured droplet radius distribution depends on the size sensitivity of the measurement technique used and also on the time droplets spend in air before measurement. The process of evaporation and sedimentation of saliva droplets involves diverse physical-chemical effects, such as high Reynolds number effects for large droplets, finite evaporation rate effects for small droplets, evaporation cooling effects, and osmotic pressure effects due to the presence of dissolved solutes. These effects are controlled by a large number of relevant parameters such as the initial droplet radius, the initial height at which droplets are produced, the ambient temperature, the relative humidity, and the initial solute volume fraction, as schematically shown in Figure 1. The prevalent theoretical strategy in the literature has been to deduce empirical relations or to numerically simulate evaporation and heat fluxes for selected parameter values. However, in order to estimate in the complete parameter space the number of virions that sediment in air given a certain droplet production rate and a finite air-exchange rate in ventilated rooms, analytical formulas for the droplet evaporation and sedimentation times that explicitly depend on all relevant system parameters are crucial.

Figure 1.

Figure 1

Open in a new tab

Overview over various physical-chemical effects and relevant parameters that control the evaporation and sedimentation times of saliva droplets and the viral air load due to speaking. The graph shows the steady-state number of virions sedimenting in air as a function of the initial radius of produced droplets due to a single infected person that constantly speaks and RH = 0.5, Φ0 = 0.01, z0 = 2 m, T = 25 °C, fdrop = 1000 s–1, and fair = 10 h–1.

In this paper, the physical-chemical mechanisms of evaporation and sedimentation of droplets with radii in the range from nm to a few hundred μm are considered, which is the range potentially relevant for airborne viral infection routes.26−29 The analytical calculations include the interplay of all relevant physical effects: (i) the finite evaporation reaction rate at the droplet surface, (ii) the effects of relative humidity, (iii) concentration-boundary as well as flow-boundary layers, (iv) droplet cooling due to the large evaporation enthalpy of water, and (v) the water vapor pressure reduction due to the presence of nonvolatile solutes (including virions) in the droplet. Analytical expressions for the evaporation rate, the time-dependent droplet radius, and the sedimentation time are derived in all relevant radius regimes as a function of all relevant parameters, from which estimates for the viral air load from speaking and the virion inhalation frequency in closed rooms including air exchange due to ventilation are derived.

Evaporation effects are typically treated on the level of the diffusion equation in the stagnant air approximation, i.e., neglecting the flow field around the droplet, and in the diffusion-limited evaporation regime. As shown here, this approximation is only accurate for droplet radii in the range 70 nm < R < 60 μm. Evaporation cooling is important and reduces the droplet surface temperature by about 10 K at a relative humidity (RH) of 0.5, which significantly slows down evaporation. For radii larger than 60 μm, the air flow around the droplet speeds up the evaporation process and at the same time becomes non-Stokesian due to nonlinear hydrodynamics effects, which is treated analytically by double-boundary-layer theory including concentration and flow boundary layers. For radii smaller than 70 nm, the evaporation at the droplet–air interface becomes reaction-rate-limited. For these small droplets, the evaporation rate is not limited by the speed with which water molecules diffuse away from the droplet surface but rather by the rate at which water evaporates from the liquid surface.

In the presence of evaporation, the sedimentation time is mainly determined by the final dried-out droplet radius, which depends on the relative humidity and the initial solute concentration. Evaporation makes large droplets remain in air much longer and thus significantly increases the airborne viral load. Using recent estimates of the SARS-CoV-2 concentration in sputum30 and droplet production rates while speaking,24,25 a single person that is infected and speaks constantly without a mouth cover is predicted to produce a steady-state airborne viral air load of more than 104 virions at a given time. In a midsize closed room, this will result in a virion inhalation frequency by a passive bystander of at least 2.5 per minute, which is for initial droplet radii larger than 20 μm only moderately reduced by air-exchange rates in the typical range of up to about 20 h–1. The quest for quantitative estimates of airborne viral infection risks still faces many challenges but also provides highly relevant future research directions, as highlighted in this Perspective.

2. Results

Droplet Sedimentation and Diffusion without Evaporation

It is useful to first recapitulate a few well-known basic equations in the absence of droplet evaporation. By balancing the Stokes friction with the gravitational force, proportional to the acceleration g, that acts on a droplet with radius R and mass density ρ, the mean sedimentation time (see Supporting Information section A) is

graphic file with name jp0c05229_m001.jpg 1

where the Stokes expression is used for the droplet diffusion constant DR = kBT/(6πηR), the droplet mass is given by m = 4πR3ρ/3, and values for the gravitational constant g, viscosity of air η, water density ρ, and thermal energy kBT at 25 °C are given in Table 1. The numerical prefactor in eq 1 turns out to be φ = 0.85 × 10–8 m s. For a droplet with radius R = 5 μm placed initially at a height of z0 = 2 m, the sedimentation time is τsed = 680 s = 11 min; other numbers are given in Table 2. The droplet radius R = 5 μm is often defined as a threshold radius below which the sedimentation time is sufficiently long to be considered relevant for infections. An exact calculation of the sedimentation time distribution is given in Supporting Information section A, which shows that the relative standard deviation of the mean sedimentation time is small for droplet radii larger than R = 10 nm. Thus, the mean sedimentation time, τsed in eq 1, is a good estimate of typical sedimentation times for all droplets with R > 10 nm.

Table 1. List of Numerical Constants Used45.

kBT thermal energy 4.1 × 10–21 J at 25 °C
η viscosity of air 1.85 × 10–5 kg/ms at 25 °C
η viscosity of air 1.73 × 10–5 kg/ms at 0 °C
ρ liquid water density 997 kg/m3 at 25 °C
g nominal gravitational constant 9.81 m/s2
Dw water diffusion constant in air 2.5 × 10–5 m2/s at 25 °C
Dw water diffusion constant in air 2.2 × 10–5 m2/s at 0 °C
Dwl water diffusion constant in liquid water 2.3 × 10–9 m2/s at 25 °C
mw water molecular mass 2.99 × 10–26 kg
vw liquid water molecular volume 3.00 × 10–29 m3 at 25 °C
vw liquid water molecular volume 2.99 × 10–29 m3 at 4 °C
cg saturated vapor water concentration 7.69 × 1023 m–3 at 25 °C
cg saturated vapor water concentration 1.62 × 1023 m–3 at 0 °C
Pvap water vapor pressure 3169 Pa at 25 °C
Pvap water vapor pressure 611 Pa at 0 °C
ρair density of air 1.18 kg m–3 at 25 °C
ν kinematic air viscosity 1.6 × 10–5 m2/s at 25 °C
kc condensation reaction rate coefficient 370 m/s
aair air thermal diffusivity 2.1 × 10–5 m2/s at 25 °C
aw liquid water thermal diffusivity 1.4 × 10–7 m2/s at 20 °C
hev molecular evaporation enthalpy of water 7.3 × 10–20 J at 25 °C
hev molecular evaporation enthalpy of water 7.5 × 10–20 J at 0 °C
hm molecular melting enthalpy of water 1.0 × 10–20 J at 0 °C
Cpl molecular heat capacity of liquid water 1.3 × 10–22 J/K at 20 °C
λair heat conductivity of air 0.026 W/mK at 25 °C
λair heat conductivity of air 0.024 W/mK at 0 °C
Open in a new tab

Table 2. List of Representative Sedimentation and Evaporation Timesa.

R0 (μm) 1 2.5 5 10 20 30 40 55
τsed (RH = 1) 5 h 45 min 11 min 170 s 43 s 19 s 11 s 5.6 s
τev (RH = 0.5) 0.0048 s 0.030 s 0.12 s 0.48 s 1.9 s 4.3 s 7.7 s 14.5 s
τsedRH (RH = 0.5) ∞ ∞ ∞ ∞ ∞ ∞ ∞ 7.6 s
τsedsol (RH = 0.5) 64 h 10 h 154 min 38 min 9 min 231 s 99.6 s 7.6 s
Open in a new tab
a

R0 denotes the initial droplet radius. τsed (RH = 1) is the sedimentation time from a height of 2 m without evaporation. τev (RH = 0.5) is the evaporation time at a relative humidity of RH = 0.5 in the absence of nonvolatile solutes in the droplet. τsedRH (RH = 0.5) is the sedimentation time in the absence of nonvolatile solutes at a relative humidity of RH = 0.5 from a height of 2 m. τsed (RH = 0.5) is the sedimentation time from a height of 2 m at a relative humidity of RH = 0.5 in the presence of an initial volume fraction Φ0 = 0.01 of nonvolatile solutes in the droplet.

Inertial effects due to the acceleration of a droplet that is initially at rest occur over the acceleration time, which is

graphic file with name jp0c05229_m002.jpg 2

where the numerical prefactor is given by ξ = 1.2 × 107 s m–2. Even for large droplets with R = 100 μm, the acceleration time is τacc = 0.12 s, showing that droplets rapidly reach their terminal velocity, so that acceleration effects can be safely neglected in the relevant radius regime.

The lateral diffusion length during the time a droplet is sedimenting in stagnant air is readily estimated. For this, the mean-squared diffusion length at the mean sedimentation time is calculated from xdiff2 = 2DRτsed. Inserting the mean sedimentation time from eq 1 results in 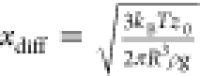Inline graphic, which for z0 = 2 m yields xdiff = 0.63 mm for a droplet of radius R = 1 μm and xdiff = 2.0 cm for a droplet of radius R = 100 nm. The lateral diffusion of droplets with radii in the micrometer range during their sedimentation time is, therefore, very limited and will be dominated by the initial emission speed, air flow, and convection effects.

Droplet Evaporation without Nonvolatile Solutes

The effect of evaporation decreases the droplet radius during its descent to the ground and therefore increases the sedimentation time. For evaporation of a droplet at rest, which defines the so-called stagnant-flow approximation, the time-dependent shrinking of the radius occurs in the diffusion-limited evaporation scenario, which is valid for radii larger than R = 70 nm, and is given by (see Supporting Information sections B and C)

graphic file with name jp0c05229_m004.jpg 3

Here R0 is the initial droplet radius and the numerical prefactor is given by

graphic file with name jp0c05229_m005.jpg 4

where θ has units of a diffusion constant. The values for the water diffusion constant in air Dw, the liquid water molecular volume vw, and the saturated water vapor concentration cg at room temperature 25 °C are given in Table 1. RH denotes the relative air humidity. The reduction of the water vapor concentration at the droplet surface due to evaporation cooling is described by the linear coefficient εC according to cgsurf ≈ cg(1 – εCΔT). Here cg denotes the water vapor concentration at the droplet surface, which has a temperature that is reduced compared to the ambient air (at a temperature 25 °C) by ΔT. The linear coefficient is given by εC = 0.032 K−1 (see Supporting Information section C). The value of the temperature reduction at the droplet surface is obtained by solving the coupled heat flux and water diffusion flux equations in a self-consistent manner and turns out to be linearly related to the relative humidity as 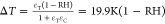Inline graphic, where the coefficient εT is given by Inline graphic (see Supporting Information section C). Interestingly, at zero relative humidity, RH = 0, the droplet surface is cooled by about 20 K: While the cooling effect is quite significant, droplet freezing does not occur at room temperatures above 20 °C (at lower temperatures, evaporation-induced freezing can very well occur and slow down evaporation even more). The factor in eq 4 that accounts for the evaporation cooling effect is given by Inline graphic, so cooling considerably slows down the evaporation process and cannot be neglected (see Supporting Information sections B and C for the derivation of eq 3). If the radius becomes smaller than 70 nm before the end of the drying process, a crossover to the reaction-rate-limited evaporation regime takes place, as is discussed in Supporting Information section D. For radii larger than 60 μm, the flow around the droplet speeds up the evaporation process and at the same time becomes non-Stokesian due to nonlinear hydrodynamics effects, which can be treated analytically by double-boundary-layer theory including concentration and flow boundary layers,31 as discussed in Supporting Information sections E, F, G, H, and I. Internal mixing due to diffusion inside the droplet is sufficiently fast for droplet radii below roughly 100 μm, and concentration inhomogeneities can be approximately neglected (see Supporting Information section J). It transpires that the stagnant-flow approximation used to derive eq 3 is valid for the initial radius range between 70 nm and 60 μm, which includes the range that produces the largest viral air load, as will be shown below.

From eq 3, it is seen that the decrease in the radius starts slowly and accelerates with time; it is therefore dominated by the initial stage of evaporation. Because of this, the time for evaporation down to a radius at which osmotic effects due to dissolved solutes (including virions) within the droplet balance the water vapor chemical potential, can be approximated as the time needed to reduce the droplet radius to zero, from eq 3 given by

graphic file with name jp0c05229_m009.jpg 5

This relation has been used by Wells in his classical work,2 but the chosen prefactor was different due to the neglect of evaporation cooling effects. Notably, the evaporation time in eq 5 increases quadratically with the initial droplet radius R0, while the sedimentation time in eq 1 decreases inversely and quadratically with the radius. Thus, at a relative humidity of RH = 0.5, a common value for room air, a droplet with an initial radius of R0 = 10 μm has an evaporation time of τev = 0.48 s but needs (neglecting the reduction of the radius) τa = 170 s to sediment to the ground. Consequently, it will dry out and stay floating for an even longer time, depending on its final dry radius. Other numerical examples for evaporation times are given in Table 2.

To accurately calculate the critical initial radius below which a droplet completely dries out before falling to the ground, one needs to take into account that evaporation changes the diffusion constant and the gravitational force during sedimentation. As detailed in Supporting Information section B, the sedimentation time in the presence of evaporation and a finite relative humidity RH < 1 is given by

graphic file with name jp0c05229_m010.jpg 6

By inserting eq 5 into eq 6, it is seen that in the limit RH = 1 the result of eq 1 is recovered. The critical radius is defined by the initial radius for which the droplet radius just vanishes as it hits the ground; it follows from equating eqs 5 and 6 as

graphic file with name jp0c05229_m011.jpg 7

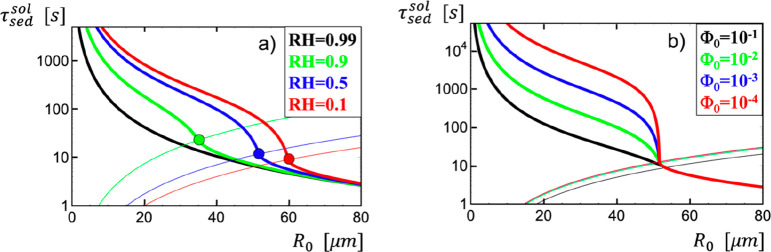
and is similar to the law established by Wells2 by simply equating the sedimentation and evaporation times. For RH = 0.5 and z0 = 2 m, one obtains R0crit = 52 μm: All droplets smaller than R0 = 52 μm will dry out before they hit the ground. In the absence of nonvolatile solutes, the droplets will thus disappear for radii smaller than R0crit. In airliners, the relative humidity is substantially lower than 0.5; in fact, for completely dry air with RH = 0, the critical radius predicted by eq 7 increases to R0 = 61 μm. Note that the results presented here hold in still air; in ventilated rooms, convection due to air circulation will prevent some droplets from falling to the ground for a long time. Figure 2 shows droplet sedimentation times τsedRH as a function of the initial radius R0 according to eq 6 for an initial height of z0 = 2 m for different relative humidities. In the limit RH = 1, no evaporation takes place and the result of eq 1 is recovered (thick black line). As the initial radius approaches the critical radius R0, given by eq 7 and indicated by a broken line, the droplet disappears. The thin solid colored lines denote the evaporation times according to eq 5; the crossing of the evaporation and sedimentation times happens at the critical radius. The qualitative shape of these curves has been empirically established by Wells.2

Figure 2.

Figure 2

Open in a new tab

Sedimentation time of droplets τsedRH in the presence of evaporation as a function of the initial radius R0 in the absence of nonvolatile solutes according to eq 6 for an initial height of z0 = 2 m. Results are shown for different relative humidities. In the limit RH = 1, no evaporation takes place and the result in eq 1 is recovered (thick black line). As the initial radius approaches the critical radius R0, given by eq 7 and indicated by a black broken line, the droplets disappear (indicated by vertical broken lines). The thin solid colored lines denote the evaporation time (eq 5).

Droplet Evaporation in the Presence of Nonvolatile Solutes

The presence of nonvolatile solutes in the initial droplet produces a lower limit for the droplet radius that can be reached by evaporation. Saliva contains a volume percentage of about 99.5% water;32 the radius of a saliva droplet thus can maximally shrink by a factor of 2001/3 = 5.8. Some of the water will stay inside the final droplet because of hydration effects. Assuming that the final state keeps 50% strongly bound hydration water, the droplet can thus maximally shrink by a factor of 1001/3 = 4.6 and the concentration of nonvolatile solutes (including virions) increases by a factor of 100. Solutes in the droplet decrease the water vapor pressure and therefore limit the droplet radius in evaporation equilibrium according to (see Supporting Information section K)

graphic file with name jp0c05229_m012.jpg 8

Here, R0 is the initial radius and Φ0 is the initial volume fraction of solutes, including strongly bound hydration water. Only for RH = 0 does a droplet dry out to the minimal possible radius of Rev = R0Φ01/3; for finite relative humidity, the droplet in evaporation equilibrium is characterized by a solute volume fraction of Φev = 1 – RH. As an example, for RH = 0.5, the free water and solute (including hydration water) volume fractions in the equilibrium state equal each other. Equation 8 is modified for solutes that perturb the water activity, but for most solutes, nonideal water solution effects can be neglected.

Taking into account the water vapor pressure reduction during the evaporation process, the radius-dependent evaporation time, which is the time it takes for the droplet radius to decrease from its initial value R0 to R, is given by

graphic file with name jp0c05229_m013.jpg 9

as derived in Supporting Information section K. Using a very accurate yet simple approximation for the scaling function Inline graphic, eq 9 can be written as

graphic file with name jp0c05229_m015.jpg 10

where τev denotes the evaporation time defined in eq 5. This expression demonstrates the logarithmic osmotic slowing down of the evaporation process due to the decreasing droplet water concentration as the droplet radius R approaches the equilibrium droplet radius Rev. Neglecting this kinetic slowing down, which is represented by the last term in eq 10, one obtains the limiting result

graphic file with name jp0c05229_m016.jpg 11

From this, an approximate expression for the evaporation time in the presence of solutes follows by setting R = Rev as

graphic file with name jp0c05229_m017.jpg 12

which for small initial solute concentrations represents a minor correction to the evaporation time given by eq 5.

Figure 3 shows the rescaled evaporation time as a function of the reduced droplet radius according to eq 9 as black lines. The presence of solutes only becomes relevant for droplet radii that are close to the final equilibrium radius Rev and gives rise to a divergent evaporation time. Except for this final stage of evaporation, the formula eq 11 (red lines) describes the evaporation very accurately and will be used for all further calculations.

Figure 3.

Figure 3

Open in a new tab

Scaling plot of the evaporation time t(R) as a function of the droplet radius R in the presence of solutes according to eq 9 (black lines). In part a, the ratio of the initial droplet radius to the final equilibrium radius is Inline graphic, and in part b, this ratio is Inline graphic. The red lines show the evaporation time when the water vapor pressure reduction is neglected (eq 11); the blue lines show the approximation (eq 10). The solute-induced water vapor pressure reduction becomes significant only for radii close to the final equilibrium radius Rev and leads to a diverging evaporation time.

The sedimentation of not too large droplets thus can approximately be split into two stages: In the first stage, the droplets shrink down to a radius given by eq 8, and in a second stage, the droplets sediment for an extended time with a fixed radius. The total sedimentation time follows as (see Supporting Information section K)

graphic file with name jp0c05229_m018.jpg 13

For droplets that are so large that they do not reach the radius Rev before they hit the ground, eq 6 describes the sedimentation time very accurately.

In Figure 4a, the droplet sedimentation time τsedsol is plotted as a function of the initial radius R0 in the presence of nonvolatile solutes with an initial solute volume fraction of Φ0 = 0.01 and an initial height of z0 = 2 m according to eq 13 for a few different relative humidities. For RH = 0.99, no evaporation takes place for Φ0 = 0.01, as follows from eq 8, and the result of eq 1 is recovered (thick black line). The thin solid colored lines denote the evaporation time (eq 12). For small droplet radii, sedimentation is a two-stage process; droplets first evaporate down to the equilibrium radius Rev and then stay floating in air for an extended time. Large droplets do not reach Rev before they hit the ground; the transition between these two scenarios is illustrated by filled circles. In Figure 4b, the droplet sedimentation time τsed is plotted for fixed relative humidity RH = 0.5 and different initial solute volume fractions Φ0. Figure 4 illustrates that the sedimentation times are significantly increased due to evaporation. In fact, as shown in Table 2, for a relative humidity of RH = 0.5 and Φ0 = 0.01, the sedimentation times of droplets increase for not too large radii by more than a factor of 10 due to evaporation.

Figure 4.

Figure 4

Open in a new tab

(a) Sedimentation time of droplets τsedsol as a function of the initial radius R0 in the presence of nonvolatile solutes with initial volume fraction Φ0 = 0.01 (which includes strongly bound hydration water) according to eq 13, for an initial height of z0 = 2 m. Results are shown for different relative humidities; in the case RH = 0.99, no evaporation takes place, and the result (eq 1) is recovered (thick black line). The thin solid colored lines denote the evaporation time (eq 12). (b) Sedimentation time of droplets τsed as a function of the initial radius R0 for fixed relative humidity RH = 0.5 and an initial height of z0 = 2 m in the presence of nonvolatile solutes with different initial volume fractions Φ0 according to eq 13.

Steady-State Number of Virions Sedimenting in Air

The virion content of a saliva droplet produced by an infected person is proportional to its initial volume. Denoting the droplet production rate of a single human who is speaking, which in principle depends on droplet radius, as fdrop, the number of humans that are simultaneously speaking as m, and the virion number concentration in saliva as cvir, the total number of virions sedimenting in air at a given time, denoted as Nvir, is in the steady state and in the absence of air exchange given by

graphic file with name jp0c05229_m019.jpg 14

and will be derived from the balance equation for the number of sedimenting droplets further below. In Figure 5a, the product of the initial droplet volume Inline graphic and the sedimentation time τsedsol, which appears in eq 14 on the right side, is plotted as a function of the initial droplet radius for a few different relative humidities. This quantity shows for RH = 0.5 a broad maximum for initial droplet radii between roughly 5 and 50 μm. This interesting property is due to the fact that smaller droplets contain less volume but evaporate faster and thus have a longer sedimentation time. This means that the precise dependence of the droplet production rate fdrop on the initial droplet radius R0 is not very important; the only important quantity is the total rate of droplets produced in the radius range between roughly 5 and 50 μm.

Figure 5.

Figure 5

Open in a new tab

(a) Product of the sedimentation time of droplets τsedsol (given by eq 13) and the initial droplet volume Inline graphic as a function of the initial radius R0 for an initial height of z0 = 2 m and an initial solute volume fraction of Φ0 = 0.01. Results are shown for different relative humidities; in the case RH = 0.99, no evaporation takes place and the result (eq 1) is recovered (thick black line). The right scale shows the steady-state number of virions Nvir sedimenting in air assuming droplet production at a rate fdrop = 103 s–1 for a single droplet producer (m = 1) and for a saliva virion concentration cvir = 106 mL–1 according to eq 14. (b) Same as part a but including the effect of air exchange with a rate fair according to eq 17. Results are shown for RH = 0.5 and for four different air-exchange rates fair in a closed room, assuming well-mixed air and a single droplet-producing speaking human, m = 1.

For the following estimate, the concentration of SARS-CoV-2 viruses in saliva will be assumed to be cvir = 106 mL–1, which is a conservative estimate given the recent measurements of viral RNA concentration in human sputum, which yielded a mean value of 7 × 106 mL–1.30 The droplet production rate from speaking was recently estimated in the droplet radius range between 12 and 21 μm as 2.6 × 103 s–1 25 and in the radius range higher than about 20 μm as ∼103 s–1,24 from which the conservative estimate fdrop ≈ 103 s–1 is constructed. Together, this gives a factor of fdropcvir = 109 s–1 mL–1 = 10–3 s–1 μm–3. For a single infected speaking human (m = 1), this factor results in a steady-state number of virions floating in air between 104 and 105 for a humidity value around RH = 0.5 and for a radius range between 5 and 50 μm, as follows from eq 14 and shown in Figure 5a on the right scale. This estimate does not depend on the room size (it also holds in open air) and assumes that the person does not wear a mask and is constantly speaking; obviously, it will be reduced if the person speaks only intermittently.

In open air, the produced droplets will dilute due to the droplet-producing person moving around and due to wind and convection effects; here the droplet concentration is difficult to evaluate quantitatively. The situation in closed rooms can be analyzed in more detail. The balance equation that describes the time-dependent number of droplets sedimenting in a room is given by

graphic file with name jp0c05229_m021.jpg 15

The first term on the right side is the droplet production term, proportional to the droplet production rate fdrop and the number of droplet producers m. The second term is the droplet loss rate due to sedimentation to the ground, where it is assumed that air mixing does not modify the mean sedimentation time. The last term is the droplet loss rate due to air exchange that is proportional to the air-exchange rate fair. In writing the last term, the assumption is made that the room air is well mixed, which should be a good approximation if the sedimentation time exceeds the time over which convection and ventilation effects mix the room air. Recommended air-exchange rates range from fair = 5/h in residential rooms up to fair = 20/h in multiply occupied offices and restaurants. In a steady state, the droplet number does not change with time and from eq 15 follows as

graphic file with name jp0c05229_m022.jpg 16

Thus, the steady-state total number of virions sedimenting in air follows as

graphic file with name jp0c05229_m023.jpg 17

which is a generalization of eq 14 that includes air exchange. The steady state is reached after the relaxation time Inline graphic, which is shorter than the sedimentation time τsedsol and also shorter than the inverse air-exchange rate 1/fair. Thus, the steady-state number of sedimenting virions is reached rather quickly and is therefore of relevance. As is seen in Figure 5b, a finite air-exchange rate reduces the total number of virions floating in air significantly for small initial radii. However, the virion number from droplets with radii above R0 = 20 μm is not affected much by a finite air-exchange rate, this is so because the sedimentation time in this range becomes shorter than the inverse air-exchange rate, which mitigates the air-exchange efficiency. Air recirculation between different rooms is a further risk, as it distributes the virion air load between all ventilated rooms.

An important question for infection-risk estimates is the number of virions that are inhaled by a person per minute. Denoting the tidal volume in normal breathing as Vtidal, the average respiratory frequency as fresp, and the room volume as Vroom, the rate at which virions are inhaled by a person is given by

graphic file with name jp0c05229_m025.jpg 18

where again the well-mixing assumption for air is used. The tidal breathing volume of adults is about Vtidal = 0.5 L, and the average respiratory frequency is about fresp = 20/min. Assuming a room volume corresponding to an area of 20 m2 and a height of 2 m, resulting in Vroom = 4 × 104 L, the prefactor in eq 18 comes out as 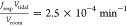Inline graphic. As seen in Figure 5, the steady-state number of sedimenting virions is even for a single speaker (m = 1) larger than Nvir ≈ 104 in the entire radius range between roughly R0 = 5 μm and R0 = 5 μm for a typical relative humidity of RH = 0.5, corresponding to a virion concentration of Inline graphic, and is only weakly reduced by increased air-exchange rates, as demonstrated in Figure 5b. The conclusion from eq 18 is that droplets produced by a constantly speaking single infected person give rise to a virion inhalation rate of a passive bystander of at least finhale = 2.5 min–1 in a wide droplet radius range.

3. Discussion and Conclusion

It is gradually becoming acknowledged that airborne infection plays a crucial role in SARS-CoV-2 spreading33−35 and that mouth covers could be instrumental,36−38 yet it is not straightforward to derive the infection risk from the virion inhalation frequency given by eq 18. It is known that SARS-CoV-2 viruses remain viable in aerosols for at least 3 h,26 which is longer than the sedimentation times in the relevant radius range, as seen in Figure 4. As a comparison, on inanimate surfaces, these viruses stay infectious for days.26,39 As a further complication, the relative humidity has a significant influence on virus stability; it was shown for bacteriophages and influenza viruses that stability is minimal at intermediate humidities around RH = 0.5 and is increased both for lower and larger humidities.40,41 Unfortunately, similar data is not yet available for SARS-CoV-2 viruses. Many factors determine the likelihood that a virus will spread from one person to another and that disease will result, but for other viruses, it is known that inhaling as few as 5 virions can cause infection,42 so the above estimate of a virion inhalation rate of finhale = 2.5 min–1, which is a conservative estimate, should be relevant for the assessment of the viral airborne infection risk not only of SARS-CoV-2 but of other viruses as well.

From the analysis in this paper, it is clear that droplet sedimentation is a complex problem. In order to come up with analytical predictions, a number of simplifying assumptions had to be made. It has been assumed that diffusion within the droplet occurs quickly enough, so that the water concentration at the droplet surface does not differ significantly from the mean water concentration in the droplet. In Supporting Information section J, it is shown that this approximation should be valid for radii below R = 100 μm, which is larger than the relevant radius range for airborne infections. Surface tension effects, which increase the water vapor pressure, are negligible for droplets with radii larger than R = 1 nm, as explained in Supporting Information section L. Likewise, the pressure increase due to evaporation and the change of droplet mass density with evaporation has been neglected.

The human sneeze was shown to produce a turbulent gas cloud of droplets mixed with hot and moist exhaled air, which can travel up to 8 m.43 It was demonstrated that the warm atmosphere in this cloud slows down evaporation for droplets that are small enough to reside inside the cloud for an extended time.44 The results presented here in principle hold also for droplets produced by sneezing once the droplets have left the sneeze cloud. Droplets larger than R = 100 μm quickly fall to the ground, but they can spread disease by ballistically landing on other people or on surfaces, which is a distinct infection mechanism and not considered here.

In summary, the evaporation of aqueous droplets with initial radii 70 nm < R0 < 60 μm can be described by the stagnant air approximation in the diffusion limit. These calculations demonstrate in terms of analytical formulas that droplets in the entire range of radii below R0crit = 52 μm for RH = 0.5 shrink significantly from evaporation before they fall to the ground and thus stay floating in air longer than their initial radius would suggest. This leads to a significant viral air load from droplets in the entire initial radius range 5 μm < R0 < 50 μm, which includes the radius range of droplets produced by speaking.24,25 A simple estimate of the viral inhalation frequency in a closed room suggests that 2.5 virions are inhaled per minute if one infected person is constantly speaking and not wearing a mask; typical air-exchange rates do not lower this number significantly. Thus, speaking and presumably more so singing are shown to increase the risk of airborne viral infections substantially, which can be reduced efficiently by wearing a mouth cover.24,25

Future work along different lines is needed to address a number of important open questions: (I) What is the precise size distribution of droplets produced by humans while speaking, while breathing, and while physically exercising? What are the deviations among individuals, and are there exceptional individuals that produce significantly more droplets than others? (II) More statistics on the virus content of saliva as a function of the infection stage is direly needed, not only for SARS-CoV-2 but also for other viruses. (III) Precise measurements of the times that viruses stay infectious in droplet nuclei for different temperatures and relative humidities. (IV) How does the viscosity inside drying saliva droplets increase, and how does that effect the evaporation kinetics? (V) How effective are face masks of various fabrication specificities in filtering out droplets of different radii from speaking? (VI) How is the sedimentation time distribution calculated in Supporting Information section A modified in the presence of convective and turbulent air-mixing effects? The analytical results presented in this work will hopefully stimulate and facilitate further research along these diverse directions.

Acknowledgments

I thank William Eaton for helpful comments and for bringing this problem to my attention. Discussions with A. Bax, L. Bocquet, J.-F. Dufreche, I. Gersonde, P. Loche, D. Lohse, M. Rezaei, and T. Zemb are gratefully acknowledged. This research has been funded by the Max-Planck Water Initiative, by the Deutsche Forschungsgemeinschaft (DFG) through grant CRC 1114 “Scaling Cascades in Complex Systems”, Grant No. 235221301, Project C02, and by the ERC Advanced Grant No. 835117.

Biography

graphic file with name jp0c05229_0001.jpg

Roland Netz studied physics at the Technical University of Berlin and at MIT and received his Ph.D. in 1994 from the University of Cologne. After postdoctoral positions at Tel-Aviv University, UC Santa Barbara, Seattle, Institute Charles Sadron in Strasbourg, CEA in Paris, and the Max-Planck Institute for Colloids and Interfaces in Potsdam, he was appointed associate professor of physics at the LMU Munich in 2002 and full professor of physics at the TU Munich in 2004. Since 2011, he has held a chair in theoretical biosoft-matter physics at the Free University of Berlin. His research focuses on the structure and dynamics of water, proteins, polymers, and charged systems using quantum, atomistic, and coarse-grained simulations as well as theoretical approaches.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpcb.0c05229.

  • Calculation of the sedimentation time distribution, stagnant droplet evaporation, convection effects on evaporation, and surface tension effects (PDF)

The author declares no competing financial interest.

Supplementary Material

jp0c05229_si_001.pdf (353KB, pdf)

References

  1. Frössling N. Über die Verdunstung fallender Tropfen. Gerlands Beitr. Geophys. 1938, 52, 170. [Google Scholar]
  2. Wells W. F. On Air-Borne Infection. Study II: Droplets and Droplet Nuclei. Am. J. Epidemiol. 1934, 20, 611. 10.1093/oxfordjournals.aje.a118097. [DOI] [Google Scholar]
  3. Duguid J. P. The size and the duration of air-carriage of respiratory droplets and droplet-nuclei. J. Hyg. 1946, 4, 471. 10.1017/s0022172400019288. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Kinzer G. D.; Gunn R. The evaporation, temperature and thermal relaxation-time of freely falling waterdrops. J. Meteorol. 1951, 8, 71.. [DOI] [Google Scholar]
  5. Best A. C. The evaporation of raindrops. Q. J. R. Meteorol. Soc. 1952, 78, 200. 10.1002/qj.49707833608. [DOI] [Google Scholar]
  6. Ranz W. E.; Marshall W. R. Evaporation from drops. Chem. Eng. Prog. 1952, 48, 141. [Google Scholar]
  7. Kukkonen J.; Vesala T.; Kulmala M. The interdependence of evaporation and settling for airborne freely falling droplets. J. Aerosol Sci. 1989, 20, 749. 10.1016/0021-8502(89)90087-6. [DOI] [Google Scholar]
  8. Xie X.; Li Y.; Chwang A. T. Y.; Ho P. L.; Seto W. H. How far droplets can move in indoor environments - revidsiting the Wells evaoporation-falling curve. Indoor Air 2007, 17, 211. 10.1111/j.1600-0668.2007.00469.x. [DOI] [PubMed] [Google Scholar]
  9. Liu L.; Wei J.; Li Y.; Ooi A. Evaporation and dispersion of respiratory droplets from coughing. Indoor Air. 2017, 27, 179. 10.1111/ina.12297. [DOI] [PubMed] [Google Scholar]
  10. Redrow J.; Mao S.; Celik I.; Posada J. A.; Feng Z.-g. Modeling the evaporation and dispersion of airborne sputum droplets expelled from a human cough. Building and Environment. 2011, 46, 2042. 10.1016/j.buildenv.2011.04.011. [DOI] [Google Scholar]
  11. Chong K. L.; Li Y.; Ng C. S.; Verzicco R.; Lohse D. Convection-dominated dissolution for single and multiple immersed sessile droplets. J. Fluid Mech. 2020, 892, A21. 10.1017/jfm.2020.175. [DOI] [Google Scholar]
  12. Fuchs N. A.Evaporation and droplet growth in gaseous media; Pergamon Press: London, 1959. [Google Scholar]
  13. Parienta D.; et al. Theoretical analysis of the motion and evaporation of exhaled respiratory droplets of mixed composition. J. Aerosol Sci. 2011, 42, 1. 10.1016/j.jaerosci.2010.10.005. [DOI] [Google Scholar]
  14. Papineni R. S.; Rosenthal F. S. The size distribution of droplets in the exhaled breath of healthy human subjects. J. Aerosol Med. 1997, 10, 105. 10.1089/jam.1997.10.105. [DOI] [PubMed] [Google Scholar]
  15. Yang S.; Lee G. W. M.; Chen C.-M.; Wu C.-C.; Yu K.-P. The size and concentration of droplets generated by coughing in human subjects. J. Aerosol Med. 2007, 20, 484. 10.1089/jam.2007.0610. [DOI] [PubMed] [Google Scholar]
  16. Xie X.; Li Y.; Sun H.; Liu L. Exhaled droplets due to talking and coughing. J. R. Soc., Interface 2009, 6, S703. 10.1098/rsif.2009.0388.focus. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Zhang H.; Li D.; Xie L.; Xiao Y. Documentary research of human resipiratory droplet characteristics. Procedia Eng. 2015, 121, 1365. 10.1016/j.proeng.2015.09.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Chao C. Y. H.; Wan M. P.; Morawska L.; Johnson G. R.; Ristovski Z. D.; Hargreaves M.; Mengersen K.; Corbett S.; Li Y.; Xie X.; Katoshevski D. Characterization of expiration air jets and droplet size distributions immediately at the mouth opening. J. Aerosol Sci. 2009, 40, 122. 10.1016/j.jaerosci.2008.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Gralton J.; Tovey E.; McLaws M.-L.; Rawlinson W. D. The role of particle size in aerosolised pathogen transmission: A review. J. Infect. 2011, 62, 1. 10.1016/j.jinf.2010.11.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Johnson G.R.; Morawska L.; Ristovski Z.D.; Hargreaves M.; Mengersen K.; Chao C.Y.H.; Wan M.P.; Li Y.; Xie X.; Katoshevski D.; Corbett S. Modality of human expired aerosol size distributions. J. Aerosol Sci. 2011, 42, 839. 10.1016/j.jaerosci.2011.07.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Somsen G. A.; van Rijn C.; Kooij S.; Bem R. A.; Bonn D. Small droplet aerosols in poorly ventilated spaces and SARS-CoV-2 transmission. Lancet Respir. Med. 2020, 8, 658. 10.1016/S2213-2600(20)30245-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Asadi S.; Wexler A. S.; Cappa C. D.; Barreda N. M.; Bouvier N. M.; Ristenpart W. D. Aerosol emission and superemission during human speech increase with voice loudness. Sci. Rep. 2019, 9, 2348. 10.1038/s41598-019-38808-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Scharfman B. E.; Techet A. H.; Bush J. W. M.; Bourouiba L. Visualization of sneeze ejactat: steps of fluid fragmentation leading to respiratory droplets. Exp. Fluids 2016, 57, 24. 10.1007/s00348-015-2078-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Anfinrud P. A.; Stadnytskyi V.; Bax C. E.; Bax A. Visualizing speech-generated oral fluid droplets with laser light scattering. N. Engl. J. Med. 2020, 382, 2061. 10.1056/NEJMc2007800. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Stadnytskyi V.; Bax C. E.; Bax A.; Anfinrud P. The airborne lifetime of small speech droplets and their potential importance in SARS-CoV-2 transmission. Proc. Natl. Acad. Sci. U. S. A. 2020, 117, 11875. 10.1073/pnas.2006874117. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. van Doremalen N.; Bushmaker T.; Morris D. H.; Holbrook M. G.; Gamble A.; Williamson B. N.; Tamin A.; Harcourt J. L.; Thornburg N. J.; Gerber S. I.; Lloyd-Smith J. O.; de Wit E.; Munster V. J. Aerosol and Surface Stability of SARS-CoV-2 as Compared with SARS-CoV-1. N. Engl. J. Med. 2020, 382, 1564. 10.1056/NEJMc2004973. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Shaman J.; Kohn M. Absolute humidity modulates influenza survival, transmission, and seasonality. Proc. Natl. Acad. Sci. U. S. A. 2009, 106, 3243. 10.1073/pnas.0806852106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Tellier R. Aerosol transmission of influenza A virus: a review of new studies. J. R. Soc., Interface 2009, 6, S783. 10.1098/rsif.2009.0302.focus. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Ai Z. T.; Melikov A. K. Airborne spread of expiratory droplet nuclei between the occupants of indoor environments: A review. Indoor Air. 2018, 28, 500. 10.1111/ina.12465. [DOI] [PubMed] [Google Scholar]
  30. Wölfel R.; Corman V. M.; Guggemos W.; Seilmaier M. Virological assessment of hospitalized patients with COVID-2019. Nature 2020, 581, 465. 10.1038/s41586-020-2196-x. [DOI] [PubMed] [Google Scholar]
  31. Batchelor G. K.An Introduction to Fluid Dynamics; Cambridge University Press: Cambridge, U.K., 1967. [Google Scholar]
  32. Humphrey S. P.; Williamson R. T. A review of saliva: Normal composition, flow, and function. J. Prosthet. Dent. 2001, 85, 162. 10.1067/mpr.2001.113778. [DOI] [PubMed] [Google Scholar]
  33. Morawska L.; Cao J. Airborne transmission of SARS-CoV-2: The world should face the reality. Environ. Int. 2020, 139, 105730. 10.1016/j.envint.2020.105730. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Zhang R.; Li Y.; Zhang A. L.; Wang Y.; Molina M. J. Identifying airborne transmission as the dominant route for the spread of COVID-19. Proc. Natl. Acad. Sci. U. S. A. 2020, 117, 14857. 10.1073/pnas.2009637117. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Liu Y.; Ning Z.; Chen Y.; Guo M.; Liu Y.; Gali N. K.; Sun L.; Duan Y.; Cai J.; Westerdahl D.; Liu X.; Xu K.; Ho K.-F.; Kan H.; Fu Q.; Lan K. Aerodynamic analysis of SARS-CoV-2 in two Wuhan hospitals. Nature 2020, 582, 557. 10.1038/s41586-020-2271-3. [DOI] [PubMed] [Google Scholar]
  36. Leung N. H. L. Respiratory virus shedding in exhaled breath and efficacy of face masks. Nat. Med. 2020, 26, 676. 10.1038/s41591-020-0843-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Stutt R. O. J. H.; Retkute R.; Bradely M.; Gilligan C. A.; Colvin J. A modelling framework to assess the likely effectiveness of facemasks in combination with ‘lock-down’ in managing the COVID-19 pandemic. Proc. R. Soc. London, Ser. A 2020, 476, 20200376. 10.1098/rspa.2020.0376. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Neupane B. B.; Mainali S.; Sharma A.; Giri B. Optical microscopic study of surface morphology and filtering efficiency of face masks. PeerJ 2019, 7, e7142 10.7717/peerj.7142. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Kampf G.; Todt D.; Pfaender S.; Steinmann E. Persistence of coronaviruses on inanimate surfaces and their inactivation with biocidal agents. Journal of Hospital Infection. 2020, 104, 246. 10.1016/j.jhin.2020.01.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Schaffer F. L.; Soergel M. E.; Straube D. C. Survival of Airborne Influenza Virus: Effects of Propa!]ating Host, Relative Humidity, and Composition of Spray Fluids. Arch. Virol. 1976, 51, 263. 10.1007/BF01317930. [DOI] [PubMed] [Google Scholar]
  41. Lin K.; Marr L. C. Humidity-Dependent Decay of Viruses, but Not Bacteria, in Aerosols and Droplets Follows Disinfection Kinetics. Environ. Sci. Technol. 2020, 54, 1024. 10.1021/acs.est.9b04959. [DOI] [PubMed] [Google Scholar]
  42. Musher D. M. How Contagious Are Common Respiratory Tract Infections?. N. Engl. J. Med. 2003, 348, 1256. 10.1056/NEJMra021771. [DOI] [PubMed] [Google Scholar]
  43. Bourouiba L. A Sneeze. N. Engl. J. Med. 2016, 375, e15 10.1056/NEJMicm1501197. [DOI] [PubMed] [Google Scholar]
  44. Bourouiba L. Turbulent Gas Clouds and Respiratory Pathogen Emissions: Potential Implications for Reducing Transmission of COVID-19. J. Am. Med. Assoc. 2020, 323, 1837. 10.1001/jama.2020.4756. [DOI] [PubMed] [Google Scholar]
  45. Lide D. R.CRC Handbook of Chemistry and Physics, 89th ed.; CRC Press: Cleveland, OH, 2008. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp0c05229_si_001.pdf (353KB, pdf)

Articles from The Journal of Physical Chemistry. B are provided here courtesy of American Chemical Society

RESOURCES