Abstract
Structural equation modeling (SEM) provides an extensive toolbox to analyze the multivariate interrelations of directly observed variables and latent constructs. Multilevel SEM integrates mixed effects to examine the covariances between observed and latent variables across many levels of analysis. However, while it is necessary to consider model fit, traditional indices are largely insufficient to analyze model fit at each level of analysis. The present paper reviews i) the partially-saturated model fit approach first suggested by Ryu and West (2009) and ii) an alternative model parameterization that removes the multilevel data structure. We next describe the implementation of an algorithm to compute partially-saturated model fit for 2-level structural equation models in the open source SEM package, OpenMx, including verification in a simulation study. Finally, an example empirical application evaluates leading theories on the structure of affect from ecological momentary assessment data collected thrice daily for two weeks from 345 participants.
Keywords: model fit, multilevel structural equation model, confirmatory factor analysis, nonindependence
Since the 1970’s, structural equation modeling (SEM) has become a highly popular data analytic approach (e.g., Hoyle, 2012). SEM facilitates integrating sets of specified covariances and regressions among specified variables into a single, cohesive model. However, research studies in many social science and medical fields (e.g., psychology, sociology, education, medicine) frequently examine processes of interest at multiple levels of analysis (Curran & Bauer, 2011; Molenaar, 2004). For example, one may use a cross-sectional design to test an interindividual (i.e., between-person) and intraindividual (i.e., within-person) theory that financial distress influences the development of psychopathology. At best, the cross-sectional design will clarify the interindividual structure (i.e., whether persons with psychopathology report higher rates of financial distress), though this does not fully test the theory. Additionally, standard SEM assumes independence of observations, which is violated if one collects data that inherently are not (e.g., due to nesting observations within person or persons within-group). This non-independence is called dependence here. Multilevel, mixed effects models and multilevel SEM (MSEM) adjust for such statistical dependence and disaggregate variance into that accounted for by each level of analysis (Raudenbush & Bryk, 2002). Therefore, MSEM allows users to specify distinct models at each level of analysis to better distinguish results by the level of analysis.
Broadly, SEM represents a multivariate extension of the general linear model that accounts for means, variances, and covariances amongst a set of variables. For example, whereas multiple regression is limited to a single dependent variable, SEM facilitates estimating multivariate multiple regression models, which can include multiple dependent and independent variables. Furthermore, within the SEM framework, one can specify covariance among multiple measures (e.g., questionnaire items) as the resulting from one or more latent (i.e., not measured) factors and residual, item-specific variance (Bentler, 1980).
In practice, users specify parameters to be estimated in order to quantify correlation and regression relationships amongst variables. These relationships are used to generate a predicted variance-covariance matrix (called a covariance matrix here for brevity) and, optionally, a vector of means for the observed data. Numerical optimization is then used to vary the parameter estimates so that the predicted covariance matrix best matches the observed data. Because all models for real data are wrong (Box, 1976), users inevitably err in specifying a model. For example, a residual covariance between items may be omitted. The resulting predicted covariance matrix is expected to depart from the observed data, which contributes to model misfit (Fan & Wang, 1998). Therefore, a necessary component of SEM analysis is the calculation of model fit (i.e., the degree of misfit between the hypothesized and observed covariance matrices). One statistic used to assess model fit is twice the difference in log-likelihood between the hypothesized model and that of a ‘saturated’ model, in which all observed variances and covariances are estimated with separate free parameters (Steiger, Shapiro, & Browne, 1985). The difference in fit between these two models may be written as TML = FML(θ) – FML(θS), where FML(θ) represents the minus twice log-likelihood fit of the hypothesized model and FML(θs) represents the −2 log-likelihood of the saturated model. Under certain regularity conditions including multivariate normality, appropriate model specification, and a sufficiently large sample size, the difference in fit between the hypothesized and saturated models (i.e., TML) is distributed following the χ2 distribution (Steiger et al., 1985). Additional indices of model fit adjust for sample size (e.g., RMSEA; Chen, Curran, Bollen, Kirby, & Paxton, 2008) or number of estimated parameters (e.g., AIC; Akaike, 1987). These indices, specifically the multivariate extensions of them, are detailed further below.
Maximum-likelihood estimation of SEM typically requires the assumption that observations are independent and identically distributed. However, when data are collected in a nested structure (e.g., multiple occasions within a person or multiple children within a classroom), this assumption of independence is violated. In such cases, data are said to be non-independent (Kenny, Kashy, & Cook, 2006). As Kenny and colleagues review, such statistical dependence of the observations does not systematically bias parameter estimates, but will typically underestimate the parameters’ standard errors.
Multilevel extensions of the general linear model (e.g., Goldstein & McDonald, 1988) have been extended to multilevel structural equation modeling (e.g., MSEM; Kim, Dedrick, Cao, & Ferron, 2016; Lee, 1990; Mehta & Neale, 2005; Muthén, 1994; Muthén & Satorra, 1995). Specifically, MSEM and multilevel regression note that E(yij) = E(yj) + E(yi|j), where the expected value of y given group j and person i is the sum of the expected value for group j and the expected value for person i conditional on group j. The variance in each variable (i.e., V(yij)) can be decomposed into variance between groups (i.e., V(yj)) and pooled variance within each group (i.e., V(yi|j)) (Raudenbush & Bryk, 2002).
MSEM relies on extending the multilevel framework to note that the covariance between two measures can be similarly decomposed, which can be expressed in matrix terms as T = B + W, where the total covariance matrix T is the sum of a between-group matrix B and a within-group matrix W (e.g., Mehta & Neale, 2005). In this framework, the within-group matrix (i.e., the lowest order of nesting) is termed level 1 while the between-group matrix is termed level 2. This notation is extended to n-levels of nesting (e.g., students who are nested within classroom within a school) by notating higher level clustering with higher integers (e.g., levels 1, 2, and 3). This notation will be used below to encourage generalizability to n-level analyses. Hence, MSEM can integrate variables assessed at multiple levels of analysis. For example, variables assessed at the group level (i.e., with only between-group variance) can be modeled along with between-group variance in variables assessed at more granular levels of analysis (e.g., within each group). However, MSEM does not require that one has assessed variables uniquely at each level of analysis. As demonstrated in the simulation study and empirical example below, MSEM allows the user to specify the covariance structure at each level of analysis, which includes variables assessed at the given level and variance in variables assessed at more granular levels of analysis that is attributable to the given level.
Maximum-Likelihood Estimation of Multilevel SEM
Maximum likelihood estimation of traditional SEM includes minimizing deviations of the expected covariance and means matrices from observed data. In the context of clustered (i.e., nested or multilevel) data, the overall model log-likelihood indexes fit at both levels 1 and 2. Specifically, this is described by equations for the −2log-likelihood aggregated over levels of analysis, which are provided comprehensively elsewhere (Lee, 1990; Liang & Bentler, 2004).
These equations show that overall model fit aggregates all levels of analysis, which obscures the source of any potential model misspecification. Moreover, overall model fit is more strongly influenced by model misspecification at level 1 than level 2 (Hsu, Kwok, Lin, & Acosta, 2015; Ryu & West, 2009; Yuan & Bentler, 2007). Ryu and West (2009) and Yuan and Bentler (2007) propose approaches to estimate model fit at each level of an n-level SEM. The Yuan and Bentler approach uses a two-step procedure to: 1) estimate saturated covariance matrices for each level, and 2) use each level-specific saturated matrix to estimate fit against fitted single-level SEM (Yuan & Bentler, 2007). Ryu and West (2009) present an alternative approach that produced a lower Type I error rate for misfit at level 2 and lower rate of non-convergence. In their approach, one estimates the hypothesized multilevel SEM along with a model in which all levels are saturated (FML[Bs,Ws]). To estimate fit at a given level, one then specifies a model in which the given level is specified based on theory while all other levels are saturated (e.g., FML[B,Ws]). Analogous to model fit in the single-level case, level-specific model fit (e.g., FMLB) is then compared as the difference in fit between the hypothesized/partially-saturated model and a fully saturated model. This approach scales to n-level models by estimating model fit for each level while keeping all other levels saturated.
However, at present, level-specific indices of model fit are not commonly incorporated into MSEM analyses. For example, in a recent review of the literature, Kim et al. (2016) report that most prior research reported fit indices (e.g., RMSEA) for the overall model, but only occasionally reported the standardized root mean square residual (SRMR), which may be able to discern model fit at each level (Hsu et al., 2015). The present paper describes the implementation of an algorithm within the open source SEM package OpenMx (Neale et al., 2016) to compute partially-saturated model fit indices (i.e., χ2, AIC, and RMSEA). Chi-squared and RMSEA statistics are included as indices of model fit to assess suitability of the model. This is comparable to the SRMR statistic provided in the Mplus statistical package (Muthén & Muthén, 1998), however RMSEA may be more robust to multivariate non-normality (see Hu & Bentler, 1998 for review). Additionally, level-specific AIC and BIC statistics are provided (see Supplement) to facilitate comparison of alternative specifications for each level. While useful to evaluate overall model fit, SRMR is not suitable to compare alternative model specifications (Hsu et al., 2015). Next, we illustrate MSEM through comparison with an alternative specification proposed by Mehta and Neale (2005). Finally, an empirical example of multilevel confirmatory factor analysis illustrates the use and benefit of level-specific model fit.
Fit Indices for MSEM
A chi-squared statistic can be computed for each level based on an empirical log-likelihood (e.g., FML[B,Ws]) derived as described above. Asymptotically, and given certain regularity conditions (Steiger et al., 1985), the level-specific difference in log-likelihood between the fully- and partially-saturated models is distributed as chi-squared with degrees of freedom equal to the difference in the number of parameters between the fully- and partially-saturated models. From this distribution, one can conduct a classical null-hypothesis test of the probability of obtaining the observed data given the specified model.
We note that one need not have observed variables at each level of analysis. Similar to variance decomposition in multilevel extensions of the general linear model, for each variable observed at a more granular level of analysis, one may specify variance at each higher level (e.g., Raudenbush & Bryk, 2002). The user can then specify a covariance structure, which includes freely estimated and constrained parameters, for all variables with variance at each level. Due to statistical dependence, we note that the user should consider variance at each higher level of analysis. For example, in fitting a saturated between-group model, one should consider between-group variance in all variables assessed within group. Omitting a variable from a higher level of analysis is akin to constraining its variance to 0. This constraint may be theoretically consistent and supported by variance decomposition analyses. However, freeing this parameter when fitting the saturated model provides an empirical test of this constraint in the context of a broader specified model. We further note that the partially-saturated approach to model fit may be limited in evaluating equality constraints between levels of analysis. For example, re-estimating the model with each level saturated may thwart a constraint of equality on the between- and within-group factor loadings for a given item.
Moreover, from the chi-squared statistic, degrees of freedom, sample size, and number of parameters, one can compute additional indices of model fit. The current paper will use RMSEA and AIC as examples. However, the approach can be extended to related fit indices. As an example, supplemental materials describe the computation of the Bayesian Information Criteria (BIC). Compared to the chi-squared statistic, RMSEA may be less sensitive to increased model complexity and robust to violations of multivariate normality (Hu & Bentler, 1998). Level-specific RMSEA is computed as the ratio (Ryu & West, 2009):
where , dfq, and Nq refer, respectively, to the chi-squared statistic, degrees of freedom, and number of observations for the q-level specified. For example, in a study where 100 participants each complete 20 assessments, level 2 (i.e., between-person) reflects the 100 participants. Level 1 reflects 20 observations per person, which, with the assumption of measurement invariance across people (i.e., level 2 groups), can be fit based on 2,000 (100 × 20) observations.
Additionally, the AIC provides a relative index of fit to facilitate comparison of multiple model specifications. AICq can be computed for each level q=1…Q, based on the chi-squared statistic adjusted for model complexity (i.e., the number of parameters in the specified model):
where refers to the chi-squared statistic for the q level specified and kq represents the number of parameters in the specified model (Akaike, 1987). One can compute additional fit indices (e.g., BIC, see supplemental materials) from these quantities.
Alternative Model Specification
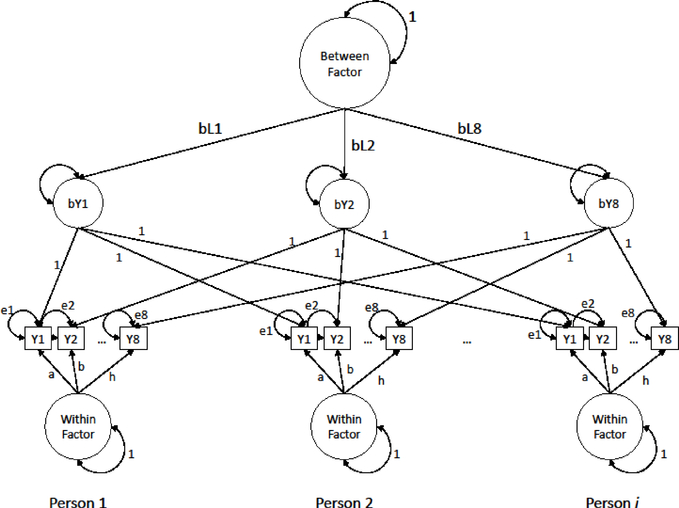
Instead of specifying a multilevel (i.e., mixed effects) structural equation model, dependence due to nested data (e.g., observations nested within person) can be alternatively specified as a single-level model at the highest level (e.g., between person) with each nested observation (e.g., observations within person) specified concurrently. Mehta and Neale (2005) detail this approach, called ML-SEM, which is illustrated in Figure 2. Specifically, the dataset is restructured so that each row represents a cluster (e.g., a person). Each variable is then represented at each occasion. Rather than specified as a separate within-person model, as detailed above, the within-person model is specified for sets of variables for each occasion. Equality constraints are added to impose stationarity and measurement invariance, which is assumed of the multilevel models described above. Mehta and Neale note that this approach facilitates empirically testing these assumptions as constraints for parameter equality can be relaxed and tested. For example, such a test might demonstrate changes in differential item functioning as a function of time in the study. One could also specify a contrast to evaluate potential measurement effects of occasion-specific variables (e.g., assessing alcohol intake on the weekend vs. weekday). However, while Mehta and Neale suggest that standard model fit indices might appropriately index model fit, they note a paucity of evidence from either mathematical or simulation-based research to confirm this notion. In the present study, we simulate data to compare and contrast the function of standard model fit indices (i.e., χ2, RMSEA, AIC) in MSEM and ML-SEM.
Figure 2.
Illustration of ML-SEM Specification for a 1-Factor Multilevel Confirmatory Factor Model. Note: Means of observed variables were generated and modeled but are omitted for visual clarity. Identical path coefficient labels (i.e., a, b, h) and residual variance labels (i.e., e1, e2, e8) denote equality constraints. Person i indicates the last person in a dataset.
Implementation
Within the open-source statistical software R (R Core Team, 2015), we developed a set of functions that generate saturated matrices and fit the correct set of models to compute model fit statistics at each level. These functions use the OpenMx package (Neale et al., 2016), a flexible SEM package that can estimate MSEM (Pritikin, Hunter, von Oertzen, Brick, & Boker, 2017). Functions and supplemental code are available at osf.io/v4mej and will be incorporated into later releases of the OpenMx package. Within the MSEMfit() function, one provides a fully specified MSEM, denotes which levels to saturate, and specifies whether-or-not to run the fully- or partially-saturated model. The function returns an mxModel object optimized or not as specified. The MSEMfitAuto() function calls on the MSEMfit() function to automatically create and optimize three models: the fully-saturated model, a model in which only level 1 is saturated, or a model in which only level 2 is saturated. Specified models for each level are retained from the user’s original, specified model. Therefore, inputting a previously optimized (i.e., fitted) model reduces computational time. The MSEMfitAuto() function returns all optimized models along with the model specific fit indices described here (e.g., χ2, RMSEA, AIC).
To saturate level 1, the MSEMfit function specifies a saturated symmetric covariance matrix for all variables included in the model (i.e., all variables specified in the manifestVars statement). All asymmetric paths are removed. To saturate level 2, the function specifies a separate latent factor at level 2 to correspond to each level 1 variable such that each level 1 variable loads into one level 2 factor. Factor loadings are fixed at 1. Similar to variance decomposition, this represents level 2 (e.g., between-person) variance in each level 1 (e.g., within-person) variable. In this manner, the partially-saturated model fit approach can evaluate the appropriateness of specified latent factors at level 2. Similar to level 1, the symmetric matrix among all latent and observed variables at level 2 is saturated; all asymmetric paths are removed. Both functions use the mxTryHard() function to automate repeated model optimization from different starting values. While the functions are presently limited to 2-level MSEM, development is underway to permit estimating model fit for n-level MSEM.
Simulation Study
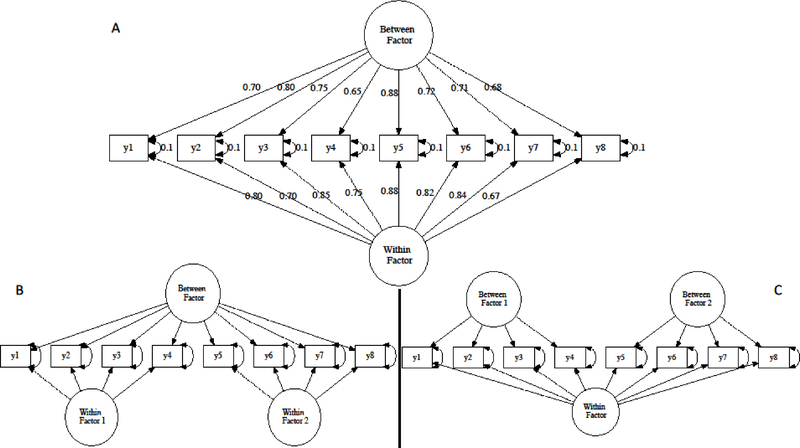
To evaluate partially-saturated model fit indices for MSEM, 500 datasets were generated under a 2-level confirmatory factor analytic (CFA) model with 8 observed variables specified as loading onto a single factor at each level (see Table 1, columns “simulated,” Figure 1A, and osf.io/v4mej for example R code). To approximate a data rich yet practically feasible sample, data were simulated with 150 observations in each of 200 clusters. Three models were then fit to the data: the correct model, one in which level 1 was mis-specified, and one in which level 2 was mis-specified (see osf.io/v4mej for example R code). In mis-specified models, the eight observed variables were modeled as indicators of two uncorrelated latent factors at level 1 (see Figure 1B) or level 2 (see Figure 1C). While omitted from Figures 1 and 2, all models estimated observed variable means and residual variance (“error”). Using the functions described above, model fit indices were computed for each model fit to each dataset.
Table 1.
Parameter Recovery from the Correctly Specified 1-Factor Multilevel Structural Equation Model
| Approach | Variable | Within Loading | Between Loading | Mean | Residual Variance | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sim. | E(X) | SD(X) | Sim. | E(X) | SD(X) | Sim. | E(X) | SD(X) | Sim. | E(X) | SD(X) | ||
| MSEM | 1 | 0.80 | 0.80 | 0.004 | 0.70 | 0.70 | 0.04 | 2 | 2.00 | 0.07 | 0.1 | 0.10 | < 0.01 |
| 2 | 0.70 | 0.70 | 0.003 | 0.80 | 0.80 | 0.04 | 3 | 3.00 | 0.08 | 0.1 | 0.10 | < 0.01 | |
| 3 | 0.85 | 0.85 | 0.004 | 0.75 | 0.75 | 0.04 | 1 | 1.00 | 0.08 | 0.1 | 0.10 | < 0.01 | |
| 4 | 0.75 | 0.75 | 0.003 | 0.65 | 0.65 | 0.03 | 2 | 2.00 | 0.07 | 0.1 | 0.10 | < 0.01 | |
| 5 | 0.88 | 0.88 | 0.004 | 0.88 | 0.88 | 0.04 | 4 | 4.00 | 0.09 | 0.1 | 0.10 | < 0.01 | |
| 6 | 0.82 | 0.82 | 0.004 | 0.72 | 0.72 | 0.04 | 2 | 2.00 | 0.07 | 0.1 | 0.10 | < 0.01 | |
| 7 | 0.84 | 0.84 | 0.004 | 0.71 | 0.71 | 0.04 | 5 | 5.00 | 0.07 | 0.1 | 0.10 | < 0.01 | |
| 8 | 0.67 | 0.67 | 0.003 | 0.68 | 0.68 | 0.03 | 3 | 3.00 | 0.07 | 0.1 | 0.10 | < 0.01 | |
| ML-SEM | 1 | 0.80 | 0.80 | 0.01 | 0.70 | 0.70 | 0.04 | 2 | 2.01 | 0.05 | 0.1 | 0.10 | < 0.01 |
| 2 | 0.70 | 0.70 | 0.01 | 0.80 | 0.80 | 0.04 | 3 | 3.01 | 0.06 | 0.1 | 0.10 | < 0.01 | |
| 3 | 0.85 | 0.85 | 0.01 | 0.75 | 0.75 | 0.04 | 1 | 1.01 | 0.06 | 0.1 | 0.10 | < 0.01 | |
| 4 | 0.75 | 0.75 | 0.01 | 0.65 | 0.65 | 0.04 | 2 | 2.00 | 0.05 | 0.1 | 0.10 | < 0.01 | |
| 5 | 0.88 | 0.88 | 0.01 | 0.88 | 0.88 | 0.05 | 4 | 4.01 | 0.07 | 0.1 | 0.10 | < 0.01 | |
| 6 | 0.82 | 0.82 | 0.01 | 0.72 | 0.72 | 0.04 | 2 | 2.01 | 0.05 | 0.1 | 0.10 | < 0.01 | |
| 7 | 0.84 | 0.84 | 0.01 | 0.71 | 0.71 | 0.04 | 5 | 5.00 | 0.05 | 0.1 | 0.10 | < 0.01 | |
| 8 | 0.67 | 0.67 | 0.01 | 0.68 | 0.68 | 0.04 | 3 | 3.00 | 0.05 | 0.1 | 0.10 | < 0.01 | |
Note. Sim. refers to simulated values; E(X) indicates the expected parameter mean, SD (X) indicates the expected parameter standard deviation over 500 samples. MSEM indicates multilevel structural equation modeling (e.g., Goldstein & McDonald, 1988; Muthén, 1990, 1994); ML-SEM indicates multilevel structural equation modeling (Mehta & Neale, 2005). Because of suspiciously high outlier χ2 values, 4 samples from the MSEM approach and 1 sample from the ML-SEM approach were removed.
Figure 1.
Illustration of Correct and Incorrect Specifications of the Simulated 1-Factor Multilevel Confirmatory Factor Model. Means of observed variables were generated and modeled but are omitted for visual clarity. Figure 1A denotes the data generating model; Figures 1B and 1C denote incorrect model specifications for level 1 and 2, respectively.
Separate models were fit to each dataset to implement the ML-SEM specification described by Mehta and Neale (2005), which evaluated prior evidence that overall model fit is particularly susceptible to misspecification at level 1. The ML-SEM specification grows linearly with the number of level 1 observations. With 8 variables at each of 150 level 1 observations, the specification would require evaluating the likelihood over 1200 observations, which would involve repeatedly inverting a 1,200 × 1,200 covariance matrix. Instead, all 200 clusters were retained but, within each level 2 cluster, only a subset of the first 13 observations were retained to reduce the considerable computational burden to a 104 × 104 covariance matrix. Because of suspiciously high outlier χ2 values, under the MSEM approach, 4 samples of the correctly-specified model and 1 sample of the model in which level 1 was mis-specified were removed. Similarly, because of a suspiciously high outlier χ2 value, 1 sample of the correctly-specified model under the ML-SEM approach was removed. Model fitting was conducted with Full Information Maximum Likelihood in the OpenMx package version 2.7.11. Analyses were run in R version 3.2.3 (R Core Team, 2015) using the psych package version 2.7.11 for data management (Revelle, 2015).
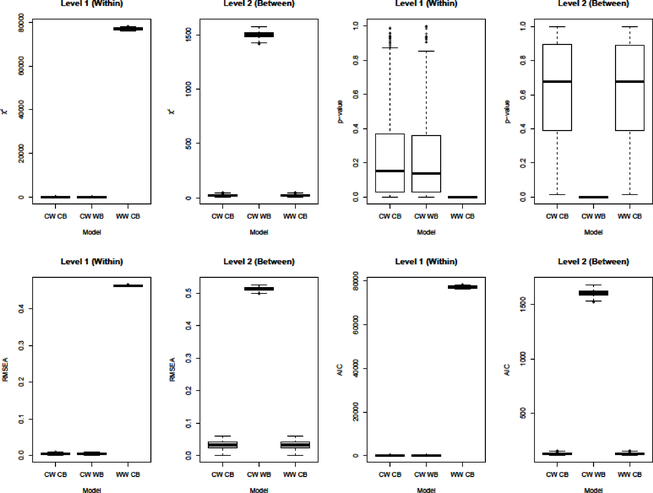
Correctly-specified MSEM and ML-SEM analyses (see Table 1) recovered the simulated observed item means, residual error, and factor loadings at both levels (see Supplemental Figure 1S). Empirical parameter estimates show high accuracy and precision around the true simulated values. The partially-saturated model fit indices (i.e., χ2, RMSEA, AIC) accurately identified correctly-specified and mis-specified models at levels 1 and 2 (see Table 2 and Figure 3). Regarding absolute model fit, a significant chi-squared statistic at p ≤ 0.05 or RMSEA ≥ 0.08 accurately indicated all cases where the level 1 or 2 model was mis-specified. Using the RMSEA ≥ 0.08 cut-off also accurately indicated all cases where the level 1 or 2 model was correctly-specified. However, consistent with prior research (e.g., Bollen, 1990; Marsh, Balla, & McDonald, 1988), the chi-squared statistic may incorrectly indicate a poor fitting model; in the present study, the chi-squared statistic incorrectly suggested poor model fit on approximately 33% of samples where the level 1 model was correctly specified and 2% of samples where the level 2 model was correctly specified. Regarding relative fit, comparison of average AIC estimates indicated that the partially-saturated model fit approach and associated function accurately index better fit of the correctly- to incorrectly-specified models. When examined separately, the AIC value for the correctly-specified model was lower than the value for the mis-specified model for both level 1 (N = 496 [100% of samples]) and 2 (N = 494 [99.6% of samples]). Comparison of BIC values also indicated the correctly-specified model at both levels on all samples.
Table 2.
Model Fit Summary for Correctly and Incorrectly Specified 1-Factor Multilevel Structural Equation Models
| Approach | Model | Level (df) | χ2 | p | RMSEA | AIC | ||
|---|---|---|---|---|---|---|---|---|
| M (SD) | M (SD) | N (%) | M (SD) | N (%) b | M (SD) | |||
| MSEM | CW, CB | 1 (12) | 18.05 (7.03) | 0.24 (0.26) | 166 (33.47) | 0.004 (0.001) | 0 (0) | 154.05 (7.03) |
| 2 (28) | 24.68 (7.44) | 0.63 (0.29) | 10 (2.02) | 0.03 (0.01) | 0 (0) | 128.68 (7.44) | ||
| WW, CB | 1 (12) | 77072.38 (326.24) | < 0.01 (< 0.01) | 499 (100) | 0.46 (0.001) | 499 (100) | 77208.38 (326.24) | |
| 2 (28) | 24.57 (7.49) | 0.62 (0.29) | 11 (2.20) | 0.03 (0.01) | 0 (0) | 128.75 (7.49) | ||
| CW, WB | 1 (12) | 18.21 (6.95) | 0.23 (0.25) | 164 (32.80) | 0.004 (0.002) | 0 (0) | 154.20 (6.95) | |
| 2 (28) | 1502.64 (28.94) | < 0.01 (< 0.01) | 500 (100) | 0.51 (0.005) | 500 (100) | 1606.64 (28.94) | ||
| ML-SEM | CW, CB | -- (4712) | 5760.57 (121.64) | < 0.01 (< 0.01) | 499 (100) | 0.03 (0.002) | 0 (0) | −18073.14 (195.91) |
| WW, CB | -- (4712) | 11913.61 (150.57) | < 0.01 (< 0.01) | 500 (100) | 0.09 (0.001) | 500 (0) | −11919.13 (217.47) | |
| CW, WB | -- (4712) | 6722.20 (131.22) | < 0.01 (< 0.01) | 500 (100) | 0.05 (0.002) | 0 (0) | −17110.54 (206.95) | |
Note. M = mean, SD = standard deviation over 500 samples
indicates the number and percent of samples where p ≤ 0.05
indicates the number and percent of samples where RMSEA ≥ 0.08
CW indicates correct within model; CB indicates correct between model; WW indicates wrong within model; WB indicates wrong between model; MSEM indicates multilevel structural equation modeling (e.g., Goldstein & McDonald, 1988; Muthén, 1990, 1994); ML-SEM indicates multilevel structural equation modeling (Mehta & Neale, 2005). Because of suspiciously high outlier χ2 values, 4 samples of the CW, CB model under the MSEM approach, 1 sample of the CW, WB model under the MSEM approach, and 1 sample of the CW, CB under the ML-SEM approach were removed. See supplemental table 1S for the Bayesian Information Criteria.
Figure 3.
Summary of Model Fit Indices from the Simulation Study. Note. CW = correct within (i.e., level 1), WW = wrong within, CB = correct between (i.e., level 2), WB = wrong between. Because of suspiciously high outlier χ2 values, 4 samples of the CW, CB and 1 sample of the CW, WB models were removed.
Finally, ML-SEM fit indices suggest that RMSEA accurately indexed the correctly-specified model, whereas, as expected, the chi-squared statistic was inflated due to sample size (Marsh et al., 1988). Both mis-specified models produced worse overall model fit as indexed by chi-squared, RMSEA, and AIC values. Results are also consistent with prior evidence: overall model fit was particularly impacted by misspecification at level 1 (e.g., Hsu et al., 2015).
Empirical Example
To illustrate the application of model fit indices for multilevel structural equation models, model fit indices were estimated to evaluate the structure of positive and negative affect in three multilevel confirmatory factor analyses (CFA). Three-hundred and forty-five undergraduate students completed an ecological momentary assessment (EMA) procedure in which they reported on current affect three times per day for 14 days using a smartphone-based app. Affect was assessed using nine items (five of which probe negative affect, e.g., “unhappy”, and four probe positive affect, e.g., “joyful”) rated from 0 (“Not at all”) to 6 (“Extremely much”) based on work by Diener and Emmons (1985). Participants completed the study for course credit; the study was approved by the Institutional Review Board of Virginia Commonwealth University, where the data were collected. Participants showed high compliance with the EMA procedure; 312 participants (90.4%) completed at least 34 (81%) of 42 scheduled assessments.
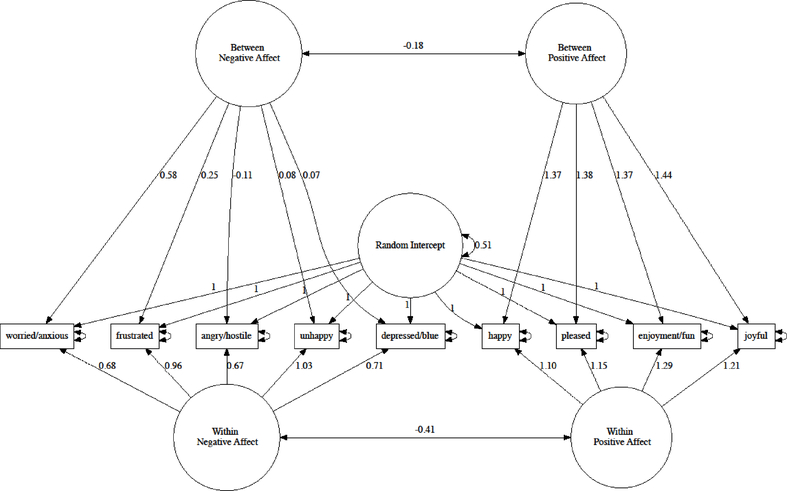
Three specifications were modeled to examine hypothesized structures for positive and negative affect. Consistent with the theory that positive and negative affect fall on a single dimension, the first model (A) included one latent factor at each level (i.e., within- and between-person; see Supplemental Figure 2S). The second model (B) examined the notion that positive and negative affect form distinct, correlated latent factors at both levels of analysis (see Supplemental Figure 3S). Using the partially-saturated model fit approach, level-specific fit is unaffected by specification at other levels of analysis (Ryu & West, 2009). Therefore, these two models are sufficient to compare the 1- and 2-factor specifications at both the within- and between-person levels of analysis. A third model (C) modified the 2-factor specification at the between-person level to include a random intercept (see Figure 4), which accounts for between-person variance such as that due to reporting style (Maydeu-Olivares & Coffman, 2006).
Figure 4.
Illustration of the Final Model for Within- and Between-Person Affect Structure.
As indexed by χ2 and RMSEA, the 1-factor model A yielded poor fit to the data at both levels of analysis (see Table 3). However, RMSEA indicates adequate fit of the 2-factor model at level 1 (i.e., within-person). A considerably smaller AIC further indicates better fit for the 2-factor model B over the 1-factor model at level 1. While AIC suggests that including the random intercept improved fit at level 2 (model C; see Table 3 and Figure 4), χ2 and RMSEA signify poor model fit at level 2. Subsequent analyses probed the source of misfit at level 2. Inspection of histograms for item means at the between-person level reveals considerable departure from multivariate normality for negative affect items (see Supplemental Figure 4S), though not for positive affect items (see Supplemental Figure 5S). Deviations from multivariate normality are known to impact traditional model fit indices, which may lead to model rejection despite a properly specified model for level 2 (Barrett, 2007). Alternatively, although model C reflects prior investigations (e.g., Diener & Emmons, 1985; Watson, Clark, & Tellegen, 1988), it may be a poor specification of the between-person structure of affect.
Table 3.
Model Fit for Multilevel Structural Equation Model of Affect
| Model | Level | χ2 | df | p | RMSEA | AIC |
|---|---|---|---|---|---|---|
| A | 2 | 12331.44 | 36 | < 0.001 | 0.99 | 12457.44 |
| 1 | 16118.07 | 18 | < 0.001 | 0.24 | 16280.07 | |
| B | 2 | 6704.73 | 35 | < 0.001 | 0.74 | 6832.73 |
| 1 | 1577.41 | 17 | < 0.001 | 0.08 | 1741.41 | |
| C | 2 | 5121.40 | 34 | < 0.001 | 0.66 | 5251.40 |
| 1 | 1552.00 | 17 | < 0.001 | 0.08 | 1716.00 |
Note. Model A includes 1 factor within- and 1 factor between-person (see Supplemental Figure 2S); Model B includes 2 factors within- and 2 factors between-person (see Supplemental Figure 3S); Model C includes 2 factors within-person / 2 factors and a random intercept between-person (see Figure 4).
Overall, the final model (i.e., model C) supports prior evidence that the 2-dimensional structure of positive and negative affect may reflect within-person variation over time (e.g., Diener & Emmons, 1985; Watson et al., 1988). Over time, within-person fluctuations in positive and negative affect are moderately negatively correlated such that fluctuations in one explain approximately 16.8% of variation in the other. This is consistent with another investigation of within-person variation in affect assessed thrice daily (Pritikin, Rappaport, & Neale, 2017). While the present data support a 2-dimensional structure of affect, they further indicate that positive and negative affect may be moderately correlated over time rather than orthogonal.
At the between-person level, the partially-saturated approach to model fit demonstrates that the present data may be inconsistent with the 1- or 2-dimensional models of affect. While others have suggested alternative, hierarchical structures to explain between-person variation in affect (e.g., Tellegen, Watson, & Clark, 1999), models A and B, evaluated here, represent the two prevailing theorized structures of affect, which have been supported in samples larger than the present study (e.g., Watson et al., 1988). It is beyond the scope of the present paper to explore alternative models for the structure of affect. A full investigation of the structure of between-person variation in affect would require a substantially larger sample. The current results illustrate that the partially-saturated model fit approach can identify that the 2-dimensional model of positive and negative affect may explain within-person variation over time but not variation between-person.
Discussion
The present study illustrates the estimation and use of partially-saturated model fit indices to evaluate level-specific fit in MSEM, as described by Ryu and West (2009). We report on new functions that create and optimize three saturated or partially-saturated models to compute level-specific fit for 2-level structural equation models. A simulation study of 500 samples demonstrates that the approach, and attendant functions, accurately identified correctly- and incorrectly-specified models while distinguishing between misspecification at each level. Moreover, we describe similarities between MSEM and ML-SEM, as described by Mehta and Neale (2005). Mehta and Neale propose the use of standard model fit indices; we demonstrate that RMSEA accurately identified a correctly-specified. Finally, we provide an empirical illustration of the use of MSEM fit indices to evaluate the within- and between-person structure of affect among university students using an EMA procedure.
MSEM, using the partially-saturated model fit indices developed by Ryu and West (2009), accurately identified when each model for level 1 and 2 were correctly- or incorrectly-specified. However, MSEM imposes several assumptions, such as measurement invariance and stationarity. In contrast, the ML-SEM approach developed by Mehta and Neale (2005) allows one to test each assumption. Nevertheless, the present simulation results suggest that overall model fit may reflect whether the level 1 model is correctly specified and may be unable to detect misspecification at level 2. The choice of approach will vary based on the goals of a given analysis. For example, ML-SEM is flexible and well-suited to test specific hypotheses and assumptions at level 1 where it is able to detect misspecification. However, research that seeks to evaluate the multivariate structure at different levels of analysis may require the MSEM approach to ensure adequate model fit for each level. Finally, the present results support prior recommendations to consider the chi-squared statistic a conservative test of model fit and encourage the use of RMSEA, which accurately detected all cases of correct and incorrect specification using the partially-saturated model fit approach.
As illustrated above, standard model fit indices assume that data are independently and identically distributed. However, many processes central to social and medical sciences rely on identifying the pertinent level of analysis. Research on one level (e.g., between-persons) is inadequate to evaluate theory relevant to another (Curran & Bauer, 2011; Molenaar, 2004). For example, poverty might contribute to psychiatric risk through direct influence on an individual (i.e., between-persons) or through influence on the surrounding community (i.e., between-communities) that creates pathogenic conditions. Additionally, changes in poverty (e.g., loss of financial security) over time for a single person (i.e., within-person) might uniquely contribute to when one experiences the onset of psychiatric distress. MSEM is well-suited to disaggregate covariance among observed variables due to various levels of a nested data structure (e.g., children within schools or observations within person; Preacher, Zyphur, & Zhang, 2010), which allows one to test theoretical models of how variables are interrelated at different levels of analysis. Additionally, MSEM allows users to specify measurement models to extract latent, unobserved factors at each level of analysis. For example, in the example above, multilevel confirmatory factor analysis of affect items evaluated whether within- and between-person covariance of affect items (e.g., “joy”) over time derives from the 2-dimensional structure. The partially-saturated model fit approach illustrates that the 2-dimensional structure fits within-person variation in affect over time though not between-person variation. Additionally, while 2 distinct dimensions, the present data indicate a moderate within-person correlation of negative with positive affect, which is consistent with recent research (Pritikin, Rappaport, et al., 2017).
However, while MSEM allows the user to specify and test unique measurement and structural models at each level of analysis, it is imperative that the specified model for each level of analysis adequately fits the empirical data. Standard log-likelihood estimates and resulting model fit indices (e.g., χ2, RMSEA, AIC) are biased towards identifying misspecification at the lowest level of analysis (i.e., level 1). Hence, researchers are strongly encouraged to evaluate level-specific model fit to both ensure adequate fit to the empirical data and to compare competing alternative models for each level of analysis. To support researchers in evaluating level-specific model fit, we demonstrate, and report on the implementation of, partially-saturated model fit indices in OpenMx, an open-source SEM and MSEM package.
Supplementary Material
Acknowledgments
The authors do not have any financial interests that might influence this research. The present work was not presented or published elsewhere. This work was supported by a grant from the National Institute of Mental Health (MH020030). This research was enabled in part by support provided by the Shared Hierarchical Academic Research Computing Network (SHARCNET: www.sharcnet.ca) and Compute/Calcul Canada (www.computecanada.ca).
References
- Akaike H (1987). Factor analysis and the AIC. Psychometrika, 52, 317–332. [Google Scholar]
- Barrett P (2007). Structural equation modelling: Adjudging model fit. Personality and Individual Differences, 42(5), 815–824. [Google Scholar]
- Bentler PM (1980). Multivariate analysis with latent variables: Causal modeling. Annual Review of Psychology, 31(1), 419–456. [Google Scholar]
- Bollen KA (1990). Overall fit in covariance structure models: Two types of sample size effects. Psychological Bulletin, 107, 256–259. [Google Scholar]
- Box GEP (1976). Science and Statistics. Journal of the American Statistical Association, 71(356), 791. [Google Scholar]
- Chen F, Curran PJ, Bollen KA, Kirby J, & Paxton P (2008). An Empirical Evaluation of the Use of Fixed Cutoff Points in RMSEA Test Statistic in Structural Equation Models. Sociological Methods & Research, 36(4), 462–494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Curran PJ, & Bauer DJ (2011). The Disaggregation of Within-Person and Between-Person Effects in Longitudinal Models of Change. Annual Review of Psychology, 62(1), 583–619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diener E, & Emmons RA (1985). The independence of positive and negative affect. Journal of Personality and Social Psychology, 47, 1105–1117. [DOI] [PubMed] [Google Scholar]
- Fan X, & Wang L (1998). Effects of potential confounding factors on fit inidices and parameter estimates for true and misspecified SEM models. Educational and Psychological Mesaurement, 58, 701–735. [Google Scholar]
- Goldstein H, & McDonald RP (1988). A general model for the analysis of multilevel data. Psychometrika, 53(4), 455–467. [Google Scholar]
- Hoyle RH (Ed.). (2012). Handbook of Structural Equation Modeling. New York, NY: Guilford Press. [Google Scholar]
- Hsu H-Y, Kwok O, Lin JH, & Acosta S (2015). Detecting Misspecified Multilevel Structural Equation Models with Common Fit Indices: A Monte Carlo Study. Multivariate Behavioral Research, 50(2), 197–215. [DOI] [PubMed] [Google Scholar]
- Hu L, & Bentler PM (1998). Fit indices in covariance structure modeling: Sensitivity to underparameterized model misspecification. Psychological Methods, 3(4), 424. [Google Scholar]
- Kenny DA, Kashy DA, & Cook WL (2006). Dyadic Data Analysis. New York, NY: Guilford Press. [Google Scholar]
- Kim ES, Dedrick RF, Cao C, & Ferron JM (2016). Multilevel Factor Analysis: Reporting Guidelines and a Review of Reporting Practices. Multivariate Behavioral Research, 0–0. [DOI] [PubMed] [Google Scholar]
- Lee S-Y (1990). Multilevel Analysis of Structural Equation Models. Biometrika, 77(4), 763. [Google Scholar]
- Liang J, & Bentler PM (2004). An EM algorithm for fitting two-level structural equation models. Psychometrika, 69(1), 101–122. [Google Scholar]
- Marsh HW, Balla JR, & McDonald RP (1988). Goodness-of-fit indexes in confirmatory factor analysis: The effect of sample size. Psychological Bulletin, 103(3), 391. [Google Scholar]
- Maydeu-Olivares A, & Coffman DL (2006). Random intercept item factor analysis. Psychological Methods, 11(4), 344–362. [DOI] [PubMed] [Google Scholar]
- Mehta PD, & Neale MC (2005). People Are Variables Too: Multilevel Structural Equations Modeling. Psychological Methods, 10(3), 259–284. [DOI] [PubMed] [Google Scholar]
- Molenaar PC (2004). A manifesto on psychology as idiographic science: Bringing the person back into scientific psychology, this time forever. Measurement, 2(4), 201–218. [Google Scholar]
- Muthén BO (1994). Multilevel covariance structure analysis. Sociological Methods & Research, 22, 376–398. [Google Scholar]
- Muthén BO, & Muthén LK (1998). Mplus User’s Guide. (Eighth Edition). Los Angeles, CA: Muthén & Muthén. [Google Scholar]
- Muthén BO, & Satorra A (1995). Complex Sample Data in Structural Equation Modeling. Sociological Methodology, 25, 267. [Google Scholar]
- Neale MC, Hunter MD, Pritikin JN, Zahery M, Brick TR, Kickpatrick RM, … Boker SM (2016). OpenMx 2.0: Extended structural equation and statistical modeling. Psychometrika, 81, 535–549. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Preacher KJ, Zyphur MJ, & Zhang Z (2010). A general multilevel SEM framework for assessing multilevel mediation. Psychological Methods, 15(3), 209–233. [DOI] [PubMed] [Google Scholar]
- Pritikin JN, Hunter MD, von Oertzen T, Brick TR, & Boker SM (2017). Many-level multilevel structural equation modeling: An efficient evaluation strategy. Structural Equation Modeling: A Multidisciplinary Journal, 24(5), 684–698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pritikin JN, Rappaport LM, & Neale MC (2017). Likelihood-based confidence intervals for a parameter with an upper or lower bound. Structural Equation Modeling: A Multidisciplinary Journal, 24, 395–401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Core Team. (2015). R: A Language and Environment for Statistical Computing.
- Raudenbush SW, & Bryk AS (2002). Hierarchical Linear Models: Applications and Data Analysis Methods (2nd ed.). Thousand Oaks, CA: Sage Publications. [Google Scholar]
- Revelle W (2015). psych: Procedures for Personality and Psychological Research (Version 1.5.8).
- Ryu E, & West SG (2009). Level-Specific Evaluation of Model Fit in Multilevel Structural Equation Modeling. Structural Equation Modeling: A Multidisciplinary Journal, 16(4), 583–601. [Google Scholar]
- Steiger JH, Shapiro A, & Browne MW (1985). On the multivariate asymptotic distribution of sequential chi-square statistics. Psychometrika, 50(3), 253–263. [Google Scholar]
- Tellegen A, Watson D, & Clark LA (1999). On the Dimensional and Hierarchical Structure of Affect. Psychological Science, 10(4), 297–303. [Google Scholar]
- Watson D, Clark LA, & Tellegen A (1988). Development and Validation of Brief Measures of Positive and Negative Affect: The PANAS Scales. Journal of Personality and Social Psychology, 54, 1063–1070. [DOI] [PubMed] [Google Scholar]
- Yuan K-H, & Bentler PM (2007). Multilevel covariance structure analysis by fitting multiple single-level models. Sociological Methodology, 37(1), 53–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.