Macrocyclic peptidomimetics as inhibitors of insulin-regulated aminopeptidase (IRAP)

The IRAP inhibition of the macrocyclic peptide, HA-08 has been explored by analogue design coupled to molecular dynamics analysis.

Abstract

Macrocyclic analogues of the linear hexapeptide, angiotensin IV (AngIV) have proved to be potent inhibitors of insulin-regulated aminopeptidase (IRAP, oxytocinase, EC 3.4.11.3). Along with higher affinity, macrocycles may also offer better metabolic stability, membrane permeability and selectivity, however predicting the outcome of particular cycle modifications is challenging. Here we describe the development of a series of macrocyclic IRAP inhibitors with either disulphide, olefin metathesis or lactam bridges and variations of ring size and other functionality. The binding mode of these compounds is proposed based on molecular dynamics analysis. Estimation of binding affinities (ΔG) and relative binding free energies (ΔΔG) with the linear interaction energy (LIE) method and free energy perturbation (FEP) method showed good general agreement with the observed inhibitory potency. Experimental and calculated data highlight the cumulative importance of an intact N-terminal peptide, the specific nature of the macrocycle, the phenolic oxygen and the C-terminal functionality.

Introduction

Insulin-regulated aminopeptidase (IRAP, oxytocinase, EC 3.4.11.3) is a member of the M1 family of aminopeptidases and has been found to participate in a wide range of physiological processes.1,2 First identified as the enzyme that degrades oxytocin in the late stages of pregnancy and in childbirth,3 IRAP has also been shown to process other peptide hormones such as vasopressin and a variety of other putative in vivo substrates.4–6 IRAP is also proposed to play a role in GLUT4 translocation to the plasma membrane upon insulin-stimulation and is known to act in the processing of peptides for presentation onto MHC class I molecules.7,8

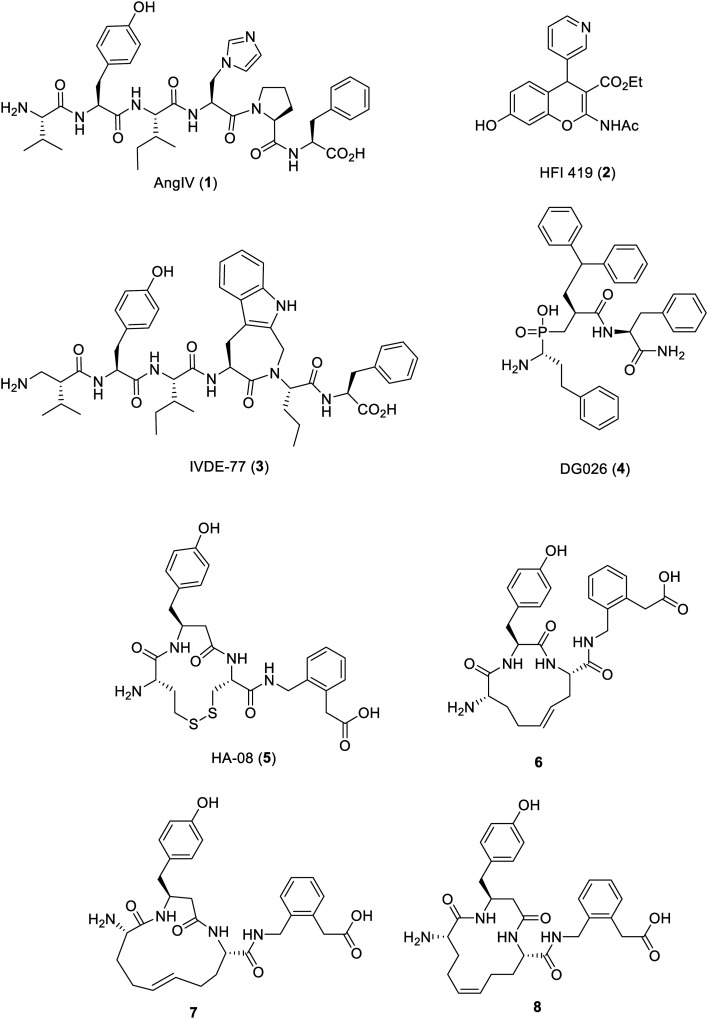
The aminopeptidase activity of IRAP has been shown to be competitively inhibited by angiotensin IV (AngIV, 1), a product of proteolytic processing of angiotensin II.6,9–15 AngIV has also been shown to improve performance in a number of memory tasks when injected into the brains of rats.9–15 This activity has provided the impetus for the development of new long-lived pharmacological IRAP inhibitors as potential therapeutics to treat Alzheimer's disease, especially given the very short in vivo half-life of AngIV. The published IRAP inhibitors described to date (Fig. 1) include small molecules such as HFI-419 (2),16 AngIV peptidomimetics, such as the β-amino acid modified compound, IVDE-77 (3),17,18 and more recently transition state mimetics such as DG026 (4) based on antigen substrate peptides, as shown in Fig. 1.19,20

Fig. 1. Reported linear peptides, cyclic peptides and non-peptide IRAP inhibitors.

From 2006–2011, details relating to macrocyclic analogues of AngIV with N-terminal disulphide or metathesis-linked peptides were published.21–25 These compounds were inspired by the structural analogy between AngIV as inhibitor and the substrate oxytocin, which is a cyclic peptide. Firstly, it was found that cyclic disulphide analogues bearing cysteine or homocysteine substitutions for valine and/or isoleucine could retain some level of inhibitory potency, in line with the capacity for IRAP to accept cyclic peptide substrates.21 Extending this concept into analogues bearing a modified C-terminus, it was found that further gains in affinity could be achieved by incorporating a β3-homotyrosine, with compound HA-08 (5), as a standout example.23 Thirdly, it was then shown that the sulfur atoms could be replaced by carbon, using ring closing metathesis to yield a trans-alkene linked macrocycle yielding compound 6 with a K_i of 4 nM as well as isomers 7 and 8 with a K_i of 1.8 nM and 30 nM respectively.24 The rationale for the activity of the compounds described in those studies was built upon pharmacophore-based models of affinity noting the effects of ring size and conformation but in the absence of any structural data relating to the IRAP protein. Such data now exists as since 2015, four structures of IRAP have been solved – two of the apo-enzyme and two with bound transition-state analogue inhibitors.26,27

The cyclic nature of 5 is of interest because macrocyclization is a structural feature that has been highlighted to convey drug-like properties of larger molecules, including oral bioavailability, in what is termed “beyond Rule of 5 space”28–32 and macrocyclic model compounds show improved membrane permeability compared to acyclic matched pairs.33,34 Macrocyclization can result in improved affinity for the target, improved selectivity and reduced metabolism.35,36 The macrocyclic HCV NS3/4A protease inhibitors, such as simeprevir conform to this notion.37

Against this background, it is important to consider how macrocyclic peptide inhibitors of IRAP exert their inhibitory potency and whether the conformation of the cyclic moiety may be involved in trapping specific conformational states of the enzyme. Here we describe our extension of the studies relating to macrocyclic peptide-based inhibitors of IRAP. A series of analogues of 5 were prepared that tested specific elements of the proposed pharmacophore. The resultant assay data was rationalised by the use of molecular dynamics (MD) analysis against X-ray structures of IRAP to support our models of binding.

Results

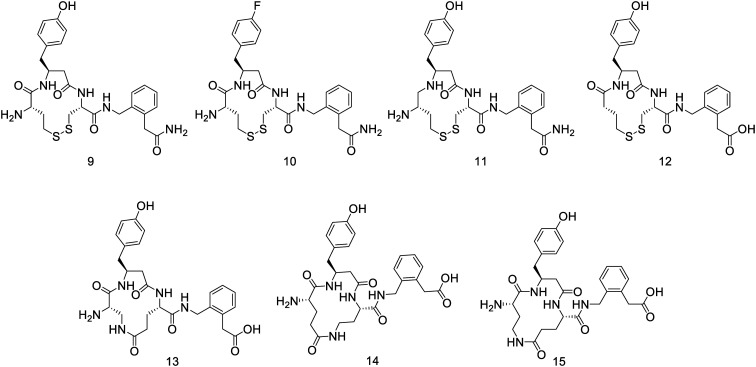
In order to expand the data set against which we could study the binding of the cyclic peptides, we prepared a series of additional novel peptides. The structure of 5 was modified in several ways that would test the basic pharmacophore. Firstly, a range of structural modifications to 5 were made to test the postulated pharmacophoric elements such as replacing the C-terminal carboxylate with an amide (9), the phenolic tyrosine with a fluorophenyl group (10), modifying the P1–P1′ amide linkage as the secondary amine (11) and removing the N-terminal amino group (12), as outlined in Fig. 2. These compounds were all synthesized by adaptation of the reported synthesis of 5.

Fig. 2. Compounds synthesized in this study to test various pharmacophoric elements of the lead compound 5.

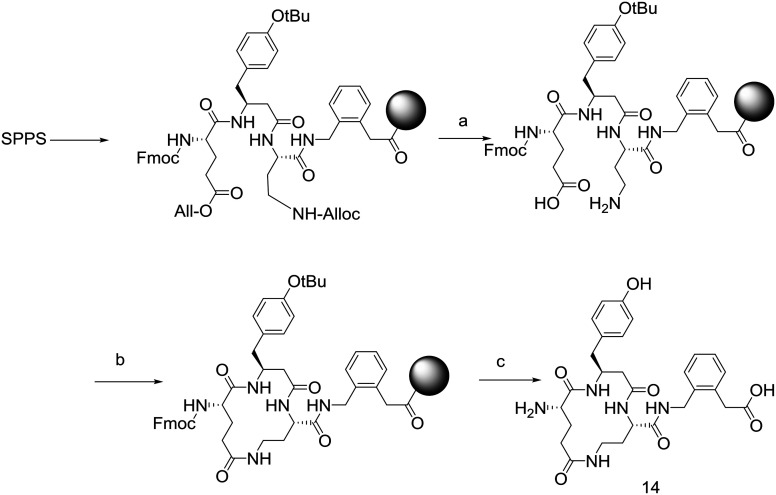
In addition the disulfide linkage of 5 was replaced by lactam bridges. In these cases, lactam bridges were constructed with Dap¹-Glu³ (13), Glu¹-Dab³ (14) and Dab¹-Glu³ (15) linkages (Fig. 3). These peptides were constructed by preparation of the corresponding linear Alloc-protected Dap or Dab residues and O-All protected Glu residue (Scheme 1). Side chain deprotection with Pd(PPh₃)₄, PhSiH₃ was followed by on-resin cyclisation using HCTU. Cleavage with TFA yielded the target cyclic peptides.

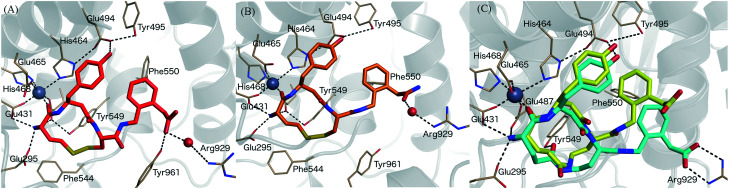
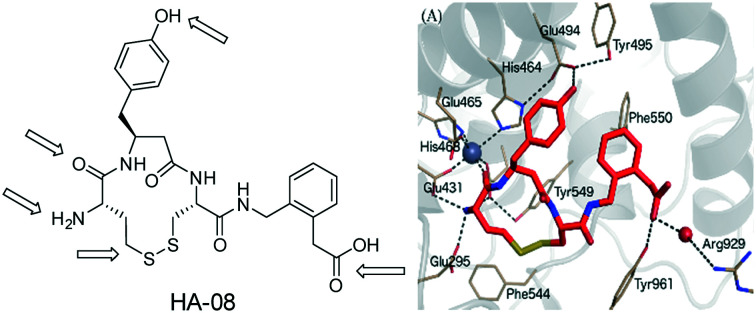
Fig. 3. Binding mode of IRAP inhibitors to the Zn²⁺ binding site. (A) Compound 5 (HA08), (B) compound 9 (C) compound 14 modelled in the cis (yellow) and trans (blue) configurations. Zn²⁺ and water molecules are represented as a grey and red spheres, respectively.

Scheme 1. Synthetic scheme to provide lactam bridged cyclic peptides using an N-alloc/O-allyl orthogonal protection strategy. (a) Pd(PPh₃)₄, PhSiH₃; (b) HCTU, DIPEA; (c) TFA, TIPS, H₂O.

The macrocyclic peptides prepared in this study were assayed for their ability to block IRAP cleavage of the substrate Leu-MCA using membrane extracts from transiently transfected HEK-293T cells. Compared to 5 which gave an IC₅₀ value of 18 nM, the new macrocycles showed a range of activities with some interesting new insights into the structure activity relationships as summarized in Table 1.

Table 1. Inhibition of IRAP by macrocyclic peptides.

Compound	IC50 (μM) ± SEM (n > 2)	K i a (nM)
5	0.018 ± 0.002	10.9
9	0.039 ± 0.03	23.7
10	0.33 ± 0.18	200.5
11	2.06 ± 0.34	1251.5
12	>100	>100
13	>100	>100
14	1.11 ± 0.20	674.4
15	1.46 ± 0.56	887.0

^a K _i was calculated using the synthetic substrate Leu-MCA; IC₅₀ = K_i (1 + [S]/K_m), where [S] and K_m were Leu-MCA K_m = 38.7 μM and [S] = 25 μM.38

The macrocyclic primary amide derivative 9 has an IC₅₀ of 39 nM, just over two-fold lower than 5. The replacement of the hydroxy group of the phenyl ring for a fluoro atom in the para position of 5 resulted in the almost 10-fold less potent IRAP inhibitor 10 with an IC₅₀ value of 330 nM, suggesting that an interaction of the hydroxyl group with the protease is important but not absolutely critical. This replacement of the para hydroxy group might be useful in a peptidomimetic to avoid rapid Phase II metabolism. Compound 11 was a weak binder in the micromolar range, while 12 was completely inactive, showing the importance of the free amine and carbonyl of the intact amino acid structure at the amino-terminus for high affinity.

The three lactam bridged peptides were all much less active than HA-08, with compounds 14 and 15 approximately 100-fold less active than 5. These two peptides have 14 membered macrocycles – larger than 5 which is a 13 membered macrocycle. In contrast compound 13, a 13-membered ring, was completely inactive. The influence of ring size in disulfide analogues of 5 has been noted previously.23

MD, LIE and FEP calculations

Four crystal structures of IRAP have been solved.26,27 We previously described a tentative model for 5 binding by applying MD simulations and calculating associated binding free energies by the linear interaction energy (LIE) method. The model predicted that the carbonyl of the N-terminal amino acid is coordinated to the Zn²⁺ ion, whereas the terminal amine is fixed by three glutamate carboxylates (Glu431, Glu487, and Glu295).39 The aromatic rings of the C-terminal phenylacetic acid and the β³-homotyrosine side chain interact and Phe550 further stabilizes aromatic/hydrophobic packing. The phenolic group of 5 is fixed by Glu494 and Tyr495 and the C-terminal carboxylate group forms a hydrogen bond to Tyr961 and interacts via a water molecule with the positively charged Arg929 (Fig. 3A). This binding mode was used as a template to model the binding of compounds 7–15 to IRAP providing insight into the effects of the substitutions (e.g. carboxylate for amide, 9, Fig. 3B) and the disulfide lactam (e.g. disulphide for lactam, 14, Fig. 3C).

After initial docking, MD simulations followed for each compound, and the associated binding free energies were calculated using the LIE method.39–41 The LIE parameters previously derived for compound 5 and related peptide analogues were retained in this work,39 given the close analogy of 5 with the present series. Briefly, the LIE parameters are scaling factors that separately weight the energy differences of both polar and non-polar ligand-surrounding interactions, between water and protein simulations [see eqn (1) in methods]. While the non-polar scaling factor is fixed to the value tested in ligands of different chemical nature (α = 0.18),39,42,53 the weighted electrostatic interactions needed to be tuned down to an empirically derived value of β = 0.19, due to the very large electrostatic environment in the binding site and the need to compensate for possible insufficient dielectric screening in the microscopic system.53 Finally, a positive offset value of γ = 7.3 was determined to account for the correct absolute binding affinities.39 The binding free energies obtained with this LIE parameterization are reported in Table 2, and are compared with the experimental binding free energies extracted from IC₅₀ values as in [eqn (2)] or K_i when indicated. The standard error of the mean (SEM) of the calculations is reported as an average of independent simulations, and is in most cases under 1 kcal mol^–1, accounting for sufficiently converged simulations.

Table 2. Experimental and LIE calculated binding free energies (in kcal mol^–1) for ligands in complex with IRAP. Errors are SEM.

Ligand	Free		Bound		ΔGobsbind kcal mol–1	ΔGcaclbind kcal mol–1
	〈Uell–s〉	〈UvdWl–s〉	〈Uell–s〉	〈UvdWl–s〉
5, HA08 a	–321.94 ± 2.5	–24.03 ± 0.1	–401.88 ± 0.7	–43.06 ± 0.2	–11.29 ± 0.1	–11.57 ± 0.5
7 b	–317.96 ± 6.7	–23.81 ± 0.2	–392.67 ± 1.6	–41.24 ± 0.4	–12.40 ± 0.0	–10.27 ± 1.3
8 b	–328.87 ± 2.0	–23.49 ± 0.1	–389.62 ± 0.4	–42.07 ± 0.2	–10.66 ± 0.0	–7.79 ± 0.4
9	–228.15 ± 1.2	–31.78 ± 0.0	–281.92 ± 1.1	–50.64 ± 0.5	–10.81 ± 0.5	–6.49 ± 0.3
10	–215.08 ± 0.8	–33.59 ± 0.1	–268.72 ± 0.5	–53.09 ± 0.4	–9.50 ± 0.3	–6.58 ± 0.2
11	–230.39 ± 1.7	–31.75 ± 0.1	–256.74 ± 0.4	–53.78 ± 0.3	–8.37 ± 0.1	–1.77 ± 0.3
12 c	–215.69 ± 3.3	–32.56 ± 0.2	–231.79 ± 1.0	–52.05 ± 0.3	≥5.71	0.67 ± 0.7
13 _cis c	–368.11 ± 4.8	–21.82 ± 0.2	–415.54 ± 1.7	–40.93 ± 0.6	≥5.71	–5.31 ± 1.0
13 _trans b	–367.98 ± 5.9	–21.58 ± 0.2	–406.59 ± 0.7	–41.90 ± 0.5	≥5.71	–3.83 ± 1.2
14 _cis	–338.68 ± 2.0	–22.91 ± 0.2	–389.26 ± 0.4	–42.07 ± 0.4	–8.75 ± 0.1	–5.93 ± 0.4
14 _trans	–325.59 ± 3.5	–24.19 ± 0.2	–389.04 ± 1.3	–42.84 ± 0.3	–8.75 ± 0.1	–8.32 ± 0.7
15 _cis	–356.17 ± 2.6	–23.04 ± 0.2	–404.53 ± 0.5	–42.80 ± 0.3	–8.58 ± 0.2	–5.61 ± 0.5
15 _trans	–341.04 ± 8.9	–23.46 ± 0.3	–404.13 ± 0.7	–41.78 ± 0.3	–8.58 ± 0.2	–8.19 ± 1.7

^aΔG_bind derived from the experimental IC₅₀ as in this work; alternatively, a value of ΔG_bind = –11.6 kcal mol^–1 was derived from the K_i from ref. 39.

^bΔG_bind derived from the experimental K_i values from Andersson et al.24

^cExperimental IC₅₀ is >100 μM.

In broad terms, the model explains the observed SAR pertaining this series, indicating the detrimental effects of the various structural changes to 5. However, the model shows a relatively high mean unassigned error (MUE) between calculated and experimental affinities of 2.5 kcal. This appears to be due to the under prediction of the positively charged compounds 9, 10 and 11, which are extraordinary sensitive to the fluctuations of the strong electrostatic interactions with the Zn²⁺. In fact, when these compounds are not considered the calculated value reduces to half (MUE = 1.2).

The results for ligands 13–15, which contain an amide bond as a bioisostere of the disulfide bridge in 5, closely matched experimental observations. Each of the cis and trans conformations of the lactam bridge were considered to assess the bioactive conformation on the basis of the predicted affinities. Thus, compound 13, which bears an amide replacement of the disulphide bond in the 13-membered macrocycle, is completely inactive, and the LIE model predicts this inactivity for either the cis or the trans conformation. Conversely, compounds 14 and 15 introduce the amide in a 14-membered ring and retain quite some affinity for IRAP. Our model predicts in both cases that the trans amide conformation is favoured, with binding affinities very much in agreement with the experimental data (see Table 2). In compound 14, the trans configuration is specifically stabilized through an interaction between Tyr549 and amide oxygen that is replacing the disulfide bond, while the carboxy-terminal group reaches directly to Arg929, making a stronger salt bridge interaction (see Fig. 3C). Compound 13, either in a cis or trans conformation does not exhibit the hydrophobic packing interaction with Phe550 and the polar interaction with Arg929, observed in the C-terminal tail in compound 5 (see Fig. 3A) and the trans conformers of 14 and 15. This causes fluctuations in the C-terminal along the MD sampling leading to instability of the key interactions with IRAP, which is ultimately translated in a relative drop of the predicted affinity by several kcal mol^–1, in agreement with the experimental data.

In considering the outcomes for 9–11, a separate LIE parameterization to account for charge differences might eventually improve the precision of the calculations. However, the small number of charged compounds precluded such an approach. Instead, we considered that these analogues were well suited to study with the first-principles free energy perturbation (FEP) method.42 Here, one calculates the relative change in binding free energy between a pairs of compounds (ΔΔG), and compare with the corresponding experimental shifts in binding affinities. During the MD simulation sampling, one compound is transformed into another by a gradual linear combination mix of their relative potentials, both in the bound and unbound states (see methods). In this case, compound 5 was used as a reference ligand to evaluate the effect caused by replacement of the terminal carboxylic acid group by an amide (to yield the positively charged compound 9), the additional loss of the carbonyl coordinating the Zn²⁺ ion (positively charged compound 11) or the effect of losing the amino group (negatively charged compound 12). The effect of substituting the hydroxyl in compound 9 by a fluorine atom (yielding the positively charged compound 10) was evaluated by a direct comparison of this pair of compounds, to improve the convergence. The results of the FEP calculations (see Table 3) show excellent agreement with the experimental data, with a MUE = 0.35 for the three pairs that have experimental affinities measured (5 → 9, 9 → 10 and 5 → 11) and strong qualitative correlation for the total loss of affinity of compound 12.

Table 3. Experimental and calculated (FEP) relative binding free energies between pairs of ligands.

Transformation a LIGA → LIGB	ΔΔGexp b (kcal mol–1 ± s.e.m.)	ΔΔGcalc (kcal mol–1 ± s.e.m.)
5 → 9	0.48 ± 0.5	1.12 ± 1.4
9 → 10	1.31 ± 0.3	1.48 ± 0.1
5 → 11	2.92 ± 0.2	2.58 ± 0.7
5 → 12	>5.11 c	7.68 ± 0.1

^aThe arrow depicts the direction of the transformation, as setup in the corresponding FEP simulation, which determines the sign of the corresponding ΔΔG_bind.

^bThe relative binding free energies (ΔΔG_exp) were calculated from experimentally determined K values using the relation .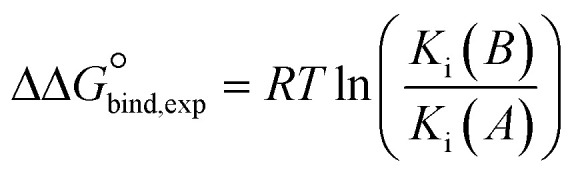

^cNo experimental value could be determined (i.e. IC₅₀ > 100 μM), and the calculated ΔΔG_exp represents the detection threshold.

The binding mode of compound 9 is depicted in Fig. 3B. One can observe that, despite the loss of the negative charge by replacement of the carboxy terminus by an amide group, the binding mode is unaltered as compared to 5 (Fig. 3A). The aromatic ring is stabilized by π-stacking interaction with Phe550 while the carbonyl of the amide group is still coordinated to Arg929 via a water molecule, explaining the modest loss in binding affinity as compared to 5. The peptide carbonyl group of the amide bond located at the N-terminal side still coordinates the Zn²⁺ ion. The interaction that is lost for compound 11 leading to an important drop in affinity of more than 2.5 kcal mol^–1, perfectly reproducing the experimental data. The positively charged amine is strongly stabilized by the cluster of glutamate residues, which explains why compound 12, lacking this amino group, does not bind to IRAP as perfectly reproduced in the corresponding FEP transformation (Table 3). Finally, the hydroxyl of the tyrosine side chain of the ligands makes hydrogen-bond with Glu494, an interaction that is lost in our FEP analysis of compound 10 explaining the moderate reduction in binding affinity as compared to the analogous compound 9.

Overall, the application of these modelling techniques provides a strong platform for rationalising the SAR of these cyclic peptidomimetics. The LIE method performed strongly in replicating conformationally driven features of ligand binding, while the “pairwise” nature of the FEP method gave excellent correlations to observed activity even when the charge state in comparator molecules was different. Either of these technical approaches might provide useful information in future IRAP inhibitor design.

Conclusion

Since its identification, IRAP has been shown to be broadly expressed and to have a diverse array of physiological roles. There is also strong evidence for the therapeutic potential of IRAP inhibitors in a variety of disease states, with dementia being the main focus historically.2 Because of the structural similarity to other aminopeptidases, the development of selective inhibitors is seen to be one of the key issues to address and in this context macrocyclic inhibitors, which echo the unique tolerance of IRAP for cyclic substrates, are strong starting points. In this study we have tried to evaluate the binding affinity of a selection of macrocyclic inhibitors that test the importance of various functional groups of the lead peptide 5. The molecular modelling of this series of compounds bears out quite closely the observed biochemical data, and supports the requirement for multiple points of interaction between the inhibitors and the enzyme in order to achieve strong affinity. The robustness of this model in rationalising the potency of the various inhibitors provides an excellent base for integrating in silico modelling as a filter in the future design of IRAP inhibitors.

Experimental section

General methods

The following reagents were purchased and were used without further purification. Fmoc protected amino acids (Chem Impex, IL, USA), Boc-S-trityl-l-cysteine (Chem Impex, IL, USA), Rink amide resin AM resin 0.3–1.2 meq g^–1 (Chem Impex, IL, USA), 2-chlorotrityl chloride resin 1.0–2.0 meq g^–1 (Chem Impex, IL, USA), piperidine (Sigma Aldrich, Australia), DIPEA (Sigma Aldrich, Australia), TFA (Sigma Aldrich, Australia), HCTU (Combi-Blocks, CA, USA), PyBOP (Combi-Blocks, CA, USA).

All compounds were analysed by LCMS using a Shimadzu LCMS-2020 fitted with a Phenomenex Luna C8 (100 × 2mm) using a gradient of 0–100% MeCN in water buffered with 0.1% TFA for 15 minutes. The UV chromatogram (λ = 214) from this analysis was used to calculate percentage purity. All compound reported were found to have a purity >95%.

High-resolution mass spectrum analysis was performed on a Agilent 6224 TOF LCMS by direct injection. All compounds were identified as either the protonated or sodiated cation with a mass error <5 ppm.

General method for SPPS

All peptides were synthesised by standard Fmoc-based SPPS. Fmoc deprotection was performed by using a solution of 20% piperidine in DMF (3 × 10 minutes) followed by washing with DMF (5 × 5 mL, min). Amino acid couplings were performed using Fmoc protected amino acid (0.6 mmol), HATU (0.6 mmol) and DIPEA (210 μL, 1.2 mmol) in DMF (5 mL) for 1 hour. The resin was then washed with DMF (2 × 1 minute), DCM (5 × 1 minute).

General synthetic method disulphide linked peptides 9–11

Peptides 9–11 were prepared on Rink amide resin (300 mg, 0.3 mmol). Cleavage from the resin was then performed by suspending the resin in a solution of triisopropylsilane (50 mL) and dithiothreitol (100 mg) in TFA (2 mL) for 3 h. The collected TFA solution was then concentrated under a stream of nitrogen and the residue was triturated in ether three times, by sonication in ether and separation by centrifuge.

For disulphide formation, the linear peptides were dissolved in TFA (4 mL) and DMSO (400 mL) added. This solution was stirred for 15 h and solvent reduce under a stream of nitrogen. The residue was taken up in a solution of 1 : 1 water–MeCN (2 mL), freeze dried overnight and purified by reverse phase HPLC.

Compound 9

Compound 9 was synthesised via the general synthetic method disulphide linked peptides (described above), employing the Fmoc protected amino acids; Fmoc-(2-aminomethylphenyl)acetic acid, Fmoc-l-Cys(Trt)-OH, Fmoc-l-β-homoTyr-OH and Fmoc-l-homoCys(Trt)-OH to yield 12 mg of 9 as a white lyophilized powder (7%). HRMS: calculated (M + H) 560.1996, found 560.2006. HPLC: Rf = 11.4 min, λ = 214, 94.7%.

Compound 10

Compound 10 was synthesised via the general synthetic method disulphide linked peptides (described above), employing the Fmoc protected amino acids; Fmoc-(2-aminomethylphenyl)acetic acid, Fmoc-l-Cys(Trt)-OH, Fmoc-4-fluoro-l-β-homoPhe-OH and Fmoc-l-homoCys(Trt)-OH to yield 20 mg of 10 as a white solid (11%). HRMS: calculated (M + H) 562.1953, found 562.1965. HPLC: Rf = 13.1 min, λ = 214, 96.0%.

Compound 11

Boc-S-trityl-l-cysteine (116 mg, 0.25 mmol) was dissolved in DCM (3 mL) and treated with PyBOP (205 mg, 0.40 mmol), CsCO₃ (126 mg, 0.4 mmol) and N,O-dimethylhydroxylamine HCl (76 mg, 0.80 mmol) for 15 hours. The reaction mixture was then diluted with DCM (50 mL), washed with 1 M KH₂PO₄ (50 mL), brine (25 mL) and dried over MgSO₄. This crude was the purified by silica gel chromatography (0–60% ethyl acetate in petroleum spirits) to provide 130 mg of Boc-S-trityl-l-Cys-N(Me)O(Me) as a colourless oil (100%). Boc-S-trityl-l-Cys-N(Me)O(Me) (130 mg, 0.25 mmol) was dissolved in dry diethyl ether (1 mL) and treated with 1 M LiAlH₄ in ether (63 μL, 0.063 mmol) at 0 °C for 10 minutes. The reaction mixture was diluted with diethyl ether (50 mL) and wash with water (50 mL), brine (25 mg) and dried over MgSO₄ to provide 110 mg of N-Boc-S-Trt-2-amino-3-mercaptopropanal as a colourless oil (95%). The linear peptide β-homoTyr-Cys-2-(2-(aminomethyl)phenyl)acetamide was prepared using the general method for SPPS (described above) using: rink amide resin, Fmoc-(2-aminomethylphenyl)acetic acid, Fmoc-l-Cys(Trt)-OH, Fmoc-l-β-homoTyr-OH. This linear peptide was cleaved from the resin and triturated as described in the general synthetic method disulphide linked peptides (described above). N-Boc-S-Trt-2-amino-3-mercaptopropanal (110 mg, 0.24 mmol) was dissolved in dry THF (2 mL) and treated with β-homoTyr-Cys-2-(2-(aminomethyl)phenyl)acetamide (70 mg, 0.16 mmol) and NaCNBH₃ (30 mg, 0.48 mmol). After stirring for 15 hours, the reaction mixture was filtered through a syringe filter, solvent removed and the crude dissolved in TFA (4 mL). After 1 hour, DMSO was added (400 μL) and the reaction mixture stirred for a further 15 hours. TFA was then removed under a stream of nitrogen and the residual lyophilised then purified by reversed phase HPLC (1–60% MeCN in water with 0.1% TFA throughout) to provide 20 mg of compound 11 as a white lyophilized powder (23%). HRMS: calculated (M + H) 546.2203, found 546.2217. HPLC: Rf = 11.1 min, λ = 214, 99.0%.

Compound 12

2-Chlorotrityl resin (300 mg, 0.3 mmol) was suspended in 5 mL of dry DCM for 30 min. Fmoc-(2-aminomethylphenyl)acetic acid (0.6 mmol) was dissolved in dry DCM (2 mL) and DIPEA (220 μL, 1.2 mmol) then added to the resin and shaken for 1 h. The resin was then washed with DCM (2 × 5 mL) and DMF (2 × 5 mL). This resin was then elaborated using the general method for SPPS (described above) using: Fmoc-l-Cys(Trt)-OH, Fmoc-l-β-homoTyr-OH and 4-tritylsulfanylbutanoic acid. Cleavage from the resin was then performed by suspending the resin in a solution of 5% water and 5% triisopropylsilane in TFA. The collected TFA solution was then concentrated under a stream of nitrogen and the residue was triturated in ether three times, followed by sonication in ether and centrifugation. The residue was purified by reverse phase HPLC to yield 15 mg of 12 as a white solid (9%). HRMS: calculated (M + H) 546.173, found 546.1727. HPLC: Rf = 13.3 min, λ = 214, 98.2%.

General synthetic method for lactam bridged compounds 13–15

The lactam bridged peptides were all prepared by SPPS on 2-chlorotrityl resin. The resin (300 mg, 0.3 mmol) was suspended in 5 mL of dry DCM for 30 min. Fmoc-(2-aminomethylphenyl)acetic acid (0.6 mmol) was dissolved in dry DCM (2 mL) and DIPEA (220 μL, 1.2 mmol) then added to the resin and shaken for 1 h. The resin was then washed with DCM (2 × 5 mL) and DMF (2 × 5 mL). The linear chain was constructed using standard SPPS as described above.

The Fmoc-protected peptide-resin was then treated with a solution of phenylsilane (108 mg, 1.0 mmol) and tetrakis(triphenylphosphine)palladium(0) (70 mg, 0.06 mmol) in DCM for 3 hours. The resin was then washed with DMF (5 × 5 mL) and treated with HCTU (124 mg, 0.3 mmol) and DIPEA (100 μL, 0.6 mmol) for 3 h then washed with DMF (5 × 5 mL). A standard deprotection step was performed and followed by a standard washing step. Cleavage from the resin was then performed by suspending the resin in a solution of 5% water and 5% triisopropylsilane in TFA. The collected TFA solution was then concentrated under a stream of nitrogen and the residue was triturated in ether three times, followed by sonication in ether and centrifugation. The residue was purified by reverse phase HPLC to provide the final lactam bridged compounds.

Compound 13

Compound 13 was synthesised via the general synthetic method for lactam bridged compounds employing the Fmoc protected amino acids; Fmoc-(2-aminomethylphenyl)acetic acid, Fmoc-Glu(OAll)-OH, Fmoc-β-homoTyr(tBu)-OH and Fmoc-Dap(Alloc)-OH. This procedure provided 5 mg of 13 (3%). HRMS: calculated (M + H) 540.2453, found 540.2451. HPLC: Rf = 11.4 min, λ = 214, 99.4%.

Compound 14

Compound 14 was synthesised via the general synthetic method for lactam bridged compounds employing the Fmoc protected amino acids; Fmoc-(2-aminomethylphenyl)acetic acid, Fmoc-Dab(Alloc)-OH, Fmoc-β-homoTyr(tBu)-OH and Fmoc-Glu(OAll)-OH. This procedure provided 3 mg of 14 (2%). HRMS: calculated (M + H) 554.2609, found 554.2608. HPLC: Rf = 11.2 min, λ = 214, 98.3%.

Synthesis of 15

Compound 15 was synthesised via the general synthetic method for lactam bridged compounds employing the Fmoc protected amino acids; Fmoc-(2-aminomethylphenyl)acetic acid, Fmoc-Glu(OtBu)-OH, Fmoc-β-homoTyr(tBu)-OH and Fmoc-Dab(Alloc)-OH. This procedure provided 7 mg of 15 (5%). HRMS: calculated (M + H) 554.2609, found 554.2615. HPLC: Rf = 11.4 min, λ = 214, 100%.

Fluorogenic enzyme assay

The source of IRAP used in the assay was obtained from solubilized membranes of HEK293T cells that overexpress recombinant full length human IRAP. The enzymatic activity of IRAP was determined by the catalysis of the synthetic substrate, l-leucine-7-amindo-4-methylcoumarin hydrochloride (Leu-MCA) to release a fluorogenic product detected at excitation and emission wavelengths of 380 and 440 nm. Assays were performed in 96-well plates with each well loaded with 2 μg solubilized membrane protein, 25 μM substrate, IRAP inhibitor (at concentrations ranging from 10^–9 to 10^–3 M) in a final volume of 100 μL of 50 mM Tris-HCl buffer, pH 7.4. Inhibitory constants (K_i) for each of the inhibitors were calculated from the GraphPad Prism 7 software (GraphPad Software Inc. San Diego, CA, USA).

Computational methods

Preparation of the IRAP structure and ligand docking

The crystal structure of human IRAP was retrieved from the protein data bank (PDB code 4PJ6),26 and chain A of the crystal dimer was retained and prepared for molecular dynamics (MD) simulations. The preparation of the structure (i.e., addition of hydrogens, rotamer assignment of Asn and His) was performed with Maestro version 9.2. (Schrödinger, LLC; NY). The series of ligands, 4–5, 8, 11–16 was built based on the previously determined binding mode for ligand 3 (HA08).39 Ligands 14–16 are built in cis and trans conformation to identify the bioactive conformation.

Molecular dynamics (MD) simulations

MD simulations were performed under spherical boundary conditions using the program Q, specially tailored for the calculation of free energies like e.g. ligand binding affinities with perturbation (FEP) or LIE methodologies.43,44 The OPLSAA (all-atom optimized potentials for liquid simulations) force field was used for protein and ligands,45 in combination with compatible parameters for the Zn²⁺ ion and the ligands, obtained with Macromodel version 10.6 (Schrödinger LLC) and translated into Q with ad hoc scripts. A simulation sphere of 25 Å radius was considered in all cases, centered on the equivalent position of the His4 Cα atom in AngIV as docked by us.39,41,46 The sphere was solvated with TIP3P water molecules47 and subjected to polarization and radial constraints according to the surface-constrained all-atom solvent model48,49 to mimic the properties of bulk water at the sphere surface. Protein atoms outside the simulation sphere were restrained to their initial positions and only interacted with the system through bonds, angles, and torsions. Excluding His, all other titratable residues within 20 Å of the Zn²⁺ ion were treated in their charged form. In addition, the residues Lys520, Lys726, Glu767, Asp773, Arg817, Glu818, Arg820, Glu825, Arg858, Glu887, Lys890, Lys892, Glu895, Arg933, and Glu1002, in the 20–25 Å layer of the sphere, were also treated as ionized because they were forming salt bridges. With this setup, the simulation sphere was overall neutral, thus avoiding the consideration of additional Born terms in the calculation of free energies of charged ligands as compared to that of the bulk solvent. Nonbonded interactions were calculated explicitly up to a 10 Å cutoff, except for the ligand atoms for which no cutoff was used. Beyond the direct cutoff, long-range electrostatics were treated with the local reaction field multipole expansion method.50 The system was slowly heated to the target temperature of 310 K during a 175 ps equilibration stage, in which initial positional restrains on all solute heavy atoms were gradually released. The subsequent data collection phase consisted of 10 replica MD simulations of 2 ns each, with randomized initial velocities (total simulation time 20 ns per ligand). A time step of 1 fs was used, with solvent bonds and angles constrained using the SHAKE algorithm.51 Nonbonded pair lists were updated every 25 steps, and the ligand-surrounding interaction energies were sampled every 50 steps. To estimate free energies of binding, ligand-surrounding energies were also sampled in parallel MD simulations of the reference state, that is, solvated in water using the same conditions as for the bound state.

Linear interaction energy binding affinity calculations

Binding free energies of every compound were calculated using the linear interaction energy (LIE) method as40,52

ΔGcalcbind = αΔΔ〈UvdWl–s〉 + + βΔΔ〈Uell–s〉 + + γ 1

where Δwhere Δ〈UvdWl–s〉 and Δ〈 and Δ〉 and Δ〈Uell–s〉 are the differences in the average nonpolar and polar ligand-surrounding interaction energies in the two states, that is, free and bound ligand. The coefficients are the differences in the average nonpolar and polar ligand-surrounding interaction energies in the two states, that is, free and bound ligand. The coefficients α and β are scaling parameters52–54 for the nonpolar and polar terms, respectively. In the standard LIE model, α was determined to have an empirical value of 0.18; the value of β follows the linear response approximation for charged ligands, while for neutral ligands or deviations of the LRA are expected which depend on the chemical nature of the ligand, and accordingly categorized values of β were derived in previous parameterizations. In the particular case of IRAP binding site, the divalent Zn²⁺ ion together with a cluster of carboxylates cause very large electrostatic interaction energies with the ligands, which are very sensitive to the force field parameters. In this situation it is recommended the treatment of β as a free parameter55 and we used previously determined an optimized value for IRAP of β = 0.19.39 Finally, the last term γ is a protein-dependent constant that does not affect the relative binding free energies53 but is used to offset the resulting calculated energies to the experimental values. The reported nonbonded energies correspond to average values over all 10 replicates, and the corresponding errors are calculated as the standard error of the mean (SEM).Experimental binding free energies (ΔGexpbind) were extracted from K_i values as

ΔGexpbind = RT ln K_i 2

Free energy perturbation

The relative binding free energy between selected pairs of ligands, LIG_A and LIG_B, was calculated using the free energy perturbation method. In this method LIG_A is transformed into LIG_B in parallel MD simulations in both the bound and the reference (water-solvated) state, and the relative binding free energy is estimated via a standard thermodynamic cycle, where the free energy of binding is calculated as the difference in the free energy resulting of transforming each ligand pair, A, B, in both the bound and the solvated, reference state as:

ΔGBbind – ΔGAbind = ΔΔG_bind = ΔGA→Bbound – ΔGA→Bfree 3

The free energy difference associated with the transformation of ligands A to B was calculated using Zwanzig's exponential formula56

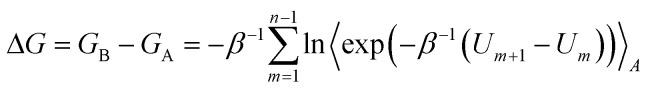4

where U_m denotes the effective potential energy function of a particular FEP window and n is the number of intermediate states. U_m is constructed as a linear combination of the initial (A) and final (B) potentials of the subperturbation

U_m = (1 – λ_m)U_A + λ_mU_B 5

where the coupling parameter λ_m is stepwise incremented from 0 to 1, in our case divided into 51 λ-windows, where every window is sampled for 10 ps.

Conflicts of interest

There are no conflicts of interest to declare.