ANALYSIS OF NON-STATIONARY RADIOMETER GAIN VIA ENSEMBLE DETECTION

Abstract

Although considered as stationary and Gaussian in general, radiometer gain is usually a fluctuating signal with non-stationary properties. Analyses of such non-stationary features is challenging as the radiometer signal cannot be observed independently. On the other hand, time series of post-gain voltages constitute an ensemble set for the radiometer gain which can be used to characterize the radiometer gain. This paper presents a novel technique called “Ensemble Detection” which can analytically retrieve the standard deviation of stationary Gaussian radiometer gain or find an equivalent stationary Gaussian process which represents the non-stationary radiometer gain under different calibration schemes. It has been found that the equivalent Gaussian process for non-stationary radiometer gain heavily depends on the calibration structure and the observation times of the measurand and the calibration references.

1. INTRODUCTION

Radiometers are typically calibrated using reference targets with well-characterized temperatures. Power measurements of calibration reference targets, with their known temperatures, reveal radiometer gain which can be used to convert measured power of an unknown source, i.e., measurand, into its antenna temperature [1–2]. Despite common assumptions of stationarity and stability, radiometer gain is usually a realization of a non-stationary random process statistics of which change in time. Therefore, accuracy and uncertainty of calibrated antenna temperatures measured by a radiometer system depend on its calibration scheme, i.e. number and temperature of calibration reference targets as well as their observation times.

Analysis of non-stationary radiometer gain is challenging, as it cannot be independently monitored and may display different characteristic under different calibration schemes. On the other hand, time series of post-gain voltages associated with calibration reference target measurements form an ensemble set for the underlying gain process from which the properties of non-stationary radiometer gain can be extracted [3–5]. This paper introduces ensemble detection, a novel technique which utilizes such ensemble sets to analyze, characterize, and model non-stationary radiometer gain according to the radiometer calibration plan.

2. RADIOMETER CALIBRATION AND ENSEMBLE DETECTION

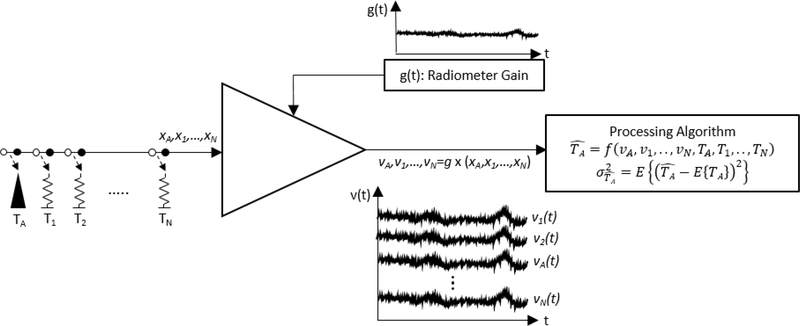
Figure 1 depicts a radiometer system with a gain represented by the signal, g(t). T_1,…,N are calibration target temperatures, x_1,..,N and ν_1,..,N are associated pre-gain signals and post-gain radiometer voltages, respectively, where v_i(t) = x_i(t) × g(t). T_A is the unknown antenna temperature, and x_A and ν_A are antenna pre-gain signal and post-gain voltage where v_A(t) = x_A(t) × g(t). The calibration scheme to estimate the antenna temperature is represented by a function f as:

$$\widehat{T_A}=f\left(v_A,v_1,\mathrm{..},v_N,T_1,\mathrm{..},T_N\right)=f\left(p_1,p_2,\dots ,p_k\right)$$ (1)

and the uncertainty in the calibrated antenna temperature is given as:

$${\sigma }_{\widehat{T_A}}^2=E\left\{{\left(\widehat{T_A}-T_A\right)}^2\right\}$$ (2)

where

$$T_A=f(\overline{p_1},\overline{p_2},\dots ,\overline{p_k},),\overline{p_l}=E\left\{p_i\right\}$$ (3)

To evaluate the uncertainty in the calibrated antenna temperature in equation (2), a multivariate Taylor series expansion about the mean value of each parameter can be performed in equation (1). Substituting the series expansion into equation (2) leads to the law of propagation of uncertainty given by [6]. Assuming the estimator is well approximated by a linear expansion for values of anticipated fluctuations, the series can be truncated at the second term. Thus, equation (2) becomes:

$${{\sigma }_{\widehat{T_A}}}^2\cong {\sum }_{i=1}^K{{\sigma }_{p_i}}^2{f_{p_i}}^2+2{\sum }_{i<j}{f}_{p_i}{f}_{p_j}cov\left(p_i{p}_j\right)$$ (4)

where

$$f_{p_i}={\frac{\partial }{\partial p_i}f\left(p_1,p_2,\dots ,p_k\right)|}_{p_1=\overline{p_1},p_2=\overline{p_2},\dots ,p_k=\overline{p_k}}$$ (5)

Equation (4) is a comprehensive uncertainty definition which includes the radiometric resolution and uncertainties due to calibration process and radiometer gain. Ensemble detection technique samples the ensemble set of post-gain voltages in a radiometer system according to the calibration scheme, and extract or model the statistical properties of the radiometer gain process separately based on this equation.

Fig. 1.

A radiometer calibration scheme with N calibration reference targets. Notice that time series voltages ν₁(t),_.., ν_Nt) form an ensemble set for the random process which defines radiometer gain.

3. STATIONARY GAUSSIAN NOISE GAIN

Assuming that pre-gain signals associated with calibration targets (x_1,..,N) and antenna (x_A), and the radiometer gain (g) are independent stationary Gaussian random processes whose samples are independent and identically distributed (IID) Gaussian random variables, equation (4) in Section 2 can be analytically solved. Thus, the relationship between the uncertainty in the calibrated antenna temperature, ${\mathrm{\sigma }}_{\widehat{\text{T}}\text{A}}$, and radiometer gain standard deviation, σ_g, can be analytically defined regardless of the calibration scheme.

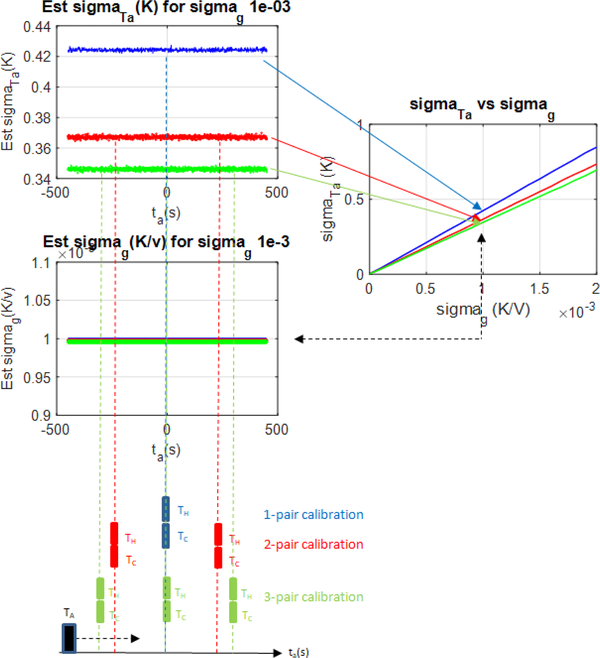
Consider a radiometer system with two calibration reference targets with temperatures 400 K and 200 K observing a 300 K target. Also, assume that the radiometer gain is a Gaussian stationary signal with mean 1 K/V and standard deviation 0.001 K/V, measurement bandwidth is 1 GHz, and integration time is 1 second. Figure 2 depicts the observed uncertainties in the calibrated antenna temperatures versus antenna observation time, their relationships with the radiometer gain standard deviation derived using equation (4), and the retrieved radiometer gain standard deviation using those relationships for three different calibration schemes, i.e., using one, two, and three measurements of the calibration pair at fixed times. As seen from the figure, the radiometer gain standard deviation can be accurately found using the uncertainty in the calibrated antenna temperatures, and the calibration scheme does not have an impact on the retrieval. It is also important to note that, since the radiometer gain is assumed to be stationary, antenna observation time with respect to calibration observation times is not important.

Fig. 2.

(Top left) Uncertainty in the estimated antenna temperature as a function of antenna observation time with fixed calibration observation times for one-, two-, and three-pair calibration. (Right) Analytical relationship between the uncertainties in radiometer gain and antenna temperature estimates. (Middle left) The direct plot of radiometer gain standard deviation as a function of antenna observation time for one-, two-, and three-pair calibration. (Bottom left) Fixed calibration observation times in one-, two-, and three-pair calibration where antenna observation time is variable.

4. NON-STATIONARY GAIN

For non-Gaussian and non-stationary radiometer gain, equation (4) does not yield a trivial analytical relationship between the statistical properties of radiometer gain and calibrated antenna temperature. However, it can still be used to model the radiometer gain as a Gaussian process, i.e., find an equivalent Gaussian radiometer gain, and calculate the associated standard deviation. Such non-Gaussian to Gaussian mapping of the radiometer gain would enable simpler analyses of radiometer systems with classical methods developed for Gaussian stationary signals.

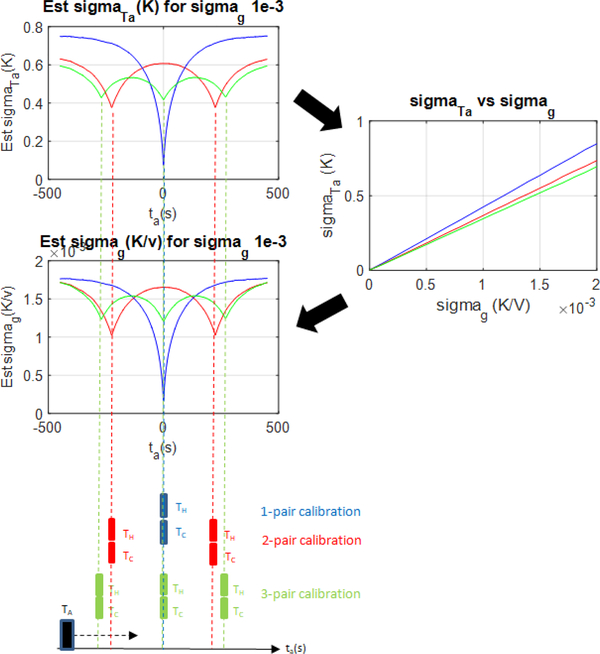
Figure 3 depicts the uncertainties in the calibrated antenna temperatures and the retrieved radiometer gain standard deviation for the same radiometer system discussed in Section 3, but with a first-order autoregressive, AR(1), radiometer gain process. The model parameter for the autoregressive process is φ=0.99, and the noise component is a zero mean Gaussian white noise with standard deviation 0.00025 K/V. Notice that, unlike the Gaussian stationary case discussed in the previous section, standard deviation of the derived equivalent Gaussian radiometer gain depends on both the calibration structure, i.e., number of measurements of the calibration pair, and the antenna observation time with respect to the calibration observation time. The standard deviation is found to be low when antenna and calibration observation times are closer, and high when they are further away from one another.

Fig. 3.

Uncertainties in the antenna temperature estimate and the retrieved gain standard deviation as a function of antenna observation time for the same calibration structures shown in Figure 2 with a first-order autoregressive gain process. Notice how the Gaussian case analytical relationship between the uncertainties in the antenna temperature estimate and radiometer gain can be used to model the non-Gaussian radiometer gain as a Gaussian process with varying standard deviations as a function of antenna observation time and calibration structure.

5. CONCLUSIONS AND DISCUSSION

This initial study has demonstrated that calibration measurements during radiometer calibration provides an ensemble set of the random process which defines the radiometer gain. Ensemble detection, then, can be applied to this set to extract the radiometer gain properties. In case of a stationary Gaussian radiometer gain, the ensemble set reveals an analytical relationship between the statistical properties of the radiometer gain and the observable uncertainty in the calibrated antenna temperature. For non-stationary radiometer gain, the same ensemble set can be used to model the radiometer gain as a Gaussian process and find the standard deviation of this equivalent Gaussian process. As expected, the statistical properties of the equivalent Gaussian gain process depend on the calibration scheme and times when the calibration reference targets are observed.

It is also important to note that retrieved parameters of the equivalent Gaussian model for a non-stationary radiometer gain process as a function of antenna observation time with respect to calibration measurement times may reveal the non-stationary properties of the radiometer gain by further analyses of equation (4). Future studies will focus on extracting such properties using the ensemble detection technique with adaptive calibration schemes.