Development of Water Content Dependent Tissue Dielectric Property Models

Abstract

We propose dielectric tissue property models dependent on both water and air content covering the microwave frequency range. Water is the largest constituent of biological tissues and its effect on the dielectric properties of biological tissue has been studied. However, dehydration effects due to thermal heating have not been fully characterized. We combined 1) Maxwell-Fricke mixture theory with a four-pole Cole-Cole equation to include water and air content dependency and as the second approach a different 2) Maxwell mixture model was coupled with a Debye function. The proposed approaches (1 and 2) were able to predict the permittivity (ε’) and conductivity (σ) of bovine liver and swine lung tissues at different hydration and inflation states from 1-15 GHz. A second approach coupling Maxwell and Debye models required fewer assumptions and modelled tissue properties with higher accuracy (less than 15% mean percent error in all tissue types). These models may help improve the accuracy of microwave ablation simulation when tissue water content changes as a result of vaporization, and may facilitate personalized treatment planning.

I. Introduction¹

Microwave ablation – the destruction of tissue through microwave heating – has gained significant clinical traction for the treatment of tumors in the abdomen and chest [1]. Microwave ablation is performed by inserting an antenna through the skin directly into a tumor and applying sufficient energy to heat the adjacent tissue to at least 60 °C for near-instantaneous cellular necrosis [1]. The dielectric permittivity and effective conductivity of a tissue determine antenna propagation characteristics and heat generation [2]. In numerical simulations of microwave ablation, accurate tissue property models (thermal and dielectric) are necessary to generate meaningful treatment predictions. Developing new ablation devices and personalized treatment planning can also be facilitated by reliable and accurate simulations [3]. Numerical models are also used in microwave sensing and imaging modalities [4].

Dielectric properties are dependent on the frequency of the applied field, temperature, and macromolecular constituents of the tissue such as water, air, lipids, and protein. One technique to account for the combined effects of these constituents is through dielectric mixture models [5]. For example, tissues can be approximated as a two compartment medium comprising low and high permittivity materials [6]. Low permittivity materials include cell membranes, proteins, air, and fat, while water has a relatively high permittivity.

While normal tissue has been described with such mixture models, significant decreases in both permittivity and conductivity have been observed around 100 °C as a result of water vaporization during microwave ablation [3], [2]. To date, these changes have only been characterized empirically by lumping temperature and vaporization effects together into a temperature-dependent model [2], [3]. However, simulations performed with these models have limited ability to predict microwave heating under arbitrary input conditions. An ability to account for more of the physics involved in microwave tissue heating may help produce more accurate simulations that can be used for device optimization and “in silico” studies of microwave heating.

Here we propose tissue dielectric property models based on an assumption that low and high permittivity tissue constituents change as a result of water vaporization and dehydration. Our objective is to model wideband temperature-dependent tissue dielectric properties beyond 60 °C. We assessed two different approaches in both liver and lung tissues (which have varying intrinsic mixtures of water, air, protein and lipids). For each tissue type, the first approach was to couple a Maxwell-Fricke mixture equation [6] with a four-pole Cole-Cole equation [7]. A second approach accounted for tissue constituents by using a Maxwell mixture equation [8] coupled to a Debye function. Each model was validated by measured liver and lung tissue properties at varying water and air contents, respectively. The proposed models may enable more accurate microwave ablation and imaging simulations by providing a wideband tissue model for multiple tissue types.

II. Methods

A. Liver Tissue Measurement

Ex-vivo bovine liver sections (8-10 g) were dehydrated in a convection food dehydrator until they lost 38%, 55%, and 79% of their water (n = 3 per group). Dehydration amount was calculated by measuring the mass of samples before and after dehydration. Ambient temperature within the dehydrator was recorded as 73±2 °C (mean ± standard deviation). Three samples were not dehydrated to serve as baseline controls. Relative permittivity and effective conductivity of all samples (n = 12) were measured by an open-ended coaxial probe 2 mm in diameter (85070E, Keysight Technologies, Santa Rosa, California) attached to a vector network analyzer (E5071C, Keysight Technologies). Before measurements, the system was calibrated with short, open, and water loads [9]. Dielectric properties were measured across at least three locations in each sample by inserting the probe tip into the tissue around 2 mn which is well beyond the penetration depth of the probe (~0.3 mn) [10]. Measurements from all samples in each group were averaged to get a single pennittivity and conductivity value for tissues with the same water and air content.

B. Lung Tissue Measurement

Ex vivo swine lung was intubated and inflated from the main bronchus. A total of four (n = 4) samples were kept in their inflation states to observe the effect of insufflation on dielectric properties. Other lung sections (n = 4) at varying inflation states were infused with dyed water. Tap water was dyed blue and injected into a peripheral airway until a color change was observed. Tissue volumes that had consistent dye coloring in a large enough volume for dielectric measurement were dissected. Since inflation caused an inhomogeneous distribution of air, sample volumes and weights were recorded to calculate densities and air contents. Dielectric properties were measured at multiple locations and averaged for each sample as described for the liver.

C. Model Parameters Optimization

1). Coupled Cole-Cole and Maxwell-Fricke Models

The Cole-Cole equation outlined in [7] was adopted to explain the frequency dependence of relative permittivity:

$$\widehat{\epsilon }={\epsilon }_{\infty }+\sum _n\frac{{\epsilon }_{s(n)}-{\epsilon }_{\infty }}{1+{\left(j\omega {\tau }_{(n)}\right)}^{1-{\alpha }_{(n)}}}+\frac{{\sigma }_i}{j\omega {\epsilon }_0},$$ (1)

where ε_s(n) is the static relative permittivity tor pole n, ε_∞ is the high frequency relative permittivity, ω (rad/s) is the angular frequency, α_(n) is a distribution parameter for pole n, σ_i (S/m) is ionic conductivity, and τ_(n) (S) is the relaxation time of pole n. The first pole static permittivity was calculated by multiplying the static permittivity of water (ε_sw) with the Maxwell-Fricke mixture team [6] in (2) to account for variablce water content. Similarly, the second pole for static permittivity was re-calculated for tissues with different water contents by multiplying an initial ε_s(2) from literature [7] with the mixture term in (2).

$${\epsilon }_{s(1,2)}={\epsilon }_{sw,s(2)}\times \left(\frac{1-p}{1+(k-1)\times p}\right)$$ (2)

Here, p is the volume fraction of low-permittivity materials (air, protein, lipid) and k accounts for the shape of suspended low permittivity particles in water. The n = 1 pole parameters in (1) were optimized at 1 GHz, 2.45 GHz, 5.8 GHz, 8 GHz, and 14.4 GHz, by fitting the measured dielectric properties to the proposed model with the non-linear least squares method. These frequencies are commonly used in ablation devices and/or are in ISM (Industrial Scientific and Medical) bands [11], [12], [13]. The parameters σ_i, and ε_sw were optimized at the same time. The remaining parameters in (1) for poles n = 2, 3, 4) were kept as reported in [7]. The fit quality was shown by mean percent errors.

Assmnptions made in the parameter optimization and mixture model application included:

• Baseline lung and liver water contents were assumed to be 79% and 70%, respectively [14].

• The suspended low-permittivity materials were assumed to be spherical (k = 2).

• The initial static permittivity of water was assumed to be 80, which was optimized with other parameters.

• Sample masses were measured before and after dehydration and percent mass reduction was calculated. The value of p in (2) was calculated by assuming that the initial water content (70%, or 0.7 volume fraction) was reduced by 79% (the most dehydrated group), which corresponded to a 55.3% reduction in mass or volume (density was assumed 1 g/ml). This means the dehydrated volume is 44.7% of the initial (100%) sample volmne. Once the tissue is dehydrated, low permittivity materials comprise a higher volume fraction. To calculate the final value of p, the initial low permittivity volume fraction was divided by the dehydrated volume of the sample. The small differences in density among protein, lipids and water were neglected in these calculations.

• Lung density, ρ (g/ml), was used to estimate the low-permittivity content from

$$p=1-(0.79\cdot \rho ).$$ (3)

2). Coupled Debye and Maxwell Models

A second approach considered only a Debye function, which is a single-pole Cole-Cole equation for the case where α_(n) is 0. Zero α_(n) means there is a single relaxation time in the frequency range of interest [15]. The Debye equation is coupled to the Maxwell mixture model [8] in (4) to account for varying water contents. Here, ε_l is the low permittivity value and is assumed to be 2.0-15.0 [16].

$${\epsilon }_s={\epsilon }_{\mathit{sw}}\frac{2{\epsilon }_{\mathit{sw}}+{\epsilon }_l-2p({\epsilon }_{\mathit{sw}}-{\epsilon }_l)}{2{\epsilon }_{sw}+{\epsilon }_l+p({\epsilon }_{\mathit{sw}}-{\epsilon }_l)}$$ (4)

The remaining model parameters were introduced in the above description of Coupled Cole-Cole and Maxwell-Fricke Models. In the coupled Debye and Maxwell model approach, Debye equation parameters (τ, ε_s, and σ_i) and mixture parameters (ε_l) in (3) were optimized by fitting measured data to this model as described above. Ionic conductivity was also scaled by the mixture model in (3), since increased water content would increase free ion concentration in tissues. The parameter ε_∞ was kept at 4.0 as in prior work [6]. Aforementioned assumptions for initial values and baseline tissue constituents help for this approach as well. The same levels of p were used in both liver and lung as described for the previous approach.

III. Results

A. Cole-Cole equation and Maxwell-Fricke Mixture Model

The values of p for 0% (baseline), 38%, 55%, and 79% water loss were 0.3, 0.41, 0.48, and 0.67, respectively, in liver. Densities of lung that were not infused with water were 0.52, 0.68, 0.78, and 1 (g/ml), corresponding to p of 0.59, 0.46, 0.38, and 0.21. Similarly, the samples that were infused with water had densities of 0.88, 0.9, 0.93, and 1 (g/ml) and p values of 0.30, 0.29, 0.27, and 0.21.

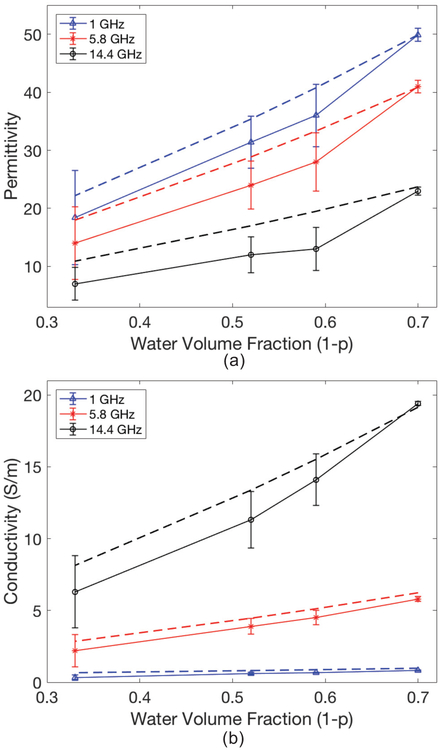
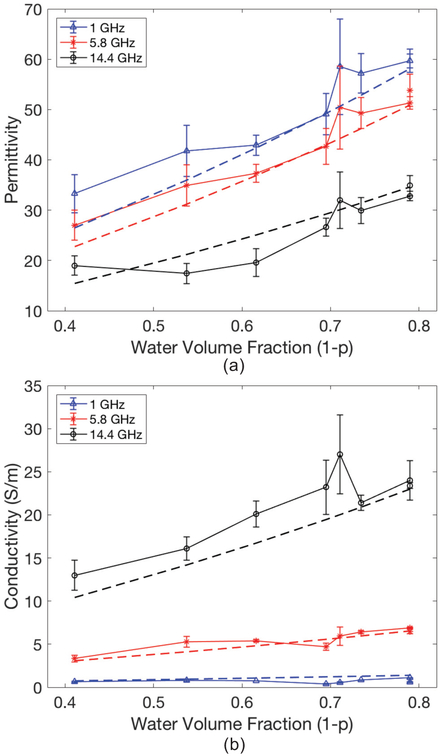
Measured dielectric properties are compared with modelled properties in Fig. 1 and Fig. 2 for liver and lung, respectively. High frequencies and water fractions (1 -p) lower than 0.5 resulted in greater model error (Fig. 1). The discrepancy in lung property modelling also increased at lower water fractions (Fig. 2). These observations corroborate previous studies, where high water content tissue properties were predicted with higher accuracy [6].

Fig. 1.

Measured (solid lines) with ±standard deviations and modelled (dashed lines) liver permittivity (a) and conductivity (S/m) (b) based on the approach where Maxwell-Fricke Mixture theory was coupled with the Cole-Cole equation. Even though modelling and measurements were done at more frequencies, only 1 GHz, 5.8 GHz, and 14.4 GHz are plotted for clarity. Properties are shown as a function of water volume fraction (1-p).

Fig. 2.

Measured (solid lines) with ±standard deviations and modelled (dashed lines) lung permittivity (a) and conductivity (S/m) (b) as a function of water volume fraction. In modelled properties Maxwell-Fricke mixture theory was coupled with the Cole-Cole equation.

Optimized parameters for the Cole-Cole and Maxwell-Fricke mixture model are shown in Table I. The relaxation times (τ) were slightly longer than pure water relaxation at 20 °C (8.5 ps) [17]. This is an expected result because water molecules in aqueous protein solutions or in tissues can show longer relaxation times due to intermolecular forces between adjacent molecules [15].

TABLE I.

Optimization Results

Parameter	Liver	Lung
εsw	75.7	81.0
σ(i)	0.21 S/m	0.9 S/m
α(1)	3.5e-14	3.5e-11
τ(1)	11.6 ps	8.6 ps
ε∞	2.0	4.0

Optimized Cole-Cole and Maxwell-Fricke Mixture equation parameters with the first approach.

Other model parameters matched expectations based on prior work. The higher values of ε_sw and ε_∞ observed in lung can be attributed to the higher water content of non-aerated lung compared to normal liver (79% vs. 70%, respectively). Both liver and lung models had very low values of α₍₁₎, which suggested that a simpler Debye model without dispersion effects might be employed for this relatively narrow frequency range (the second approach).

The optimized value for σ_i was higher in lung than liver. Tins was somewhat counterintuitive given that liver is generally a more electrically conductive medium than normal lung.

However, we note that the conductivity value in our optimized parameters is for the non-air portion of lung, which has a higher water content, which would coexist with ions, than liver (79% compared to 70%). This might have contributed the higher σ_i value in lung, however, it is also important consider that all model parameters are used and considered holistically during data fitting.

A. Debye equation and Maxwell Mixture Model

The second approach of a Debye function coupled to a Maxwell mixture model yielded more accurate tissue models for both liver and lung than the first approach. In Fig. 3 and Fig. 4, liver and lung dielectric properties are plotted against the water volume fraction, respectively. Parameters that were optimized by the second approach are shown in Table II.

Fig. 3.

Comparison of measured (solid lines) with ± standard deviation and modelled dielectric properties (dashed lines) of liver samples. Second modelling approach was used in predictions.

Fig. 4.

Lung permittivity (a) and conductivity (b) that were acquired by the second approach (dashed lines) and measured dielectric properties with ± standard deviation (solid lines).

TABLE II.

Optimization Results

Parameter	Liver	Lung
εsw	77.4	80
σi	0.036 S/m	0.9 S/m
εl	2.0	12.0
τ	13.0 ps	11.9 ps
ε∞	4.0	4.0

Optimized Debye and Maxwell Mixture equation parameters with the second approach.

A similar relationship between lung and liver tissue parameters was observed with this approach, such as higher values in ε_sw and σ_i in lung compared to liver.

In contrast to the first approach, this second approach was more accurate across the spectrum of water contents studied. Overall, conductivity was predicted with a higher error. This might be due to very low values of conductivity at 1 GHz, which is around 1 (S/m). A physically small difference between modelled and predicted conductivity can result in a high percent error.

Percent errors were calculated between predicted and measured dielectric properties at all tissue inflation levels (for lung), hydration levels (for liver) and at aforementioned frequencies. Table III shows mean percent errors that were acquired from both approaches used in this study.

TABLE III.

Mean Percent Errors

Tissue Type – Property	Approach 1	Approach 2
Liver – Permittivity	20.4%	10.8%
Liver – Conductivity	23.5%	13.6%
Lung – Permittivity	8.1%	6.0%
Lung – Conductivity	27.3%	14.5%

Mean percent errors between predicted and modelled dielectric properties.

IV. Discussion

This preliminary study shows that mixture models can be used to predict tissue dielectric properties in the microwave range as functions of water content for liver and lung, respectively. Coupled Maxwell and Debye models (second approach) were more accurate, with a mean percent error of less than 15% across tissue types.

After parameter optimization, ε_sw was in the range of 75 to 81 (Table I and Table II) from both approaches, which is very close to the normally assumed static permittivity of water at 20 °C [18]. This suggests that the basic premise of tissue being modeled as a suspension of particulates in water was reasonable.

The parameter α₍₁₎ represents the distribution of relaxation times in a mixture and was found to be close to zero because the data were fit in a limited frequency range of 1 GHz – 15 GHz [19], [20]. In this frequency range, water polarization and relaxation is the dominant source of dispersion, specifically gamma dispersion [15]. Therefore, a value of α₍₁₎ close to zero was not surprising. Having minimal impact from dispersion also suggested that a Debye function can characterize the dielectric properties in this frequency range [15], which we observed to be true in the second approach.

There was a sharp increase in dielectric properties around 1-p = 0.7 that was not expected from the more linear mixture theory model. Given the high variance observed at this point, we surmise that this result could have been affected by the lung density measurement technique. The density of each tissue sample was measured in bulk; it was not possible to map density or air/water distribution in the tissue samples at the point of measurement. The dielectric probe has a limited sensing region, so fluctuations in dielectric properties for that set of samples might have been the result of inhomogeneous air/water distribution in the tissue.

The low permittivity parameter ε_l in (4) represents the aggregate effect of low permittivity materials in a mixture – proteins, lipids, air, etc. Different values were found for lung (ε_l = 12) and liver (ε_l = 2) with the second approach. It has been shown that permittivity of proteins in aqueous solutions can be in the range of 2 to 80, and that there are multiple factors, such as the type of the protein, temperature and pH of the mixture, that influence this value [16]. Without a more complete analysis of each tissues structure, we are not able to comment on the reason for this difference. However, the excellent match between the models and experimental data supports the use of these parameters.

V. Conclusion

Simple dielectric mixture models can be coupled with Debye or Cole-Cole equations to account for tissue water content when modeling dielectric properties. The coupled Maxwell mixture model and Debye equation (approach 2) was the more accurate approach, with a mean percent error of less than 15% across tissue types. Such models may enable wideband simulation of different tissue types at varying hydration states.

Biography

Sevde Etoz (S’16) received Bachelor of Science degree in Biomedical Engineering from Erciyes University, Kayseri, Turkey in 2013 and Master of Science degree in Biomedical Engineering in 2017 at University of Wisconsin-Madison, USA.

She is currently working toward the PhD degree in Biomedical Engineering in University of Wisconsin-Madison, USA. Her current research interests include microwave ablation antenna optimization, image guidance in microwave tumor ablation, and development of tissue models for microwave ablation simulations.

Christopher L. Brace (M’01-SM’11) received the B.S. degree in physics and the B.S.E.E. degree from the University of Wisconsin, Milwaukee, Milwaukee, WI, in 2001, and the M.S.E.E. and Ph.D. degrees from the University of Wisconsin, Madison, Madison, WI, in 2003 and 2005, respectively.

He is currently an Associate Professor in the Departments of Radiology and Biomedical Engineering, at the University of Wisconsin, Madison. His research interests include image-guided interventional oncology, thermal therapies such as radiofrequency and microwave ablation, medical imaging, and applications of electromagnetics in medicine.

Dr. Brace a member of the Society of Thermal Medicine, Biomedical Engineering Society and American Society for Engineering Education.