A protocol for preparing explicitly solvated systems for stable molecular dynamics simulations

Abstract

Before beginning the production phase of molecular dynamics simulations, i.e., the phase that produces the data to be analyzed, it is often necessary to first perform a series of one or more preparatory minimizations and/or molecular dynamics simulations in order to ensure that subsequent production simulations are stable. This is particularly important for simulations with explicit solvent molecules. Despite the preparatory minimizations and simulations being ubiquitous and essential for stable production simulations, there are currently no general recommended procedures to perform them and very few criteria to decide whether the system is capable of producing a stable simulation trajectory. Here, we propose a simple and well-defined ten step simulation preparation protocol for explicitly solvated biomolecules, which can be applied to a wide variety of system types, as well as a simple test based on the system density for determining whether the simulation is stabilized.

INTRODUCTION

Molecular dynamics (MD) simulations of biomolecules have become an important tool for studying a wide variety of biological phenomena such as protein structure and function, protein–ligand drug-like interactions, and macromolecular complexes.^1–3 Although it is, in theory, possible to simulate systems with no a priori knowledge of structures,^4,5 in general, most MD simulations begin with a structure that has been determined via some experimental methods such as x-ray diffraction or NMR spectroscopy.

In practice, a structure obtained via experimental methods requires some preparation before it can be used for all-atom MD simulation. This preparation may involve adding missing atoms or residues, removing unwanted ligands or molecular tags, addition of solvent molecules and ions, etc. Once the system has been built, for a variety of reasons it may not be ready for the production phase of MD, i.e., MD simulation that will produce useful data for analysis. First, the structures obtained from experimental methods usually represent an average of an ensemble of structures and may include artifacts due to poor resolution, crystal packing effects, issues with refining the raw experimental data (electron density, chemical shifts, etc.) into structural data, and so on. Second, there may be issues with the system resulting from how it was built; for example, the system density may be off depending on how the solvent was placed, or there may be atoms in close contact, which may result in large initial forces and system instability, etc.

Although proper preparation of a system is critical for ensuring MD simulations of that system are well-behaved, i.e., they are able to generate useful data and do not experience catastrophic initial forces and velocities (i.e., “blow up”), there are surprisingly few specific recommended protocols for preparing systems for MD simulation in the literature. For example, in the popular computational simulation reference “Molecular Modeling” by Leach, only a very general description of such a procedure is given: “During equilibration, various parameters are monitored together … When these parameters achieve stable values then the production phase can commence.”⁶ Molecular dynamics reviews often only mention that some sort of equilibration should be done to prepare systems for production but provide either a very general description of what equilibration means or no further details on how to accomplish it.^1,7–12 When a protocol is given in detail, it is often presented as specific to that system and not as a general protocol.^13–15 Protocols with more detailed steps are available (such as that detailed by Galindo-Murillo et al.¹⁶), but often provide ranges instead of specific values (e.g., simulate for 10 ps–100 ps and minimize for 1000 to 5000 steps). Other protocols are both detailed and specific, but are presented in the context of very specific systems (e.g., CHARMM-GUI and protein–membrane systems¹⁷). Gelpí et al. have developed a minimization and equilibration procedure based on classical molecular interaction potentials; however, this procedure is based more on using a different functional form of the force field for setting up the system of interest and less on a specific set of steps to be used.¹⁸ Walton and VanVliet presented a very well-defined protocol for identifying equilibration time based on normal mode analysis.¹⁹ However, the work was focused more on identifying equilibration than system preparation; their procedure consisted only of a single minimization followed by a single MD simulation for equilibration and was tested on a single small (58 amino acid residue) protein, and it is unclear whether this procedure can be generalized to larger systems or systems containing other molecule types (e.g., nucleic acids and lipids). Similarly, Chodera presented a method that attempts to identify the production region of a trajectory as one that maximizes the number of uncorrelated samples (with equilibration considered everything prior to the production region) but no specific recommendations on how to conduct the simulation in the equilibration region.²⁰

Here, we present a specific ten step protocol for preparing any explicitly solvated system for stable dynamics. The protocol relies on general features such as steepest descent (SD) minimization and harmonic Cartesian positional restraints. We then apply the protocol to almost 400 systems, comprising protein, nucleic acid, protein/nucleic acid, and protein/membrane systems, as well as a cellulose fiber. All systems were successfully prepared for MD, and the protocol was run on these systems until the density “stabilized” as determined by a novel but simple density plateau test. The protocol was tested with various thermostats and barostats to evaluate their effect on the efficacy of the protocol.

We note that this is explicitly not an “equilibration” protocol per se but can be considered the beginning of one. In practice, virtually every degree of freedom in macromolecular simulation will need to be equilibrated. Most degrees of freedom can be equilibrated very quickly, such as a distorted bond or angle, but some degrees of freedom require much longer equilibration times. The amount of equilibration needed is thus related to the correlation times of the slower degrees of freedom, and since correlation times tend to be longer for larger systems, the equilibration time lengths should be longer for larger systems. A good equilibration scheme is the one in which every degree of freedom can be equilibrated nearly independently from all others. For example, the heat generated from relaxing a bad bond distance or angle must not be allowed to distort the nearby environment. Thus, the focus of this protocol involving multiple steps of both minimization and molecular dynamics is to provide a generally applicable framework for performing these sometimes difficult initial relaxations, which will in turn allow subsequent system equilibration to proceed in a stable manner.

SYSTEM PREPARATION PROTOCOL

The protocol itself consists of a series of energy minimizations and “relaxations” (i.e., short MD simulations) designed to allow the system to relax gradually. Over the first nine steps of the protocol, there are 4000 total steps of minimization and 40 000 steps of MD (totaling 45 ps in all). The final step of the protocol is run until the density plateau criteria are satisfied; this is described below in detail.

The system is divided into two types of molecules: (1) “mobile” molecules, which are the relatively fast diffusing molecules in the system, such as solvents (e.g., water) and ions and (2) “large” molecules, which are slower to diffuse, such as proteins and lipids. In this protocol, the mobile molecules are allowed to relax before the large molecules; this is accomplished via positional restraints on “large” molecules. In addition, for proteins and nucleic acids, the substituents (amino acid side chains for proteins and nucleobases for nucleic acids) of the “backbone” (i.e., the main polymer chain) are allowed to relax prior to the backbone in order to allow, e.g., close atomic contacts to relax with minimal disruption to secondary structural elements. Each step after the first uses the final coordinates (and velocities if available) of the previous step as its starting coordinates. No coordinate “wrapping” (i.e., molecules outside the periodic box being translated back into the primary unit cell) should be used in order to avoid potential issues with positional restraints (for example, positional restraints in Amber do not take periodic boundary conditions into account).

Note that since many modern graphics processing unit (GPU) codes use a fixed-precision model that is somewhere between single and double precision, it is possible that extremely large forces (such as those that might result from atomic overlaps) will result in numerical overflows. Therefore, it is recommended that the minimization steps be done with full double precision. If double precision GPU codes are not available, one can switch to double precision central processing unit (CPU) codes for the minimization steps, and then use GPU codes for MD simulations.

To test whether the simulation protocol is sensitive to the choice of thermostat/barostat, the steps of the protocol that require them were tested with various combinations of a weak-coupling thermostat/barostat, a Langevin-style thermostat, and a Monte Carlo barostat. The weak-coupling algorithms²¹ were tested since they are available in almost all major MD engines (e.g., Amber,²² CHARMM,²³ Gromacs,²⁴ NAMD,²⁵ and LAMMPS²⁶). It should be noted that although it has previously been shown that the weak-coupling thermostat can still provide correct dynamical properties, it still results in the wrong energy distribution.²⁷ It has also been shown that the weak-coupling barostat can introduce artifacts into simulations, particularly for inhomogenous systems.²⁸ When used, the Langevin thermostat was used with a collision frequency of 5 ps⁻¹ and the Monte Carlo barostat was used with volume change attempts occurring every 100 steps. Settings for the weak coupling thermostat/barostat are noted in the specific steps below.

• Step 1: Initial minimization of mobile molecules The first step is 1000 steps of SD minimization with strong positional restraints applied to the heavy (i.e., non-hydrogen) atoms of the large molecules using a force constant of 5.0 kcal/mol Å and the initial coordinates as a reference. No other constraints (e.g., SHAKE²⁹) should be applied during this step.

• Step 2: Initial relaxation of mobile molecules

The second step is 15 ps of MD simulation using a time step of 1 fs (15 000 steps in total) at constant volume and temperature (NVT). Initial velocities should be assigned for the desired temperature via a Maxwell–Boltzmann distribution. Positional restraints are applied to the heavy atoms of the large molecules using a force constant of 5.0 kcal/mol Å and the initial coordinates as a reference. Any necessary constraints (e.g., SHAKE for hydrogen atoms) should be applied. When using a weak-coupling thermostat to regulate the temperature, the time constant should be set to 0.5 ps.

• Step 3: Initial minimization of large molecules

The third step is 1000 steps of SD minimization with medium positional restraints applied to the heavy atoms of the large molecules using a force constant of 2.0 kcal/mol Å and the initial coordinates as a reference. No other constraints (e.g., SHAKE) should be applied during this step.

• Step 4: Continued minimization of large molecules

The fourth step is 1000 additional steps of SD minimization with weak heavy atom positional restraints on large molecules using a force constant of 0.1 kcal/mol Å and the initial coordinates as a reference. No other constraints (e.g., SHAKE) should be applied during this step.

• Step 5: Final minimization of the system

The fifth step is 1000 steps of SD minimization with no positional restraints. No other constraints (e.g., SHAKE) should be applied during this step.

• Step 6: Initial relaxation of large molecules

The sixth step is 5 ps of MD simulation using a time step of 1 fs (5000 steps in total) at constant pressure and temperature (NPT). Initial velocities should be assigned for the desired temperature via a Maxwell–Boltzmann distribution. Positional restraints are applied to the heavy atoms of large molecules using a force constant of 1.0 kcal/mol Å and the initial coordinates (final coordinates of step 5) as a reference. Any necessary constraints (e.g., SHAKE for hydrogen atoms) should be applied. When using the weak-coupling thermostat and/or barostat to regulate temperature/pressure, the time constant for both should be 1.0 ps.

• Step 7: Continued relaxation of large molecules

The seventh step is 5 additional ps of MD simulation using a time step of 1 fs (5000 steps in total) in the NPT ensemble. Initial velocities should be the final velocities from step 6. Positional restraints are applied to the heavy atoms of large molecules using a force constant of 0.5 kcal/mol Å and the final coordinates of step 5 as a reference. Any necessary constraints (e.g., SHAKE for hydrogen atoms) should be applied. When using the weak-coupling thermostat and/or barostat to regulate temperature/pressure, the time constant for both should be 1.0 ps.

• Step 8: Relaxation of non-backbone atoms

The eighth step is 10 additional ps of MD simulation using a time step of 1 fs (10 000 steps in total) in the NPT ensemble. Initial velocities should be the final velocities from step 7. Positional restraints are applied to the non-hydrogen backbone atoms of protein and nucleic acid residues and to the heavy atoms of all other large molecules using a force constant of 0.5 kcal/mol Å and the final coordinates of step 5 as a reference. Any necessary constraints (e.g., SHAKE for hydrogen atoms) should be applied. When using the weak-coupling thermostat and/or barostat to regulate temperature/pressure, the time constant for both should be 1.0 ps.

• Step 9: Unrestrained relaxation

The ninth step is 10 additional ps of MD simulation using a time step of 2 fs (5000 steps in total) in the NPT ensemble. Initial velocities should be the final velocities from step 8. No restraints are used. Any necessary constraints (e.g., SHAKE for hydrogen atoms) should be applied. When using the weak-coupling thermostat and/or barostat to regulate temperature/pressure, the time constant for both should be 1.0 ps.

• Step 10: Final density stabilization

The tenth step involves the MD simulation using whatever settings are desired for the production simulation; however, it must be performed in the NPT ensemble since the final density relaxation occurs during this step. This step will be performed as long as the final density plateau criteria (described in detail below) have not been met. In this study, this step was run in 1 ns increments as long as the density criteria were not satisfied. Initial velocities should be the final velocities from step 9. Unless required for some reason, it is recommended that a thermostat and barostat with better properties than the weak-coupling versions be used (e.g., Langevin dynamics, Langevin piston,²⁸ Nosé–Hoover,³⁰ and Monte Carlo barostat³¹). When used, the Langevin thermostat was used with a collision frequency of 5 ps⁻¹, the Monte Carlo barostat was used with volume change attempts occurring every 100 steps, and the weak-coupling thermostat/barostat was used with a time constant of 5.0 ps.

DENSITY PLATEAU CRITERIA

Although determining precisely when a system is “equilibrated” (when the probability density of the system has no time dependence) can be difficult, in general, an explicitly solvated system can be considered ready for generating stable MD trajectories when the initial rapid changes in the system (due to things like too-close contacts between atoms or a system density unsuitable for the desired simulation temperature) have finished. For explicitly solvated systems, we propose that a system cannot be considered ready for production dynamics until at least the system density has stabilized (i.e., reached a plateau). We further propose the following systematic and automatable procedure for determining whether the system density has finished its initial relaxation.

The first step is to fit the density data to an equation that seeks predicting the longer-time behavior of the system density. It is assumed that the relaxation of the density from its initial value to its final value is two-state; the density data are fit to a single exponential of the form

$$D\left(t\right)=D_I+\left(\left(D_F-D_I\right)\text{*}\left(1-e^{-k\text{*}t}\right)\right),$$

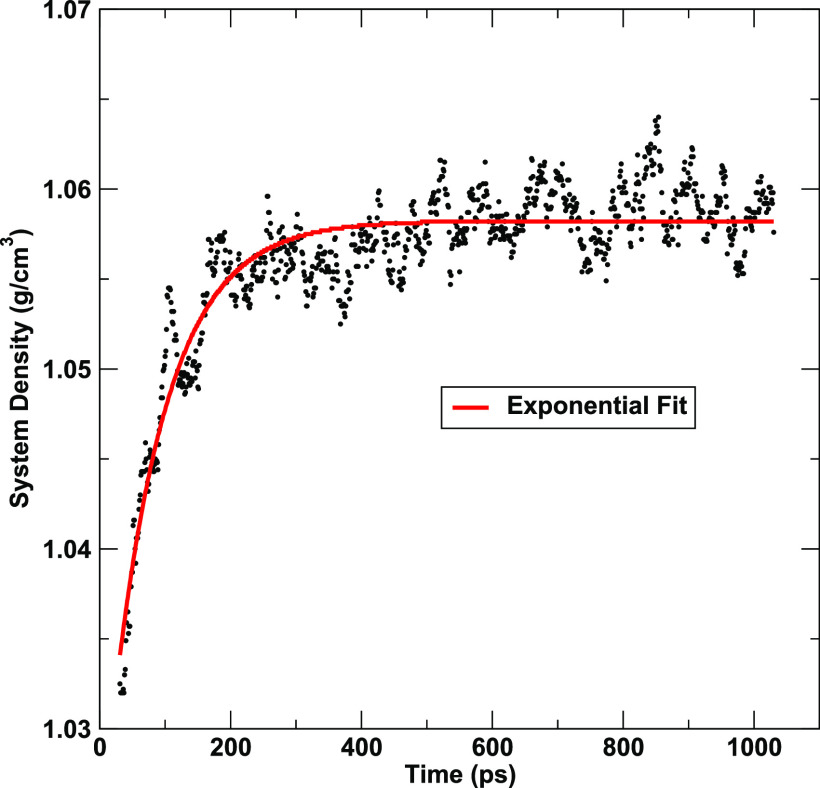
where D(t) is the density at time t, D_I is the initial density, D_F is the “final” (long-time estimated) density, and k is a relaxation constant. The average of the first 1% of the density data is used as the initial guess for D_I. The average of the second half of the density data is used as the initial guess for D_F. The initial guess for k is set to 0.1. When performing the fit, the density time values are shifted so that the initial density value occurs at t = 0. An example of the exponential fit to density is shown in Fig. 1.

FIG. 1.

Example of fit to density for the system from PDB 4F4L. The values for the exponential fit are D_I = 1.0341 g/cm³, D_F = 1.0582 g/cm³, and k = 0.0121 ps⁻¹. The plot time starts from step 10 of the preparation protocol (31 ps), but the fit was performed with time values shifted to 0. The density plateau criteria were satisfied at 501 ps. The difference of D_F to the average of the second half of the density data is 0.0005 g/cm³ and the chi-squared value of the fit is 0.0035.

The second step is to measure the slope of the fitted line. The final slope of the fitted exponential must be less than 1 × 10⁻⁶ g cm⁻³/ps for the density to be considered as having plateaued. The exponential fit to a smooth function better captures the longer-term behavior of the density and makes it possible to use the slope as a strict criterion since it is not subject to fluctuations in the density. In addition to the fitted slope, there are two additional criteria: (1) the absolute difference of D_F from the average of the second half of the density data must be less than 0.02 g cm⁻³ and (2) the chi-squared value of the fitted exponential must be less than 0.5. All three checks must be satisfied for the density to be considered as having plateaued.

The cutoffs for slope, absolute difference of D_F, and chi-squared were chosen empirically based on observations of what gave reasonable exponential fits. The slope cutoff was chosen since at a slope of 1 × 10⁻⁶ g cm⁻³/ps, the line appears “reasonably flat”; if the slope was to remain constant, the density would change by only 0.02 g cm⁻³ over 20 ns. The absolute difference cutoff of 0.02 g cm⁻³ was chosen since this seemed a reasonable difference from the long-time average based on the slope cutoff. The chi-squared cutoff of 0.5 is used to filter out extremely poor fits of the exponential function to density data and corresponds to a total deviation of about 0.71 g cm⁻³ (note that the largest chi-squared value observed for any of the runs in this study was 0.1009). It is likely that there is room for improving these values, but for the systems studied here, they give reasonable results.

METHODS

The preparation protocol was tested on a handful of systems including 391 randomly selected structures from the protein data bank (PDB) and three additional structures, including two with lipid bilayers: (1) a voltage-gated sodium ion channel (PDB ID 4f4l) in a POPE bilayer, (2) two WALP19³² peptides on a DOPC bilayer (referred to in this manuscript as xxx1), and (3) the cellulose fiber benchmark included with Amber (referred to in this manuscript as xxx3). In terms of composition, there were 2 protein–lipid, 1 carbohydrate, 161 protein, 187 DNA, 24 RNA, 6 protein–DNA, 3 protein–RNA, and 10 DNA–RNA systems.

The lipid bilayer systems were prepared using CHARMM-GUI^17,33 with the CHARMM 36 force field.^34,35 The topology and coordinates from step 5 (assembly) were used and converted to Amber topology and restart formats. The cellulose fiber system was prepared using the “Run.leap” script provided with Amber (in the Amber home directory, subdirectory “benchmarks/cellulose/setup”) to generate the un-minimized system. The remaining systems (from the PDB) were prepared according to the following protocol.

Since the focus of this study is on preparing systems for stable MD simulation, not perfect parameterization, a very simple protocol was followed when building structures selected from the PDB. First, the PDB was run through the program pdb4amber from AmberTools 19 to remove hydrogen atoms, strip water molecules, choose any alternate atom locations (when present, “A” was always used), and identify non-standard residues (typically ligands or co-factors). In general, non-standard residues were removed using CPPTRAJ³⁶ version 4.19.2, with the exception of residues such as NH₂ (C-terminal amine), ACE (N-terminal acetyl), and TCL (triclosan). Parameters for TCL were available from previous work and obtained using the Antechamber program from Amber, AM1-BCC³⁷ charges, and parameters from the General AMBER force field (GAFF).³⁸ In addition, the 5′-terminal phosphate groups were removed from nucleic acid molecules since these are typically not present in common molecular mechanics force field residue templates. Existing metal centers and ions (potassium, chloride, sodium, magnesium, and zinc) were also removed. Parameters were assigned using LEaP from AmberTools 19, using the FF14SB³⁹ force field parameters for protein residues, BSC1⁴⁰ parameters for DNA residues, and OL3^41,42 parameters for RNA residues. The structure was then solvated using TIP3P⁴³ waters with a 10 Å buffer around the solute in a truncated octahedral unit cell. If the system contained a net charge, enough sodium and/or chloride ions to achieve neutral charge were added by swapping them with randomly selected solvent molecules (via the “addionsrand” command in LEaP); ion parameters of Joung and Cheatham⁴⁴ were used. The final solvated system sizes ranged from ∼5 k to ∼857 k atoms, with the median system size being ∼16 k; only seven systems had more than 100 k atoms. A complete list of the systems used in this study along with final system sizes can be found in the supplementary material.

Before applying the protocol, the final structure from the build (LEaP or CHARMM-GUI) was then checked for close atomic overlaps (<0.8 Å) and unusually long bonds (equilibrium length plus 1.15 Å) with the “check” command from CPPTRAJ; the structure was run through the preparation protocol even if these problems were detected. Unusually long bonds could occur when the input PDB contained missing residues. No attempt was made to ameliorate sequence gaps; these were considered an extra “stress test” for the preparation protocol, i.e., to see if it can recover structures with particularly bad starting configurations. Every run for a given system used the same initial coordinates, but different initial velocities (corresponding to a temperature of 300 K) and random seeds.

To test whether the simulation protocol is sensitive to the choice of thermostat/barostat, the protocol was tested with various combinations of a weak-coupling thermostat/barostat, a Langevin-style thermostat, and a Monte Carlo barostat. Three sets of runs were performed: (1) initial nine steps done with a weak-coupling thermostat/barostat and final density stabilization done with a Langevin thermostat/Monte Carlo barostat (referred to as “Combined”), (2) all steps done with a Langevin thermostat/Monte Carlo barostat (referred to as “Langevin/MC”), and (3) all steps done with a weak-coupling thermostat/barostat (referred to as “Weak-coupling”). See the section titled “System preparation protocol” for specific thermostat/barostat settings.

The pressure control was isotropic for all systems except for those containing lipid membranes (where the pressure control was anisotropic).

During MD, the center of mass motion was removed every 1000 steps from step 9 onward. Long range electrostatics were handled using the particle mesh Ewald method with a cutoff of 8.0 Å and default Amber parameters. Long range Lennard-Jones interactions were handled using a cutoff of 8.0 Å and a long range correction.⁴⁵ The system preparation protocol is not expected to be very sensitive to reasonable choices for the above settings, and it is expected that they can be adjusted as needed.

RESULTS

All 394 systems tested were successfully prepared with no errors and produced stable trajectories as evaluated by no system “explosions” due to large forces, no errors due to constraint violations (namely SHAKE), and satisfaction of the density plateau criteria. This includes systems that started with very close atomic overlaps and/or very long bonds due to structural gaps. The density plateau times and final estimated density values for each system and each run can be found in the supplementary material.

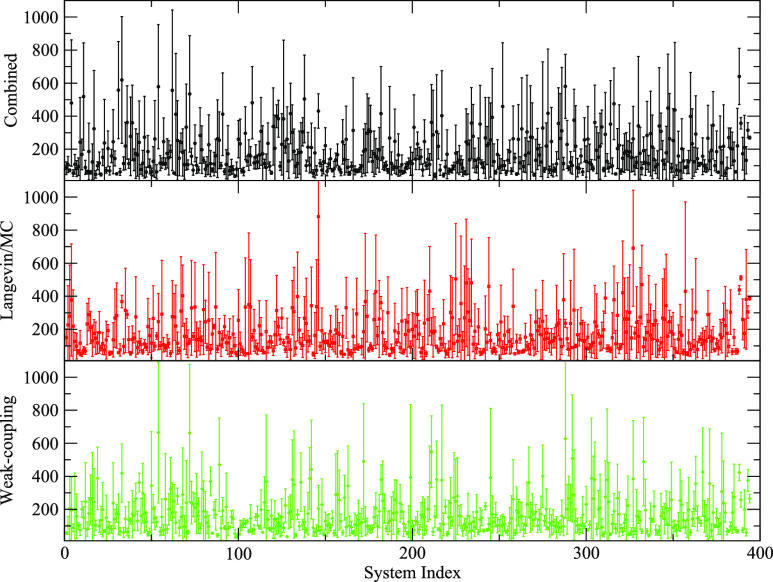
The overall average time taken to satisfy the density plateau criteria was 180 ± 188 ps for the Combined runs, 175 ± 181 ps for the Langevin/MC runs, and 166 ± 170 ps for the Weak-coupling runs. The minimum density plateau time observed for all cases was 31 ps (note that this is the shortest possible time as it is the time needed to complete steps 1–9); this was observed four times for the Combined runs, five times for the Langevin/MC runs, and six times for the Weak-coupling runs. The maximum density plateau time observed was 1215 (134d run 0), 1851 (17gs run 2), and 1309 ps (2pd3 run 2), respectively. A plot of average time to satisfy the density plateau criteria for each system is shown in Fig. 2. It is notable that the standard deviations for individual systems can be quite large, indicating that the time needed to satisfy the density plateau criteria for a given system can vary quite significantly. This is due to the stochastic nature of MD simulations with different random seeds/initial velocities.

FIG. 2.

For each system tested, the average plateau time for the Combined (black), Langevin/MC (red), and Weak-coupling (green) runs. Error bars represent 1 standard deviation.

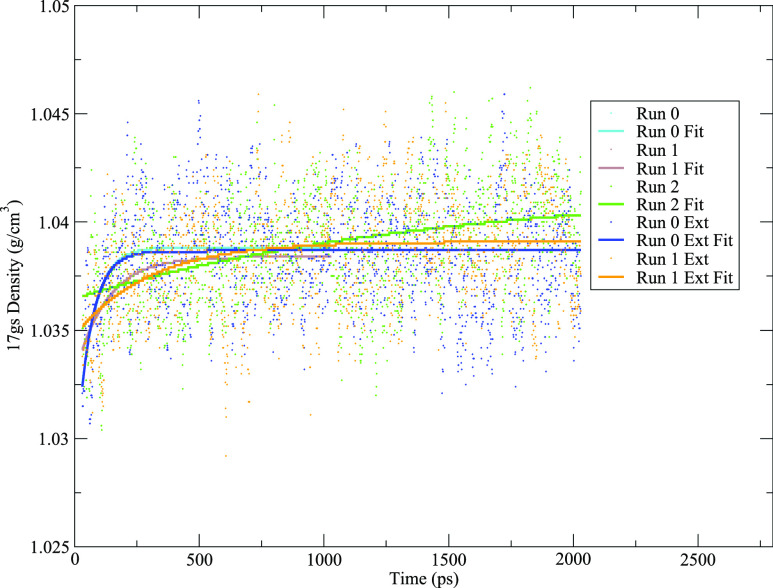
For example, the three Langevin/MC runs for the 17gs system had density plateau times of 321 ps, 474 ps, and 1851 ps, and final estimated densities of 1.0388 g/cm³, 1.0384 g/cm³, and 1.0417 g/cm³, respectively. The densities averaged over the last quarter of each simulation were 1.0381 g/cm³, 1.0387 g/cm³, and 1.0402 g/cm³, respectively. Figure 3 shows the system density and calculated fits for each of these simulations plus two extra runs, where the first two simulations (with original plateau times of 321 ps and 474 ps) were each extended an extra 1 ns to match the length of the third simulation; the new plateau times for these extended runs were 304 ps and 799 ps, and the new final estimated densities were 1.0387 g/cm³ and 1.0391 g/cm³, respectively. The original plateau time estimates were reasonably close given that the new plateau times are still within the original 1 ns simulation time and the new final densities are within 0.001 g/cm³ of the original final estimated densities. It is noted that since the point of this protocol is to ensure a system that will generate stable MD trajectories, not necessarily predict the equilibrium density of the system, the protocol is still performing well for these runs.

FIG. 3.

System density for the three Langevin/MC runs for the system 17gs. The first two runs were extended an extra 1 ns to make them the same length as the third run.

No correlation was observed between the change in density (i.e., D_F–D_I) and the time to satisfy the density plateau criteria (max correlation after linear regression was 0.07 for the Langevin/MC third set of runs). Similarly, no correlation was observed between the system size (i.e., total number of atoms) and the time to satisfy the density plateau criteria (max correlation after linear regression was 0.13 for the Langevin/MC first set of runs).

For comparison, we then ran all systems with a much simpler protocol, referred to hereafter as “Simple”: 100 steps of steepest descent minimization followed by 1 ns of NPT MD using the exact same settings as step 10 of the System Preparation Protocol. As with the other runs, these runs were repeated three times. Interestingly, 385 of the 394 runs were able to complete and satisfy our density plateau criteria (supplementary material, Table 4). However, nine of the MD runs failed to complete, in all cases, due to large forces leading to errors or overflows. The failed systems were 13gs, 149d, 156d, 208l, 239d, 254d, 261d, 275d, and 333d. These failed systems are structurally disparate; they range in size from 7684 to 37 081 atoms, some are nucleic acid systems and some are protein systems, and some of them had initial structures with problems (e.g., unusually long bond lengths) while others had no problems at all. In other words, there is nothing that stands out about these systems that would indicate a priori that MD simulations of the systems would fail.

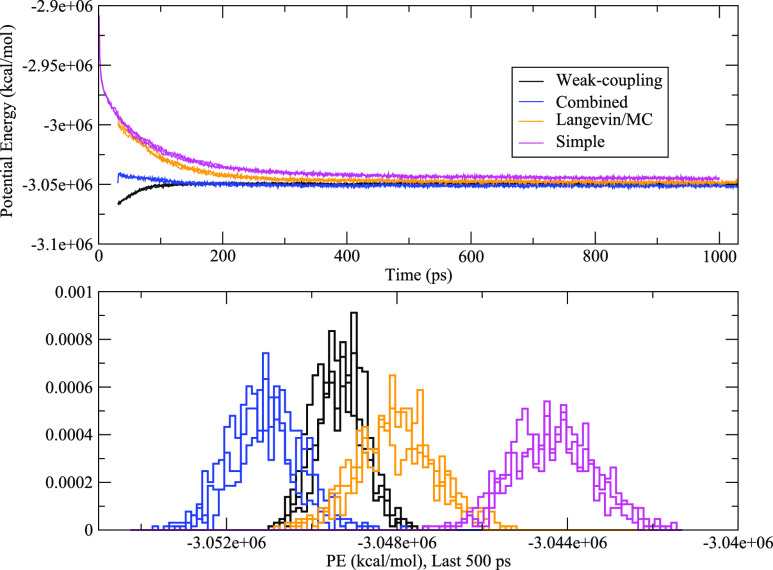
While the Simple protocol “worked” for the majority of the systems tested here, that does not necessarily mean it is equivalent to the protocol presented here. However, it is difficult to compare the two protocols from a structural standpoint (for example, comparing the heavy atom root-mean-square deviation (RMSD) of the final structure to the initial PDB coordinates) for three reasons: (1) the fully solvated structure may in fact differ somewhat from the crystal structure due to things like crystal packing and the simple fact that the solution environment in the simulations differs from crystal conditions, (2) there may be issues with the force field used that causes the simulated structure to drift away from the crystal structure, and (3) the extremely simple system construction protocol used in this study (where, for example, missing residues in the PDB were ignored) may itself cause the simulation structure to differ from the PDB structure. However, there are still some checks that can be done. For example, the largest system studied here is the ribosomal subunit from Thermus thermophilus (857 343 atoms), PDB 4kvb. Due to its high charge, this system required the addition of the largest amount of counterions (906 Na+) of all systems studied. Figure 4 shows the potential energies for each 4kvb run using the System Preparation Protocol and the Simple protocol. In each case, the potential energies of the runs using the System Preparation Protocol are lower than those using the Simple protocol (largely due to the electrostatic component of the potential energy), indicating a more favorable system relaxation. It is interesting to note that, in this system, the choice of thermostat/barostat appears to have a measureable effect on the resulting potential energies, specifically that using a weak-coupling thermostat/barostat in the initial stages of the protocol may be beneficial. The potential energy plots of several other large systems did not exhibit this phenomenon. Therefore, we conclude that this effect is likely observable in 4kvb due to the large number of ions in this system. We plan to explore this result in detail in future work.

FIG. 4.

(Top) Potential energy vs time for all 4kvb runs. (Bottom) Potential energy histograms of the last 500 ps of each run.

CONCLUSIONS

In this work, we have outlined a specific ten-step protocol that can be used to prepare a wide variety of systems for stable MD simulations in explicit solvents. The protocol is relatively simple and requires only basic features that are available in all major MD engines. We have also introduced a simple criterion based on the system density, which can be used to evaluate whether a system is ready for further simulation. The simulation protocol has been shown to be both effective and general and was tested on a wide variety of protein/nucleic acid systems. We emphasize that even though this protocol worked for a wide variety of systems, existing protocols that have been well-refined for specific system types (e.g., the Charmm-GUI protocol for membrane systems¹⁷) will still likely perform better for those system types. We envision that the primary utilization of this protocol will be for systems where no such protocol already exists, as the first step in obtaining a well-equilibrated system.

Based on the results of this work, in most cases, a weak-coupling thermostat/barostat should be avoided. However, it appears that for systems with large numbers (on the order of hundreds) of ions, there may be some benefits in using a weak-coupling thermostat/barostat for the initial steps of the protocol. This may be due to of the ability of a weak-coupling thermostat/barostat to be tuned to respond rapidly to changes in the system. For the final density equilibration (and any subsequent production runs), the results of this work combined with the now well-known deficiencies in the weak-coupling thermostat/barostat support the use of a more robust thermostat. It is also recommended to run the final density stabilization step for at least 1 ns of simulation time. When using the Langevin thermostat and Monte Carlo barostat, all but three simulations (out of 1182 for that thermostat/barostat) satisfied the density plateau criteria within 1 ns.

It is likely that the specific results shown here may change somewhat for different system construction protocols. In particular, how the system is solvated (e.g., if using another program like Packmol⁴⁶) may impact the final density plateau times. However, it is expected that this protocol is general enough that it will work for different types of system preparation. Future work will focus on how robust the protocol is with respect to different solvent models and/or slightly different force fields (e.g., when polarizability is present).

SUPPLEMENTARY MATERIAL

See the supplementary material for the table of systems used and final system sizes after solvation, table of density plateau times for each protocol run, table of final estimated density for each protocol run, and table of density plateau times and final estimated density values for “Simple” protocol runs.

DATA AVAILABILITY

The data that support the findings of this study are available from the corresponding author upon reasonable request.