Forecasting and planning during a pandemic: COVID-19 growth rates, supply chain disruptions, and governmental decisions

Highlights

• •We provide predictive analytics tools for immediate use during COVID-19.
• •We use data from the UK, USA, India, Germany, Singapore up to mid-April 2020.
• •We forecast COVID-19 growth rates at country-level.
• •We use auxiliary data (Google trends) to model excess demand.
• •We forecast the excess demand for products and services at country-level.

Abstract

Policymakers during COVID-19 operate in uncharted territory and must make tough decisions. Operational Research – the ubiquitous ‘science of better’ – plays a vital role in supporting this decision-making process. To that end, using data from the USA, India, UK, Germany, and Singapore up to mid-April 2020, we provide predictive analytics tools for forecasting and planning during a pandemic. We forecast COVID-19 growth rates with statistical, epidemiological, machine- and deep-learning models, and a new hybrid forecasting method based on nearest neighbors and clustering. We further model and forecast the excess demand for products and services during the pandemic using auxiliary data (google trends) and simulating governmental decisions (lockdown). Our empirical results can immediately help policymakers and planners make better decisions during the ongoing and future pandemics.

1. Introduction and motivation

First spotted in Wuhan in China, the ongoing COVID-19 pandemic has triggered the most severe recession in nearly a century and, according to the OECD's latest Economic Outlook,2 it has been causing enormous damage to people's health, jobs, and well-being. COVID-19 has affected almost all countries in the world and, has practically put the entire planet on hold for more than 2 months. At the time this paper was being revised, the number of confirmed global cases was more than 13 million; the number of deaths crossed the mark of 500,000 in late June 2020 – standing at 571,689 as of 13–7–2020 (WHO, 2020). Unfortunately, the number of cases and deaths is still exhibiting significant growth in many countries, with the Americas (most notably the USA and Brazil) been in the pandemic's epicenter.3

Our generation has never met anything remotely similar to this pandemic. Despite HIV/AIDS been associated with far more deaths,4 the speed with which COVID-19 can kill even-perfectly-healthy humans (sometimes within just a few days), and the unprecedented disruption in work and social life that it has brought (getting workers furloughed for months, and the vulnerable part of the population in strict isolation for 12 weeks), makes this pandemic unique.

Furthermore, due to this pandemic and the associated global healthcare crisis, supply chains have faced significant disruptions in the upstream, while hoarding and panic buying caused equally significant disruptions to the downstream. The balance of supply and demand was further impacted by the travel restrictions and lockdowns implemented by several countries worldwide. Due to these disruptions, short-term real time forecasts (daily and weekly) about the pandemic and its effect on the supply chain have become a very important managerial and policy-making imperative. Mid-and long-term forecasts are essential too for supply chain planning (at monthly, quarterly and annual frequency). However, research on these is more likely to be conclusive after the first wave of the pandemic is over, when more – and more reliable – supply chain data becomes available.

An accurate forecast of the evolution of new cases enables the more effective management of the resulting excess demand across the supply chain. Common sense and recent experience suggest that the acceleration and progression of COVID-19 across countries drives changes in immediate actual needs (healthcare and food) and in consumer behavior (for example panic buying and overstocking at home5 ). Such changes put an enormous strain to the respective supply chains. For instance, when consumers start panic buying dry pasta, eventually, the whole supply chain involving eggs, flour, wheat, is affected. A phenomenon, which is likely to be significantly exacerbated by the well-known implications of the Bullwhip effect (Chen, Drezner, Ryan & Simchi-Levi, 2000; Kahn, 1987; Lee, Padmanabhan & Whang, 1997; Wang & Disney, 2016).

Therefore, forecasting during the pandemic becomes essential for effective governmental decision making, for managing supply chain resources, and for informing very difficult political decisions as, for example, imposing a lockdown or curfews. Yet, forecasting the evolution of the pandemic i.e. the growth in the number of cases per country, or even to greater spatial detail, is a complex task because of the limited history of pandemic data and the multidimensionality of the problem. For instance, there are several, and at times unknown, factors that affect the contagiousness and the severity of the disease. To that end, forecasting in real time and while new data becomes available is a complex exercise for both government and supply chain managers (Beliën & Forcé, 2012; Nikolopoulos, 2020).

Epidemiologists have been applying traditional models for outbreak prediction (Nsoesie, Marathe & Brownstein, 2013; Yang et al., 2020). Applied mathematicians, decision scientists, and operational researchers have been employing time-series, and machine-learning techniques. As a result, for COVID-19, since the onset of the crisis, a few statistical and regression-based forecasts have been available online (Al-Shammari et al., 2020; Team IHME COVID-19 & Murray, 2020a, 2020b). Yet, and despite the contribution of these models for predicting the progress of the virus and its impact on the supply chain, their proliferation generates confusion. The most profound manifestations of this confusion have been the different approaches taken by companies and governments to deal with the pandemic, e.g. timings and extents of lockdown, processes of reopening the economy etc. and the differing, and often confusing, views about the onset of a second wave. This has been exacerbated by the wider recognition that different countries and, even, different regions are structurally diverse. Thus, using a single forecasting model may not accurately predict how the pandemic evolves. As a result, there is an emergent and urgent need for, on the one hand, more of these models (Petropoulos, Makridakis, Assimakopoulos & Nikolopoulos, 2014) and, on the other, a methodology that enables decision makers to select the one, which is likely to be the more applicable in their own context.

To address this need, in this article we forecast the growth of the pandemic at the country-level and evaluate 52 time-series, epidemiological, machine-learning, and deep-learning techniques. Furthermore, we propose a new hybrid forecasting method tailored to the task that is using cross-country information. To achieve generalizable results, we use data from a diverse set of countries (UK, USA, India, Germany, and Singapore), and perform a rolling forecasting evaluation consisting of 46 daily and 6 weekly forecasts. Our research can easily be extended into all the countries affected by the pandemic. We further use these forecasts in order to estimate the excess demand for products and services during the pandemic. Therefore, this study provides a methodological contribution as it illustrates how to perform such a forecasting exercise. A prerequisite for this is that data from the academic and policymaking community becomes available in accessible formats.6

For the remainder of this paper in Section 2 we review the literature while in Section 3 we present our empirical forecasting competition. In Section 4 we provide models for estimating the excess demand and respective supply chains disruptions. In the final section we provide our conclusions and implications for practice.

2. Background literature

In Section 2.1, we provide a targeted review on different techniques and methods used for the forecasting of the evolution of a pandemic. After that, in Section 2.2, we provide a review of the literature on forecasting the demand and supply in a supply chain in view of the evolution of a pandemic. In the last sub-section, we present our research questions and our methodological approach.

2.1. Forecasting the evolution of a pandemic7

Forecasting methods for pandemic evolution can be divided into time-series methods, compartmental epidemiological models, agent-based models, metapopulation models, and approaches in metrology (Nsoesie et al., 2013). A recent addition to this long list is machine learning (ML) and deep learning (DL) methods (Yang et al., 2020). Soebiyanto, Adimi and Kiang (2010) proposed the use of ARIMA models for one-step ahead forecasting of influenza weekly cases. Andersson et al. (2008) proposed the use of regression methods for the prediction of the peak time and volume (of cases) for a pandemic and provided promising empirical evidence to that end from seven outbreaks (in Sweden). Shaman and Karspeck (2012) used the Kalman filter based SIR epidemiological model to forecast the peak time of influenza and claimed that the peak can be predicted 6–7 weeks in advance.

An extensive evaluation of multiple time series methods for forecasting the evolution of an epidemic (Hantavirus) with data from CDC8  was performed by Yaffee et al. (2008) in which they compared casual methods with 16 time-series univariate methods and found that univariate methods were better at prediction than causal models. For COVID-19, Petropoulos and Makridakis (2020) applied ETS (Hyndman, Koehler, Snyder & Grose, 2002) models for predicting the evolution of the number of cases at a global scale. They reported very successful results in terms of real accuracy both for their point forecasts and the prediction intervals they provided. This is an open-access article in PLOS ONE that has already drawn significant attention with 70,852 views up to 29–05–2020 while available online for only 2 months, providing evidence of the interest and importance of such quantitative studies for academia and practice. Finally, there has been a series of studies focusing on predicting deaths in the USA and European countries for the next few months of the first wave of the COVID-19 pandemic (Team, IHME COVID-19 & Murray, 2020a, 2020b).

Furthremore, researchers and software companies have also rapidly during the COVID-19 pandemic developed live-simulators which make use of simulation models9 integrating governmental decisions (e.g. lockdown) and have been made available online via freely accessible websites and portals.

2.2. Supply chain disruptions due to a pandemic

Supply chain disruptions have been known to cause significant challenges and can affect organization performance (Hendricks & Singhal, 2003). Famous incidents, such as the tsunami that hit Japan in 2011 and the financial crisis of 2008 have illustrated how the interconnectedness and global nature of the supply chains can amplify even the smallest of “glitches” (Hendricks & Singhal, 2003). As a result, there have been several studies that attempt to explain the antecedents of resilient supply chains, both at the network (Kim, Chen & Linderman, 2015) and the organization levels (Bode, Wagner, Petersen & Ellram, 2011). Pettit, Croxton and Fiksel (2019) and Pettit, Fiksel and Croxton (2010) offer a good review of the literature on supply chain resilience that predates COVID-19.

The severity of the business disruption of COVID-19 pandemic has challenged much of our previous understanding of what constitutes a resilient supply chain. Recent reports have clearly indicated that this crisis has led to the rapid deterioration of several business and economic indicators, including productivity and global GDP (Harris, 2020). In addition, a few studies also estimated the impact of COVID-19 on the labor demand, a 16.24% decrease in the demand of working hours (Castro, Duarte & Brinca, 2020). These impacts are due to the imposition of travel and trade (Baveja, Kapoor & Melamed, 2020) restrictions and the shutting down of work places.

As a result, Araz, Choi, Olson and Salman (2020) asserted that COVID-19 is, probably the most severe disruption to the global supply chain in the last decade. Ivanov (2020), who considered the pandemic and the respective supply chain risks, provided a simulation model for global supply chain disruption and predicted the severity of COVID-19′s impact on supply chain performance. Similarly, Team IHME COVID-19 and Murray (2020a) predicted that COVID-19 will place unprecedented stress on hospitals, ICUs, and ventilators, and that the overall demand will be beyond the healthcare system's current capacity. In a follow up study, Team IHME COVID-19 and Murray (2020b) predicted the impact of COVID-19 on hospitals and deaths for Europe and US and suggested measures to temporarily increase the supply of critical products and services. Govindan, Mina and Alavi (2020) presented a decision support system to manage the demand for healthcare supplies based on physicians' knowledge and Fuzzy Inference System (FIS). They claimed that the use of their propositions leads to efficient and accurate managing of the supply chain disruptions in case of an outbreak.

Finally, Hobbs (2020) assessed the implications of COVID-19 on the food supply chains and reported that demand and supply shocks created during a pandemic are due to a shift in consumer behaviors. For instance, the sudden panic buying shift to ready-meals caused demand shocks, which then led to labor shortages, and disruptions of the transportation network. Furthermore, restrictions on cross-border goods movement led to further supply side shocks to the food supply chains. As a result, it would be reasonable to conclude that COVID-19 will have long-lasting effects on consumer habits and supply chains.

In summary, COVID-19 has put some significant and unprecedented strain on global supply chains across most product categories. Past literature on forecasting and on supply chain disruption has been able to provide some indication of the factors that can lead to it. However, and at the same time, it has exposed some of the challenges associated with identifying and responding to significant changes in the demand patterns during a pandemic. The ability to forecast excess demand during the pandemic early could, however, has significant implications for both supply chain managers and policy makers. The former can benefit from early warnings about where resources will be needed and the latter from a data driven approach to government interventions, e.g. by prioritizing critical supply chains.

2.3. Research questions, methodological approach, and implications for theory

Considering the targeted literature presented, our research aims to address the following research questions:

R1

What are the best models for forecasting the evolution of the pandemic at the country-level?

R2

How can we forecast the excess demand for products and services during the pandemic, before even actual supply and demand data become available?

We need to emphasize that we address the aforementioned research questions during the pandemic and not after it, and thus the urgency and importance of our ongoing research. This caveat constitutes a contribution by itself, as it evidences the ubiquitousness, responsiveness, and the timeliness of OR research.

We deploy an exploratory methodological approach in order to find the best forecasting methods (the ‘horses for courses’ – Petropoulos et al., 2014) – as we do not prescribe which methods/models we expect to perform better via a set of formal hypotheses. Then via a series of simulations we forecast the excess demand of products and services, i.e. the excess demand that is driven from the growth of COVID-19 cases. Our analysis covers a major part of the current wave of the pandemic, the period from the 22 January 2020 to 15 April 2020. From a methodological standpoint, we contribute to the stream of Phenomenon-based research as we engage in a very early phase of a scientific inquiry, observing, researching, and providing solutions for a developing a novel phenomenon (von Krogh, Rossi-Lamastra & Haefliger, 2012).

We further contribute both to the fields of Operations Research (OR) and Supply Chain Management (SCM). For the former, we provide an exhaustive empirical investigation that identifies the most accurate method for forecasting growth rates during a pandemic. We do so during the phenomenon and before the start-growth-maturity-decline sequence is complete. We contribute to the latter, the field of SCM, by providing an input (the demand forecasts for the new cases and the selected products), which is essential to decision-making algorithms that involve stock-control, replenishment, advance purchasing, and even rationing,10 i.e. situations that require a mean forecasted demand over the lead-time. We further provide simulations for the excess demand for products and services during the pandemic.

Finally, we contribute to the theory of predictive analytics, as we propose new data-driven predictive methodologies. We do so by building on theory from non-parametric regression smoothing on Nearest Neighbors (Härdle, 1990), and by using machine-learning clustering approaches. We capitalize on the experience of those countries where the outbreak of the pandemic came earlier to forecast the evolution of the pandemic. We also contribute to policymaking as we take into account the impact of political decisions – specifically the enforcing of a lockdown/curfew11 - on both the evolution of the pandemic and the resilience of the affected supply chains.

3. Forecasting the evolution of the pandemic

Following the influential12 empirical forecasting evaluation at the global level of Petropoulos and Makridakis (2020), we perform our empirical forecasting analysis at the country-level. This is also the most common geographical level for decision-making during the pandemic. Although at the time of writing there was data from 215 countries we decided to focus our study on five of these. We did so for both brevity and for providing a clearer illustration of the benefits of the methods we used. The countries we selected are: Germany, India, Singapore, the United Kingdom, and the USA as they cover a wide range of national systems and government responses. More specifically:

• •Germany because it is the country with the best response in Europe. This is despite neighboring with badly affected countries and being very close to the epicenter of the outbreak in Europe: Italy. Germany is also of interest as it followed a very aggressive testing policy early on, trying to identify each and every case as early as possible. As of 12/07/2020 a total of 200,047cases with 9135 deaths have been confirmed, bringing the deaths per capita at 109/1 M of population, much lower than most G20 countries.
• •India because it is the most populous country in the world still affected by the pandemic (with a population more than 1380 M, second largest in the planet). On this basis we did not include China because it is considered to have completed the first wave in April 2020. As of 12/07/2020 a total of 888,944 cases has been reported (third-most in the world) with 23,333 deaths.
• •Singapore because it is the country with one of the most advanced healthcare systems in the planet,13 a claim supported profoundly during this pandemic as well. Despite Singapore not employing extremely strict lockdown measures, it had a very aggressive testing approach, deployed a very effective tracking mobile application14 and has been in the forefront of technology adoption and development e.g. it developed a wearable device to obtain better results than those achieved by the mobile app15 . As of 12/07/2020 a total of 46,283 cases has been reported and a total of only 26 deaths, with 42,285 confirmed recoveries. This performance equals to a mortality rate at 0.06%, which is less than long term average for the seasonal flu (0.1%16 ) for which both a vaccine17 and a first-line antiviral treatment18 is available, rendering this country's response arguably the best in the planet. This is despite Singapore being one of the first hit by the pandemic, right after China and Taiwan.
• •the UK because it has been the most-affected country in Europe and the one with the most deaths per capita at 660 deaths per 1 M of population (worst among countries with population over 15 M). As of 12/07/2020 the UK had reported a total of 289,603 cases and 44,819deaths. The UK is also of interest as it has the largest public healthcare system in Europe19 (and 2nd largest single-payer healthcare system in the world). It also followed a different approach early in the pandemic – aiming for “herd immunity” rather than virus containment.20
• •And finally, the USA because it has been the most-affected country in the world by the outbreak (up to the time of this submission). As of 12/07/2020 it had reported a total of 3,415,573 cases and 137,797 deaths.

We collected all data on COVID-19 cases and respective healthcare and socioeconomic variables from credible international publicly available sources (listed in Appendix A).

3.1. Forecasting methods

We used a set of 52 models (from more than 20 methods21 ), ranging from simple to complex, and from time-series and epidemiological, to machine- and deep-learning. We produced forecasts for the growth rates at various stages of the pandemic for each nation. In total we produced forecasts 46 times for daily data and 6 times for weekly data. We identified the top-three methods per country that exhibit the smaller Mean Absolute Scaled Error (MASE), and used the equal-weighted combination of these methods for the follow-up simulations in Section 4. We used the simple average of forecasts, as it is a simple and effective method for combining forecasts (Makridakis & Winkler, 1983). We used MASE as our primary accuracy metric (Hyndman & Koehler, 2006) because it is scale-independent and widely accepted metric for forecast evaluations (Makridakis, Spiliotis & Assimakopoulos, 2020).

In Table 1 we provide a list of competing models. For details on these popular methods, the interested reader may revisit either the article on the latest forecasting competition (the M4 competition – Makridakis et al., 2020) or the free online forecasting textbook from Hyndman and Athanassopoulos.22   For the more advanced machine- and deep-learning methods we provide a brief description in Appendix A.

Table 1.

Forecasting methods.

Category	Method
Time-series	Naïve, Moving Averages (four models 2,3,4,7), SES, ETS, ARIMA, Theta, TBATS, ANN_AR, G&M (1985)-Damped trend (Gardner & McKenzie, 1985), Holt - Trend, ns-HW (non-seasonal Holt-Winters), ARFIMA, GARCH(1,1) (six models, wih: GED, SGED, NORM, SNORM, STD, SSTD), ARIMAx, Naïve-d with drift (ten models with step of 0.1 for the drifta)
Machine Learning	Multiple linear regression (MLR), Ridge regression, Decision Trees (DT), Random forest (RF), Neural Network (NN), Support vector machine (SVM).
Deep Learning	Long-Short Term Memory networks (LSTM)
Others	Splines, Sigmoid, Partial Curve Nearest Neighbor methods (PC—NN), Multivariate Clustering based Partial Curve Nearest Neighbor methods (CPC—NN)
Epidemiological	SIR (two models with: beta = 1.16, gamma = 0.38b; beta = 1.4, gamma = 0.3c)

^aFor the Naïve with drift approaches the reader can revisit Nikolopoulos, Buxton, Khammash and Stern (2016).

^bhttps://science.sciencemag.org/content/368/6492/742.abstract.

^chttps://www.r-bloggers.com/sir-model-with-desolve-ggplot2/.

3.1.1. A new forecasting proposition: nearest neighbor approaches for forecasting the evolution of a pandemic

The new proposition is data-driven and designed to use historical data from several countries to produce better forecasts for a target country. This is a classic adaptation of a Nearest Neighbor approach (Härdle, 1990; Kyriazi & Thomakos, 2020). We have named it Partial Curve Nearest Neighbor Forecasting (PC—NN) because it tries to find similarities in between parts of curves (from the start of the time series of a pandemic in a country until the date the forecast is made, as depicted in Fig. 1 ). The method involves the following steps:

• I.Collecting the data for a period of T days on daily cases growth for a set of N countries. The data vectors for N countries can be represented as: $\left[Y_1;Y_2;\dots ;Y_N\right]$.
• II.Fitting a smooth curve to each data series from each country separately, $\left[Y_1^{\prime };Y_2^{\prime };\dots ;Y_N^{\prime }\right]$. This is done by selecting the best fit (min squared distances optimization) from a pool of moving averages methods like 2-MA, 3-MA, 4-MA, and 5-MA
• III.Calculating the daily changes in the smooth curve (fitted in Step II) for each nation, $\left[\Delta Y_1^{\prime };\Delta Y_2^{\prime };\dots ;\Delta Y_N\right]$.
• IV.Comparing the daily changes curve of country (A) to those of other countries. To do so in a simple and effective manner, we normalized the data and we calculated the Euclidean distance between curves as the squared root of the sum of squared differences between the selected country's curve (e.g. India) and those of others. Based on the values of the$\left(r_{ij}\right)$, we selected the nearest neighbors.

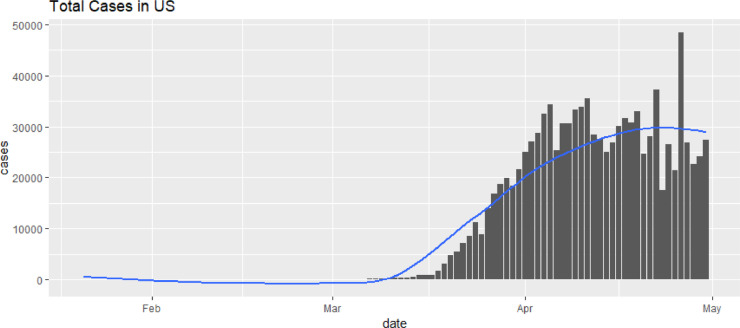
Fig. 1.

An example of COVID-19 cases and a fitted smooth curve (USA).

$NNDistanceForumulation:$

$\text{For}\mathrm{a}\text{country}\left(\mathrm{A}\right),$

$$N{N}_{dist}=[\sqrt{{\left(Y_{A{t}_1}^{\prime }-Y_{2t_1}^{\prime }\right)}^2+{\left(Y_{A{t}_2}^{\prime }-Y_{2t_2}^{\prime }\right)}^2+\dots +{\left(Y_{A{t}_T}^{\prime }-Y_{2t_T}^{\prime }\right)}^2};$$

$$\sqrt{{\left(Y_{At\_1}^{\prime }-Y_{3t\_1}^{\prime }\right)}^2+{\left(Y_{At\_2}^{\prime }-Y_{3t\_2}^{\prime }\right)}^2+\dots +{\left(Y_{A{t}_T}^{\prime }-Y_{3t_T}^{\prime }\right)}^2};$$

$$\sqrt{{\left(Y_{A{t}_1}^{\prime }-Y_{N{t}_1}^{\prime }\right)}^2+{\left(Y_{A{t}_2}^{\prime }-Y_{N{t}_2}^{\prime }\right)}^2+\dots +{\left(Y_{A{t}_T}^{\prime }-Y_{N{t}_T}^{\prime }\right)}^2}],$$

or

$$\begin{array}{cc}\hfill N{N}_{dist}& =\left[r_{A2},r_{A3},\dots ,r_{AN}\right],r_{AB}=\sqrt{\sum _{i=1}^T{\left(Y_{A{t}_i}^{\prime }-Y_{B{t}_i}^{\prime }\right)}^2}\hfill \\ & =1,2,\dots ,T,andA\ne B.\hfill \end{array}$$

• V.Defining groups using the $r_{1j}$values for a country (A): PC—NN1 (A and its closest nation), PC—NN3 (A and its two closest countries), PC—NN5 (A and its 4 closest countries), and PC—NN-all (all countries).
• VI.Finally, using the PC—NN groups identified in Step V for a country A and the ($N+1)$th period naïve forecasts for these countries, the ($N+1)$th period forecast is produced for country A using a simple average of all PC—NN's naïve forecasts. In the case of PC—NN3 we can either use equal weightings for the three neighbors (PC—NN3ew), or uneven/triangular ones (PC—NN3uw). This would mean that a 50% weighting is given to the nearest neighbor and 25% to the other two. For future research, we would recommend employing the next actual values of the neighbors instead of a naïve forecast.

We further extend this approach by using a multivariate dataset and a clustering algorithm. We performed the clustering with data on socioeconomic, climate, and COVID-19 related factors and grouped them according to whether they are facing, or they are about to face similar challenges. We used the K-means23 clustering algorithm to find the clusters of the countries. The countries that are in the same cluster will probably face a similar situations and challenges related to COVID-19 in the future, especially if they adopt similar policies. We consider this a very important feature of this forecasting method as it allows the clustering. The policy implication here is that there may be policies that some can learn from some but not from others. We call this method hereafter: Clustering and Partial Curves and Nearest Neighbor Forecasting (CPC—NN). We use similar notations for the variations of this latter extension too: CPC—NN1, CPC—NN3ew, CPC—NN3uw, CPC—NN5, and CPC—NNall.

3.2. Country-level forecasting

We produced forecasts for the growth rates at various stages of the pandemic for each of the five nations. In total we conducted this process 46 times for daily data and 6 times for weekly data for the period of 22 January 2020 to 15 April 2020. We derived the time series of percentage daily changes in COVID-19 cases from the daily new case series. We calculated the daily percentage growth with the following equation.

$$DailyGrowthin\%=\left(\frac{Case{s}_{t+1}-Case{s}_t}{Case{s}_t}\right)*100$$

We used the forecasting methods listed in Table 1 for forecasting for all the countries across all time periods. We used the death and recovery rates as the independent variables for the multivariate forecasting methods. We calculated the Mean Absolute Scaled Error (MASE) and the Symmetric Mean Absolute Percentage Error (SMAPE) for each iteration (Makridakis et al., 2020; Shankar, Ilavarasan, Punia & Singh, 2019). We calculated the relative errors by dividing with the corresponding error from the naïve method (Punia, Nikolopoulos, Singh, Madaan & Litsiou, 2020). We report in Table 2 the relative (to naïve) medians for: MASE (RelMdMASE), and SMAPE (RelMdMAPE).24

Table 2.

Forecasting accuracy: MASE and SMAPE (Relative median errors to Naïve) for all methods across all weeks (days) and across all countries, by proposed method. [Methods listed alphabetically].

Model	Weekly		Daily
	RelMdMASE	RelMdSMAPE	RelMdMASE	RelMdSMAPE
MA3 (best MA for weekly)	1.1527	1.2385	0.3402	0.3438
MA7 (best MA for daily)	1.2443	1.2265	0.2602	0.3336
ARFIMA	1.3828	1.4207	0.2709	0.3373
ARIMA	1.3828	1.4209	0.3297	0.3371
ARIMAx	2.0763	1.9343	0.3798	0.3926
DT	1.4219	1.5663	0.3400	0.3445
ETS	1.0427	1.2353	0.2813	0.2284
G&M (1985)–Damped trend	1.8048	1.4603	0.3459	0.3640
GARCH(1,1) model with SGED(best GARCH for daily)	1.2893	1.5166	0.2064	0.2160
GARCH(1,1) model with SSTD (best GARCH for weekly)	1.2236	1.3250	0.3312	0.4423
holt – trend	2.0588	1.6877	0.3543	0.3470
LSTM	1.9028	1.4825	0.3170	0.3885
MLR	1.4504	1.4187	0.3284	0.3515
Naive-d 0.1 (best Naïve-d for weekly)	1.0015	1.0022	1.0754	1.0687
Naive-d 0.9 (best Naïve-d for daily)	1.6488	1.5895	0.4130	0.5409
NN	1.2093	1.3848	0.3164	0.3745
NN_AR	1.9233	1.6155	0.3877	0.4467
ns-HW	1.3949	1.4220	0.2778	0.2443
RF	1.4180	1.5813	0.5024	0.4814
Ridge	1.4621	1.3408	0.3438	0.3147
SES	1.3949	1.4211	0.2765	0.3372
Sigmoid	2.1129	1.8262	1.5698	1.9833
Splines (CV)	0.9846	1.2572	1.2826	1.1985
SVM	1.2678	1.1858	2.1718	1.8120
TBATS	2.2840	1.9044	0.3597	0.4578
Theta	1.4200	1.5195	0.3844	0.4546
SIR-1	3.4664	2.0000	11.8852	2.0000
SIR-2	3.2383	2.0000	10.6193	2.0000

Since we are interested in finding the overall ‘winner’ across the competing methods, we need to evaluate the methods across the five countries simultaneously. To do so, we produced forecasts for all competing methods, for each period and country. We then calculated the medians of the forecasting errors across all countries. Table 2 includes the results.25

We observe from Table 2 that the performance of the Naïve method was very difficult to beat for the weekly data: only Splines (CV) did better. This led us to develop models using the PC—NN/CPC—NN method. In Table 3 and in the next subsection we demonstrate that these models do outperform all other methods for weekly data, but at a computational cost. Given that many policy decisions are taken weekly, a weekly frequency and forecasting horizon becomes very important for planning. For instance, the UK revised its social distancing measures based on forecasts and actual data for the pandemic every 3 weeks.

Table 3.

Relative median errors across all weeks, from the average of the top-3 performing methods for each country.^a

Country	Weekly		Daily		Top-3 models
	RelMdMASE	RelMdSMAPE	RelMdMASE	RelMdSMAPE	(Weekly forecasts)
Germany	0.1758	0.2264	0.2573	0.2672	Naive-d 0.5; Naive-d 0.4; Naive
India	0.1484	0.1252	0.2357	0.2727	CPC—NN3uw; PC—NN5; CPC—NN3ew
Singapore	0.1260	0.1290	0.1292	0.1363	PC—NN5 PC—NNall; PC—NN3ew
United Kingdom	0.2674	0.2792	0.2221	0.2584	Naïve; PC—NNall; CPC—NNall
USA	0.1907	0.2254	0.3032	0.2877	PC—NN3uw; PC—NN3ew; CPC—NN3uw

^aFor the sake of robustness checks, we also repeated this analysis (Tables 2 and 3) for 22 countries as well with similar results.

For the daily data the picture is very different, with many methods outperforming the Naive method. The GARCH(1,1) model with SGED with 0.2064 ranks first and MA7 with 0.2602 for MASE ranks second. On the other hand, for SMAPE, GARCH(1,1) model with SGED with 0.2160 ranks first and ETS with 0.2284 ranks second. The two epidemiological models did not perform well.

However, for the weekly data at country level (Table 3), the average of top-three methods performs significantly better than the naïve forecast. Most of the relative errors are less than 0.5 indicating the large performance improvement over naïve by the proposed methodology, and the respected anticipated benefits of combinations (Makridakis et al., 2020).

One key conclusion from Table 3, is that the level of error is not the same across all countries and for some it is easier to forecast than others. For example, for Singapore the error on the weekly data is 0.1260 and the one for daily 0.1292. At the other end, for the UK the error on the weekly data is 0.2674 for the USA 0.3032 (on the daily ones). Therefore, a key conclusion is that forecasting at the country level is more likely to lead to effective local guidance and would need to consider different underlying time series.

A second key conclusion is that different methods perform better in different countries. For example, for Germany Naïve and two variants of Naïve with drift are the top-performing models; while for the USA the two variants of PC—NN3 and CPC—NN3uw are the top-performing ones. Thus, the forecasting evaluation needs to be performed in every country separately: this is a consistent result with the ‘horses for courses’ doctrine (Petropoulos et al., 2014) as well as the Makridakis forecasting competitions (Makridakis et al., 2020). In Table 3 we present the results on the weekly data, as this is the frequency where all methods competed. This is because the PC—NN/CPC—NN family is computationally intensive and thus we only evaluated it over the six weekly forecasts.

Following the analysis and recommendations of Makridakis et al. (2020) we further calculated the prediction intervals for our competing methods. We also assessed the respective performance with MSIS, Cover Rate and ACD in a very similar fashion as in the M4 competition. The results are presented in Table 4 . The GARCH(1,1) model with SGED gives the best MSIS for both weekly and daily data -with a perfect cover rate for the weekly; while for the daily data LSTM and Naive-d 0.1 present a perfect cover rate of 100%. The cover rate is the most comprehensive metric as it measures the percentage of times that the next actual observation falls within the forecasting prediction interval and thus gives a perfect score (100%).

Table 4.

Forecasting uncertainty: MSIS, Cover Rate and ACD as in Makridakis et al. (2020) (Relative median errors to Naïve) for all methods across all weeks (days) and across all countries, by proposed method. [Methods listed alphabetically].

Method	Weekly			Daily
	RelMdMSIS	Cover Rate	ACD	RelMdMSIS	Cover Rate	ACD
MA2	1.0014	1.0000	0.0500	0.8424	0.9956	0.0456
MA7	0.9068	1.0000	0.0500	0.7444	0.9913	0.0413
ARFIMA	0.7311	1.0000	0.0500	0.6981	0.9652	0.0152
ARIMA	0.7664	1.0000	0.0500	0.7034	0.9652	0.0152
ARIMAx	0.6880	0.8696	0.0804	0.4657	0.9620	0.0120
DT	0.7219	1.0000	0.0500	0.5194	0.9851	0.0351
ETS	0.8070	1.0000	0.0500	0.7081	0.9652	0.0152
G&M (1985)-Damped trend	0.9558	1.0000	0.0500	0.7167	0.9783	0.0283
GARCH(1,1) model with SGED	0.4814	1.0000	0.0500	0.3693	0.9340	0.0160
GARCH(1,1) with NORM	0.6485	1.0000	0.0500	0.5706	0.9522	0.0022
holt - trend	0.9233	1.0000	0.0500	0.7146	0.9696	0.0196
LSTM	0.8146	0.9500	0.0000	0.7017	1.0000	0.0500
MLR	0.7209	1.0000	0.0500	0.6991	0.9652	0.0152
Naive-d 0.1	0.9823	1.0000	0.0500	0.9996	1.0000	0.0500
Naive-d 1.0	0.8947	1.0000	0.0500	1.0334	0.9737	0.0237
NN	0.7915	1.0000	0.0500	0.9714	0.9769	0.0269
NN_AR	0.6864	0.9667	0.0167	0.6963	0.9609	0.0109
ns-HW	0.8306	1.0000	0.0500	0.7095	0.9652	0.0152
RF	0.7982	1.0000	0.0500	0.7987	0.9817	0.0317
Ridge	0.8135	1.0000	0.0500	0.8250	0.9742	0.0242
SES	0.8306	1.0000	0.0500	0.7094	0.9652	0.0152
Sigmoid	0.9354	1.0000	0.0500	0.9486	0.9315	0.0185
Splines (CV)	0.7974	1.0000	0.0500	0.7892	0.9260	0.0240
SVM	0.8413	1.0000	0.0500	0.8486	0.9264	0.0236
TBATS	0.7011	1.0000	0.0500	0.7031	0.9565	0.0065
Theta	0.8306	1.0000	0.0500	0.7094	0.9609	0.0109

3.3. Forecasting with PC-NN/CPC-NN

We first produce forecasts with the five models for PC—NN for the weekly data following the steps prescribed in 3.1.1. Then we proceed at implementing the five models for CPC—NN by using the K-means algorithm for clustering the multivariate data we collected. The data consists of the variables listed in Table 5 .

Table 5.

List of variables used for clustering for the CPC—NN method.

Name	Description
Travel restrictions	When no ban (0), for days with ban (1)
Reproductive number	Average R value of the country
Temperature	Average temperature of the country
Humidity	Average humidity of the country
Population density	Population density
Population median age	Median age of the population
Lung disease	Deaths by lung diseases per 100,000 people
Diabetes	Diabetes prevalence of the population
Coronary heart disease	Deaths by heart disease per 100,000 people
Distance Wuhan	Distance as vector from Wuhan
Air pollution	Air pollution measured by PM 2.5
GDP spending on healthcare	Percentage of GDP spent for the healthcare sector in US dollars
Global healthcare ranking	Development ranking from 0 to 100
Growth of cases on daily basis	Normalized growth in percent

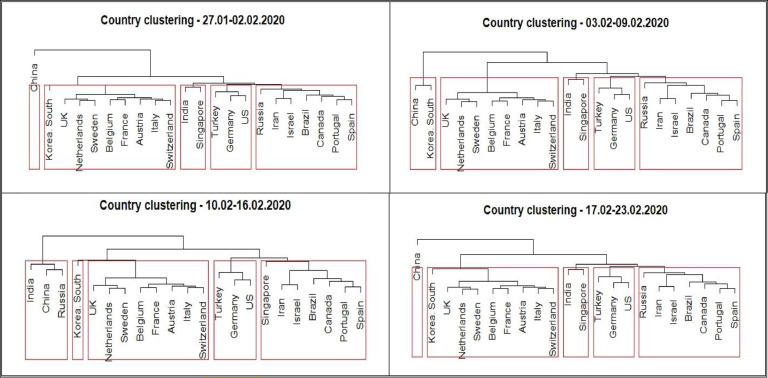
We performed the clustering at each step of the rolling forecasting evaluation because we expect clusters to change with the evolution of the pandemic in different countries. Fig. 2 presents the results for four instances of the clustering of countries. The clusters evolve over time and countries are changing clusters due to changes in both the spread COVID-19 and the decisions policy makers are taking. The algorithm selects the number of clusters based on maximum height in the dendrograms. Many other clustering algorithms could be employed before forecasting (see for example Vangumalli, Nikolopoulos & Litsiou, 2019), but we leave this for future research.

Fig. 2.

Clusters of Countries at different points of time.

Table 6 presents the performance of PC—NN/CPC—NN. The results are better than the Naïve method, with eight models outperforming the best method of Table 2 (Splines (CV)) for the weekly data. PC—NNall is the overall winner with MASE of 0.3604 and SMAPE of 0.4703. Only the PC—NN/CPC—NN methods that picked only one nearest neighbor are performing worse than Naïve.

Table 6.

Forecasting performance of the PC—NN & CPC—NN models on weekly data.

Method	RelMdMASE	RelMdSMAPE
PC—NNall	0.3604	0.4703
PC—NN3ew	0.4436	0.4928
CPC—NN3uw	0.4664	0.5683
PC—NN5	0.4821	0.4080
PC—NN3uw	0.5827	0.6299
CPC—NNall	0.6262	0.6767
CPC—NN5	0.6434	0.5800
CPC—NN3ew	0.8499	0.5949
Splines (CV)	0.9846	1.2572
Naive-drift-0.1	1.0015	1.0022

This concludes our investigation for R1, as we have identified many models and combinations that perform better than the standard forecasting benchmarks at multiple frequencies.

4. Forecasting the excess demand for products and services

In this section, we advance our work towards addressing the second research question (R2), which aims at exploring how we can forecast the excess demand for products and services during the pandemic. In normal conditions, the demand for some of these products and services is relatively non-volatile and, as a result, does not exhibit complex patterns. It is, thus, not very difficult to forecast. This is especially so for products in more mature markets such as pasta, rice, toiletries. However, during a pandemic, we expect the purchasing behaviors will become significantly more volatile because of consumer biases on the potential for scarcity (Chandon & Wansink, 2006). In such cases, customers become less able to evaluate both their own inventory of supplies and the risk of scarcity of the products they are planning to panic. This leads to “panic buying” (Tsao, Raj & Yu, 2019), which was particularly prevalent in the COVID-19 pandemic (Gray, 2020).

4.1. Modeling excess demand

We consider the excess demand for the quantity of different products and services including groceries, electronics, automotive and fashion. We start by considering the following equation as our benchmark model.

$$Q_{Dt}=aCov{19}_{t-b}$$ (1)

Where $Q_{Dt}$ is the quantity of the excess demand at time t. $Cov{19}_{t-b}$ is the growth rate of incidents of COVID-19 that took place at time t-b with b being the respective lag. We assume that the effect on the quantity demanded will take place after society becomes aware of the evolution of the infectious disease. Parameter a captures the effect of Cov19 on $Q_{Dt}.$

If a government decides to impose measures to reduce the spread of the virus, it could force a lockdown. The lockdown could generate further anxiety and as a result further change in consumer behavior. To capture this effect, we introduce a dummy, which takes the value of one (1) after the date that the government imposed lockdown and zero (0) before.

$$Q_{Dt}=aCov{19}_{t-b}+n{D}_t$$ (2)

4.2. Forecasting excess demand

For the estimation of the demand quantities, we use as a proxy the searches for products from the Google trends (Jun, Yoo & Choi, 2018) of four different sectors (Groceries, Electronics, Fashion, Automotive) for the five countries we research. We decided to use auxiliary data as confirmed supply chain demand data will not be available for the months to come and as such no demand modeling would be possible until then. This is not an option for policymakers however and to that end we believe we provide here an essential set of tools to inform decision making.

For the values of variable COVID-19 in Eq. (2) we use the average of the top-3 forecasts prepared in Section 3. We then use ordinary least squares to estimate the coefficients in Eq. (2). We model the excess demand over and above normal stable demand. We make the implicit assumption that the products we are looking at follow a relatively stable average demand in the long-run. Since we are focusing on the impact of the COVID-19 on the supply chains of these products we assume that the pandemic leads to an intermittent demand pattern over and above the mainstream (Nikolopoulos, 2020).

4.3. Using Google trends data to estimate the coefficients a and n for different sectors

To estimate a, we need the demand of the relevant products and the growth of the confirmed COVID-19 cases. Since demand patterns and data are not available yet, we extracted the Google search trends for certain goods to get an estimation of how the demand changed on a daily basis during the COVID-19 pandemic as shown in Table 7 .

Table 7.

Daily Google Trends data extracted.

Sector\Product	Product 1	Product 2	Product 3
Grocery	Bread	Meat	Vegetables
Electronics	TV sets	Smartphone	Notebook
Fashion	Shoes	Dresses	Handbags
Automotive	New Car	Used car	Car rental

We used several consumer products per sector, which allowed us to get a more holistic trend. We chose sectors that have different underlying supply chains. We extracted Google trends data for a 90-day window, starting from the beginning of February and ending on the 30th of April 2020. We estimated parameter a by running regressions between the daily growth and the daily search trend, resulting in Table 8 .

Table 8.

Estimation of parameter a. ***, **, and * indicate statistical significance at the 1%, 5% and 10% levels respectively. Robust standard errors presented in the parenthesis.

Country\Industry	Grocery	Electronics	Fashion	Automotive
Germany	14.3***(3.1)	12.9**(2.1)	4.2***(1.9)	0.5***(0.2)
India	16.4***(2.4)	8.9***(3.2)	−3.9***(1.0)	−5.8***(2.3)
UK	14.9***(2.0)	9.3***(3.4)	1.0***(0.2)	−6.3***(2.4)
USA	15.9***(5.3)	8.0***(2.1)	−0.2***(0.0)	−2.2*(1.2)
Singapore	13.7***(4.3)	4.1***(2.0)	−0.8***(0.2)	−0.5***(0.1)

Model: $\text{Country}\_\text{search}\_\text{trend}\sim \text{Country}\_\text{growth}\_\text{normalized}-1.$

To consider the impact of imposing lockdowns, we use the same data from Google trends and add the variable lockdown as a binary classifier. It takes the values of 0, when there is no travel ban or curfew, and 1 when a curfew or travel ban are in place. Re-running the regressions leads to Table 9 :

Table 9.

Estimation of parameter a and n. ***, **, and * indicate statistical significance at the 1%, 5% and 10% levels, respectively. Robust standard errors presented in the parenthesis.

Country\ Industry	Grocery		Electronics		Fashion		Automotive
	α	n	α	n	α	n	α	n
Germany	26.1***(10.4)	88.5***(14.5)	36.7***(18.1)	108.7**(52.3)	−30.3**(15.3)	75.7**(38.3)	−28.3**(15.0)	63.1**(34.2)
India	8.9***(4.7)	77.0***(20.4)	12.4***(6.3)	65.0**(32.1)	−21.5**(12.2)	53.4(25.0)	−21.5*(12.2)	47.7**(26.0)
UK	15.8***(3.9)	83.9***(18.3)	16.4***(7.7)	70.3***(35.1)	−21.3**(13.6)	61.0**(36.5)	−28.6**(15.0)	60.8**(31.2)
USA	19.4***(4.6)	88.5***(43.2)	27.7***(12.1)	92.4***(45.7)	−26.6**(14.0)	68.3**(38.2)	−30.8**(16.3)	73.9***(35.5)
Singapore	6.2***(2.3)	65.2***(25.7)	12.4***(6.9)	53.8***(22.3)	−14.8*(8.1)	45.8**(23.2)	−12.8**(6.6)	40.4***(19.8)

Model: $Country\_search\_trend\sim Country\_growth\_normalized+Lockdown-1.$

4.4. Simulations

Considering a 21 day Lockdown (3 weeks), starting from week 1 (thus Lag =3), we estimate the excess demand from the lagged values of COVID-19 growth rates in a country. We simulate four product categories for all five countries: Groceries (P1), Electronics (P2), Fashion (P3), and Automotive (P4).

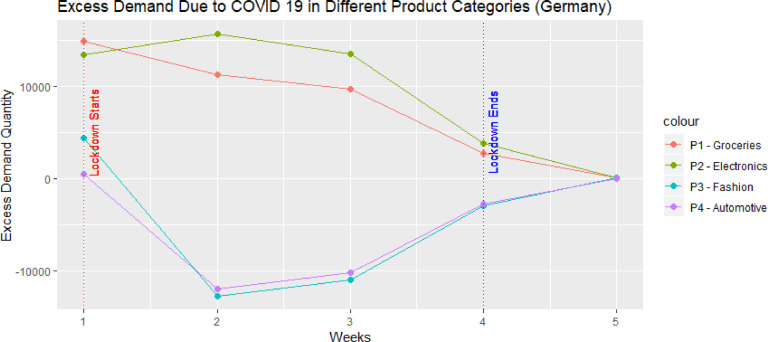
Fig. 3 depicts the projected excess demand of the different sectors due to the pandemic from the onset of the lockdown.

Fig. 3.

The impact of Lockdown in Germany: excess demand for products due to the pandemic.

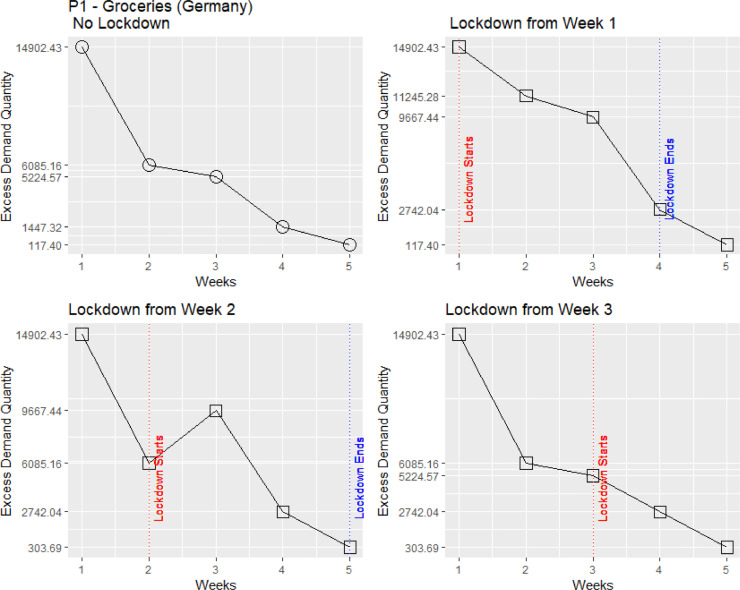
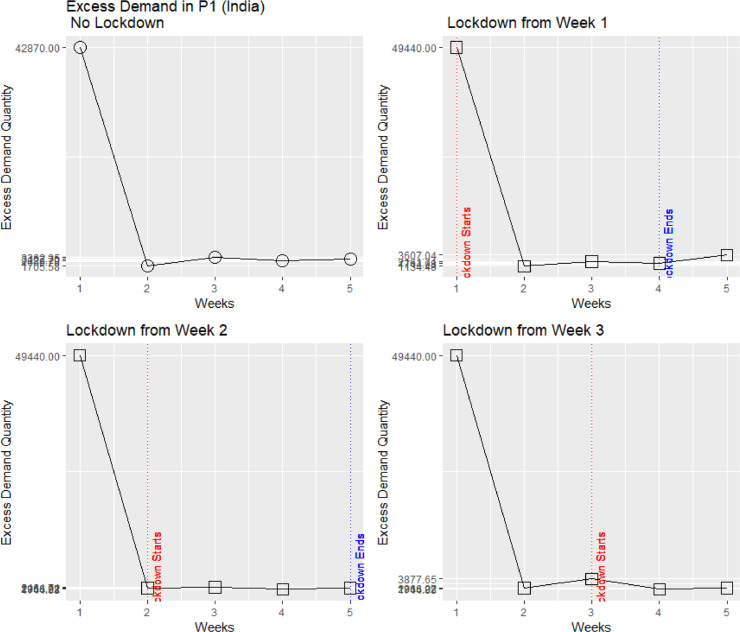
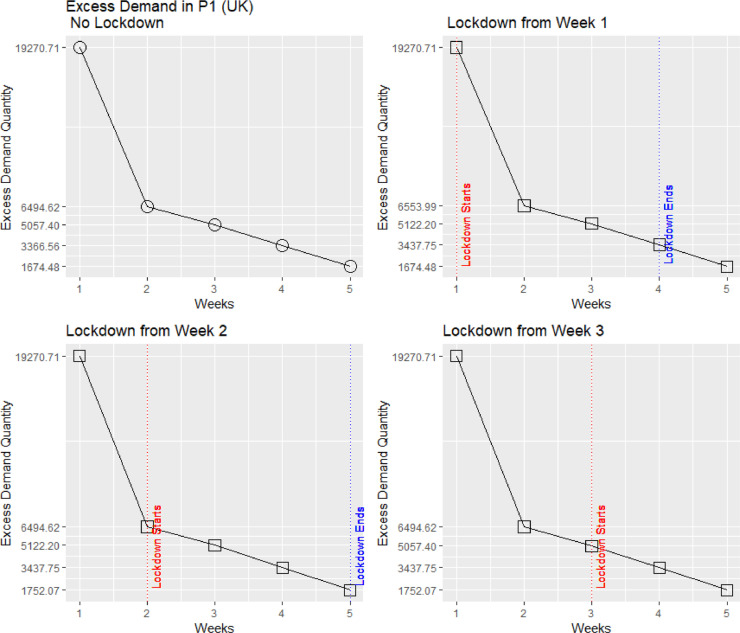
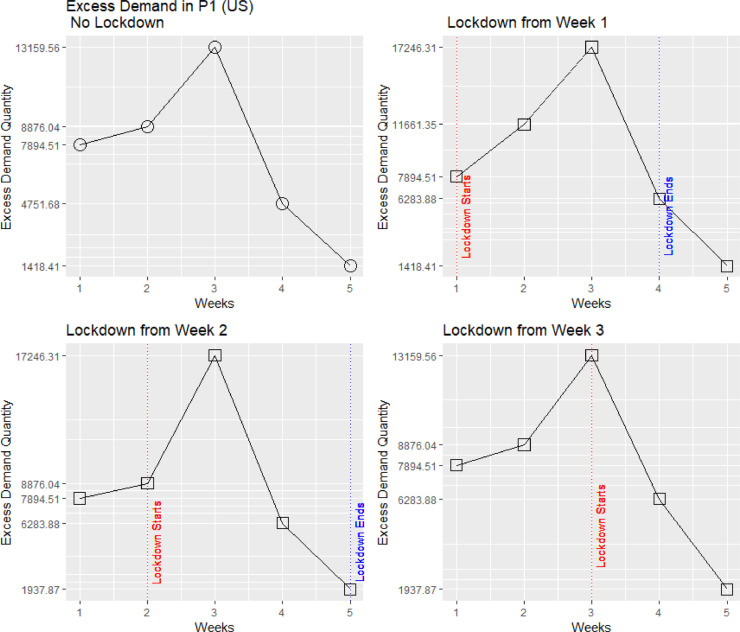
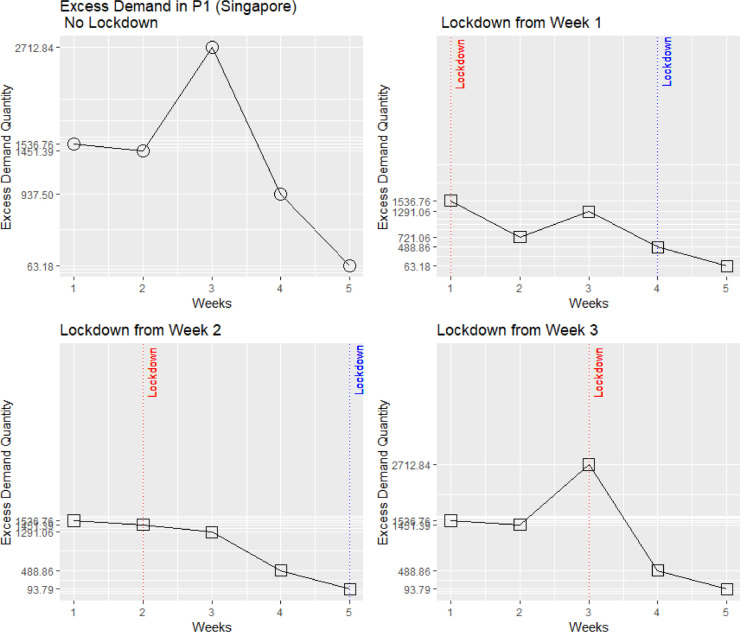
We further investigate the impact of moving the lockdown over the weeks to create alternative scenarios (Fig. 4 ). We consider four scenarios: (a) no lockdown, (b) lockdown from week 1, (c) lockdown from week 2, and (d) lockdown from week 3. We focus on the more critical products, that of Product category 1 – Groceries, as these are essential during the pandemic. We provide the simulations for groceries (P1) for the remaining four countries in Appendix C.

Fig. 4.

The impact of alternative Lockdown decisions in excess demand for Groceries in Germany.

Our results show that the onset and the amount of the excess demand are dependent upon the type of product and the timing of the lockdown. Demand for groceries (P1) and electronics (P2) becomes excessive, whereas that for fashion (P3) and automotive related items (P4) reduces (Fig. 3). These trends have been confirmed by articles in the daily press. Furthermore, Fig. 4, shows that for groceries, the earlier the lockdown is imposed, the higher the excess demand. Finally, the longer the lockdown lasts the higher the cumulative excess demand. We find similar results for India, the UK, the USA and Singapore (Appendix C).

Our results therefore point to various directions for both the process of forecasting and the management of the supply chain. First, we demonstrate that the process of forecasting during the pandemic needs to be dynamic and to take into account the changes in the external circumstances. Research that focuses on responses to humanitarian crises data (van der Laan, van Dalen, Rohrmoser & Simpson, 2016) has also argued for a flexible approach to forecasting. As more information becomes available and decisions about the response to the pandemic are being taken, the approach to forecasting needs to be readjusted. Therefore, our results extend those for the management of more localized humanitarian crisis by illustrating the implications for forecasting at the time of a global pandemic.

Furthermore, our results illustrate the challenge of making forecasts and making supply chain decisions for products where consumers need to make judgments about their own immediate needs. In the case of groceries, previous research indicates that when consumers make estimates about their own inventory levels (e.g. the amount of toilet paper they have at home), they do so with unrealistic assumptions and limited data (Chandon & Wansink, 2006). As a result, they are very likely biased and influenced by the external environment. Our results forecast that similar effects are at play with other product categories such as electronics, where consumers have to make evaluations about the capability of their own equipment and the potential for scarcity, e.g. the combined effect of fear of failure of one's own laptop and the potential for stockouts.

Therefore, we can make two recommendations because of our results. The first for policy makers and relates to efforts to secure high volumes of inventory for products in those categories (P1 and P2) before the lockdown. Our analysis shows that this should not be based only on data of actual needs, but should take into account consumers’, often biased and at times irrational, behavior. The second recommendation is for supply chain managers of companies in the product categories we analyzed above. In addition to the preparations for fluctuations in demand, particularly in view of a lockdown, our results indicate that the approach to forecasting needs to continuously adjust to take into account the changing needs. This would imply changes to the forecasting models as well.

This concludes our investigation for R2, as we have identified ways to forecast the excess demand for products and link that to governmental decisions.

5. Conclusions, implications for practice and policymaking, and the future

This paper has examined urgently and extraordinarily the predictability of COVID-19 growth in five countries and modeled the dependent short-term supply chain disruptions. We evaluated existing state-of-the-art and proposed new data-driven methods for forecasting pandemic evolution while working with limited, volatile, and constantly revised data. Countries have different healthcare systems, run the COVID-19 tests in different places (hospitals, GPs, community centers, airports), apply different policies (track and trace, lockdowns, legislation, etc.), test with different devices and protocols, and report differently new cases and deaths (including or excluding deaths at home or in care homes). All these complicate and limit the extent of accuracy that can be achieved from forecasting models. There is, therefore, an immediate need for a homogenous credible database to enable more accurate and comparable forecasting by the academic community, policy makers and supply chain professionals. Nevertheless, forecasting remains an essential part of many decision-making processes, and as such, this motivates us further for this research endeavor. We also modeled the excess demand for products and services during the pandemic via using auxiliary data (Google trends) as actual supply & demand data are not yet publicly available: our models rightly predicted the panic buying effect and respective excess demand for groceries and electronics during the current wave of COVID-19.

Many operational decisions are affected by our research including those associated with planning, production, shipping, stock-control (Prak, Teunter & Syntetos, 2017), ordering, and allocating of resources (Nikolopoulos, Metaxiotis, Lekatis & Assimakopoulos, 2003). They are all decisions where an accurate forecast is an essential input and as such, our study is relevant. Furthermore, the results of our research can inform government decisions. We show that the earlier a lockdown is imposed, the higher the excess demand will be for groceries. Furthermore, the longer the lockdown lasts the higher the cumulative excess demand and thus the higher the need for planning for production and inventory. Consequently, a policy recommendation for the governments will be to secure high volumes of inventory for such products before the lockdown; and if not possible, consider radical interventions such as rationing.

During a health emergency response, leaders need to make a numerous critical decisions for the supply chain, and for prevention strategies (Glasser, Hupert, McCauley & Hatchett, 2011). The decisions occur in a rapidly changing environment and they might be misinformed or biased. Consequently, forecasting becomes an essential tool for helping and providing guidance for the utility and timing of prevention strategies. However, the use of infectious disease forecasts for decision-making is challenging because most existing infectious diseases require different methods for different countries. Each forecasting model has limitations. Furthermore, data may not be reliable because it may have been recorded during the emergency situations. As a result, comparing forecasts at the country level remains challenging, potentially limiting the development and utility of forecasts.

Despite these limitations, COVID-19 forecasts provide indications and quantify the needs that appear in an emergency, and thus more research should be directed towards identifying the best forecasting models for all geographical contexts and temporal frequencies.

Appendix A. Data sources

The following publicly available data sources has been used.

• •Confirmed, recovered and deceased cases were obtained from Johns Hopkins university, this data set is derived from multiple sources, including WHO and national governmental organization and is updated on a daily basis: (https://data.humdata.org/dataset/novel-coronavirus-2019-ncov-cases) and https://coronavirus.jhu.edu/ (Johns Hopkins Coronavirus Resource Center). Initially the process was done manually at a daily basis and at a later stage automated via https://github.com/CSSEGISandData/COVID
• •Climate information a s well as the reproduction number is derived from the Covid 19 reseaerch team from Beihan university in China: (http://covid19-report.com/#/forecasting, https://github.com/bigscity/nCov-predict)
• •The information about the specific date of travel restrictions and curfews by country were obtained from Mayer Brown: Mayer Brown's COVID-19 Global Travel Restrictions by Country (https://www.mayerbrown.com/-/media/files/perspectives-eve- nts/publications/2020/02/mayer-brown_covid19-global-travel-restrictions-by-country2.pdf)
• •Information about populations, including median age, population density were obtained from the world population review (https://worldpopulationreview.com/countries/median-age/)
• •Rate of lung diseases per 100.000 inhabitants by country was obtained from: (https://www.worldlifeexpectancy.com/cause-of-death/lung-disease/by-country/)
• •Rate of coronary heart diseases per 100.000 inhabitants by country was obtained from: (https://www.worldlifeexpectancy.com/cause-of-death/coronary-heart-disease/by-country/)
• •Diabetes prevalence by country derived from the world bank:(https://data.worldbank.org/indicator/SH.STA.DIAB.ZS)
• •Percentage of GDP spent on healthcare by country was obtained from the world bank: (https://data.worldbank.org/indicator/SH.XPD.CHEX.GD.ZS)
• •The PM 2.5 concentration as metric for air pollution by country was derived from the world bank:(https://data.worldbank.org/indicator/EN.ATM.PM25.MC.M3)
• •Import data from OECD: https://stats.oecd.org/Index.aspx?DataSetCode=BTDIXE#
• •Google trends: https://trends.google.com

Appendix B. Description of machine- and deep-learning forecasting methods

Decision tree

The decision tree is supervised machine learning algorithm used for the classification and regression application. We used the continuous variable, regression decision tree with classification and regression tree (CART) algorithm. The Caret package from R is used for the implementation of the method (Kuhn, 2008). The parameter optimization was performed using grid search.

Random forest

Random forest was developed by Breiman, (2001); Ho, (1995) and it generates multiple random samples and perform the bagging of decision tree applied on random sample of data, thus called random forest. The algorithm is implemented using Caret package in R (Kuhn, 2008) and grid search was used to search best combination of parameters. The literature is referred for optimal implementation of the random forest fore forecasting (Fischer & Krauss, 2018; Punia, Singh & Madaan, 2020).

Artificial Neural Network (ANN)

ANN have three layers for data modeling, namely, an input layer, an output layer, and hidden layers. The inputs $\left(X_1,X_2,\dots ,X_p\right)$and outputs $\left({\mathrm{y}}_{\mathrm{t}}\right)$ are modeled through $y_t={\alpha }_o+{\sum }_{j=1}^q{\alpha }_{j}g\left({\beta }_{oj}+{\sum }_{i=1}^p{\beta }_{ij}{X}_{t-i}\right)+{\epsilon }_t,$ where $\alpha$s and $\beta$s are connection weights, p is the number of input nodes and q is the number of hidden nodes. The output from the ANN is a non-linear function that maps the inputs to outputs with the help connection weights. ANN were applied for the forecasting using death rate and recovery rate as the input and cases growth as the output variable in R.

LSTM

The LSTM networks are state-of-the-art sequencing modeling methods which comes under deep learning. The sequence modeling feature of LSTM can be used for time-series forecasting specially to model non-linear time series variations. The LSTM were implemented using Keras library in R (Chollet, 2015). The work of Punia, Nikolopoulos et al. (2020) was followed for implementation and hyperparameter optimization of the LSTM networks.

Ridge regression

Ridge regression is an advanced regression technique that allows to perform L2 regularization i.e. adding penalty equals to square of coefficients along with minimizing the sum of squared error between actual and forecast. The linear ridge regression was implemented using ridge library in the R.

Support Vector Machines (SVM)

SVM are the machine learning techniques that is based on classification and regression algorithms and can be used for the forecasting purposes using regression method. SVM were implemented using e1071 package in R. The “linear” kernel were used along with “eps-regression” type from the parameters for the implementation of the method.

Splines and sigmoid

The splines are used to fir a smoothing function to the data just like the regression. Different smoothing splines can be fitted to the data using different non-linear functions and best one can be selected for the purpose of forecasting. We have used the sigmoid, logistics functions to fit the data. The functions smooth.spline and nls (non-linear least square estimates) were used from the base package of the R.

Appendix C. Groceries demand (simulations) for India, UK, USA, and Singapore [Simulations for P2, P3 and P4 are available upon request]

Fig. 5.

The impact of alternative Lockdown decisions in excess demand for Groceries in India.

Fig. 6.

The impact of alternative Lockdown decisions in excess demand for Groceries in UK.

Fig. 7.

The impact of alternative Lockdown decisions in excess demand for Groceries in US.

Fig. 8.

The impact of alternative Lockdown decisions in excess demand for Groceries in Singapore.