A Fast and Accurate Method for Genome-Wide Time-to-Event Data Analysis and Its Application to UK Biobank

Abstract

With increasing biobanking efforts connecting electronic health records and national registries to germline genetics, the time-to-event data analysis has attracted increasing attention in the genetics studies of human diseases. In time-to-event data analysis, the Cox proportional hazards (PH) regression model is one of the most used approaches. However, existing methods and tools are not scalable when analyzing a large biobank with hundreds of thousands of samples and endpoints, and they are not accurate when testing low-frequency and rare variants. Here, we propose a scalable and accurate method, SPACox (a saddlepoint approximation implementation based on the Cox PH regression model), that is applicable for genome-wide scale time-to-event data analysis. SPACox requires fitting a Cox PH regression model only once across the genome-wide analysis and then uses a saddlepoint approximation (SPA) to calibrate the test statistics. Simulation studies show that SPACox is 76–252 times faster than other existing alternatives, such as gwasurvivr, 185–511 times faster than the standard Wald test, and more than 6,000 times faster than the Firth correction and can control type I error rates at the genome-wide significance level regardless of minor allele frequencies. Through the analysis of UK Biobank inpatient data of 282,871 white British European ancestry samples, we show that SPACox can efficiently analyze large sample sizes and accurately control type I error rates. We identified 611 loci associated with time-to-event phenotypes of 12 common diseases, of which 38 loci would be missed within a logistic regression framework with a binary phenotype defined as event occurrence status during the follow-up period.

Introduction

With increasing use of electronic health records (EHRs) and biobanks for genetics research, time-to-event data analysis is becoming more common to genetic studies of human diseases. The time-to-event data analysis can be more powerful than the analysis of binary outcome defined as event occurrence status at a fixed time point and allows for the identification of genetic variants predicting the prognosis of diseases.^{1, 2, 3, 4, 5, 6, 7, 8} Although the time-to-event data analysis has been routinely used in clinical practice, it has not been extensively performed in genome-wide association studies (GWASs), partly because of the unavailability of such information in many studies. EHR-linked biobanks potentially resolve the phenotype-availability issues and can even provide phenome-wide diagnosis and prognosis information. A motivating example is the UK Biobank, which includes genome-wide scale genetic data, diagnoses of more than 1,000 phenotypes, and the corresponding in-patient dates from 500,000 participants.^9,10 The time-stamped longitudinal data enables one to extract age of onset information in UK Biobank. In the absence of a national health system, such as that in the UK, major hospital-based biobanks around the world have been linked to National or State Death Indexes or other disease registries to derive time-to-event phenotypes.¹¹

Another key challenge of genome-wide, and potentially phenome-wide, time-to-event data analysis is computational cost. In time-to-event data analysis, one of the standard approaches is the Cox proportional hazards (PH) regression model. Cox PH is a semi-parametric method and can adjust for features such as censoring, stratification, and time-varying covariates.^12,13 Based on the Cox PH model, optimized tools such as gwasurvivr and SurvivalGWAS have been developed for genome-wide scale analysis.^{14, 15, 16, 17} However, these tools are not scalable when the sample size is large (>100,000) because they are based on a Wald test that requires fitting a separate alternative model for each genetic variant. For example, when analyzing 400,000 subjects while adjusting for ten covariates, R package gwasurvivar would take ∼300 days to test 20 million genetic variants (∼1.3 s per variant, see Numeric Simulations). In addition, as shown in our simulation studies and real data analysis, Wald tests cannot control type I error rates when testing low-frequency variants and/or when the event rate is low.

Compared to the Wald-test-based approaches, a score test takes much less time because it only requires fitting one null model across the genome-wide tests.^{18, 19, 20, 21} A regular score test uses a normal distribution to calculate p values. However, when testing low-frequency variants, the underlying null distribution could be highly skewed.^22,23 In these cases, the normal approximation is inaccurate at extreme tails, which will result in inflated type I error rates. To overcome this, the saddlepoint approximation (SPA) method uses an entire cumulative generating function (CGF) to approximate the null distribution. Superior performance of the SPA method has been shown in case-control and gene-environment interaction (G$\times$E) studies.^{18, 19, 20, 21,24, 25, 26}

In this paper, we propose an SPA implement based on the Cox PH regression model (SPACox), a fast and accurate approach that is scalable for a genome-wide scale single-variant time-to-event data analysis and is well calibrated for controlling type I error rates. SPACox fits a null Cox PH model only once for the genome-wide analysis. We then estimate the empirical CGF of the martingale residuals and apply the SPA to calibrate p values. Important features embedded in the classic Cox PH model, such as censoring, time-varying covariates, and stratification, can also be incorporated in SPACox. Through simulation studies and application to UK Biobank data of 282,871 unrelated samples from white British participants, we demonstrate that SPACox is computationally feasible, correctly controls type I error rates, and is sufficiently powerful to identify 611 loci associated with 12 common phenotypes, 38 loci of which are not found within a logistic regression framework with a binary phenotype defined as event occurrence status at the end of the follow-up period.

Material and Methods

Cox Proportional Hazard Model and Score Statistics

For subject $i$, let $G_i$ denote hard-called genotype $\left(G_i=0,1,2\right)$ or dosage value of a genetic variant to be tested. Dominant or recessive genotype coding $\left(G_i=0,1\right)$ can also be used.²⁷ The Cox PH model specifies the hazard function for the failure (event phenotype) time $T_i^{\ast }$ associated with $G_i$ and a $p\times 1$ vector of covariates $X_i$ in the form of

$$\lambda \left(t;X_i,G_i\right)={\lambda }_0\left(t\right)\exp \left(X_i^T\beta +G_i\gamma \right),$$

where ${\lambda }_0\left(t\right)$ is a baseline hazard function, $\beta$ is a $p\times 1$ vector corresponding to the effect of covariates, and $\gamma$ is the genetic effect. Let $C_i$ denote the censoring time for subject $i$. Suppose that the data consist of $n$ independent samples of $(T_i,{\delta }_i,X_i,G_i)$, where $T_i=\min (T_i^{\ast },C_i)$ denotes the observed time-to-event, ${\delta }_i=I(T_i^{\ast }\le C_i)$ indicates that failure is observed, and $I(.)$ is the indicator function.

To perform the score test for the null hypothesis $H_0:\gamma =0$, we need to fit the null Cox PH model as

$$\lambda \left(t;X_i\right)={\lambda }_0\left(t\right)\exp \left(X_i^T\beta \right).$$

We note that the null model is the same for all genetic variants, so the null model will be fit only once across the genome-wide analysis. To fit the null model, we use a well-developed R package survival, which can incorporate extensions of time-dependent variables and time-dependent strata and can handle tied event time with three possible choices, including Breslow’s approximation, Efron’s approximation, and exact partial likelihood.^{28, 29, 30} The package also returns martingale residuals $R_i,i\le n$ for all subjects. In Appendix A, we give more details about the likelihood and its derivatives and the definition of the martingale residuals under Breslow’s approximation. Chen et al. also gave similar derivations under Efron’s approximation.²²

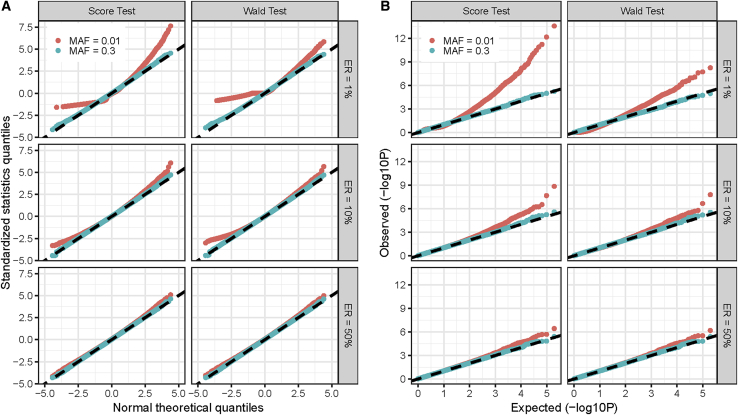
For any genetic variant, the score statistic is $S=\sum _{i=1}^n{G}_i{R}_i$, and its asymptotic variance is estimated by $\widehat{Var}\left(S\right)=G^{T}VG-G^{T}VX{\left(X^{T}VX\right)}^{-1}{X}^{T}VG$, where $G={(G_1,\dots ,G_n)}^T$, $X={(X_1,\dots ,X_n)}^T$, and $V$ is defined in Appendix A. The score statistic $S$ asymptotically follows a normal distribution with a mean of 0. However, when the event rate is low, the martingale residuals are highly skewed, which results in a right-skewed null distribution of $S$, especially when testing low-frequency variants (Figure 1). This indicates that the normal approximation cannot control type I error rates at stringent genome-wide significance levels.³¹ The inflated type I error rate of the score test has been observed in previous studies.^22,23

Figure 1.

Quantile-Quantile (QQ) Plots for Standardized Statistics and −log₁₀(P) of Score and Wald Tests

(A and B) Normal QQ plots for standardized statistics (A) and QQ plots for -log10(P) of score and Wald tests (B). Standardized statistics were calculated as raw statistics $\text{S}$ divided by the estimated variance $\widehat{\text{Var}}\left(\text{S}\right)$. p values were calculated from a normal approximation. We simulated 2$\times$10⁵ replications under three event rates (ERs) of 1%, 10%, and 50%. The sample size was 4,000, and we considered common variants (MAF = 0.3, expected MAC = 2,400) and low-frequency variants (MAF = 0.01, expected MAC = 80). MAF, minor allele frequency; MAC, minor allele counts.

Saddlepoint Approximation and Empirical CGF

Compared to the normal approximation that only uses the first two moments, SPA is more accurate because it uses an entire CGF to approximate the null distribution of scores.^18,19 For the Cox PH model, the null distribution of score statistic $S=\sum _{i=1}^n{R}_i{G}_i$ is complicated, and its theoretical CGF cannot be expressed in a closed form. In this paper, we use an empirical method to approximate the CGF.

For any genetic variant, to approximate the null distribution of $S$, we consider $G_i,i\le n$ as fixed values and $R_i,i\le n$ as random variables. In addition, because martingale residuals should satisfy linear restrictions of $\sum _{i=1}^n{X}_i{R}_i=0$ and $\sum _{i=1}^n{R}_i=0$, we use a projection scheme on $G$. Suppose $\tilde{X}=\left[1_{\mathit{n}},X\right]$, which includes a column of 1 in the design matrix, and $R={(R_1,\dots ,R_n)}^T.$ The linear restrictions can be expressed as ${\tilde{X}}^{T}R=0$, that is, random vector $R$ is restricted at the null space of the matrix $\tilde{X}$. Let $Q=I_n-\tilde{X}{\left({\tilde{X}}^T\tilde{X}\right)}^{-1}{\tilde{X}}^T$ be an orthogonal projection matrix onto the null space of the matrix $\tilde{X}$. We assume that $R=Q\tilde{R},$ where $\tilde{R}$ is a latent random vector without the linear restriction, then the score statistic can be rewritten as $S=R^{T}G={\tilde{R}}^{T}QG={\tilde{R}}^T\tilde{G}$, where $\tilde{G}=QG=G-\tilde{X}{\left({\tilde{X}}^T\tilde{X}\right)}^{-1}{\tilde{X}}^{T}G$ is a centered covariate-adjusted genotype vector. Because $R=QR$, $R$ is a natural representative of $\tilde{R}$, and we use the observed martingale residuals $R_i,i\le n$ to estimate the empirical distribution of $\tilde{R}$.

To construct the CGF of $S$, we first estimate the moment generating function (MGF) of $R_i$. Following an analogous approach used in Feuerverger,³² the empirical MGF of $R_i$ is given by

$${\hat{M}}_0\left(z\right)=E\left(e^{zR}\right)\approx \frac{1}{n}\sum _{i=1}^n{e}^{z{R}_i},$$

and its first and second derivatives are

$${\hat{M}}_0\text{'}\left(z\right)\approx \frac{1}{n}\sum _{i=1}^n{R}_i\cdot e^{z{R}_i},{\hat{M}}_0\text{''}\left(z\right)\approx \frac{1}{n}\sum _{i=1}^n{R}_i^2\cdot e^{z{R}_i}.$$

The empirical CGF of $R_i$ is then ${\hat{K}}_0\left(z\right)=\ln {\hat{M}}_0\left(z\right)$, and the derivatives are

$${\hat{K}}_0^{\text{'}}\left(z\right)=\frac{{\hat{M}}_0\text{'}\left(z\right)}{{\hat{M}}_0\left(z\right)},{\hat{K}}_0^{\text{''}}\left(z\right)=\frac{{\hat{M}}_0\text{''}\left(z\right){\hat{M}}_0\left(z\right)-{\left[{\hat{M}}_0\text{'}\left(z\right)\right]}^2}{{\left[{\hat{M}}_0\left(z\right)\right]}^2}.$$

The properties of uniform consistency, moment structure, and weak convergence to normality have been established.³² Considering ${\tilde{G}}_i,i\le n$ as constant coefficients, we obtain the empirical variance of the score statistic $S=\sum _{i=1}^n{\tilde{G}}_i{\tilde{R}}_i$ as ${\widehat{Var}}_{emp}\left(S\right)=\sum _{i=1}^n{\tilde{G}}_i^2\cdot {\hat{M}}_0^{\text{'}\text{'}}\left(0\right)$, and its estimated CGF is

$$\hat{K}\left(z\right)=\sum _{i=1}^n{\hat{K}}_0\left({\tilde{G}}_{i}z\right).$$

The first and second derivatives are

$${\hat{K}}^{\text{'}}\left(z\right)=\sum _{i=1}^n{\tilde{G}}_i{\hat{K}}_0\text{'}\left({\tilde{G}}_{i}z\right),{\hat{K}}^{\text{''}}\left(z\right)=\sum _{i=1}^n{\tilde{G}}_i^2{\hat{K}}_0\text{''}\left({\tilde{G}}_{i}z\right).$$

Given an observed score $S=s$, we first calculate $\text{ζ}$ such that ${\hat{K}}^{\text{'}}\left(\zeta \right)=s$, then we calculate $\omega =\text{sgn}\left(\text{ζ}\right)\sqrt{2\left(\text{ζ}s-\hat{K}\left(\text{ζ}\right)\right)}$and $\nu =\text{ζ}\sqrt{\hat{K}\text{'}\text{'}\left(\text{ζ}\right)}$. According to the saddlepoint method (Barndorff-Nielson),³³ the null distribution is

$$\mathrm{Pr}\left(S<s\right)\approx \Phi \left\{\omega +\frac{1}{\omega }\cdot \log \left(\frac{\nu }{\omega }\right)\right\},$$

where $\Phi$ is the standard normal distribution function.

Implementation Details and Computation Complexity

To obtain empirical CGF, ${\hat{K}}_0\left(z\right)$, and its derivatives ${\hat{K}}_0\text{'}\left(z\right)$ and ${\hat{K}}_0\text{'}\text{'}\left(z\right)$, we compute (${\hat{K}}_0\left(z_j\right)$, ${\hat{K}}_0\text{'}\left(z_j\right)$, ${\hat{K}}_0\text{'}\text{'}\left(z_j\right)$), for pre-determined knots $z_j,j=1,\dots ,q$, and then use linear interpolation. To select knots, we first calculate $q$-quantiles of a standard Cauchy distribution and then scale them up to a pre-determined range. We use Cauchy distribution because (1) the bell shape leads to more knots close to 0 and (2) the heavy tail ensures enough knots far away from 0. In our simulation studies and real-data analyses, we used $q=\mathrm{10,000}$ knots and set the location of knots bounded by $\left(-10,10\right)$.

Because the normal approximation behaves well near the mean of the distribution, it can be used to obtain the p value when the observed score statistic lies close to 0, the mean value under the null hypothesis.¹⁸ We apply the normal approximation by using the empirical variance ${\widehat{Var}}_{emp}\left(S\right)$ if the absolute value of the observed score statistic $\left|S\right|<r\sqrt{{\widehat{Var}}_{emp}\left(S\right)}$, where $r$ is a pre-specified value. Because using the normal approximation takes less time than using the SPA, this approach can reduce the computation time. We consider $r=2$, following the recommendation by Dey et al.¹⁸

Confounding can be controlled by replacing the raw genotype $G$ with a covariate-adjusted genotype $\tilde{G}$. This projection is motivated by linear regression but is not necessarily the best choice.²⁶ A computationally efficient alternative is to use the centered genotype $\hat{G}=G-\bar{G},$ where $\bar{G}$ is the mean value of the genotype. Numeric simulations demonstrate that using $\hat{G}$ also works well in most cases, although it might result in slightly inflated type I error rates when the raw genotype is strongly associated with covariates. Hence, we recommend beginning with $\hat{G}$ to calculate the p value and then updating the result with $\tilde{G}$ only if the p value is less than 0.001. In this way, we can improve the computational efficiency while avoiding false positive discoveries.

Implementation of the SPACox method mainly comprises two steps. In step 1, we use R package survival^29,30 to fit a null Cox PH model and then empirically estimate (${\hat{K}}_0\left(z\right)$, ${\hat{K}}_0\text{'}\left(z\right)$, ${\hat{K}}_0\text{'}\text{'}\left(z\right)$) of the martingale residuals. In step 2, for each genetic variant, we calculate score statistic $S$ and its empirical variance ${\widehat{Var}}_{emp}\left(S\right).$Then, the normal approximation or SPA is used to calculate p values. Note that the matrix $\tilde{X}{\left({\tilde{X}}^T\tilde{X}\right)}^{-1}$, function ${\hat{K}}_0\left(z\right)$, and its derivatives will be pre-calculated in step 1. It takes (pn) multiplications to calculate $\tilde{G}$ and takes (n) multiplications to calculate $\hat{K}\left(z\right)$ and its derivatives in step 2. The total computation complexity for testing one SNP is (pn).

Numeric Simulations

We carried out simulation studies to evaluate computation time, type I error rates, and powers of SPACox. For subject $i$, we first generated the censoring time $C_i$ and the underlying failure time $T_i^{\ast }$ and then calculated the time-to-event phenotype $T_i=\min (T_i^{\ast },C_i)$ and ${\delta }_i=I(T_i^{\ast }\le C_i)$. The censoring time $C_i$ was simulated following a Weibull distribution with the scale parameter of 0.15 and the shape parameter of 1. The underlying failure time $T_i^{\ast }$ was generated from a Cox PH model with a Weibull baseline hazard function as

$$T_i^{\text{∗}}=\lambda \sqrt{\frac{-\log U_i}{\exp \left({\eta }_i\right)}},\left(1\right),$$

where $U_i$ was simulated from a uniform (0,1) distribution and linear predictor ${\eta }_i=0.5x_{i1}+0.5x_{i2}+\gamma G_i,$ where $\gamma$ is the genotypic effect, $G_i$ is the genotype simulated following Hardy-Weinberg equilibrium, and $x_{i1}$ and $x_{i2}$are two covariates simulated following the standard normal distribution and a Bernoulli (0.5), respectively. The scale parameter $\lambda$ is selected to correspond to an event rate $\sum _{i=1}^n{\delta }_i/n$.

We first simulated small datasets of 4,000 samples ($n$ = 4,000) to evaluate the null distributions of regular score and Wald test statistics and compare them to the standard normal distribution. The score and Wald test statistics were standardized to have mean zero and variance unity. The asymptotic variance $\widehat{Var}\left(S\right)$ was estimated from the observed information matrix. We considered three event rates of 1%, 10%, and 50%. For each event rate, we simulated 2$\times$10⁵ replications for common variants (minor allele frequency [MAF] = 0.3) and low-frequency variants (MAF = 0.01). We also compared the asymptotic variance estimated from the observed information matrix $\widehat{Var}\left(S\right)$ and the empirical variances ${\widehat{Var}}_{emp}\left(S\right)$ and evaluated SPACox-NoSPA in which p values were calculated via a normal approximation with variance ${\widehat{Var}}_{emp}\left(S\right)$.

To evaluate computation time in realistic scenarios, we randomly sampled MAFs from the MAF distribution in the UK Biobank data and then simulated 10,000 null variants. We considered two event rates of 1% and 50%, incorporated 10 covariates in the model, and increased the sample size from 1,000 to 400,000. We compared four different tests: the proposed saddlepoint approximation score test (SPACox), the Wald-based Cox PH regression via R package survival (Wald), Firth’s penalized likelihood ratio test via R package coxphf (Firth), and a fast version of the Wald test via R package gwasurvivr (gwasurvivr).¹⁴ We did not evaluate other genome-wide survival analysis software, such as genipe, SurvivalGWAS, and GWASTools, because Rizvi et al. has shown that gwasurvivr is significantly faster than them.¹⁴ The evaluation process is on an Intel Xeon Platinum 8176 CPU at 2.10 GHz.

To evaluate type I error rates, we fixed the sample size at 100,000 and simulated phenotypes under the null model $\gamma =0$. We considered common, low-frequency, and rare variants with MAFs of 0.3, 0.01, and 0.001 and simulated 10⁶ genetic variants for each MAF. We considered five event rates of 0.2%, 1%, 10%, 20%, and 50% and simulated 1,000 datasets of time-to-event phenotypes for each event rate. Hence, for each pair of MAF and event rate, 10⁹ replications were evaluated in total. We compared type I error rates of SPACox, SPACox-NoSPA, Score, Wald, and Firth tests at significance levels $\alpha =5\times {10}^{-5}$ and $5\times {10}^{-8}$. As a result of the heavy computational burden, we performed a hybrid approach in which we used Score, Wald, and Firth tests only when the SPACox p values were smaller than $1\times {10}^{-3}$. We did not evaluate R package gwasurvivr because its p value is the same as the p value calculated via R package survival.

To evaluate powers, we fixed the sample size at 100,000 and simulated 50 datasets under the alternative model. For each dataset, we simulated 20 genetic variants and a phenotype by setting

$${\eta }_i=0.5x_{i1}+0.5x_{i2}+\gamma \sum _{k=1}^{20}{G}_i^k.$$

We compared empirical powers of SPACox, Score, Wald, and Firth tests. To compare the powers of using time-to-event phenotypes and using case-control phenotypes, we considered the SPA method for case-control study (SPACC).¹⁸ Event indicator ${\delta }_i$ was treated as a binary outcome. SPACC used $x_{i1}$, $x_{i2}$, and time-to-event $T_i$ as covariates; SPACC0 only used $x_{i1}$ and $x_{i2}$ as covariates.

Application to the UK Biobank Data

To illustrate the performance in a real-data application, we applied SPACox to analyze UK Biobank.^9,10 UK Biobank includes 408,961 white British samples. We used FastIndep³⁴ to select 344,340 unrelated samples, of which 282,871 samples with in-patient data were analyzed. UK Biobank includes in-patient diagnosis data from various providers with different censoring dates. More details about the providers, including sample size and censoring dates, are presented in Table S2.

We defined affected and unaffected individuals by using the PheWAS code system based on the International Statistical Classification of Diseases and Related Health Problems (ICD) (PheCode, Web Resources).^35,36 For example, individuals with hypertension (PheCode: 401.1) were identified as the individuals who had at least one observed ICD-10 diagnosis code I10 or its subcodes. In total, we analyzed 12 phenotypes, including hypertension, type 2 diabetes, and Alzheimer disease. The detailed summary information is presented in Table 1. For each phenotype, if we observe at least one in-patient diagnosis for patient $i$, we let the event indicator ${\delta }_i=1$ and time-to-event $T_i$ be the age at the first in-patient diagnosis date. Otherwise, we let ${\delta }_i=0$ and time-to-event $T_i$ be the age at right-censoring date or lost to follow-up date. The observed survival time was left truncated at the in-patient data collection date.

Table 1.

Summary Information of the 12 Phenotypes in UK Biobank Data Analysis

Phenotype	PheCode	# of Events (Affected Individual)	Event Rate	Mean (SD) of Age at Event	# of Significant Locia
Essential hypertension	401.1	76,566	27.09%	62.7 (7.67)	204 (23)
Abdominal hernia	550	45,957	16.26%	59.88 (9)	45 (0)
Hyperlipidemia	272.1	35,623	12.60%	63.4 (7.52)	70 (1)
Osteoarthrosis	740	29,071	10.29%	62.88 (7.96)	22 (5)
Cardiac dysrhythmias	427	25,585	9.05%	63.08 (8.58)	29 (1)
Asthma	495	25,240	8.93%	58.33 (9.74)	74 (2)
Cataract	366	22,635	8.01%	65.94 (7.3)	24 (2)
Coronary atherosclerosis	411.4	19,079	6.75%	62.38 (7.41)	69 (2)
Type 2 diabetes	250.2	18,557	6.57%	62.76 (7.91)	70 (2)
Parkinson disease	332	1,345	0.48%	66.7 (7.08)	1 (0)
Alzheimer disease	290.11	641	0.23%	70.53 (5.09)	2 (0)
Schizophrenia	295.1	551	0.19%	65.26 (8.24)	1 (0)

^aNumber of significant loci based on the SPACox method (and number of not significant loci based on SPACC). Using significance level 5$\times$10^-8, we identified a total of 611 loci with a SPACox p value < 5 × 10^-8, of which, 38 loci did not reach genome-wide significance in SPACC (p value > 5 × 10^-8). We clustered variants within the 200 kb region or at the same gene region as one locus.

For all diseases, we used the top four principal components (PCs) and gender as covariates. We restricted our analyses to markers imputed by the Haplotype Reference Consortium (HRC)³⁷ panel. Approximately 24 million markers with minor allele counts (MAC) $\ge$ 20 and imputation info score > 0.3 were used in the analyses.

Results

Normal Approximation: Score Test, Wald Test, and SPACox-NoSPA

We first evaluated the null distributions of regular score and Wald test statistics. The normal quantile-quantile (QQ) plots for standardized statistics and QQ plots for p values of regular score and Wald tests are presented in Figure 1. For score and Wald tests, a lack of symmetry in departures from the null hypothesis is observed, especially when testing low-frequency variants and/or when the event rate is low. The variance $\widehat{Var}\left(S\right)$ was underestimated for positive statistic and was overestimated for negative statistic. This asymmetry is because the information matrix of the Cox PH model behaves differently for large positive $\gamma$ and large negative $\gamma$.³¹ For a genome-wide time-to-event analysis, the right-skewed null distribution would result in inflated type I error rates. We compared the regular score test, which uses $\widehat{Var}\left(S\right)$ from the information matrix, and SPACox-NoSPA, which uses the empirical variance ${\widehat{Var}}_{emp}\left(S\right)$ (Figure S1). In general, $\widehat{Var}\left(S\right)$ and ${\widehat{Var}}_{emp}\left(S\right)$ were comparable. For common variants with an MAF of 0.3, p values of SPACox-NoSPA were similar to score test p values. For low-frequency variants with an MAF of 0.01, p values of SPACox-NoSPA were slightly different from score test p values. Interestingly, the QQ plot suggests that, when event rates were low (1% and 10%), the score test had more inflated type I error rates than SPACox-NoSPA for low-frequency variants.

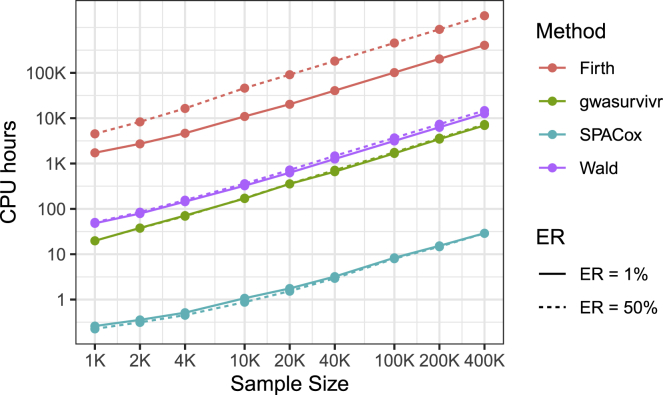
Comparison of Computation Time

The projected computation time for 20 million variants is presented in Figure 2. SPACox was 76–252 times faster than gwasurvivr, 185–511 times faster than the Wald test (R package survival), and more than 6,000 times faster than Firth (R package coxphf). For example, when analyzing a large cohort with 400,000 samples, SPACox took 29 CPU h (without reading data). Meanwhile, gwasurvivr, Wald, and Firth took 302.9, 614.3, and more than 15,000 CPU days, respectively. SPACox, Wald, and gwasurvivr took similar computation times under different event rates. However, Firth took more time when ER = 50%. This may be because the R package coxphf is not as well optimized as other packages.

Figure 2.

Projected Computation Time for a Genome-wide Time-to-Event Data Analysis of 20 Million Variants

The projected time is based on computation time for 10,000 variants on an Intel Xeon Platinum 8176 CPU at 2.10 GHz. For example, suppose it takes $\text{α}$ h to analyze 10,000 variants, then the projected time for 20 million variants is 2,000 $\times \text{α}$ h. Solid and dashed lines represent ERs of 1% and 50%, respectively. The MAFs are randomly generated from the MAF distribution of UK Biobank, and we considered 10 covariates.

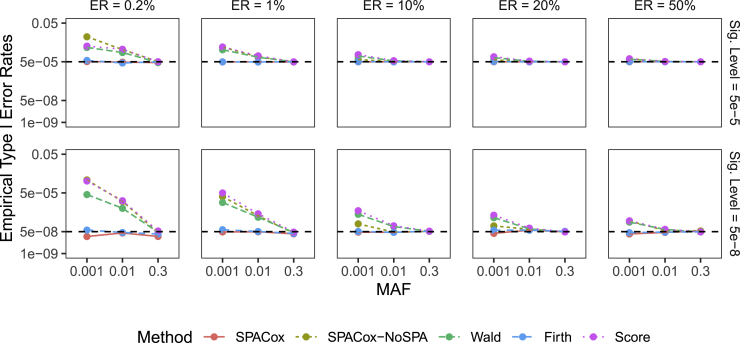
Type I Error Simulation Results

The empirical type I error rates based on ${10}^9$ replications are presented in Figure 3 and Table S1. At significance levels $\alpha =5\times {10}^{-5}$ and $5\times {10}^{-8}$, SPACox and Firth can control type I error rates under all settings of MAFs and event rates. However, Wald, Score, and SPACox-NoSPA had inflated type I error rates when testing low-frequency variants (MAF = 0.01 and 0.001), especially when the event rate is low. For example, at $\alpha =5\times {10}^{-8}$, when testing variants with an MAF = 0.001 and event rate of 1%, type I error rates of SPACox and Firth were $4.75\times {10}^{-8}$and$7.10\times {10}^{-8}$, respectively, and type I error rates of Wald, Score, and SPACox-NoSPA were $9.14\times {10}^{-6}$, $5.04\times {10}^{-5}$, and 2.61 $\times {10}^{-5}$. We further evaluated Wald in terms of type I error rates based on the signs of the estimated $\hat{\gamma }$. Figure S3 shows that the Wald test was inflated when $\hat{\gamma }>0$ and was deflated when $\hat{\gamma }<0$, which is consistent to the right skewed distribution of Wald statistics as shown in Figure 1.

Figure 3.

Empirical Type I Error Rates of SPACox, SPACox-NoSPA, Wald, Firth, and Score Tests

From left to right, the plots considered five event rates (ERs) of 0.2%, 1%, 10%, 20%, and 50%. Top and bottom plots are for empirical type I error rates at $\text{α}=5\times {10}^{-5}$ and $5\times {10}^{-8}$, respectively. Sample size $\text{n}$ = 100,000. For each pair of MAF and event rate, we simulated ${10}^9$ replications.

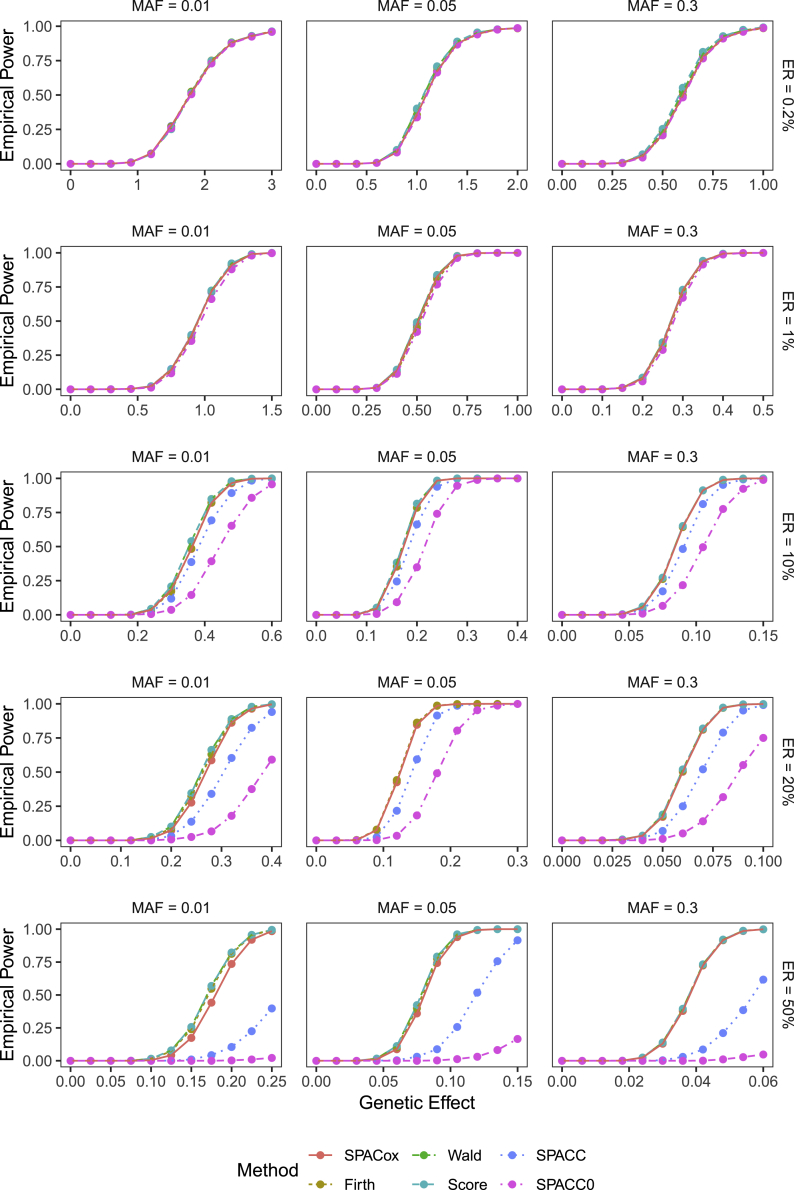
Power Simulation Results

The empirical powers with positive and negative $\gamma$ are presented in Figures 4 and S4, respectively. Since Wald and Score tests cannot control type I error rates when testing low-frequency variants, we used their empirical significance levels estimated from type I error simulations to calculate the empirical powers. When the event rate was less than 10%, the powers of all six tests were almost the same, and when the event rate was greater than 10%, powers of SPACC and SPACC0 were significantly lower than the other four methods (SPACox, Firth, Wald, and Score tests) based on the Cox PH model. For example, at $\alpha =5\times {10}^{-8}$, when testing common variants with an MAF = 0.3, event rate of 50%, and genetic effect size $\gamma =0.05$, powers of SPACC and SPACC0 were less than 0.211, and powers of the other four methods were higher than 0.916. This validates that the time-to-event phenotype (i.e., when an event occurs) is more informative than the corresponding case-control outcome (i.e., whether an event occurs during the follow-up period).

Figure 4.

Empirical Powers of SPACox, Firth, Wald, Score, and SPACC Tests When $\text{γ}$ Is Positive

From left to right, the plots considered three MAFs of 0.01, 0.05, and 0.3. From top to bottom, the plots considered five ERs of 0.2%, 1%, 10%, 20%, and 50%. Empirical powers were evaluated at the significance level $5\times {10}^{-8}$. Sample size $\text{n}$ = 100,000. For each pair of MAF and event rate, we simulated 1,000 replications.

When testing common variants (MAF $\ge$ 0.05), the powers of SPACox, Firth, Wald, and Score tests were almost the same. When MAF = 0.01 and the event rate is greater than 20%, powers were slightly different. Similar to type I error rates, the differences depend on the sign of $\gamma$: when $\gamma >0$, powers of Firth, Wald, and Score tests were slightly greater than that of SPACox, and when $\gamma <0$, powers of Firth and SPACox were slightly greater than those of Wald and Score tests. The differences were slightly larger when testing rare variants with an MAF = 0.001 (Figure S5).

Application to UK Biobank Data

We applied SPACox to UK Biobank data to analyze 12 phenotypes (Table 1). The Manhattan plots (Figure 5) and QQ plots (Figure S6) show that SPACox successfully identified a large number of loci. We also evaluated SPACox-NoSPA and Wald tests, both of which used normal approximation to calculate p values for all genetic variants (Figures S7–S9). QQ plots suggest that tests using normal approximation produced many potentially spurious associations, and SPACox gave a better type I error rates control, especially when testing low-frequency and rare variants. These results indicate the advantages of the SPA over normal approximation in terms of type I error rates control.

Figure 5.

Manhattan Plots for 12 Phenotypes from UK Biobank

Manhattan plots were based on p values calculated from the SPACox method. The red line represents the genome-wide significance level $\alpha =5\times {10}^{-8}$.

At a genome-wide significance level $\alpha =5\times {10}^{-8}$, we identified a total of 611 loci, of which 88.2% (539 loci) are common SNPs with an MAF > 0.05 (Figure S10). We clustered variants within 200 kb region or at the same gene region as one locus. For each locus, we treated the case-control status as a binary phenotype, included the top four PCs, birth year, and gender as covariates, and calculated p values using SPACC.¹⁸ Figure S11 shows that p values of SPACox and SPACC were comparable and that most of the loci identified by SPACox could also be identified by SPACC. This is expected because they use the same set of data to indicate affected (event) or unaffected (right-censoring) individuals, and event rate is generally low. Figure S12 shows the survival curves of the strongest SNP associations for each disease.

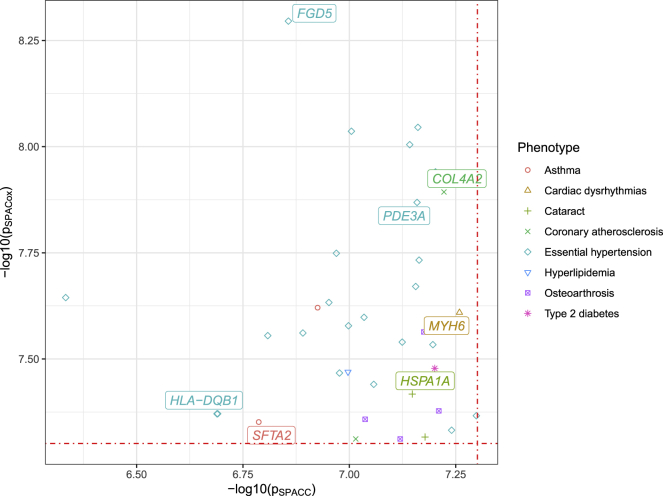
We highlighted 38 loci (of the 611 loci) that were not significantly associated in SPACC at $\alpha =5\times {10}^{-8}$. Detailed information including hazard ratios, p values, and gene annotation³⁸ can be seen in Table S3 and Figure 6. The Wald test produced p values that were very close to the SPACox p values. Several of the observed associations have been previously identified. For example, SPACox identified a genome-wide significant association between hypertension and a variant in FGD5 (MIM: 614788, rs13062241, p = 5.06$\times$10^-9), whereas SPACC did not (p = 1.39$\times$10^-7). FGD5 is a protein coding gene and belongs to the family of FGD5-guanine nucleotide exchange factors (FGD5-GEFs). Several GWAS studies have identified the association of FGD5 with different blood pressure-related phenotypes.^{39, 40, 41} Other examples include the association between coronary atherosclerosis and COL4A2 (MIM: 120090, rs9515203, SPACox p = 1.28$\times$10^-8, SPACC p = 5.99$\times$10^-8) and the association between hypertension and HLA-DQB1 (MIM: 604305, rs28724242, SPACox p = 4.26$\times$10^-8, SPACC p = 2.05$\times$10^-7).^{42, 43, 44, 45, 46, 47, 48, 49, 50} We also conducted another SPACC analysis in which time-to-event was used to replace the birth year as a covariate. The results show that, of the 611 significant loci identified by SPACox, 188 loci did not pass significance level $5\times {10}^{-8}$ (Figure S11).

Figure 6.

p Values of SPACC and SPACox for 38 Highlighted SNPs from UK Biobank

We highlight 38 loci that are significant on the basis of SPACox but not significant on the basis of SPACC. The red lines represent the genome-wide significance level $\alpha =5\times {10}^{-8}$.

The genome-wide summary information of the 12 phenotypes and the cumulative risk curves of the identified 611 loci can be downloaded via our personal website (Web Resources). Of the 611 loci, SPACox p values of 375 loci (61.4%) are smaller than the corresponding SPACC p values, and SPACC gave smaller p values for the remaining 236 loci (38.6%). We further extended the SPACC analysis (with birth year as a covariate) to all loci and identified 17 loci whose SPACox p values > 5$\times$10^-8 and SPACC p values < 5$\times$10^-8 (Table S4).

Discussion

In this paper, we have proposed SPACox, a fast and accurate approach to perform genome-wide time-to-event data analyses in large cohorts. The method fits a null Cox PH model only once for genome-wide analysis, which greatly improves the computational efficiency. Empirical SPA is used to calibrate p values so that type I error rates can be well controlled. Through extensive simulation studies and application to UK Biobank data, we have demonstrated that SPACox is much faster than currently existing methods, while retaining well-controlled type I error rates and powers. We implemented SPACox in the R package SPACox (see Data and Code Availability). Another computationally efficient two-step strategy is to use a logistic regression for the genome-wide analysis and then apply the Cox regression to analyze variants with p values less than a pre-selected cutoff.^51,52 In terms of computation time, this strategy is similar to SPACox because they both only need to fit one model for the genome-wide analysis.

When we calculate empirical CGF, we use a covariate adjusted genotype $\tilde{G}=G-\tilde{X}{\left({\tilde{X}}^T\tilde{X}\right)}^{-1}{\tilde{X}}^{T}G$ to account for the linear restrictions in martingale residuals. Another covariate-adjusted genotype $\dot{G}=G-X{\left(X^{T}VX\right)}^{-1}{X}^{T}VG$ is possible because the score statistic $S={\dot{G}}^{T}R$ and variance $Var\left(S\right)={\dot{G}}^{T}V\dot{G}$. That is, when $\dot{G}$ is used to replace $G$, the score statistic remains the same and its asymptotic variance does not explicitly depend on the covariate matrix $X$. However, we have found that using $\dot{G}$, the empirical variance ${\widehat{Var}}_{emp}\left(S\right){|}_{\dot{G}}=\sum _{i=1}^n{\dot{G}}_i^2\cdot {\hat{M}}_0^{\text{'}\text{'}}\left(0\right)$ greatly deviates from $\widehat{Var}\left(S\right)$, which resulted in deflated p values (Figure S2). This might be because $\dot{G}$ is not centered, that is, $\sum _{i=1}^n{\dot{G}}_i\ne 0$. Another possible approach is using$G-\tilde{X}{\left({\tilde{X}}^{T}V\tilde{X}\right)}^{-1}{\tilde{X}}^{T}VG$ as the covariate-adjusted genotype vector in which $\tilde{X}=\left[1_{\mathit{n}},X\right]$. However, because ${\tilde{X}}^{T}V\tilde{X}$ is irreversible (Appendix A), the covariate-adjusted genotype vector cannot be directly calculated. Thus, we did not consider this adjustment.

Family relatedness is commonly observed in a large biobank dataset. To adjust for the sample relatedness, BOLT-LMM and SAIGE methods used several optimization strategies so that a generalized linear mixed model could be computationally feasible in large cohorts.^19,53 As for the Cox PH model, some approaches have been proposed to adjust for sample relatedness. However, most of them are based on a sparse kinship matrix, not a dense genetic relationship matrix (GRM). In the future, we plan to extend the current method to adjust for sample relatedness via a GRM. As a score test, SPACox cannot estimate the genetic effect size. We recommend using SPACox as the first step to identify potential genetic variants, followed by time-to-event analysis of Firth correction for more details about the identified variants. In the future, we plan to extend our method to efficiently estimate the genome-wide effect sizes, which is important for some applications, such as meta-analysis.²⁶ Another future research of interest is to design a fast and accurate algorithm to identify rare variants based on a gene- or region-based multiple-variant test.^54,55 In Supplemental Methods, we discussed how to apply SPACox to analyze time-varying covariates, and we showed that the SPA correctly controls type I error rates at genome-wide significant levels. However, the considered scenarios for the time-varying covariates were limited. Additional simulations covering more extensive scenarios are still needed, and these are left to future work.

A time-to-event phenotype is different from binary, continuous, and counts phenotypes because the outcome of interest is not only whether an event occurred, but also when the event occurred. A unique feature of the time-to-event phenotype is censoring, that is, not all subjects experience the event by the end of the follow-up period. In medical studies, time-to-event phenotypes were often used to characterize outcomes such as death and cancer progression. With the expansion of biobanks and EHRs data, time-to-event phenotypes will become more readily available for genetic studies. SPACox is scalable to analyze hundreds of thousands of samples and is well calibrated for common, low-frequency, and rare variants. Given all advantages, SPACox will facilitate the genome-wide time-to-event data analysis in large biobanks and contribute to the discovery of the genetic causes underlying complex diseases.

Declaration of Interests

The authors declare no competing interests.

Published: June 25, 2020

Appendix A

From the Breslow’s approximation for the tied survival time, the log partial likelihood with respect to $\beta$ and $\gamma$ is

$$l\left(\beta ,\gamma \right)=\sum _{i=1}^n{\delta }_i\left(X_i^T\beta +G_i\gamma -\log \left(\sum _{k\in {\mathcal{R}}_{t_i}}{e}^{X_k^T\beta +G_k\gamma }\right)\right),$$

where ${\mathcal{R}}_{t_i}=\left\{k;t_k\ge t_i\right\}$ is the set of subjects at risk at time point $t_i$. Let $\hat{\beta }$and $\hat{\gamma }$ be the estimates from the log partial likelihood and $P$ be an $n\times n$ matrix with the ($i,j$)-th element

$$p_{ij}\left(\hat{\beta },\hat{\gamma }\right)=\frac{I\left(i\in {\mathcal{R}}_{t_j}\right)\cdot {\delta }_j\cdot e^{X_i^T\hat{\beta }+G_i\hat{\gamma }}}{{\sum }_{k\in {\mathcal{R}}_{t_j}}{e}^{X_k^T\hat{\beta }+G_k\hat{\gamma }}}$$

denoting the hazard of subject $i$ at time point $t_j$. Then, ${\hat{\Lambda }}_i=\sum _{j=1}^n{p}_{ij}\left(\hat{\beta },\hat{\gamma }\right)$ is an estimate of cumulative hazard of subject $i$ prior to time point $t_i$, and the corresponding martingale residual is $R_i={\delta }_i-{\hat{\Lambda }}_i$. In addition, based on the definition of the matrix $P$,

$$\sum _{i=1}^n{p}_{ij}\left(\hat{\beta },\hat{\gamma }\right)=\frac{{\sum }_{i\in {\mathcal{R}}_{t_j}}{e}^{X_i^T\hat{\beta }+G_i\hat{\gamma }}}{{\sum }_{k\in {\mathcal{R}}_{t_j}}{e}^{X_k^T\hat{\beta }+G_k\hat{\gamma }}}\cdot {\delta }_j={\delta }_j,\sum _{j=1}^n{p}_{ij}\left(\hat{\beta },\hat{\gamma }\right){\delta }_j=\sum _{j=1}^n{p}_{ij}\left(\hat{\beta },\hat{\gamma }\right)={\hat{\Lambda }}_i,$$

that is, $P^T\cdot 1_{\mathit{n}}=\delta$and $P\cdot \delta =\hat{\Lambda },$ where $1_{\mathit{n}},\delta ,\hat{\Lambda }$ are $n\times 1$ vectors with the $i$-th element’s being $1,{\delta }_i,{\hat{\Lambda }}_i$, respectively.

Let $X={\left(X_1,\dots ,X_n\right)}^T$ be an $n\times p$ covariate matrix,$G$ be an $n\times 1$ vector with the $i$-th element being $G_i$, and $V=diag\left({\hat{\Lambda }}_1,\dots ,{\hat{\Lambda }}_n\right)-P{P}^T$, then the score vector $S(\hat{\beta },\hat{\gamma })$ and the observed information matrix $J(\beta ,\gamma )$ are

$$S\left(\hat{\beta },\hat{\gamma }\right)=\left(\begin{array}{c}\frac{\partial l\left(\hat{\beta },\hat{\gamma }\right)}{\partial \beta }\\ \frac{\partial l\left(\hat{\beta },\hat{\gamma }\right)}{\partial \gamma }\end{array}\right)=\left(\begin{array}{c}\sum _{i=1}^n{X}_i{R}_i\\ \sum _{i=1}^n{G}_i{R}_i\end{array}\right),J\left(\hat{\beta },\hat{\gamma }\right)=-\left(\begin{array}{c}\frac{{\partial }^{2}l\left(\hat{\beta },\hat{\gamma }\right)}{\partial \beta \partial {\beta }^T},\\ \frac{{\partial }^{2}l\left(\hat{\beta },\hat{\gamma }\right)}{\partial \gamma \partial {\beta }^T},\end{array}\begin{array}{c}\frac{{\partial }^{2}l\left(\hat{\beta },\hat{\gamma }\right)}{\partial \beta \partial {\gamma }^T}\\ \frac{{\partial }^{2}l\left(\hat{\beta },\hat{\gamma }\right)}{\partial \gamma \partial {\gamma }^T}\end{array}\right)=\left(\begin{array}{c}{X}^{T}VX,\\ G^{T}VX,\end{array}\begin{array}{c}{X}^{T}VG\\ G^{T}VG\end{array}\right)$$

For any genetic variant, the score statistic $S=\sum _{i=1}^n{G}_i{R}_i$ and its asymptotic variance Var (S) = G^TVG −G^TVX(X^TVX)⁻¹X^TVG

Because $P^T\cdot 1_{\mathit{n}}=\delta$and $P\cdot \delta =\hat{\Lambda }$, we can deduce that $V\cdot 1_{\mathit{n}}=\hat{\Lambda }-P{P}^T\cdot 1_{\mathit{n}}=0$. Define $\tilde{X}=\left[1_{\mathit{n}},X\right]$, then the matrix

$${\tilde{X}}^{T}V\tilde{X}=\left[\begin{array}{cc}{1}_{\mathit{n}}^T\cdot V\cdot 1_{\mathit{n}}& V\cdot 1_{\mathit{n}}\\ 1_{\mathit{n}}^T\cdot V& X^{T}VX\end{array}\right]=\left[\begin{array}{cc}0& 0\\ 0& X^{T}VX\end{array}\right]$$

is irreversible.

Data and Code Availability

The codes generated during this study are available at https://github.com/WenjianBI/SPACox.

Web Resources

• Firth’s correct R package, https://cran.r-project.org/web/packages/coxphf

• Genome-wide summary statistics and the cumulative risk curves of the identified 611 loci, https://www.leelabsg.org/resources

• gwasurvivr R package, http://bioconductor.org/packages/release/bioc/html/gwasurvivr.html

• PheCode, https://phewascatalog.org/phecodes, https://phewascatalog.org/phecodes_icd10

• SPACC R package, https://cran.rstudio.com/web/packages/SPAtest

• Survival R package, https://cran.r-project.org/web/packages/survival/

• UK Biobank, https://www.ukbiobank.ac.uk/