Reconfigurable microbots folded from simple colloidal chains

Significance

Most microscale swimmers and some larger animals utilize long filaments or slender bodies for propulsion, since one-dimensional chains are the simplest structure that can be bent, twisted, braided, or folded into a wide range of geometrically or topologically complex morphologies. Inspired by this, here, we fabricate flexible magnetic colloidal chains that can enable significant freedom of morphology change and motion using an applied precessing magnetic field. As a result of their reconfigurability, these systems can switch propulsion mode from free swimming to surface-enabled translation, enabling navigation through complex 3D environments such as channels that mimic arteries, veins, and capillaries. The demonstrated shape change and adaptability are ubiquitous in natural systems and are necessary for microbot navigation in complex environments.

Abstract

To overcome the reversible nature of low-Reynolds-number flow, a variety of biomimetic microrobotic propulsion schemes and devices capable of rapid transport have been developed. However, these approaches have been typically optimized for a specific function or environment and do not have the flexibility that many real organisms exhibit to thrive in complex microenvironments. Here, inspired by adaptable microbes and using a combination of experiment and simulation, we demonstrate that one-dimensional colloidal chains can fold into geometrically complex morphologies, including helices, plectonemes, lassos, and coils, and translate via multiple mechanisms that can be varied with applied magnetic field. With chains of multiblock asymmetry, the propulsion mode can be switched from bulk to surface-enabled, mimicking the swimming of microorganisms such as flagella-rotating bacteria and tail-whipping sperm and the surface-enabled motion of arching and stretching inchworms and sidewinding snakes. We also demonstrate that reconfigurability enables navigation through three-dimensional and narrow channels simulating capillary blood vessels. Our results show that flexible microdevices based on simple chains can transform both shape and motility under varying magnetic fields, a capability we expect will be particularly beneficial in complex in vivo microenvironments.

Propulsion at the microscale is challenging due to the reversible nature of low-Reynolds flow (1). Despite this, microorganisms such as prokaryotes and sperm are able to swim in complicated biological environments by waving their flagella or cilia to drive processes essential for life, ranging from nutrient transport to pathogen clearance. To control their motion, these biological motors have evolved to be flexible, adaptive, and polymorphic. For example, the flagellum morphology of the photosynthetic bacterium Rhodobacter sphaeroides can shift from a helix to an in-plane coil to slow down and reorient the cell (2). Escherichia coli, when sensing nutrients, can change the rotating direction of flagella from counter-clockwise to clockwise, where the flagellum bundle falls apart (3). And the flagellum of an entrapped Shewanella putrefaciens bacterium can adapt a radical change into a spiral-like shape that wraps around the cell body to generate a large force to escape (4). Flexibility is also used by animals outside of the low-Reynolds-number regime. Snakes, for example, take advantage of underlying surfaces to achieve multiple movements, such as concertina, serpentine, sidewinding, and rectilinear locomotion (5).

Although significant progress has been made in mimicking natural swimmers by synthetic microbots (6–12), most of them have been fabricated with rigid structure, preventing shape change and adaptation. Recently, reconfigurable artificial swimmers based on millimeter-scale magnetic hydrogel nanocomposites or three-dimensional (3D) printing have been fabricated (13–17). With preprogrammed ferromagnetic domain distributions and changing external magnetic field, such systems can deform into 3D architectures (16) to roll, jump, swim, crawl, and transport cargo under command (15). However, their sizes are large compared with their biological counterparts, preventing in situ applications. Other types of shape-morphing micromachines have also been reported based on the origami principle and spatial patterning of heterogeneous materials (18–21). They, however, have either been limited to one type of transformation or have relied on sophisticated fabrication techniques (20, 21).

For propulsion, most biological swimmers utilize one-dimensional (1D) elastic filaments, the simplest structure that can be bent, twisted, braided, or folded into a wide range of geometrically or topologically complex morphologies. Indeed, flexible chains such as polypeptides and polynucleotides are ubiquitous in biological systems. Although they have relatively simple backbones, by virtue of site-specific interactions between rather limited sets of subunits along the chains, they can fold into proteins and DNA molecules with well-defined 3D structures of exquisite complexity and functionality. Inspired by the polymorphic nature of linear chains, we extend our previous work on the assembly of magnetic wheel-based translating microbots (22, 23) to incorporate flexible linkages between component colloidal building blocks to fabricate magnetic colloidal polymers that enable significantly greater freedom of motion. We then demonstrate that magnetic-chain microbots can readily undergo shape transformation with a precessing magnetic-field change. These systems, both homogeneous and heterogeneous suggestive of cargo transport, can switch propulsion modes, and, as a result of their flexibility and reconfigurability, they can adapt within complicated 3D environments, such as confined channels.

Results and Discussion

Fabrication of Semiflexible Magnetic Chains.

Magnetic chains were fabricated by chemically linking superparamagnetic particles (Dynabead MyOne; diameter 2a = 1.05 µm, density ρ = 1.8 g/cm³) with four-arm polyethylene glycol (PEG) maleimide (SI Appendix, section 1 and Figs. S1 and S2). In this, available carboxylic acid groups on the particle surface were converted into thiols via carbodiimide chemistry. Under a 1D direct-current (DC) magnetic field, surface-modified particles suspended in dimethyl sulfoxide (DMSO) chain together due to dipolar attractions. The thiol functional groups on the particle surfaces then react with maleimides in the PEG linkers via a Michael addition reaction; as a result, chemically stable, but flexible, linkages form between neighboring particles (24). With this approach, the maximum chain length L is ∼60 µm. The chain-bending modulus κ_bend = EI (where E is the Young’s modulus and I = πa⁴/4 is the moment of inertia) can be determined by bending an initially straight chain into a U shape along the orthogonal direction (SI Appendix, Fig. S3). Based on the measured separation between two legs of the U-shaped chain (25, 26), we have determined that κ_bend = 10⁻²⁴ to 10⁻²⁶ J⋅m, tunable by fabrication-field strength and degrees of thiol functionalization (SI Appendix, Fig. S2E). By comparing the spring constant k₀ of a single PEG linker and the overall spring constant of the colloidal chains k_tot and assuming that the PEG linkers are springs that are connected in parallel between particles, we have estimated that the number of PEG linkers between neighboring particles ranges from 2 to 160 (SI Appendix, sec. 4 and Fig. S5). In this work, we focus on semiflexible chains, for which the ratio of the chain-contour length L to the persistent length L_p (L_p = k_bend/k_BT, where k_BT is the thermal energy) is of order 1 to 10. This ratio is comparable with those found in real flagella (27) and other synthetic magnetic chains (28–30), indicating similar flexibilities. While chain diameters are 50 times larger than those of flagella with a corresponding moment of inertia 10⁷ times larger, an effective Young’s modulus 10⁷ times smaller leads to a bending modulus of similar magnitude. Comparable flexibilities enable chains to fold and propel similarly to their smaller-scale natural counterparts. All of the experiments described here were performed by dispersing fabricated chains in DMSO (viscosity = 1.996 cP) to prevent sticking. In deionized water, we observed that chains adhered to glass surfaces quickly with apparent electrostatic attractions and zeta potential reduction due to the conversion of carboxylic acid surface-functional groups into thiols and dissociation of nitrogen atoms from linker maleimide groups. With observed propulsion velocities of 1 to 10 µm/s, we calculated Reynolds numbers of order 10⁻⁴ to 10⁻⁵, well within the Stokes regime. Note that, given the smooth nature and low surface roughness (∼10 nm) of glass slides, the impact of surface topography on chain propulsion can be neglected.

Folding and Propulsion of Chains under Precessing Magnetic Fields.

We and others have shown that flexible magnetic chains can be folded into “U” and “S” shapes under 1D fields (25, 26, 31, 32) or coiled into “lassos” under two-dimensional (2D) rotating magnetic fields (29, 33, 34). Theories have predicted that spiral or helical shapes are possible under 3D precessing fields (35, 36). No experimental work, however, has so far demonstrated the folding of colloidal chains into helices, primarily due to the challenge in making chains of sufficient flexibility. As shown in SI Appendix, Fig. S4, we applied a precessing magnetic field, i.e., the superposition of a DC field along the x axis, and a circularly rotating field in the y–z plane

$$\mathbf{B}=B_x\hat{\mathbf{x}}+B_{yz}\sin \left({\omega }_{M}t\right)\hat{\mathbf{y}}+B_{yz}\cos \left({\omega }_{M}t\right)\hat{\mathbf{z}},$$ [1]

where ω_M is the angular frequency of the applied field, B_x and B_yz are the magnetic flux densities, $\hat{\mathbf{x}}$ and $\hat{\mathbf{y}}$ are in-plane unit vectors parallel to the substrate, and $\hat{\mathbf{z}}$ is perpendicular to the substrate. The unit vector $\hat{\mathbf{B}}=\left(cos\beta ,sin\beta \sin \left({\omega }_{M}t\right),\sin \beta \cos \left({\omega }_{M}t\right)\right)$ points toward the magnetic-field direction, where β = tan⁻¹(B_yz/B_x) is the so-called cone angle. This specific field orientation was chosen to aid visualization of chain morphologies under optical microscopy. By tuning both field strength and cone angle, we have been able to fold individual chains into helices (Fig. 1A and Movie S1A). In this case, the two ends of an initially straight chain coil with opposite chirality and rotate due to the rotating field in the y–z plane. Subsequent chain coiling then propagates toward the center, and one of the chiralities “wins,” potentially due to small perturbation during folding or some mild heterogeneity in chain flexibility, and a stable helix is formed.

Fig. 1.

Folding of magnetic chains under precessing magnetic fields. (A) Snapshots showing the dynamics of chain folding in experiments (Left) and simulations (Right). (Scale bar, 10 µm.) (B) The phase diagram of chain morphologies with varying field strengths in B_yz and B_x. The regime highlighted in green corresponds to the helix morphology predicted by numerical simulation. The red dashed line corresponds to the magic cone angle β = 54.7°. (C) The helical geometry (p/πD) with magnetoelastic constant M_n. C, Inset shows all relevant geometric parameters. The snapshots show the helix geometry at corresponding points. (D) The propulsion efficiency (V/ωD) of the helix as a function of its geometry for several strengths of the magnetic field (Inset) keeping the ratio B_x/B_yz fixed. The solid line comes from Eq. 5 with measured helix parameters p and D.

Qualitatively, the formation of a helix results from the competition between the x–DC field and the y–z rotating field. If the rotating field B_xy is strong, the chain folds into a closed-loop lasso in the y–z plane, while the chain will be stretched into a rigid rod if the DC field B_x is strong. We have found that a helix only formed within a narrow regime of the full phase diagram (Fig. 1B) where the cone angle was slightly larger than the magic angle $\beta =acos\sqrt{1/3}=54.7°$, for which the time-averaged dipolar magnetic interactions nearly vanished, consistent with theoretical predictions (35, 36). Moreover, as shown in Fig. 1C, the helical morphology, characterized by the ratio of pitch to perimeter, p/πD, can also be conveniently controlled by the so-called magnetoelastic parameter (35) M_n = πa²χ²B²L²(1 − 3cos²β)/36k_bendμ₀, where μ₀ is the permeability of free space, χ is the magnetic susceptibility of the particle, and $B=\sqrt{B_x^2+B_{yz}^2}$. Compared with prefabricated and rigid microhelices (7–9), our chains are able to fold into flexible helices with the corresponding helix angles θ = cot⁻¹(p/πD) ranging from ∼60° to 90° solely by manipulating external magnetic-field conditions.

Helices, once formed, demonstrated unique 3D propulsion capability due to their intrinsic broken symmetry under the same precessing field. Also shown in Movie S2A, the helix propelled along both the x and y axes. Its motion in the y axis was due to its interaction with the wall and a rotation–translation coupling arising from the circularly rotating y–z field, similar to the rolling of both lassos and rods (Movie S2 B and C). The translation of a helix along the x axis was, however, due to its helical shape. Based on resistive force theory (37–39), the propulsion velocity V and applied torque Γ on a helix are related to the applied force F and its angular frequency ω via the matrix

$$\left(\begin{array}{c}\mathit{V}\\ \mathrm{\Gamma }\end{array}\right)=\left(\begin{array}{cc}A& -B\\ B& C\end{array}\right)\left(\begin{array}{c}\mathit{F}\\ \mathit{\omega }\end{array}\right),$$ [2]

where the constants A, B, and C are

$$\begin{array}{c}A=\frac{\sin \theta }{N\pi D\left({\zeta }_{\parallel }{\cos }^2\theta +{\zeta }_{\perp }{\sin }^2\theta \right)}\\ B=\frac{D\left({\zeta }_{\parallel }-{\zeta }_{\perp }\right)\tan \theta }{2\left({\zeta }_{\parallel }+{\zeta }_{\perp }{\tan }^2\theta \right)}\\ C=\frac{N\pi D^3{\zeta }_{\perp }{\zeta }_{\parallel }}{4\sin \theta \left({\zeta }_{\parallel }{\cos }^2\theta +{\zeta }_{\perp }{\sin }^2\theta \right)}\end{array},$$ [3]

and N is the number of turns in the helix, with tanθ = πD/p. Here ξ_⊥ and ξ_|| are the viscous drag coefficients perpendicular and parallel to the helix segment, respectively (40).

$${\zeta }_{\perp }=\frac{4\pi \eta }{\ln \left[\frac{0.18\pi D}{a\sin \theta }\right]+0.5}\hspace{1em}{\zeta }_{\parallel }=\frac{2\pi \eta }{\ln \left[\frac{0.18\pi D}{a\sin \theta }\right]}.$$ [4]

Since the helix is actuated under a uniform magnetic field, there is no magnetophoretic force, and the chain is force-free, F = 0, and Eq. 2 can then be simplified as

$$\frac{V}{\omega D}=\frac{\left(1-{\gamma }_k\right)p}{2\pi D\left[{\gamma }_k{\left(p/\pi D\right)}^2+1\right]}\hspace{0.17em},$$ [5]

where γ_k = ξ_||/ξ_⊥. This scaling matches well with our experimental data of helical motion along the x direction (Fig. 1D). The highest propulsion coefficient that can be achieved in our chains is V/ωD ∼ 0.08, slightly smaller than rigid helices (9), but comparable with that of E. coli (∼0.1 with V ∼ 25 µm/s, ω ∼ 628 rad/s, and D ∼ 0.4 µm) (41).

Numerical Simulation of Chain Folding and Propulsion.

To further understand the response of colloidal chains under different magnetic fields, we used numerical simulation, where the colloidal chain was modeled as linked spherical beads of radius a. In the model, the magnetic force on bead i due to the interaction with neighboring bead j is (42)

$${\mathit{F}}_{i,j}^{\text{mag}}=\frac{F_0}{{\left(r_{i,j}/a\right)}^4}\left(2\left(\hat{\mathit{m}}\cdot {\hat{\mathit{r}}}_{i,j}\right)\stackrel{}{\hat{\mathit{m}}}-\left(5{\left(\hat{\mathit{m}}\cdot {\hat{\mathit{r}}}_{i,j}\right)}^2-1\right){\hat{\mathit{r}}}_{i,j}\right),$$ [6]

where $F_0=3{\mu }_0{m}_0^2/4\pi a^4$, $m_0=4\pi a^3\chi B_0/3{\mu }_0$, and $\widehat{\mathit{m}}=\mathit{m}/m_0$ is the scaled magnetic moment of a bead; magnetic interactions between nonneighboring beads are neglected. Since the beads are superparamagnetic, we assume that the direction of the induced magnetic moment aligns instantaneously with the direction of the applied field B(t). We resolve the time dependence of the magnetic field instead of averaging the magnetic interactions over one period of oscillation, as done in prior theoretical work (36). This requires that the time-step size be much smaller than the period of the alternating current (AC) component of the applied field. Using at least 20 time steps per period resolved the time dependence of the magnetic forces adequately.

The chain elasticity was modeled by using a penalized (slightly extensible) discrete version of the Kirchhoff continuum model of an inextensible rod, following work by others (43, 44) and explained in more detail in SI Appendix. We obtained the bending modulus κ_bend from the response of a straight chain to a perpendicular DC field, as we will elaborate on later. The twist modulus κ_twist cannot be independently measured, so we have selected its value to closely reproduce the dynamics of helix formation in the experiments.

We used the fast, minimally resolved Brownian dynamics method presented in ref. 45 to simulate the dynamics of folding and propulsion of colloidal chains. This method is based off of Stokesian dynamics (46), but omits stresslets and only uses the Rotne–Prager–Blake (47, 48) tensor to compute the translational and rotational hydrodynamic mobility between particles of radius a suspended above a bottom wall. We included near-field lubrication corrections to the hydrodynamics following Brady et al. (46) for both neighboring pairs of particles along the magnetic chain and between individual particles and the bottom wall. These lubrication corrections improved the accuracy of the hydrodynamic model. Accounting for lubrication also allowed us to use a more short-ranged and stiff steric repulsion to impose nearly strict inextensibility of the chain, without incurring a severe restriction on the time-step size, primarily because of the strong reduction of the mutual mobility for nearly touching particles. Further details of our simulation method are described in SI Appendix, section 3.

To validate our simulation method and obtain values for the bending modulus, we first simulated the bending of a straight chain under an applied DC field in the direction orthogonal to the initial chain alignment. As shown in SI Appendix, Fig. S3 and Movie S3, a chain of 40 beads gradually bent into a U shape. The separation between two legs Δ depended on the field condition and the bending modulus of the chain. By substituting the properties of Dynabeads and the exact experimental conditions, and tuning the bending modulus ${\kappa }_{bend}={\kappa }_{bend}^{const}=2.0\times {10}^{-24}$ J·m, we were able to match the simulated Δ with experiments. We note that this value of κ_bend is also consistent with what we measured in experiments. The time scale of the chain folding in simulation is also in fair agreement with experiments. After obtaining the bending modulus, we simulated the folding of a 60-mer chain under a 3D precessing field (Movie S1B), and the snapshots are shown in Fig. 1A. The chain morphologies as a function of time matched well with our experiments, validating our simulation method. For this simulation, we took the bending modulus to be variable along the length of the chain, such that $k_{bend}\left(s\right)={\kappa }_{bend}^{const}\left(3+2s/L\right)/5$, where s is the arc length. This variable form of k_bend(s) was chosen ad hoc to give the chain some flexural heterogeneity, and its actual form is not critical. This heterogeneity, however, was important to be included in the simulations of swimming helices, as perfectly homogeneous chains typically develop a kink in their chirality in the middle of the chain, thus exhibiting no preferred swimming direction. In experiments, however, the development of chain chirality was eventually dominated from one of the two ends, likely due to mild heterogeneity in the bending modulus, which is unavoidable during the linking stage. For shorter chains, such as 40 mers, however, an initial small perturbation of the chain configuration (Config.) was enough to break the symmetry, without having to include flexibility heterogeneity (Fig. 2 and SI Appendix, Fig. S3, with simulation conditions summarized in SI Appendix, Table S2).

Fig. 2.

Sequential folding and motion of a homogeneous chain under different magnetic-field conditions in experiments (upper or left half of images) and simulations (lower or right half of images). (A) Under a DC magnetic field, the chain can adopt line, U, and S shapes, depending on initial conditions. (B) By further applying an in-plane (x–y) undulatory magnetic field, they fold into oscillating arc, “U,” and “S” shapes, respectively. (C) The 3D precessing magnetic field makes the oscillating arc-, U-, and S-shaped chains fold into helical, plectoneme, and coiled structures. The arrows indicate the net propulsion direction. The scale bar (10 µm) applies to all images.

Sequential Folding and Motion of Homogeneous Chains.

We note that the morphology of a folded chain depends on its initial configuration and the magnetic-field conditions. Therefore, we were able to fold the chain sequentially along different pathways, as shown in Fig. 2A (Configs. 1 to 3), where a linear chain was prealigned with the DC field in the x direction. The addition of an AC field along the y direction induced oscillation in the same direction. Further superposition of an AC field in the z direction, i.e., a 3D precessing field, eventually folded the chain into a helix, as we have demonstrated. On the other hand, the U- and S-shaped chains in Fig. 2 B and C formed depending on the initial chain configurations along the x direction. If both ends of the chain initially curve inward slightly, the chain will transform into a U-shaped chain when a DC field is applied in the y direction. In contrast, if one end curves inward and the other end curves outward slightly, the chain forms an S shape when the y–DC field is applied, as shown in simulations (31). Further application of the 3D precessing field allowed the two parallel legs of the U-shaped chain to twist together, forming a plectoneme (Config. 8), while the S-shaped chain folded into a coiled configuration (Config. 9). These chain morphologies and folding pathways were also reproduced in our numerical simulations by using the same experimental conditions (Fig. 2, with simulation conditions summarized in SI Appendix, Table S2).

Chain morphology determines whether a chain exhibits net propulsion or not. Under 2D fields, no net translation was observed for oscillating linear and “S”-shaped chains since their fore–aft symmetries were not broken. The “U”-shaped chain, however, was asymmetric. Its two free legs oscillated with higher amplitude than its bent head, and, as a result, it translated toward the tail (Movie S4). Under 3D precessing fields, on the other hand, both helices and plectonemes exhibited net propulsion perpendicular to their rotating directions, depending on their chirality (Movie S4). The highly coiled chain in Config. 9 cannot move because its overall shape is approximately isotropic.

Multimodal Propulsion of Heterogeneous Chains.

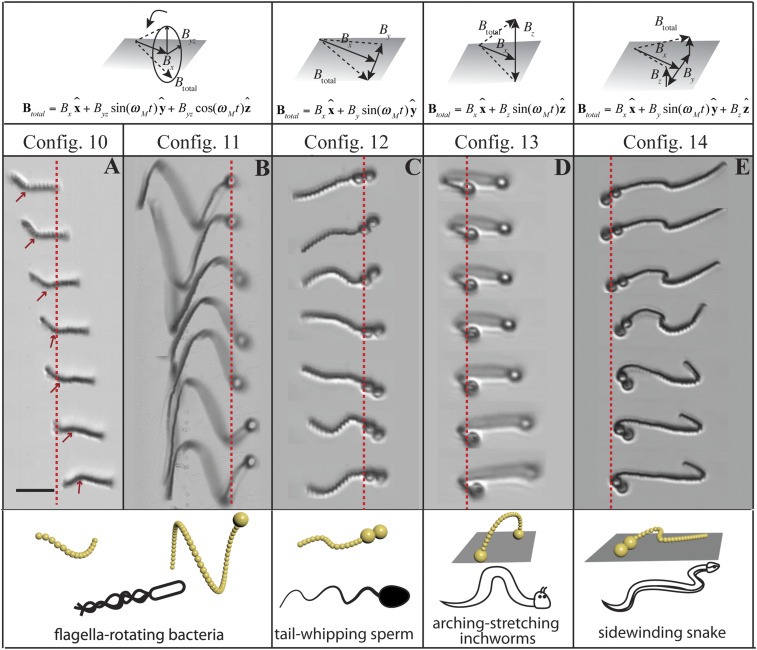
Unlike homonuclear polymers, our colloidal chains, even when fabricated with monodisperse magnetic colloids, occasionally exhibited noticeable bending-stiffness heterogeneities along the chain. For example, Fig. 3A shows a chain with one malformed point defect highlighted by the red arrows, where the tail is curved. This breaks the fore–aft symmetry and allows the tail to rotate as a rigid helix under a 3D precessing field (Movie S5A). As a result, the chain moved with its rigid head leading along the x axis, with minimal rolling in the orthogonal y direction. More controlled heterogeneous diblock or triblock chains can be fabricated by sequentially attaching larger particles to the ends of single block chains composed of smaller particles. Such structures could also be investigated within the context of cargo transport, where the rigid head, even if inert, is to be moved and delivered to a desired target. Fig. 3B shows a long and flexible chain linked to a large 2.7-μm magnetic bead. Under the same field, its helical motion mimicked a rotating bacteria flagellum (Movie S5B). A comparison between these two types of chains sheds light on their differences. The tail in Fig. 3A retained its shape during rotation and behaved like a rigid helix. As a result, its axial swimming velocity was considerably larger than lateral rolling. On the other hand, the chain in Fig. 3B was so flexible that one can see the propagation of waves along the chain. Interestingly, the chain flexibility lowered its axial velocity. Significant rolling along the orthogonal direction due to the nearby wall was observed. For both cases, we were able to reverse the propulsion direction by switching the rotation direction.

Fig. 3.

Multimodal motion of heterogeneous chains that mimic natural swimmers and propellers. Snapshots in equal time intervals of 0.44 s are shown top to bottom, with the red dashed line denoting a fixed reference position in the x direction. (A) Rotation of a single block chain (14-mer) with a malformed point defect (red arrow, between the fifth and sixth particles) under a 3D precessing field. (B) Helical motion of a diblock chain (54-mer tail with one 2.7-µm particle head) with a long and flexible tail under the same precessing field. Configs. 10 and 11 mimic rotating bacteria flagella. (C) In-plane undulatory motion of a diblock chain (13-mer tail with a 2 × 2.7-µm particle dimer head) under an x–y undulatory field, mimicking tail-whipping sperm. (D) Inchworm motion of a triblock chain (21-mer chain with a 2.7-µm particle head and a 2.7-µm particle tail) under an x–z undulatory field, mimicking arching and stretching inchworms. (E) Sidewinding of a diblock chain (29-mer tail with a 2 × 2.7-µm particle dimer head) under a 3D undulatory magnetic field, mimicking sidewinding snakes. The scale bar (10 µm) applies to all images.

More complicated bio-inspired propulsion modes, reminiscent of animal propulsion not necessarily relying on low-Reynolds-number flow, can be created by taking further advantage of the nearby substrate. For example, a diblock chain can undergo undulatory beating (Fig. 3C and Movie S6) on a substrate in a 2D field of $\mathbf{B}=B_x\hat{\mathbf{x}}+B_y\sin \left({\omega }_{M}t\right)\hat{\mathbf{y}}$, mimicking the planar beating of spermatozoa. We note that our diblock chains swam with the larger magnetic beads leading. The bending wave propagated from its larger head toward the free end, which was in the opposite direction from chains that were attached to red blood cells (6). When a 2D magnetic field was applied in the x–z plane, $\mathbf{B}=B_x\hat{\mathbf{x}}+B_z\cos \left({\omega }_{M}t\right)\hat{\mathbf{z}}$, a triblock chain underwent inchworm-like motion (Fig. 3D and Movie S7). The chain bent into a tilted asymmetric arch on the substrate because of the DC field along the z direction and some chain heterogeneity. As one end was closer to the substrate than the other end, the difference in hydrodynamic drag caused a net propulsion via cyclic bending and stretching. When a 3D field such as $\mathbf{B}=B_x\hat{\mathbf{x}}+B_y\sin \left({\omega }_{M}t\right)\hat{y}+B_z\hat{\mathbf{z}}$ was applied, a diblock chain also tended to curve into an arch. With the middle part of its body lifting up, the undulatory field in the y direction propelled it on the substrate like a sidewinding snake (Fig. 3E and Movie S8).

Comparison of Propulsion Modes.

We compare different propulsion modes reported in the literature with the propulsion mechanisms of our colloidal chains in Fig. 4. The radial axis of the polar plot represents the characteristic length D, and the angle axis corresponds to the helix angle θ (defined in Fig. 1C). All 2D swimmers, including undulating chains, rolling rods, and rotating lassos, lie on the radius axis since their helix angles are 90°. The propulsion coefficient is defined as V/ωD, where D, the characteristic length, is chosen to be the diameter of the cross-section for a helix, lasso, and plectoneme. For 2D swimmers, D is twice the actuation amplitude as chosen in previous studies (37). We can see from Fig. 4 that the propulsion of 3D swimmers was overwhelmingly more efficient than their 2D counterparts. One exception was the microlasso reported by us (34) (Fig. 4, green square, V/ωD ∼ 0.075). As our chains are reconfigurable, we can readily switch the propulsion modes from 2D to 3D with the same length-scale D, but varying helix angles θ. For a homogeneous chain, the helical rotation (Config. 7) was the most efficient 3D propulsion mode compared with the rotation of plectonemes and coils (Configs. 8 and 9). From Eq. 5, we see the that the maximum propulsion efficiency, ${\left(V/\omega D\right)}_{\max }=\left(1-{\gamma }_k\right)/4\sqrt{{\gamma }_k}$, occurs at the optimal helix angle θ = arctan $\left(\sqrt{{\gamma }_k}\right)$. Thus, the smaller γ_k is, i.e., the larger the aspect ratio of helix length to single-particle diameter is, the more efficient the propeller is. This is why high-aspect-ratio microswimmers like E. coli (Config. 15) or synthetic nanohelix (Config. 19) are more efficient than helical chains, which are primarily limited by the maximal chain length obtained to date.

Fig. 4.

Comparison of Configs. 4 to 14 with microswimmers in the literature. The radius axis of the polar plot is the length scale, angle axis the helical angle θ in Fig. 1 C, Inset. For 2D swimmers, θ = 90°. The propulsion efficiency V/ωD is marked with different color in the colormap. For helical swimmers, D is the helix diameter. For 2D swimmers, D is twice the actuation amplitude. Config. 15 is the result from Turner et al. (2000) (41), Config. 16 is from Gray and Hancock (1955) (37), Config. 17 is from Dreyfus et al. (2005) (6), Config. 18 is from Zhang et al. (2009) (8), Config. 19 is from Ghosh et al. (2009) (7), Config. 20 is from Tottori et al. (2012) (9), Config. 21 is from Jang et al. (2015) (12), and Config. 22 is from Yang et al. (2017) (34).

Chain Locomotion in Straight and Curved Channels.

To better mimic microorganisms in nature, artificial microswimmers must be able to adapt within complicated external environments. Most recently, Huang et al. (17) demonstrated that soft magnetic hydrogel composites can fit into complicated 3D microchannels. Here, we show that our 1D semiflexible magnetic chains navigate within different environments through transformation of both shapes and propulsion modes solely controlled by magnetic fields.

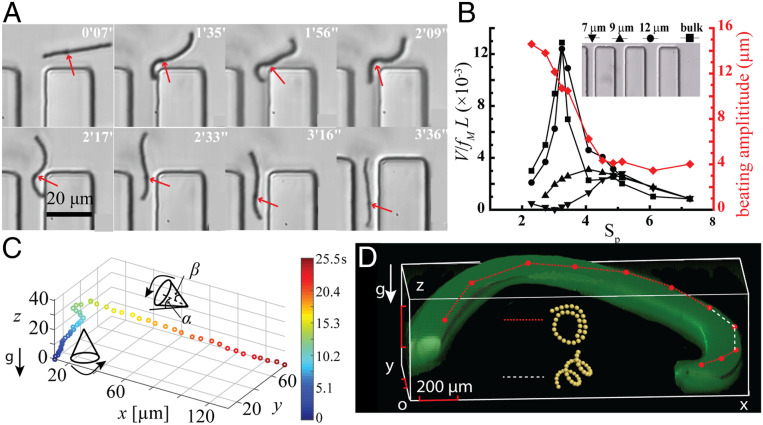
First, linear chains can pass through straight polydimethylsiloxane (PDMS) channels ranging from 7 to 20 µm in width and height ∼10 µm. As shown in Fig. 5A, a chain of length L = 21 µm with a single point defect underwent an in-plane undulatory motion entered and moved through a channel of 9 µm wide (Movie S9). As expected, the chain-propulsion efficiency, characterized by the ratio of chain velocity and the product of beating frequency and chain length V/(f_ML), depended on both beating frequency f_M and the channel width w. For a given channel, the efficiency first increased with increasing frequency—or, here, equivalently, the sperm number, $S_p={\left(\frac{2\pi f_M{\zeta }_{\perp }{L}^4}{{\kappa }_{bend}}\right)}^{\frac{1}{4}}$—because chain motion becomes nonreciprocal in time. As frequency increased further, the chain-beating amplitude, shown in the red curve in Fig. 5B, became smaller, and the efficiency dropped quickly. Therefore, the existence of an optimal efficiency results from the competition between the bending force and the viscous force. When the channel width is large (e.g., w = 12 μm), the propulsion efficiency reaches the maximum when the sperm number is ∼3, the same as a chain propelling in the bulk (6, 49–51). However, when the chain is confined within a narrower channel, the sperm number associated with maximum propulsion efficiency will be shifted. This is because the channel width becomes smaller than the maximal chain-beating amplitude, so that the chain propulsion is hindered by the channel walls. For all cases, the optimum propulsion efficiency occurred at the frequency where the beating amplitude was comparable to the channel width. In our work, the narrowest channel which our chain can navigate is ∼7 µm, comparable to the size of typical capillary blood vessels.

Fig. 5.

Navigation of microchains into complicated environments including narrow channels and 3D curved channels. (A) Typical dynamics of a defected linear chain (length ∼21 µm) passing through a narrow channel (width 9 µm) under an in-plane undulatory magnetic field $B_x\widehat{\mathit{x}}+B_y\sin \left({\omega }_{M}t\right)\widehat{\mathit{y}}$. The propulsion direction was controlled by the ratio of B_x and B_y. The red arrows indicate the point defect. (B) The dependence of chain-propulsion efficiency on the sperm number $S_p={\left(\frac{2\pi f_M{\zeta }_{\perp }{L}^4}{k_{bend}}\right)}^{\frac{1}{4}}$, in channels with different widths. The chain-beating amplitudes were measured in bulk. (C) Directed propulsion of a helical chain in bulk fluid by tuning the cone orientation α, including swimming against gravity (blue/green dots). We plot the 3D position of the center of mass of the chain as a function of time (indicated by the color scale). (D) Multimodal chain propulsion within a 3D curved channel (1.78 × 0.80 × 0.55 mm; 3D reconstruction from confocal microscopy images and labeled by green fluorescent dyes) under tilted precessing magnetic fields. The red dots indicate chain positions every 2 min. The segments connecting the red dots indicate sections of the trajectory where the chain is a helix (white) or a lasso (red), as controlled via the magnetic field.

Beyond straight channels at the same elevation, we can also achieve 3D propulsion in both bulk fluid and curved channels. This is possible because chain Configs. 10 to 12 allow for propulsion modes that do not rely on the existence of nearby walls. For example, Fig. 5C and Movie S10 show that a helical chain can overcome the gravitational force and undergo directed 3D propulsion. To achieve this, we applied a 3D precessing field $\hat{B}=\left(\cos \alpha \cos \beta -\sin \alpha \sin \beta \cos \left({\omega }_{M}t\right)\right)\hat{\mathbf{x}}+\sin \beta \sin \left({\omega }_{M}t\right)\hat{\mathbf{y}}+\left(\sin \alpha \cos \beta +\cos \alpha \sin \beta \cos \left({\omega }_{M}t\right)\right)\hat{\mathbf{z}}$ and reoriented the magnetic cone-orientation angle α (SI Appendix, Fig. S4, Inset), which allowed us to control the direction of the helix propulsion. To demonstrate this, we fabricated a 3D curved PDMS channel (1.78 × 0.80 × 0.55 mm), as reconstructed from confocal microscopy images and labeled by green fluorescent dyes in Fig. 5D, by pouring the PDMS precursor around a thin, curved polymer thread, followed by dissolving the polymer with solvent (SI Appendix, sections 1.4 and 1.5). The red trajectory in Fig. 5D and Movie S11 demonstrate chain navigation within this curved channel over the change of 500 μm in elevation and 2 mm in length. For most of the trajectory, we folded the chain into lassos which rolled along the channel wall quickly. Whenever the chain encountered steep slopes where the surface-enabled propulsion mode became ineffective, we altered the field condition to transform the lasso into a helix, which allowed for free swimming within the channel (white trajectory in Fig. 5D). This example demonstrates that a colloidal chain can navigate through a curved channel and against gravity by changing both chain morphology and propulsion modes with different field conditions, mimicking the adaptation of propulsion mechanisms in different environments seen in biological swimmers.

Conclusions

We fabricated 1D semiflexible superparamagnetic colloidal chains and demonstrated that they can fold into a variety of 2D and 3D shapes, including helices, plectonemes, lassos, and coils, under varying magnetic fields. Under similar fields, the folded chains can be tuned to move either by surface-enabled or free swimming, allowing for 3D propulsion. We have shown that free swimming can be achieved to overcome limitations due to low-Reynolds-number fluid mechanics by breaking chain symmetry with heterogeneity in stiffness along a homonuclear chain or with multiple blocks. Other heterogeneous chains instead take advantage of nearby surfaces and exhibit different propulsion modes that closely mimic arching and stretching inchworms and sidewinding snakes. The transformation between different chain morphologies and locomotion modes, solely controlled by external magnetic fields, enables these high-aspect-ratio colloidal chains to navigate through complex 3D environments, such as long and curved channels and narrow channels similar to capillary blood vessels.

Data Availability.

All experimental data discussed in the paper are available in Figs. 1, 4, and 5 and SI Appendix. The codes used in this work are available publicly in the GitHub repository (https://github.com/stochasticHydroTools/).