Keratoconus Detection Based on a Single Scheimpflug Image

Abstract

Purpose

To introduce a new approach for keratoconus detection based on corneal microstructure observed in vivo derived from a single Scheimpflug image.

Methods

Scheimpflug single-image snapshots from 25 control subjects and 25 keratoconus eyes were analyzed; from each group, five subjects were randomly selected to provide out-of-sample data. Each corneal image was segmented, after which the stromal pixel intensities were statistically modeled with a Weibull distribution. Distribution estimated parameters α and β, characterizing corneal microstructure, were used in combination with a macrostructure parameter, central corneal thickness (CCT), for the detection of keratoconus. In addition, receiver operating characteristic curves were used to determine the sensitivity and specificity of each parameter for keratoconus detection.

Results

The combination of CCT (sensitivity = 88%; specificity = 84%) with microscopic parameters extracted from statistical modeling of light intensity distribution, α (sensitivity = 76%; specificity = 76%) and β (sensitivity = 96%; specificity = 88%), from a single Scheimpflug image was found to be a successful tool to differentiate between keratoconus and control eyes with no misclassifications (sensitivity = 100%; specificity = 100%) with coefficients of variation up to 2.5%.

Conclusions

The combination of microscopic and macroscopic corneal parameters extracted from a static Scheimpflug image is a promising, non-invasive tool to differentiate corneal diseases without the need to perform measurements based on induced deformation of the corneal structure.

Translational Relevance

The proposed methodology has the potential to support clinicians in the detection of keratoconus, without compromising patient comfort.

Introduction

Keratoconus (KC) is an ocular disorder in which the cornea gradually thins and deforms, and it remains a major cause of vision impairment worldwide.¹ The epidemiology of the condition is unclear, but recent studies suggest that the prevalence of keratoconus is higher than 1 in 2000,² and it occurs more often in young people. With the continuing development of methods to support the diagnosis of keratoconus, this prevalence will rise as earlier forms of the disease are detected.

The evolution of corneal imaging techniques, supported by computer-aided corneal image analysis, played an important role in the detection of keratoconus; however, detection of the disease in its early stages remains a clinical challenge but is especially important to avoid complications after refractive surgery.^3,4 Today, Scheimpflug tomography is considered the key technology for keratoconus detection, as this technology offers a non-contact, three-dimensional evaluation of the corneal shape. Such data can be used to derive pachymetry, topography, and keratometry maps⁵ to assist ophthalmologists in their clinical decision-making process. It is also known that keratoconus is associated with a biomechanical weakening of the corneal stroma,⁶ suggesting that corneal biomechanics should be also considered for keratoconus detection.^7,8 To this end, the Corvis ST (Oculus, Wetzlar, Germany), a high-speed dynamic Scheimpflug imaging system based on mechanical stimulation of the cornea, was introduced to investigate the corneal biomechanical characteristics in vivo. However, all of these techniques are based on analysis of the cornea at the macroscopic level.

A more sensitive characterization of the cornea should involve analysis in vivo at both the macroscopic and microscopic levels, although the latter is not yet clinically available. Recently, it was demonstrated that statistical modeling of optical coherence tomography (OCT) image speckles can reveal information related to corneal tissue and in vivo corneal biomechanics.^9–11 Inspired by these recent findings, our team utilized this methodology to investigate the statistical light intensity distribution in dynamic Scheimpflug images.¹² By combining traditional macroscopic parameters, including central corneal thickness (CCT) and intraocular pressure (IOP), with microscopic tissue-related parameters obtained from Scheimpflug image processing, acquired with the Corvis ST, it was possible to discriminate mild keratoconus from control eyes successfully.¹² These first results also suggested that the proposed technique may even have potential discriminative power when applied to a single image taken before the air-puff excitation, rather than using all 140 images obtained by each Corvis ST measurement. This suggests that it is feasible to investigate the in vivo corneal microstructure from a single Scheimpflug image, without air-puff excitation. The aim of this work was to devise a methodology combining both macroscopic and microscopic corneal properties derived from a single Scheimpflug image to discriminate between keratoconus and control eyes.

Methodology

Subjects and Data Collection

Fifty participants (50 eyes) were included in this study. They were adult participants (31 females, 19 males) between 18 and 29 years of age (mean ± SD, 23.7 ± 3.0 years). The keratoconus group (KC) consisted of 25 participants. The remaining 25 participants served as the healthy control eyes, with IOP falling within a narrow range of 15 to 17 mm Hg and corneal astigmatism less than 0.75D. Each group was randomly subdivided into two groups. The first group contained 20 KC and 20 control eyes that were included for statistical analysis, and the second group had five KC and five control eyes to be used as an out-of-sample dataset for benchmarking the method (10% from the whole available data). This sample size was chosen based on calculations conducted using previously published data on statistical light intensity distribution from Scheimpflug images which suggested that a sample size of 10 control and 10 keratoconus participants would yield a 90% power to distinguish between control and keratoconus eyes at the 0.05 significance level.¹²

Keratoconus patients were recruited from the keratoconus clinic at the Antwerp University Hospital (Edegem, Belgium). Their eyes represented various stages of keratoconus, including clear cornea, non-severe corneal thinning, Fleischer ring at the apex base, and anterior or posterior corneal steepening. In addition, the KC eyes were not crosslinked or planned for crosslinking in the year following recruitment. Besides prior crosslinking, other exclusion criteria included corneal scarring, recent contact lens wear, known retinal or corneal pathologies (apart from keratoconus), known ocular procedures or treatments, and known systemic diseases (e.g., diabetes, HIV/AIDS, hypertension). In patients diagnosed with keratoconus in only one eye, the pathological eye was selected for measurement. For participants with keratoconus in both eyes and for control subjects, one eye was randomly selected for measurement and further statistical analysis. All participants underwent a comprehensive ophthalmological examination, including an interview and corneal biomechanics assessment with the Corvis ST (software version 1.4r1755). Corvis ST offers a complete set of biomechanical parameters derived from corneal deformation which were considered in a previous work¹² and were used exclusively in this work for descriptive purposes (keratoconus vs. control). Rather than including all of these parameters for analysis, the present study incorporates only CCT as a macro parameter that can be inferred from a single image without the need for mechanical stimulation. In addition to the Corvis ST assessment, for the purposes of severity classification the keratoconus patients also had their eyes imaged during the same visit with the Oculus Pentacam HR. Based on all available clinical data, the subjects were classified by an experienced ophthalmologist into four groups of keratoconus severity: early, mild, moderate, or advanced (Table 1). All assessments were performed around the same time of day (11 AM to 1 PM) during a single visit to avoid the effect of diurnal fluctuations in corneal shape.¹³

Table 1.

Structural and Biomechanical Parameters for the 25 Control and 25 Keratoconus Subjects Classified According to Disease Severity

	Keratoconus				Control
Parameter	Early	Mild	Moderate	Advanced
Corvis ST
Number of eyes	7	9	7	2	25
CCT, µm	524 ± 31	499 ± 15	464 ± 22	414 ± 5	548 ± 35
Maximum deformation amplitude, mm	1.12 ± 0.06	1.18 ± 0.13	1.23 ± 0.08	1.34 ± 0.03	1.01 ± 0.09
Radius of curvature, mm	6.33 ± 0.58	5.75 ± 1.01	5.13 ± 0.65	4.18 ± 0.09	7.1 ± 0.7
Corvis Biomechanical Index	0.3 ± 0.1	0.9 ± 0.1	1.0 ± 0.0	1.0 ± 0.0	0.2 ± 0.3
Pentacam HR
Astigmatism, D	1.15 ± 0.75	3.13 ± 0.77	2.92 ± 1.60	1.40 ± 0.30
Kmax, D	45.5 ± 0.8	51.3 ± 1.2	58.2 ± 4.3	63.3 ± 2.1
TCT, µm	504 ± 9	462 ± 7	436 ± 24	371 ± 3	n/a
BAD-D index	2.15 ± 1.14	6.37 ± 0.62	10.10 ± 2.99	16.55 ± 1.93
TKC index	0.1 ± 0.2	1.7 ± 0.4	2.9 ± 0.3	3.25 ± 0.25

K_max, maximum corneal curvature; TCT, thinnest corneal thickness; BAD-D, Belin/Ambrósio Deviation; TKC, topographic keratoconus classification.

To assess the repeatability of the proposed method, a subject from the control group was randomly chosen and asked to have their eye measured with Corvis ST 20 times. The subject had at least a 3-minute break between measurements, ensuring new positioning and alignment for every measurement. The coefficient of variation (CoV) was calculated for each of the parameters under investigation.

The study was approved by the Antwerp University Hospital Ethical Committee and adhered to the tenets of the Declaration of Helsinki. All participants gave written informed consent prior to their participation and after the nature and possible consequences of the study were explained.

Data Analysis

After data acquisition with the Corvis ST, the very first image (fixed size of 200 × 576 pixels) of each measurement from each subject was exported for further analysis. This image corresponds to an image obtained before air stimulus, with the cornea in a static position; consequently, the methodology explained here could be applied to any other Scheimpflug-based tomographers. The method of data analysis consisted of two main stages: (1) corneal segmentation and (2) statistical modeling of the pixel intensity distribution. The process of corneal segmentation consisted of various steps. First, median filtering was applied as a smoothing technique to eliminate noise from the image. Border detection using Canny edge detection was then performed. Canny edge detection uses a multi-stage algorithm to detect a wide range of edges in images, so no information is missed in areas where the difference between the corneal edge and background is subtle. After border detection, anterior and posterior corneal layers were detected, subsequently creating a mask that would separate the pixels of interest (i.e., those corresponding to the cornea) from unwanted pixels (i.e., those corresponding to the background of the image or other ocular structures).

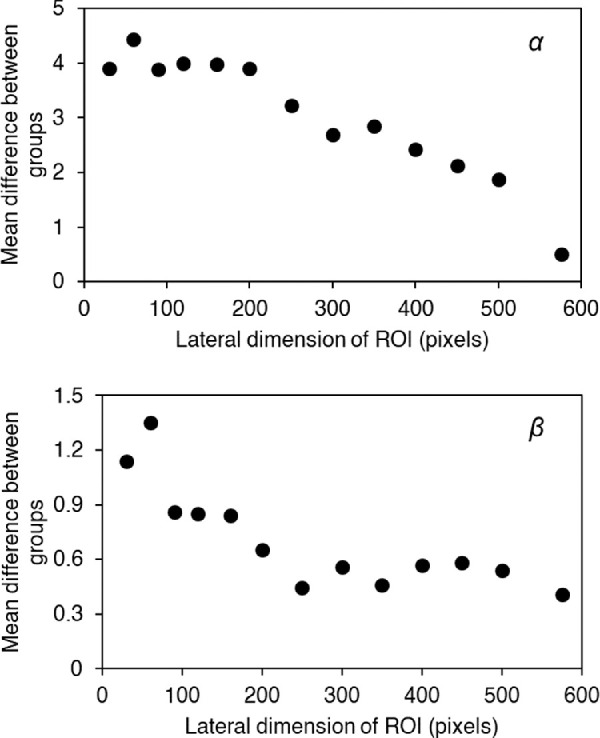
After segmentation, a central region of interest (ROI) was selected automatically (Fig. 1). For ROI selection, the anterior and posterior corneal profiles automatically defined by corneal segmentation were considered. The axial and lateral dimensions of the ROI were optimized to achieve the highest discriminative power of the statistical parameters of the cornea. Regarding the vertical (axial) dimension, image pixels corresponding to corneal epithelium were omitted, as they carry different statistical information compared to those from the stroma.⁹ Because the epithelial border (Bowman's layer) was barely visible in the Scheimpflug images, it was decided to use an epithelial length equivalent to 12% of the whole central corneal thickness previously delineated by corneal segmentation.¹⁴ This epithelial length was subtracted from the automatically delineated anterior corneal profile. Consequently, the vertical (axial) dimension of the ROI depended on corneal thickness. The horizontal (lateral) dimension of the ROI (60 pixels) was optimized to maximize the amount of signal-carrying data (Fig. 2).

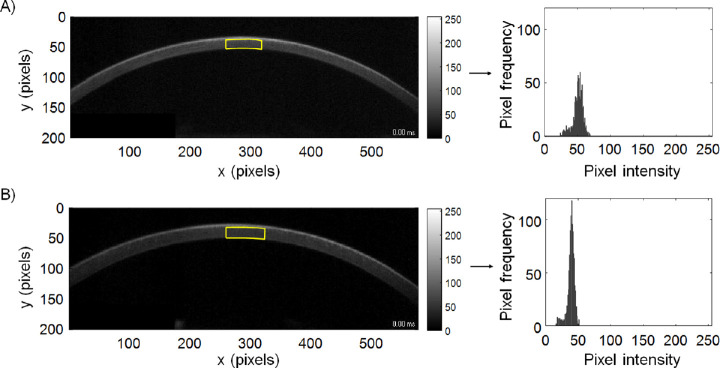
Figure 1.

Corneal Scheimpflug images and the central ROI (indicated by yellow lines) selected for analysis for a randomly chosen keratoconus participant (A) and a randomly chosen control participant (B). On the right are the corresponding histograms of pixel intensities for each ROI.

Figure 2.

The mean differences between the groups (KC vs. control) for parameters α (top) and β (bottom) as a function of the lateral dimension of ROI (number of pixels).

To assess to what extent the size of ROI affects the parameter estimates and whether there is a need to keep the number of pixels in a given ROI constant—in other words, to assess whether or not corneal thickness might be a source of bias—two different tests were performed: (1) bootstrap statistical analysis and (2) comparing a standard ROI size with half the ROI size. The bootstrap method is a resampling technique used to estimate statistics for a population by sampling a dataset with replacement. To perform the analysis, based on 1000 independent repetitions, the two most extreme cases in terms of ROI size were used for the analysis: (1) the keratoconic subject with the thinnest cornea, for which CCT = 409 µm and the ROI was 600 pixels (60 × 10 pixels), and (2) the control subject with the thickest cornea, for which CCT = 620 µm and the ROI was 1140 pixels (60 × 19 pixels). The bootstrap method allows calculating characteristics of the parameter estimators, such as the mean, standard deviation, and confidence intervals. In addition to the bootstrap method, a second test was performed to ensure that the size of the ROI did not affect the parameter estimates. This test consisted of randomly choosing a subject from each group (KC and control) and comparing the parameter estimates for a standard ROI size and half of the ROI size randomly chosen over 100 iterations.

Pixels corresponding to a given ROI were grouped in a histogram according to pixel intensity (Fig. 1). The resulting histogram was further approximated by the two-parameter distribution functions that scored higher in the statistical analysis of OCT corneal speckle (i.e., Weibull, gamma, and lognormal distributions).⁹ The parameters of the Weibull probability density function are

$$\begin{array}{c}\hfill f\left(x\right)=\frac{\beta }{\alpha }{\left(\frac{x}{\alpha }\right)}^{\beta -1}{e}^{-{\left(\frac{x}{\alpha }\right)}^{\beta }}ifx\ge 0\mathrm{or}0\mathrm{otherwise}\end{array}$$

where α > 0 is the scale parameter and β > 0 is the shape parameter. Both parameters were estimated using the method of maximum likelihood from the pixel intensities of the selected ROI in each image. The same procedure was followed with the parameters of the Gamma probability density function:

$$\begin{array}{c}\hfill f\left(x\right)=\frac{{\theta }^k}{\Gamma \left(k\right)}{x}^{k-1}{e}^{-\theta x}\end{array}$$

where k is the shape parameter, θ is the rate parameter, and Γ(k) is the standard gamma function. Finally, a similar procedure was followed with the two parameters of the lognormal distribution (x > 0):

$$\begin{array}{c}\hfill f\left(x\right)=\frac{1}{x\sigma \surd 2\pi }{e}^{-{(ln\left(x\right)-\mu )}^2/2{\sigma }^2}\end{array}$$

where µ and σ are the mean and standard deviation of the variable's natural logarithm, respectively. For all the distributions, the parameters were estimated using the method of maximum likelihood. The goodness of fit was assessed by means of the root mean squared error (RMSE) for the three candidate distributions. The Shapiro–Wilk test was used to test the distribution type (Gaussian or non-Gaussian) of all continuous variables. The independent two-sample t-test was used to assess differences in CCT and image-derived parameters between the KC and the control groups. The level of significance was set to 0.05.

Further, a two-class linear classifier based on a support vector machine (SVM) in combination with 5-fold cross-validation was used to obtain the optimal linear equations that would separate the two clusters under investigation (i.e., KC vs. control eyes). SVM is considered to be a powerful and highly accurate binary classifier.¹³ It was chosen over other classifiers because it is generally able to handle overfitting, it has a more balanced boundary between two given categories, and its hypothesis is a discriminator function producing 1 or 0, unlike other classifiers that do not offer an absolute prediction but rather a given probability of belonging to a certain group.¹⁵ In 5-fold cross-validation, the original dataset, consisting of 40 eyes (i.e., 20 keratoconus and 20 control), is randomly partitioned into five equally sized subsamples of 32 eyes per subsample (i.e., 16 keratoconus and 16 control). Of the five subsamples, a single subsample is retained as the validation data for testing the model (equivalent to 20% of the original dataset), and the remaining four subsamples are used as training data (equivalent to 80% of the original dataset) to define the line that would separate both groups (i.e., KC vs. control eyes). The cross-validation process is then repeated five times, with each of the five subsamples being used exactly once as the validation data. The five results can then be averaged to produce a single delimiting line. The advantage of this method over repeated random subsampling is that all observations are used for both training and validation.¹⁵ In addition to the method of 5-fold cross-validation, an out-of-sample dataset (consisting of 10 eyes: five KC and five control) was used to benchmark the model.

Receiver operating characteristic (ROC) curves were used to determine the sensitivity (true positive rate) and specificity (proportion of negatives correctly identified as such) of each considered discriminant parameter individually. This is to determine how well a given parameter can discriminate KC on its own. From each ROC curve, in addition to the sensitivity and specificity, other statistical parameters that provide information on the discrimination performance of the method were extracted,¹⁵ such as accuracy (ratio of correct classifications to the total number of classifications), precision (proportion of positive results that are true positives), cutoff value (maximum distance between the ROC and the diagonal), and the area under the ROC curve (AUC), computed using trapezoidal numerical integration. The AUC ranges from 0 to 1. The closer to 1, the better the performance of the method is.

Results

Participants

Table 1 shows the results of the structural and biomechanical parameters extracted from the Corvis ST that are regarded as being the most discriminative for diagnosing keratoconus eyes. Corneal thickness of the control eyes (group average, 548 ± 35 µm; range, 482–620 µm) was found to be statistically significantly different from the corneal thicknesses of the mild, moderate, and advanced keratoconic eyes (Mann–Whitney U test; P = 0.006, P < 0.001, and P < 0.001, respectively) but not statistically significantly different from the corneal thickness of early keratoconus eyes (Mann–Whitney U test; P = 0.100). Similarly, the Corvis Biomechanical Index (CBI) in control eyes (group average, 0.18 ± 0.31; range, 0.0–1.0) was found to be statistically significantly different from the index values for the mild, moderate, and advanced keratoconic eyes (Mann–Whitney U test; all P < 0.001) but was not statistically significantly different from that for early keratoconus (Mann–Whitney U test; P = 0.070).

ROI Selection

After corneal segmentation, the ROI was automatically chosen for every individual. The horizontal (lateral) dimension of the ROI was fixed for all participants and set to 60 pixels, which approximately represents 1 mm. Different lateral dimensions of the ROI were tested, ranging from 30 pixels to 576 pixels (576 pixels corresponding to the whole cornea) as shown in Figure 2. The lateral dimension for which the difference between keratoconus and control eyes is maximized (i.e., α and β parameters more distinguishable between classes) was considered optimal. A ROI of 60 pixels lateral length increases the difference in both α and β parameters between groups (Fig. 2).

Model Selection

The Weibull probability density distribution was found to be the best candidate function to fit pixel intensity distribution within the ROI in single corneal Scheimpflug images. The mean probability density functions (PDFs) corresponding to the different candidate modeling functions to describe pixel intensity distribution (gamma, Weibull, and lognormal) are shown in Figure 3.

Figure 3.

Mean PDF of the raw data fitted to Weibull, gamma, and lognormal distributions for 20 KC eyes (left) and 20 control eyes (right), overlapping the mean histograms of scaled pixel frequency (SPF) from each group.

The Weibull distribution was chosen to fit the pixel intensity distribution in single corneal Scheimpflug images because it reported the smallest RMSE, as shown in Table 2. The RMSE of each probability density distribution was found to be statistically significantly different from the other probability density distributions under analysis (i.e., Weibull vs. gamma, Weibull vs. lognormal, and gamma vs. lognormal). In all cases, P < 0.001 for both keratoconus and control groups.

Table 2.

Goodness of Fit in Terms of RMSE of the Different Candidate Models to Fit Corneal Pixel Intensity Distribution, Expressed in Arbitrary Units, for Keratoconus and Control Subjects

Model	KC (n = 20)	Control (n = 20)
Weibull	0.006 ± 0.0008	0.006 ± 0.0003
Gamma	0.010 ± 0.002	0.011 ± 0.001
Lognormal	0.011 ± 0.002	0.012 ± 0.001

Figure 4 illustrates the Weibull PDF of Figure 3 for the control and KC groups. Keratoconus expands the distribution around its center and causes a shift toward brighter pixel intensities. The parameters of the Weibull fit were significantly different between KC and control eyes (t-test α, P < 0.001; t-test β, P < 0.001). Table 3 shows the results of bootstrap analysis including the estimated means, standard deviations, 95% confidence intervals (CIs) and the coefficient of variation for the parameters α and β for the two extreme cases of ROI (i.e., the largest ROI that corresponds to a control subject and the smallest ROI that corresponds to a KC subject). Even though the standard deviation of the α estimator is twice as large for the keratoconic subject than for the control subject, suggesting that the data may have to be normalized for the sample size, the differences in the mean values of the α estimator are sufficiently large so those differences in standard deviations are negligible. There is no overlap between the 95% CI of a keratoconic subject and that of the control subject for either of the two parameters. Also, the coefficients of variation are very small for all of the parameter estimators. Thus, from these results, it can be concluded that there is no need to adjust for the difference in sample size or, in other words, to keep the number of pixels in a given ROI constant. Differences in corneal thickness would not affect the estimation of α and β parameters.

Figure 4.

PDF of the Weibull distribution for the keratoconus and control groups (20 participants in each group).

Table 3.

Results from the Bootstrap Analysis Method (1000 Independent Repetitions) Applied to the Keratoconus Participant with the Thinnest Cornea (Smallest ROI) and to the Control Participant with the Thickest Cornea (Largest ROI)

	α t hickest	α thinnest	β thickest	β thinnest
Mean	41.25	50.57	9.00	7.47
SD	0.14	0.28	0.26	0.31
95% CI	40.98–41.53	49.99–51.12	8.49–9.51	6.88–8.13
CoV, %	0.003	0.005	0.029	0.041

Parameters α and β estimators are calculated from the Weibull fitting.

To ensure the assumption that differences in corneal thickness would not affect the estimation of α and β parameters, a second test besides bootstrap was performed. A subject was randomly chosen from the control group (CCT = 576 µm), and a second subject was randomly chosen from the KC group (CCT = 495 µm). First, we performed the standard analysis to calculate α and β parameters in each case (control: α = 40.01, β = 8.57; KC: α = 44.78, β = 8.09). Further, the calculation of α and β parameters was repeated but randomly, taking only half of the pixels of the ROI. This analysis was repeated 100 times for each subject. The results indicate that α and β parameters are stable independently of the size of the ROI (control: α = 40.00 ± 0.08, β = 8.57 ± 0.14; KC: α = 44.78 ± 0.13, β = 8.10 ± 0.14).

Repeatability

The results from the repeatability test, where a single control eye was measured consecutively 20 times, showed CoV values of 2.0% for α, 2.5% for β, and 0.7% for CCT (see Table 4), indicating high repeatability of the light-intensity distribution parameters used for detecting keratoconus.

Table 4.

Repeatability of the Method Calculated for a Control Subject Measured 20 Times with Corvis ST

Parameter	Mean	SD	Range	CoV (%)
α	45.8	0.9	43.9–47.6	2.0
β	10.0	0.3	9.5–10.5	2.5
CCT, µm	556	4	551–566	0.7

Data corresponding to α and β are expressed in arbitrary units.

Keratoconus Detection

Parameters directly extracted from the statistical modeling of the corneal light-intensity distributions (α and β), in combination with CCT, all acquired from a single Scheimpflug image, were found to be good discriminators between keratoconus and control eyes (Fig. 5, Table 5). The mean CCT from the 20 KC participants amounted, on average, to 473 ± 27 µm, whereas the CCT from the 20 control participants amounted, on average, to 554 ± 34 µm.

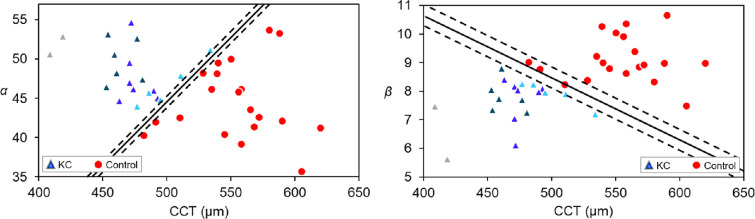
Figure 5.

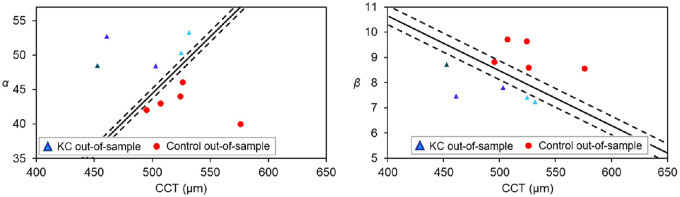
Scatterplots showing the discriminative power of the combination of CCT and a parameter extracted from statistical modeling of the light-intensity distribution—scale parameter α (left) and shape parameter β (right)—to distinguish between KC (n = 20) and control eyes (n = 20). KC eyes are represented in various colors depending on KC severity: early (light blue, n = 5), mild (bright blue, n = 7), moderate (dark blue, n = 6), and advanced (gray, n = 2). All parameters were acquired from a single Scheimpflug image. The discriminant solid lines were calculated by SVM and 5-fold cross validation. The confidence intervals represented as dashed lines were calculated according the coefficients of variance of α (2.0%) and β (2.5%).

Table 5.

Sensitivity and Specificity of the Combination of Micro Parameters (α, β) with a Macro Parameter (CCT) for Detection of KC

Combination of Parameters	Sensitivity (%)	Specificity (%)
α and CCT	100	100
β and CCT	100	95

The lines separating the keratoconus group from the control group in Figure 5 were calculated by the method of SVM in combination with 5-fold cross-validation. They are defined as:

$$\begin{array}{c}\hfill \begin{array}{c}\alpha =0.16·\mathrm{CCT}-37.18\hfill \\ \beta =-0.02·\mathrm{CCT}+19.4\hfill \end{array}\end{array}$$

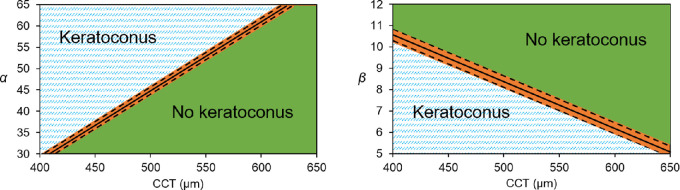
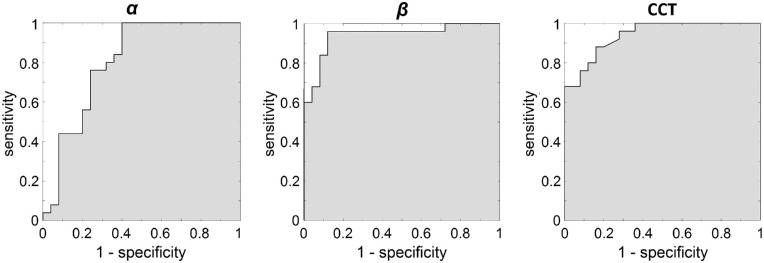
Details of the performance of the combination of parameters for keratoconus detection are presented in Table 5. According to these results and depending on the values of α, β, and CCT obtained for a given eye, Figure 6 can be of use to classify an unlabeled eye as KC or non-KC. ROC curve analysis was performed to assess the discriminant power of every considered parameter on its own (Fig. 7). Corresponding statistics are presented in Table 6.

Figure 6.

Charts to identify whether or not an eye suffers from keratoconus, based on parameters α and β of the Weibull distribution and CCT. The orange area, estimated based on the coefficient of variation of the study parameters, demarcates an inconclusive result.

Figure 7.

ROC curves corresponding to α (left), β (middle), and CCT (right) parameters for 20 keratoconus and 20 control eyes. Related statistics are presented in Table 6.

Table 6.

Statistical Parameters That Determine the Efficacy of Diagnosing KC for the Three Considered Parameters

Parameter	Sensitivity (%)	Specificity (%)	Accuracy (%)	Precision (%)	AUC	Cutoff Value
α	76	76	76	76	0.81	46.3a
β	96	88	92	89	0.94	8.2a
CCT	88	84	86	85	0.94	505 µm

^aArbitrary units.

Results Validation

An out-of-sample dataset consisting of five randomly preselected keratoconic subjects (CCT, 495 ± 32 µm) and five randomly preselected control subjects (CCT, 526 ± 28 µm) that were not included in the analysis (Fig. 5) was utilized exclusively for validation purposes. The light-intensity distribution of those 10 extra participants was analyzed using the Weibull probability density distribution. As presented in Figure 8, the obtained parameters (α and β) in combination with the CCT from the extra participants matched the previously defined discriminant lines.

Figure 8.

Classification of the out-of-sample dataset consisting on five KC and five control eyes. KC eyes are represented in different colors depending on KC severity: early (light blue, n = 2), mild (bright blue, n = 2) and moderate (dark blue, n = 1).

Discussion

To the best of our knowledge, this study showed for the first time that from a single Scheimpflug image it is possible to discriminate between control and keratoconus eyes without misclassifications. The method presented is based on combining central corneal thickness with parameters derived from the analysis of light-intensity distributions in the cornea. From among the two-parameter functions considered, the Weibull distribution performed best in fitting the corneal pixel intensity distribution in terms of the RMSE (Table 2). Both distribution parameters (α and β) were found to be statistically significantly different among the groups.

Many previous clinical studies have attempted to discriminate between keratoconus and control eyes using Scheimpflug imaging solely based on macroscopic parameters derived from both tomography data^16–18 and biomechanical parameters indirectly acquired from corneal mechanical excitation.^19–23 However, the results were often inconclusive, especially in early keratoconus.^20,22 Some more recent approaches added more sophisticated analysis techniques based on artificial intelligence (AI) and machine learning algorithms to enhance the detection rate of the early cases.^15,24–26 These AI-based techniques, although solely based on macroscopic parameters, tend to be more accurate than traditional methods; however, they require large datasets for their development.

This work shows that it is possible to investigate corneal tissue at the microscopic level in vivo using statistical modeling of light scattering in the cornea, without the necessity of using an air-puff to induce corneal deformation. Light scattering refers to how corneal tissue reflects light. Inner differences in the corneal tissue (control vs. pathological) would make the light travel differently through the tissue. Even though this work does not provide sufficient data to make a statement regarding the origin of the observed differences in pixel intensity distributions between control and keratoconus eyes, one may consider a physical interpretation based on the distribution parameters in previous works,^9,27 along with the well-known fact that corneal biomechanics are compromised in keratoconus.^6,7 We therefore hypothesize that the mechanism underlying the difference between healthy and pathologic tissue may be associated with scattering by microstructural modifications that manifest themselves in the intensity distribution. This leaves the door open for further studies on investigating corneal tissue in vivo, such as in different corneal pathologies or age-related corneal changes.

It is worth noting that statistically significant differences were found in our analysis in spite of the relatively small number of pixels in each image (200 × 576 pixels compared to, for example, 600 × 800 pixels in the Pentacam HR). This suggests that the presented methodology would be easily transferrable to other, higher resolution Scheimpflug devices. Standard commercial Scheimpflug tomographers incorporate a rotating camera that images different sections of the cornea. Consequently, the methodology presented here could be potentially used to investigate regional tissue differences in the cornea, such as those in astigmatic or keratoconic eyes. However, despite built-in commercial software offering the possibility of visualizing different corneal sections, it is limited in terms of accessing all raw data, which is essential for successful image processing analysis. It is also important to remark that, as is common in image processing, technical details such as ROI size or model selection were optimized for the current Corvis ST dataset and the problem of differentiating keratoconus from control eyes. Technical details might not be directly transferrable to other types of images or to a different problem, and their optimization for successful data analysis might be required. In the current work, a ROI of 60-pixel horizontal length was found optimal to maximize the difference between the groups (keratoconus vs. control) for both parameters α and β. However, as seen in Figure 2, incrementing the ROI length, and consequently the corneal area, will not substantially affect the discriminant power of α. Hence, for a larger corneal coverage, it is recommended to use the scale parameter (α) on its own, as the shape parameter (β) might be a weaker discriminator. On the other hand, no clear distinction was observed among the different keratoconus groups (Fig. 5). This does not mean that the presented methodology is not able to successfully grade keratoconus severity, but rather that the technical details were not optimized to such an end and should be considered in further research.

Note that, although the size of the study cohort was relatively small, this proof-of-concept study was able to present several statistically significant differences. In addition, for validation purposes, we used a subset of data for randomly chosen eyes that was not used for designing the separating lines between keratoconus and control eyes, and no misclassifications were found (Fig. 8). The proposed parameters related to corneal microstructure (α and β) proved to be good discriminators of keratoconus on their own, especially β (Fig. 7, Table 5), showing discriminant power even greater than that of CCT. However, the combination of these parameters (α and β) with a macrostructure parameter (CCT) was shown to be an even better discriminatory tool (Table 5). The results of the different tests applied indicate that the combination of α with CCT is able to correctly differentiate control subjects from keratoconus with no misclassifications (sensitivity = 100%; specificity = 100%).

It is important to notice, however, that in addition to the good performance of the classifier, the final result might be altered by the inherent variance in the calculation of the α (2%) and β (2.5%) parameters (Table 4). This constraint is shown as an orange area in the final classifying chart (Fig. 6), indicating that if an eye would fall in that area the classification results should be taken with caution. This was observed in one of the control eyes from the out-of-sample dataset (Fig. 8). In this example, all eyes were perfectly classified using α and CCT, but one of the control eyes, even though it is properly classified, fell within the confidence intervals using β and CCT. In case of doubt, it is important to bear in mind that the combination of α with CCT has shown to have a higher performance (sensitivity = 100%, specificity = 100 %) than data of β (sensitivity = 100%, specificity = 95 %) while α also has shown a smaller coefficient of variation.

To avoid systematic bias in pixel intensity distributions between keratoconus and control eyes, the groups were age matched, with each data acquisition being performed on a different day, and the same instrumental setting was used for acquisition. Corneal thickness could be considered as a potential source of systematic bias. However, the results from the performed bootstrap analysis (Table 3) indicate that corneal thickness is not a confounding factor that would affect the calculation of α and β.

It is also worth considering that, in general, methods based on pixel intensity detection are dependent on the alignment of the eye. Changes in ocular alignment could induce changes in pixel intensity distribution that might decrease measurement repeatability. Nevertheless, results from the repeatability test performed showed small coefficients of variation for α and β parameters (Table 4), indicating that the two parameters are not substantially affected throughout different imaging sessions.

In conclusion, we investigated the usefulness of a single Scheimpflug image to discriminate keratoconus from control eyes. The microscopic parameters extracted from static images have the potential to become an effective tool for evaluating corneal disease without performing measurements based on induced deformation of the corneal structure, thus reducing patient discomfort.