Abstract
Magnetic reconnection is a fundamental plasma process, by which magnetic energy is explosively released in the current sheet to energize charged particles and to create bi-directional Alfvénic plasma jets. Numerical simulations predicted that evolution of the reconnecting current sheet is dominated by formation and interaction of magnetic flux ropes, which finally leads to turbulence. Accordingly, most volume of the reconnecting current sheet is occupied by the ropes, and energy dissipation occurs via multiple relevant mechanisms, e.g., the parallel electric field, the rope coalescence and the rope contraction. As an essential element of the reconnecting current sheet, however, how these ropes evolve has been elusive. Here, we present direct evidence of secondary reconnection in the filamentary currents within the ropes. The observations indicate that secondary reconnection can make a significant contribution to energy conversion in the kinetic scale during turbulent reconnection.
Subject terms: Planetary science, Magnetospheric physics
Magnetic reconnection is a fundamental plasma process of magnetic energy conversion to kinetic energy. Here, the authors show direct evidence of secondary reconnection in the filamentary currents within the flux ropes indicating a significant contribution to energy conversion in the kinetic scale during turbulent reconnection.
Introduction
A macroscale current sheet is one necessary condition for occurrence of magnetic reconnection. When the current sheet thins to ion-scale, it becomes unstable to produce a train of ion-scale magnetic flux ropes characterized by the helical magnetic structures1–4. The roles of these flux ropes in reconnection have been extensively investigated, e.g., energizing electrons1,5–9, realizing fast reconnection10,11, mixing plasma at two sides of current sheet12,13, and transferring magnetic fluxes14,15. In this process, magnetic free energy is injected at large spatial scale, then transferred from the large scale into the small scale and dissipated at the kinetic scale. This kind of cross-scale energy cascade has been verified16,17. The current density within the flux rope was previously derived from magnetic field via Ampere’s law and exhibits a singular compact layer, primarily along the axis17. By the accurate plasma moment data in high time resolution recently achieved by magnetospheric multiscale (MMS) mission18, the researchers found that the singular compact current layer can be composed of many filamentary electron currents19,20, and the filamentary currents were directed at any direction other than only along the rope axis20. It suggests that the free energy is transferred into the much-smaller filamentary currents inside the ion-scale flux ropes. How this energy transfer actually occurs and how this energy is finally dissipated inside the flux ropes remain issues.
Here we show identification of series of varied magnetic field pulses inside the flux ropes downstream of a primary reconnection site at the magnetopause. These pulses represent small-scale flux rope-like structures and, within these pulses, a few filamentary currents are observed. Secondary reconnection is detected inside the filamentary currents of the pulses.
Results
Overview of the reconnection event
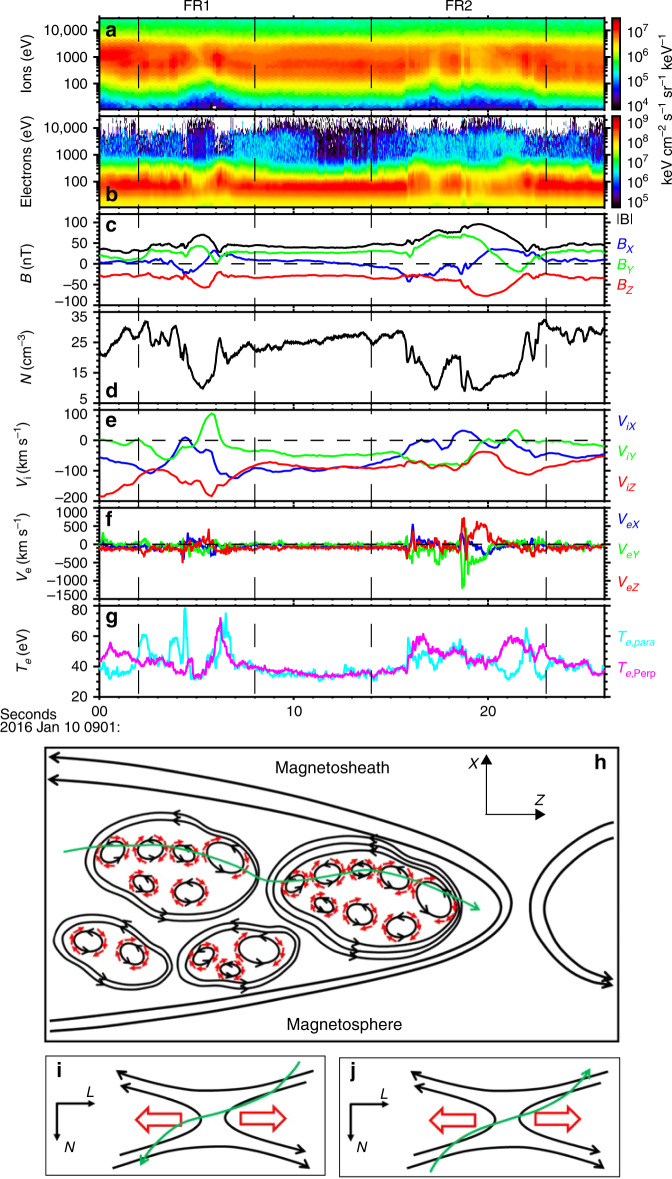
Figure 1 shows an overview of the MMS observations dawn-side of Earth’s magnetopause, in the geocentric solar magnetospheric (GSM) coordinates, during 09:01:00–09:01:26 UT on 10 Jan 2016. In this time interval, the spacecraft was located in the magnetopause boundary layer characterized by the southward magnetic field component (Fig. 1c), dominant low-energy (<200 eV) electron population and subordinate high-energy (>1 keV) electron population (Fig. 1b). The continuous southward ion flows were observed in this interval and the average speed was about −100 km s−1 (Fig. 1e), ~0.8 vA, where vA was the local Alfvén speed based on Bz ≈ 30 nT and N ≈ 25 cm−3. It suggests that a primary reconnection event was occurring north of the spacecraft21. The MMS spacecraft detected many magnetic flux ropes inside the ion diffusion region21, closely analogous to the previous observations in the magnetotail17. Here, we focus on the two flux ropes with the longest duration since the microphysics within the flux ropes can be analyzed in detail.
Fig. 1. Overview of MMS3 observations.
The data are presented in the geocentric solar magnetospheric (GSM) coordinates. The vertical dashed lines mark the leading and trailing edges of the flux ropes. a, b The ion and electron energy-time spectrograms of differential energy fluxes (color scale, in units of keV cm−2 s−1 sr−1 keV−1). c The magnitude and components of the magnetic field. d Electron density. e Ion velocity. f Electron velocity. g Electron temperature. h Schematic showing the varied magnetic field pulses and electron vortices in magnetic flux ropes. Black lines with arrows represent magnetic field lines, red arrows represent electron flows, and green curve with an arrow represents MMS trajectory. i, j A simplified schematic of reconnection in varied magnetic field pulses. The oppositely directed electron outflows were observed.
The two flux ropes, named as FR1 and FR2, are characterized by the bipolar Bx signatures accompanied with the enhancements of magnetic field magnitude and By near the reversal points of Bx (Fig. 1c), and were bounded by the vertical dashed lines in Fig. 1. The boundary was determined as the location where the magnetic field strength varied from and returned to the ambient value (black curve in Fig. 1c). By the time delay of Bx = 0 between the four satellites, the timing method22 was used to estimate their velocities and the speeds of the two flux ropes were ~119 and ~72 km s−1, respectively. The durations of FR1 and FR2 were ~6.0 s (09:01:02.0–09:01:08.0 UT) and ~9.0 s (09:01:14.0–09:01:23.0 UT). Thus, the radii of the two flux ropes were estimated to be ~357.0 km (~7.8 di) and ~324.0 km (~7.1 di) respectively, where di was ion inertial length, di = 45.6 km based on N ≈ 25 cm−3.
Inside the two flux ropes, the electron density was largely depressed and had the minimum near the centers (Fig. 1d), with some localized peaks. The electron temperature increased inside the flux ropes and fluctuated strongly (Fig. 1g). Remarkably, a series of electron flow spikes were observed and the speed occasionally exceeded ~1000 km s−1 (Fig. 1f), much larger than the ion flow speed (≤200 km s−1, Fig. 1e). These electron flow spikes referred to the thin electron current layers inside the flux ropes and would be explored later.
Varied magnetic field pulses inside flux ropes
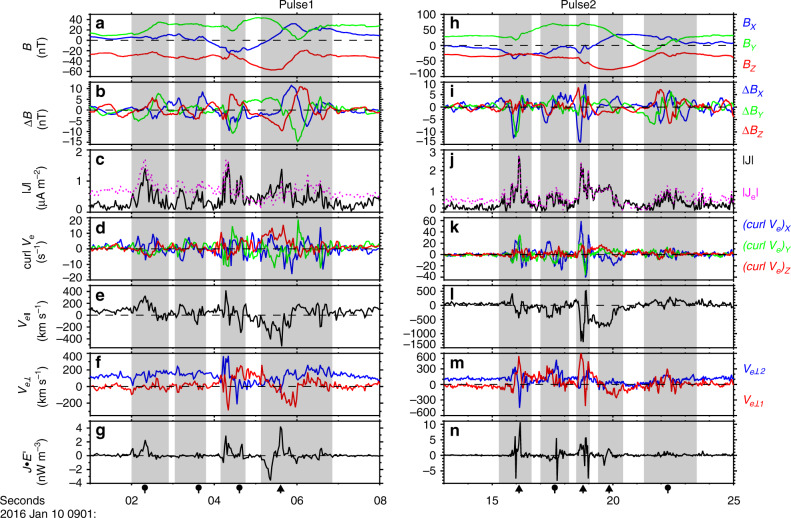
The features of the magnetic field and electron data inside the two flux ropes are enlarged in Fig. 2a–n. The signatures of magnetic flux ropes are evident from Fig. 2a, h. Figure 2b, i show the varied magnetic field in the three directions with the 1-s average data removed. The magnetic field fluctuations were strong inside the flux ropes and a train of the varied magnetic field pulses were observed in both flux ropes, marked by the vertical shadows. Figure 2c, j display the total (black trace) and electron (pink trace) current density intensities. A number of the current density peaks were observed within both flux ropes, i.e., the filamentary currents19,20. The total current density was nearly equal to the electron current density at most of peaks within the FR1 (Fig. 2c) and almost all peaks inside the FR2 (Fig. 2j). It appears that most of the filamentary currents were primarily carried by the electrons. These filamentary currents were all located within the varied magnetic field pulses and were the reason for the magnetic pulses within the ropes. At least two components of the varied magnetic field reversed inside each pulse (Fig. 2b, i). On average, ΔB was up to 10 nT, ~ 0.2|B|. It means that the varied magnetic field pulses signify a kind of helical magnetic topology, similar to the magnetic flux ropes in small-scale, which was very evident even in the three magnetic field components, in the pulses at ~09:01:06 UT (dubbed Pulse1 at the top of Fig. 2) within FR1 and at ~09:01:19 UT (Pulse2) within FR2. It was illustrated in Fig. 1h.
Fig. 2. Enlarged view of two flux ropes.
The two ropes correspond to the left and right columns. The vertical shadows mark the varied magnetic field pulses. Different black arrows below the vertical shadows represent two kinds of varied magnetic field pulses with different signatures. a Three components of the magnetic field in GSM coordinates. b The perturbation in magnetic field B with the 1-s average data removed. c The total (black trace) and electron (pink trace) current density intensity. The total current density intensity , the electron current density intensity , where e is the elementary charge, N is the electron number density, and Vi and Ve are the ion and electron velocity. d The curl of electron velocity. e The parallel electron velocity. f The two perpendicular components of the electron velocity, ⊥1 along (ve × b) and ⊥2 along b × (ve × b), where b and ve are unit vectors of the background magnetic field and the electron flow, respectively, calculated with the background average value outside the flux ropes. Here, b = (0.188, 0.679, −0.709) and ve = (−0.500, −0.124, −0.857) determined from interval 09:01:10.0–09:01:11.5 UT. gJ • E′ = J • (E + Ve × B). h–n The data of the rope FR2 are displayed in the same form and b = (0.176, 0.657, −0.733) and ve = (−0.502, −0.334, −0.798) for FR2 determined from interval 09:01:24.5–09:01:26.0 UT.
Figure 2d, k show the electron flow vorticity calculated by the flow measurements at four satellites. All three components of electron vorticity were significant in each varied magnetic field pulse. It means that the electron flows were very complicated inside the pulses and there were the electron vortices in the pulses. In order to figure out the electron vortices, the electron flows were transferred into the field-aligned coordinates (//, ⊥1, ⊥2), where // along b direction, ⊥1 along (ve × b) direction, and ⊥2 along b × (ve × b) direction, where b and ve are the unit vectors of the background magnetic field and the background electron flow, respectively, calculated with the background average value outside the flux ropes. The parallel electron flows are displayed in Fig. 2e, l while the two perpendicular components are shown in Fig. 2f, m. The parallel electron flow reversed inside all of the varied magnetic field pulses and, sometimes, changed sign multiple times in a single pulse, e.g. at ~09:01:04.3 UT, ~09:01:06.0 UT, ~09:01:16.0 UT, ~09:01:19.0 UT. The perpendicular component Ve⊥1 reversed as well within each varied magnetic field pulse (red curves in Fig. 2f, m). In the pulses with multiple reversals of Ve|| listed above, the electron flow in the Ve⊥2 also changed sign. It appears that the electron flow reversed at least in two directions inside all of the pulses. During some of the pulses, all three components of the electron flows changed direction. Thus, it is concluded that there were electron vortices inside the varied magnetic field pulses. Sometimes, the electron vortices were three-dimension eddies.
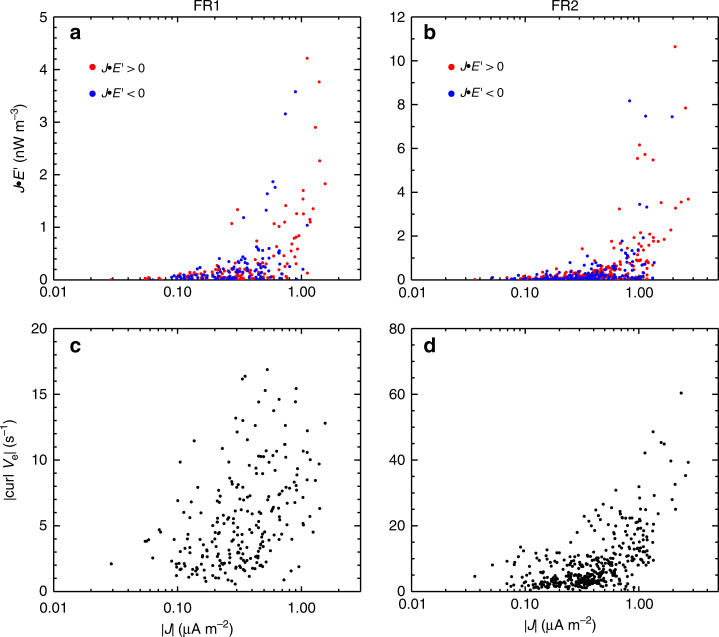
Figure 2g, n show J • E′, where E′ = E + Ve × B, and J • E′ denotes the energy conversion from electromagnetic field to plasmas in the electron rest frame23. J • E′ had a few peaks and valleys inside most of the varied magnetic field pulses, and the J • E′ peaks and valleys persisted for a short while (<0.5 s). In other words, the strong energy conversion occurred in the extremely localized area within the pulses. In order to figure out where the energy conversion happened, the scatter plot of J • E′ and |J| inside FR1 and FR2 are, respectively, displayed in Fig. 3a, b. It is clear that the energy conversion mainly occurred in the region with strong current density. The most intense energy conversion (|J • E′| > 2 nW m−3) only appeared at |J| ≥ 0.8 µA m−2. Such a relation has been demonstrated in the plasma turbulence using numerical simulations24. Furthermore, the total amount of all J • E′ data points was 16.2 nW m−3 inside FR1 and 65.7 nW m−3 inside FR2. This means that magnetic free energy was converted into the plasma energy inside both big flux ropes. The relation between the electron vorticity and the current density intensity was shown in Fig. 3c, d. Basically, the electron vorticity was intensified as increase of the total current density. The relation between the electron vorticity and the filamentary currents was observed also in the reconnection exhaust region25.
Fig. 3. The scatter plots of J • E′, |∇ × Ve| and |J|.
a, b The scatter plot of J • E′ and current density intensity |J| inside FR1 and FR2. The red (blue) dots represent the positive (negative) J • E′ data points. c, d The scatter plot of intensity of the electron velocity curl and |J| inside FR1 and FR2.
Reconnection in the varied magnetic field pulses
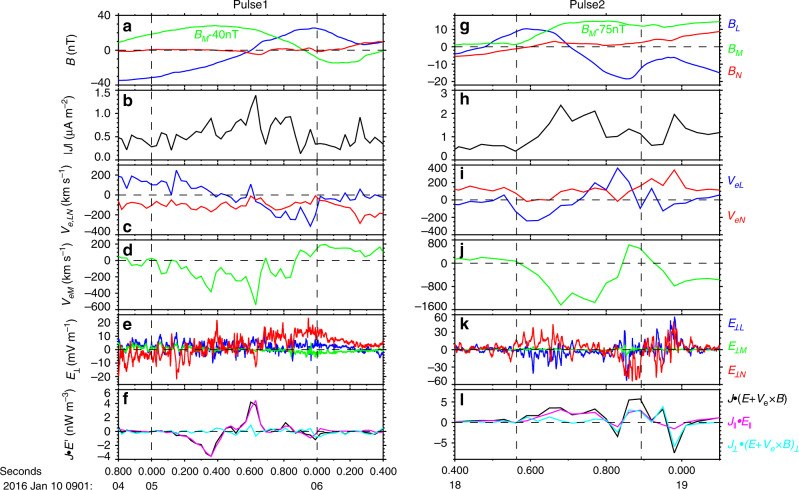
We examined carefully each of the filamentary currents inside the varied magnetic field pulses and transferred the data of each varied magnetic field pulse into its local current (LMN) coordinates derived from the hybrid minimum variance analysis: M was determined as the direction of maximum current density in each varied magnetic field pulses; then N = L′ × M, where L′ is the direction of the maximum variance of the magnetic field; L = M × N (specific results of each varied magnetic field pulses are displayed in Supplementary Table 1). As a result, the signatures associated with reconnection were observed in all of the pulses. Especially, the bidirectional electron outflow jets, the related Hall electric field and significant energy conversion were simultaneously observed inside the four pulses at ~09:01:06, 09:01:16, 09:01:19, and 09:01:20 UT, marked by the arrow at the bottom of Fig. 2. The bidirectional plasma jets were the direct evidence of the ongoing reconnection. The two ongoing reconnection events dubbed Pulses 1 and 2 are exhibited in Fig. 4 in their individual local current layer coordinate. The other events can be found in the Supplementary Figs. 2 and 4.
Fig. 4. Direct evidence of the reconnection in Pulse1 and Pulse2.
The data are shown in a local current (LMN) coordinate with L = (0.88, −0.47, −0.01)GSE, M = (0.25, 0.50, −0.83)GSE and N = (0.39, 0.73, 0.56)GSE for Pulse1, and L = (−0.92, 0.05, 0.39)GSE, M = (−0.18, 0.82, −0.55)GSE, and N = (−0.35, −0.57, −0.74)GSE for Pulse2. a, g Magnetic field BLMN, with BM shifted by −40 nT for Pulse1 and −75 nT for Pulse2. b, h The total current density intensity. c, i Electron velocity Ve,LN. d, j Electron velocity VeM. e, k Perpendicular electric field E⊥LMN in the spacecraft frame. The perpendicular electric fields mean electric field component perpendicular to the local magnetic field. f, lJ • E′ = J • (E + Ve × B).
There existed a few filamentary currents within the Pulse1 (Fig. 2c). We mainly focused on the first filamentary current at ~09:01:05.6 UT. The duration was about 1.0 s (~09:01:05.0 to ~09:01:06.0 UT). In order to accurately obtain its speed, we chose the magnetic signatures of the filamentary current with an evident time delay between any two of the four satellites. The timing method was finally performed to the points of BL = 0 for this filamentary current and the speed was calculated to be 130.8 km s−1. So, the half-thickness of this filamentary current was estimated to be 65.4 km ~1.4 di. Inside this filamentary current (Fig. 4a–f), BL changed sign from negative to positive (Fig. 4a), BM exhibited a bipolar variation with respect to the strong background field (~50 nT), and the current density peaked at the reversal point of BL at 09:01:05.6 UT (Fig. 4b). It shows that the spacecraft crossed the thin filamentary current. In this crossing, the electron bulk flows in the L direction reversed from positive to negative with a speed up to 200 km s−1 ~4.1 vA (blue trace, Fig. 4c) and veM got the minimum value just at the veL and BL reversal point, veM ~ −500 km s−1 (Fig. 4d). Meanwhile, the perpendicular electric field in the normal direction of the current sheet E⊥N changed sign also (red trace, Fig. 4e). It was basically negative in the positive veL and became positive in the negative veL, consistent with the simulation for reconnection with a strong guide field26. At the center of the veL reversal point (09:01:05.6 UT, expected location of electron diffusion region), the energy dissipation J • E′ (Fig. 4f) was positive, up to 4 nW m−3. Thus, magnetic energy was releasing. At the two sides of the reconnection outflows, J • E′ was negative. This kind of the J • E′ distribution in the vicinity of the X-line is in good agreement with the simulation results27. Based on these observations, it is concluded that the spacecraft crossed the reconnection diffusion region from one outflow to the other, as illustrated in Fig. 1i. Immediately after the reconnection diffusion region, the spacecraft encountered another filamentary current at 09:01:06.3 UT, its half-thickness was estimated to be 0.14 di, and reconnection signature was not observed there.
Figure 4g–l show one filamentary current at 09:01:18.7 UT inside the Pulse2. The duration of the current was ~0.32 s (~09:01:18.57 to ~09:01:18.89 UT) and the timing method was performed to the BL maximum for this filamentary current. Finally, its speed and half-thickness were obtained to be 106.3 km s−1 and 17.0 km (~0.37 di), respectively. The spacecraft crossed the filamentary current (Fig. 4g) and detected a strong guide field (BM ~80 nT). In this crossing, the electron flow in the L direction reversed from negative (approximately −200 km s−1) to positive (approximately 300 km s−1, Fig. 4i) and −veM had the maximum value around the veL reversal (Fig. 4j). Meanwhile, the electric field component E⊥N was positive in the negative veL and negative in the positive veL. Furthermore, J • E′ was positive (~3 nW m−3) around the veM peak. Based on the analysis above, the reconnection with a strong guide field was indeed happening in this current and the schematic was displayed in Fig. 1j. The analogous reconnection events were detected also in the filamentary currents of pulses at ~09:01:16, and ~09:01:20 UT (see Supplementary Figs. 2 and 4).
Inside the rest pulses, although the bidirectional electron flows in the L direction were not observed, the reconnection outflow jets veL, larger than the local Alfven speed, were always observed in some of the filamentary currents, as indicated by the arrows with round heads at the bottom of Fig. 2. It indicates that the reconnection was occurring but the spacecraft did not pass through the reconnection X-line region (see Supplementary Figs. 5–9). According to the observations, the reconnection was common in these varied magnetic field pulses and there was no ion-couple detected in these reconnection events, similar to the observations in the magnetosheath28 and in the magnetotail29. Moreover, the secondary reconnection was always with a strong guide field.
Discussion
In the process of primary reconnection, magnetic energy is transferred from the large-scale current sheet into the ion-scale magnetic flux ropes. The energy dissipation via interaction between these flux ropes has been extensively studied17,30,31. Remarkably intense electric field structure32–34 and energy dissipation35,36 were detected inside flux ropes. However, it is confusing that why the energy dissipation can occur inside the simple helical magnetic structures. Focusing on the two big flux ropes embedded in the reconnection ion outflows, we find a few small-scale flux rope-like structures or the varied magnetic pulses inside each big flux rope. In all of these small-scale flux rope-like structures, the electron flow reversed at least at two directions, i.e., the parallel and one of the perpendicular directions. In some pulses, the electron flow reversed at all three directions. Namely, the electron vortices were three-dimensional. Furthermore, the electron vorticity was enhanced within each pulse.
It is well known that the electron flow shear can lead to excitation of the KH instability. The nonlinear evolution of the electron KH instability can lead to the vortices, which can explain the observed electron vortices inside the pulses here. The magnetic field component along the shear flow can be wrapped up with the evolving KH vortices and results in the compressed thin current layers where magnetic reconnection can be triggered37–39. The similar process was found in a large flux rope via a PIC simulation40, where the magnetic flux rope was bounded by two X-lines at the two ends, and thus the colliding reconnection outflows towards the center of the flux ropes were important to the electron dynamics. In our event reported here, there were no such colliding ion flows were observed.
In order to verify whether the KH instability can be excited here, we examined the instability criterion41–43 ΔveL > veA/2, where ΔveL is the electron velocity variation across the filamentary currents and is the local electron Alfven speed. It is found that ΔveL was substantially smaller than veA/2 around all of the filamentary currents (see Supplementary Figs. 1–9), i.e., the KH instability inside the big flux ropes was stable as the spacecraft passed through them. This discrepancy can be caused by the fact that the shear flow speed decreases as the KH instability evolves and can be very low during the nonlinear stage. Another scenario for occurrence of the observed varied magnetic field pulses is the secondary instability or the tearing-type instability16, driven by the strong magnetic shear across the electron current layer. As a result, secondary reconnection can occur in the filamentary currents. The formed flux rope was unstable to interchange instability as well driven by density gradients predicted by simulations44 and secondary reconnection was verified in the resulting narrow current layers. In our event, the intense density gradient was clear in both big flux ropes, consistent with the simulation results44. At present, we cannot distinguish which mechanism(s) is responsible for the generation of the varied magnetic field pulses.
According to our observation, it is undoubted that magnetic energy was released inside magnetic flux ropes via secondary reconnection. Given a number of the secondary reconnection inside the flux ropes, they may make a significant role on energy conversion during reconnection. More efforts are needed to devote the total energy budget in reconnection.
Methods
Local current coordinate system determination
To find secondary reconnection signatures, the spacecraft data should be examined in the local current coordinate system (LMN). A hybrid minimum variance analysis was used to determine the LMN coordinate system: M was along the direction of maximum current density in the filamentary current. N = L′ × M, where L′ was the direction of maximum variance of the magnetic field. L = M × N. The results are shown in Supplementary Table 1.
Estimation of the filamentary currents speed
A multi‐spacecraft method was used to determine the speed of the filamentary currents. This method (timing method) is based on the time delay between the passages of the current sheet over four satellites. The relative position of the four MMS satellites can be found from MMS data. Then we chose the magnetic signatures of the filamentary currents with an evident time delay between any two of the four satellites. The timing method was performed to these signatures to obtain the speeds. The timing method was performed to the BL maximum for the events E3, E5, E7, E8, and E9, to the BL minimum for the events E2 and E6, and to the points of BL = 0 for the events E1 and E4. The results are shown in Supplementary Table 2.
Supplementary information
Acknowledgements
We thank the entire MMS team and instrument principal investigators for providing data. R.W. appreciates the valuable comments and discussion with T.K.M. Nakamura at Space Research Institute, Austrian Academy of Sciences and helpful discussion from C. Huang at Institute of Geology and Geophysics, Chinese Academy of Sciences. This work is supported by the B-type Strategic Priority Program of the Chinese Academy of Sciences (XDB41000000), the National Science Foundation of China (NSFC) grants (41674143, 41922030, and 41527804), the key research program of frontier sciences CAS (QYZDJ-SSW-DQC010), and the Fundamental Research Funds for the Central Universities.
Author contributions
S.M.W. and R.S.W. carried out data analysis and wrote the paper. R.S.W. and Q.L. supervised the work and provided the theoretical analysis. H.F. reconstructed the magnetic topology via the FOTE method. S.W. gave the valuable suggestions and comments. All of the authors discussed the results and commented on the paper.
Data availability
All the MMS data used in this work are available at the MMS data center (https://lasp.colorado.edu/mms/sdc/public/). Magnetic field and electric field data are available at https://lasp.colorado.edu/mms/sdc/public/datasets/fields/. The electron and ion moment data can be found at https://lasp.colorado.edu/mms/sdc/public/datasets/fpi/.
Code availability
All the spacecraft data in this study are collected and analyzed with the IDL software (spedas) available to the public in the MMS database website. The IDL spedas package is available at https://lasp.colorado.edu/mms/sdc/public/software/.
Competing interests
The authors declare no competing interests.
Footnotes
Peer review informationNature Communications thanks the anonymous reviewers for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Rongsheng Wang, Email: rswan@ustc.edu.cn.
Quanming Lu, Email: qmlu@ustc.edu.cn.
Supplementary information
Supplementary information is available for this paper at 10.1038/s41467-020-17803-3.
References
- 1.Chen LJ, et al. Observation of energetic electrons within magnetic islands. Nat. Phys. 2008;4:19–23. [Google Scholar]
- 2.Sibeck DG, et al. Magnetotail flux ropes. Geophys. Res. Lett. 1984;11:1090–1093. [Google Scholar]
- 3.Olson J, et al. Experimental demonstration of the collisionless plasmoid instability below the ion kinetic scale during magnetic reconnection. Phys. Rev. Lett. 2016;116:255001. doi: 10.1103/PhysRevLett.116.255001. [DOI] [PubMed] [Google Scholar]
- 4.Slavin JA, et al. Geotail observations of magnetic flux ropes in the plasma sheet. J. Geophys. Res. 2003;108:1015. [Google Scholar]
- 5.Drake JF, Swisdak M, Che H, Shay MA. Electron acceleration from contracting magnetic islands during reconnection. Nature. 2006;443:553–556. doi: 10.1038/nature05116. [DOI] [PubMed] [Google Scholar]
- 6.Du SB, Guo F, Zank GP, Li XC, Stanier A. Plasma energization in colliding magnetic flux ropes. Astrophys. J. 2018;867:16. [Google Scholar]
- 7.Fu XR, Lu QM, Wang S. The process of electron acceleration during collisionless magnetic reconnection. Phys. Plasmas. 2006;13:012309. [Google Scholar]
- 8.Oka M, Phan TD, Krucker S, Fujimoto M, Shinohara I. Electron acceleration by multi-island coalescence. Astrophys. J. 2010;714:915–926. [Google Scholar]
- 9.Wang RS, Lu QM, Du AM, Wang S. In situ observations of a secondary magnetic island in an ion diffusion region and associated energetic electrons. Phys. Rev. Lett. 2010;104:175003. doi: 10.1103/PhysRevLett.104.175003. [DOI] [PubMed] [Google Scholar]
- 10.Daughton W, Scudder J, Karimabadi H. Fully kinetic simulations of undriven magnetic reconnection with open boundary conditions. Phys. Plasmas. 2006;13:072101. [Google Scholar]
- 11.Karimabadi H, Daughton W, Scudder J. Multi-scale structure of the electron diffusion region. Geophys. Res. Lett. 2007;34:L13104. [Google Scholar]
- 12.Paschmann G, et al. Plasma and magnetic field characteristics of magnetic flux transfer events. J. Geophys. Res. 1982;87:2159–2168. [Google Scholar]
- 13.Russell CT, Elphic RC. Initial ISEE magnetometer results: magnetopause observations. Space Sci. Rev. 1978;22:681–715. [Google Scholar]
- 14.Pu ZY, et al. Magnetic topologies of an in vivo FTE observed by Double Star/TC-1 at Earth’s magnetopause. Geophys. Res. Lett. 2013;40:3502–3506. [Google Scholar]
- 15.Lee LC, Fu ZF. A theory of magnetic flux transfer at the Earth’s magnetopause. Geophys. Res. Lett. 1985;12:105–108. [Google Scholar]
- 16.Daughton W, et al. Role of electron physics in the development of turbulent magnetic reconnection in collisionless plasmas. Nat. Phys. 2011;7:539–542. [Google Scholar]
- 17.Wang RS, et al. Coalescence of magnetic flux ropes in the ion diffusion region of magnetic reconnection. Nat. Phys. 2016;12:263–267. [Google Scholar]
- 18.Burch JL, Moore TE, Torbert RB, Giles BL. Magnetospheric multiscale overview and science objectives. Space Sci. Rev. 2016;199:5–21. [Google Scholar]
- 19.Eastwood JP, et al. Ion-scale secondary flux ropes generated by magnetopause reconnection as resolved by MMS. Geophys. Res. Lett. 2016;43:4716–4724. doi: 10.1002/2016GL068747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Wang RS, et al. Interaction of magnetic flux ropes via magnetic reconnection observed at the magnetopause. J. Geophys. Res. 2017;122:10436–10447. [Google Scholar]
- 21.Wang SM, et al. Anisotropic electron distributions and whistler waves in a series of the flux transfer events at the magnetopause. J. Geophys. Res. 2019;124:1753–1769. [Google Scholar]
- 22.Schwartz SJ. Shock and discontinuity normals, Mach numbers, and related parameters. ISSI Sci. Rep. Ser. 1998;1:249–270. [Google Scholar]
- 23.Zenitani S, Hesse M, Klimas A, Kuznetsova M. New measure of the dissipation region in collisionless magnetic reconnection. Phys. Rev. Lett. 2011;106:195003. doi: 10.1103/PhysRevLett.106.195003. [DOI] [PubMed] [Google Scholar]
- 24.Wan M, et al. Intermittency, coherent structures and dissipation in plasma turbulence. Phys. Plasmas. 2016;23:042307. [Google Scholar]
- 25.Phan TD, et al. MMS observations of electron-scale filamentary currents in the reconnection exhaust and near the X line. Geophys. Res. Lett. 2016;43:6060–6069. [Google Scholar]
- 26.Oieroset M, et al. MMS observations of large guide field symmetric reconnection between colliding reconnection jets at the center of a magnetic flux rope at the magnetopause. Geophys. Res. Lett. 2016;43:5536–5544. [Google Scholar]
- 27.Zenitani S, Hesse M, Klimas A, Black C, Kuznetsova M. The inner structure of collisionless magnetic reconnection: the electron-frame dissipation measure and Hall fields. Phys. Plasmas. 2011;18:122108. [Google Scholar]
- 28.Phan TD, et al. Electron magnetic reconnection without ion coupling in Earth’s turbulent magnetosheath. Nature. 2018;557:202–206. doi: 10.1038/s41586-018-0091-5. [DOI] [PubMed] [Google Scholar]
- 29.Wang RS, et al. An electron-scale current sheet without bursty reconnection signatures observed in the near-Earth tail. Geophys. Res. Lett. 2018;45:4542–4549. [Google Scholar]
- 30.Pritchett PL. Kinetic properties of magnetic merging in the coalescence process. Phys. Plasmas. 2007;14:052102. [Google Scholar]
- 31.Zhou M, et al. Coalescence of macroscopic flux ropes at the subsolar magnetopause: magnetospheric multiscale observations. Phys. Rev. Lett. 2017;119:055101. doi: 10.1103/PhysRevLett.119.055101. [DOI] [PubMed] [Google Scholar]
- 32.Hwang KJ, et al. Small-scale flux transfer events formed in the reconnection exhaust region between two X lines. J. Geophys. Res. 2018;123:8473–8488. [Google Scholar]
- 33.Stawarz JE, et al. Intense electric fields and electron-scale substructure within magnetotail flux ropes as revealed by the magnetospheric multiscale mission. Geophys. Res. Lett. 2018;45:8783–8792. [Google Scholar]
- 34.Wang RS, et al. Electrostatic and electromagnetic fluctuations detected inside magnetic flux ropes during magnetic reconnection. J. Geophys. Res. 2016;121:9473–9482. [Google Scholar]
- 35.Fu HS, et al. Intermittent energy dissipation by turbulent reconnection. Geophys. Res. Lett. 2017;44:37–43. [Google Scholar]
- 36.Huang SY, et al. Observations of flux ropes with strong energy dissipation in the magnetotail. Geophys. Res. Lett. 2019;46:580–589. [Google Scholar]
- 37.Nakamura TKM, Daughton W, Karimabadi H, Eriksson S. Three-dimensional dynamics of vortex-induced reconnection and comparison with THEMIS observations. J. Geophys. Res. 2013;118:5742–5757. [Google Scholar]
- 38.Nakamura TKM, Hasegawa H, Shinohara I, Fujimoto M. Evolution of an MHD-scale Kelvin-Helmholtz vortex accompanied by magnetic reconnection: two-dimensional particle simulations. J. Geophys. Res. 2011;116:A03227. [Google Scholar]
- 39.Nykyri K, Otto A. Plasma transport at the magnetospheric boundary due to reconnection in Kelvin-Helmholtz vortices. Geophys. Res. Lett. 2001;28:3565–3568. [Google Scholar]
- 40.Huang C, et al. Development of turbulent magnetic reconnection in a magnetic island. Astrophys. J. 2017;835:245. [Google Scholar]
- 41.Fermo RL, Drake JF, Swisdak M. Secondary magnetic islands generated by the Kelvin-Helmholtz instability in a reconnecting current sheet. Phys. Rev. Lett. 2012;108:255005. doi: 10.1103/PhysRevLett.108.255005. [DOI] [PubMed] [Google Scholar]
- 42.Huang C, et al. Magnetic islands formed due to the Kelvin-Helmholtz instability in the outflow region of collisionless magnetic reconnection. Geophys. Res. Lett. 2015;42:7282–7286. [Google Scholar]
- 43.Zhong ZH, et al. Evidence for secondary flux rope generated by the electron Kelvin-Helmholtz instability in a magnetic reconnection diffusion region. Phys. Rev. Lett. 2018;120:075101. doi: 10.1103/PhysRevLett.120.075101. [DOI] [PubMed] [Google Scholar]
- 44.Lapenta G, Markidis S, Goldman MV, Newman DL. Secondary reconnection sites in reconnection-generated flux ropes and reconnection fronts. Nat. Phys. 2015;11:690–695. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All the MMS data used in this work are available at the MMS data center (https://lasp.colorado.edu/mms/sdc/public/). Magnetic field and electric field data are available at https://lasp.colorado.edu/mms/sdc/public/datasets/fields/. The electron and ion moment data can be found at https://lasp.colorado.edu/mms/sdc/public/datasets/fpi/.
All the spacecraft data in this study are collected and analyzed with the IDL software (spedas) available to the public in the MMS database website. The IDL spedas package is available at https://lasp.colorado.edu/mms/sdc/public/software/.