Biomechanics of vertical posture and control with referent joint configurations

Abstract

Our study compared the results of two methods of analysis of postural sway during human quiet standing, the rambling-trembling (Rm-Tr) decomposition and the analysis of the point of intersection of the ground reaction forces (zIP analysis). Young, healthy subjects were required to stand naturally and with an increased level of leg/trunk muscle co-activation under visual feedback on the magnitude of a combined index of muscle activation (muscle mode). The main findings included the shift of zIP toward higher frequencies and strong correlations between Tr and zIP when the subjects stood with increased muscle co-activation. We interpret the results within the idea of whole-body control with a set of primitives associated with referent coordinates in the joint configuration space.

Introduction

This study is based on several theoretical concepts related to the control of posture and movement. We assume, in particular, that the neural control of movement and posture can be adequately described as setting time-varying referent coordinates (RCs) for the effectors, including RCs for the whole body (cf. Feldman 2015). This type of control is organized in a hierarchical way: At the task level, a low-dimensional set of RCs is defined, which is then transformed into lower-level, higher-dimensional RCs, e.g., at the level of individual limbs, digits, and joints (Latash 2010). At the muscle level, RC is equivalent to threshold of the stretch reflex (λ) as in the classical equilibrium-point hypothesis (Feldman 1966, 1986).

During quiet stance, spontaneous postural sway is typically described using time-varying patterns of mechanical variables such as trajectories of the center of mass (COM) and of the center of pressure (COP) of the ground-reaction force on the feet (F). Zatsiorsky and Duarte (1999, 2000) have suggested that balance is kept with respect to a moving, rather than stationary, coordinate. They operationalized this idea with decomposition of the COP(t) time series during quiet stance into two components termed rambling (Rm) and trembling (Tr). Rm(t) was computed as an interpolation of COP points when the component of F along the selected axis (e.g. anterior-posterior) was zero; thus, it approximated the equilibrium trajectory of the body reflecting its time-varying RC. Tr(t) was computed as the difference between COP(t) and Rm(t) and interpreted as a reflection of peripheral mechanisms including the mechanical properties of the effectors and spinal reflex circuitry.

Recently, a novel method of analysis of biomechanical variables during quiet standing has been suggested (Boehm, Nichols, & Gruben, 2019). It is based on the non-trivial observation that the F(t) vectors within a plane (e.g., a sagittal plane), quantified within relatively narrow frequency ranges covering a wide total range (0.6–6.0 Hz at 0.4 Hz increments), nearly intersect in a point (IP) at a height above the support surface (zIP). This observation suggests proportional scaling of the joint moments acting in the plane of analysis (Gruben & Boehm 2012). In terms of control with joint RCs, proportional joint moment scaling implies that shifts from one RC to another traverse along a line in the joint configuration space. Note that this is true assuming that actual body configuration shows relatively small changes during quiet standing (cf. Hsu et al. 2007). We will refer to such a line as an RC_J template. Such templates may be seen as control primitives (cf. Bizzi, Giszter, Loeb, Mussa-Ivaldi, & Saltiel, 1995; D’Avella, Saltiel, & Bizzi, 2003; Kargo, Ramakrishnan, Hart, Rome, & Giszter, 2010), which may be combined to produce different behaviors. Thus, changes in F that are characterized by an IP are consistent with using a single RC_J-primitive. The observation that zIP varies systematically with frequency (Boehm et al., 2019) indicates a preference to shift RC in the joint configuration space along a line that could correspond to the combination of a few RC_J-primitives with weights selected in a frequency-dependent manner.

We suggest that Tr and zIP reflect linked processes related to the natural control of vertical posture with RCs. The original studies have documented consistent changes in zIP with the frequency band: It drops as an approximately inverse relationship from values above the COM height for low frequencies to values below the COM for higher frequencies (Boehm et al., 2019). Across participants, consistent zIP values are observed for frequencies over 0.5 Hz suggesting a link between zIP and Tr as the typical Rm range is below 0.5 Hz while the Tr range is within the range 0.4–2.5 Hz (Zatsiorsky & Duarte, 2000). Hence, we expected the Tr power to correlate with zIP across frequencies (Hypothesis-1). We also expected Tr and zIP to show parallel changes during quiet stance while producing a prescribed elevated level of agonist-antagonist co-activation in the leg/trunk muscles. Our earlier study has documented faster Rm and Tr with increased co-activation (Yamagata, Falaki, & Latash, 2019); hence, we expected a shift of zIP toward higher frequencies or, equivalently, toward higher values for a fixed frequency range (Hypothesis-2) given that zIP drops smoothly for higher frequencies.

Methods

Participants

Five women and six men (age 26.9 ± 5.6 years old, body mass 70.6 ± 16.9 kg, height 1.7 ± 0.1 m; mean ± SD) without known neurological, muscular, and/or orthopedic conditions took part in this study. They all were right-leg dominant as defined by preferred leg during stepping up and kicking a ball. Written informed consent for the study, approved by the Office for Research Protections of the Pennsylvania State University, was obtained from all participants.

Apparatus

Subjects were tested during standing on a force platform (AMTI, OR-6, Watertown, MA, USA). Three force (F_X, F_Y, F_Z) and three moment components (M_X, M_Y, M_Z) were recorded at 1 kHz. The three axes corresponded to the anterior-posterior (X), medio-lateral (Y) and vertical (Z) directions with respect to the subject’s body. A 21-inch monitor located at the eye level about 1 m away from the subject was used for two types of visual feedback at a time delay of approximately 10 ms. Changes in COP coordinates in the anterior-posterior and medio-lateral directions (COP_AP and COP_ML) caused displacement of a 5-mm cursor up/down and left/right. The visual feedback on the muscle activation level was provided as a bar; higher muscle activation moved the bar upward. For the feedback, we used the magnitude of one of the two first muscle modes (Krishnamoorthy, Goodman, Latash, & Zatsiorsky, 2003), namely the M2-mode, which contained significantly loaded ventral muscles. The computation of the M2-mode magnitude is described later. A more detailed description of the setup can be found in Yamagata et al. (2019a).

To record surface muscle electrical activity (electromyogram, EMG), we used a Trigno wireless system (Delsys Inc., Natick, MA, USA). After cleaning the skin, electrodes were attached over the following 14 muscles on the right side of the body: tibialis anterior (TA), soleus (SOL), gastrocnemius medialis (GM), gastrocnemius lateralis (GL), biceps femoris (BF), semitendinosus (ST), vastus lateralis (VL), rectus femoris (RF), vastus medialis (VM), tensor fascia latae (TFL), rectus abdominis (RA), lumbar erector spinae (LES), thoracic erector spinae (TES), and flexor digitorum superficialis (FDS). Prior to transmission to the data collection computer (Dell, Core™ i7, 2.93 GHz), EMG signals were pre-amplified and band-pass filtered (20–450 Hz). The EMG and force platform data were recording using a customized LabVIEW program (National Instruments Corp., Austin, TX, USA) with a sample frequency of 1 kHz with the 16-bit resolution (PCI-6225, National Instruments Corp.).

Procedure

Subjects stood on the force platform with their feet parallel at the hip width; the foot position was marked to make the position consistent across conditions. Subjects crossed their arms over the chest and placed the fingertips on the shoulders. This posture was selected as a comfortable one that was relatively easy to reproduce across trials; in addition, this posture facilitated FDS voluntary contraction in a corresponding condition (see later) without changing the body position. Three tasks were performed in this study: 1) control trials; 2) voluntary sway (VS) task; and 3) quiet standing task.

The purpose of the control trials was to normalize the EMG signals. In these tasks, subjects stood with the arms crossed over the chest, and two instructions were provided: subjects were asked to co-contract the muscles in the lower limbs as hard as possible, or they were asked to press with their right hand on the left shoulder muscle as strongly as possible. Each task was performed once; the duration of each task was 5 s. To avoid fatigue, a 30-s rest period was provided between trials. The purpose of these trials was to make signals recorded in the main experimental series comparable across subjects.

VS task was performed to define muscle groups with parallel activation levels (M-modes, see the next section). In this task, the subjects swayed the whole body to ensure that the COP cursor moved between the two target lines shown on the monitor at 0.5 Hz, paced by a metronome. Note that swaying at the frequency of 0.5 Hz is typically performed about the ankle joints. In addition, an earlier study of Danna-dos-Santos et al. (2007) has shown that the composition of M-modes does not change significantly with changes in the sway frequency within a wide range, even when the participants use the hip joint to a large extent. The lines were set at 3 cm anterior and posterior from the preferred COP location. Visual feedback on the COP_AP and COP_ML coordinates was shown on the monitor, without visual feedback of muscle activation. The COP_AP and COP_ML were computed as follows (Winter, Prince, Frank, Powell, & Zabjek, 1996):

$$CO{P}_{AP}= -\frac{M_Y+\left(F_X\cdot d_Z\right)}{F_Z}$$ (1)

$$CO{P}_{ML}= \frac{M_X+\left(F_Y\cdot d_Z\right)}{F_Z}$$ (2)

where d_Z is the distance between the surface and the platform origin (0.043 m). Following three practice trials, each subject performed three trials with 30-s rest periods between trials; the duration of each trial was 35 s. Subjects were instructed to sway mainly about the ankle joints in the AP direction and keep full contact of both feet with the platform surface (cf. Danna-dos-Santos, Slomka, Zatsiorsky, & Latash, 2007). The participants were always watched by an experimenter to ensure compliance with this (relatively easy) task.

In the quiet standing trials, we used the M-mode data calculated using the M-modes from the VS task. M-modes (addressed in some studies as “muscle synergies”, Ivanenko, Poppele, & Lacquaniti, 2004; Ting & McKay, 2007) have been defined as muscle groups with parallel changes in activation levels. Their existence has been viewed as a means of alleviating the famous problem of motor redundancy (Bernstein, 1967) at the muscle activation level by using one neural control variable per muscle group (M-mode).

For each subject, M-modes were computed as in previous studies (Krishnamoorthy et al., 2003; Danna-Dos-Santos et al. 2007; Krishnan, Aruin, & Latash, 2011). The M-modes were classified into a “dorsal-M-mode” (with significantly loaded dorsal muscles; M1-mode), a “ventral-M-mode” (with significantly loaded ventral muscles; M2-mode), and a “mixed M-mode” (commonly this M-mode included significantly loaded RA; M3-mode). This step is described in more detail in the section on data processing. During quiet standing, subjects stood naturally on the force platform for 65 s with three levels of leg muscle co-activation: the natural level of muscle activation (No-C), twice the baseline muscle activation level (Low-C), and three times the baseline activation level (High-C). Separate 65-s trials were performed for each of the conditions. The baseline level was defined using muscle activation signals (rectified EMGs) averaged over 5 s when the subject stood quietly with the COP_AP shifted forward by 3 cm from the natural standing posture. The EMG signals were used to compute the baseline M2-mode magnitude. On average, across subjects, this value corresponded to about 5% of the muscle activation measured in the control trials.

In the Low-C and High-C conditions, subjects were given visual feedback on the M2-mode level. The subjects were asked to keep the bar at the corresponding target by contracting muscles in the lower limbs without trunk or arm motions. In the No-C condition, subjects were provided visual feedback on the FDS activity and instructed to keep the FDS activity at twice the level observed during quiet standing. The participants squeezed the left shoulder with the right hand without changing the body position to match the signal of the screen with the target; this natural action involved activation of many muscles, but feedback on FDS only was provided. This was done to ensure that the double-tasking conditions were met across all quiet standing trials. No visual feedback on COP location was provided. The order of co-activation conditions was randomized across subjects. To minimize fatigue, 1-min rest periods were provided between conditions.

Data processing

We used a customized MATLAB R2016a program (Mathworks Corp., Natick, MA, USA) for all calculations. Force signals were low-pass filtered at 10 Hz with a 4^th order, zero-lag Butterworth filter.

Defining M-modes

First, raw EMG signals were band-pass filtered (20–360 Hz) using a 4^th order, zero-lag Butterworth filter, rectified, and then filtered using a moving average 100-ms window. Each EMG signal was corrected for the baseline activity and normalized using the following equation (Krishnamoorthy et al., 2003; Klous, Mikulic, & Latash. 2011):

$${EMG}_{\mathit{\text{norm}}}=\mathrm{ }\frac{EMG-{EMG}_{qs}}{{EMG}_{MAX}}$$ (3)

where EMG_qs is the average filtered EMG within the {6 s; 10 s} interval in the No-C condition, and EMG_MAX is the maximal EMG activity across all VS tasks. In all conditions, EMG signals over the 5-s intervals in control trials were used for the normalization procedure. Prior to performing principal component analysis (PCA), we used EMG signals recorded in the VS tasks for normalization of the individual EMG values. To define visual feedback, EMG signals recorded in the control trials were used for normalization.

The rectified and normalized EMG signals from all muscles, except FDS, during the VS tasks were integrated over 50-ms time windows (IEMG_norm). Further, PCA using Varimax rotation and factor extraction was applied to the IEMG_norm correlation matrix (Krishnamoorthy et al., 2003). Based on the Kaiser criterion, we accepted three factors addressed further as M1-mode, M2-mode, and M3-mode.

M2-mode (which significantly loaded ventral muscles) was utilized for real-time visual feedback of the muscle activation level. For visual feedback, a moving average 250-ms window was applied to rectified EMG signals to produce a smooth envelope of M2-mode. The maximum values during control trials were used to normalize M2-mode and FDS EMG signals.

Analysis of zIP

COP_AP and the angle of the force vector (θ_F) signals from the quiet standing task were band-pass filtered using a 2^nd order, zero-lag Butterworth filter centered on frequencies from 0.6–6.0 Hz at 0.4 Hz increments. The θ_F was calculated as follows (Boehm, et al., 2019): ${\theta }_F=\mathrm{ }\mathrm{a}\mathrm{t}\mathrm{a}\mathrm{n}\left(\frac{F_X}{F_Z}\right)$, where the subscript X represents the anterior-posterior axis and Z represents the vertical axis. The first 5 s of the COP_AP and θ_F data were removed to eliminate filtering edge effects. The remaining data over 60 s were used to identify IP height (zIP).

To calculate zIP, we used principal component analysis (PCA) applied to the COP_AP versus θ_F correlation matrix. The eigenvector of the first principal component (EV₁) in each frequency band was evaluated, and zIP was defined as the slope of the EV₁. For further statistical analysis, zIP was averaged within three frequency intervals, < 1.5 Hz (Interval-1), 1.5–3.0 Hz (Interval-2), and > 3.0 Hz (Interval-3). These intervals were selected based on an earlier study quantifying zIP (Boehm et al., 2019). COM height was estimated as 56% of body height (Croskey, Dawson, Luessen, Marohn, & Wright, 1922). The average COM height across subjects was 96.5±6.7 cm.

Rambling (Rm) and trembling (Tr) analysis

To eliminate edge effects, the first 5 s of the COP data were removed from further analysis. The remaining data over 60 s in each trial were used to calculate Rm and Tr in the AP direction.

To identify instantaneous equilibrium points (IEPs; Zatsiorsky & Duarte, 1999, 2000), the instances when F_AP was zero were found as the midpoints between two consecutive samples when F_AP changes sign. Given the frequency of data acquisition, this corresponded to the maximal error of 1 ms. The IEP coordinates were interpolated with a cubic spline, which was defined as Rm(t). Tr(t) was defined as the difference between the COP(t) and Rm(t) trajectories. To minimize possible edge effects, we removed the first and the last one-second intervals of the remaining 60-s time series of Rm(t) and Tr(t) from further analysis over the remaining 58 s. The power spectrum analysis of Rm and Tr was also performed.

Statistics

We used SPSS to perform all statistical tests (IBM Corp., Armonk, NY, USA). Data are presented in the text and figures as means ± standard errors. To test whether muscle co-activation affected zIP (Hypothesis 2), a two-way repeated-measure ANOVA was performed to evaluate the effects of Coactivation (No-C, Low-C, and High-C) and Frequency-Interval (Interval-1, Interval-2, and Interval-3). For parametric statistics, the assumptions of normality and sphericity were checked. In cases of violations of normality, log-transformation to satisfy the normality assumptions was used, and in case of violations of sphericity, the Greenhouse-Geisser procedure was used. Pairwise contrasts with Bonferroni corrections were used to explore significant effects. The significance level was set at p = 0.05.

Results

During the voluntary sway tasks, all subjects showed similar grouping of muscles into muscle modes (M-modes) revealed by the PCA with rotation and factor extraction. Based on our criteria, we accepted three M-modes for each subject, which accounted, on average, for 74.4 ± 0.9% of the total variance in the muscle activation space. The first two M-modes showed consistent patterns with the dorsal muscles (such as SOL, GM, GL, BF, ST, and ES) loading significantly on one of those two M-modes and the ventral muscles (such as TA, RF, VM, VL, and sometimes RA) – on the other M-mode. The third M-mode was variable across subjects, commonly with RA significantly loaded. Averaged across subjects loading factors for the three M-modes are presented in Table 1.

Table 1.

M-mode loading factors

	M1-mode	M2-mode	M3-mode
SOL	0.734 (0.099)	−.150 (0.112)	−0.022 (0.040)
GL	0.797 (0.052)	−0.126 (0.107)	0.017 (0.033)
GM	0.821 (0.024)	−0.174 (0.082)	0.030 (0.046)
BF	0.701 (0.080)	0.001 (0.122)	0.138 (0.062)
ST	0.644 (0.087)	0.076 (0.125)	0.062 (0.081)
TA	−0.485 (0.079)	0.549 (0.093)	0.005 (0.059)
RF	−0.418 (0.063)	0.710 (0.097)	0.024 (0.036)
VL	−0.306 (0.063)	0.757 (0.095)	0.007 (0.041)
VM	−0.234 (0.068)	0.749 (0.094)	0.008 (0.036)
TFL	−0.118 (0.082)	0.385 (0.078)	0.164 (0.127)
ESL	0.667 (0.094)	−0.142 (0.065)	0.234 (0.129)
EST	0.651 (0.093)	−0.114 (0.062)	0.241 (0.128)
RA	−0.007 (0.048)	0.165 (0.078)	0.513 (0.157)

Averaged loading factors across subjects are shown for the individual muscles. The values in parentheses represent standard errors. Significant loadings (>0.5) are shown in bold. Note the consistent patterns with dorsal muscles significantly loaded in the M1-mode and ventral muscles significantly loaded in the M2-mode. There was no significant loading for TFL because it was not consistently included in a specific mode across subjects. TA – tibialis anterior; SOL – soleus;l GL and GM – lateral and medial heads of gastrocnemius; BF – biceps femoris; SM – semitendinosus; RF – rectus femoris; VL and VM – lateral and medial vastii; TFL – tensor facsia latae; ESL and EST – lumbar and thoracic portions of erector spinae; and RA – rectus abdominis.

Computation of the zIP across frequency bands showed a consistent pattern involving a drop in zIP from values comparable to the subject’s height at low frequencies to about 50% of CM height for higher frequencies (the solid line in Fig. 1A). The zIP(ƒ) characteristic crossed the COM height at about 1.5 Hz. When the subjects stood with additional contraction of the leg/trunk muscles, the zIP(ƒ) line shifted to the right (or, equivalently, upwards). This is illustrated for the High-C condition in Fig. 1A with the dashed line. For statistical comparisons, the data were analyzed within three frequency intervals shown in Fig. 1A with vertical dashed lines (see also Methods). Two-way ANOVA confirmed significant effects of Coactivation (F_{[2, 10]} = 13.6; p < 0.001) and Frequency-Interval (F_{[2, 10]} = 1645.3; p < 0.001) without an interaction. zIP values in all conditions decreased with increasing frequency. zIP values in the High-C and Low-C conditions were significantly greater than in the No-C condition,

Figure 1.

Height of the intersection point of the ground reaction force vectors (zIP). Panel A: Time profiles of zIP across frequency bands. Averaged data across subjects are shown with standard error shades for the No-C and High-C conditions. Interval-1, Interval-2, and Interval-3 are defined as < 1.5 Hz, 1.5 – 3.0 Hz, and > 3.0 Hz.

Panel B: zIP for the No-C, Low-C, and High-C conditions. Averaged data across subjects are shown with standard error bars. Statistically significant differences are shown with one star (p < 0.05).

No-C -natural level of muscle activation; Low-C – low muscle co-activation level; and High-C – high muscle co-activation level.

The Rm–Tr decomposition of COP(t) during quiet standing trials showed that the average Rm power peaked at about 0.02 Hz and dropped below 10% of its peak at about ƒ = 0.3 Hz. Average Tr power peaked close to 0.60 Hz and covered a broader frequency range. At frequencies analyzed in our study, both Rm and Tr power dropped exponentially with frequency and had comparable magnitudes (our analysis was performed at relatively high frequencies where the powers of Rm and Tr were comparable). Figure 2 illustrates the average frequency profile of Rm and Tr across subjects for the No-C condition. Shear force in the anterior-posterior direction (F_X) correlated strongly with Tr but not with Rm. Across subjects, the median correlation coefficient (R) between F_X and Rm was 0.19 in the No-C condition (quartiles 0.14 – 0.22), 0.20 in the Low-C condition (quartiles 0.15 – 0.24), and 0.19 in the High-C condition (quartiles 0.17 – 0.28), whereas R was much higher for the F_X vs. Tr correlation (median 0.88; quartiles 0.86 – 0.89 in No-C condition, median 0.88; quartiles 0.85 – 0.91 in Low–C condition, and median 0.89; quartiles 0.82 – 0.90 in High–C condition).

Figure 2.

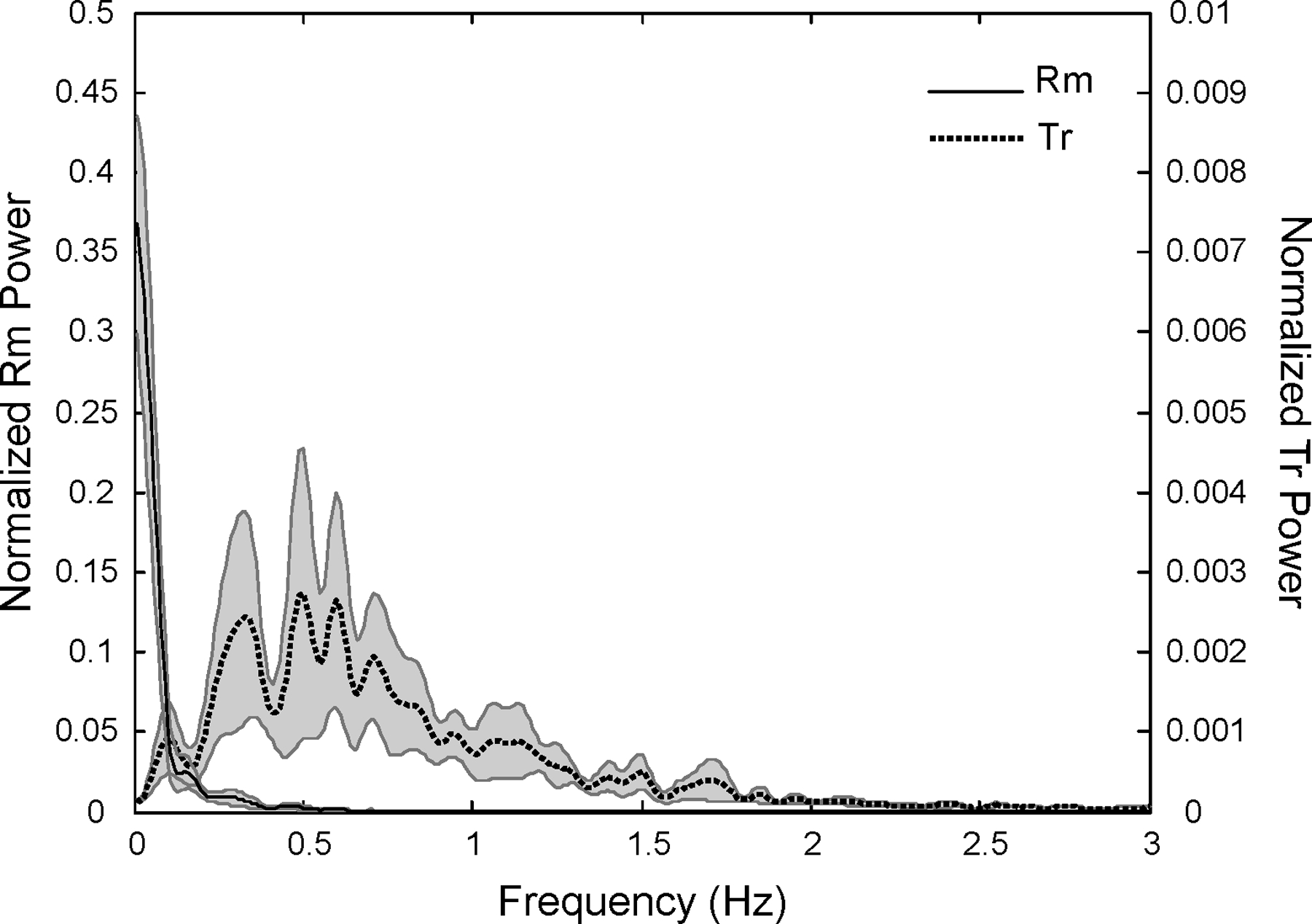
Frequency profiles of rambling (Rm; solid line) and trembling (Tr; dashed line) in the No-C condition. Averaged data across subjects are shown with standard error shades. For abbreviations, see the caption for Fig. 1.

There was a significant correlation between zIP and Tr power across frequencies. For this analysis, power magnitudes were averaged over 0.4-Hz bins from 0.6–6.0 Hz, and log-transformed to satisfy the normality assumption. The median correlation coefficient (R) was 0.91 in the No-C condition, 0.93 in the Low-C condition, and 0.91 in the High-C condition. Similar analysis performed for the correlation between zIP and Rm showed higher correlation coefficients: The median R was 0.97 in the No-C condition, 0.97 in Low-C condition, and 0.98 in High-C condition. The R values for the Tr analysis were significantly lower than for the Rm analysis (p < 0.05; Wilcoxon’s signed-rank test).

Discussion

Both specific hypotheses have been supported in the experiment. Indeed, there were strong correlations between the Tr power and zIP across frequencies of analysis as predicted by Hypothesis-1, while weaker correlations were seen between Rm power and zIP. When the subjects produced increased levels of muscle co-activation, Tr showed an increase in its speed (cf. Yamagata et al., 2019a) while zIP shifted toward higher values (for comparable frequency ranges) or to higher frequencies (for comparable zIP values), as predicted by Hypothesis-2.

Our secondary analyses have confirmed some of the facts from earlier publications. These include significant correlations between Tr and shear force magnitude in the absence of comparable correlations between shear forces and Rm (cf. Zatsiorsky & Duarte, 2000). We would like to emphasize that our first hypothesis considers not only the correlation between Tr and shear force but more specifically how the slope of that correlation (zIP) varies with frequency. The authors are unaware of any other reports of that frequency dependence (except the cited Boehm et al., 2019). The observation of Zatsiorsky and Duarte (2000) that the Tr and shear force have similar power spectra is not sufficient to indicate that the slope varies with frequency (and co-activation level).

We also confirmed the typical frequency ranges of Rm and Tr (cf. Zatsiorsky & Duarte, 1999, 2000) and the frequency-dependence of zIP (Boehm et al., 2019). There are differences in the power spectra between our findings and those by Zatsiorsky and Duarte, in particular the lack of a clear peak of Rm, which could be due to our experimental conditions with visual feedback on EMG signals. Note that using such feedback can lead to large-power very slow components of Rm, addressed as “COP drift” (Yamagata, Popow, & Latash 2019).

In the rest of the Discussion, we use these observations to support and develop the idea of postural control with RCs at the whole-body and joint configuration levels. In particular, we link this idea to the concepts of multi-muscle synergies (d’Avella et al. 2003; d’Avella & Bizzi, 2005; Ivanenko et al., 2004; Ting & McKay, 2007) or muscle modes (M-modes, Krishnamoorthy et al. 2003) and to the idea of control with a few scalable primitives (cf. Kargo et al., 2010) formed by RCs defined in the joint configuration space. Our long-term goal is to merge the data from studies of posture in spaces of kinetic, kinematic, and muscle activation variables into a single coherent hierarchical control scheme with RCs.

Referent joint configurations as the basis for control primitives

The idea of the neural control of movement with spatial referent coordinates (RCs) for the effectors has been developed based on the classical equilibrium-point hypothesis (Feldman, 1986, 2015). This idea is a specific realization of the physical approach to motor control, which searches for laws of nature that define properties of biological movements (Latash, 2016, 2017). Within this approach, RCs are viewed as parameters of relevant laws of nature, while variables measured in typical experiments, kinetic, kinematic, and electromyographic, emerge as consequences of interactions within the body and between the body and the environment.

The idea of control with RCs can be applied at different levels of analysis, from whole-body to individual muscle actions. During whole-body actions (such as quiet standing), RC at the task level is relatively low-dimensional and its conversion into action mechanics involves a sequence of few-to-many transformations, to the higher-dimensional joint configuration level RCs (RC_J), and to the very high-dimensional muscle level (Latash, 2010). At this time, only at the muscle level, RCs have a physiological interpretation; they are equivalent to stretch reflex thresholds, which are in turn associated with subthreshold depolarization of the alpha-motoneuronal pools (Feldman, 2015). Neuronal mechanisms of higher-level RCs remain unknown, although important progress has been made recently (Feldman, 2019).

In this study, we focus on joint-level RCs. For a given body configuration, RC_J changes result in the generation of joint torques, which, in the first approximation, are linearly related to the deviations between individual joint RCs and their actual positions. This transformation involves a stiffness-like coefficient k (addressed as apparent stiffness, Latash & Zatsiorsky, 1993). During quiet standing, muscle activation levels are typically low, and the amount of agonist-antagonist co-activation is also low (e.g., Aruin & Latash, 1995), although recently, changes in the ankle joint stiffness have been reported during natural sway (Amiri & Kearney, 2019) suggesting modifications in the amount of agonist-antagonist co-activation. These observations allow assuming that individual joint k values are relatively constant. Within this approximation, scaling of joint moments is a direct reflection of scaling of RCs for the individual joints. The observation of a single point of intersection of the force vectors within a narrow range of frequencies of force change suggests proportional changes in the joint moments (Gruben & Boehm, 2012). Given that joint displacements during natural postural sway in healthy persons are relatively small, proportional joint moment changes imply proportional changes in the respective RCs along a line in the joint configuration space. So, for a specific narrow range of frequencies, joint RC change may be viewed as resulting from a single template scaled with a time-varying coefficient. We will address such a hypothetical RC_J pattern as an RC_J-primitive.

The idea of primitives (similar concepts have been addressed as basis functions, synergies, principal components, factors, strategies, modes, etc., Bizzi et al., 1995; d’Avella et al., 2003; Kargo et al., 2010) assumes that the brain combines the available numerous elemental variables (degrees of freedom) into groups and then uses a single variable per group to modulate its involvement into action. Until recently, this idea was applied to groups of variables measured in the periphery such as muscle activations, joint rotations, joint torques, etc. Recently, the idea of primitives has been used to quantify and interpret activation patterns of neuronal populations in brain structures including the primary motor cortex (Holdefer & Miller, 2002; Overduin, d’Avella, Roh, Carmena, & Bizzi, 2015; Shay, Chen, Garcea, & Mahon, 2019). Here we generalize this idea to hypothetical control variables, RCs, representing parameters of physical laws leading to actions.

By definition, a particular RC_J-primitive produces a specific zIP value observed within a narrow frequency range (Boehm et al., 2019), which means that COP location and shear force along the same axis are tightly correlated to keep zIP constant. This prediction has been confirmed in both earlier experiments exploring Tr (Zatsiorsky & Duarte, 2000) and our current data.

Kinetic and muscle activation consequences of control with RC-primitives

Using a time-varying single RC_J-primitive to control vertical posture is expected to produce proportional changes in joint moments of force, which naturally leads to intersection of forces in a point at a specific height (Boehm et al., 2019). (Note that we assume here planar analysis and no major changes in posture and in the individual joint apparent stiffness magnitudes.) This prediction is supported by the data, whereas specific zIP values are observed within relatively narrow frequency bands. The consistent major changes in the height of zIP with frequency suggest that the controller uses more than one RC_J-primitive, distinct primitives for different frequencies, or combines them, e.g., using a linear combination, in a frequency-dependent manner. As a simplest case, we can assume that two RC_J-primitives are used. One of them is typical of actions at relatively low frequencies (under 1.5 Hz; zIP > COM height), while the other one is typical for higher frequencies (over 1.5 Hz; zIP < COM height; see the top panel in Fig. 1). Linear combination of these two primitives could produce the intervening heights.

This assumption is compatible with earlier suggestions of “simultaneously co-existing excitable modes” (Alexandrov, Frolov, & Massion, 2001; Alexandrov, Frolov, Horak, Carlson-Kuhta, & Park, 2005; Creath. Kiemel, Horak, Peterka, & Jeka, 2005) that are both involved during quiet stance tasks. In particular, Creath and colleagues (2005) described two modes in the joint angle space similar to the earlier introduced notions of ankle strategy and hip strategy (Horak & Nashner, 1986). The former was supposed to dominate at frequencies under 1 Hz while the latter – at higher frequencies. This view may also be seen as an alternative to the idea of competing coordination modes (cf. Bardy, Marin, Stoffregen, & Bootsma, 1999; Bardy, Oullier, Bootsma, & Stoffregen, 2002). Note, however, that, in contrast to the mentioned earlier studies, our assumption is formulated at the level of control variables, which are reflected in consistent patterns at the level of joint kinetics and kinematics.

Note also that using a single RC_J-primitive is expected to lead to proportional changes in activation levels of muscles crossing the main joints along the vertical body axis since muscle activation, similarly to joint torque, is a monotonic function of the difference between the actual and referent muscle length (Feldman, 2015). This leads to a prediction of muscle groups with proportional scaling of activation levels, which has been supported in many studies of postural tasks (Krishnamoorthy et al., 2003; Ting & McKay, 2007; Danna-dos-Santos et al., 2007; Klous et al., 2011). Such groups have been referred to as muscle synergies or M-modes, which is our preferred term to avoid confusion with performance-stabilizing synergies (cf. Latash & Zatsiorsky, 2016). In the absence of major muscle co-activation, a single RC_J-primitive may lead to two M-modes acting in opposite directions: This is a typical finding in studies of postural tasks, which are associated with a “push back” and “push forward” M-modes (Krishnamoorthy et al., 2003; Danna-dos-Santos et al., 2007). However, the present observation of a range of IP heights (zIP) suggest the necessity of multiple RC_J primitives.

Most of the cited studies explored tasks involving relatively slow whole-body actions and associated changes in the shear forces. When a standing person is required to produce a very quick pulse of the shear force in the anterior-posterior direction into a target, a different pattern of M-modes is observed suggesting a different RC_J-primitive (Robert, Zatsiorsky, & Latash, 2008). The patterns of the two sets of RC_J-primitives (e.g., Fig. 12 in Robert et al., 2008) suggest similarity of those patterns to the aforementioned notions of ankle strategy and hip strategy. In particular, the more commonly described pattern typical of slower actions is similar to the ankle strategy, while the faster RC_J-primitive resembles the hip strategy. As described in an earlier paper (Boehm et al., 2019), zIP is related to the relative body segment accelerations produced such that, when zIP > COM height, predominance of ankle acceleration leads to a kinematic profile typical of the ankle strategy, whereas when zIP < COM height, predominance of hip acceleration leads to a pattern resembling the hip strategy.

The patterns of the two RC_J-primitives are also similar to the patterns of two out of the three “eigenmovements” defined as joint motion patterns along new coordinates representing linear joint angle combinations that allow decoupling the equations of motion along each of the new coordinates (Alexandrov et al., 2001). The third eigenmovement involves action resembling squatting, which is probably not typical of natural quiet standing.

Note that Tr accounts for a relatively small fraction of the total power of the COP(t) signal (Zatsiorsky & Duarte, 2000). This is particularly true for the portion of the Tr signal corresponding to higher frequencies, e.g. > 1.5 Hz. So, most of the postural sway corresponds to a single RC_J-primitive typical of lower frequencies, i.e. the one resembling the ankle strategy (cf. Horak & Nashner, 1986).

Effects of agonist-antagonist co-activation on postural sway

Agonist-antagonist co-activation is a common phenomenon across effectors and tasks (reviewed in Smith, 1981; Latash, 2018). Most commonly, co-activation has been discussed as a means of increasing apparent stiffness of the joints crossed by the muscles with possible effects on action speed and joint stability (Frysinger, Bourbonnais, Kalaska, & Smith, 1984; Hirokawa, Solomonow, Luo, Lu, & D’Ambrosia, 1991; Nielsen & Kagamihara, 1992). An increase in apparent stiffness is expected to lead to an increase in the natural frequency of the effector. This may be the primary reason for an increase in the speed of Tr observed in our experiment. The increase in Rm speed reported earlier (Yamagata et al., 2019a) may be viewed as adaptive to the increased speed of Tr. Indeed, consider the aforementioned example of a pole balanced on the fingertip (see the Introduction). If the pole is short and its natural frequency is high, faster finger motion (analogous to Rm) is needed to keep it vertical. For a longer pole with lower natural frequency, the fingertip motion may be slower.

Given that the vertical force during quiet standing is nearly constant, the increase in Tr speed is naturally coupled to an increase in the horizontal force and the rate of change of the angle of the force vector with the vertical. This is due to the aforementioned correlation between Tr and shear force (Zatsiorsky & Duarte, 2000 and our data). This is expected to lead to faster characteristic frequencies, ƒ, for a given zIP value, i.e., a shift of the zIP(ƒ) curve toward higher frequencies. Given the monotonic drop of zIP with ƒ (Boehm et al., 2019), a shift of this curve toward higher frequencies is equivalent to its shift upwards - toward higher zIP for a given frequency bin. This was indeed observed in the experiment (Fig. 1, top panel).

Overall, our results, such as an increase in the speed of Tr and Rm, do not support the idea that increasing agonist-antagonist co-activation improves stability of vertical posture (see also Yamagata et al., 2019a). In addition, as described briefly in a previous paper (Boehm, Nichols, & Gruben, 2019) the height of the zIP is related to the relative body segment accelerations produced. The multi-segmented body has various modes with which it can deviate from vertical (e.g., fall), coordinated muscle activation must be tuned to restore balance by acting along those modes (cf. the concept of “acting along the most nimble direction”, Akulin, Carlier, Solnik, & Latash 2019). Thus, to be able to resist a variety of disturbances, a controller must have a variety of responses corresponding to a range of zIP values, including values above and below the COM. With and without co-activation, the zIP curves we calculated, while distinct, indicate a similar range of zIP and thus similar range of disturbance rejection. One possible speculation that remains to be tested is that the co-activation curve may indicate improved disturbance rejection in the low frequency region and less robust rejection in the high frequency region. For some environmental conditions, that may be desirable while in others detrimental. Thus, we do not see signs of improved overall stability due to co-activation.

Note, however, that increased co-activation has been reported across a variety of subpopulations with impaired postural control (Arias, Espinosa, Robles-García, Cao, & Cudeiro, 2012; Boudreau & Falla, 2014; Hammond, Fitts, Kraft, Nutter, Trotter, & Robinson, 1988; Hirai, Miyazaki, Naritomi, et al., 2015; Keshner, Allum, & Pfaltz, 1987; Mari, Serrao, Casali, et al. 2014; Rinaldi, Ranavolo, Conforto, et al. 2017) as well as in healthy persons in challenging conditions (Berger, Trippel, Discher, & Dietz, 1992; Shiratori & Latash, 2000; Krishnamoorthy et al. 2004; Asaka, Wang, Fukushima, & Latash, 2008; Asaka, Yahata K, Mani, & Wang, 2011). An alternative interpretation of this phenomenon has been suggested recently (Latash, 2018; Yamagata et al., 2019a). It is related to the concept of synergies stabilizing performance in abundant spaces of control variables (Ambike, Mattos, Zatsiorsky, & Latash, 2016; Reschechtko & Latash, 2017). According to this idea, non-zero co-activation provides abundance of control variables to stabilize performance. If co-activation is zero, changes in one of the basic commands (the so-called c-command, Feldman, 2015) have no effects on performance, and the control space becomes non-abundant or degenerate.

Concluding comments

Our study compared the results of two methods of analysis of postural sway, the Rm-Tr decomposition and the zIP analysis, and produced results compatible with the idea of whole-body control with a set of primitives associated with RCs in the joint configuration space. The findings included strong correlations between Tr and zIP and the shift of zIP toward higher frequencies when the subjects stood with increased muscle co-activation.