Abstract
The Fontan procedure is a common palliative surgery for congenital single ventricle patients. In silico and in vitro patient-specific modeling approaches are widely utilized to investigate potential improvements of Fontan hemodynamics that are related to long-term complications. However, there is a lack of consensus regarding the use of non-Newtonian rheology, warranting a systematic investigation. This study conducted in silico patientspecific modeling for twelve Fontan patients, using a Newtonian and a non-Newtonian model for each patient. Differences were quantified by examining clinically relevant metrics: indexed power loss (iPL), indexed viscous dissipation rate (iVDR), hepatic flow distribution (HFD), and regions of low wall shear stress (AWSS). Four sets of “non-Newtonian importance factors” were calculated to explore their effectiveness in identifying the non-Newtonian effect. No statistical differences were observed in iPL, iVDR, and HFD between the two models at the population-level, but large inter-patient variations exist. Significant differences were detected regarding AWSS, and its correlations with non-Newtonian importance factors were discussed. Additionally, simulations using the non-Newtonian model were computationally faster than those using the Newtonian model. These findings distinguish good importance factors for identifying non-Newtonian rheology and encourage the use of a non-Newtonian model to assess Fontan hemodynamics.
Keywords: Non-Newtonian Rheology, Patient-specific Modeling, Congenital Heart Defects, Computational Fluid Dynamics, Fontan Hemodynamics, non-Newtonian model
2. INTRODUCTION
The Fontan procedure is a common palliation for patients suffering from congenital single ventricle defects. This procedure is a staged surgery that culminates in a total cavopulmonary connection (TCPC), rerouting venous return from the subpulmonary ventricle to the pulmonary arteries. The TCPC separates oxygenated and de-oxygenated blood flow and, in general, results in favorable short-term outcomes. However, long-term complications such as limited exercise capacity, pulmonary arteriovenous malformations (PAVMs), and underdeveloped pulmonary vessels affect Fontan patients. Previous studies have explored the relationship between these complications and compromised Fontan hemodynamics while emphasizing the importance of understanding the hemodynamics to improve surgical techniques and enhance outcomes for individual surgeries.
Both in silico and in vitro studies have been conducted to assess hemodynamic metrics in the TCPC. Despite being characterized as a non-Newtonian fluid, several studies assume that blood is a Newtonian fluid7, 14, 36, 38, 39. This assumption is generally acceptable for Fontan studies involving prevalent high shear rates induced by high velocities44, such as pump support of TCPC circulation35 or TCPC hemodynamics under exercise conditions3, 33. However, it is well known that red blood cells induce nonNewtonian rheology30. In the size of the vessels comprising a TCPC, this non-Newtonian rheology occurs for two primary reasons: (1) red cell aggregation at low shear rate regimes (shear-thinning effect), determining a decrement of the apparent viscosity at high shear rate regimes; (2) red-cell deformability and intercellular collisions1, 49. The latter effect generally requires substantial modification of the mathematical model, with an additional set of differential equations, e.g., Oldroyd-B models1. The shear-thinning effect, which is generally more important, can be addressed by Generalized-Newton models, which express the effective viscosity as a monotonically decreasing function of the shear rate. Therefore, many previous publications have used Generalized-Newton models to incorporate the shear-thinning nature of blood into cardiovascular modeling. Some recent Fontan studies have begun to utilize Generalized-Newton models to simulate blood in Fontan patients, but the coefficients of these models were derived from the healthy population7, 13. While Chitra et al.12 attempted to examine the non-Newtonian effect on Fontan simulations, their findings were based on an idealized two-dimensional model and flow conditions. Recently, Cheng et al.11 conducted hemorheological investigations in a cohort of Fontan patients. Later, the same group experimentally demonstrated the non-Newtonian impact on three-dimensional (3D) modeling of Fontan hemodynamics10. However, considering the importance of patient-specific modeling for Fontan hemodynamics15, 31, their findings were limited by the use of an idealized Fontan anatomy (number of patients= 1) and flow conditions. Therefore, in this study, the effects of using a non-Newtonian model for Fontan hemodynamic assessment were systematically investigated using a larger number of patient-specific models.
Twelve Fontan patients were included in this study. Both patient-specific anatomy and blood flow data were acquired from medical images. For each patient, 3D computational fluid dynamic (CFD) simulations were performed using both Newtonian and non-Newtonian models to describe the properties of blood10, 11. The Generalized-Newton shear-thinning model was derived from the viscosity curve for a typical Fontan patient, and its effect was quantified in terms of clinically relevant TCPC hemodynamic metrics: indexed power loss (iPL), indexed viscous dissipation rate (iVDR), hepatic flow distribution (HFD), and regions of low wall shear stress (AWSS).
3. MATERIALS AND METHODS
3.1. Patient Information
The patients included in this study were retrospectively selected from the Georgia Tech Cardiovascular Fluid Mechanics Fontan Database. Special efforts were made to select datasets that included a range of cardiac outputs and flow pulsatility. Informed consent was obtained, and the protocol was approved by the Georgia Institute of Technology and Children’s Hospital of Philadelphia institutional review boards (IRB: H05236).
3.2. Anatomical Reconstruction, Velocity Segmentation, and Analysis
Both cardiac magnetic resonance imaging (MRI) and phase-contrast MRI (PC-MRI) were acquired at the Children’s Hospital of Philadelphia. 3D patient-specific anatomies were reconstructed from cardiac MRI using 3D Slicer (http://www.slicer.org)18. Then, the anatomies were imported to Geomagic Studio (Geomagic Inc., NC, USA) for surface mesh generation. Vascular Modeling Toolkit (VMTK, Orobix, Bergamo, Italy) was utilized to obtain anatomical characteristics of all TCPCs, including the mean diameter of each vessel, as well as offsets and angles between vessels. To eliminate the effect of interpatient variations, vessel diameters and offsets were normalized by the square root of patient body surface area (BSA) and mean IVC diameter of each patient, respectively.
Blood flow velocities were extracted from PC-MRI using Medviso Segment (http://segment.heiberg.se)20. The flow pulsatility (PI) of each vessel was calculated as
| (1) |
where Qavg, Qmin, and Qmax were the average, minimum and maximum flow rates across the vessel over one cardiac cycle, respectively. A total weighted pulsatility index (wPI) was obtained to quantify the overall flow pulsatility level of the individual Fontan patient.
| (2) |
3.3. CFD Model Solution
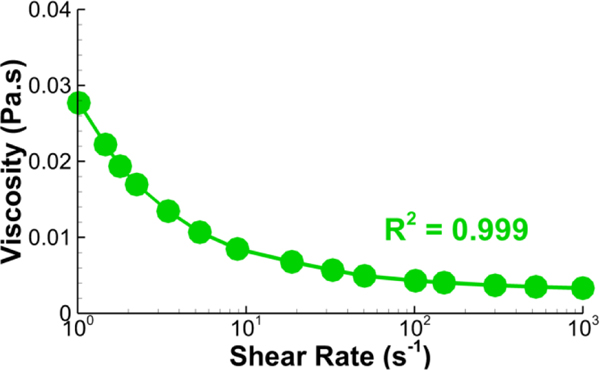
Transient CFD simulations were conducted using ANSYS Fluent (v17.0, ANSYS Inc., Canonsburg, PA). For simulations using the Newtonian fluid assumption, the dynamic viscosity of blood, μ∞ was set to be 3.3×10−3 Pa-s, which is in the physiological range for human blood. With standard notation, we denoted the velocity and pressure of blood by u and p respectively and the rate-of-deformation tensor by The shear rate is defined here as the second invariant of the tensor For the non-Newtonian fluid simulations, the dynamic viscosity was modeled with a Carreau model expressed in Eq. 3 and reported in Fig. 1 with viscosity and the following coefficients: time constant λ = 3.34 (s), power-law index n = 0.3025, zero shear viscosity η0 = 0.06109 (kg/m-s), and infinite shear viscosity η∞= 0.0033 (kg/m-s). It is worth noting that this rheological model may need to be changed when modeling pediatric versus adult patients19. The model from Cheng et al.11 was experimentally measured from Fontan patients with similar age (10.8±3.9 years), indicating the validity of using this model in simulations of our patient-cohort.
Figure 1.
The Carreau model that fits the relation between viscosity and shear rate. The solid line is the Carreau model used in this study, and the circles are from Cheng et al.11.
| (3) |
The vessel walls were assumed to be rigid, and blood had a density of ρ = 1060 kg-m−3. The polyhedral mesh with near-wall refinements was generated with the ANSYS Meshing module. As suggested by Ref.43, the mesh-independence study was conducted with two mesh sizes: Davg/50 and Davg/62.5, where Davg was the average diameter of all TCPC inlets and outlets. The discrepancies between the use of these two mesh sizes were 0.4%, 4.6%, 1.5%, and 3.6% for power loss, viscous dissipation rate, hepatic flow distribution, and AWSS, respectively. It is, therefore, reasonable to conclude that the former mesh size (Davg/50) can provide acceptable grid-independent results. User-defined functions were utilized to apply patient-specific, time-varying flow rate waveforms to inlet boundaries and time-varying flow ratios derived from clinical measurement to outlet boundaries. All simulations were run for 10 cardiac cycles, and the last cycle was used to post-process results. Detailed meshing and numerical setups can be found in Wei et al. 46.
3.4. Hemodynamic Metrics
Clinically relevant hemodynamic metrics involved in this study include hepatic flow distribution (HFD), indexed power loss (iPL), indexed viscous dissipation rate (iVDR), and the low shear stress area of the TCPC wall (AWSS<T). HFD is related to the formation and progression of pulmonary arteriovenous malformations28, 32 and was quantified by calculating the percentage of flow from the inferior vena cava (IVC) to the left pulmonary artery (LPA). AWSS<τ, a parameter associated with thrombosis risk24, 48, was defined as the time-averaged percentage of TCPC surface area where the norm of the wall shear stress vector was lower than a specified threshold; this study chose T = 0.5, 1, and 2 dyne/cm2 as the thresholds. Previous studies have additionally reported correlations between power loss through the TCPC and a patient’s exercise intolerance29, 33 and quality of life25. The definition of iPL is:
| (4) |
where Qs,avg, is time-averaged systemic venous flow, and BSA is body surface area. PLavg is a time-averaged power loss, and the corresponding instantaneous value was calculated by:
| (5) |
where n is the outward normal unit vector and dA denotes the infinitesimal integration area.
The indexed viscous dissipation rate (iVDR) serves as a good surrogate of iPL45. These two metrics are highly correlated but not the same. Though very fine mesh resolutions were adopted, iVDR still contains ~5% discretization error, while iPL has only ~0.1%. iPL represents the true power loss through the TCPC, but it does not have spatial distribution. This study, therefore, calculates iVDR and plots its distribution contours for additional engineering and clinical insights. The definition of indexed viscous dissipation rate is:
| (6) |
The instantaneous value of VDR was calculated by using
| (7) |
where Vol represents the control volume, i.e. the TCPC volume.
The effects of using a non-Newtonian fluid model were quantified via discrepancies in the aforementioned hemodynamic metrics between the Newtonian and non-Newtonian fluid models: ΔiPL, ΔiVDR, ΔHFD, and ΔAWSS<T. The equations are:
| (8) |
| (9) |
| (10) |
| (11) |
where “NF” and “NNF” refer to the “Newtonian Fluid” and “non-Newtonian Fluid” models, respectively.
Four sets of non-Newtonian importance factors were calculated to quantify non-Newtonian effects. The first set includes VolSR<100/s and ASR<100/s, which are percentages of TCPC volume and wall surface with a shear rate (SR) lower than 100 s−1, respectively19, 26. The rationale of using these two non-Newtonian importance factors is that, in general, it is reasonable to consider blood as Newtonian fluid when the SR > 100 s-1. Another two sets are IL and IG, expressed in Eqs. (12) & (13), which adhere to their definitions from the previous literature5, 21:
| (12) |
| (13) |
where CV is the coefficient of variation and μeff was the effective viscosity obtained from the non-Newtonian blood model during the simulation. In Eq. (13), N is the number of cells in the TCPC volume for (IG)Vol or number of faces on the TCPC surface for (IG)S. It is worth noting that this index can be regarded as the percent quotient of the sampling standard deviation between the non-Newtonian and the Newtonian viscosities divided by √N. Although widely used in many previous studies8, 16, 21, IG is clearly dependent on the number of elements (either volumetric or superficial), therefore reducing its significance, as a uniform numerical refinement of the mesh would invariably induce a reduction of the index, not to mention the effects of non-uniform reticulations. Ideally, the normalization factor should be discarded to obtain a mesh-independent index. With an awareness of this defect, a fourth factor, IG*, was also calculated in this study. This factor was derived from recent studies4 and has not been widely used. However, it does not suffer from the limitations of the previous index. This study will compare the effects of these three importance factors.
| (14) |
3.5. Statistical Analysis
Statistical analyses were performed using IBM SPSS Statistics (IBM, Inc., Aramark, NY). The metrics were first analyzed for normality using the Shapiro-Wilk test. Depending on normality results, either a Paired T-test or a Wilcoxon-Sign test was used to determine differences between results from the NF and NNF models. Bivariate correlations were also analyzed using either Spearman’s or Pearson’s correlation test. P < 0.05 was considered as statistical significance.
4. RESULTS
4.1. Patient Cohort
Patient characteristics are shown in Table I. This cohort of patients possessed a wide range of outputs (range = [2.1, 6.3] L/min) and weighted pulsatility indices (range = [21.5, 117.1]%).
Table I.
Patient demographic and hemodynamic information (n = 12)
| Fontan Type (Intra-Cardiac:Extra-Cardiac) | 9:3 |
| Age (years) | 13.5±4.5 |
| BSA (m2) | 1.4±0.4 |
| Sex (Male/Female) | 5/7 |
| Cardiac Output (L/min) | 4.0±1.4 |
| wPI | 50.5±26.7% |
Data reported as mean ± standard deviation
4.2. Flow Fields
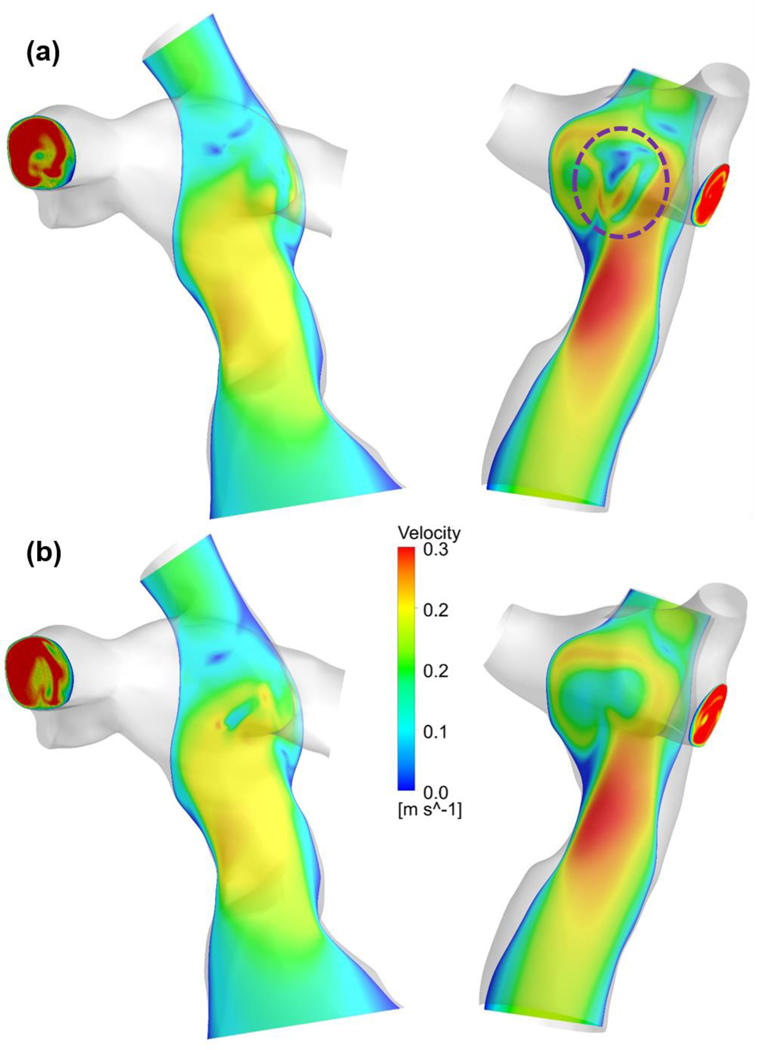
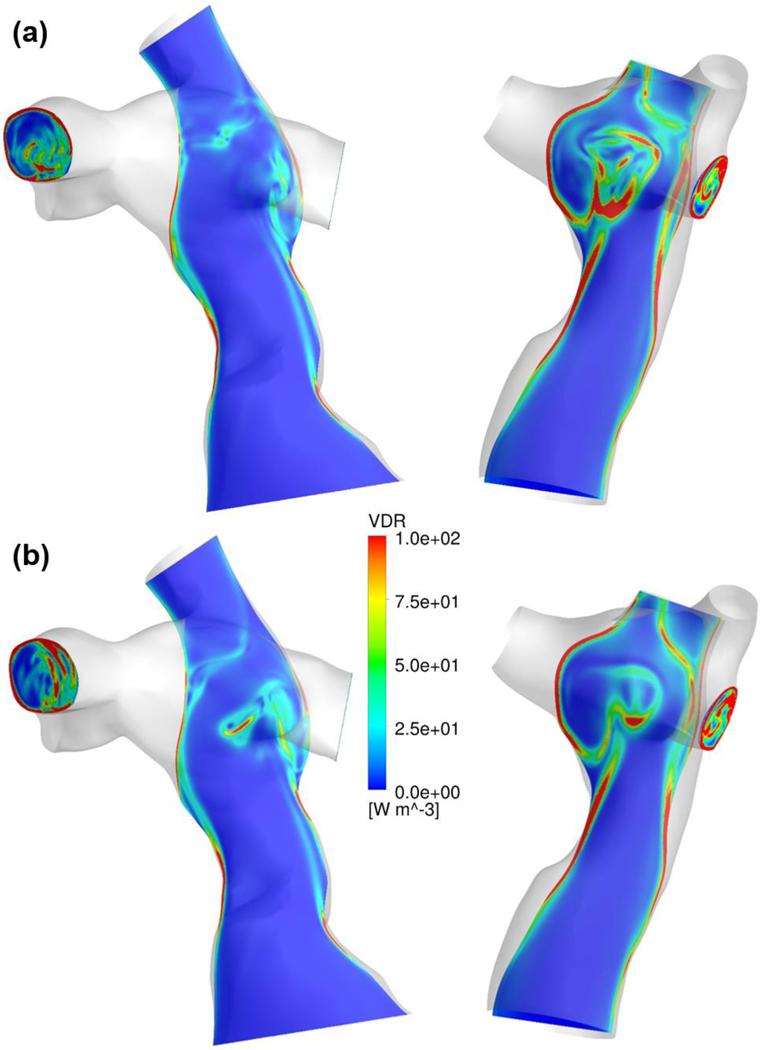
Figures 2 and 3 illustrate flow fields and VDR distributions of representative patients using the NF and NNF models. The primary flow patterns were similar between these two models, while visible differences in detailed flow structure can be observed. The flow contours demonstrate that using the NNF model diminishes flow unsteadiness, especially in the region where the IVC and superior vena cava (SVC) flow streams collide (the region circled by the dashed purple line in Figure 2).
Figure 2.
Comparison of velocity contours between the (a) NF and (b) NNF models for two representative patients. The dashed purple circle indicates the region where flow streams from the inferior and superior vena cava collide.
Figure 3.
Comparison of VDR contours between the (a) NF and (b) NNF models for two representative patients
4.3. Hemodynamic Metrics & Bland-Altman Plots
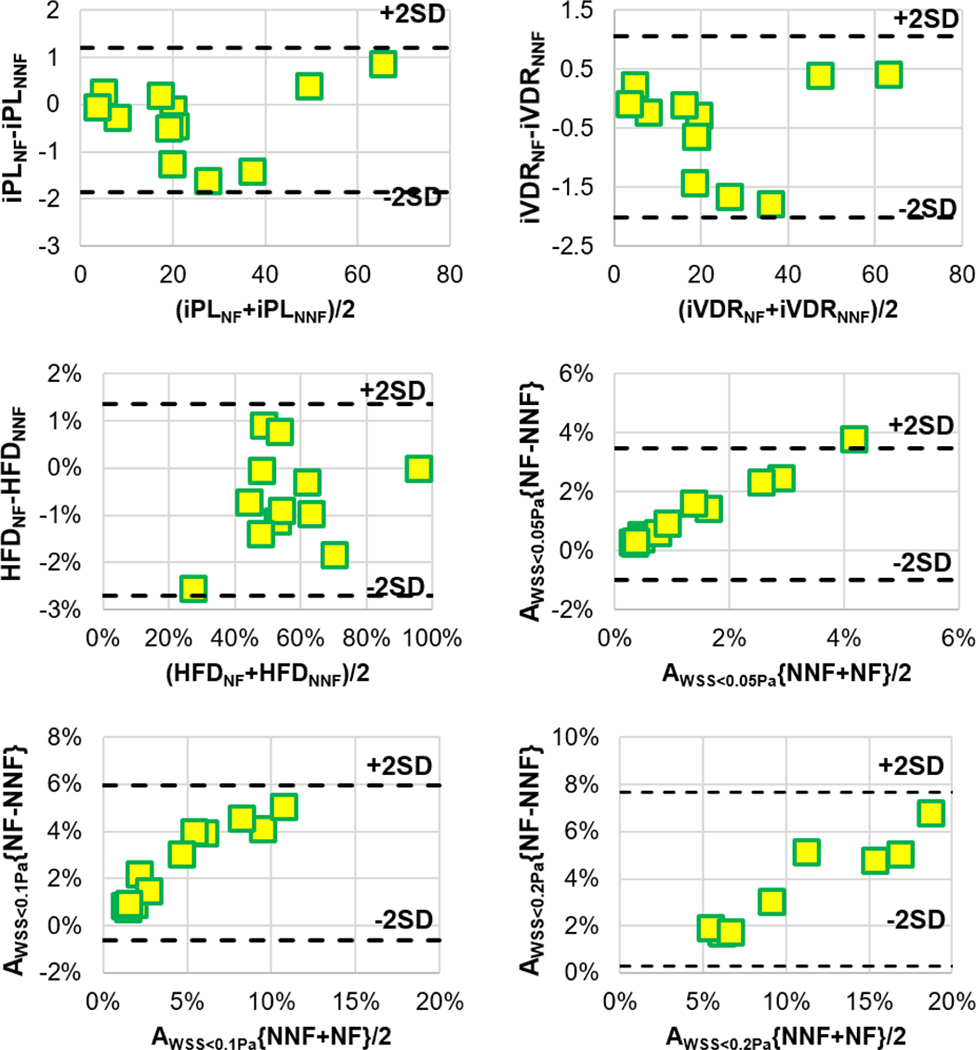
Table II tabulates results from statistical analyses comparing the clinically relevant hemodynamic metrics between simulations using the NF and NNF models. No statistical significances were observed in iPL and iVDR, and differences in these two metrics (ΔiPL = −2.1±3.4% and iVDR = −1.4±3.3%) do not have any clinical significance neither. Significant differences were observed for all metrics related to AWSS<T. Though significance is also seen in the differences between HFD values, the Bland-Altman plots in Figure 4 show that the maximum difference in HFD is ~3%, which would not result in any clinical difference
Table II.
Statistical results comparing hemodynamic metrics between the Newtonian and non-Newtonian blood models
| Newtonian | non-Newtonian | p-value | |
|---|---|---|---|
| iPL (×10−6) | 24.22±18.46 | 24.54±18.30 | 0.173 |
| iVDR (×10−6) | 23.13±17.71 | 23.60±17.63 | 0.055 |
| HFD | 55.3±16.7% | 56.0±16.4% | 0.041* |
| AWSS<0.05Pa | 2.0±1.8% | 0.72±0.69% | 0.002* |
| AWSS<0.1Pa | 6.0±4.1% | 3.3±2.6% | <0.001* |
| AWSS<0.2Pa | 15.5±7.8% | 11.6±6.2% | <0.001* |
p < 0.05
Figure 4.
Bland-Altman plots for clinically relevant hemodynamic metrics. AWSS<T{NF-NNF} indicates the result of AWSS<T from using the NF model subtracted by the respective value from using the NNF model. AWSS<T{NF+NNF} indicates the summation of AWSS<T from using the NF and the NNF models.
4.4. Discrepancies in Hemodynamic Metrics & Importance Factors
Statistical analysis was conducted to explore correlations between the four sets of non-Newtonian importance factors and discrepancies in the hemodynamic metrics. No correlation was found between the volumetric importance factors and ΔiPL, ΔiVDR, and ΔHFD, as shown in Table III.
Table III.
Bivariate correlation analyses between volumetric importance factors and ΔiPL, ΔiVDR, and ΔHFD
| Values | Bivariate Correlations (p-values) | |||
|---|---|---|---|---|
| ΔiPL | ΔiVDR | ΔHFD | ||
| VolSA<100/s | 73.2±10.2% | 0.381 | 0.691 | 0.625 |
| (IL)Vol | 1.60±0.18 | 0.781 | 0.996 | 0.344 |
| (IG)Vol | 0.037±0.013 | 0.882 | 0.416 | 0.476 |
| (IG*)Vol | 0.78±0.27 | 0.675 | 0.884 | 0.507 |
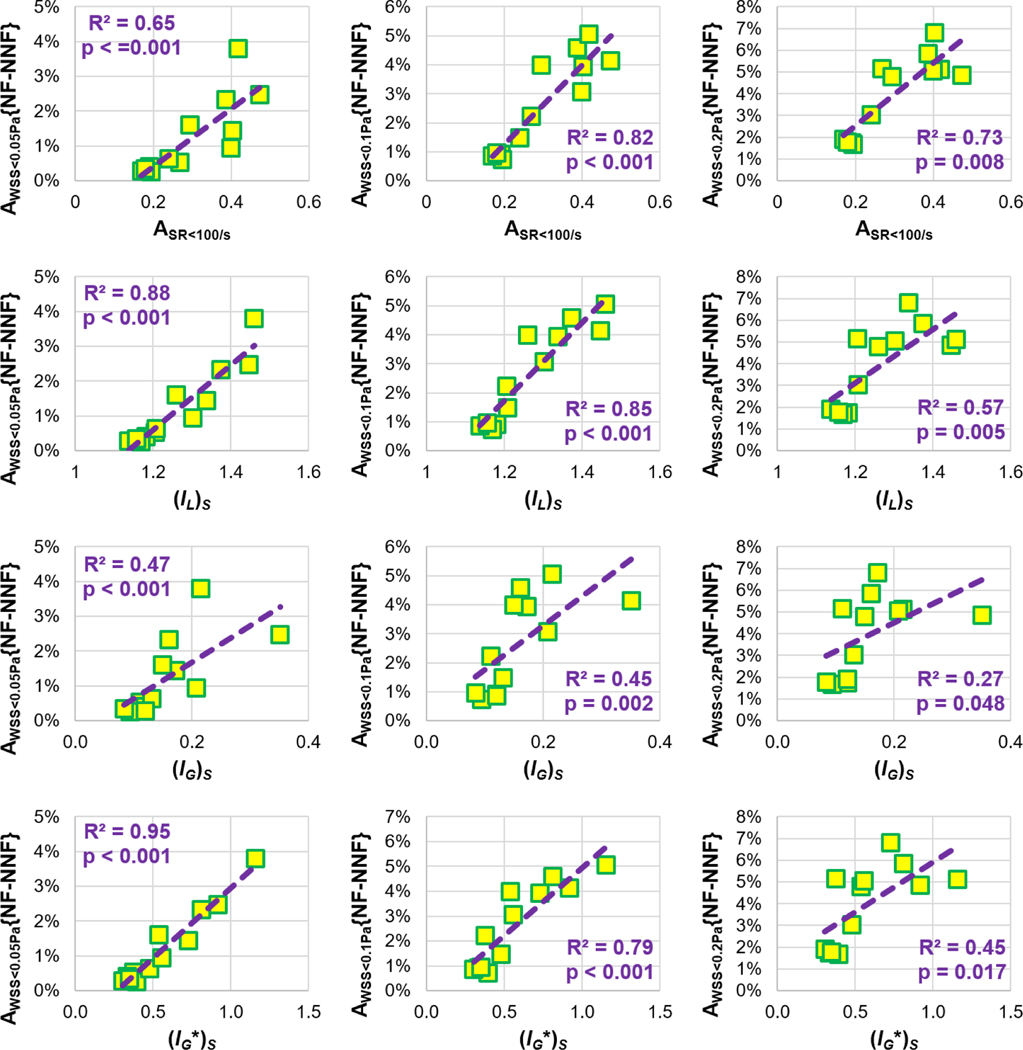
Figure 5 exhibits the statistical correlations between ΔAWSS<T and the area factors ASA<100/s (30.2±10.9%), (IL)S (1.27±0.11), (IG)S (0.16±0.07), and (IG*)S (0.58±0.27). It is worth noting that (IL)S for all cases was lower than 1.75, which was the cut-off value for significant non-Newtonian effects introduced in previous studies5, 21.
Figure 5.
Statistical correlations between areal importance factors and AWSS<T{NF-NNF}, which is the result of AWSS<T from using the NF model subtracted by its value from using the NNF model.
4.5. Relationship with Anatomical and Flow Characteristics
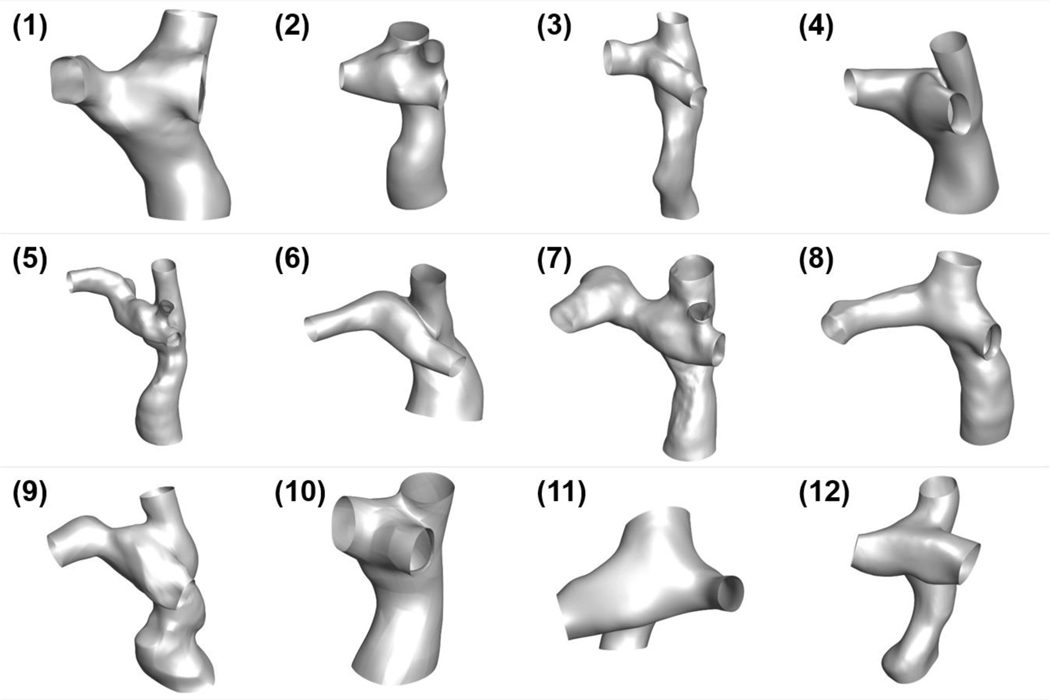
Figure 6 illustrates the anatomical reconstructions of the twelve patients included in this study. Visible differences can easily be observed in these anatomies. The anatomical characteristics are tabulated in Table IV. The same table summarizes statistical analyses that investigate the relationship between metrics representing non-Newtonian effects and patient-specific anatomical and flow characteristics. No statistical correlations were detected.
Figure 6.
Patient-specific 3D anatomies for all patients included in this study. The inferior vena cava and superior vena cava are located at the bottom and top of each anatomy, respectively. The left pulmonary artery is toward the left side, and the right pulmonary artery and right upper pulmonary artery are toward the right side of each model.
Table IV.
Summary of statistical analysis exploring the relationship between non-Newtonian effects on hemodynamics and anatomical and flow characteristics
| Value | Bivariate Correlations (p-values) | ||||||
|---|---|---|---|---|---|---|---|
| ΔiPL | ΔiVDR | ΔHFD | ΔAWSS<0.05Pa | ΔAWSS<0.1Pa | ΔAWSS<0.2Pa | ||
| Normalized Vessel Diameter (mm/m) | |||||||
| DIVC | 16.0±3.4 | 0.84 | 0.57 | 0.87 | 0.06 | 0.11 | 0.86 |
| DSVC | 13.30±1.52 | 0.44 | 0.71 | 0.64 | 0.48 | 0.63 | 0.83 |
| DLPA | 12.2±2.5 | 0.53 | 0.80 | 0.81 | 0.22 | 0.35 | 1.00 |
| DRPA | 10.9±2.1 | 0.48 | 0.75 | 0.90 | 0.11 | 0.12 | 0.42 |
| The angle between vessels (degrees) | |||||||
| IVC-LPA | 113.9±19.2 | 0.23 | 0.18 | 0.83 | 0.54 | 0.63 | 0.73 |
| IVC-RPA | 83.3±10.4 | 0.49 | 0.71 | 0.83 | 0.38 | 0.34 | 0.35 |
| SVC-LPA | 102.8±13.1 | 0.31 | 0.41 | 0.23 | 0.90 | 0.83 | 0.95 |
| SVC-RPA | 102.5±9.6 | 0.40 | 0.40 | 0.56 | 0.98 | 0.83 | 0.68 |
| IVC-SVC | 128.5±16.2 | 0.43 | 0.49 | 0.81 | 0.28 | 0.19 | 1.00 |
| LPA-RPA | 117.2±20.1 | 0.69 | 0.84 | 0.48 | 0.54 | 0.56 | 0.35 |
| Offsets between vessels (mm/mm) | |||||||
| IVC-SVC* | 0.13±0.18 | 0.12 | 0.13 | 0.79 | 0.13 | 0.14 | 0.14 |
| VC-PA** | 0.39±0.17 | 0.90 | 0.42 | 0.12 | 0.44 | 0.76 | 0.83 |
| Flow characteristics | |||||||
| CO (L/min) | 4.0±1.4 | 0.43 | 0.28 | 0.57 | 0.34 | 0.47 | 0.59 |
| wPI (%) | 50.5±26.7 | 0.72 | 0.44 | 0.98 | 0.53 | 0.78 | 0.37 |
IVC/SVC: inferior/superior vena cava; LPA/RPA: left/right pulmonary artery; CO: cardiac output.
Offset between IVC-SVC: the offset between IVC and SVC on the lateral direction (from left to right)
Offset between vena cava and pulmonary arteries (VC-PA): the offset between two centerlines from IVC to SVC and from LPA to RPA
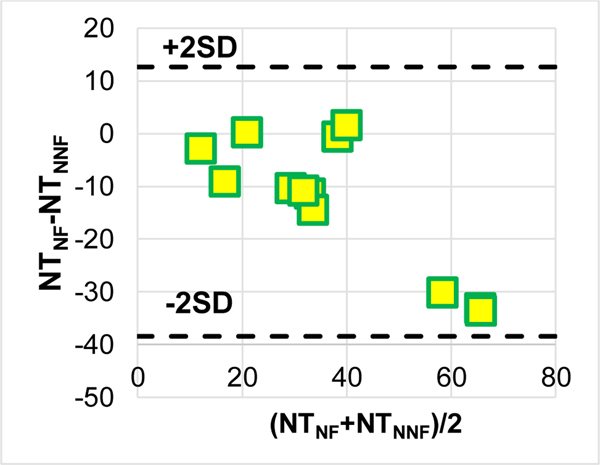
4.6. Computational Time
The Bland-Altman plots in Figure 7 show that using the non-Newtonian model requires significantly less computational time than using a Newtonian model (p = 0.006).
Figure 7.
A Bland-Altman plot for NT = “the number of computational time steps per hour”.
5. DISCUSSION
Many previous studies have found that the use of NNF models results in different flow fields when compared to the use of NF models, e.g. in the modeling of blood flow through axisymmetric stenosis22, an ascending aorta19, and large arteries2. Conversely, others have found that the differences between NF and NNF models were not significant, e.g. in the modeling of abdominal aortic aneurysm26, cerebral aneurysm9, and left ventricle16 hemodynamics. However, not many studies have investigated the impact of differences in clinical practice. One study of the middle cerebral artery, though exhibiting notable differences in WSS between NF and NNF models, concluded that the evaluation of these differences against a set of risk factors showed little to no significance6.
A common drawback for many previous studies examining the non-Newtonian effect was a lack of large patient cohorts. Most used only one to few cases and could not, therefore, generalize their findings. Moreover, the investigation of non-Newtonian effects on Fontan modeling is limited, and the only existing literature is based on single, idealized models either in silico27 or in vitro4. To overcome these limitations, the current study is the first to investigate the non-Newtonian (Generalized Newton) effects on patient-specific Fontan modeling using a larger patient cohort. It allows statistical analysis and extrapolation of the findings to clinical applications, such as Fontan surgical planning37.
This study observed that the NNF model resulted in altered flow details inside the TCPC and led to higher AWSS<T where T = 0.05, 0.1, and 0.2 Pa. This increase is intuitive and analogous to the Hagen-Poiseuille flow, where the NNF model increases WSS. The Hagen-Poiseuille law also indicates that an increase in flow rate amplifies the difference in WSS between the NF and NNF models, thereby enhancing power loss differences. Interestingly, the results of this study did not demonstrate a correlation between the cardiac output (CO) increase and the difference in power loss between the NF and NNF models, i.e. ΔiPL and ΔiVDR. The primary explanation for this finding is that flow collision between the IVC and SVC flow streams also contributes to power loss throughout the TCPC. The higher viscosity in the NNF model may diminish the unsteadiness of this flow collision and, therefore, reduce power loss. In the case of a higher CO, the flow in TCPC became more unsteady, and the power loss reduction stemming from the flow unsteadiness suppression could be more prominent. In other words, an increase in CO leads to (1) more difference in power loss because using the NNF model elevates WSS, and (2) less difference in power loss because it generates more flow unsteadiness for the NNF model to suppress. This compounding effect of CO on the difference in power loss results in the fact that this study observed no correlations between CO and differences in iPL and iVDR. Similarly, wPI has a compounding effect on the difference in power loss: the increase in wPI lessens the non-Newtonian effect on WSS5 while potentially enhancing the suppression of flow unsteadiness. Moreover, no correlation between anatomical characteristics and the difference in power loss may also be caused by similar compounding effects. For example, a decrease in vessel diameters leads to increasing WSS based on the Hagen-Poiseuille law but also results in more flow unsteadiness and corresponding suppression. In conclusion, both anatomical and flow characteristics have compounding effects on the differences in power loss between the NF and NNF models. Therefore, neither anatomical nor flow metrics obtain correlations with the differences in power loss. Also, the differences in power loss are not monotonic amongst all patients involved in this study.
This study showed no statistically significant difference in iPL and iVDR between the NF and NNF models. Also, the cohort-averaged ΔiPL and ΔiVDR indicate no clinical significance between using these two models at the population-level. These observations support the rationale of using NF models for previous large-cohort Fontan studies. However, remarkable patient-to-patient variations exist in these differences, which can reach 10% and may potentially be clinically significant. Consequently, the NNF model is recommended for future investigations, especially those substantially relying on absolute values of Fontan hemodynamic metrics, e.g. “future” Fontan surgical planning37. Clinical insights from previous Fontan surgical planning cases are still valid as these cases focused on comparing iPL and HFD between different surgical options37, 41, i.e. relative values of iPL and HFD. The non-Newtonian effect should not influence the relative ranking of iPL and/or HFD because it is much less than the effect of anatomy on iPL and HFD from different surgical options47. Furthermore, although a statistically significant difference was detected in HFD between the NF and NNF models, this difference does not have any clinical implications, as indicated by the Bland-Altman plot for HFD and the value of ΔHFD.
In addition, four sets of non-Newtonian importance factors were calculated, and their effectiveness in identifying the non-Newtonian effect was investigated. Volumetric importance factors, VolSR<100/s, (IL)Vol, (IG)Vol, and (IG*)Vol, did not exhibit any statistical correlations with the discrepancies in volumetric hemodynamic metrics between the NF and NNF models: ΔiPL, ΔiVDR, and ΔHFD. This lack of significant correlation can be primarily attributed to the insignificant differences in ΔiPL, iVDR, and HFD between the models. In contrast, statistical correlations were observed between area importance factors, ASA<100/s, (IL)S, (IG)S, and (IG*)S, and the discrepancies in AWSS<T (T = 0.05, 0.1, and 0.2 Pa). However, the correlation coefficients (R2 values) of (IG)S were markedly lower than those of other factors. Along with its mathematical defects described below Eq. (13), IG is not recommended as a factor in identifying the non-Newtonian effect due to its dependence on the mesh size.
It is intriguing that previous Fontan studies10, 12 witnessed a nearly two-fold increase in power loss between the use of NF and NNF fluids while, for all patients involved in this study, the difference in power loss between the NF and NNF models never exceeded 15%. This discrepancy between the current work and previous studies can be primarily attributed to the selection of outlet boundary conditions. The current study applied the same patient-specific flow conditions for outlet flow boundaries (at pulmonary arteries) in both simulations the NF and NNF models, isolating the differences observed between these two models. On the contrary, the change of flow distributions at pulmonary arteries presented in previous studies may contribute to the differences seen between the NF and NNF models/fluids observed in their studies, as demonstrated in Ref.17.
Furthermore, it was found that the simulations using the NNF model cost significantly less computational time than those using the NF model. This seems counterintuitive, since solving the NNF model theoretically adds a computational burden. However, there might be two primary reasons leading to the reduction of computational time observed in this study. First, though the NNF model introduces the non-linear expression regarding the viscosity in the numerical model, ANSYS Fluent treated it in a semi-implicit manner. This means that at a generic time step, the viscosity, in Eq. (1), was obtained by using the extrapolation of the shear rate at the current time step based on the previous time steps. Consequently, the calculation of the non-linear viscosity is simplified, and the computational burden of the calculation becomes minor. Secondly, the higher viscosity of the NNF model mathematically improves the algebraic properties of the linear systems and diminishes flow unsteadiness from a physical point of view, thus enhancing the convergence rate and computational rate. This effect may not be able to overpower the computational burden in simulations where low strain rates barely exist in the main flow stream, e.g. under exercise conditions. Another example is simulations of blood flow through the aorta: previous studies have shown that simulations using an NNF model were slower26. On the contrary, the collision caused by the flow streams from the IVC and superior vena cava (SVC) creates a low shear rate region inside the TCPC. In this scenario, the effect of diminishing flow unsteadiness by an NNF model may overcome the computational burden, and consequently, reduce the computational time in comparison with using an NF model. Similar findings were also reported in simulations of abdominal aortic aneurysms26.
The authors acknowledge the limited number of Fontan patients involved in this study. A large-cohort study is essential to examine the generalization of the findings, although the current study made special efforts to cover a range of possible cardiac outputs and flow pulsatilities. The rigid vessel wall assumption was utilized for all simulations, considering the negligible impact of compliant vessel walls on the hemodynamic metrics involved in this study23, 34. Moreover, this study investigated non-Newtonian effects on Fontan hemodynamic metrics under resting conditions but not exercise conditions. The primary change between resting and exercise conditions is increased cardiac output40, 42. No correlation was observed between cardiac output and the effect of the NNF model on simulated Fontan hemodynamic metrics; it is reasonable to believe that the findings from this study can also be applied to Fontan hemodynamics under exercise conditions.
Furthermore, a cohort-averaged relationship between the viscosity and shear rate for Fontan patients was utilized in simulations for the current study. Cheng at al.11 demonstrated that the inter-patient variation in viscosity for their Fontan patient cohort is approximately ±10% when shear rate = 50–1000 s−1 (the spectrum of shear rate values obtained from simulations of this study). This 10% variation would affect the values of WSS-related metrics but not the population-level statistical results related to these metrics. Also, viscosity has a compounding effect on the difference in power loss: it increases (or decreases) the WSS while enhancing (or suppressing) diminishing flow unsteadiness. Therefore, inter-patient variation in the relationship between viscosity and shear rate for Fontan patients should not affect population-level findings regarding power loss (both iPL and iVDR). Lastly, the effect of this variation should not significantly change the bulk flow, thereby affecting the HFD. Nevertheless, the variation presented by Cheng et al. confirmed that blood rheology varies considerably from patient to patient due to multiple factors, including variations in patient-specific hematocrit levels, age, follow-up time after surgery. Therefore, future studies are warranted to assess the effect of patient-specific blood rheology on Fontan hemodynamics. Similarly, when the shear rate is in the range of [50, 1000] s−1, the viscosities from the NNF model for a “healthy population”7, 13 are around 10% higher than the cohort-averaged viscosities for Fontan patients. Therefore, using NNF models for “healthy populations” is acceptable for population-level Fontan studies but is not recommended for investigating patient-specific Fontan hemodynamics.
Last but not least, it is worth pointing out that the NNF model employed in this study includes the shear-thinning nature of blood and ignored other effects like those induced by the red-cell collisions that require more sophisticated NNF models. In general, shear-thinning is the most apparent non-Newtonian effect. Red-cell collisions may play a role in colliding flow streams, like in the TCPC. Therefore, the effects of red-cell collisions merit careful future investigations.
This study is the first to systemically investigate non-Newtonian effects on patient-specific Fontan hemodynamics. Using the non-Newtonian model (with appropriate numerical treatments) demands less computational costs and leads to significant impacts on AWSS<T (T = 0.05, 0.1, and 0.2 Pa). With the twelve patients involved, though no clinically significant difference was observed at the population-level regarding iPL, iVDR, and HFD, large inter-patient variations exist, and the differences in individual patients may influence patient-specific clinical decisions. Therefore, the use of a non-Newtonian model is recommended for future patient-specific assessment of Fontan hemodynamics. Additionally, statistical correlations were observed between non-Newtonian area importance factors and AWSS<τ. However, (IG)S has mathematical defects and weaker correlations in comparison with ASA<100/s, (IL)S and (IG*)S. This finding suggests that the latter three factors are more effective in identifying the non-Newtonian effect.
6. ACKNOWLEDGMENTS
This study was supported by the National Heart, Lung, and Blood Institute Grants HL67622 and HL098252. The authors acknowledge the use of ANSYS software which was provided through an Academic Partnership between ANSYS, Inc. and the Cardiovascular Fluid Mechanics Lab at the Georgia Institute of Technology.
Footnotes
Publisher's Disclaimer: This Author Accepted Manuscript is a PDF file of an unedited peer-reviewed manuscript that has been accepted for publication but has not been copyedited or corrected. The official version of record that is published in the journal is kept up to date and so may therefore differ from this version.
7 REFERENCES
- 1.Anand M, Kwack J. and Masud A.. A new generalized Oldroyd-B model for blood flow in complex geometries. International Journal of Engineering Science 72: 78–88, 2013. [Google Scholar]
- 2.Arzani A. Accounting for residence-time in blood rheology models: do we really need non-Newtonian blood flow modelling in large arteries? J R Soc Interface 15: 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Avitabile CM, Goldberg DJ, Leonard MB, Wei ZA, Tang E, Paridon SM, Yoganathan AP, Fogel MA and Whitehead KK. Leg lean mass correlates with exercise systemic output in young Fontan patients. Heart 104: 680–684, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Aycock KI, Campbell RL, Lynch FC, Manning KB and Craven BA. The Importance of Hemorheology and Patient Anatomy on the Hemodynamics in the Inferior Vena Cava. Ann Biomed Eng 44: 3568–3582, 2016. [DOI] [PubMed] [Google Scholar]
- 5.Ballyk PD, Steinman DA and Ethier CR. Simulation of non-Newtonian blood flow in an end-to-side anastomosis. Biorheology 31: 565–586, 1994. [DOI] [PubMed] [Google Scholar]
- 6.Bernabeu MO, Nash RW, Groen D, Carver HB, Hetherington J, Kruger T. and Coveney PV. Impact of blood rheology on wall shear stress in a model of the middle cerebral artery. Interface Focus 3: 20120094, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Bossers SSM, Cibis M, Gijsen FJ, Schokking M, Strengers JLM, Verhaart RF, Moelker A, Wentzel JJ and Helbing W. a.. Computational fluid dynamics in Fontan patients to evaluate power loss during simulated exercise. Heart (British Cardiac Society) 100: 696–701, 2014. [DOI] [PubMed] [Google Scholar]
- 8.Caballero AD and Lain S.. Numerical simulation of non-Newtonian blood flow dynamics in human thoracic aorta. Comput Methods Biomech Biomed Engin 18: 1200–1216, 2015. [DOI] [PubMed] [Google Scholar]
- 9.Castro MA, Ahumada Olivares MC, Putman CM and Cebral JR. Unsteady wall shear stress analysis from image-based computational fluid dynamic aneurysm models under Newtonian and Casson rheological models. Med Biol Eng Comput 52: 827–839, 2014. [DOI] [PubMed] [Google Scholar]
- 10.Cheng AL, Pahlevan NM, Rinderknecht DG, Wood JC and Gharib M.. Experimental investigation of the effect of non-Newtonian behavior of blood flow in the Fontan circulation. European Journal of Mechanics-B/Fluids 68: 184–192, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Cheng AL, Takao CM, Wenby RB, Meiselman HJ, Wood JC and Detterich JA. Elevated Low-Shear Blood Viscosity is Associated with Decreased Pulmonary Blood Flow in Children with Univentricular Heart Defects. Pediatric cardiology 37: 789–801, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Chitra K, Sundararajan T, Vengadesan S. and Nithiarasu P.. Non-Newtonian blood flow study in a model cavopulmonary vascular system. International Journal for Numerical Methods in Fluids 66: 269–283, 2011. [Google Scholar]
- 13.Cibis M, Jarvis K, Markl M, Rose M, Rigsby C, Barker AJ and Wentzel JJ. The effect of resolution on viscous dissipation measured with 4D flow MRI in patients with Fontan circulation: Evaluation using computational fluid dynamics. Journal of Biomechanics 48: 2984–2989, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Corsini C, Baker C, Baretta A, Biglino G, Hlavacek AM, Hsia T-Y, Kung E, Marsden A, Migliavacca F, Vignon-Clementel I. and Pennati G.. Integration of Clinical Data Collected at Different Times for Virtual Surgery in Single Ventricle Patients: A Case Study. Annals of Biomedical Engineering 43: 1310–1320, 2014. [DOI] [PubMed] [Google Scholar]
- 15.DeGroff CG Modeling the Fontan Circulation: Where We Are and Where We Need to Go. Pediatric cardiology 29: 3–12, 2008. [DOI] [PubMed] [Google Scholar]
- 16.Doost SN, Zhong L, Su B. and Morsi YS. The numerical analysis of non-Newtonian blood flow in human patient-specific left ventricle. Computer methods and programs in biomedicine 127: 232–247, 2015. [DOI] [PubMed] [Google Scholar]
- 17.Ensley AE, Lynch P, Chatzimavroudis GP, Lucas C, Sharma S. and Yoganathan AP. Toward designing the optimal total cavopulmonary connection: an in vitro study. The Annals of thoracic surgery 68: 1384–1390, 1999. [DOI] [PubMed] [Google Scholar]
- 18.Fedorov A, Beichel R, Kalpathy-Cramer J, Finet J, Fillion-Robin JC, Pujol S, Bauer C, Jennings D, Fennessy F, Sonka M, Buatti J, Aylward S, Miller JV, Pieper S. and Kikinis R.. 3D Slicer as an image computing platform for the Quantitative Imaging Network. Magn Reson Imaging 30: 1323–1341, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Good BC, Deutsch S. and Manning KB. Hemodynamics in a Pediatric Ascending Aorta Using a Viscoelastic Pediatric Blood Model. Annals of Biomedical Engineering 44: 1019–1035, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Heiberg E, Sjögren J, Ugander M, Carlsson M, Engblom H. and Arheden H.. Design and validation of Segment-freely available software for cardiovascular image analysis. BMC Med Imaging 10: 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Johnston BM, Johnston PR, Corney S. and Kilpatrick D.. Non-Newtonian blood flow in human right coronary arteries: Steady state simulations. Journal of Biomechanics 37: 709–720, 2004. [DOI] [PubMed] [Google Scholar]
- 22.Liu X, Fan Y, Xu XY and Deng X.. Nitric oxide transport in an axisymmetric stenosis. J R Soc Interface 9: 2468–2478, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Long CC, M. C. C. M. c. Hsu, Y. Bazilevs, J. A. Feinstein and A. L. Marsden. Fluid – structure interaction simulations of the Fontan procedure using variable wall properties. International Journal for Numerical Methods in Biomedical Engineering 28: 513–527, 2012. [DOI] [PubMed] [Google Scholar]
- 24.Malek AM, Alper SL and Izumo S.. Hemodynamic shear stress and its role in atherosclerosis. Jama 282: 2035–2042, 1999. [DOI] [PubMed] [Google Scholar]
- 25.Marino BS, Fogel M, Mercer-Rosa LM-R, Wei ZAW, Trusty PM, Tree M, Tang E, Restrepo M, Whitehead KK, Paridon SM and Yoganathan A.. Poor Fontan Geometry, Hemodynamics, and Computational Fluid Dynamics Are Associated With Worse Quality of Life. In: Circulation2017, p. A18082-A18082. [Google Scholar]
- 26.Marrero VL, Tichy JA, Sahni O. and Jansen KE. Numerical study of purely viscous non-Newtonian flow in an abdominal aortic aneurysm. J Biomech Eng 136: 101001, 2014. [DOI] [PubMed] [Google Scholar]
- 27.Pennati G, Corsini C, Cosentino D, Hsia TY, Luisi V, Dubini G. and Migliacca F.. Boundary conditions of patient-specific fluid dynamics modelling of cavopulmonary connections: possible adaptation of pulmonary resistances results in a critical issue for a virtual surgical planning. Interface Focus 1: 297–307, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Pike NA, Vricella LA, Feinstein JA, Black MD and Reitz BA. Regression of severe pulmonary arteriovenous malformations after Fontan revision and “hepatic factor” rerouting. The Annals of thoracic surgery 78: 697–699, 2004. [DOI] [PubMed] [Google Scholar]
- 29.Rijnberg FM, Hazekamp MG, Wentzel JJ, de Koning PJH, Westenberg JJM, Jongbloed MRM, Blom NA and Roest AAW. Energetics of Blood Flow in Cardiovascular Disease: Concept and Clinical Implications of Adverse Energetics in Patients With a Fontan Circulation. Circulation 137: 2393–2407, 2018. [DOI] [PubMed] [Google Scholar]
- 30.Robertson AM, Sequeira A. and Owens RG. Rheological models for blood In: Cardiovascular Mathematics: Modeling and simulation of the circulatory system, edited by Formaggia L, Quarteroni A. and Veneziani A.. Milano: Springer Milan, 2009, pp. 211–241. [Google Scholar]
- 31.Ryu K, Healy TM, Ensley AE, Sharma S, Lucas C. and Yoganathan AP. Importance of accurate geometry in the study of the total cavopulmonary connection: computational simulations and in vitro experiments. Ann Biomed Eng 29: 844–853, 2001. [DOI] [PubMed] [Google Scholar]
- 32.Tang E, Wei ZA, Trusty PM, Whitehead KK, Mirabella L, Veneziani A, Fogel MA and Yoganathan AP. The effect of respiration-driven flow waveforms on hemodynamic metrics used in Fontan surgical planning. Journal of Biomechanics 82: 87–95, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Tang E, Wei ZA, Whitehead KK, Khiabani RH, Restrepo M, Mirabella L, Bethel J, Paridon SM, Marino BS, Fogel MA and Yoganathan AP. Effect of Fontan geometry on exercise haemodynamics and its potential implications. Heart 103: 1806–1812, 2017. [DOI] [PubMed] [Google Scholar]
- 34.Tang TLE Effect of Geometry, Respiration and Vessel Deformability on Fontan Hemodynamics: a Numerical Investigation. Georgia Institute of Technology, 2015. [Google Scholar]
- 35.Throckmorton AL, Lopez-Isaza S. and Moskowitz W.. Dual-pump support in the inferior and superior vena cavae of a patient-specific fontan physiology. Artificial Organs 37: 513–522, 2013. [DOI] [PubMed] [Google Scholar]
- 36.Tree M, Wei ZA, Trusty PM, Raghav V, Fogel M, Maher K. and Yoganathan A.. Using a Novel In Vitro Fontan Model and Condition-Specific Real-Time MRI Data to Examine Hemodynamic Effects of Respiration and Exercise. Annals of Biomedical Engineering 46: 135–147, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Trusty PM, Slesnick TC, Wei ZA, Rossignac J, Kanter KR, Fogel MA and Yoganathan AP. Fontan Surgical Planning: Previous Accomplishments, Current Challenges, and Future Directions. J Cardiovasc Transl Res 11: 133–144, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Trusty PM, Wei Z, Rychik J, Graham A, Russo PA, Surrey LF, Goldberg DJ, Yoganathan AP and Fogel MA. Cardiac Magnetic Resonance Derived Metrics are Predictive of Liver Fibrosis in Fontan Patients. Annals of Thoracic Surgery Accepted. [DOI] [PubMed] [Google Scholar]
- 39.Trusty PM, Wei Z, Rychik J, Russo PA, Surrey LF, Goldberg DJ, Fogel MA and Yoganathan AP. Impact of hemodynamics and fluid energetics on liver fibrosis after Fontan operation. J Thorac Cardiovasc Surg 156: 267–275, 2018. [DOI] [PubMed] [Google Scholar]
- 40.Trusty PM, Wei Z, Tree M, Kanter KR, Fogel MA, Yoganathan AP and Slesnick TC. Local Hemodynamic Differences Between Commercially Available Y-Grafts and Traditional Fontan Baffles Under Simulated Exercise Conditions: Implications for Exercise Tolerance. Cardiovasc Eng Technol 8: 390–399, 2017. [DOI] [PubMed] [Google Scholar]
- 41.Trusty PM, Wei ZA, Slesnick TC, Kanter KR, Spray TL, Fogel MA and Yoganathan AP. The first cohort of prospective Fontan surgical planning patients with follow-up data: How accurate is surgical planning? The Journal of thoracic and cardiovascular surgery 157: 1146–1155, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Wei Z, Whitehead KK, Khiabani RH, Tree M, Tang E, Paridon SM, Fogel MA and Yoganathan AP. Respiratory Effects on Fontan Circulation During Rest and Exercise Using Real-Time Cardiac Magnetic Resonance Imaging. Ann Thorac Surg 101: 1818–1825, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Wei ZA, Huddleston C, Trusty PM, Singh-Gryzbon S, Fogel MA, Veneziani A. and Yoganathan AP. Analysis of Inlet Velocity Profiles in Numerical Assessment of Fontan Hemodynamics. Ann Biomed Eng 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Wei ZA, Sonntag SJ, Toma M, Singh-Gryzbon S. and Sun W.. Computational Fluid Dynamics Assessment Associated with Transcatheter Heart Valve Prostheses: A Position Paper of the ISO Working Group. Cardiovasc Eng Technol 9: 289–299, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Wei ZA, Tree M, Trusty PM, Wu W, Singh-Gryzbon S. and Yoganathan A.. The Advantages of Viscous Dissipation Rate over Simplified Power Loss as a Fontan Hemodynamic Metric. Annals of Biomedical Engineering 46: 404–416, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Wei ZA, Trusty PM, Tree M, Haggerty CM, Tang E, Fogel M. and Yoganathan AP. Can time-averaged flow boundary conditions be used to meet the clinical timeline for Fontan surgical planning? J Biomech 50: 172–179, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Wei ZA, Trusty PM, Zhang Y, Tang E, Whitehead KK, Fogel MA and Yoganathan AP. Impact of Free-Breathing Phase-Contrast MRI on Decision-Making in Fontan Surgical Planning. J Cardiovasc Transl Res 2019. [DOI] [PubMed] [Google Scholar]
- 48.Yang W, Chan FP, Reddy VM, Marsden AL and Feinstein JA. Flow simulations and validation for the first cohort of patients undergoing the Y-graft Fontan procedure. The Journal of thoracic and cardiovascular surgery 149: 247–255, 2015. [DOI] [PubMed] [Google Scholar]
- 49.Yeleswarapu KK, Kameneva MV, Rajagopal KR and Antaki JF. The flow of blood in tubes: Theory and experiment. Mechanics Research Communications 25: 257–262, 1998. [Google Scholar]