Mechanisms and modeling of electrohydrodynamic phenomena

Abstract

The purpose of this paper is to review the mechanisms of electrohydrodynamic (EHD) phenomenon. From this review, researchers and students can learn principles and development history of EHD. Significant progress has been identified in research and development of EHD high-resolution deposition as a direct additive manufacturing method, and more effort will be driven to this direction soon. An introduction is given about current trend of additive manufacturing and advantages of EHD inkjet printing. Both theoretical models and experiment approaches about the formation of cone, development of cone-jet transition and stability of jet are presented. The formation of a stable cone-jet is the key factor for precision EHD printing which will be discussed. Different scaling laws can be used to predict the diameter of jet and emitted current in different parametrical ranges. The information available in this review builds a bridge between EHD phenomenon and three-dimensional high-resolution inkjet printing.

1 Introduction

Due to the current trend toward the miniaturization of devices, traditional manufacturing methods such as casting, injection molding, and computer numerical control machining cannot satisfy the developing needs of industries. The lithography-based microfabrication experiences inherent limitations in processing diverse materials, and extending fabrication into the third dimension[1]. In addition, it is a time-consuming process to use masks and photo-resistant chemicals, and also expensive when the manufacturing process requires a sophisticated, clean room and state-of-the-art lithographic equipment[2]. Additive manufacturing, based on localized deposition of material and a layer-by-layer printing process, is able to build customized products in a short time-frame and offers significant advantages over traditional manufacturing processes in the area of design freedom and reduction of assembly time and cost. Inkjet printing, which is a low cost, high speed and large area additive manufacturing process[3], relies on the generation of droplets at or near a nozzle aperture, followed by non-contact deposition onto a substrate with high spatial control. Unfortunately, inkjet printing systems share the same drawback, namely that the droplet size is solely dependent on the nozzle diameter, with droplet diameter about twice the nozzle diameter[4], and the nozzle diameter cannot be scaled down continuously.

To overcome the above limitations, electrohydrodynamic (EHD) inkjet printing (also called “EHD jet printing”) has been proposed as a solution to the limited resolution of the conventional inkjet printer system, because EHD printing can generate small droplets without the need to miniaturize the nozzle. The process involved, called “electrospray in the cone-jet mode,” uses electrical (“Maxwell”) forces to pull the liquids from the nozzle tip, rather than apply thermal or acoustic energy to push liquid from a fine capillary. The EHD inkjet printing can be a high-resolution inkjet printing technology because there is a large “neck-down ratio” between the inner diameter of the nozzle and the jet: The jet diameter is about two orders of magnitude smaller than the nozzle diameter. Thus, in EHD jet printing the nozzle inner diameter can be much larger than that used in thermal or piezoelectric inkjet printing (about 20 μm); this makes blockages much less likely and makes it easy to employ a highly viscous liquid[5]. EHD ink-jet printing is a mask-less, non-contact, direct-write, and additive process, and it is used in the field of micro or nanomanufacturing for patterning of a large class of materials on a variety of substrates without adversely affecting the chemical properties of the deposited materials. Park[6] developed an EHD inkjet printing system, and they used a microcapillary with diameter from 0.3 to 30 μm to produce single droplet with sub-micrometer size. Followed by their seminal work, a series of applications appear in recent years, and applications include varied electronics, biotechnology, and three-dimensional (3D) printing. Liang[7] used the coaxial nozzle to print microscale 3D cell-laden constructs, and Liu[8] investigated that influence of EHD jetting parameters on the morphology of PCL scaffolds. Designs of EHD printing system and recent applications of high-resolution printing will be introduced in the following paper due to the limitation of length. In the remaining sections of this paper, we provide a brief account of the history of EHDs and related technology. Then, we review the known theories and principles related to EHD printing, especially the theory of Taylor cone formation, mechanism of cone-jet transition, and criteria for jet stability.

2 History of EHDs and Jet Formation Technology

The phenomenon of a liquid drop subject to sufficiently strong electric forces adopting a roughly conical shape has been reported by Gilbert in 1600[9,10]. The electrically induced formation of a cone-jet and its breakup into droplets were first reported by Grey in the 1700s[11]. In 1882, Rayleigh conducted research on the theoretical analysis of the breakup of a spherical liquid droplet under electrical stress and derived an instability condition for an electrically charged spherical droplets[12]. His result implies that (for a spherical droplet) the stability criterion is equivalent to the condition that the electric stress outward is equal to the surface tension stress inwards. The rapid EHD pulsation of the electrified liquid surface, now known as the cone-jet transition that a thin liquid jet is ejected from the tip of an electrified cone shape, is discovered first time by Zeleny in 1915[13]. Zeleny also characterized the resulting spray as a function of the nature of the solvent, high voltage and pressure of the liquid at the tip of the tube (which is linked to the flow rate in modern electrospray experiments)[12,14]. Before1960s most work focused on the behavior of perfect conductors (mercury or water) or perfect dielectrics (a polar liquid such as benzene), but Allan and Mason (1962) started to study on poorly conducting liquids - and established the leaky dielectrics model or ohmic model[15,16]. In 1969 Taylor derived a pioneering theory to adequately explain the peculiar form of meniscus cones, referred as Taylor cone, and the related concept is only recently extended for use in micro patterning[17]. Then, Cloupeau and Prunch proposed a classification of EHD jetting modes on the basis of their observations in the air at atmospheric pressure[18]. Specially, Cloupeau and Prunet-Foch organized EHD jetting modes according to liquid flows from the meniscus in a continuous or pulsating manner into: (1) Continuous manner including cone-jet, multi-jet, simple jet, and ramified jet modes and (2) pulsating manner including dripping, micro dripping produced at the end of the capillary or meniscus, pulsed cone-jet produced by breakup of a jet, and spindle mode[18]. In terms of location where drops are formed, spraying modes can also be divided into two different groups: Electrified droplets pinched off either from a protruding meniscus or from a jet emerging from a conical meniscus[18,19]. It should be noted that the release of charged droplets directly from the apex of a cone is not possible in competition with the formation of a cone-jet[20]. Fenn et al. found that flowing solution of large polymers and proteins can be formed by electrostatic atomization of their solutions from a Taylor cone in a bath gas, and this led to the 2002 Nobel Prize in Chemistry received by Fenn et al.[21,22]. Early reports on the use of this phenomenon for the controlled deposition of materials drew inspiration from electrospray techniques for the generation of charged droplets[23-25]. De la Mora and Loscertales explored the relationship between the various parameter and emitted current and jet diameter for high conducting liquid. Ganan-Calvo proposed six different scaling laws to define cone-jet transition[26]. Chen performed a series of studies on the generation and placement of droplets with a high positioning accuracy about 4±2 μm[27,28]. Park et al. used the EHD method to eject different types of ink from microcapillary nozzles of different sizes and obtained printing resolution up to 1 μm[6,29]. Maginean et al.[30] and Chen[28] separately investigated pulsating cone-jet formation and summarized scaling law for oscillation frequency in the two different scenarios.

3 Theory and Mechanism of EHD Inkjet Printing

The mechanisms of EHD jetting are complicated, and the physics behind this phenomenon is not completely known. This paper summarizes some of the contributions in this area and gives readers a basic introduction to some important theories related to EHD inkjet printing. The following section specially discusses liquid cone formation, the cone-jet transition, and jet stability.

3.1 Formation of the Liquid Cone Shape

Figure 1A shows a common setup for EHD printing. The pressure head of the liquid in the cylindrical nozzle is initially adjusted by the pressure regulator until the meniscus “A” in Figure 1A is almost flat at the nozzle exit. Then, a high voltage is applied between the metal nozzle and a grounded electrode to create an electrical potential difference. The electric field strength near the apex of an operating jet can be close to the threshold for electrical breakdown of air (3 × 10⁶ V/m), but a cone-jet only forms in the absence of gas discharge[31]. As the voltage is increased, the increasing Maxwell stress causes liquid deformation, from a hemispherical droplet in Figure 1B to a roughly conical meniscus in Figure 1C. The process of surface deformation is triggered by small perturbations of the surface, which, in turn, enhance the local electric field through charge concentration, and further increase the electrostatic pull in a cascading effect[32]. The conical meniscus is maintained over a certain critical limit of electric potential[33], and a limiting case is reached when the apex of the cone approaches a point, i.e., a singularity[32]. Inside the conducting nozzle, the liquid is electrically neutral before emerging from the nozzle outlet, and there is no charge separation in the nozzle regardless of liquid conductivity because the electric field inside the nozzle is zero.

Figure 1.

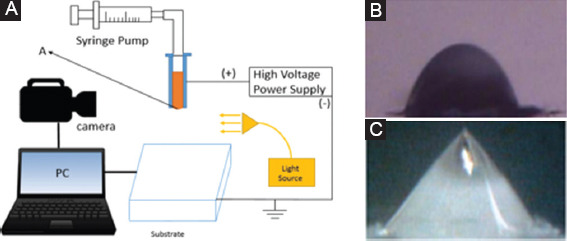
(A) A schematic of electrohydrodynamic printing setup. Ethylene glycol liquid meniscus (B) at 0 volts; (C) at 2.5kV[34]. Adapted by permission from Lozano et al. (2004) under the Elsevier license.

In 1964, Taylor obtained the first analytical model for the cone structure and constructed a modal analysis of a conducting liquid cone at equilibrium (without a jet from the apex)[32,35]. In 1969, Taylor used the two plate experimental setup to explore the criteria for the deformation from a sphere to a cone. At the critical potential difference, the spherical cap above the tip of the tube is taken to be in an equilibrium defined by electrostatic force, hydrodynamic force, the surface tension force, and weight of the spherical cap. The force balance is given in equation (1):

F+Δpπr²=2πrγcosθ+W (1)

In this two plate experimental geometry, the value of the force, F, exerted on a cylinder of length, L, is[17]:

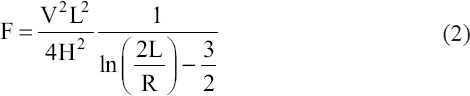
Above, F is the attractive force due to the imposed field; ΔP is the pressure difference between inside the liquid cone at its base and ambient pressure; γ is the surface tension; R is the nozzle radius; L is the distance between the end of nozzle and plate E; W is the hydrodynamic force including the weight of liquid in the spherical cap above the orifice; and θ is the semi-cone angle. The hydrodynamic force ΔP continuously supplies fluid to the emerging droplet[33].

In the classical theory of dielectrics, the charge is situated at the interface between two substances, which have different dielectric constants[36]. Thus, electro forces, which stem from two isotropic media which have different electrical conductivity and dielectric constant within or across the phase boundaries[37], induces electrical charges which exist in the fluid along the fluid interface[38]. While surface tension tends to keep the pendant droplet in spherical shape which has the smallest surface-to-volume ratio, and also to reduce interfacial energy[39], the repulsion between the surface charges acts against the surface tension force to deform the sphere into cone[38].

If pressure (ΔP) at the top of the fluid equal to zero, the cone semi-vertical angle (θ) is 49.3°. If the weight of the fluid is also neglected, the critical voltage (static equilibrium would no longer be maintained) for the appearance of cone with a straight generatrix[40] before the jet forms can be predicted by equation (3) which is derived by substituting equation (2) into equation (1)[17]:

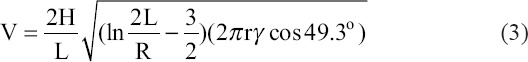
Above the critical voltage, the static equilibrium value would no longer be maintained[17]. For a liquid meniscus formed at the exit of a conducting needle, like electrodes of the needle to plate setup, the critical voltage can be approximately calculated as[41,42]:

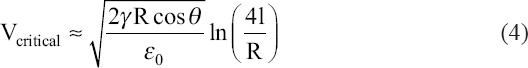
Where l is the distance between the electrode of nozzle and electrode of substrate. This expression is valid when the electrode separation l is much larger than the radius of nozzle r[5]. This formula only gives an approximation to the required starting voltage (experimentally verified within 10%) for each simulation[32].

The Taylor angle (θ_T=49.3^o) is theoretically calculated from the balance of surface-tension stress and electric stress under no fluid motion (hydrostatic pressure P, as shown above, equal to zero)[33]. Thus, the critical voltage, which Taylor predicted, is only valid in the limit of no liquid jet emission and it does not account for any EHD effect caused by subsequent jet emission[38]. The semi-vertical angle, which Taylor predicted above, is not always 49.3° and Fernandez de la Mora showed that several factors, including liquid loss through the cone, space charge, flow rate, and ambient pressure, might result in cones established at different semi-vertical angles[19,43-45]. Cloupeau and Prunet-Foch also showed that there are stable conical menisci for certain range of variation in the hydrostatic pressure and applied potential difference, but the value of the angle at the apex is variable, and the generatrix of the cone may be either concave or convex[18,40]. In addition, the actual electrode setup in experiments may not replicate the geometry of Taylor’s model[32].

In a word, it is important to obtain starting electric potential for initiation of EHD printing, and equations (3, 4) are used to estimate the critical value of the voltage. The semi-vertical angle from experiments can be different from Taylor angle applied to these equations, and this is a reason to cause a discrepancy between theoretical and experimental critical voltage. Another reason arises from factors which are not counted in equations, such as space charge and shape of nozzle.

3.2 The Cone-jet Transition Stage

As shown in Figure 2A, when the electric field is absent or small, the liquid flow out from a nozzle by the assistance of gravitational force occurs by the dripping mode at a small flow rate or the jetting mode at high flow rate[1,46,47]. At a critical potential difference the Taylor cone is formed, and with further increase of field strength, the cone becomes unstable and then a small droplet or a very thin jet (small and thin compared with the capillary diameter) is emitted from the conical apex[17]. Juraschek and Rollgen classified spray of axisymmetric regimes into three modes, based on current measurements[19,20]. With the increase of voltage, a pulsating jet (axial mode I) appears, with pulsations frequencies existing in the low kilohertz range or less[20]. Marginean considered axial mode I, which exhibits two periods, as burst regimen[19]. As the voltage grows to the axial mode II, only high-frequency pulsation at the low kilohertz is observed[20]. The intrinsic or natural pulsating modes are caused by an imbalance between the supply and loss of liquid in the entire cone volume (low frequencies) or the cone’s apex (high frequencies)[20,28,48]. Juraschek and Rollgen claimed that capillary current is linearly dependent on the pulsation frequency and independent of the capillary potential applied in the high pulsation mode[20]. Chen et al. observed steady-state results from a long exposure time (0.4 ms), but the intrinsic pulsating mode in the kilohertz range was observed when the exposure time is reduced to 0.1 ms or less[28]. Marginean et al., first, used a set of sequential images (Figure 2B) to show spontaneous Taylor cone deformation and a similar intrinsic pulsation at 1μs per frame[14]. Figure 2B clearly shows periodic formation, relaxation of meniscus, and cone-jet, and they provide a direct connection between Taylor cone pulsation and electrospray current oscillations[14,28]. Yogi et al. used an external stimuli method to generate picoliter droplets by applying a 1000V, and 10ms pulse voltage to the tip of a capillary tube and drop-on-demand (D-O-D) deposition can be achieved using external stimuli[24]. In contrast to deposition in a small area by electrospray, pulsating jet caused by either intrinsic or external stimuli approaches are able to generate single micro-scale droplet on the substrate. In addition, D-O-D pulsating jet deposition can achieve higher sensitivity and generate the customized volume of droplets by changing pulse duration. In general, pulsation frequency depends on flow rate, properties of liquid and nozzle diameter. Several models were proposed to express the relationship between frequency and parameters, and these models will be discussed in section 3.2.3.

Figure 2.

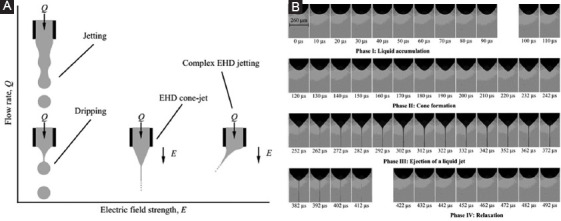
(A) Phase diagram depicting flow transitions that occur as flow rate and/or electric field strength is varied[46]. Adapted by permission from Robert T. Collins et al. (2007) under the Cambridge University Press. (B) Time images of the pulsating Taylor cone with the four phases of the cycle. Delay time values measured from the most retracted meniscus (Δt) are shown under the individual images. Each frame is an average of 100 exposures with the same delay[14]. Adapted by permission from Marginean et al. (2004) under the ACS Publications.

When the applied potential difference is further increased, continuous emission of liquid through cone jet is developed. This mode is known as axial mode III[20]. In addition, a concavely shape cone observed in the two pulsation mode is changed to a nearly straight cone in the continuous spray mode[20]. Marginean et al. revealed that a complex transition into an astable regime may exist between pulsating and continuous cone-jet regime[19]. In Figure 2A a complex jetting behavior, like tilted jets, is shown at higher electric field strength, but these phenomena are not considered to be controllable in a precision deposition. When the applied voltage is slightly lower than the voltage required to obtain a single permanent jet, the jet may be emitted only intermittently, which means the apex of meniscus alternately takes on a pointed or rounded form, and emission phases may occur at perfectly regular time intervals[18]. This intermittent or pulsed cone-jet is similar to the axial mode I and II. The diameter of the jet varies during these emission phases, and thus the distribution of droplet size is never narrow[18]. These studies suggest that pulsating and continuous cone-jet can be obtained by adjusting the voltage and flow rate. However, there are noteworthy exceptions, and polycaprolactone is one of them. A stream of pulsating droplets has not been observed since it is hard to accumulate enough charges to overcome the surface tension and high viscous force[49]. For paraffin wax, pulsating cone-jet was only formed[50], and this result may attribute to its low viscosity and electrical conductivity. In one word, generation of pulsating or continuous cone-jet is controlled not only by changes of voltage and flow rate but also material properties, such as surface tension, electrical conductivity, and viscosity.

Zeleny first investigated the continuous production of drops by the breakup of a permanent jet extending from a meniscus in the conical form[13,51], and then Vonnegut and Neubauer acquired the same mode during their experiments on liquids[52]. Cloupeau and Prunet used the compound word “cone-jet” to describe the phenomenon that a permanent jet extending from an axisymmetric conical volume of liquid and jet is stretched along the capillary axis[18]. The creation of a jet requires penetration of the field lines into the liquid with a dielectric liquid, and only penetration will allow the appearance of a component of the electric field tangent to the surface; this acts on the surface charges and creates a force that drives the liquid and an acceleration of the jet downstream[18]. Melcher and Taylor also pointed out that for an interface to be subjected to shear stress, the surface must simultaneously support the surface charge and be subjected to a tangential electric field[53,54]. In addition, Melcher et al. mentioned two limiting cases and the first one is the perfectly conducting interface[53]. In this case, electrical surface forces always act perpendicularly to the surface and thus interface supports no tangential electric stress[53]. The second limiting case is a perfectly insulated surface with no free charge density while the polarization force density is operative at the interface. Therefore, the electric surface force density acts in the direction of permittivity gradient (−∇ε), which is perpendicular to an interface[53]. Thus, the liquid must not be perfectly conducting or insulating[18], and for a leaky dielectric liquid, the tangential component of the electric field can develop a shear force along the conical surface.

When a steady flow rate is issuing from the cone’s tip in the form of a microjet, an electric field toward liquid surface must appear in the cone to supply the electric current, which is emitted by the microjet in the form of charged droplets[55]. The tangential electrical stress pulls the charged surface toward the tip, and tangential electrical stress provokes sufficient axial momentum to transfer onto the liquid to begin a progressive deformation of the cone into a jet[55]. Hayati et al. showed an axisymmetric circulation pattern where the particles travel downward along the surface of the cone and reverse upward along its axis in the conical base[54]. The electric field drives free charges to the surface of the cone; hence, the surface is charged and is subjected to a normal electric field E_n. A potential difference will exist between the base of the cone at the end of the capillary and the tip of the cone due to the semiconducting nature of the liquid[54]. This potential difference ensures that the interface is subjected to a tangential electric field E in the direction of flow[54]. Barrero et al. observed a similar recirculating meridional motion and an additional vigorous swirl coupled to the meridional motion, and they attributed the appearance of different motion to a distinct value of liquid conductivity and viscosity[56]. The meridional motion can be considered as a proof of the existence of tangential electrical stress on the cone surface. De la Mora considered the domain of cone as hydrostatic since recirculating flow is slow and have little influence on jet formation[45].

Even though the phenomenon of cone-jet transition has been known for over 200 years, the actual process is not understood completely. It is complex to analyze theoretical multi-physical free surface flow by mathematical methods, and there are also limitations in simplifying assumptions in models[5]. In addition, based on the complexity of EHD phenomenon controlled by multi-parameters, it is not always possible to know beforehand the mode obtained when the values of main parameters are given[18]. According to data obtained from experiments, Cloupeau and Prunet found that the cone-jet mode only appears at a certain range of voltage and flow rate, and instabilities including skewed and multiple-jet regime appear in a larger electric field[57]. At specific conditions, operating diagram of cone-jet can be described as changes of flow rate and electric field strength[5,57]. Domains of cone-jet may become different by small changes in the selection of parameters mentioned above (such as working fluid, setup of the experiment, and geometry of nozzle). Furthermore, experimental measurements are also difficult for the flow fields in a free jet whose diameter is often on the verge of optical resolution[5].

3.2.1 Dimensional Analysis

In this section, the effect of parameters on the transition process is reviewed. The cone-jet transition is confined to the region near the conical apex. First, the dimensional analysis is used to give a qualitative description of the jet diameter, D_j, and emitted current, I_j[38]. The jet diameter and current are related to the operating parameters (flow rate Q and electric field strength E), liquid material properties (density ρ, viscosity μ, electrical conductivity K, gas-liquid surface tension γ, and fluid relative permittivity ε_r), and geometrical parameters (nozzle diameter D_n and distance between two electrodes H). If parameters ρ, γ, K, and the va`cuum permittivity, ε₀, are selected as dimensionally independent variables in this functional relation for the jet diameter and current, dimensions of these related variable are [ρ] =ML⁻³, [γ] = MT⁻², [K] = MLT⁻³V⁻², and . Next, the Buckingham’s Π theorem can be applied to perform a dimensional analysis[38,55]:

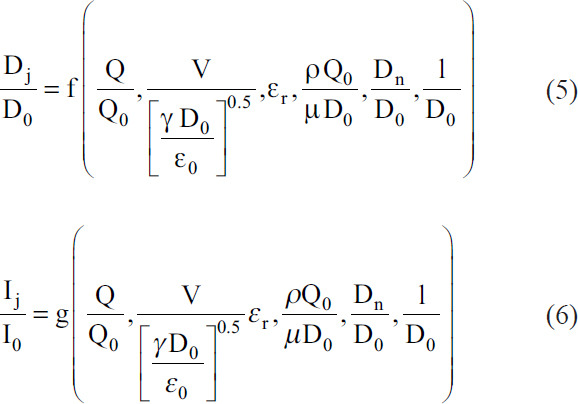
Where f() and g() are dimensionless functions. Lee et al. add a ratio of two characteristic times, t_e/t_h, where t_e is charge relaxation time, which is the characteristic time of charge transport determined by the electrical properties of the fluid, and t_h is hydrodynamic time, which is the characteristic time of the fluid supply[33,55]. The charge relaxation time is 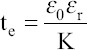and hydrodynamic time is 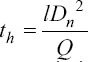. The characteristic flow rate is , characteristic distance 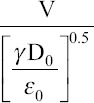and characteristic current .

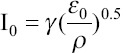These dimensionless groups have a certain influence on jet diameter and current, qualitatively. In the classical EHD jetting system, the charge relaxation time is smaller than the hydrodynamic time (t_e<t_h); most of EHD printing, electrospray, and electrospinning belong to this category[33]. Charges are induced toward the surface of the liquid to form a thin layer of charge under the liquid-gas interface[33], and both the shape of the liquid cone and the jet stability are affected by the amount of electric charge on the liquid surface[38]. For liquids with relatively high conductivities (above 10⁻⁴ S/m), the electrical relaxation time is short and sufficient charge can accumulate on the surface to counteract the surface tension force[38]. The jet formation zone is limited to the apex of the conical meniscus[57]. The remaining surface is practically equipotential, and an almost static equilibrium of forces exists at each point[57]. The shape of the cone may have a practically straight generatrix with a very fine jet (Figure 3A) or exhibit a shape as in Figure 3B[18]. In Figure 3C and D, the acceleration zone extends further toward the base of the cone and the profile of liquid has a similar shape of cone-jet with an open cone for decreasing conductivities[57]. Flow rate required for stable cone-jet mode moves toward a lower threshold with an increase in conductivity when all other parameters are kept same[57]. In the non-classical EHD (t_e >t_h), there is insufficient time to develop an appreciable surface charge, and electrically forced jet may appear, like a ball cone-jet[33,58,59]. Although it is not possible to obtain very fine jets with liquid of low conductivity unless special methods are used[57], it is still possible to produce a jet for liquids with low electrical conductivities (10⁻¹³ S/m)[58]. The conical shape ultimately disappears when the liquid has a very low conductivity[57]. Electrical stress cannot counteract the surface tension to deform the meniscus into a cone, and the pendant droplet grows in volume and finally drips off.

Figure 3.

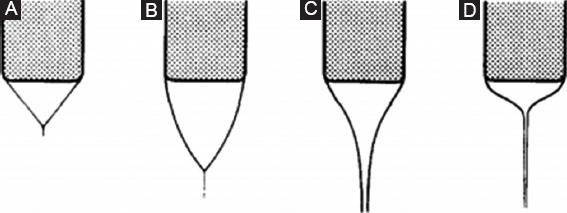
(A-D) Different forms of the meniscus in cone-jet mode[57]. Adapted by permission from Michel Cloupeau et al. (1989) under the Elsevier.

In the experiment of Juraschek and Rollgen, both high and low pulsation frequencies weakly increase with the increase of electrical conductivities, since the dielectric relaxation time of liquid without the addition of electrolyte concentration is already shorter than the time scale of a single pulse period[20]. The addition of the electrolyte causes decreases of capillary potential, and as a result the measured average capillary current increases due to an increase of emitted electric charges during a single pulse[20].

The first one (Q/Q₀) in the dimensionless group is the dimensionless flow rate 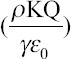and the jet diameter can be varied by two orders of magnitude by changing the flow rate[55]. The potential required for the formation of steady cone-jet transition is affected by flow rate and the resulting shape of the liquid cone[38]. The minimum flow rate and its associated electric field are considered as a stability boundary of cone-jet[5], and Q₀ is of the order of the minimum flow rate for a given liquid[60]. The minimum flow rate is not, simply, the flow rate due to the upstream pressure, but rather the specific flow rate that causes electrical stress to strip off (or shear) the surface charge layer of the fluid[33,61]. The cone-jet mode only appears within a limited range of values of flow rate for a given conductivity[18]. The value of the current and diameter of jet grow with the increase of flow rate[57]. Chen provided operating modes of steady cone-jet in the E-Q diagram for the conductivity of liquids above 10⁻⁴ S/m when other materials and geometry parameters are kept fixed[5]. In the experiment of Juraschek and Rollgen, the “low” frequency of the appearance of current pulse sequence increases with the increase of liquid flow rate, since a shorter time is needed to build up the required large cone volume with a critical radius for the onset of a liquid emission process[20]. The number of pulses in a sequence also slightly increases due to the extension of emission time by raised liquid supply[20]. The “high” pulsation frequency is weakly changed by liquid flow rate, but the amplitude and width of the pulse increase with flow rate accordingly. In conclusion, the duty cycle of the “high” frequency pulsations is affected by liquid supply to the apex region of the cone and weakly affected by liquid supply to the bulk of the cone.

The second is dimensionless electrical voltage related to Taylor’s critical voltage 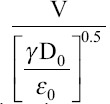[55]. The electric field promotes the charge migration away from the electrode partly through the solution bulk after the charge is produced electrochemically at the emitter liquid interface, partly along the liquid surface[19]. The value of an electric field on the liquid is not only depends on value of voltage but also varied with a dimension of the capillary, the shape, and dimensions of the bottom electrode and distance between two electrodes[57]. With the increase of electric field strength, there are many different forms of cone-jet transition[18]. Within the regime of the steady cone-jet transition, the liquid meniscus of a Taylor cone recedes toward the nozzle base as the electric field strength is increased[44]. Within the operating envelope, the range of applied voltage for steady cone-jet transition is <7% for a given flow rate[55], which is small in comparison with the changes due to the liquid flow rate. Since the range of electric field strengths for the steady cone-jet transition is fairly narrow, this group can be considered as an invariant[55].

The third is the relative permittivity of fluid ε_r, which is determined by the amount of the alignment of dipoles[33]. When two liquids have a similar value of the fourth dimensionless group, the liquid with higher relative permittivity has a smaller charge relaxation length, and thus a larger potential is required to achieve lower threshold for cone-jet formation[33].

The fourth dimensionless group is 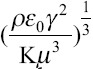, which only depends on the liquid properties. It can be considered as the ratio of the propagation velocity of a perturbation across the jet by the velocity of liquid 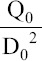and viscous diffusion 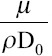[55]. The axial velocity profile of the liquid jet depends on the viscous dimensionless parameter. Viscosity does not explicitly affect the jet diameter. The viscosity of the liquid mainly affects the stability of the jet, especially with polymer jets where the huge viscoelastic effects and elongational viscosity associated with polymers prevent the capillary instability[62,63]. Thus, higher viscosity liquids form thicker jets under the cone-jet transition[38]. In the cone-jet mode, the length of the jets increases with the viscosity, the resistivity, and the flow rate of the liquid[18].

The following dimensionless group relates to the nozzle diameter D_n, which has a small influence on the diameter of jet D_j, particularly for conductive liquids. For high conductivity liquids (10⁻⁴ S/m and above), De la Mora et al. demonstrated that the current is independent of the needle voltage and geometry of the electrodes as long as a stable cone is formed[31]. This conclusion is consistent with the result that current becomes decreasingly dependent on needle voltage at increasing conductivities in I-Q curves[57]. The jet diameter becomes irrelevant to nozzle diameter when the ratio of the two diameters approaches to zero[60]. Under these conditions, the dynamic effect due to the jet emission is negligible and limited to the vicinity of the conical apex (e.g., d_n/d₀>>1 in the derivation). However, this simple behavior does not hold for liquids with small electrical conductivities and area of stable conical meniscus depends on electrode geometry[31]. Choi et al. claimed the dependence of jet diameter on nozzle diameter from their study, and this different result from above can be attributed to the lower electrical conductivity of ink[64]. At this circumstance, smaller droplets can be the outcome of using a thinner nozzle. In a stable cone-jet transition, smaller nozzle diameters will extend both the low and high flow rate limit for a given liquid conductivity[57]. The electric field strength near the nozzle depends on both the applied voltage and the nozzle diameter. Thus, with decreasing outer diameter, the field strength increases and the resulting electrostatic forces, as well as the entrance velocity, raise up[20]. Furthermore, a smaller nozzle diameter or distance between two electrodes, the required onset voltage is lower[44,65]. It is favorable for high-resolution printing and precise placement to keep a short distance “l” (usually smaller than 5 mm) between nozzle and ground electrode due to reduction of lateral variations[6]. As printing complex feature with sharp turns or small corners, a small distance “l” enables the process to response promptly to the abrupt path change. Another key factor for high-resolution printing is plotting speed, and it is also important to consider compatibility between plotting speed and jetting speed. As a stable jet emits from the tip of the cone, the speed of jetting depends on flow rate and electrical potential. The plotting speed is the movement speed of the substrate. If two speeds match each other, a straight jet appears, and a uniform continuous plotted line is deposited on the substrate. In the pulsating mode, it shows an equal space between droplets. Material properties also need to be added into consideration in regard to the matching process.

Finally, the effect of surface tension needs to be considered. In Taylor’s theory, the formation of a jet in the cone-jet transition only occurs when the stress induced by the electrical field (ε₀E2/2) is larger than the stress induced by surface tension (2γ/r), and a square dependence exists between the onset voltage and the surface tension. If the surface tension of the liquid is too high, triggering of corona discharges prevents electrostatic atomization in the air[57]. The effect of lowering surface tension stress at the liquid apex by adding surfactants is the same as an increase of the Maxwell stress[20]. The suppression of low-frequency spray and the reduction of cone length at low surfactant concentrations is probably related to a weak reduction of the surface tension of the liquid cone[20]. The phenomenon of corona discharge usually occurs with liquids having a high surface tension and thus requiring high fields to overcome the surface tension stress[57]. The corona can be suppressed by increasing the dielectric strength of the surrounding medium, such as Freon 12, CO₂, and SF₆[41] or lowering the temperature of the ambient air[31,57]. The hysteresis phenomenon that the minimum voltage needed to maintain the cone-jet mode is lower than the voltage needed to initiate the cone-jet mode needs to be considered[57].

Wettability of capillary may cause a liquid ridge over the entire periphery of the nozzle outlet or only on the small part of it. During the growth of the ridge, the flow rate of the atomized liquid is lower than the total rate, causing the electric field to decrease due to the increase in the section of the capillary[57]. Wettability can be reduced by coating non-wettable substance around nozzle except on the outlet section[57].

3.2.2 Characteristic Dimensions and Scaling Law Related to Cone-jet Transition

3.2.2.1 Ganan-Calvo’s Scaling Law for Four Different Conditions

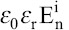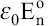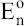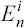In the model of Ganan-Calvo[66], EHD spraying in steady cone-jet mode is a quasi-electrostatic quasi-one-dimensional (1D) condition based on two assumptions: (1) The inner electric displacement , is small compared to the displacement, , where and are the normal outer and inner electric fields on the jet’s surface, respectively; (2) the radial variations of the liquid velocity are small compared to the average velocity for most liquids and EHD spraying conditions. Since the transverse section of the cone region is very large compared to that of the emitted microjet, and the liquid velocity is small compared to that in the microjet, the bulk ohmic electric conduction is dominant in the cone with very small inner electric fields [55,60,67]. Thus, the cone region is considered as perfectly electrostatic[35,60]. The axial electric field E_z should be of the order of the normal electric field at the cone:

In the ohmic model or “leaky dielectric” model[5,16], an ohmic constitutive law for the current in the cone-jet transition region is assumed[53,66].

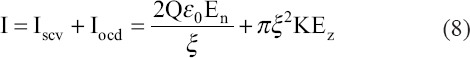
where I_scv is surface convection current, I_ocd is ohmic bulk conduction current, Q is emitted flow rate, is normal electric field on the jet’s surface, ξ is radius of jet, and K is liquid electric conductivity[66,68]. The point where the surface convection current equals the ohmic bulk conduction current is located close to the jet’s origin[67].

The pressure difference across the jet’s surface is balanced by the normal electrostatic stress. The polarization stress 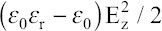is negligible[66]. Thus,

The kinetic energy per unit volume of the liquid becomes of the order of the electrostatic stress once the jet is developed and the gradient of the kinetic energy in the axial direction is mostly balanced by the tangential electric stress resultant on the jet’s surface[66]:

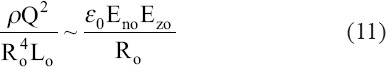
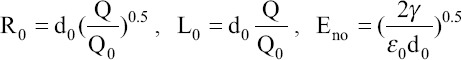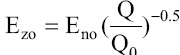Here , and are the characteristic values of the jet’s radius, axial length, outer normal electric field, and tangential electric field. The characteristic flow rate 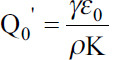, characteristic distance 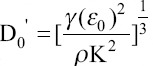, and characteristic current 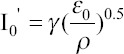are shown in the dimensionless analysis above[66].

Ganan-Calvo defined two dimensionless expressions for flow rate[26]:

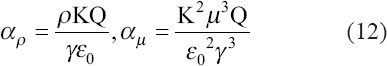
When the inertia stress is large, the dimensionless flow rate is the ratio of flow rate, Q, and dimensional variable sets (γε₀/ρK). When viscous stress is large, the dimensionless flow rate is the ratio of flow rate, Q, and dimensional variable sets 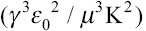. The dominance of surface tension is a marginal situation[26].

For six different situations, Ganan-Calvo et al. identified different scaling laws for the jet diameter D_j and the electric current I[26]. Three of them have been found in published experimental data, and they are presented below:

• IE-scaling: Dominance of inertia and electrostatic suction in the limits of 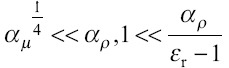Where, D_j is the same as the characteristic value (R₀)[26]:

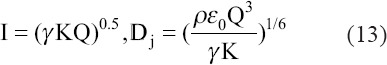
The IE scaling law is the most common regime. It has been widely verified in numerous experimental works[26,66,69-71], and data for octanol were accord with this scaling law[26,31].

• IP-scaling: Dominance of inertia and polarization forces in the limit of 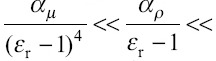[26]:

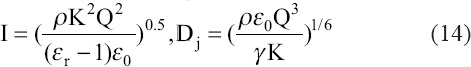
The IP scaling law is used for polar liquids, and the scaling of jet diameter is the same as for IE scaling, no matter whether the dominant factor is electrostatic or polarization force[26]. Data for water and formamide tend to match with the IP scaling solution[26,31].

·• VE-scaling: Dominance of viscous force and electrostatic suction in the limit of 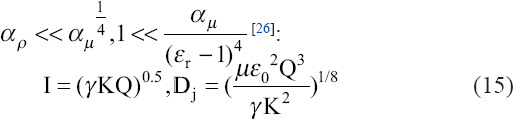[26]:

The IP scaling law is applicable to high viscosity liquids with a sufficiently large electric conductivity. The trend of this scaling law has been confirmed by experiments that use glycerol with different electrical conductivities[26].

3.2.2.2 De la Mora’s Scaling Law

In the model of De la Mora and Loscertales, the conductivities of the tested liquids are all in the range of 10^–4 S/m and above; hence, these are considered as high conductivity liquids. They concluded that the current and jet structure for liquids with high conductivities are insensitive to changes of needle voltage, diameter, the distance between two electrodes, the meniscus shape, and the spray structure[31]. The static Taylor equilibrium is maintained to the point where the flow time becomes shorter than the electrical relaxation time. Beyond this point, there is a rapid transition to a cone-jet. After the same point, the ohmic bulk conduction current (I_ocd) that is dominated in the cone also fast transfer to surface free charge convection current (I_scv) by the accelerating liquid stream, which is dominant close to jet’s end where is very small cross-section and large liquid velocity[31,32,55]. In the cone-jet transition area between these two regions, both conduction and convection are of the same order[55].

A non-dimensional factor, η², can be defined as the ratio of inertia pressure (ρQ2/r⁴) where ρ is liquid density, Q is the flow rate, and r is local radius, and capillary pressure is (γ/r)[31,32].

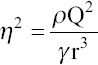
The formation of the jet may be determined either by inertia or by charge relaxation, depending on which of these two phenomena acts first as the cone apex is approached[31]. When η is smaller than unity, the diameter of jet scale as characteristic length r*. In the opposite limit, where η is much larger than one, the diameter of jet scales as characteristic length R*[31]. A characteristic distance λ from the cone apex is closely related to the jet radius[31], and it also relates to the thickness of surface charge layer, which is built up by the bulk conduction[72]. When the jet scaling length r*, which is the same magnitude of charge relaxation length, λ, where hydrodynamic time, t_h is of the order of the electrical relaxation time, t_e, the characteristic distance, r*, is expressed as the following equation[31,32].

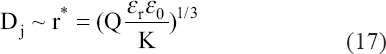
When η equals to one and r equals to r*, the minimum flow rate for the stable cone-jet structure is found, and it is also known as the characteristic flow rate[31,32]. The minimum flow rate is expressed as:

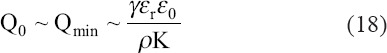
The characteristic distance, d₀, can be obtained from the characteristic flow rate, Q₀, through the equation below:

When the dynamic pressure 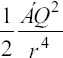becomes comparable with surface tension, γ/r, the diameter of jet scale as characteristic length, R*[31].

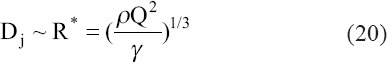
The intermediate region which is analyzed in the model of Ganan-Calvo provides consistent for matching the cone to transition region[26]. Interestingly, when two characteristic distances (r* and R*) are multiplied together, the product of these two characteristic distances is similar with the expression of jet diameter for IE or IP scaling. In the liquid meniscus, charges are transmitted by convection and conduction at the charged interface and only by conduction through the bulk[31]. In this model, the surface conduction term is ignored since it is small compared to surface convective term, and the surface convection current is then given by[31]:

I_scv=2πru_sσ (21)

Where u_s is the liquid speed at the interface and the free surface charge density, σ, equals to 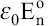. At the point where charge relaxation become non-negligible and the current I which jet carries is given[31]:

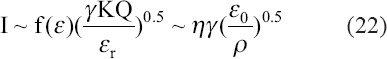
Where f(ε), as obtained from experiment, is a function of ε. Scaling law expressed in equation (22) is similar with scaling law of current in IE regime of Ganan-Calvo model, and actually f(ε) become very small when the dielectric constant is small. When η is equal to one, characteristic current, I₀, is closely related to current, I, and can be obtained from:

The parameter Z which equals to 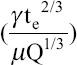is defined to measure the radial variation in the axial velocity profile of the jet[31]. The electrical shear stresses which tend to make the liquid velocity larger at the surface than at the core, while viscosity tends to make the axial velocity radially uniform.

In conclusion, the scaling model presented above has been confirmed by asymptotically self-similar solutions, and it shows that the emitted current and diameter of jet mainly depend on flow rate and liquid properties. They argue that the jet radius is independent of the boundary condition and applied potential since the typical jet radius is sufficiently smaller than the local size of the tip region. Table 1 summarizes scaling laws that describe the dependence of jet diameter and magnitude of current on working parameters.

Table 1.

A summary of scaling laws that outline the relationship between processing parameters and diameter of jet or emitting current

Name	Dominant conditions	Scaling of jet diameter	Scaling of current	Material	Reference
GanonCalvo scaling law for high electric conductivity (Above 10−4 S/m)	IEscaling (inertia stress and electrostatic suction)		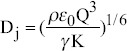I=(γKQ)0.5	Nonpolar liquid with low viscosity, such as Octanol
	IPscaling (inertia stress and polarization force)		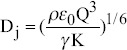	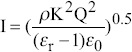Polar liquid with low viscosity, such as water, and formamide
	VEscaling (viscous force and electrostatic suction)		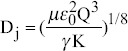I=(γKQ)1	Ink material with high electric conductivity, such as glycerol
	VPscaling (Viscous force and polarization force)		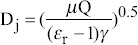	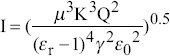Not found in published paper
De la Mora scaling law for high electronic conductivity (Above 10−4 S/m)	Hydrodynamic time and electrical relaxation time		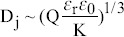	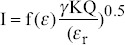Ethylene glycol
	Inertia stress and surface tension		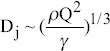	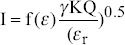Glycerine solution
Choi scaling law	Electrical field force and surface tension		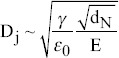Not mentioned in the reference paper	Water (0.1 mM KBr added), and Glycerine

However, Hohman et al. obtained a different scaling law from electrospinning experiments, and they found current not only depends on flow rate and material properties but also applied voltage, shape, and material of nozzle[73]. Discrepancies in scaling laws of electrospray and electrospinning may be attributed to the following reasons. Solutions from steady-state equations for electrospray are a function of imposed flow rate, current, and voltage drop between two electrodes. Boundary condition on a surface charge is that jet shape is matched to a perfectly conducting nozzle. However, the current is determined dynamically in electrospinning experiment, and flow rate and field strength are only independent parameters. Hohman et al. found that the radius of the jet has already decreased substantially before entering the asymptotic regime. Thus, current is determined more than just the behavior in the asymptotic regime. Numerical steady solutions have only been obtained for low conductivity material (10⁻⁶ S/m) at the high electric field after counting fringe fields of the nozzle and considering small surface charge density as a boundary condition at the nozzle[73]. The electric field around nozzle and boundary condition become key factors to influence shape and charge densities on the liquid jet. It is helpful for understanding this influence to explore what the predominant charge transport mechanism near the nozzle is. Differences in geometry setup are also a possible reason to lead different scaling law.

3.2.3 Pulsating Cone-jet Regime

Although most attention is focused on the “continuous regime” where a jet is continuously ejected from its apex, a continuous regime only happens for certain ranges of the operating parameters. Changes in liquid properties can also cause instabilities[30]. The D-O-D pulsate printing as produced by an external voltage pulse has become more popular due to low reagent consumption and high ion transmission efficiency at small flow rate[28]. The frequency of the lowest excitation mode for a negligible amount of charge is expressed as [30] and can be calculated by equation (24) which is derived from the frequency spectrum for the capillary waves on the surface of a charged droplet proposed by Rayleigh[12].

Where r is the droplet radius. Marginean et al. found[30] that equation (24) can also express the relationship between the square of the pulsation frequency and the cube of the anchoring radius of the menisci (the position of the contact line at the tip of the capillary during the liquid recoil phase) for low-conductivity liquids and relatively large nozzle radius. They also found that the effect of charge in this region is negligible.

Another finding is that the capillary waves not only governs transitions associated with the meniscus (dripping mode to spindle mode) but also influences the breakup of the liquid filament (varicose to kink)[30]. Choi et al. proposed a scaling law for jet diameter in the pulsating cone-jet regime, based on data from their experiments and literature[64]. They defined the ratio between the surface tension and the electric field forces as the “electrical capillary number (Ca),” and considered D_j and D_n as characteristic length scales associated with the surface tension force and the electrical field force separately[64]. The scaling law for jet diameter is:

This scaling law is different from those in section 3.2.2; a simple reason is that Choi et al. obtained diameter of the jet at initiation condition where the jet is the widest. Choi et al. substituted equation (25) into equation (24) to derive a scaling law without droplet radius. The pulsation frequency read as:

Chen et al. proposed a different model for the intrinsic pulsations frequency; this is related to the drop formation rate, Q, in equation (27), (28).

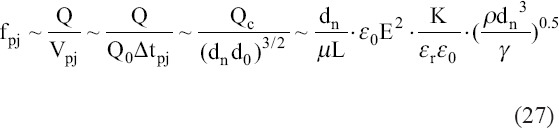
In conclusion, as upstream flow rates are low, the cone formation rate is affected by stress at the liquid-to-air interface and by viscous drag in the thin nozzle, and Taylor cone only deforms at the tip[28]. Equation (27) is used to obtain frequency at a low flow rate, and the drop formation rate scales as d4E2L⁻¹ where d is inner diameter of nozzle, E is the nominal electric field, and L is the nozzle length[28]. However, as supplied flow rate is not limited by upstream conditions, the equation (24) is applied to acquire frequency (Chen, 2011). Since equation (25) reveals a 0.5 power dependence between the diameter of jet and nozzle, it implies this equation may not be employed for high conductivity liquid (≥10⁻⁴ S/m).

3.3 Theory and Analysis of Jet Stability

In EHD inkjet printing, a continuous fine jet is generated at the apex of a liquid cone in the cone-jet mode and the length of jet increases with the viscosity, the resistivity and flow rate of liquid[18]. The field strength at the tip of the jet increases with the length of the jet, due to a decrease of the electrical field shielding by the large outer diameter of the capillary and also a decrease of the diameter of the accelerated jet, which behaves as a vena contracta[74]. This corresponds to increasing field stress at the tip of the jet in the direction toward the counter electrode[20]. It is difficult to stabilize and control the trajectory of submicron jets under an electric field and jet may have different instable status. When the charge of the jet is not too high, liquid jet is broken up into drops by varicose instabilities as shown in Figure 4 and satellite droplets may be created at the moment of the breakups[18]. The process of a breakup may degrade resolution on the substrate. The smaller droplets move away from the axis of the jet, which is faster than the larger ones[18]. For slightly higher voltages, lateral kink-type instabilities appear, and the jet stretches out into fine droplets of different sizes[18]. Thus, a big challenge for utilizing the electrically driven cone-jet transition as a writing device still exist in overcoming the rapid disintegration in electrospray and controlling the whipping of the jet in electrospinning[38]. The common feature of them is no boundary jetting methods, but axisymmetric instability is applied on breaking up the jet into numerous tiny droplets in electrospraying, and non-axisymmetric, known as whipping action, is used to thin the liquid jet and deposit it as a fiber filament in electrospinning. However, both of instabilities need to be prevented from high resolution printing process. In the following part, the theory of the jet stabilization is discussed, and then the stabilization of jet under an electric field is considered.

Figure 4.

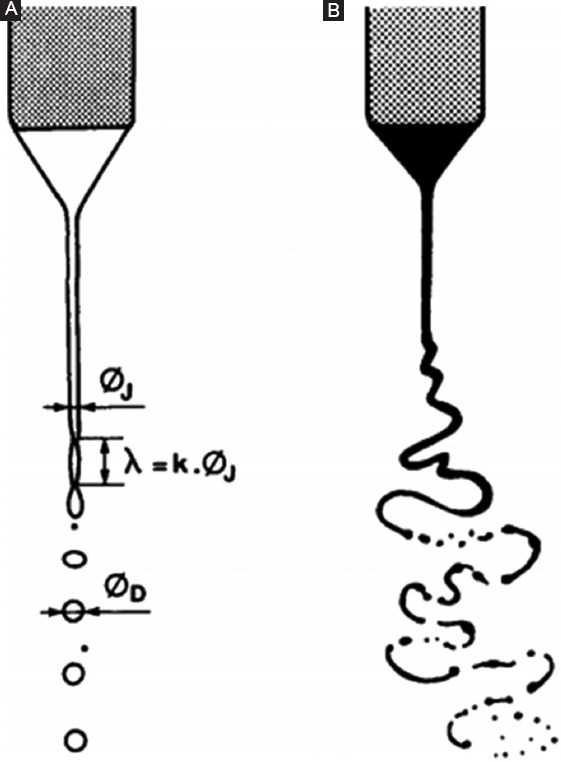
Cone-jet mode: (A) Varicose instabilities; (B) kink instabilities[18]. Adapted by permission from Michel Cloupeau et al. (1994) under the Elsevier.

When a liquid jet is either neutral or lower surface charging under the condition of lower field strengths, the breakup of a jet into droplets is attributed to the effect of surface waves[75]. Surface waves propagating along the surface of a jet are generated by disturbances of the jet[61]. As the amplitude of surface waves of an appropriate wavelength (“varicose waves”) is enhanced by surface tension forces, they lead to the breakup of a cylindrical jet into droplets with radius r=1.89α[20]. This mechanism is well established for uncharged jets and was first described by Rayleigh[76]. Rayleigh reveals that disturbances on a jet with wavelengths greater than the circumference of the jet will grow, and rapid growing disturbance will control the breakup of jet[77].

3.3.1 Three Instability Modes of a Charged Jet

Saville performed qualitative analysis for the stability of an uncharged liquid cylinder in the longitudinal electric field[62], and this analysis ignores the presence of surface charge on the jet and thinning of the radius[78,79]. Another analysis of stability is for a charged cylinder in a radial electric field (without tangential field) and a constant radius jet[80]. Hohman et al. developed a 1D model for a long and slender object made of a leaky dielectric material, and this model is asymptotically valid in the assumption that tangential stress caused by the electric field must be much smaller than the radial viscous stress[79]. They performed a local linear stability analysis by considering axisymmetric perturbation to a charged cylinder of constant radius under an assumption that the wavelength of the perturbation is much smaller than the characteristic decay length of jet[79]. They identified three different instability modes that are axisymmetric extensions of the classical Rayleigh instability, and two conducting modes, which only exist when the conductivity of fluid is finite, including the axisymmetric conducting mode motivated by different time scale for fluid response and axial surface charge arrangement, and a whipping conducting mode caused by static charge density of jet, which dominated in local electric field. Rayleigh instability is suppressed when the electrical pressure per unit length of the jet exceeds the surface tension pressure per unit length with an increase of electric field and surface charge density, and conducting mode which is raised from the interaction of electric field with a surface charge on the jet makes jet unstable[79]. Both the axisymmetric modes are stronger than the whipping mode at low fields by adding the effect of viscosity and surface charge, but the whipping mode is stronger than both of the axisymmetric modes at high fields[79]. Figure 5 compares the theoretical operating diagrams for glycerol and PEO jet with experimental measurements of the instability thresholds[73]. The shape of operating diagram for a less viscous and highly conducting fluids is similar to the range of cone-jet mode in electrospray[73]. The lower threshold of onset of cone-jet is identified as cessation of varicose instability, and upper threshold is considered as onset of whipping. With increase of electrical conductivity, the critical flow rate of cone-jet mode decreases. A higher surface charge density in higher conductivity fluids leads a stable jet at a lower flow rate due to suppression of Rayleigh mode[18,57]. In other words, steady cone-jet which is most used for EHD high-resolution printing should locate in the area between varicose and whipping instability in E-Q operating diagram.

Figure 5.

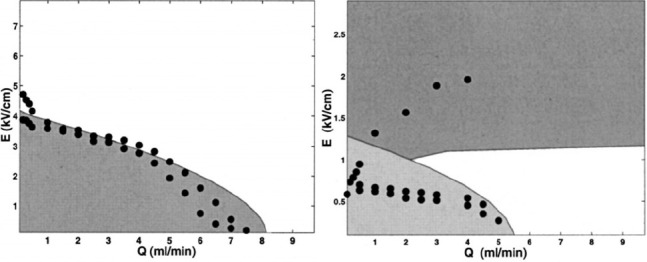
Operating diagram for (a) glycerol jet (K = 0.1 × 10⁻⁵S/m), ρ = 1.26 × 10³ Kg/m³, μ = 1.87 Pa·s). The shaded region is varicose perturbations, and no whipping instability is present. (b) PEO jet (K = 1.2 × 10⁻² S/m, ρ = 1.2 × 10³ Kg/m³, μ = 2 Pa·s). The lower shaded region is varicose perturbation, and the upper shaded region is whipping instability. The points represent experimental measurements are consistent with theoretical prediction[73]. Adapted by permission from Moses Hohman et al. (2001) under the AIP Publishing LLC.

In Table 2, the main models mentioned in this review are summarized by the phenomenon, the name of models, assumptions, advantages, and disadvantages of the model.

Table 2.

A summary of theoretical models for three phenomena under different assumptions, and their advantages and disadvantages

Phenomenon	Theories or models	Assumption and conditions	Advantages	Disadvantages
Conical meniscus	Taylor electrohydrostatic model (Taylor cone)	Semivertical angle of cone is 49.3°; Pressure is zero; Neglected weight of the liquid cone	Obtaining critical voltage value for jet emission from the tip of the cone	Semiangle is not always 49.3°; Approximate 10% difference from the critical voltage of experiment
Conejet transition	Leaky dielectric model; Surface couple model	Penetration of electric field lines into liquid; Appearance of surface electric charges	Described operating diagram of conejet for inks with partial electrical conductivity	Only for leaky dielectric material and stable conejet mode; Complexity in a mathematical method
Stability of a long and slender jet	Onedimensional model	Tangential stress caused by electric field must be much smaller than the radial viscous stress; Wavelength of the perturbation is much smaller than the characteristic decay length of the jet	Identified three instability modes based on electric field strength; Represented operating diagram of varicose and whipping instability thresholds	Inaccurate in low viscosity and/or imperfect conductor jet

3.3.2 Stability Analysis in Finite Conductivity and Permittivity Jets

Herrera et al. studied influence of arbitrary liquid viscosity, permittivity, and conductivity in the presence of a DC radial electric field, and found 1D average models are inaccurate in low viscosity imperfect conductor jet since an interfacial boundary layer may exist in the axial velocity profile[81]. These results show that the accuracy of 1D approximation increases with the increase of liquids’ electrical conductivity and/or viscosity by comparing results obtained from 1D approximation and two-dimensional leaky dielectric model[82]. They focused on axisymmetric capillary jet instability modes that are dominant in the moderate range of Weber number that is the ratio of average axial velocity, U, to capillary velocity (v_c).

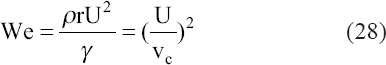
In the developed EHD jet, the axial electric field can be neglected since it is much less than radial electric field that is created by surface charge density located at the interface[60,69]. According to cubic roots of dispersion relation, Hohman et al. found three instable modes in the presence of an axial electric field[79], but Herrera obtained four-order dispersion relation (four modes) in the presence of radial electric field[81]. Artana et al. indicated that the intact length of the jet is proportional to the inverse of growth rate σ_m in the fastest growing mode under the assumption of electrified inviscid limit and perfect conductor limit[83]. Effects of relaxation parameter (α) that is the ratio of the capillary time (t_c) to the electrical relaxation time (t_e), liquid’s relative permittivity (β) and electric bond number (χ), which is the ratio of the electric pressure to capillary pressure are explored in this study.

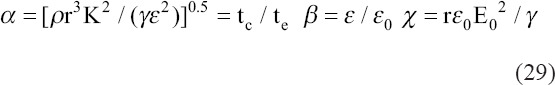
Where ε₀E₀ is surface charge density and E₀ is a radial electric field. With the increase of conductivity, the maximum growth rate σ_m increases and the wave number k_m decreases in the fastest growing mode in Figure 6A. Growing relative permittivity leads to a similar trend[81]. This figure shows that instability increases with the rise of breakup wavelength. The conductivity and permittivity do not influence a range of stability, but in Figure 6C, the instability lobe expands with an increase of electrical bond number[81]. Herrera et al. pointed out that tangential electric stress will attenuate the growth of perturbations and may promote longer liquid jets with moderate viscosity in the non-whipping jet regime for an imperfect conductor[81].

Figure 6.

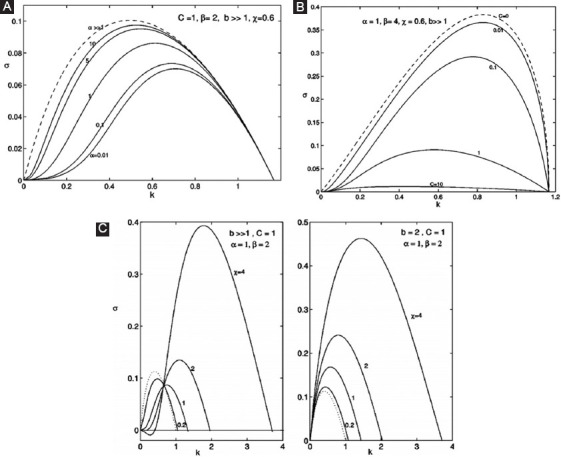
(A) Growth rate σ versus the wavenumber k for a jet with b (distance between two radial electrodes) >>1, χ = 0.6, C (Ohnesorge number) = 1, and β (liquid relative permittivity) = 2 and several values of the relaxation parameter α; (B) Growth rate σ versus the wavenumber k for a jet with different values of the Ohnesorge number C (b >>1, α=1, β=1, χ=0.6). (C) Growth rate σ versus the wave number k for a jet with b>>1 and b=2. The other parameters are fixed at C=1, α=1, and β=2. Several values of the electrification number χ are plotted[81]. Adapted by permission from Jose Lopez-Herrera et al. (2005) under the AIP Publishing LLC.

The effects of the viscosity can be reflected by comparing growth curves having different Ohnesorge numbers, C, defined as a ratio of viscous forces to capillary forces,

Viscosity does not change the stability limits, but it lowers the growth rate of any perturbation. The most unstable wavelength becomes longer with an increase of Ohnesorge number in Figure 6B, whereas the growth rate decreases[81]. A narrow interfacial boundary layer with high radial velocity gradients is produced by an axial electric field for quasi-inviscid free jets, and the axial field boundary layer is based on the balancing of axial stress and viscous term[81]. In a radial electric field, boundary layer becomes conspicuous when liquid is a poor-conductor, and the radial field boundary layer is formed by competition between oscillatory acceleration and viscous term[81]. The core velocity profile of poor conductor is insensitive to liquid conductivity, permittivity, and electric bond number because viscous stress is too small to counterbalance any electric shear stress, while the velocity of the boundary layer is changing with a distance of two electrodes[81].

The meniscus may globally be either stable or unstable up to values of the operational parameters, and the global stability of the liquid meniscus is a prerequisite for steady jetting[84]. The liquid flow accelerates from a subcritical to a supercritical regime at a critical point near the exit of feeding needle by considering self-induction effects and jets issued from Taylor cone are always supercritical at region before breakup point[67]. A point of instability is defined as a boundary line to separate the supercritical region and the breakup regions and supercritical region prevents upstream propagation of disturbance as long as the point of instability is far away from the critical point[67]. Transition between jetting and dripping is related to transition between convective and absolute instability transitions[85]. Convective instability is defined as the surface energy that is sufficiently smaller than the kinetic energy per unit jet length, and the disturbance can only propagate and increase downstream[85]. The disturbance can propagate and increase both upstream and downstream for absolute instability. The critical convective velocity in the developed jet that relates to critical Weber number mainly depends on the viscosity of fluid that scale as the Reynolds number during the transition between the absolute and convective instability. Herrera et al. introduced different electric parameters (relaxation parameter α, liquid relative permittivity β, and electric bond number χ) to the classical Leib and Goldstein curve and range of electric bond number χ are limited between 0 and 1 to avoid growth of kink instability[85]. In conclusion, final results disclose that the critical Weber number is not significantly influenced by the electric parameters at high Reynolds range[85]. Figure 7 shows experimental values of the Reynolds number as a function of the capillary number and most of the points are in stable cone-jet region which is above the continuous line (theoretical critical curves)[85]. At the low Reynold numbers, the stable region of the jet is affected by three electric parameters. At equipotential limit (α>>1), a relatively larger jet velocity is required for smaller jet diameter to achieve a stable region of jet and liquid relative permittivity β has no effect in this limit. However, at the frozen charge limit (α=0), critical limit of the stable region depends on β and electric bond number, χ, only. In sum, E-Q operating diagram in Figure 5 anticipates a range of steady cone-jet well, while the accurate shape of cone-jet stability for a specific material depends on dominated parameters at each region and boundary conditions.

Figure 7.

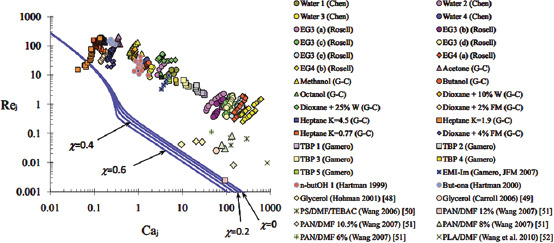
The continuous curve is theoretical predictions of the transition between absolute and convective instability. Most of the points from experimental values are in the region of convective instability[85]. Adapted by permission from Jose Lopez-Herrera et al. (2010) under the AIP Publishing LLC.

4. Conclusion

Although the EHD phenomenon has been known for more than 200 years, its working mechanism is still not fully understood. EHD phenomenon are controlled by multiple parameters, and they are coupled each other. On the one hand, it is complicated to simulate multi-physical free surface flow, and there are also limitations in simplifying assumptions in physics model. A ”Leaky-dielectric” model is only successfully applied to materials with relatively high conductivity. On the other hand, it is not always attainable before the mode obtained in experiments when the values of working parameters are given.

This paper reviews the initiation condition of cone-jet. The critical voltage predicted by Taylor does not account for EHD effect caused by subsequent jet emission, and the semi-vertical angle is not always Taylor angle. The following section study effects of processing parameters and materials properties on the operating diagram of cone-jet. Domain of cone-jet may become different by small changes in the selection of parameters. The minimum flow rate in operating diagram is not, simply, the flow rate due to the upstream pressure, but rather the specific flow rate that causes electrical stress to strip off (or shear) the surface charge layer of the fluid. Several scaling laws have been proposed to predict jet diameter and emitted current, and each of them is applied to different parametric ranges according to material attribute and working condition. Communities have not reached an agreement on the charge transport mechanism. In the future, it is helpful to study what the predominant transport mechanism is, especially near the nozzle. It is difficult to measure a thin free jet whose diameter is usually at the verge of optical resolution experimentally. It is known that a stable jet is a prerequisite condition for acquiring high printing resolution, but the theoretical prediction of jet stability still remains to be a difficulty. Understanding of this physical process requires more systematical studies on the formation of a stable cone-jet.

3D high-resolution printing as one of an important branch of EHD family is rising rapidly in recent ten years. In contrast to deposition in a small area by electrospray or thinning and bending process by electrospinning, high-resolution EHD printing can generate single droplet or continuous line at single micro-scale. Designs and recent applications of EHD 3D printing will be discussed in the next paper due to length limitation.