SUMMARY
The microtubule cytoskeleton plays critically important roles in numerous cellular functions in eukaryotes, and it does so across a functionally diverse and morphologically disparate range of cell types [1]. In these roles, microtubule assemblies must adopt distinct morphologies and physical dimensions to perform specific functions [2–5]. As such, these macromolecular assemblies—as well as the dynamics of the individual microtubule polymers from which they are made—must scale and change in accordance with cell size, geometry, and function. Microtubules in cells typically assemble to a steady state in mass, leaving enough of their tubulin subunits soluble to allow rapid growth and turnover. This suggests some negative feedback that limits the extent of assembly, for example decrease in growth rate, or increase in catastrophe rate, as the soluble subunit pool decreases. Although these ideas have informed the field for decades, they have not been observed experimentally. Here, we describe the application of an experimental approach that combines cell-free extracts with photo-patterned hydrogel micro-enclosures as a means to investigate microtubule dynamics in cytoplasmic volumes of defined size and shape. Our measurements reveal a negative correlation between microtubule plus-end density and microtubule growth rates, and suggest that these rates are sensitive to the presence of nearby growing ends.
RESULTS AND DISCUSSION
Microtubule-based assemblies, specifically interphase microtubule asters and mitotic spindles, have been characterized in discrete droplets of cell-free Xenopus egg extract to study microtubule self-organization and scaling phenomena [6–9]. In these emulsion droplets, however, it is difficult to collect images with a high enough signal-to-noise ratio and sufficient temporal resolution to characterize dynamic molecular-scale phenomena such as microtubule growth. To circumvent these limitations in a way that would still allow for precise control of extract volume, we used hydrogel photolithography [10] to confine cell-free extracts and microtubule asters within microscale enclosures of precise geometrical shape and size (Figure 1A).
Figure 1. Extract-laden hydrogel micro-enclosures.
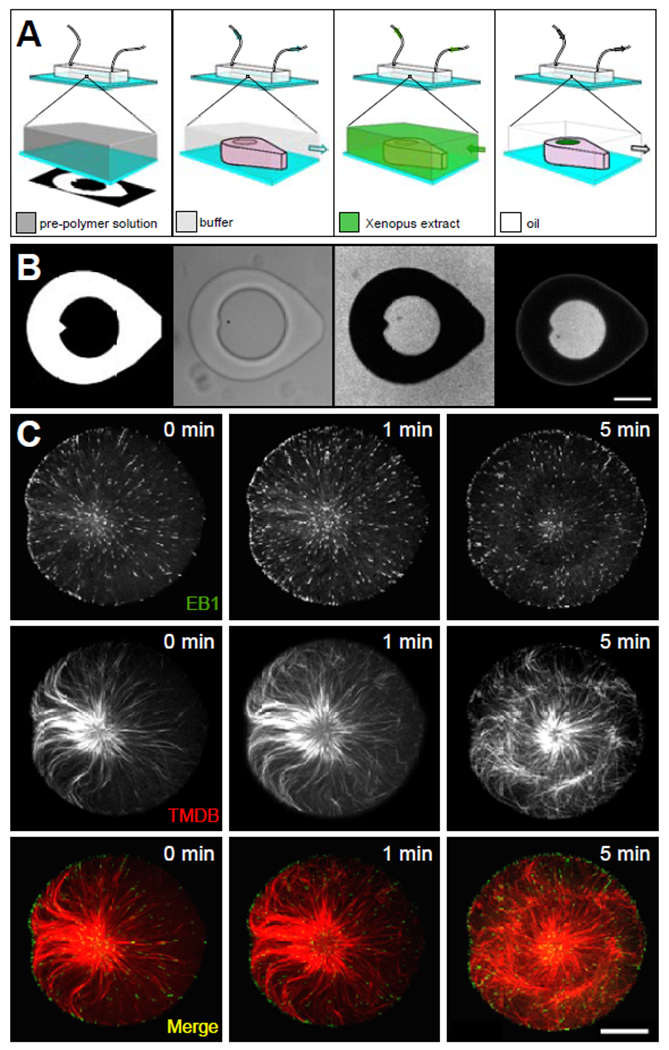
Schematic (A) and captured images (B) corresponding to the process for isolating discrete volumes of cytoplasmic extract in hydrogel micro-enclosures. The calibrated digital mask used to create hydrogel structures are pictured in the leftmost panels (see Figure S1A and Video S1). Schematic and bright-field image of the micro-enclosure (center-left panels), which is filled with Xenopus extract containing a soluble fluorophore (center-right panels) and then isolated by oil crossflow (rightmost panels). Center-right and the rightmost panel in (B) show fluorescent images of the micro-well and cytoplasmic extract visualized through EB1-GFP (scale bar in b = 50 μm). Microtubule aster formation (C) in micro-well enclosures visualized through EB1-GFP and a Tau-based fluorescent protein, mCherry-TBMD [13] (scale bar = 25 μm). 0 min corresponds to the start of the image series.
To generate photo-patterned structures on the coverslip surface, we placed a digital micromirror array in the optical path of a microscope and projected light patterns onto a pre-polymer solution of poly(ethylene glycol) diacrylate (PEGDA) contained within a polydimethylsiloxane (PDMS) microfluidic flow chamber 30 μm in height (Figure 1A, B; leftmost and center-left panels; Figure S1A). The positions of these enclosures within the device were dictated by the random spatial arrangement of artificial microtubule organizing centers (aMTOCs; [11]) within the pre-polymer solution (Video S1). By first generating a flow of extract into the device from one direction to fill the enclosures (Figure 1A, B; center-right panel), and then subsequently flowing in an oil phase (fluorinated oil/surfactant) from the opposite direction (Figure 1A, B; rightmost panel), we could trap aqueous volumes of extract within the confines of the hydrogel micro-enclosures (Figure 1A, B). It should be noted that the exterior tear-drop shape of the enclosures was important for isolating extract (or other aqueous phases) in hydrogel structures using oil crossflow (Figure S1B). With this experimental paradigm, we successfully isolated discrete volumes of cell-free extracts at the coverslip surface (Figure 1A, B; rightmost panel) with precise control of geometry and volume. aMTOCs confined in this manner were able to nucleate MTs and generate microtubule asters as described previously in bulk interphase egg extracts [11, 12] (Figure 1C). microtubule plus-ends and the microtubule lattice were visualized at the coverslip surface using EB1-GFP and a fluorescent microtubule-associated protein, mCherry-TBMD ([13]; Figure 1C).
Given that the size of macromolecular microtubule-based assemblies has been shown to scale with changes in the size of the cell in which they are made [6, 7, 14, 15], we predicted that changes in cytoplasmic volume might affect microtubule growth rates. To test this hypothesis, we used our hydrogel experimental platform to capture aMTOCs in cylindrical micro-enclosures of increasing diameter. The range of diameters tested (equivalent to spherical cells ranging from 30 to 115 μm in diameter [Ø]) was chosen based on the range of blastomere sizes in which in vivo mitotic spindle scaling has been observed ([15]; Figure 2A). The extracts used in these experiments were supplemented with a low concentration of EB1-GFP (60 nM) to visualize and track growing microtubule plus-ends. Subsequent analysis of time-lapse recordings of EB1 comets using both automated tracking and manual kymographs allowed us to measure microtubule growth rates and plot them versus micro-enclosure volume (Figure 2B; Figure S1E).
Figure 2. Effects of cytoplasmic volume on microtubule growth rates.
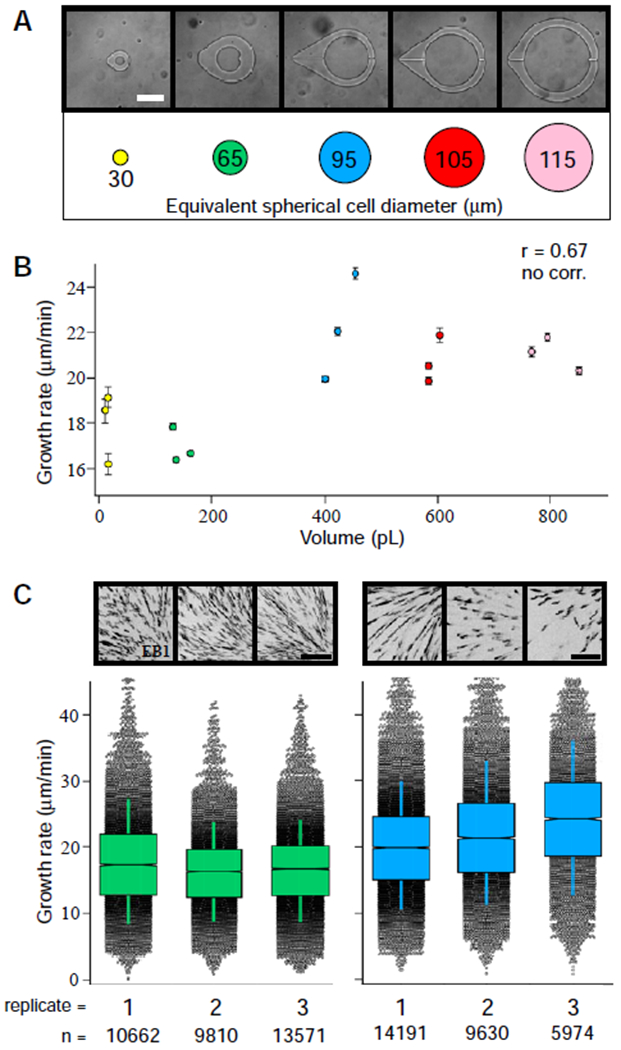
(A) Cylindrical micro-enclosures of increasing internal diameters are shown along with their equivalent spherical cell diameters (scale bar = 75 μm). (B) Microtubule growth rates plotted as a function of cytoplasmic volume (see also Figure S2E). Error bars equal two SEMs. The Pearson correlation coefficient (r) is indicated at the top of the graph and is significant if p < 0.01 (the absence of a correlation is indicated otherwise). A comparison of microtubule growth rates (C) in the experimental replicates for ~160-pL (left) and ~400-pL (right) volumes (~65 μm and ~95 μm Ø, respectfully; scale bar = 5 μm). See also Figure S1C, D and Video S2 and Video S3. Box plots feature a Tukey-style interquartile range, with whiskers indicating one SD of the median. Notches approximate the 95% confidence interval for the median. Representative max-intensity projections for each imaging series displaying EB1 signal in black are shown above the graphical data. The total number of EB1 tracks (n) recorded for each imaging series are displayed at the bottom for reference.
Microtubule growth rates showed some correlation with cytoplasmic volume within our system, however, most of the observed variation could not be explained by a linear model (R2 = 0.45). For example, in volumes as low as ~13 pL, we observed growth rates that were statistically higher or indistinguishable from those found in ~160 pL enclosures (corresponding to spherical cells of ~30 and 65 μm Ø, respectively), and microtubule growth rates seemed to plateau at volumes above ~400 pL (spherical cells of ~95 μm Ø; Figure 2B). We also observed large, statistically significant differences in microtubule growth rates under near-isovolumetric conditions (e.g., see the spread observed in the data points for enclosures around 400 pL in volume in Figure 2B; Figure S1D). Taken as a whole, these observations prompted us to identify other factors that might better account for the observed variation of microtubule growth rates. Indeed, when we compared EB1-GFP signal densities within each ~400-pL device, we found large differences in the total number of tracked microtubule growing ends (Figure 2C; Video S2). In contrast, both EB1 signal density and microtubule growth rates observed in ~160 pL devices (cell diameter of ~65 μm) showed less device-to-device variation (Figure 2C; Figure S1C; Video S3). We speculated that the measured differences in microtubule growth rates observed in similar cytoplasmic volumes might be caused by differences in microtubule plus-end density, rather than changes in cytoplasmic volume. This would be consistent with a scenario in which each growing microtubule plus-end acts as a sink for structural components (i.e., tubulin) and/or +TIP proteins [16–19].
To determine whether microtubule plus-end density is a more reliable predictor of microtubule growth rates within our system, we re-plotted microtubule growth rates versus EB1 density (Figure 3A). Over the range of EB1 comet densities measured, microtubule plus-end density negatively correlated with microtubule growth rates and better accounted for the device-to-device variation found in microtubule growth rates under near-isovolumetric conditions (Figure 3A; R2 = 0.88. This observation was confirmed using manually recorded growth rates and EB1 densities, suggesting this trend is not an artifact of automated tracking (Figure S1F). These data are consistent with the idea that growth rates are regulated by growing-end competition for a limited supply of components or local regulators [20–22].
Figure 3. Microtubule growth rates as a function of microtubule plus-end density.
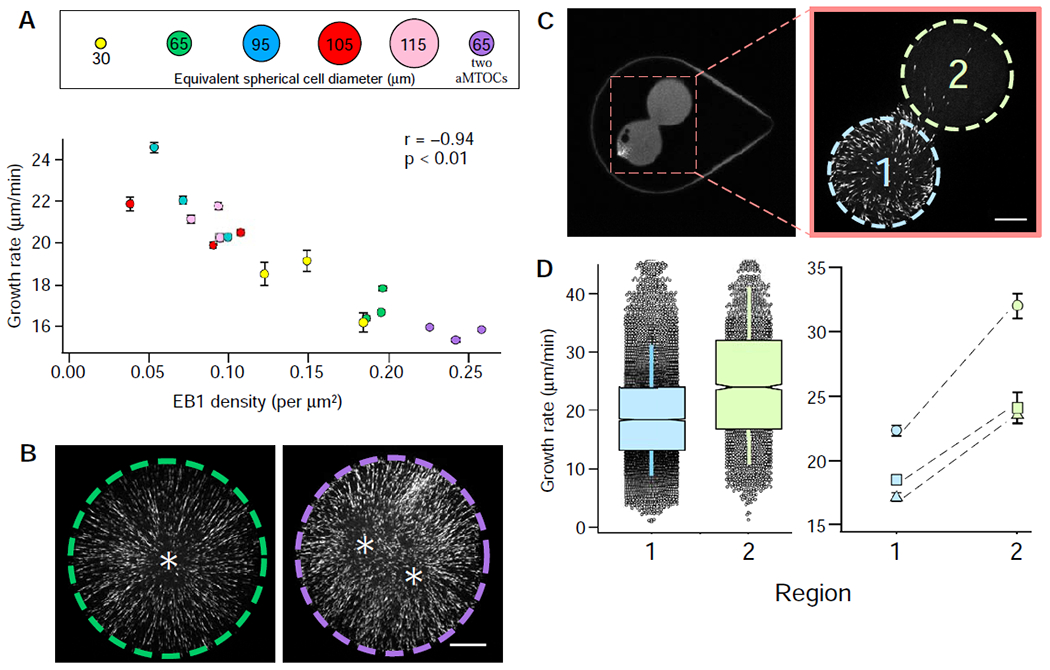
(A) Microtubule growth rates displayed as a function of EB1 comet density (see also Figure S2F). Error bars equal two SEMs. Pearson’s correlation coefficient (r) is indicated at the top of the graph and is significant if p < 0.01. (B) The effect of an additional aMTOC, with representative images showing EB1 signal from captured time-lapse series (see also Video S4). The left micro-enclosure (green dashed line) has one aMTOC, whereas the right micro-enclosure (purple dashed line) has two. Quantified microtubule growth rates are displayed in the graph in (A). Asterisks denote the relative positions of the aMTOCs (scale bar = 15 μm). (C) Hourglass-shaped micro-enclosure. The area indicated in the left panel is shown at higher magnification in the right panel and includes the two lobes of the hourglass enclosure (region 1 in light blue and region 2 in light green; scale bar = 15 μm). The left and right images were acquired from two different hourglass-shaped micro-enclosures. (D) Microtubule growth rates from the two regions of the hourglass micro-enclosures. The left graph displays grouped microtubule growth rates from the two regions of the micro-enclosure as box plots featuring a Tukey-style interquartile range (IQR), with whiskers indicating one SD of the median. Notches approximate the 95% confidence interval of the median for three different micro-enclosures. The right graph shows paired microtubule growth rates from the two regions of the hourglass micro-enclosure for three different enclosures. Error bars equal two SEMs. See also Figure S1.
By this logic, we hypothesized that changes in microtubule plus-end density would lead to correlative changes in microtubule growth rates. To test this, we increased microtubule plus-end density by capturing two aMTOCs in ~160-pL micro-enclosures (Figure 3B; Video S4). With the additional aMTOC, we indeed observed greater densities of EB1 comets, which resulted in measured decreases in microtubule growth rates (Figure 3A; “2 aMTOC”). Increased EB1 comet density resulting from the additional aMTOC suggests that the nucleation capacity of the extract is not taxed by a single aMTOC. However, analysis of nucleation rates from single aMTOCs suggests that volume-dependent changes in aMTOC nucleation rates plateau at volumes above ~130 pL (Figure 1G). Overall, these observations confirm that microtubule growth rates are sensitive to changes in global microtubule plus-end density. Importantly, we did not observe the same trend between microtubule plus-end density and catastrophe frequency, which was relatively constant across all extract volumes tested (Figure S2A; R2 = 0.23). Though we acknowledge that changing the number of aMTOC microtubule-nucleation sights might affect microtubule growth rates via a different mechanism (see Discussion), we reasoned that the link between microtubule plus-end density and microtubule growth rates might depend on the availability of key microtubule associated proteins (MAPs) and their diffusion and capture at microtubule growing ends [17, 23].
If microtubule growth rates are diffusion-limited in our system, one would expect spatial differences in microtubule plus-end densities to impart a local effect on microtubule growth rates. To test this, we generated hourglass-shaped micro-enclosures and trapped a single aMTOCs in one of the two connected lobes (Figure 3C). In each of these experiments, the lobe containing the aMTOC exhibited a locally higher EB1 comet density than the unoccupied lobe. A comparison of microtubule growth rates in each lobe showed significant differences in microtubule growth rates (Figure 3D), despite all growing ends being contained within the same continuous cytoplasm. Consistent with our previous findings, the regions containing lower microtubule plus-end densities displayed the highest microtubule growth rates (Figure 3D). This result suggested a possible role for a diffusion-limited mechanism in regulating microtubule growth rates [17, 24].
The observed variation in microtubule growth rates within a single cytoplasm led us to explore the length scales over which microtubule growth rates might be sensitive to spatial differences in microtubule plus-end density. To identify the local plus-end density experienced by each EB1 comet over its lifetime, we developed a custom MATLAB code that uses positional data obtained from u-track software [25, 26]. This code allowed us to define a search area projected from the center of each comet and then to identify and count the number of neighboring EB1 comets found within that area over the lifetime of the tracked comet (Figure 4A). This analysis, termed “local plus-end density”, was then repeated for all tracked EB1 comets in the image series.
Figure 4. Microtubule growth rates as a function of local microtubule plus-end density.
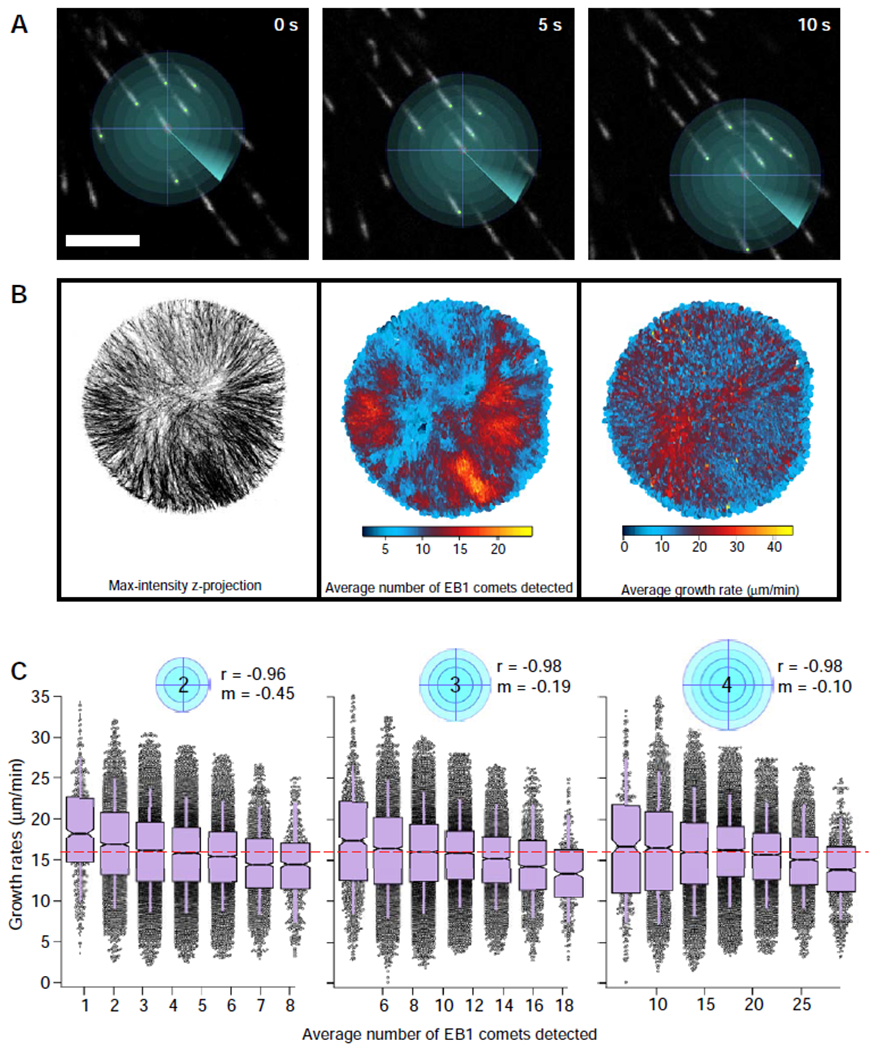
Pictorial representation (A) of local density analysis, showing a series of search radii projected from the center of an EB1 comet over its lifetime (scale bar = 5 μm). (B) A micro-enclosure supplemented with two aMTOCs depicted as a max-intensity z-projection (left panel). The average velocity and average local density of each EB1 comet plotted at each coordinate position of the comet’s lifetime (center and right panel, respectively). The average local density indicates the number of EB1 comets detected within a 3 μm search radius. See also Figure S3. (C) Average local density as a function of the search radius (indicated by blue circles), displayed as a box plot with bin sizes being equal to a 10% increment of the maximum density observed at that search radius (red dashed line indicates global density of the micro-enclosure). Box plots feature a Tukey-style IQR, with whiskers indicating one SD of the median. Notches approximate the 95% confidence interval of the median. See also Figure S2D and S4. See also Video S4.
We first analyzed the relationship between local plus-end density and microtubule growth rates in a time-lapse image series in which spatial variation in growing plus-end density was qualitatively evident (one of the “two aMTOCs” time series in Figure 3A, B; see also Video S4). This allowed us to compare regions of varying plus-end density at similar radial distances from the aMTOC. Moreover, the simple cylindrical geometry of the extract as confined in this device allowed us to rule out the possibility that spatial signaling gradients emanating from the aMTOC might contribute to the differences in microtubule growth rates observed in our two-lobed devices (Figure 3c, d). After determining the local plus-end density experienced by each EB1 comet within a 3-μm search radius, we plotted the average local density and average growth rate for each EB1 comet over its lifetime against the x-y position (Figure 4B; center and right panel, respectively). Consistent with the negative correlation we observed between global plus- end density and mean microtubule growth rate (Figure 2A), regions with lower microtubule growth rates showed higher local microtubule plus-end densities (Figure 4B). Comparisons of EB1 comet speeds using kymographs generated from two regions with distinct EB1 comet densities within the same micro-enclosure (Figure S2E) confirmed a similar relationship.
To better characterize the relationship between local microtubule plus-end density and microtubule growth rates, we performed the local density analysis over a range of different search radii (Figure 4C). The output from each search radius was binned and plotted, with each bin centered on the average local density contained within that bin (see Figure 2D). This analysis revealed that local microtubule growth rates were negatively correlated with local microtubule plus-end densities (Figure 4c). Not surprisingly, at smaller search radii, microtubule growth rates were more sensitive to local growing-end density (reflected in the larger negative slopes of linear fits). In contrast, as the search radius was increased, the slope of the linear fits approached zero, with the average velocity of each bin closer to the mean global microtubule growth rate of the entire micro-enclosure (red dashed lines, Figure 4C). This relationship between local microtubule plus-end density and microtubule growth rates was also observed across a range of cytoplasmic volumes (Figure S3, S4), suggesting that diffusion of components, rather than the absolute protein content of the cytoplasm, is responsible for the observed local density effect. In addition, these measurements indicate that the ability of a growing microtubule end to “sense” differences in growing microtubule plus end density is most acute at distances shorter than a few microns. Though we repeated these analyses using smaller search radii, the small sample sizes that resulted precluded a rigorous statistical analysis of the data (not shown).
Mechanistically, these results suggest (i) that each microtubule growing end might act as a local sink for either tubulin or key regulators of microtubule growth (microtubule plus-end competition), or (ii) that steric hindrance and changes in viscosity within dense microtubule polymer networks impede the loading of components onto microtubule plus-ends [24, 27]. Mechanism (i) requires either a limited source of structural components or the limited translation or rotational diffusion of these same key elements. Predictions for mechanism (ii) are less clear, as crowding effects due to large crowding agents (e.g. BSA, PEG, etc.) typically increase rates of chemical reactions through an “excluded volume effect”, whereas small crowding agents (e.g ethylene glycol, glycerol) slow down the same reactions in a diffusion-limited manner [24, 27, 28].
In summary, our local density analyses suggest that a steady-state dynamic microtubule assembly can experience a global depletion of components, whereas an individual microtubule plus-end might experience a local component gradient dictated by the presence and proximity of other growing microtubule ends. We speculate that these density-dependent effects likely exist because of constraints imposed by the slow diffusion of microtubule structural components and/or +TIP-localized growth–promoting factors. The case could be made for free α/β-tubulin heterodimers (tubulin), but a steady-state mean-field model for the concentration of tubulin near a growing microtubule end predicted that local tubulin concentration returned to the bulk concentration at ~50 nm from the growing microtubule tip [16], a distance well below the measured length scale of the density-dependent effect we have observed. We note that the in extract conditions used in our studies differ considerably from those assumed by Odde, and argue that the availability of tubulin is most likely not limiting microtubule growth rates in our system, based on its relatively large diffusion coefficient [29] and high total concentration in Xenopus egg extracts (estimated to be ~15–20 μM; [30]). We acknowledge, however, that it is unclear how much of the total tubulin in a cell is incorporated into aster MTs at steady-state, and that differences in the ratio of cytoplasmic volume to the number of aMTOC nucleating sites might affect the steady-state partitioning of tubulin in unpredictable ways. Indeed, several labs have characterized a negative correlation between centrosomal nucleation rates and microtubule growth rates [31, 32]
Rather than implicating tubulin as the responsible limiting component, we favor a model that implicates local depletion of some larger, and less abundant, microtubule growth regulator as the mechanistic link between microtubule growing-end density and growth rate. A putative candidate is the processive microtubule polymerase XMAP215, whose activity is known to increase microtubule growth rates in vitro [33–35]. XMAP215 has also been shown to modulate spindle microtubule growth rates and ultimately set spindle mass in Xenopus egg extracts [23] and to regulate spindle size in Xenopus laevis embryos [36]. Reductions in microtubule growth rates of approximately 4 μm/min have also been observed in chTOG, the human homolog of XMAP215, RNAi treated CRC cells [37], which mirrors reductions in growth rates observed in the EB1 dense regions of our micro-enclosures (see Figure 4C; 2-μm search radius). Furthermore, biochemical characterizations and physical measurements indicate XMAP215 is a large, highly elongated molecule in solution (~220kDa and approximately 60 nm in length, and 3.2 nm wide; [33, 34, 38]) and its concentration in extract has been estimated to be ~120 nM [23]. In the absence of concrete measurements, we can only speculate, however, that expected differences in diffusion coefficients and known differences in relative concentrations of tubulin and XMAP215 are sufficient to account for the disparate length scales predicted by theory and those observed here.
The observation that microtubule dynamics are affected by local growing-end density might explain, in part, the variability of published microtubule growth rates, even those measured within the same organism and during similar stages of the cell cycle. In Xenopus egg extracts, interphase microtubule growth rates range from as low as ~7 μm/min to as high as ~30 μm/min [12, 39, 40]. In systems such as the C. elegans embryo and LLCPK tissue culture cells, reported microtubule growth rates can vary within interphase by as much as 20% [31, 41] and 47% [42–44], respectively. This variability in measured microtubule growth rates far exceeds the ~2% variability that would be expected from a simple Poisson model of tubulin addition to the microtubule plus-end [45]. Explanations for this variation have been numerous and experimentally intractable, as many reasonable causes have been evoked, e.g., proximity to membranes, spatial effects resulting from changes in MAP function and post-translational modifications, and steric crowding effects [24, 46, 47]. Our results suggest that some of this variability can be accounted for simply by spatial differences in growing microtubule plus-end density.
In summary, our observations suggest that microtubule growth rates are regulated by the presence and proximity of other microtubule plus-ends, and that this spatial regulation can impart local changes in the dynamics of microtubule subpopulations within a single, continuous cytoplasm. This might explain recently observed differences in astral microtubule and spindle microtubule growth rates in C. elegans embryos [14]. We postulate that this mechanism might also be biologically significant in several additional contexts, such as mitotic spindle size scaling during development, as relatively small changes in microtubule growth rates have been shown to correlate with large changes in mitotic spindle size [23, 36], and at animal cell kinetochores and centromeres, which represent discrete foci of particularly high microtubule growing-end density.
STAR METHODS:
RESOURCE AVAILABILITY
Lead Contact
Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Jesse C. Gatlin (jgatlin@uwyo.edu).
Materials Availability
This study did not generate any unique reagents.
Data and Code Availability
The microtubule growth rate data sets and “local plus-end density” MATLAB script generated during this study are available at Mendeley Data (DOI: 10.17632/fj8rrmgwny.1).
EXPERIMENTAL MODEL AND SUBJECT DETAILS
CSF-arrested egg extract preparation
Cytostatic factor (CSF)-arrested extracts were prepared from freshly laid Xenopus laevis eggs as described previously [48]. Briefly, gravid female frogs (3-8 years of age) were primed by injection of 100U of pregnant mare serum gonadotropin 1-2 weeks prior to a 500U injection of human chorionic gonadotropin to induce laying. Eggs arrested in metaphase of meiosis-II were then collected, dejellied, packed, and fractionated via centrifugation. The cytoplasmic fraction was collected and supplemented with 10 μg/mL each of the protease inhibitors leupeptin, pepstatin, and chymostatin (LPC) and 10 μg/mL cytochalasin D (to prevent f-actin dependent gelation and contraction of the bulk extract). These CSF-arrested extracts were kept on ice until induction into interphase 1 h prior to imaging via the addition of Ca2+ to a final concentration of 400 μM. Translation was inhibited in these extracts 1 h prior to imaging through the addition of cycloheximide to a final concentration of 355 μM.
All Xenopus laevis frogs used in these studies were purchased from Nasco which maintains a closed colony of frogs at least five generations removed from wild stock. The frogs were housed in filtered re-circulating aquaria rack systems (XenRackTM; Aquatic Enterprises) and allowed at least 4 months to replenish oocytes between induced egg-laying cycles. Husbandry facilities and all experimental protocols involving frogs were reviewed and approved by the University of Wyoming Institutional Animal Care and Use Committee. All studies using Xenopus laevis followed the guidelines of the U.S. Department of Health and Human Service for the Care and Use of Laboratory Animals, and all experiments were performed in accordance with national regulatory standards and ethical rules.
METHOD DETAILS
Preparation of microfluidic flow chambers
Preparation of microfluidic flow chambers was carried out as previously described in [49], with the following modifications. The coverslips used for the preparation of the chambers were first soaked in 1M HCl at 50°C for 16 h before being extensively rinsed with double distilled water. After acid washing, the coverslips were then rinsed with 100% ethanol and left to dry between sheets of Whatman filter paper. In addition, the single-use microfluidic devices cast in PDMS feature a flow channel of ~3 mm in width and ~45 mm in length, with a height of 30 μm, as opposed to a T-junction.
Microfluidic flow chambers were PEGylated to ensure a biologically inert glass surface. This was accomplished by first treating the microfluidic flow chamber with 2% (v/v) 3-(trimethoxysilyl)propyl methacrylate in 95% ethanol for 15 min after plasma treatment. The chambers were then flushed with 30 channel volumes of 95% ethanol and heated at 70°C for 15 min. After an additional flush with ddH2O, these devices were then kept in the dark and left to dry at room temperature. These devices were then filled with a solution containing 10% (w/w) poly(ethylene glycol) methacrylate and 0.1% (w/w) lithium phenyl-2,4,6-trimethylbenzoylphosphinate. Each device was then exposed for 3 seconds to 10 mW of UV light (352 nm) at a distance of 15 cm on a reflective surface. After exposure, the device was then immediately flushed with five channel volumes of the same solution and exposed once more. This process was repeated for three exposures in total. After PEGylation, the flow chambers were flushed with 30 channel volumes of ddH2O and left to soak in ddH20 at 4°C until use.
Microfluidic encapsulation of Xenopus egg extract
To create PEGDA micro-enclosures, passivated microfluidic flow chambers were filled with a solution containing 20% (w/w) PEGDA 700, 0.5% (w/w) lithium phenyl-2,4,6-trimethylbenzoylphosphinate and aMTOCs in CSF-XB buffer. The devices were then placed on an IX81 stand (Olympus) equipped with a digital micromirror device (DMD; Polygon 400dense from Mightex) (Figure S1A; rightmost panel). With the use of calibrated digital masks projecting micro-enclosure negatives, the solution within the device was then selectively exposed to 405-nm light until full gelation of the micro-enclosure wall was observed (see Video S1). It should be noted that exposure conditions varied slightly per device because of inconsistencies with the coverslip orientation with respect to the light path. Unused polymer solution was then flushed out of the channel using 30 channel volumes of CSF-XB buffer pumped in through Tygon microbore tubing (0.010-inch ID × 0.030-inch OD; Saint-Gobain Performance Plastics) at a continuous rate of 7 μl/min. Fluid flow to the device was established using a syringe pump (neMESYS, CETONI GmbH). The channels containing PEGDA micro-enclosures were then stored in CSF-XB buffer for at least 10 h prior to filling the device with Xenopus extract to limit liquid permeability through the PDMS device walls. Xenopus extract containing our soluble fluorophore was then pumped into the device at a rate of 7 μl/min for a total of 30 channel volumes in a 4°C cold room to prevent microtubule nucleation. A crossflow of Novak 7500 containing 2% surfactant (PicoSurf 1, Sphere Fluidics) was then pulsed into the device from the opposite outlet at a rate of 23 μ/min in 5-μl increments for a total of 15 μl (Figure 1A, B; rightmost panel). The device was then transported on ice to a temperature-controlled room for imaging.
Microscopy and imaging
All microscopy experiments were performed at 17°C, using a scientific CMOS (complementary metal oxide semiconductor) camera (Flash 4.0, Hamamatsu) mounted on an IX81 stand equipped with a spinning-disk confocal head (CSU-X1, Yokogawa). Confocal illumination was provided to the system by a LMM5 laser launch (Spectral Applied Research). Integration of all imaging system components was provided by Biovision Technologies. Image acquisition was performed using Metamorph 7.7 software (Molecular Devices). Images were acquired at the coverslip surface at 0.5-sec intervals for 1 min using Olympus objectives of varying magnification: 20× (0.85 NA) and 60× (1.35 NA) immersed in Olympus immersion oil (IMMOIL-F30CC). All time images were acquired within 20 min of the device being taken off ice. Multidimensional z-stack imaging of encapsulated extract allowed for precise determination of the encapsulated micro-enclosure diameter and height (as determined by the fluorescent signal), which were then used to calculate the volume of each micro-enclosure.
QUANTIFICACTION AND STATISTICAL ANALYSIS
Measurements of microtubule growth rates and EB1 density
Microtubule growth rates and EB1 positional data were quantified using u-track particle tracking software (ver. 2.0; [25, 26]). Object tracking was done using “Microtubule plus-ends”, with “Comet Detection” being used to identify EB1 comets. The “High-pass Gaussian filter” and “Watershed minimum threshold” were determined in part by the NA of the objective, the bit depth of the camera, and the aspect ratio of the EB1 comets (typically, a High-pass Gaussian filter of 7 and a Watershed minimum threshold of 5 were used). For tracking, a minimum track length of three frames was kept constant across all treatments. The upper and lower bounds for the “frame-to-frame linking” were set at twice the mean growth rate in pixels per second of EB1 comets measured by manual kymographs for each specific treatment to reduce false-linking events. No forward reclassification was used in post-processing of tracks, and tracks starting in the first frame and those ending in the last frame were removed for volume and density comparisons (Figures 2, 3). Note that these tracks were included in the local-density analysis for ease of indexing and coding (Figure 4). All parameters set for automated detection were evaluated against a reference frame, in which automated detection of EB1 comets was compared to manual detection for a representative area. A 95% accuracy rate (for both false-positive and false-negative detections) was deemed sufficient for this analysis. Microtubule growth rates were also manually measured using kymographs in Metamorph 7.7 software. For each image sequence, at least 30 kymographs were generated, tracking EB1 comets at random radial positions and distances from the aMTOC (Figure S1E, F and Figure S2E).
The global EB1 density (per μm2) was calculated using the total number of tracks (n), the average track lifetime (l) in frames for the time series, the number of frames in the time series (f), and the area (A) of the micro-enclosures (Eq. 1).
| (1) |
Measurement of nucleation rate
To quantify nucleation rate from our aMTOCs, we generated a MATLAB script modeled after a similar analysis included in [12]. In brief, the custom MATLAB script counted EB1 tracks that crossed a circle of a user defined radius projected from the center of the aMTOC. The radius of the circle used to detect the nucleation rate was set at one fifth the diameter of the micro-enclosure.
Statistical analysis
Indicated statistical tests were conducted using Igor Pro 7 software (ver. 8.0.3.3; Wavemetrics) and confirmed in Excel. For each condition, measurements were taken from at least three independently prepared extracts.
Supplementary Material
Video S1. Formation of PEGDA micro-enclosure. Related to Figure 1.
Video S2. EB1 comets in ~400-pL micro-enclosures. Related to Figure 2.
Video S3. EB1 comets in ~160-pL micro-enclosures. Related to Figure 2.
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Chemicals, Peptides, and Recombinant Proteins | ||
| Leupeptin | EMD Millipore | Cat#EI8 |
| Pepstatin | EMD Millipore | Cat#EI10; CAS: 26305-03-3 |
| Chymostatin | EMD Millipore | Cat#EI6 |
| Cycloheximide | Sigma-Aldrich | Cat#C7698; CAS: 66-81-9 |
| Cytochalasin D | Sigma-Aldrich | Cat#C6762; CAS: 14930-96-2 |
| PMSG | Prospec-Tany Technogene | Cat#hor-272; Lot#718PGSMP |
| hCG | Prospec-Tany Technogene | Cat#hor-250; Lot#119PHCG13 |
| SYLGARD 184 Silicone elastomer | Dow Corning | Material Number 99109937 |
| 3-(trimethoxysilyl)propyl methacrylate | Sigma-Aldrich | Cat#440159 CAS: 2530-85-0 |
| Poly(ethylene glycol) methacrylate | Sigma-Aldrich | Cat#409537 CAS: 25736-86-1 |
| Poly(ethylene glycol) diacrylate | Sigma-Aldrich | Cat#455008 CAS: 26570-48-9 |
| Lithium phenyl-2,4,6-trimethylbenzoylphosphinate | Sigma-Aldrich | Cat#900889 |
| Pico-Surf | Sphere Fluidics | SKU: C021 |
| EB1-GFP | Gatlin Lab | N/A |
| mCherry-TMBD | Gatlin Lab [13] | N/A |
| Experimental Models: Organisms/Strains | ||
| Xenopus laevis adult female | NASCO | https://www.enasco.com/c/Education-Supplies/Xenopus-Frogs |
| Software and Algorithms | ||
| Metamorph 7.7 software | Molecular Devices | https://www.moleculardevices.com/products/cellular-imaging-systems/acquisition-and-analysis-software/metamorph-microscopy |
| ImageJ | National Institutes of Health | https://imagej.net/Fiji/Downloads |
| MATLAB | MathWorks | https://www.mathworks.com/products/matlab.html |
| Excel | Microsoft | https://products.office.com/en-us/excel |
| u-track | Danuser Lab | https://github.com/DanuserLab/u-track |
| Local density analysis | Gatlin Lab | http://dx.doi.org/10.17632/fj8rrmgwny.1 |
| IgorPro | WaveMetrics | https://www.wavemetrics.com/products/igorpro |
ACKNOWLEDGMENTS
We thank Keisuke Ishihara for helpful discussions. We would also like to thank Priscilla Phan for preparation of Xenopus extracts, and Alexandre Matov for his consultation and time in getting our lab set up to use u-track. We also received support from Marko Horb and the National Xenopus Resource at the Marine Biological Laboratory. This work was made possible by an Institutional Development Award (IDeA) from the National Institute of General Medical Sciences of the National Institutes of Health under Grant # 2P20GM103432. It was also supported by additional funding provided by the NIGMS under Grant #R01GM113028, Whitman Center fellowships at the Marine Biological Laboratory, and the Biomedical Scholars program of the Pew Charitable Trusts.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
DECLARATION OF INTERESTS
The authors declare no competing interests.
Contributor Information
Zachary M. Geisterfer, Department of Molecular Biology, University of Wyoming, 1000 E. University Ave., Laramie, WY 82070
Daniel Y. Zhu, Department of Molecular Biology, University of Wyoming, 1000 E. University Ave., Laramie, WY 82070
Timothy J. Mitchison, Department of Systems Biology, Harvard Medical School, 25 Shattuck St., Boston, MA 02115; Marine Biological Laboratory, Cell Division and Organization Group, 7 MBL Street, Woods Hole, MA 02543, USA
John Oakey, Department of Chemical Engineering, University of Wyoming, 1000 E. University Ave., Laramie, WY 82070.; Marine Biological Laboratory, Cell Division and Organization Group, 7 MBL Street, Woods Hole, MA 02543, USA.
Jesse C. Gatlin, Department of Molecular Biology, University of Wyoming, 1000 E. University Ave., Laramie, WY 82070.; Marine Biological Laboratory, Cell Division and Organization Group, 7 MBL Street, Woods Hole, MA 02543, USA
REFERENCES
- 1.Nogales E (2000). Structural Insights into Microtubule Function. Annual Review of Biochemistry 69, 277–302. [DOI] [PubMed] [Google Scholar]
- 2.Brugues J, and Needleman D (2014). Physical basis of spindle self-organization. Proc Natl Acad Sci U S A 111, 18496–18500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Dumont S, and Mitchison TJ (2009). Compression Regulates Mitotic Spindle Length by a Mechanochemical Switch at the Poles. Curr. Biol. 19, 1086–1095 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Dumont S, and Mitchison TJ (2009). Force and length in the mitotic spindle. Curr. Biol. 19, R749–761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ishihara K, Korolev KS, and Mitchison TJ (2016). Physical basis of large microtubule aster growth. Elife 5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Good MC, Vahey MD, Skandarajah A, Fletcher DA, and Heald R (2013). Cytoplasmic volume modulates spindle size during embryogenesis. Science 342, 856–860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hazel J, Krutkramelis K, Mooney P, Tomschik M, Gerow K, Oakey J, and Gatlin JC (2013). Changes in cytoplasmic volume are sufficient to drive spindle scaling. Science 342, 853–856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Jimenez AM, Roche M, Pinot M, Panizza P, Courbin L, and Gueroui Z (2011). Towards high throughput production of artificial egg oocytes using microfluidics. Lab Chip 11, 429–434. [DOI] [PubMed] [Google Scholar]
- 9.Pinot M, Chesnel F, Kubiak JZ, Arnal I, Nedelec FJ, and Gueroui Z (2009). Effects of confinement on the self-organization of microtubules and motors. Curr. Biol 19, 954–960. [DOI] [PubMed] [Google Scholar]
- 10.Revzin A, Russell RJ, Yadavalli VK, Koh W-G, Deister C, Hile DD, Mellott MB, and Pishko MV (2001). Fabrication of Poly(ethylene glycol) Hydrogel Microstructures Using Photolithography. Langmuir 17, 5440–5447. [DOI] [PubMed] [Google Scholar]
- 11.Tsai MY, and Zheng Y (2005). Aurora A kinase-coated beads function as microtubule-organizing centers and enhance RanGTP-induced spindle assembly. Curr. Biol. 15, 2156–2163. [DOI] [PubMed] [Google Scholar]
- 12.Ishihara K, Nguyen PA, Groen AC, Field CM, and Mitchison TJ (2014). Microtubule nucleation remote from centrosomes may explain how asters span large cells. Proc Natl Acad Sci U S A 111, 17715–17722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Mooney P, Sulerud T, Pelletier JF, Dilsaver MR, Tomschik M, Geisler C, and Gatlin JC (2017). Tau-based fluorescent protein fusions to visualize microtubules. Cytoskeleton (Hoboken) 74, 221–232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Lacroix B, Letort G, Pitayu L, Salle J, Stefanutti M, Maton G, Ladouceur AM, Canman JC, Maddox PS, Maddox AS, et al. (2018). Microtubule Dynamics Scale with Cell Size to Set Spindle Length and Assembly Timing. Dev Cell 45, 496–511 e496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Wuhr M, Chen Y, Dumont S, Groen AC, Needleman DJ, Salic A, and Mitchison TJ (2008). Evidence for an upper limit to mitotic spindle length. Curr. Biol 18, 1256–1261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Odde DJ (1997). Estimation of the diffusion-limited rate of microtubule assembly. Biophys J 73, 88–96. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Dogterom M, and Leibler S (1993). Physical aspects of the growth and regulation of microtubule structures. Physical Review Letters 70, 1347–1350. [DOI] [PubMed] [Google Scholar]
- 18.Novak IL, Slepchenko BM, and Mogilner A (2008). Quantitative Analysis of G-Actin Transport in Motile Cells. Biophys J 95, 1627–1638. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Van Goor D, Hyland C, Schaefer AW, and Forscher P (2012). The Role of Actin Turnover in Retrograde Actin Network Flow in Neuronal Growth Cones. PLOS ONE 7, e30959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Schulze E, and Kirschner M (1987). Dynamic and stable populations of microtubules in cells. J Cell Biol 104, 277–288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Caudron N, Valiron O, Usson Y, Valiron P, and Job D (2000). A reassessment of the factors affecting microtubule assembly and disassembly in Vitro. Edited by A. Klug. Journal of Molecular Biology 297, 211–220. [DOI] [PubMed] [Google Scholar]
- 22.Reber S, and Goehring NW (2015). Intracellular Scaling Mechanisms. Cold Spring Harb Perspect Biol 7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Reber SB, Baumgart J, Widlund PO, Pozniakovsky A, Howard J, Hyman AA, and Julicher F (2013). XMAP215 activity sets spindle length by controlling the total mass of spindle microtubules. Nat Cell Biol 15, 1116–1122. [DOI] [PubMed] [Google Scholar]
- 24.Wieczorek M, Chaaban S, and Brouhard GJ (2013). Macromolecular Crowding Pushes Catalyzed Microtubule Growth to Near the Theoretical Limit. Cellular and Molecular Bioengineering 6, 383–392. [Google Scholar]
- 25.Applegate KT, Besson S, Matov A, Bagonis MH, Jaqaman K, and Danuser G (2011). plusTipTracker: Quantitative image analysis software for the measurement of microtubule dynamics. J Struct Biol 176, 168–184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Jaqaman K, Loerke D, Mettlen M, Kuwata H, Grinstein S, Schmid SL, and Danuser G (2008). Robust single-particle tracking in live-cell time-lapse sequences. Nature Methods 5, 695–702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Minton AP (1981). Excluded volume as a determinant of macromolecular structure and reactivity. Biopolymers 20, 2093–2120. [Google Scholar]
- 28.Drenckhahn D, and Pollard TD (1986). Elongation of actin filaments is a diffusion-limited reaction at the barbed end and is accelerated by inert macromolecules. Journal of Biological Chemistry 261, 12754–12758. [PubMed] [Google Scholar]
- 29.Salmon ED, Saxton WM, Leslie RJ, Karow ML, and McIntosh JR (1984). Diffusion coefficient of fluorescein-labeled tubulin in the cytoplasm of embryonic cells of a sea urchin: video image analysis of fluorescence redistribution after photobleaching. J Cell Biol 99, 2157–2164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Parsons SF, and Salmon ED (1997). Microtubule assembly in clarified Xenopus egg extracts. Cell Motil Cytoskeleton 36, 1–11. [DOI] [PubMed] [Google Scholar]
- 31.Srayko M, Kaya A, Stamford J, and Hyman AA (2005). Identification and Characterization of Factors Required for Microtubule Growth and Nucleation in the Early C. elegans Embryo. Developmental Cell 9, 223–236. [DOI] [PubMed] [Google Scholar]
- 32.Wordeman L, Decarreau J, Vicente JJ, and Wagenbach M (2016). Divergent microtubule assembly rates after short- versus long-term loss of end-modulating kinesins. Mol Biol Cell 27, 1300–1309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Cassimeris L, Gard D, Tran PT, and Erickson HP (2001). XMAP215 is a long thin molecule that does not increase microtubule stiffness. Journal of Cell Science 114, 3025. [DOI] [PubMed] [Google Scholar]
- 34.Brouhard GJ, Stear JH, Noetzel TL, Al-Bassam J, Kinoshita K, Harrison SC, Howard J, and Hyman AA (2008). XMAP215 is a processive microtubule polymerase. Cell 132, 79–88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Gard DL, and Kirschner MW (1987). A microtubule-associated protein from Xenopus eggs that specifically promotes assembly at the plus-end. J Cell Biol 105, 2203–2215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Milunovic-Jevtic A, Jevtic P, Levy DL, and Gatlin JC (2018). In vivo mitotic spindle scaling can be modulated by changing the levels of a single protein: the microtubule polymerase XMAP215. Mol Biol Cell 29, 1311–1317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Ertych N, Stolz A, Stenzinger A, Weichert W, Kaulfuß S, Burfeind P, Aigner A, Wordeman L, and Bastians H (2014). Increased microtubule assembly rates influence chromosomal instability in colorectal cancer cells. Nat Cell Biol 16, 779–791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Gard DL, and Kirschner MW (1987). A microtubule-associated protein from Xenopus eggs that specifically promotes assembly at the plus-end. J Cell Biol 105, 2203–2215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Verde F, Labbé J-C, Dorée M, and Karsenti E (1990). Regulation of microtubule dynamics by cdc2 protein kinase in cell-free extracts of Xenopus eggs. Nature 343, 233–238. [DOI] [PubMed] [Google Scholar]
- 40.Belmont LD, Hyman AA, Sawin KE, and Mitchison TJ (1990). Real-time visualization of cell cycle-dependent changes in microtubule dynamics in cytoplasmic extracts. Cell 62, 579–589. [DOI] [PubMed] [Google Scholar]
- 41.O’Rourke SM, Christensen SN, and Bowerman B (2010). Caenorhabditis elegans EFA-6 limits microtubule growth at the cell cortex. Nat Cell Biol 12, 1235–1241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Piehl M, and Cassimeris L (2003). Organization and dynamics of growing microtubule plus ends during early mitosis. Mol Biol Cell 14, 916–925. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Rusan NM, Fagerstrom CJ, Yvon AM, and Wadsworth P (2001). Cell cycle-dependent changes in microtubule dynamics in living cells expressing green fluorescent protein-alpha tubulin. Mol Biol Cell 12, 971–980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Alieva IB, Zemskov EA, Kireev II, Gorshkov BA, Wiseman DA, Black SM, and Verin AD (2010). Microtubules growth rate alteration in human endothelial cells. J Biomed Biotechnol 2010, 671536–671536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Pedigo S, and Williams RC Jr. (2002). Concentration dependence of variability in growth rates of microtubules. Biophys J 83, 1809–1819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Zeitz M, and Kierfeld J (2014). Feedback mechanism for microtubule length regulation by stathmin gradients. Biophys J 107, 2860–2871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Shaebani MR, Pasula A, Ott A, and Santen L (2016). Tracking of plus-ends reveals microtubule functional diversity in different cell types. Scientific Reports 6, 30285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Maresca TJ, and Heald R (2006). Methods for studying spindle assembly and chromosome condensation in Xenopus egg extracts. Methods Mol Biol 322, 459–474. [DOI] [PubMed] [Google Scholar]
- 49.Oakey J, and Gatlin JC (2018). Microfluidic Encapsulation of Demembranated Sperm Nuclei in Xenopus Egg Extracts. Cold Spring Harbor Protocols 2018, pdb.prot102913. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Video S1. Formation of PEGDA micro-enclosure. Related to Figure 1.
Video S2. EB1 comets in ~400-pL micro-enclosures. Related to Figure 2.
Video S3. EB1 comets in ~160-pL micro-enclosures. Related to Figure 2.
Data Availability Statement
The microtubule growth rate data sets and “local plus-end density” MATLAB script generated during this study are available at Mendeley Data (DOI: 10.17632/fj8rrmgwny.1).


